算法题解----最短路 ： 单源最短路 朴素Dijsktra算法

今天来介绍一下十分经典的一个最短路算法：朴素Dijsktra算法

题目要求:　

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

输入样例：

3 3

1 2 2 

2 3 1

1 3 4 

输出样例：

3

 

那么这个算法的思路是怎么样的呢？

我们要找到一条从1号点到n号点的最短路 ， 不妨把我们已经走过的点当成一个集合，去更新我们没有走过的点

如下图所示：

 

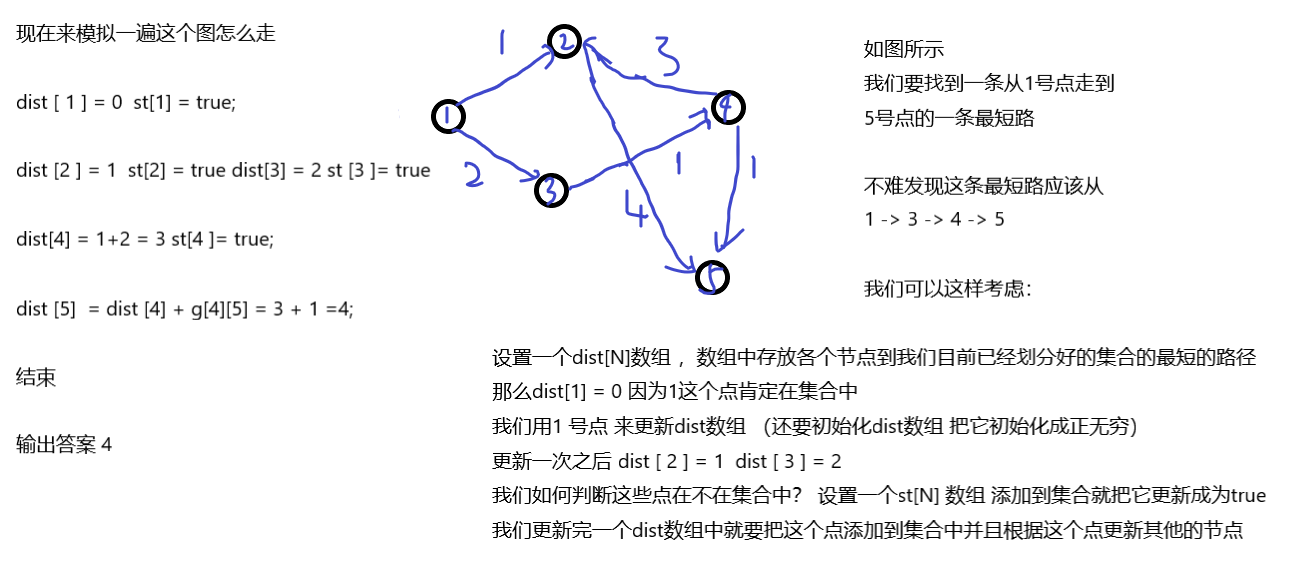
总结一下：朴素迪杰斯特拉算法 O(n^2)

 　　　　①  dist[1] = 0  其他点赋值为 正无穷

　　　　 ②  for (i : 0 - n)

　　　　　　    t <-  不在s中的 距离最近的点

　　　　　　　s <-  t

　　　　　　   用t更新其他点的距离

 

这题适用于稠密图  所以用邻接矩阵来存储图

 

 

# include <iostream>
# include <cstring>

# include <algorithm>

using namespace std;

 

const int N= 510;

 

bool st[N];     //判断状态

int dist[N];

int g[N][N];   //邻接矩阵，存储图

int n,m;

 

int dijsktra()

{

　　memset (dist , 0x3f,sizeof dist);　  //初始化 dist数组

　    dist[1] = 0;          //1号点肯定在集合里面

　 

　　for(int i=0;i<n;i++)

　　{

　　　　int t = -1;

　　　　for(int j = 1;j <= n ; j++)

　　　　　　if( !st[j] && (t==-1 || dist[t] > dist[j] ) )     //找到目前距离集合最近的点 并且添加进去

　　　　　　　　　　t = j;

　　　　st[t] = true;

　　　　for(int j = 1; j<=n; j ++)

　　　　　　dist[j] = min (dist [j] ,dist[j] + g[t][j]);     //添加完点之后就可以更新其他点

　　}

　　if(dist[n]  == 0x3f3f3f3f) return -1;              //如果n号点没有被更新的话说明走不到n，就没有最短路

　　return dist[n];

}

int main()

{

　　cin.tie(0);

　　cin>>n>>m;

　　memset(g,0x3f,sizeof g);

　　for(int i=1;i<=m;i++)

　　{

　　      int a,b,w;

             cin>>a>>b>>w;

            g[a][b] = min(g[a][b],w);        //因为这题可能有重边所以要取最小值

　　}　　

　　int t = dijsktra();

       cout <<t <<endl;  

　　return 0;

}