算法题解----ACWing 125. 耍杂技的牛

题目描述：

农民约翰的 N 头奶牛（编号为 1....N）计划逃跑并加入马戏团，为此它们决定练习表演杂技。

奶牛们不是非常有创意，只提出了一个杂技表演：

叠罗汉，表演时，奶牛们站在彼此的身上，形成一个高高的垂直堆叠。

奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。

这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强壮程度 Si。

一头牛支撑不住的可能性取决于它头上所有牛的总重量（不包括它自己）减去它的身体强壮程度的值，现在称该数值为风险值，风险值越大，这只牛撑不住的可能性越高。

您的任务是确定奶牛的排序，使得所有奶牛的风险值中的最大值尽可能的小。

输入格式：

 

第一行输入整数 N，表示奶牛数量。

 

接下来 N行，每行输入两个整数，表示牛的重量和强壮程度，第 i 行表示第 i 头牛的重量 Wi 以及它的强壮程度 Si。

输出格式：

输出一个整数，表示最大风险值的最小可能值。

数据范围：

1 ≤ N ≤ 50000,

1 ≤ Wi ≤ 10,000

1 ≤ Si ≤ 1,000,000,000

输入样例：

3

10 3 

2 5

3 3

输出样例：

2

 

思路：

　　这题要用到贪心的思想，而Y总评价时说诸多算法中最难的是dp和贪心算法，因为他没有一个固定的模板

　我们如果想要严格解题的话就需要写出严格的证明，推出公式并且证明可行，很多时候显然的结论想要去证明它

   还是不容易的。

　　那么这题我先把结论说一下再证明一遍：

　　这题我们首先要对每头牛进行排序，排序的规则是：按照 Wi + Si 来排序，然后再从这些牛中找到风险值最大的那头牛。

　　下面就是证明:

　　

　　

 

　　

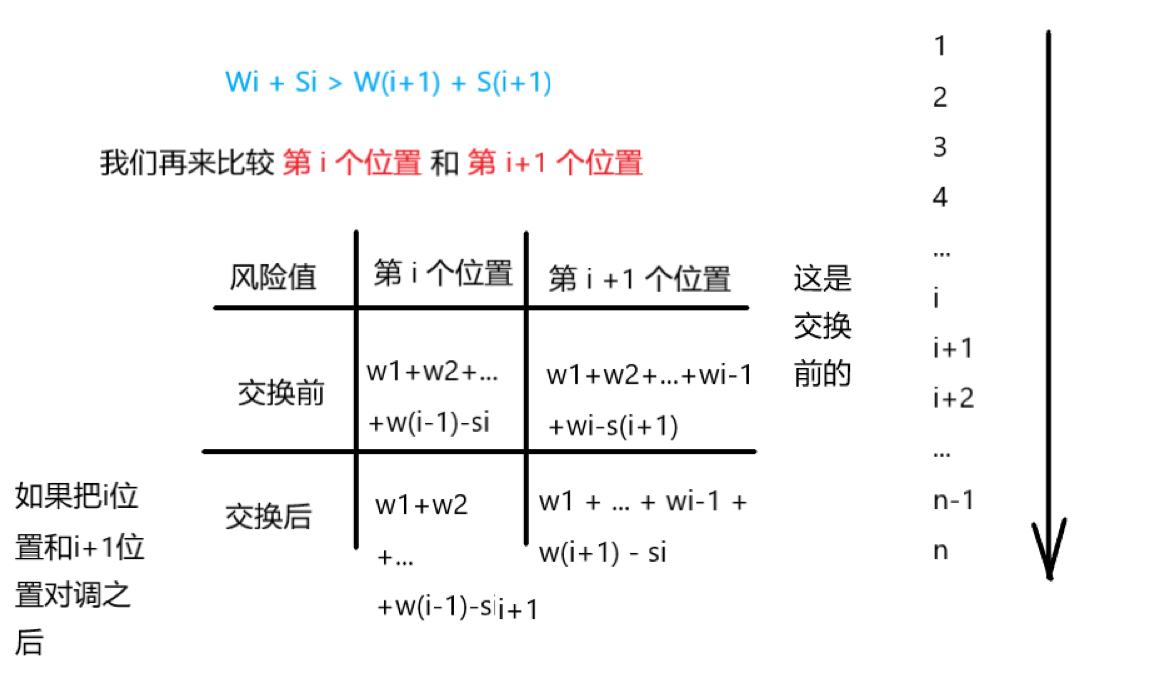
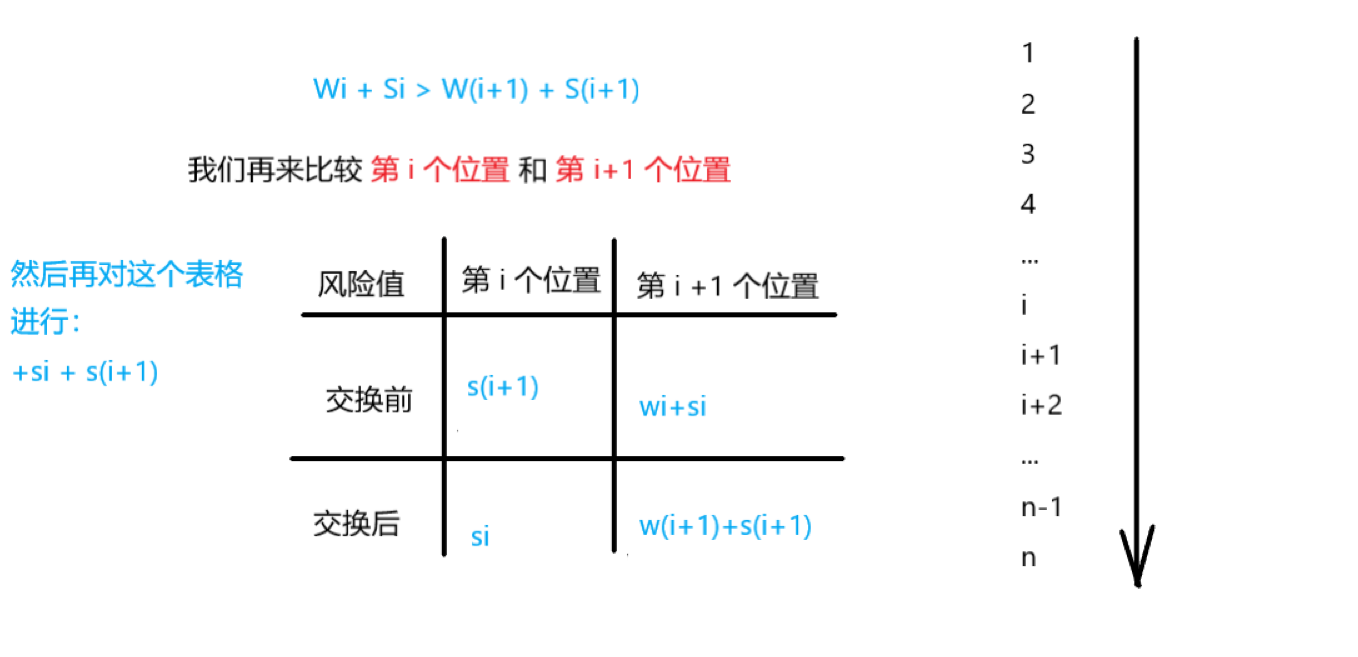
师爷，你来给我翻译翻译他妈的什么叫他妈的惊喜！

 

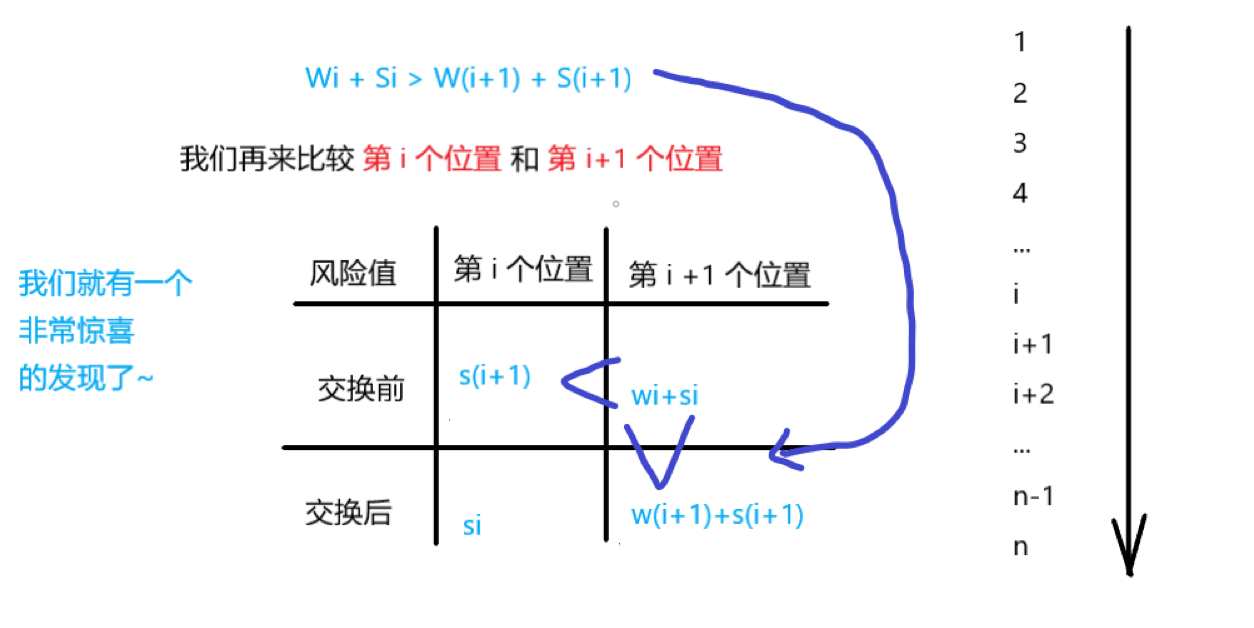
惊喜就是我们发现我们在序列中如果存在 Wi + Si > Wi+1 + Si+1的逆序对的时候

我们都有唯一的方法去把这个逆序对变成顺序对，反之则不可以

也就是说，我们按照数列的想法这个应该是最后答案的形式

所以这题的排序就一定要以 Wi + Si 的大小来排序。

 

 

话不多说 上代码~

 

# include <iostream>
# include <algorithm>
using namespace std;

 

const int N = 50000+10;

 

struct Cow
{
　　int w,s;
　　bool operator< (const Cow& c) const    //重载小于号
　　{
　　　　return (w+s) < (c.w+c.s);
　　}
}cow[N];        //声明这么些牛

 

int main()
{
　　cin.tie(0);
　　int n;
　　cin>>n;
　　for(int i =0;i<n;i++)
　　{
　　　　int w,s;
　　　　cin>>w>>s;
　　　　cow[i]={w,s};
　　}

　　sort(cow,cow+n);       //对这些牛排序

　　int res = -2e9;         //我们的结果，初始化为负无穷
　　int sum = 0;            //这是这头牛上面的牛的重量之和
　　for(int i=0;i<n;i++)
　　{
　　　　res = max(res,sum-cow[i].s);       //答案要找出最小风险值中的最大值
　　　　sum += cow[i].w;              //前面牛的体重要加上去
　　}
　　cout<<res;
　　return 0;
}