斯坦福 CS228 概率图模型中文讲义 四、贝叶斯网络

四、贝叶斯网络

原文：Bayesian networks

译者：飞龙

协议：CC BY-NC-SA 4.0

自豪地采用谷歌翻译

我们从表示的话题开始：我们如何选择概率分布来为世界的一些有趣方面建模？ 建立一个好的模型并不容易：我们在介绍中看到，垃圾邮件分类的朴素模型需要我们指定一些参数，这些参数对于英文单词数量是指数级的！

在本章中，我们将了解避免这类复杂事物的一种方法。 我们将要：

• 学习有效和通用的技术，仅使用少数参数来参数化概率分布。
• 了解如何通过有向无环图（DAG）来优雅地描述所得模型。
• 研究 DAG 结构与所描述的分布的模型假设之间的联系；这不仅会使这些模型假设更加明确，而且还会帮助我们设计更有效的推理算法。

我们将在这里看到的模型称为贝叶斯网络。 在下一章中，我们还会看到第二种方法，它涉及无向图，也称为马尔可夫随机场。

概率建模与贝叶斯网络

有向图模型（也称为贝叶斯网络）是一系列概率分布，它们允许紧凑的参数化，可以使用有向图来自然描述。

这个参数化背后的总体思路非常简单。

回想一下，通过链式法则，我们可以将任意概率p写为：

紧凑贝叶斯网络是一种分布，右侧的每个因子仅依赖于少量的祖先变量 ：

例如，在一个有五个变量的模型中，我们可以选择用 来近似因子 。 在这种情况下，我们写作 。

当变量是离散的时候（我们会认为问题通常会是这种情况），我们可以将因子 看作概率表，其中行对应于 的赋值，并且列对应于 的值；条目包含实际概率 。 如果每个变量取d个值并且最多有k个祖先，那么整个表将包含最多O(dk + 1)个条目。 由于每个变量都有一个表，因此只用O(ndk + 1)个参数（与朴素方法的O(dn)相比），就可以简洁地描述整个概率分布。

图表示

这种形式的分布可以自然地表示为有向无环图，其中顶点对应于变量xi并且边表明了依赖关系。 特别是，我们将每个节点的父母设置为 的祖先 。

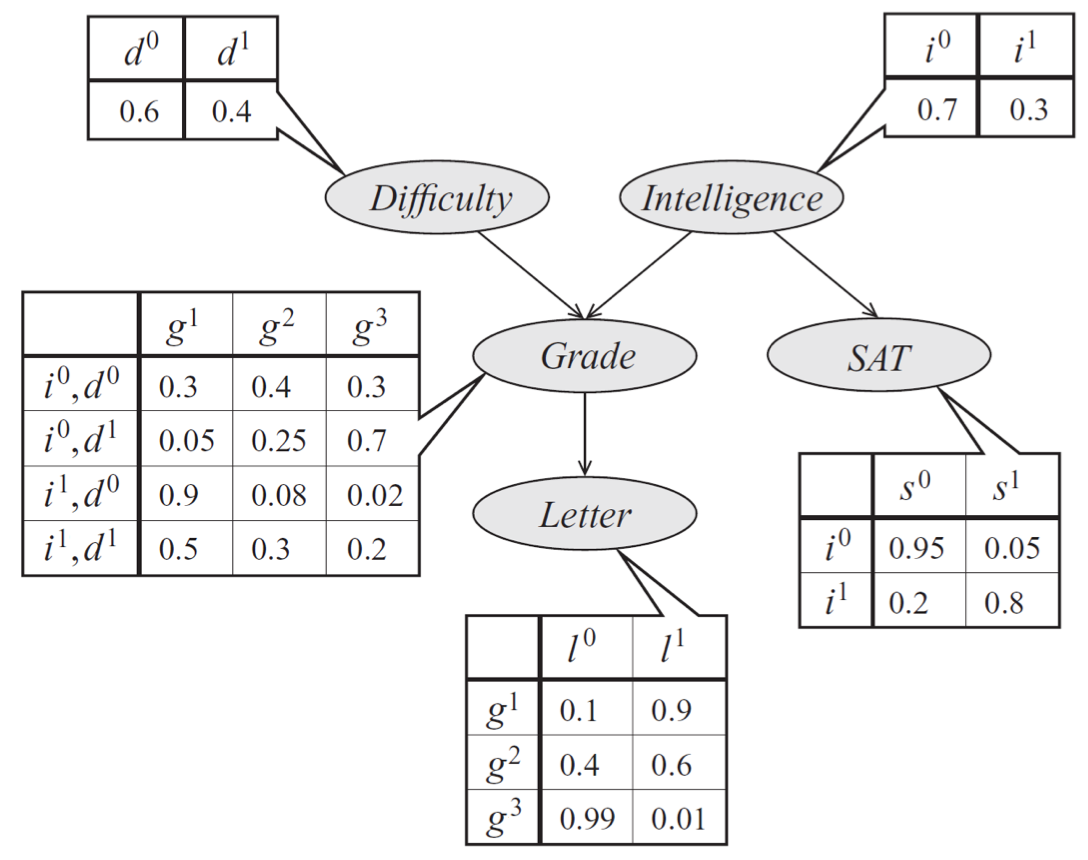
作为一个例子，考虑考试中的学生成绩g的模型; 成绩取决于几个因素：考试的难度d，学生的智力i，他的 SAT 分数s; 它也会影响教授课程的教授的推荐信的质量l。 每个变量都是二元的，除了g，它取 3 个可能的值。

描述考试中学生表现的贝叶斯网络模型。 分布可以表示为条件概率分布的乘积，由表指定。 这些分布的形式由图中的边描述。

5 个变量的联合概率分布自然因式分解如下：

这个分布的图表示是一个 DAG，它可视化地规定随机变量如何相互依赖。 图清楚地表明信件取决于年级，而它又取决于学生的智力和考试的难度。

解释有向图的另一种方式是根据数据如何生成的故事。 在上面的例子中，为了确定推荐信的质量，我们可以首先抽取一个智力水平和一个考试难度；然后，根据这些参数抽取学生的成绩；最后，推荐信是基于该成绩生成的。

在之前的垃圾邮件分类示例中，我们隐式假设电子邮件根据两步过程来生成：首先，我们选择垃圾邮件/非垃圾邮件标签y；然后我们独立地抽取每个词是否存在，并以该标签为条件。

形式定义

形式上，贝叶斯网络是一个有向图G =(V, E)：

每个节点i∈V都是随机变量 。
一个节点有一个条件概率分布（CPD），规定 以父值为条件的概率。

因此，贝叶斯网络定义了概率分布p。 相反，我们说如果概率p可以分解为因式乘积，由G所规定，那么它可以在 DAG G上因式分解。

不难看出，由贝叶斯网络表示的概率将是有效的：显然，它将是非负的，并且可以使用归纳论证（以及使用 CPD 是有效概率的事实）来证明，所有变量赋值的和将为一。 相反，我们也可以通过反例说明，当G包含环时，其相关概率可能不会为一。

贝叶斯网络的依赖

总而言之，贝叶斯网络表示概率分布，它们可以通过更小的，局部条件概率分布（每个变量一个）来产生。 通过以这种形式表达概率，我们向模型中引入了一些假设，即某些变量是独立的。

这就产生了一个问题：通过使用模型贝叶斯网络，以及由G描述的给定结构，我们做了哪些独立性假设？ 这个问题很重要，有两个原因：我们应该确切地知道我们正在做什么模型假设（以及它们是否正确）；此外，这些信息将有助于我们稍后设计更高效的推理算法。

让我们使用符号I(p)来表示对于联合分布p成立的，所有条件独立性的集合。 例如，如果p(x,y)=p(x)p(y)，那么我们说x⊥y∈I(p)。

由有向图描述的独立性

结果表明，贝叶斯网络p非常优雅地描述了I(p)中的许多独立性；通过查看三种类型的结构，可以从图中恢复这些独立性。

为了简单起见，我们首先看看具有三个节点A, B, C的贝叶斯网络G。在这种情况下，G基本上只有三种可能的结构，每种结构产生不同的独立性假设。 感兴趣的读者可以使用一些代数来轻松证明这些结果。

三个变量上的贝叶斯网络，编码了不同类型的依赖关系：级联（a，b），公共父级（c）和 V 结构（d）。

• 公共父级：如果G的形式是A←B→C，并且观察到了B，则A⊥C|B。 但是，如果B未被观察到，则 。 直观地说，这源于一个事实，B包含决定A和C结果的所有信息；一旦观察到，没有其他因素影响这些变量的结果。
• 级联：如果G等于A→B→C，并且再次观察到了B，则再次A⊥C|B。 但是，如果B未被观察到，则 。 这里的直觉是，B再次拥有决定C的结果的所有信息; 因此，A取什么样的值并不重要。
• V 结构（也称为 Explaining Away）：如果G是A→C←B，则知道C就结合了A和B。换句话说，如果C未被观察，则A⊥B，但如果观察到了C，。

最后一种情况需要额外的解释。假设C是一个布尔变量，表明我们的草坪在早上是否潮湿；A和B对潮湿有两种解释：下雨（用A表示）或喷水器打开（用B表示）。如果我们知道草地是湿的（C为真）并且喷水器没有打开（B是假的），那么A为真的概率必须是 1，因为这是唯一可能的解释。因此，A和B并不是独立的。

这些结构清楚地描述了由三变量贝叶斯网络编码的独立性。我们可以通过在任何更大的图上递归地应用它们，来将它们扩展到通用网络。这产生了一种被称为 D-分离的概念（其中d代表有向）。

我们说，如果变量Q和W没有由活动路径连接，观察到变量O时，Q和W是 D-分离的。如果对于路径上的每三个连续的变量X, Y, Z，满足下列条件之一，贝叶斯网络结构G中的无向路径被称为在观察变量O条件下活动的：

• X←Y←Z，Y未被观测，Y∉O
• X→Y→Z，Y未被观测，Y∉O
• X←Y→Z，Y未被观测，Y∉O
• X→Y←Z，Y或任何后继被观测

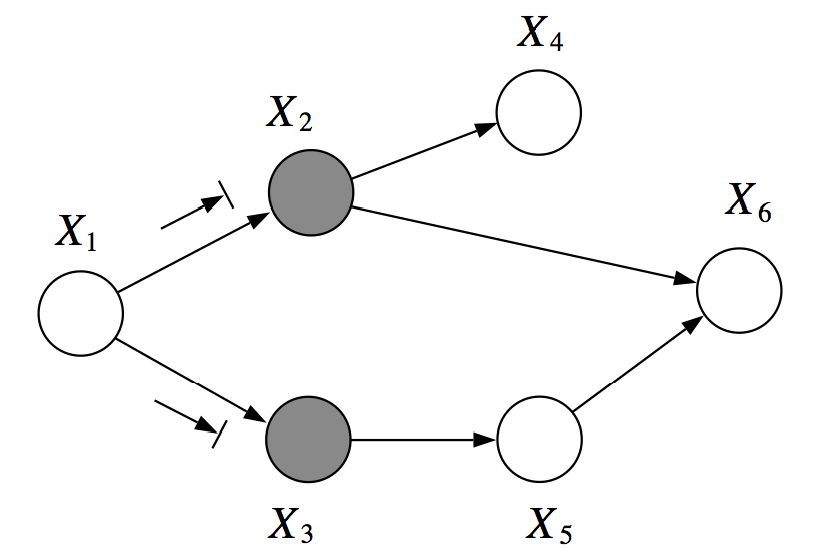
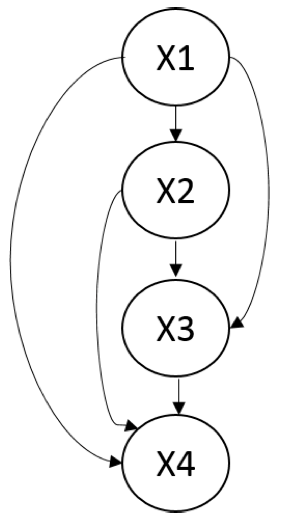
例如，在上面的图中，X1和X6在X2, X3条件下是 D-分离的。

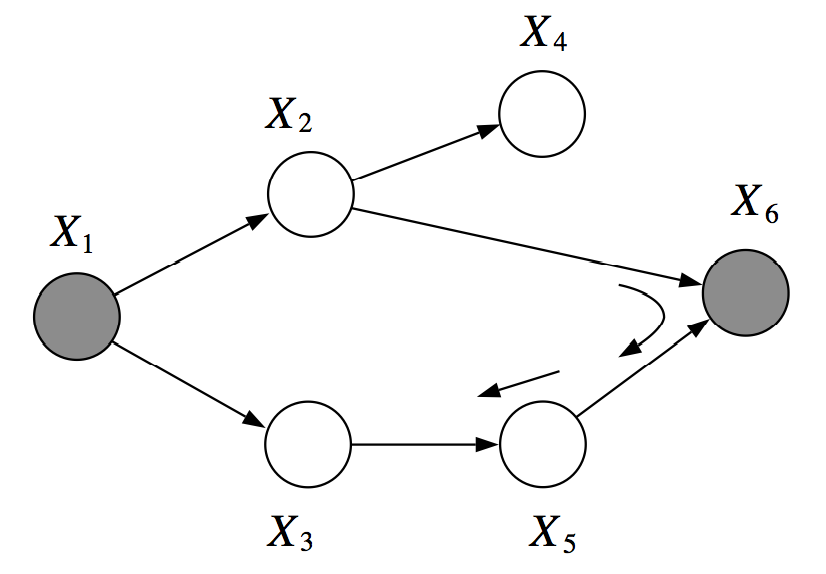
但是，X2, X3在X1, X6条件下不是 D-分离的，因为我们可以找到活动路径(X2, X6, X5, X3)。

之前有个 CS228 学生创建了一个交互式网络模拟来测试 D-分离。 随意使用它，如果是这样，请通过 Web 应用程序上的反馈按钮提交任何反馈或错误。

D-分离的概念很有用，因为它让我们描述了我们模型中很大一部分依赖关系。 令I(G)={(X⊥Y|Z)}，其中X, Y是条件Z下的 D-分离，它是G中 D-分离变量的集合。

事实 [1]：如果p在G上隐式分解，那么I(G)⊆I(p)。这里，我们说G是p的 I-map（独立性映射）。

[1] 我们不会正式证明它，但直觉是，如果X, Y和Y, Z是相互依赖的，那么X, Z也是如此。 因此，我们可以根据上面概述的本地依赖性结构，查看相邻节点并传播依赖关系。

换句话说，用G编码的所有独立性都是合理的：G中的 D-分离的变量，在p中是真正独立的。 然而，相反的情况并非如此：分布可能在G上因式分解，但具有在G中未捕获的独立性。

在某种程度上，这几乎是一个无意义的陈述。 如果p(x,y)=p(x)p(y)，那么这个分布仍然在图y→x上因式分解，因为我们总是可以使用 CPD ​p(x|y)，把它写成p(x,y)=p(x|y)p(y)，其中x的概率实际上并不随y变化。 但是，我们可以通过简单地删除不必要的边来构造一个图，匹配p的结构。

有向图的表现力

这引发了我们最后的也许是最重要的问题：有向图可以表示任何分布p的所有独立性吗？ 更正式地说，给定一个分布p，我们是否可以构造一个图G，使得I(G)=I(p)？

首先，请注意，构造G使得I(G)⊆I(p)非常容易。 因为I(G)=∅，全连通的 DAG G是任何分布的 I-map。

四个变量的全连通贝叶斯网络。这个模型中没有独立性，并且它是任何分布的 I-map。

一个更有意思的问题是，我们能找到p的最小 I-map G，也就是一个 I-map，从G中移除单个边将导致它不再是一个 I-map。这很简单：我们可以从一个完全连接的G开始，并删除边，直到G不再是 I-map。一种方法是遵循图的自然拓扑排序，并删除节点祖先，直到不再可能这样；我们将在进行结构学习时回顾这种修剪方法。

然而，我们真正感兴趣的是，确定概率p是否拥有完美的映射G，其中I(p)=I(G)。不幸的是，答案是否定的。例如，考虑三个变量X, Y, Z的以下分布p：我们从伯努利分布中抽样X,Y~Ber(0.5)，并且我们让Z = X xor Y（我们称之为 noisy-xor 示例） 。我们可以使用一些代数来检查，{X⊥Y，Z⊥Y，X⊥Z}∈I(p)，但Z⊥{Y,X}∉I(p)。因此，X→Z←Y是p的一个 I-map，但我们讨论的三节点图结构都没有完美描述I(p)，因此这种分布没有完美的映射。

一个相关的问题是，当存在完美的映射时，它是否是唯一的。 同样，情况并非如此，因为X→Y和X←Y编码了相同的独立性，但形成不同的图。 更一般地说，如果两个贝叶斯网络G1，G2编码相同的依赖性I(G1)=I(G2)，它们就是 I-等价的。

两个贝叶斯网络什么时候是 I-等价的？ 为了回答这个问题，让我们回到三个变量的简单例子。 我们说下面的每个图都有相同的骨架，这意味着如果我们放弃箭头的方向性，每种情况下我们会获得相同的无向图。

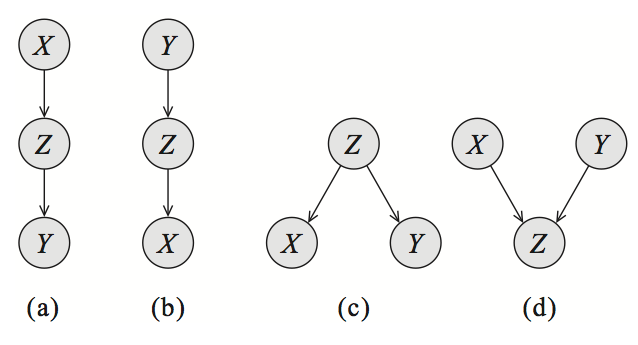
三个变量上的贝叶斯网络

级联结构（a，b）显然是对称的，箭头的方向性并不重要。 实际上，（a，b，c）编码了完全相同的依赖关系。 只要我们不将它们变成 V 结构（d），我们就可以改变箭头的方向。 然而，当我们有 V 结构时，我们不能改变任何箭头：结构（d）是唯一描述依赖关系 的图。 这些例子提供了 I-等价性的下列一般结果的直觉。

事实：如果G, G′具有相同的骨架和相同的 V 结构，则I(G)=I(G′)。

同样，直观理解为什么这是真的，这很容易。 如果变量之间的 D-分离相同，则两个图是 I-等价的。 我们可以翻转任何边的方向，除非它形成一个 V 结构，并且图的 D-连通性将保持不变。 我们提请读者阅读 Koller 和 Friedman 的教科书来获得充分的证据。