重新整理数据结构与算法(c#)——算法套路k克鲁斯算法[三十]
前言
这个和前面一节有关系,是这样子的,前面是用顶点作为参照条件,这个是用边作为参照条件。
正文
图解如下:
每次选择最小的边。
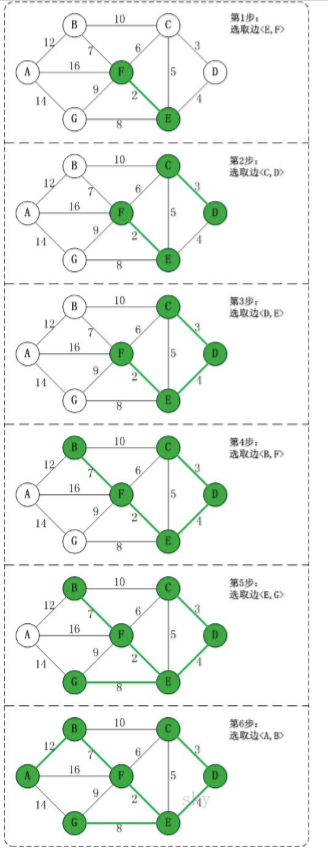
但是会遇到一个小问题,就是会构成回路。
比如说第四步中,最小边是CE,但是没有选择CE,因为CE会形成回路。
那么如何判断是否有回路呢?

判断两个点的终点,是否一致。
这个是怎么来的呢?为什么判断终点是否一致就可以判断有回路呢?
是这样子的,如何两个点可以共同到达任何一个点,那么他们之间一定是通的,这一点是肯定的,如果他们本来就是通的,再在他们之间加一条那么肯定回路的。
那么为什么选择终点呢?是这样子的,假如他们之间选来不相通,他们肯定在两条路上。
假设选了cd和ef这两条路。那么他们这两条路的终点分别是d(c->d)和f(e->f),他们的终点不同,那么他们没有在一条路上,所以把c->d的终点d的终点设置为e->另一条路的终点也就是f,连接后所有节点都有公共的终点,那么终点就可以作为判断依据,这样就不用去遍历了。
代码如下:
private static int INF = int.MaxValue;
static void Main(string[] args)
{
char[] vertexs = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
//克鲁斯卡尔算法的邻接矩阵
int[,] matrix = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF
},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
KruskaCase kruskaCase = new KruskaCase(vertexs,matrix);
kruskaCase.kruskal();
Console.ReadKey();
}
}
public class KruskaCase
{
private int edgeNum;//边的个数
private char[] vertexs;//顶点数组
private int[,] matrix;//邻接矩阵
private static int INF = int.MaxValue;
public KruskaCase(char[] vertexs, int[,] matrix)
{
int vlen = vertexs.Length;
//初始化顶点,避免污染数据
this.vertexs = new char[vlen];
for (int i=0;i<vlen;i++)
{
this.vertexs[i] = vertexs[i];
}
//初始化边, 避免污染数据
this.matrix = new int[vlen,vlen];
for (int i = 0; i < vlen; i++)
{
for (int j = 0; j < vlen; j++)
{
this.matrix[i,j] = matrix[i,j];
}
}
for (int i = 0; i < vlen; i++)
{
for (int j = i+1; j < vlen; j++)
{
if (matrix[i, j] != INF)
{
edgeNum++;
}
}
}
}
public void kruskal()
{
//表示第几条边加入最后的结果
int index = 0;
//记录每个顶点的终点
int[] ends = new int[edgeNum];
//最后边的个数肯定是节点数量-1
EData[] result = new EData[vertexs.Length-1];
EData[] edges = getEData();
sortEData(edges);
for (int i=0;i<edgeNum;i++)
{
var start = getPosition(edges[i].start);
var end = getPosition(edges[i].end);
int startEndPoint = getEnd(ends,start);
int endEndPoint = getEnd(ends, end);
if (startEndPoint != endEndPoint)
{
ends[startEndPoint] = endEndPoint;
result[index++] = edges[i];
}
}
Console.WriteLine("最小生成树为:");
for (int i=0;i<result.Length;i++)
{
Console.WriteLine(result[i]);
}
}
private int getPosition(char ch)
{
for (int i = 0; i < vertexs.Length; i++)
{
if (vertexs[i] == ch)
{
return i;
}
}
return -1;
}
private int getEnd(int[] ends, int i)
{ // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
while (ends[i] != 0)
{
i = ends[i];
}
return i;
}
/// <summary>
/// 对边数组进行排序
/// </summary>
/// <param name="edges">需要排序的边数组</param>
private void sortEData(EData[] edges)
{
for (int i = 0; i < edges.Length - 1; i++)
{
for (int j = 0; j < edges.Length - 1 - i; j++)
{
if (edges[j].weight > edges[j + 1].weight)
{//交换
EData tmp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = tmp;
}
}
}
}
结果:
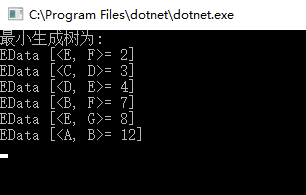


 浙公网安备 33010602011771号
浙公网安备 33010602011771号