重新整理数据结构与算法(c#)—— 平衡二叉树[二十三]
前言
因为有些树是这样子的:
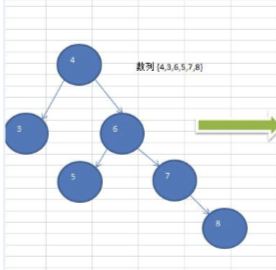
这样子的树有个坏处就是查询效率低,因为左边只有一层,而右边有3层,这就说明如果查找一个数字大于根元素的数字,那么查询判断就更多。
解决方法就是降低两边的层数差距:
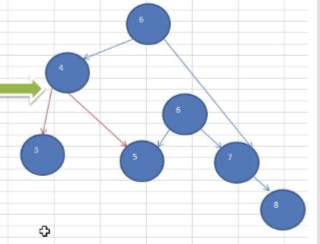
变成这样。
那么如何这样做呢?
如果右边比左边层次大于1,进行左旋转规格:

如果左边比右边层次大于1,进行右旋转:

为什么是这样处理呢?
我拿左旋转来说:
左边是1,右边是3,那么需要右边的给一层给左边。
这时候就是6作为根节点,6作为根节点,本身呢,就是一颗二叉树。
这时候呢,6大于4,所以4在6的右边,而6的左节点肯定大于4(原理的根节点)小于6,所以作为4的左节点代替,4也就成了6的左节点。
右旋转同理。
旋转会出现的问题
就是这样通过右旋转之后,可能达不到目标。
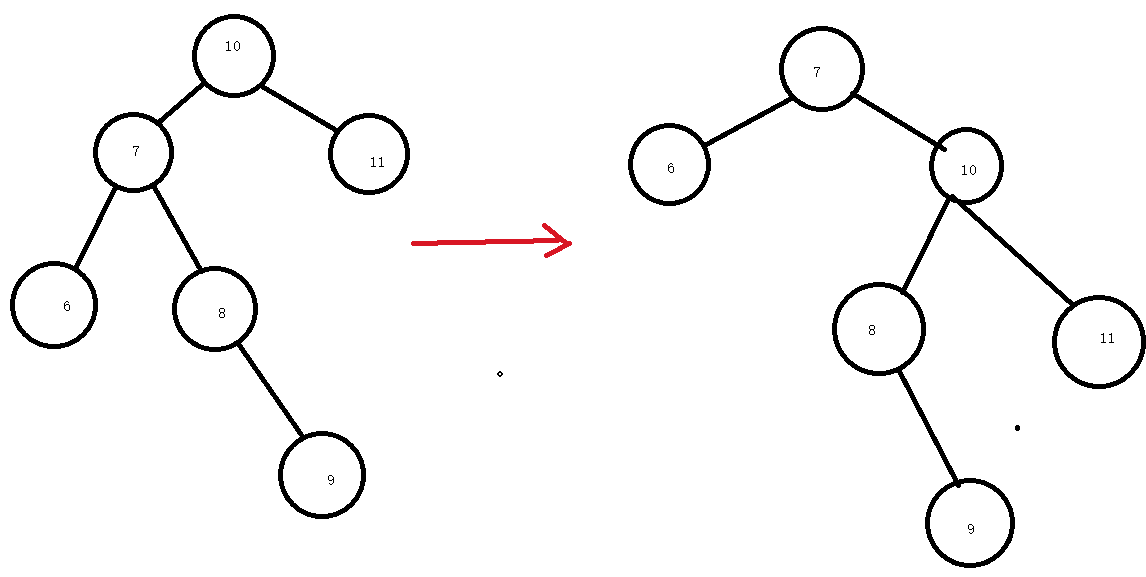
看上面这张图,右旋转后还是不平衡,为什么会这样呢?原因是这样的,我们来看下本质问题,右旋转干了什么?右旋转其实是重新分配元素的过程。
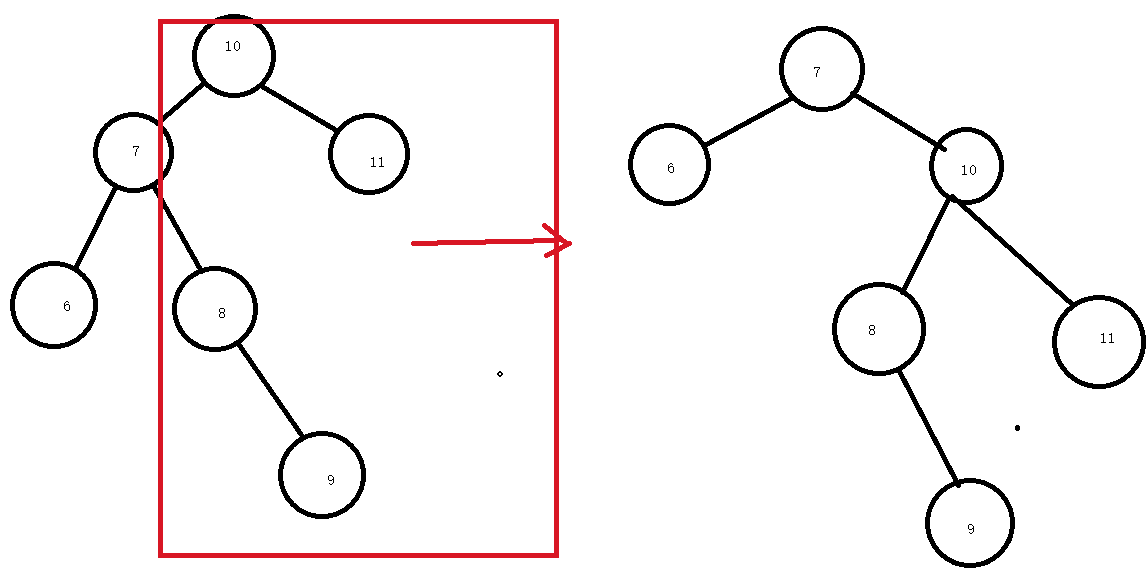
看我这种图红色部分,其实是将红色部门分给了右边,这时候会存在元素个数差异过大的问题。
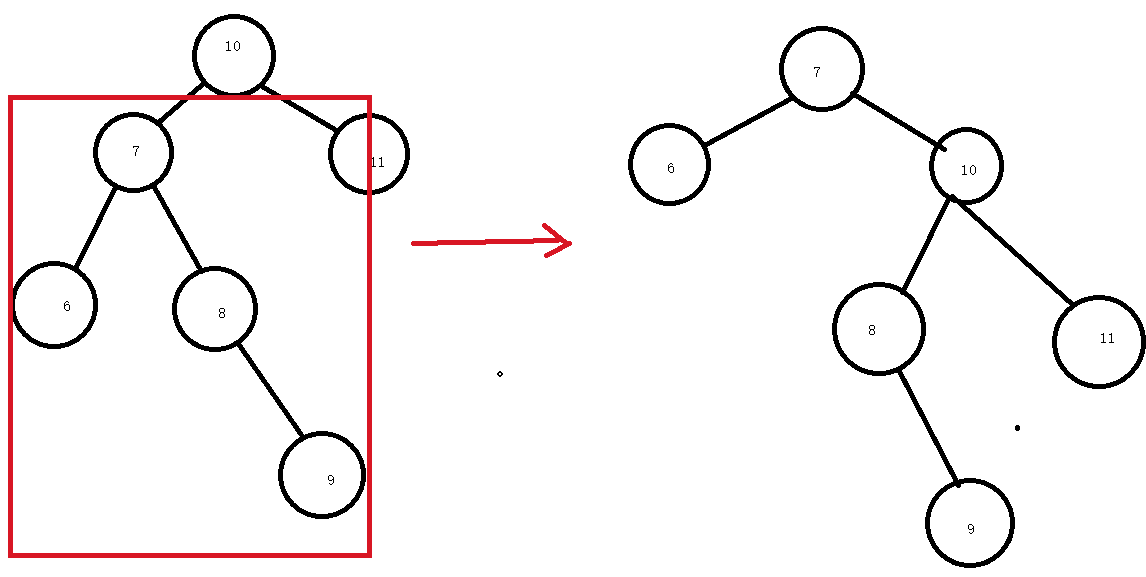
那么这时候该怎么办呢?
要让红框部分进行左旋转才行,那么看代码吧。
正文
节点模型:
public class Node
{
public Node left;
public Node right;
int value;
public int Value { get => value; set => this.value = value; }
public Node(int value)
{
this.Value = value;
}
//中序排序
public void infixOrder()
{
if (this.left != null)
{
this.left.infixOrder();
}
Console.WriteLine(this);
if (this.right != null)
{
this.right.infixOrder();
}
}
//左子树高度
public int leftHeight() {
if (left == null)
{
return 0;
}
return this.left.height();
}
//右子树高度
public int rightHeight() {
if (right == null)
{
return 0;
}
return this.right.height();
}
//计算高度
public int height()
{
return Math.Max(left==null?0:this.left.height(),right==null?0:this.right.height())+1;
}
//进行左旋转
private void leftRotate()
{
Node newNode = new Node(value);
newNode.left = left;
newNode.right = right.left;
//将右节点变成根节点
value =right.value;
//原先右节点被抛弃
right=right.right;
//左节点设置为
left = newNode;
}
//进行右旋转
private void rightRotate()
{
Node newNode = new Node(value);
newNode.left = left.right;
newNode.right = right;
value = this.left.value;
left = left.left;
right = newNode;
}
public override string ToString()
{
return Value.ToString();
}
//增加元素
public void addNode(Node node)
{
if (node.Value < this.Value)
{
if (this.left == null)
{
this.left = node;
}
else
{
this.left.addNode(node);
}
}
else {
if (this.right == null)
{
this.right = node;
}else {
this.right.addNode(node);
}
}
if (rightHeight() > leftHeight() + 1)
{
if (right.leftHeight() > right.rightHeight())
{
right.rightRotate();
}
this.leftRotate();
}
else if (leftHeight() > rightHeight() + 1)
{
if (left.rightHeight() > left.leftHeight())
{
left.leftRotate();
}
this.rightRotate();
}
}
public Node searchParentNode(int value)
{
if ((this.left != null && this.left.value == value || (this.right != null && this.right.value == value)))
{
return this;
}
else
{
if (this.value < value && this.left != null)
{
return this.left.searchParentNode(value);
}
else if (this.value >= value && this.right != null)
{
return this.right.searchParentNode(value);
}
else
{
return null;
}
}
}
//查找元素
public Node searchNode(int value)
{
if (this.Value == value)
{
return this;
}
if (this.Value > value)
{
if (this.left != null)
{
return this.right.searchNode(value);
}
else
{
return null;
}
}
else
{
if (this.left != null)
{
return this.left.searchNode(value);
}
else
{
return null;
}
}
}
}
树模型:
public class BinarySortTree
{
//根节点
Node root;
internal Node Root { get => root; set => root = value; }
public BinarySortTree(Node root)
{
this.Root = root;
}
public BinarySortTree() : this(null)
{
}
public void add(Node node)
{
if (Root == null)
{
Root = node;
}
else
{
this.Root.addNode(node);
}
}
public void infixOrder()
{
if (Root == null)
{
Console.WriteLine("root 为空");
}
else
{
Root.infixOrder();
}
}
public Node searchNode(int value)
{
if (Root==null)
{
Console.WriteLine("root 为空");
}
return Root.searchNode(value);
}
public int delRightTreeMin(Node node)
{
Node tagert = node;
while (tagert.left!=null)
{
tagert = tagert.left;
}
delNode(tagert.Value);
return tagert.Value;
}
public Node searchParentNode(int value)
{
if (Root != null)
{
return Root.searchParentNode(value);
}
return null;
}
public void delNode(int value)
{
if (Root == null)
{
return;
}
Node node=searchNode(value);
if (node == null)
{
return;
}
if (node.Value == Root.Value)
{
Root = null;
return;
}
Node parent = searchParentNode(value);
if (node.left == null && node.right == null)
{
if (parent.left.Value == value)
{
parent.left = null;
}
else
{
parent.right = null;
}
}
else if (node.left != null && node.right != null)
{
//删除左边最大值或者右边最小值,然后修改值为删除的值
parent.right.Value=delRightTreeMin(node.right);
}
else
{
if (node.left != null)
{
if (parent.left.Value == value)
{
parent.left = node.left;
}
else
{
parent.right = node.left;
}
}
else {
if (parent.left.Value == value)
{
parent.left = node.right;
}
else
{
parent.right = node.right;
}
}
}
}
}
测试代码:
static void Main(string[] args)
{
int[] arr = { 10, 11, 7, 6, 8, 9 };
BinarySortTree binarySortTree = new BinarySortTree();
//循环的添加结点到二叉排序树
for (int i = 0; i < arr.Length; i++)
{
binarySortTree.add(new Node(arr[i]));
}
//中序遍历后的数据
Console.WriteLine("树的高度=" + binarySortTree.Root.height()); //3
Console.WriteLine("树的左子树高度=" + binarySortTree.Root.leftHeight()); // 2
Console.WriteLine("树的右子树高度=" + binarySortTree.Root.rightHeight()); // 2
Console.WriteLine("当前的根结点=" + binarySortTree.Root);//8
Console.Read();
}
结果: