[论文理解] Meta Pseudo Labels

Intro

GOOGLE 21年的CVPR，提出了一种Teacher、Student都在训练中进行优化的基于伪标签的优化方法，最重要的是性能好，是目前参数量同等情况下在IMAGENET上精度最高的方法，TOP1 ACC高达90.2%。

文章的贡献主要有：

1. 提出一种形式化的蒸馏方法，该方法利用伪标签同时更新Teacher网络和Student网络。
2. 文章提出的方法具有超高的性能，同参数量情况下率先将IMAGENET准确率提升到90+。

Model

直入主题，文章提出的方法叫Meta Pseudo Labels，因而相较于传统的Pseudo Labels方法多了Meta建模的过程。传统的基于伪标签的蒸馏方法是基于一个预训练好的Teacher模型，利用Teacher模型提供的伪标签作为Student模型的Target，进行训练。而本文的方法可以通过Student模型在有标签数据上的表现（Loss）来帮助Teacher模型优化。与其他半监督模型不太一样的是，Teacher模型并非是通过EMA方式进行更新的，而是梯度方式。

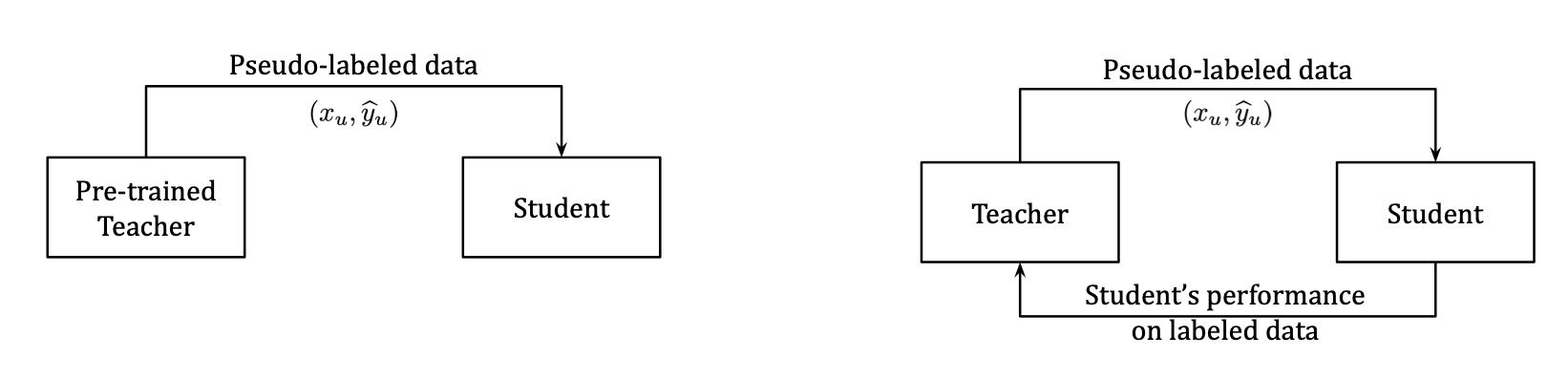
Method

对于传统的蒸馏方法，用伪标签方式进行优化的过程可以描述为：

\[\theta_{S}^{\mathrm{PL}}=\underset{\theta_{S}}{\operatorname{argmin}} \underbrace{\mathbb{E}_{x_{u}}\left[\operatorname{CE}\left(T\left(x_{u} ; \theta_{T}\right), S\left(x_{u} ; \theta_{S}\right)\right)\right]}_{:=\mathcal{L}_{u}\left(\theta_{T}, \theta_{S}\right)} \]

其中\(T\)表示Teacher模型，\(S\)表示Student模型，\(\theta\)表示该模型的参数，\(CE\)为交叉熵损失函数，\(\theta_S^{PL}\)为利用伪标签方法得到的最优Student模型参数。该部分是在无标签的数据上进行的，因为传统的半监督学习方法就是有标签部分损失加上无标签部分的一致性损失，蒸馏过程对应无标签部分的一致性损失。

本文的想法是，利用Student模型在有标签数据上的表现，来更新Teacher模型，那么这种“表现”数学化其实对应的就是Student模型在有标签数据上的Loss，因此可以表示为：

\[\mathbb{E}_{x_{l}, y_{l}}\left[\operatorname{CE}\left(y_{l}, S\left(x_{l} ; \theta_{S}^{\mathrm{PL}}\right)\right)\right]:=\mathcal{L}_{l}\left(\theta_{S}^{\mathrm{PL}}\right) \]

上式的公式有一个参数\(\theta_{S}^{\mathrm{PL}}\)，可以看到这个参数其实由上面第一个公式定义，因而可以看作是以\(\theta_T\)作为输入变量，\(\theta_S\)作为优化参数的函数形式，因而可以写为\(\theta_{S}^{\mathrm{PL}}(\theta_T)\)，那么上面第二个公式的损失可以定义为\(\mathcal{L}_{l}\left(\theta_{S}^{\mathrm{PL}}(\theta_T)\right)\)。

这样其实就已经完成了Meta模型的建模，即将一个模型的参数作为某一函数表达的输入，另一模型的参数作为该函数表达的参数，经过对该参数表达的损失函数的优化，得到最优参数。

因此，要在这一过程中更新Teacher模型，则需要最小化第二个公式的损失：

\[\begin{aligned}\min _{\theta_{T}} & \mathcal{L}_{l}\left(\theta_{S}^{\mathrm{PL}}\left(\theta_{T}\right)\right), \\\text { where } & \theta_{S}^{\mathrm{PL}}\left(\theta_{T}\right)=\underset{\theta_{S}}{\operatorname{argmin}} \mathcal{L}_{u}\left(\theta_{T}, \theta_{S}\right)\end{aligned} \]

很显然，上式的argmin函数没法用梯度方式来优化，因为得等到\(\theta_S\)达到最优，才能进行下一步，显然会导致训练无法端到端。文章对该问题做了一个one-step的近似：

\[\theta_{S}^{\mathrm{PL}}\left(\theta_{T}\right) \approx \theta_{S}-\eta_{S} \cdot \nabla_{\theta_{S}} \mathcal{L}_{u}\left(\theta_{T}, \theta_{S}\right) \]

到这里，上式的优化目标变成了：

\[\min _{\theta_{T}} \quad \mathcal{L}_{l}\left(\theta_{S}-\eta_{S} \cdot \nabla_{\theta_{S}} \mathcal{L}_{u}\left(\theta_{T}, \theta_{S}\right)\right) \]

OK，那么讲道理如果能对该式求\(\theta_T\)的梯度，就可以利用梯度下降方法来端到端优化了，定义上式为\(R\)，那么具体求解过程为：

\[\underbrace{\frac{\partial R}{\partial \theta_{T}}}_{1 \times|T|}=\frac{\partial}{\partial \theta_{T}} \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}\left[\theta_{S}-\eta_{S} \nabla_{\theta_{S}} \operatorname{CE}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)\right]\right)\right) \]

为简化表示，定义：

\[\underbrace{\bar{\theta}_{S}^{\prime}}_{|S| \times 1}=\mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}\left[\theta_{S}-\eta_{S} \nabla_{\theta_{S}} \mathbf{C E}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)\right] \]

则上式可以表示为：

\[\begin{aligned}\underbrace{\frac{\partial R}{\partial \theta_{T}}}_{1 \times|T|} &=\frac{\partial}{\partial \theta_{T}} \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}\left[\theta_{S}-\eta_{S} \nabla_{\theta_{S}} \mathbf{C E}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)\right]\right)\right) \\&=\frac{\partial}{\partial \theta_{T}} \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \bar{\theta}_{S}^{\prime}\right)\right) \\&=\underbrace{\left.\frac{\partial \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \bar{\theta}_{S}^{\prime}\right)\right)}{\partial \theta_{S}}\right|_{\left.\theta_{S}=\bar{\theta}_{S}^{\prime}\right)}}_{|\times| S \mid} \cdot \underbrace{\frac{\partial \bar{\theta}_{S}^{\prime}}{\partial \theta_{T}}}_{|S| \times|T|}\end{aligned} \]

上式的左边其实是很容易利用梯度下降求解的，因为可以利用Student模型在有标签数据集上更新前后参数相减得到梯度：

由于

\[\theta_{S}^*=\theta_{S}-\eta_{S} \nabla_{\theta_{S}} \mathbf{C E}\left(y_{l}, S\left(x_{l} ; \theta_{S}\right)\right) \]

因此很容易利用更新前后\(\theta_S\)进行相减得到其梯度：

\[\eta_{S} \nabla_{\theta_{S}} \mathbf{C E}\left(y_{l}, S\left(x_{l} ; \theta_{S}\right)\right) =\theta_{S}-\theta_{S}^* \]

所以现在需要聚焦到前面式子的右侧项\(\frac{\partial \bar{\theta}_{S}^{\prime}}{\partial \theta_{T}}\)：

将这该式展开：

\[\begin{aligned}\underbrace{\frac{\partial \bar{\theta}_{S}^{\prime}}{\partial \theta_{T}}}_{|S| \times|T|} &=\frac{\partial}{\partial \theta_{T}} \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}\left[\theta_{S}-\eta_{S} \nabla_{\theta_{S}} \operatorname{CE}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)\right] \\&=\frac{\partial}{\partial \theta_{T}} \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}\left[\theta_{S}-\eta_{S} \cdot\left(\left.\frac{\partial \operatorname{CE}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)}{\partial \theta_{S}}\right|_{\theta_{S}=\theta_{S}}\right)^{\top}\right]\end{aligned} \]

为了简化表示，我们再次定义：

\[\underbrace{g_{S}\left(\widehat{y}_{u}\right)}_{|S| \times|1|}=\left(\left.\frac{\partial \operatorname{CE}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)}{\partial \theta_{S}}\right|_{\theta_{S}=\theta_{S}}\right)^{\top} \]

那么上式就变成了：

\[\underbrace{\frac{\partial \bar{\theta}_{S}^{\prime}}{\partial \theta_{T}}}_{|S| \times|T|}=-\eta_{S} \cdot \frac{\partial}{\partial \theta_{T}} \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}[\underbrace{g_{S}\left(\widehat{y}_{u}\right)}_{|S| \times 1}] \]

这里的\(g_{S}\left(\widehat{y}_{u}\right)\)并不依赖\(\theta_T\)的，只是\(\widehat{y}_{u}\)需要利用伪标签算法依赖Teacher模型的参数罢了，这里其实用到了Leibniz积分法则，举一个例子：

\[\frac{\partial }{\partial \theta} \mathbb{E}_{x \sim p(x;\theta)}f(x) \]

这个式子要求梯度可以这么做：

\[\frac{\partial }{\partial \theta} \mathbb{E}_{x \sim p(x;\theta)}f(x) \\ = \frac{\partial}{\partial \theta} \int p(x;\theta)f(x)dx \\ = \int \frac{\partial}{\partial \theta}p(x;\theta)f(x)dx \\ = \int p(x;\theta) \nabla_\theta log(p(x;\theta))f(x)dx \\ =\mathbb{E}_{x \sim p(x;\theta)} f(x)\nabla_\theta log(p(x;\theta)) \]

那么同理呀，上式可以写成：

\[\frac{\partial }{\partial \theta_T} \mathbb{E}_{\hat{y}_u \sim T(x_u;\theta_T)}[g_s(\hat{y}_u)] \\ = \frac{\partial}{\partial \theta_T} \sum_{\hat{y}_u} p(\hat{y}_u|x_u;\theta_T)g_s(\hat{y}_u) \\ = \sum_{\hat{y}_u} \frac{\partial}{\partial \theta_T}p(\hat{y}_u|x_u;\theta_T)g_s(\hat{y}_u) \\ = \sum_{\hat{y}_u} p(\hat{y}_u|x_u;\theta_T) \frac{\partial}{\partial \theta_T} log(p(\hat{y}_u|x_u;\theta_T)g_s(\hat{y}_u) \\ =\mathbb{E}_{\hat{y}_u \sim T(x_u;\theta_T)} [g_s(\hat{y}_u) \frac{\partial}{\partial \theta_T} log(p(\hat{y}_u|x_u;\theta_T)] \]

因此有：

\[\begin{aligned}\underbrace{\frac{\partial \bar{\theta}_{S}^{(t+1)}}{\partial \theta_{T}}}_{|S| \times|T|} &=-\eta_{S} \cdot \frac{\partial}{\partial \theta_{T}} \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}\left[g_{S}\left(\widehat{y}_{u}\right)\right] \\&=-\eta_{S} \cdot \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}[\underbrace{g_{S}\left(\widehat{y}_{u}\right)}_{|S| \times 1} \underbrace{\cdot \underbrace{\frac{\partial \log P\left(\widehat{y}_{u} \mid x_{u} ; \theta_{T}\right)}{\partial \theta_{T}}}_{1 \times|T|}]}\\&=\eta_{S} \cdot \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}[\underbrace{g_{S}\left(\widehat{y}_{u}\right)}_{|S| \times 1} \cdot \underbrace{\frac{\partial \operatorname{CE}\left(\widehat{y}_{u}, T\left(x_{u} ; \theta_{T}\right)\right)}{\partial \theta_{T}}}_{1 \times|T|}]\end{aligned} \]

到这一步就可以利用交叉熵损失项来计算该部分梯度了。

到这里，再整理一下上面提到的左项和右项：

\[\begin{aligned}\underbrace{\frac{\partial R}{\partial \theta_{T}}}_{1 \times|T|} &=\underbrace{\left.\frac{\partial \mathbf{C E}\left(y_{l}, S\left(x_{l} ; \bar{\theta}_{S}^{\prime}\right)\right)}{\partial \theta_{S}}\right|_{\theta_{S}=\bar{\theta}_{S}^{\prime}}}_{1 \times|S|} \underbrace{\frac{\partial \bar{\theta}_{S}^{\prime}}{\partial \theta_{T}}}_{|S| \times|T|} \\&=\eta_{S} \cdot \underbrace{\left.\frac{\partial \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \bar{\theta}_{S}^{\prime}\right)\right)}{\partial \theta_{S}}\right|_{\theta_{S}=\bar{\theta}_{S}^{\prime}}}_{1 \times|S|} \cdot \mathbb{E}_{\widehat{y}_{u} \sim T\left(x_{u} ; \theta_{T}\right)}[\underbrace{g_{S}\left(\widehat{y}_{u}\right)}_{|S| \times 1} \cdot \underbrace{\frac{\partial \operatorname{CE}\left(\widehat{y}_{u}, T\left(x_{u} ; \theta_{T}\right)\right)}{\partial \theta_{T}}}_{1 \times|T|}]\end{aligned} \]

上式均值项需要进行采样才能计算(过程就是对batch内样本计算)，以batch内一个样本为例，其梯度为：

\[\begin{aligned}\nabla_{\theta_{T}} \mathcal{L}_{l} &=\eta_{S} \cdot \underbrace{\frac{\partial \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \theta_{S}^{\prime}\right)\right)}{\partial \theta_{S}}}_{1 \times|S|} \cdot \underbrace{\left(\left.\frac{\partial \mathbf{C E}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)}{\partial \theta_{S}}\right|_{\theta_{S}=\theta_{S}}\right)^{\top}}_{|S| \times 1} \cdot \underbrace{\frac{\partial \operatorname{CE}\left(\widehat{y}_{u}, T\left(x_{u} ; \theta_{T}\right)\right)}{\partial \theta_{T}}}_{1 \times|T|} \\&=\underbrace{\eta_{S} \cdot\left(\left(\nabla_{\theta_{S}^{\prime}} \operatorname{CE}\left(y_{l}, S\left(x_{l} ; \theta_{S}^{\prime}\right)\right)^{\top} \cdot \nabla_{\theta_{S}} \operatorname{CE}\left(\widehat{y}_{u}, S\left(x_{u} ; \theta_{S}\right)\right)\right)\right.}_{\text {A scalar }:=h} \cdot \nabla_{\theta_{T}} \mathbf{C E}\left(\widehat{y}_{u}, T\left(x_{u} ; \theta_{T}\right)\right)\end{aligned} \]

可以看到左端项其实利用矩阵乘法已经是一个scalar了，右端项为一vector。

h的泰勒估计

已知

\[\theta'_S = \theta_S - \eta \]

且根据Student参数更新过程

\[\eta = \eta_S \nabla_{\theta_S}CE(\hat{y}_u, S(x_u;\theta_S)) \]

令

\[L(\theta_S) = CE(y_l, S(x)) \]

根据泰勒公式，

\[L(\theta_S') = L(\theta_S - \eta) \approx L(\theta_S) - \eta \nabla_{\theta_S}L(\theta_S) \\ =L(\theta_S) - \eta_S \nabla_{\theta_S}CE(\hat{y}_u, S(x_u;\theta_S)) \nabla_{\theta_S}L(\theta_S) \\ =L(\theta_S) - \eta_S \nabla_{\theta_S}CE(\hat{y}_u, S(x_u;\theta_S)) \nabla_{\theta_S}CE(y_l, S(x)) \\ = L(\theta_S) - h \]

所以

\[h = L(\theta_S) - L(\theta_S') \]

到这里，理论推导部分就结束了。

Algorithm

算法部分相当简单，和UDA损失一起使用，那么基本分为两个过程，首先利用Teacher模型提供伪标签，优化更新Student模型，然后利用上面计算的公式，求出scalar h，代入求得梯度项，更新Teacher模型；Teacher和Student模型交替进行优化。

Experiments

实验上，一般先在CIFAR10等这样的小数据集上进行一轮比较：

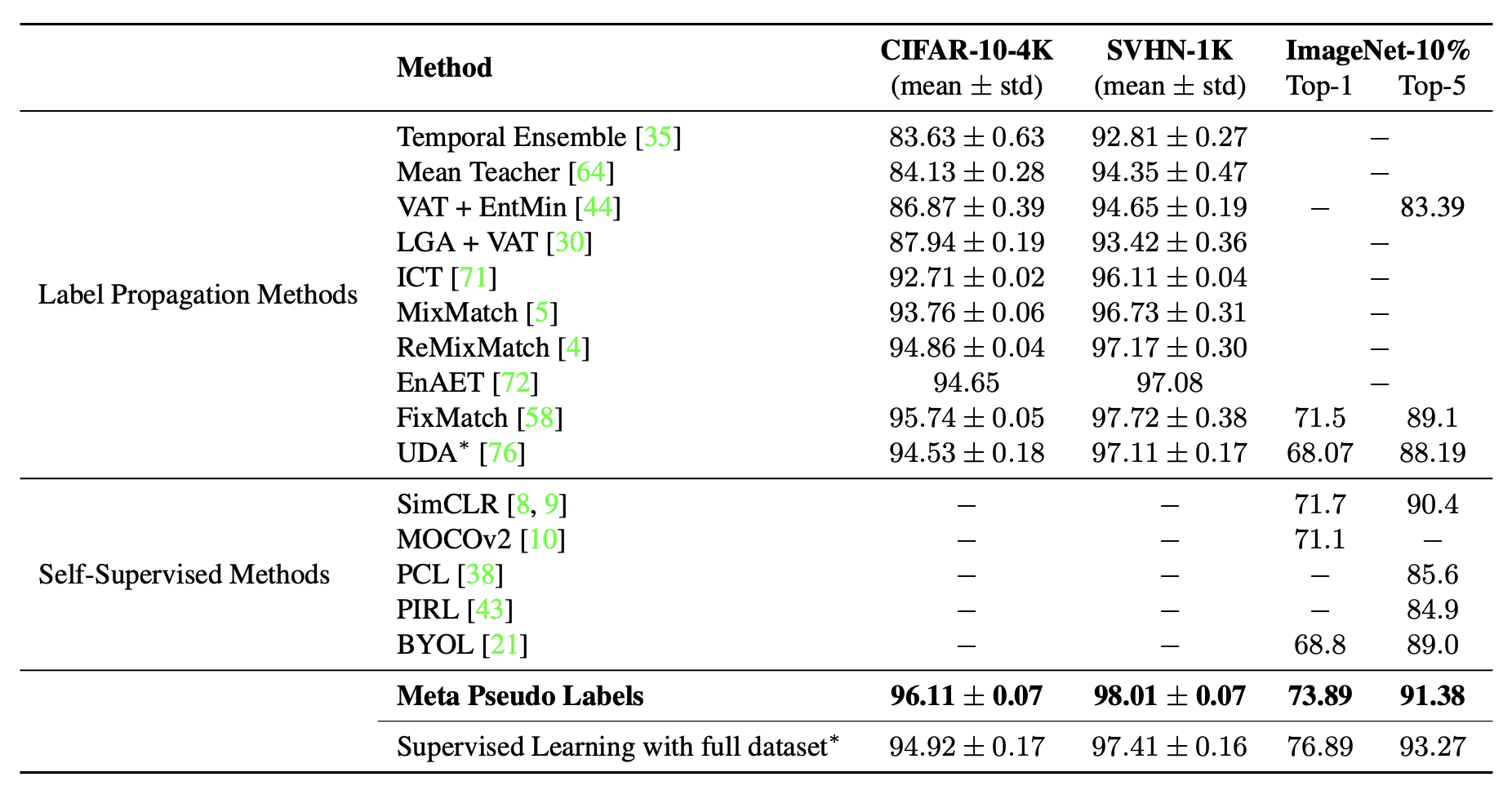
基本是最优的。

在IMAGENET上进行全监督实验时，其实也是按半监督的方式来做的，只是将IMAGENET的全部样本当作有标签的样本，然后再用了1.3亿张JFT数据集当无标签样本训练的。

其实验结果：

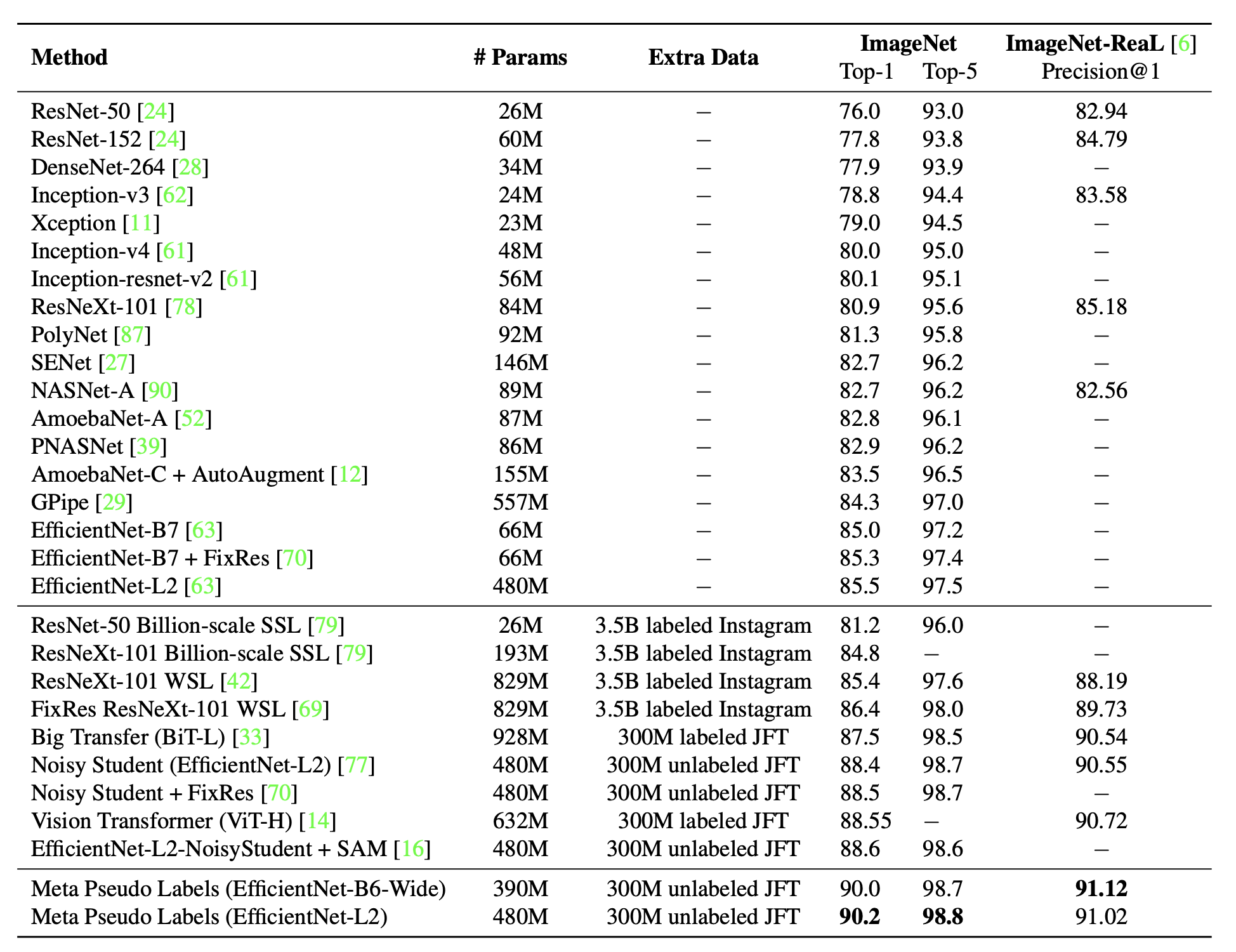
300+M的模型就已经达到90%的acc了。。

Code

Ref: https://github.com/kekmodel/MPL-pytorch

batch_size = images_l.shape[0]
t_images = torch.cat((images_l, images_uw, images_us))
t_logits = teacher_model(t_images)
t_logits_l = t_logits[:batch_size]
t_logits_uw, t_logits_us = t_logits[batch_size:].chunk(2)
del t_logits

t_loss_l = criterion(t_logits_l, targets)

soft_pseudo_label = torch.softmax(t_logits_uw.detach()/args.temperature, dim=-1)
max_probs, hard_pseudo_label = torch.max(soft_pseudo_label, dim=-1)
mask = max_probs.ge(args.threshold).float()
t_loss_u = torch.mean(
    -(soft_pseudo_label * torch.log_softmax(t_logits_us, dim=-1)).sum(dim=-1) * mask
)
weight_u = args.lambda_u * min(1., (step+1) / args.uda_steps)
t_loss_uda = t_loss_l + weight_u * t_loss_u

s_images = torch.cat((images_l, images_us))
s_logits = student_model(s_images)
s_logits_l = s_logits[:batch_size]
s_logits_us = s_logits[batch_size:]
del s_logits

s_loss_l_old = F.cross_entropy(s_logits_l.detach(), targets)
s_loss = criterion(s_logits_us, hard_pseudo_label)

s_scaler.scale(s_loss).backward()
if args.grad_clip > 0:
    s_scaler.unscale_(s_optimizer)
    nn.utils.clip_grad_norm_(student_model.parameters(), args.grad_clip)
s_scaler.step(s_optimizer)
s_scaler.update()
s_scheduler.step()
if args.ema > 0:
    avg_student_model.update_parameters(student_model)

with amp.autocast(enabled=args.amp):
    with torch.no_grad():
        s_logits_l = student_model(images_l)
    s_loss_l_new = F.cross_entropy(s_logits_l.detach(), targets)
    # dot_product = s_loss_l_new - s_loss_l_old
    # test
    dot_product = s_loss_l_old - s_loss_l_new
    # moving_dot_product = moving_dot_product * 0.99 + dot_product * 0.01
    # dot_product = dot_product - moving_dot_product
    _, hard_pseudo_label = torch.max(t_logits_us.detach(), dim=-1)
    t_loss_mpl = dot_product * F.cross_entropy(t_logits_us, hard_pseudo_label)
    t_loss = t_loss_uda + t_loss_mpl

t_scaler.scale(t_loss).backward()
if args.grad_clip > 0:
    t_scaler.unscale_(t_optimizer)
    nn.utils.clip_grad_norm_(teacher_model.parameters(), args.grad_clip)
t_scaler.step(t_optimizer)
t_scaler.update()
t_scheduler.step()

teacher_model.zero_grad()
student_model.zero_grad()

if args.world_size > 1:
    s_loss = reduce_tensor(s_loss.detach(), args.world_size)
    t_loss = reduce_tensor(t_loss.detach(), args.world_size)
    t_loss_l = reduce_tensor(t_loss_l.detach(), args.world_size)
    t_loss_u = reduce_tensor(t_loss_u.detach(), args.world_size)
    t_loss_mpl = reduce_tensor(t_loss_mpl.detach(), args.world_size)
    mask = reduce_tensor(mask, args.world_size)