[论文理解] Temporal Shift Module for Efficient Video Understanding
Temporal Shift Module for Efficient Video Understanding
Intro
文章是提出了一种颇为有效的跨帧处理模块，能够提升2DCNN对于视频数据的特征提取能力，大大提升视频分类的准确率，同时，该模块还是0参数量的模块，即插即用。
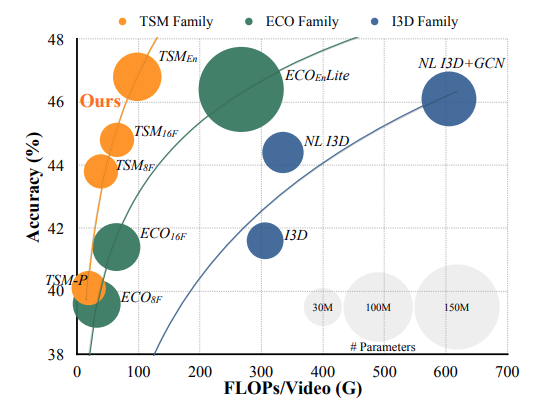
Intution
本文的Intution其实很明显，是想要借鉴一维卷积的移位、乘加操作的分解，将其利用到视频处理中，而恰巧2D卷积本质上是对通道维度的乘加，恰巧满足卷积的第二个操作，那么只要实现了卷积的移位操作，就可以将视频序列在时间维度上当成一维序列进行卷积化处理了。
首先我们先回顾一下一维卷积的过程：
对于序列\(X\)，假定我们需要使用大小为3的卷积对其进行处理，卷积核权重为 \(W =(w_1, w_2, w_3)\),
那么首先需要对输入序列\(X\)进行移位处理：
然后进行乘加处理：
这一块简单证明一下：
原始的1D卷积公式：
但是需要考虑到padding，所以y的0位置要和x的padding后的初始位置对应（之所以需要考虑padding，是因为公式默认从第一个非0的x位置开始索引），所以上面公式考虑padding之后可以写为:
其中k为kernel size，现在假定k=3，那么有：
考虑h的取值只能是0，1，2，所以i的取值只有n,n-1和n-2：
所以
基于此，作者想到，如果想要对时序维度进行信息利用，其实并不一定需要参数量更大的3D卷积网络，而是可以利用卷积对通道维度的乘加处理，再单独加上时间维度的移位操作，这样就可以实现在时间维度上的1D卷积了。
Method
文章对TSM进行了这样一张图的解释：
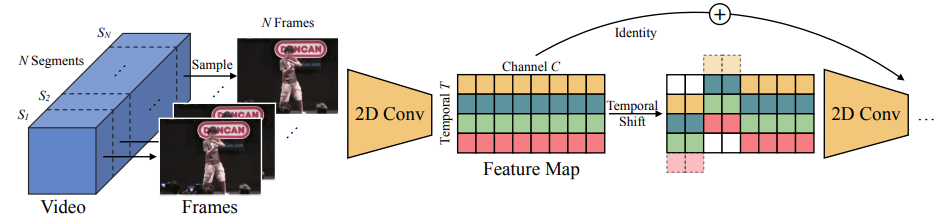
怎奈右边部分怎么也看不懂。。然后就去看了代码，其实还是不太懂。
研究了下我画了个更好理解的图：
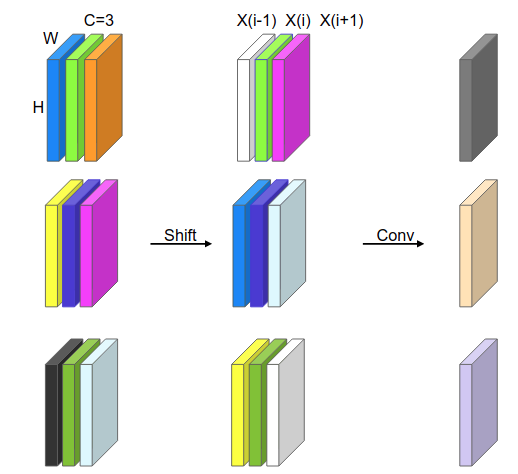
以通道为3的特征层为例，每组3个通道为一张图对应的特征层，因此从上往下是对应不同帧的特征层。对这个图进行解释，shift操作对所有特征层的第一层向下进行平移，于是可以看到shift之后第一列对应shift之前第一列是向下平移的了，其中白色的层表示0填充，第二层不动，第三层向上平移，那么第一层第二层第三层的序列就可以表示成X(i-1)、X(i)和X(i+1)的三个序列了，由于卷积本身是对所有通道的一个加权，因此2D卷积处理后就把三个特征层加权求和变成了一个特征层，从而实现了1D卷积的乘加操作(kernel size = 3)。
需要说明的是，原文是对很多相邻的通道同时进行平移，而我的例子只是平移了一个通道，显然对于kernel size为3的1D卷积，如果channel数量大于3，只能是同时对channel size / 3数量的channel进行平移，这样做就是将相邻多个通道看成一个通道进行处理，当然也是可以这么做的；但是原文中是四分之一的通道上移，四分之一的通道下移，二分之一的通道不移动(移动先后顺序无关，因为最后是求和)，我画的图是三个通道的例子；为什么原文那样做比较好，后面作者简单做了个实验：
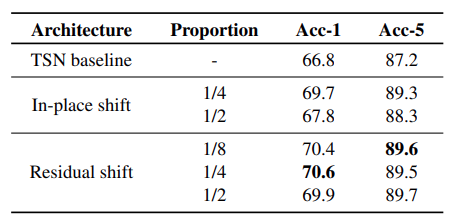
每个shift占比四分之一可能是个比较合适的值，但其实这里的实验明显是不够的，感觉不能充分说明四分之一的超参足够优秀。。。
Training
训练的话其实是参考TSN的，TSN的训练是下面几个过程：
- 将视频划分为若干clip
- 每个clip的图像被按当成batch处理，使用2d卷积
- 所有clip处理完之后进行fuse
- fuse之后对整个视频分类。
基本也就是把一些卷积结构换成TSM，不再赘述。
Code
out = torch.zeros_like(x)
fold = c // fold_div
out[:, :-1, :fold] = x[:, 1:, :fold] # shift left
out[:, 1:, fold: 2 * fold] = x[:, :-1, fold: 2 * fold] # shift right
out[:, :, 2 * fold:] = x[:, :, 2 * fold:] # not shift
return out
