[论文理解] Quantizing Deep Convolutional Networks For Efficient Inference A Whitepaper

Quantizing Deep Convolutional Networks For Efficient Inference A Whitepaper

Question：到底加速在哪？

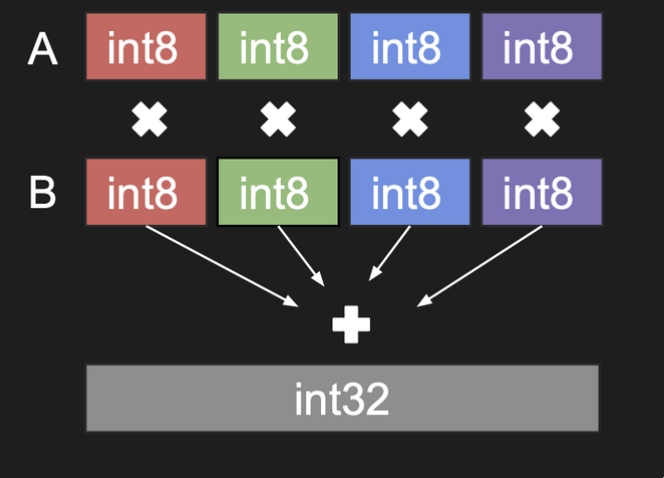
Nvidia官网上的一张图

非对称量化

\[\begin{aligned}x_{i n t} &=\operatorname{round}\left(\frac{x}{\Delta}\right)+z \\x_{Q} &=\operatorname{clamp}\left(0, N_{\text {levels }}-1, x_{i n t}\right)\end{aligned} \]

第一步，先转int32，对原始数据除以delta + zero-point

第二步，把int8之外的数据剔除，将其存储在8bit存储单元中。

反量化：

\[x_{\text {float }}=\left(x_{Q}-z\right) \Delta \]

需要注意一点，反量化没有误差。

假设量化后的数据和量化前的数据可以一一对应，那么反量化操作是可以完全恢复原始数据的！！

那有了量化后的数据我们怎么得到算子运算之后的数据呢？？

卷积量化：

\[\begin{aligned}y(k, l, n) &=\Delta_{w} \Delta_{x} \operatorname{conv}\left(w_{Q}(k, l, m ; n)-z_{w}, x_{Q}(k, l, m)-z_{x}\right) \\y(k, l, n) &=\operatorname{conv}\left(w_{Q}(k, l, m ; n), x_{Q}(k, l, m)\right)-z_{w} \sum_{k=0}^{K-1} \sum_{l=0}^{K-1} \sum_{m=0}^{N-1} x_{Q}(k, l, m) \\&-z_{x} \sum_{k=0}^{K-1} \sum_{l=0}^{K-1} \sum_{m=0}^{N-1} w_{Q}(k, l, m ; n)+z_{x} z_{w}\end{aligned} \]

缺点是计算略微复杂了一点。z！！

对称量化

让z=0

原因：

zero-padding 不要有误差。

缺点，对不关于0对称的数据不友好，比如relu激活后的数据，浪费比特了。

随机量化

\[\begin{aligned}x_{\text {int }} &=\operatorname{round}\left(\frac{x+\epsilon}{\Delta}\right)+z, \quad \epsilon \sim \operatorname{Unif}\left(-\frac{1}{2}, \frac{1}{2}\right) \\x_{Q} &=\operatorname{clamp}\left(0, N_{\text {levels }}-1, x_{i n t}\right)\end{aligned} \]

论文中说：

不解。说是对梯度计算有好处？ 从这个公式怎么看出来对梯度有好处？

感知量化

量化训练的问题：clamp不可导 → 梯度几乎处处为0；

解决：跳过clamp函数，梯度计算直接用量化前的权重计算，而不是量化反量化之后的权重计算。

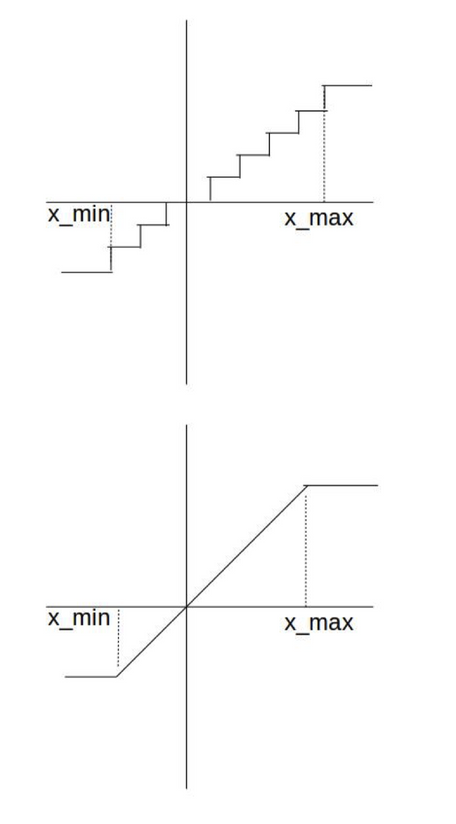
量化参数选取

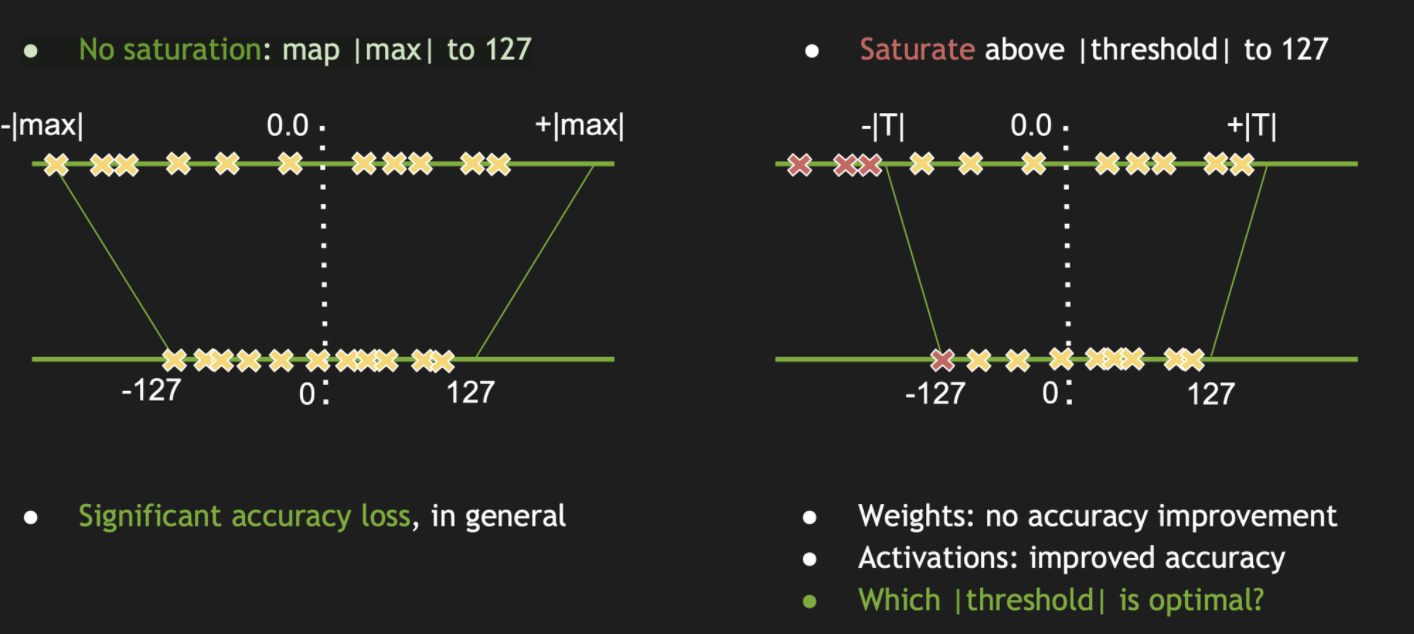
KL div

Intuition： KL散度衡量的是用Q分布来编码真实分布P时产生的信息损耗；如果这个信息损失够小，那么这显然是很好的量化结果。

目的：

得到一个最佳threshold

算法：

从一个最小值（应该是超参）到包含所有数据的最大值开始依次试，每次计算量化前后的KL div，取最小的那个结果对应的thre。

量化粒度

层间量化的效果不如每个channel量化的效果。粒度越细效果越好。

训后量化

1. 只量化权重 ： 不需要数据
2. 权重和激活值都量化： 需要数据

（1）per-channel量化的效果跟原始结果已经非常接近了。

（2）数据量化几乎是没损失的，因为bn使得数据变得0均值小方差，relu6这样的激活函数将数值限制在了0到6，这都有利于量化。

（3）越大的模型（resnet）对量化越robust（相比于mibilenet）

（4）层间量化精度掉的非常多。

（5）几乎所有的精度损失都来自于权重量化，而非数据量化。

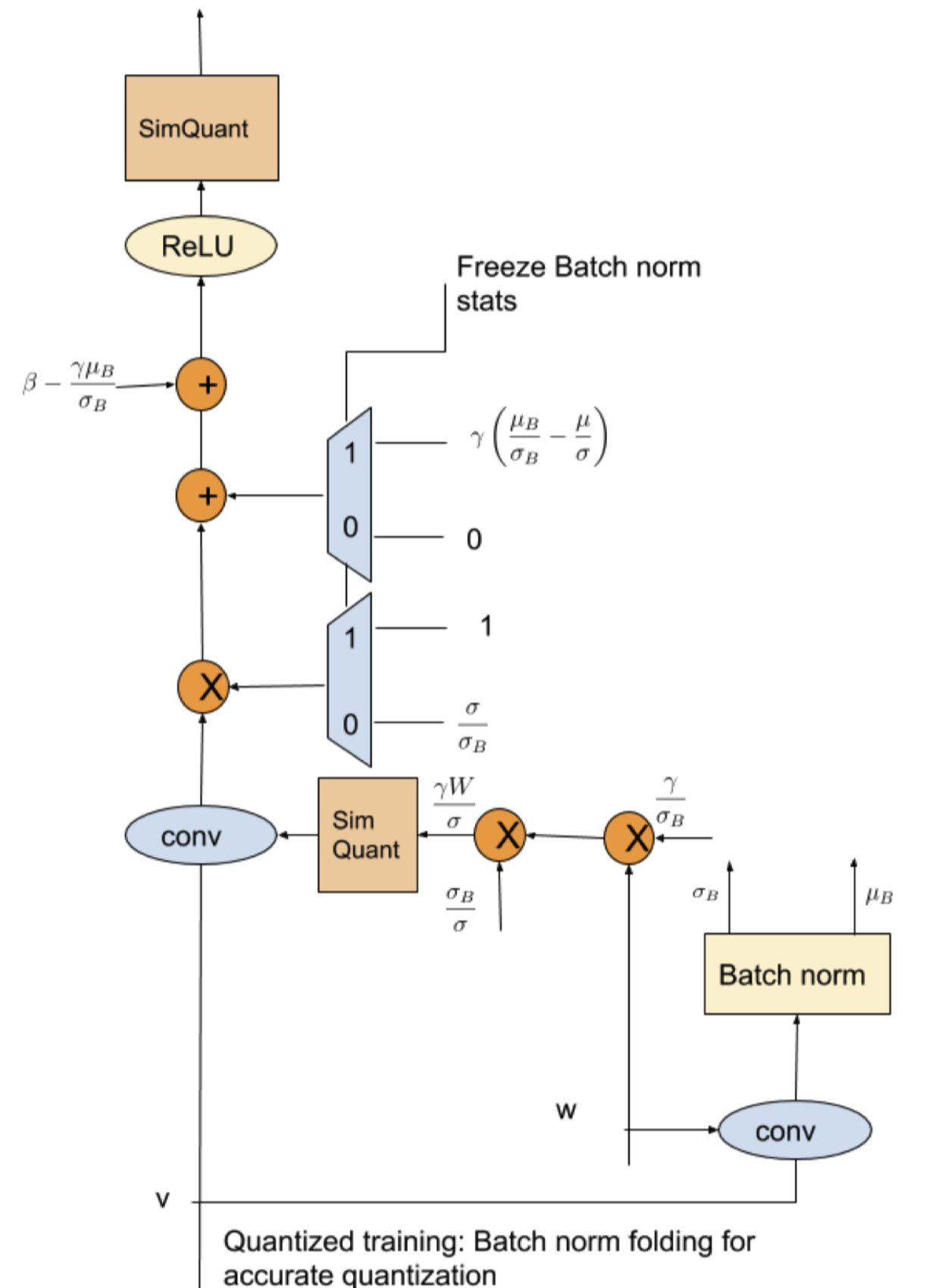
BN的一些问题

merge加速

\[x_{b n}=\gamma\left(\frac{x-\mu_{B}}{\sigma_{B}}\right)+\beta \]

相当于对上一层的卷积的权重相乘，加上一个新bias

\[\begin{aligned}W_{i n f} &=\frac{\gamma W}{\sigma} \\\text { Bias }_{i n f} &=\beta-\frac{\gamma \mu}{\sigma}\end{aligned} \]

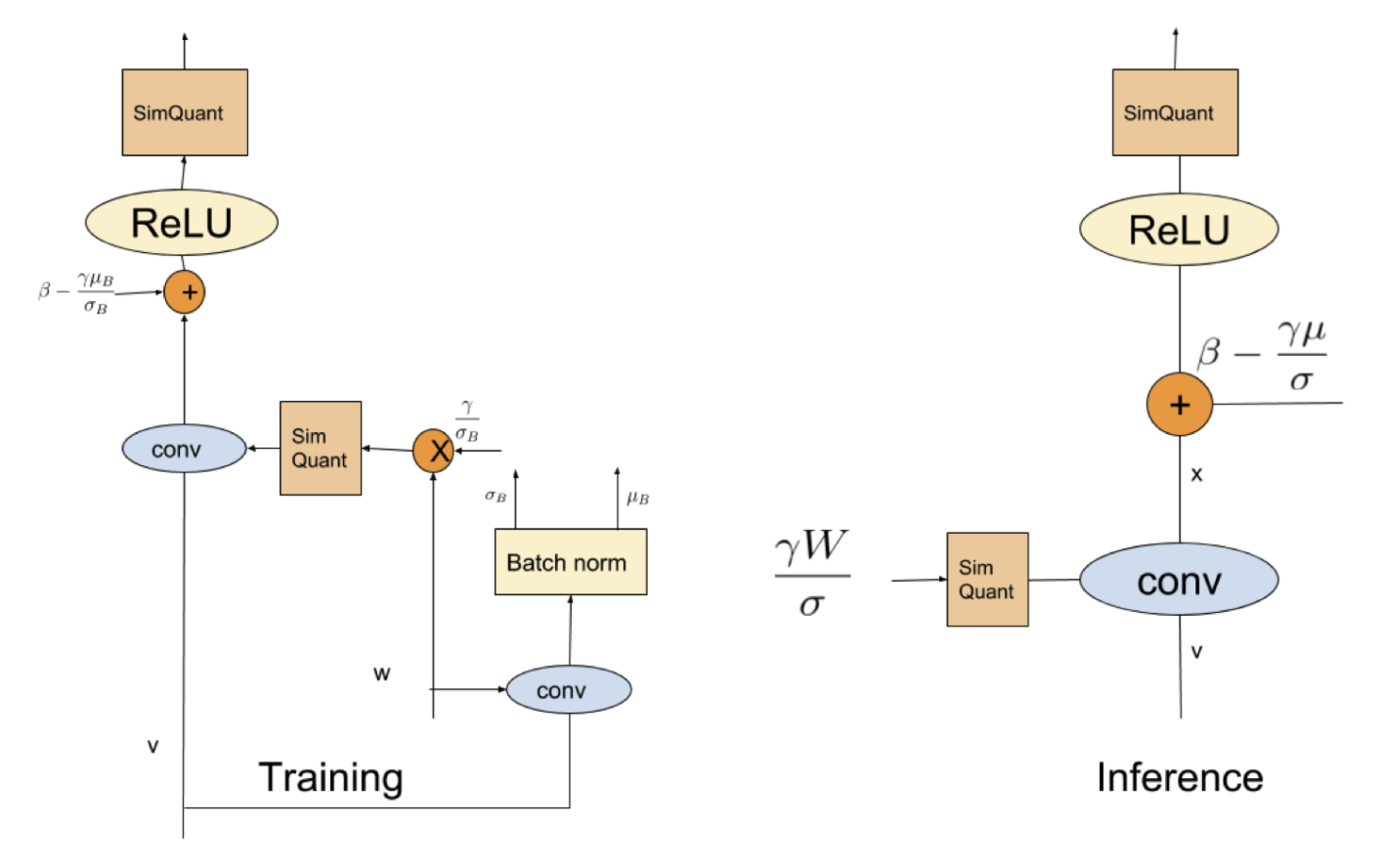
但是由于训练过程中sigma和u都是和数据有关的，而且是和batch内数据非常相关，因此sim quant权重可能会因此不稳定。

Solution：量化反量化前用滑动平均，之后再恢复。