[论文理解] 半监督论文总结（一）

Semi-supervised Papers Review

CatGAN

arxiv：https://arxiv.org/pdf/1511.06390.pdf

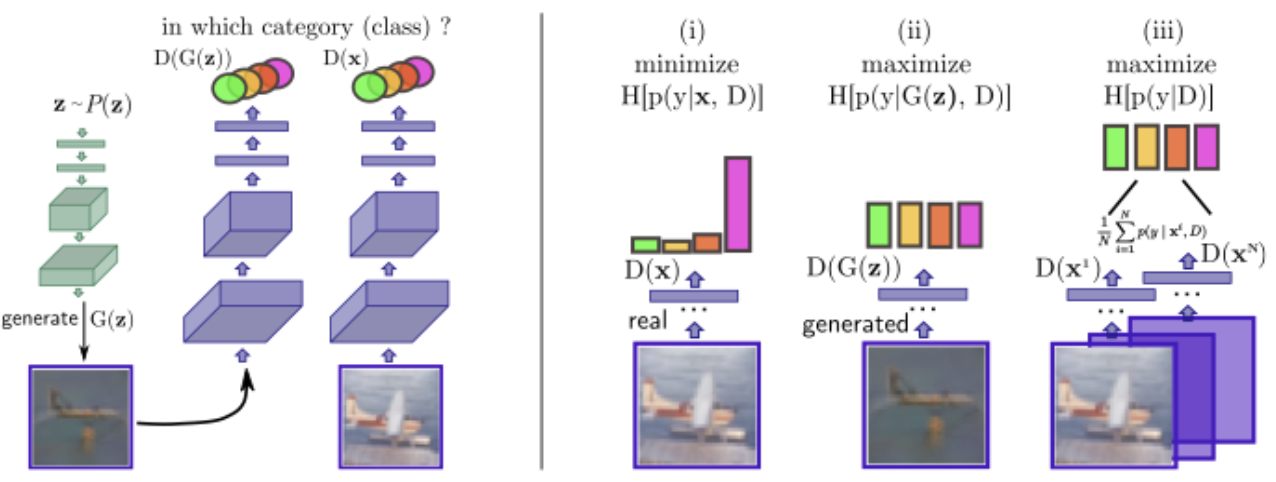
主要贡献：

修改原始GAN的目标函数为

1）对于有标签样本，训练判别器时直接交叉熵

2）对于无标签样本和生成样本，训练判别器时最小化无标签样本的条件熵，最大化生成样本的条件熵，其中还要保证判别器对生成样本所在的整个数据分布的预测在各个类别之间是均匀的，这个可以用边缘熵来计算，由于我们认为生成的分布和当前真实数据的分布是一致的，因此可以直接用真实数据集的边缘熵最大来实现（之所以用边缘熵是希望标签y是均匀采样的）。

3）对于无标签样本和生成样本，训练生成器时对于无标签样本需要最小化生成样本的条件熵。同样也需要边缘熵最大化。

生成器角度的需求：

i）确定样本的类别分配，（ii）不确定生成的样本的分配，以及（iii）平等地使用所有类别(平均分布)。

判别器角度的需求：

i）生成具有高度确定类别分配的样本，（ii）在所有K类中平均分配样本。

CCGAN

paper：https://arxiv.org/abs/1611.06430v1

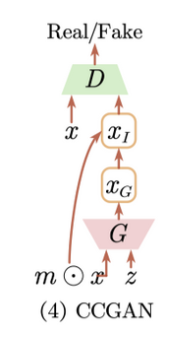
主要贡献：

1）主要认为给图像提供边界之后让生成器生成中间部分会使得判别器真正理解生成图像的语义，从而可以利用来做半监督。（可能人脸比较适合？）

2）判别器和分类器并不共用，倒数第二层共用，最后一层单独header连接任务。

Improved GAN

arxiv：https://arxiv.org/abs/1606.03498

1. 把判别器改为K+1分类，前K类区分id的类别，最后一类分真假样本。
2. feature matching

BadGAN

生成低密度区域的数据。惩罚高密度点。写过博客了BadGAN。

Localized GAN

Global versus Localized Generative Adversarial Nets ！important

arxiv：https://arxiv.org/pdf/1711.06020

这篇文章主要观点是，传统的GAN的latent space z是从一个坐标系采样并控制图像的生成的，这导致了想要通过图像反向得到latent space的坐标z并不容易，虽然也是可以得到的，但是其实并没有办法保证每张图片在latent space里都存在一个坐标z。

文章觉得每个样本应该都有一个局部的坐标系，并且以样本自身为原点，在latent space中对应的局部坐标系的坐标应该为0，这样就保证了任意样本在latent space中都有坐标对应（以自身为原点的相对坐标系）。

两个正则化要求：

1. locality： \(G(x, 0) = x\)， 局部坐标系原点必须是该样本本身
2. orthonormality： \(J^Tx Jx = I_N\)，N维坐标对应的切空间向量之间必须正交

为啥切向量必须正交？

因为如果不正交，那么就意味着该坐标系可以被更低维表示，这样会存在局部改变切空间坐标值而结果不变的模式崩塌。

用在半监督里：

判别器损失

\[\begin{aligned}&\max _{P} \mathbb{E}_{\left(\mathbf{x}_{l}, y_{l}\right) \sim P_{\mathcal{L}}} \log P\left(y_{l} \mid \mathbf{x}_{l}\right)+\mathbb{E}_{\mathbf{x}_{u} \sim P_{\mathcal{X}}} \log P\left(y_{u} \leq K \mid \mathbf{x}_{u}\right) \\& +\mathbb{E}_{\mathbf{x} \sim P_{\mathcal{X}}, \mathbf{z} \sim P_{\mathcal{Z}}} \log P(y=K+1 \mid G(\mathbf{x}, \mathbf{z})) \\& -\sum_{k=1}^{K} \mathbb{E}_{\mathbf{x} \sim P_{\mathcal{X}}}\left\|\nabla_{\mathbf{x}}^{G} \log P(y=k \mid \mathbf{x})\right\|^{2}\end{aligned} \]

注意

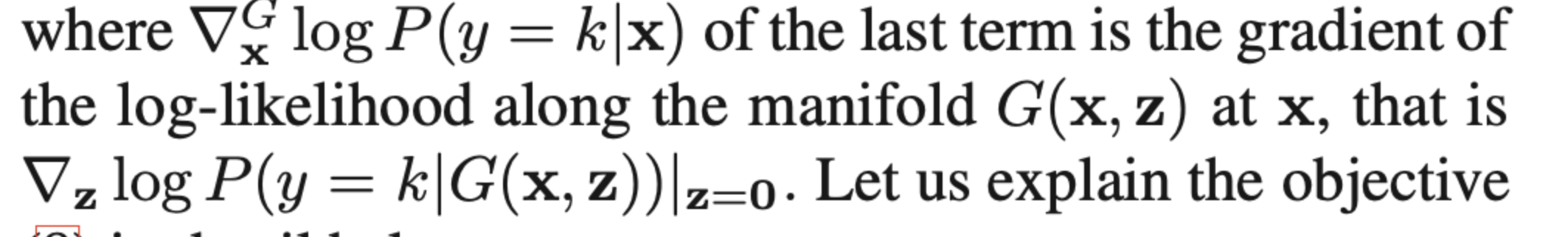
最后一项满足locality正则化要求。惩罚z的改变对结果的影响，也即局部perturb不改变模型输出，一致性正则。

生成器损失

\[\min _{G} \mathcal{K}_{G}+\mathcal{L}_{G}+\mathbb{E}_{\mathbf{x} \sim P_{\mathcal{X}}} \Omega_{G}(\mathbf{x}) \]

\[\mathcal{K}_{G}=-\mathbb{E}_{\left(\mathbf{x}_{l}, y_{l}\right) \sim P_{\mathcal{L}}, \mathbf{z} \sim P_{\mathcal{Z}}} \log P\left(y_{l} \mid G\left(\mathbf{x}_{l}, \mathbf{z}\right)\right) \]

对有标签样本，生成器生成的样本要保证类别不变，没有标签的样本和原始样本之间做feature matching loss， 最后一项是上面提到的两个正则项。

文章这样用生成的样本，生成器能够保证生成的样本满足两个正则项、而且用了feature matching。

他的目标其实和badgan不太一样，他要的是生成流形附近的样本，并且在判别器里相当于对生成的样本和原始样本做一致性正则，惩罚的是z变化最大的样本，让结果更bound。

感觉这个其实是一篇很启发性的文章，但从他生成图像的效果来看其实并不好，说不定可以在这个文章基础上继续做一些工作会很有帮助。

文章表示通过直接对生成图片的每个类别进行梯度惩罚，可以得到一个相对鲁棒的分类器：

\[|D(G(x, z+\sigma z))-D(G(x, z))|^{2} \approx\left\|\nabla_{x}^{G} D(x)\right\|^{2} \sigma z \]

具体的可以实现为：

\[\sum_{k=1}^{K} \mathbb{E}_{x \sim p_{x}}\left\|\nabla_{x}^{G} \log p(y=k \mid x)\right\|^{2} \]

CTGAN

arxiv：https://arxiv.org/pdf/1803.01541.pdf

1. 判别器K+1分类
2. 判别器损失添加一致性正则，一致性方式为：(1)给输入加随机噪声 (2) 给hidden layer 加随机噪声
3. 在WGAN的基础上进行的工作，WGAN本身是要达到L1连续性，L1连续

论文结果：

Mnist Test Error：0.89 ± 0.13 4,000 labels

CIFAR-10： 9.98 ± 0.21 4,000 labeles

Bidirectional Generative Adversarial Networks

arxiv：https://arxiv.org/pdf/1605.09782v7.pdf

ADVERSARIAL FEATURE LEARNING

是一篇偏理论的文章。

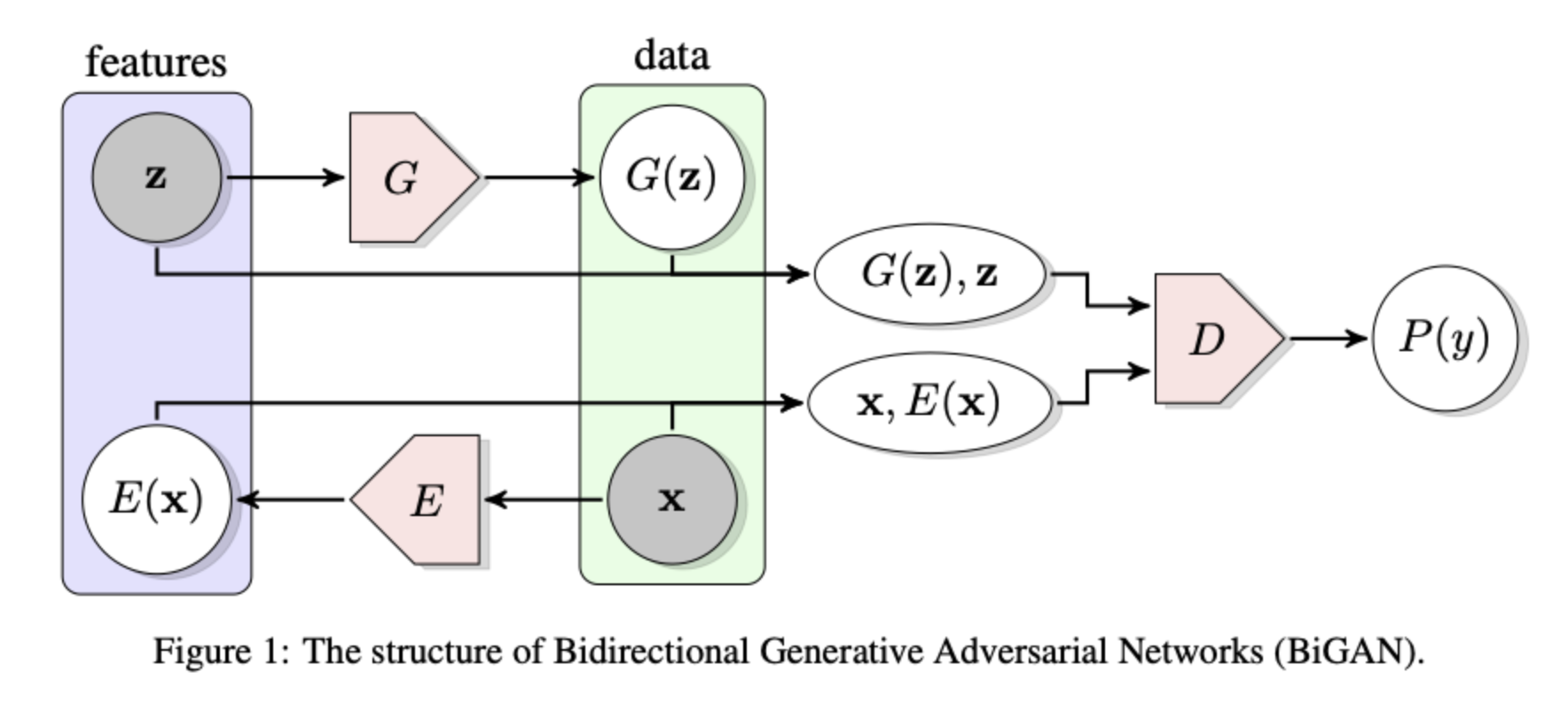
主要贡献：

1. 感觉主要贡献是提出了如图所示的训练结构，引入一个新的encoder E，将原图映射回latent space，判别器判断(x, E(x))元组和(G(z),z)组。
2. 剩下的很多理论证明，主要结论是这样训练的GAN会使得E和G成为互逆变换。

从直觉上来理解一下而非公式，为什么E能够学习到与G相反的变换呢？

假设生成器G生成的分布就是真实分布x，那么如果E(x)和z不是对应的分布，此时判别器D可以根据此以及配对情况分辨开他俩，而生成器我们认为是固定的，此时只有通过优化E使得E(x)和z对应才能再次欺骗判别器，因此最终E可以学习到与G相逆的变换。

主要评估的是无监督性能。

Adversarially Learned Inference

arxiv：https://arxiv.org/pdf/1606.00704.pdf

把BiGAN（上面这篇文章）改成了K+1-class。

Augmented BiGAN

Semi-supervised Learning with GANs: Manifold Invariance with Improved Inference

arxiv: https://arxiv.org/pdf/1705.08850.pdf

看起来是一篇比较偏理论的文章，4月8日研究一下

简单思想

1. 相对BiGAN加了FM损失
2. 添加loss term防止生成的样本类别改变

\[\mathbb{E}_{x \sim p(x)}\left[\log \left(1-D\left(E(x), G_{x}(E(x))\right)\right)\right] \]

TripleGAN

Triple Generative Adversarial Networks

arxiv: https://arxiv.org/pdf/1912.09784.pdf

3-player-game:

三个player分别是

1. classifier C 负责给定真实样本x，得到\(p_C(y|x)\)
2. generator G condition on 标签y，得到\(p_G(x|y)\)
3. discriminator D 负责区分样本对\((x, y)\)，这样的样本对其实是\(p(x,y)\)联合概率，对于真实样本，\(p(x,y) = p(y|x)p(x)\)，而对于生成对样本，则\(p(x,y) = p(x|y)p(y)\)

本文的基本假设是\(p(x)和p(y)\)均可以很容易获得，x的分布可以由训练集采样得到，y的分布假设是均匀分布可以采样得到。

这样的一个基本过程对应的损失为：

\[\begin{gathered}\min _{C, G} \max _{D} \mathbb{E}_{p(x, y)}[\log D(x, y)]+\alpha \mathbb{E}_{p_{c}(x, y)}[\log (1-D(x, y))] \\+(1-\alpha) \mathbb{E}_{p_{g}(x, y)}[\log (1-D(G(y, z), y))]\end{gathered} \]

第一项对应真实样本真实标签，第二项对应真实样本伪标签，第三项对应真实标签生成的样本。

因此很好理解，C是为了给真实样本产生伪标签，G是为了给真实存在的标签产生对应的样本。

然而有个问题，就是\(p(x)p_C(y|x)\)和\(p(x,y)\)、\(p_G(x|y)p(y)\)不能保证三者是相等的，问题就是公式(11)并没有确保这三者相等的约束，而我们的假设又是基于这三者相等，为了满足这一条件，文章加了两个KL散度的正则使得训练结果是三者相等的。

最终的损失对应为：

\[\begin{gathered}\min _{C, G} \max _{D} \mathbb{E}_{p(x, y)}[\log D(x, y)]+\alpha \mathbb{E}_{p_{c}(x, y)}[\log (1-D(x, y))] \\+(1-\alpha) \mathbb{E}_{p_{g}(x, y)}[\log (1-D(G(y, z), y))]+\mathcal{R}_{\mathcal{C}}+\alpha_{\mathcal{P}} \mathcal{R}_{\mathcal{P}},\end{gathered} \]

理论上讲应该是加三个KL散度的正则项，但是\(p(x,y)\)和\(p_G(x|y)p(y)\)之间的KL散度起不到优化作用，前者的概率可以认为是均匀分布的概率（整个数据集认为是均匀分布，样本之间相互独立，因此sample一个小batch内的样本也是均匀分布的），后者是一均匀分布和。这样需要计算KL散度的是\(KL(p(x,y)||p_C(y|x)p(x))\)，由于\(p(x)\)在batch内是均匀采样的，分类器得到的直接是条件概率，所以可计算。还有就是要求\(p_C(y|x)p(x)\)和\(p_G(x|y)p(y)\)的KL散度，文章在appendix中推导出了这个式子和优化下式等价：

\[\mathcal{R}_{\mathcal{P}}=\mathbb{E}_{p_{g}(x, y)}\left[-\log p_{c}(y \mid x)\right] \]

这里是将生成器生成的样本和标签对通过分类器正确分类，希望分类器也能正常分类生成的样本和对应的标签。

Enhanced TGAN

Enhancing TripleGAN for Semi-Supervised Conditional Instance Synthesis and Classification

CVPR：https://openaccess.thecvf.com/content_CVPR_2019/papers/Wu_Enhancing_TripleGAN_for_Semi-Supervised_Conditional_Instance_Synthesis_and_Classification_CVPR_2019_paper.pdf

Margin GAN

MarginGAN: Adversarial Training in Semi-Supervised Learning

NIPS：https://papers.nips.cc/paper/2019/file/517f24c02e620d5a4dac1db388664a63-Paper.pdf

在半监督领域，一般是用伪标签手段来实现margin最大化，对于无标签样本，我们根据其输出给其分配一伪标签，计算伪标签和输出值的交叉熵损失来优化结果，使得网络对自己的输出更加确定，从而实现最大化margin的效果。

本文提出的Margin GAN受到最大化分类间隔和Bad GAN的影响，主要方法为：

1. 对于判别器，需要其区分真实样本和生成的样本，损失为

\[\operatorname{Loss}(D)=-\left\{E_{x \sim p^{[l]}(x)}[\log (D(x))]+E_{\widetilde{x} \sim p^{[u]}(\widetilde{x})}[\log (D(\widetilde{x}))]+E_{z \sim p(z)}[\log (1-D(G(z)))]\right\} \]

2. 对于分类器，有标签样本即正常分类，无标签样本伪标签分类（最大化margin），对生成的样本用ICE损失（ICE损失具体过程为为生成样本分配伪标签，增大伪标签的交叉熵损失而非减小）。ICE损失会让margin减小，也就是让结果趋于不确定化（最优解为均匀分布），而margin减小会使得分类面穿过生成的样本，而生成的样本是低密度的“Bad”样本，从而可以保证分类面不穿过流形而经过低密度区域。

3. 对于生成器，需要同时欺骗判别器和分类器，对于欺骗判别器很简单，而需要欺骗分类器是由于分类器会减小生成样本的margin，所以生成器需要生成使得margin尽可能大的样本，因此损失为：

\[\operatorname{Loss}(G)=-E_{z \sim p(z)}[\log (D(G(z)))]+E_{z \sim p(z)}\left[\operatorname{Loss}_{C E}\left(\widetilde{y}^{[g]}, C(G(z))\right)\right] \]

最后生成结果图像是和badgan类似的效果，也就是说这么的损失最后能得到低密度的bad样本，分类器将其margin减小确实符合预期，但是为什么这样的3-player game可以保证生成低密度样本呢？

文章没有给出数学证明，但可以简单分析一下。

生成器最后生成的样本对应判别器肯定是没法分辨的，那就可以认为可以生成id的样本，而对应分类器得到的是margin为0的样本，而margin为0则表示该类样本就在分类面上，因此可以认为，最终生成的样本应该是类别之间的分类面上的样本。无标签数据的利用使得分类面很难落穿过真实流形，而我认为生成网络的作用是鼓励分类面往远离流形的方向走，如果生成的样本过真，则需要margin既大又小，可能并没有优化效果，如果生成的样本欠真，则分类面肯定会往欠真的样本方向移动，此时鼓励的分类面的移动，从而具有优化效果。

从结果上看远超badgan，一方面可能badgan那种用pixelcnn来估算样本密度的方式并不可靠，而通过margin惩罚的方式相对更能达到这种效果，另一方面也确实说明了低密度样本对半监督的有效作用。

Triangle GAN

Triangle Generative Adversarial Networks

arxiv：https://arxiv.org/pdf/1709.06548.pdf

Structured GAN

arxiv：https://arxiv.org/pdf/1711.00889.pdf

Mean Teacher = EMA 的 proposal model

perturb的large margin有很大的关系，会促进学习large margin，取决于perturb的步长

Ladder Network

arxiv：https://arxiv.org/pdf/1507.02672.pdf

将加噪声、去噪声的任务用于半监督学习，其中不仅最后输出层加噪声去噪声，中间层也需要完成加噪声去噪声的任务。

本身加噪声去噪声的任务是为了让网络学习到内在不变信息，并不一定是分类信息，自编码器希望保留大多数信息以便重构，而分类器希望只学习到与任务相关的、具有不变性的信息，那么其他的信息，对于分类器就相当于某种噪声，换句话说，分类器学习的过程，也可以解释为是一种降噪的过程。

降噪自编码器，在编码时进行去噪，在解码时进行重构。因此降噪自编码器的编码过程，很好地符合了分类器希望去噪（去掉与任务无关的信息）的目的。因为降噪自编码器的训练学习，强化了分类器的降噪能力，而且因为是无监督降噪，这种降噪是一种通用降噪，可以提升分类器的泛化能力。