[论文理解] Improving the imporved training of Wasserstesin GANS: A consistency term and its dual effect

IMPROVING THE IMPROVED TRAINING OF WASSERSTEIN GANS: A CONSISTENCY TERM AND ITS DUAL EFFECT

Intro

本文是对wgan的扩展，通过添加对真实样本周围的gp，使得网络处处gp不仅在真实样本和生成的样本之间能够work，也能在真实样本周围work，从而使得discriminator更加满足Lipschitz连续。在结果上比较意外的是，不仅能够生成相对比较真实的样本，半监督的效果也非常好，在cifar10上，4000个有标签样本的基础上可以达到90+的top 1 acc(这些天做了很多实验，我们的方法也才70+ ～ 80+)，还不能达到这个效果，所以感觉还是挺惊叹的。这个结果和badgan其实差不多了，都是80+。

Pros and Cons

对于WGAN，有一个基本的要求是discriminator要满足1-Lipschitz连续，为了满足这一条件，最初的做法是梯度裁剪，但是梯度裁剪却使得网络的拟合能力受限了，有时候也会出现梯度消失的问题。为了解决这一问题，WGAN在接下来的文章中以梯度惩罚项的损失来代替梯度裁剪，具体形式为：

\[GP|_{\hat{x}} = \mathbb{E}_{\hat{x}}[(||\nabla_{\hat{x}}D(\hat{x})||_2 -1)^2] \]

这里\(\hat{x}\)从真实分布和生成的图像分布中sample的样本，因此直接的方式就是对真实样本和生成的样本做线性加权求和。

但是这样做却只保证了判别器在真实样本和生成样本之间连续，没有保证在真实分布上连续。在训练的初始阶段，真实分布和生成分布离得比较远，这时gp其实并没有起左右，而真正gp起作用的时候是训练中后期，当真实分布和生成分布比较接近的时候，因此这也是gp的一个问题。

Approach

对于Lipschitz连续，我们有

\[d(D(x_1), D(x_2)) \leq M \cdot d(x_1, x_2) \]

即存在一个\(M\)，对任意\(x\)上式均成立。

为了让discriminator在真实样本附近也是Lipschitz连续的，添加如下损失

\[CT|_{x_1, x_2} = \mathbb{E}_{x_1, x_2} [max(0, \frac{d(D(x_1), D(x_2))}{d(x_1, x_2)}) - M'] \]

文章也是尝试了各种perturb的方法，起初是对真实样本\(x\)随机加noise，发现会让生成的图像比较模糊，然后也尝试了不同的方法，最终确定为，对同一输入\(x\)，对discriminator的中间隐藏层随机dropout，认为dropout后的样本为perturb后的样本，计算两perturb后样本的距离。标记perturb后的样本经过discriminator的结果分别为\(D(x')\)和\(D(x'')\)

文章假设\(d(x_1, x_2)\)是有界的，根据上面第一条公式，显然可以将超参(常数项)\(M\)和\(d\)合并，因此最终的惩罚项变为了：

\[CT|_{x', x''} = \mathbb{E}_{x \backsim \mathbb{P}_r} [\max(0, d(D(x'), D(x'')) + 0.1 \cdot d(D\_{(x')}, D_\_{(x'')}) - M')] \]

其中\(D_\_\)是从第二层到最后一层均使用dropout的，\(D\)仅仅对中间某一层使用dropout。作者也是实验发现加上这一项效果比较不错。

Experiments

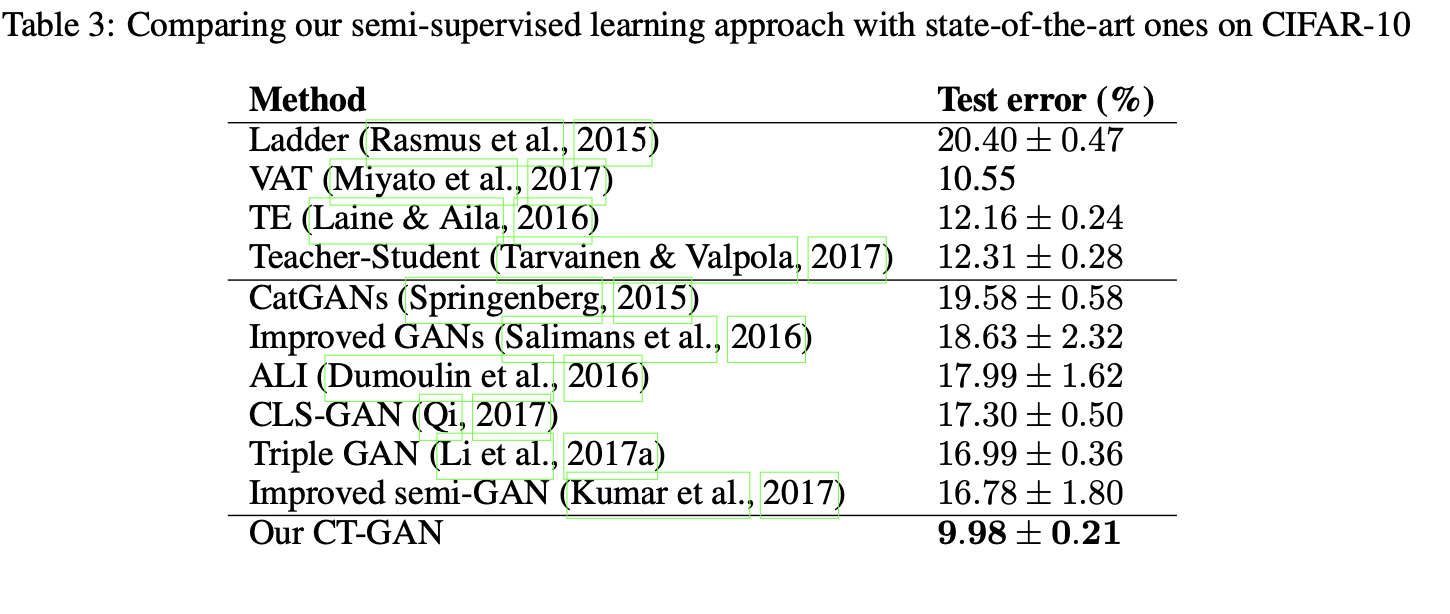
在Mnist和CIFAR10上均很不错(虽然现在大家都在IMAGENET上比了)。