[论文理解] Good Semi-supervised Learning That Requires a Bad GAN

Good Semi-supervised Learning That Requires a Bad GAN

恢复博客更新，最近没那么忙了，记录一下学习。

Intro

本文是一篇稍微偏理论的半监督学习的文章，通过证明一个能够生成非目标分布的、低样本密度的样本的生成器，对半监督学习的效果有很大的提升，这样的生成器作者称之为Complement Generator，而提升的原因是生成的bad样本填充了特征空间的低密度区域，从而使得分类的分类面在低密度区域，从而避免了分类面穿过流形的情况，因而能够提升分类的精度。为了得到这样的生成器，首先利用最大熵使得生成器的熵最大，一方面最大熵可以防止mode collapse，第二方面可以增加生成样本的丰富度，从而保证生成器能够生成低密度区域的样本；然后，利用pixel cnn来估计生成样本的概率密度，惩罚过于接近流形的生成器生成的样本。

参考了官方的代码，复现了一下本文的算法。

Theoretical Analysis

GAN-Based Semi-Supervised Learning

GAN-Based半监督学习一般采用K+1分类的方式来训练，与传统的两分类的GAN不同的是，用于半监督学习的GAN前K个类别负责预测具体类别，最后一个（K+1）负责预测true or fake。

因此，对于有标签的样本，我们大可将其分为前K类中的一类，对于无标签的样本，我们认为它们是真实样本，因此可以将前K个类别的和和第K+1类看成是二分类问题，对于生成的fake样本同理。

因此，GAN-Based半监督学习的Loss一般为：

\[\max_D \mathbb{E}_{x,y \backsim \ell} \log P_D(y|x,y\le K) + \mathbb{E}_{x \backsim p} \log P_D(y\leq K|x) + \mathbb{E}_{x \backsim p_G} \log P_D(K+1|x) \]

其中\(\ell\) 代表有标签的数据，\(p\)代表无标签的数据，\(p_G\)代表生成器生成的数据。

而“Improved techniques for training gans”中则提到，可以将第K+1类的权重设为0，这样可以减少全连接的参数，事实上，这样会让第K+1类的概率的分子项变为常值1，仍然满足K+1个类别的和为1.所以与原来K+1分类是等价的。

这里我记得代码里还有个trick是，计算log softmax可以减去一个值防止上溢，即：

\[Softmax(x_i) = \frac{exp(x_i)}{\sum exp(x_j)} \\ LogSoftmax(x_i) = Log \frac{exp(x_i - c + c)}{\sum exp(x_j - c + c)} \\ = Log \frac{exp(x_i - c)}{\sum exp(x_j - c)} \cdot \frac{exp(c)}{exp(c)} \\ = Log \frac{exp(x_i - c)}{\sum exp(x_j - c)} \\ = (x_i - c) - Log \sum exp(x_j - c) \]

Perfect Generator

一个完美的生成器，当然是生成图像的概率分布\(p_G\)和真实图像的概率分布\(p\)完全一致，即\(p_G = p\)，此时作者给出了命题1:

Proposition 1

如果一个生成器是Perfect Generator，并且D有infinite capacity，那么对其实下式Loss的任意一个最优解D，都可以找到上面的Loss的最优解\(D^*\)，使得\(P_D(y|x,y \le K) = P_{D^*}(y|x,y \leq K)\)。而下式的Loss则完全只包含分类的Loss，因此当生成器很完美的时候，很容易退化为下面的Loss，则相当于只做了有监督部分，而无标签的数据并没有得到充分利用。

\[\max_D \mathbb{E}_{x,y \backsim \ell} \log P_D(y|x, y \le K) \]

命题1的证明也很简单：

可以看出来，我们要让\(J_D\)取得最大值，所以要同时使得\(L_D\)和后面那一项最大，而后面那一项取得最大值的结果就是\(P_D(K+1|x) = \frac{1}{2}\)，然后根据(6)，是可以找到这样一组解的。因此证明了可以得到一组解，可以使得只用有监督部分的Loss和两者都用的Loss一样，从而证明了其实存在局部解可以使半监督部分失去意义。

Complement Generator

假定映射\(f\)可以将输入空间映射到特征空间，令\(p_k(f)\)表示第k类样本在特征空间的概率密度，给定一个阈值\(\epsilon_k\),令\(F_k = {f:p_k(f) > \epsilon_k}\)，并且假定给定\(\{\epsilon_k\}_{k=1}^{K}\)，\(F_k\)之间都有一个margin，这就可以理解为，可以找到一组\(\epsilon\)使得任意两个分类面的流形完全分开，分开的距离是一个margin，当然，最好的情况就是\(\epsilon\)足够小，这样才能保证泛化性能。那么Complement Generator做的就是生成这些流形之外的样本，也就是流形与流形之间的样本。

以一维为例，则就是下图所示的样子了：

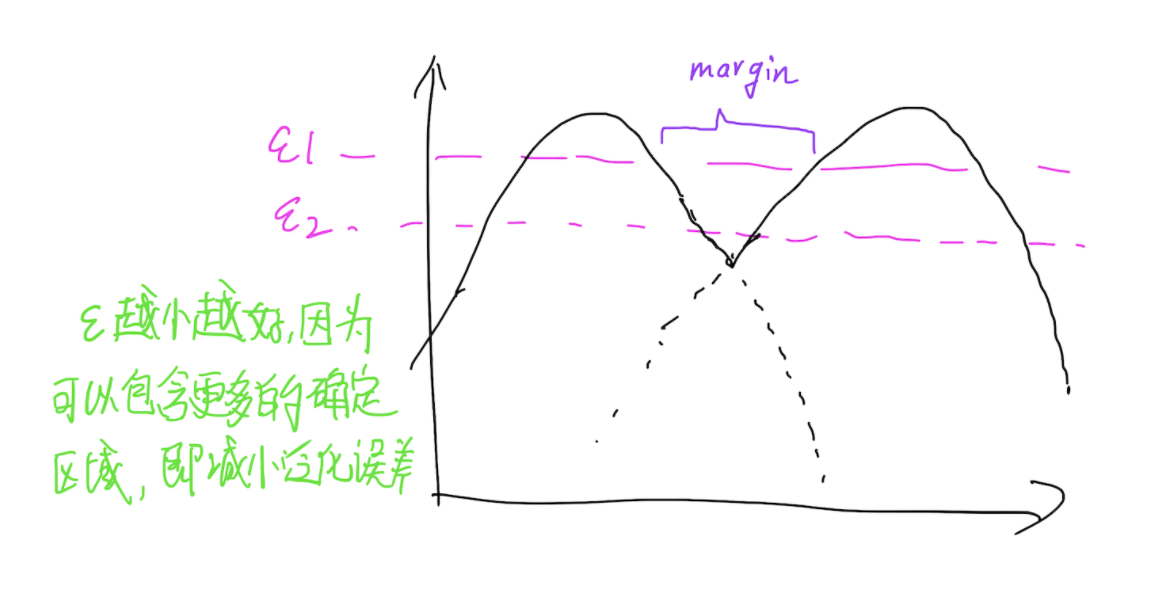
Assumption 1. Convergence conditions.

当\(D\)收敛之后，认为\(D\)能够学习到一个很好的分类面使得所有的训练的不同类别样本都可以分开，也就是说，必须满足以下三个条件：

1. 对于任意的\((x,y) \in \ell\)均有\(w^T_yf(x) > w_k^Tf(x)\)成立，k表示其他类别(\(k \neq y\))
2. 对于任意的\(x \in \mathcal{G}\)，均有\(\max_{k=1}^Kw_k^Tf(x)<0\)成立
3. 对于任意的\(x\in \mathcal{U}\)，均有\(\max_{k=1}^Kw_k^Tf(x) > 0\)成立

由此，提出引理1

Lemma 1

假设对于所有的k，都有\(||w_k||_2 \leq C\)，假设存在一\(\epsilon >0\)，使得对于任意的\(f_G \in F_G\),存在一\(f'_G \in \mathcal{G}\)使得\(||f_G - f_G'||_2 \leq \epsilon\)， 根据假设1，则有对任意\(k \leq K\)，都有\(w_k^Tf_G < C\epsilon\)。

证明比较简单：

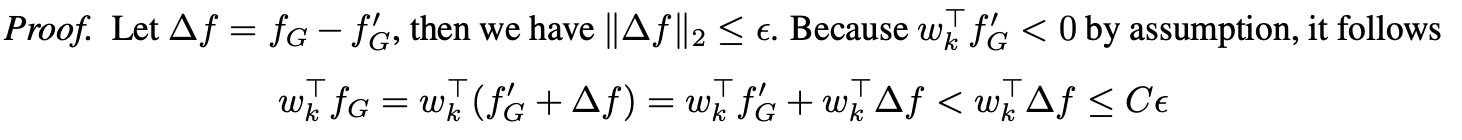
因此可以得到下面的推论

Corollary 1

如果能够生成无穷的样本，则有\(\lim_{|\mathcal{G}| \to \infty}w_k^Tf_G \leq 0\)

Proposition 2

在引理1的条件下，对于任意类别\(k \leq K\)，对于任意特征空间中的点\(f_k \in F_k\)，都有\(w_k^T f_k > w_j^Tf_k\)成立，其中\(j \neq k\)

可以用反证法来证明，如果假设\(w_k^T f_k \leq w_j^Tf_j\)，那么一定存在一个\(\alpha\)，得到一个特征空间中的点\(f_G = \alpha w^T_kf_k + (1 - \alpha)w^T_j f_j\)在流形之外，则有\(w_j^Tf_G \leq 0\)，而\(w_k^Tf_k >0\)并且\(w_j^Tf_j>0\)矛盾了。

事实上，如果生成的样本把流形之外的空间填充的足够好，这样相当于强行让分类面落在流形的边界处，从而避免了分类面穿过流形的情况。

Case Study on Synthetic Data

上面都是偏理论的分析，然后作者以简单的demo来浅显的说明上述观点的可行性。

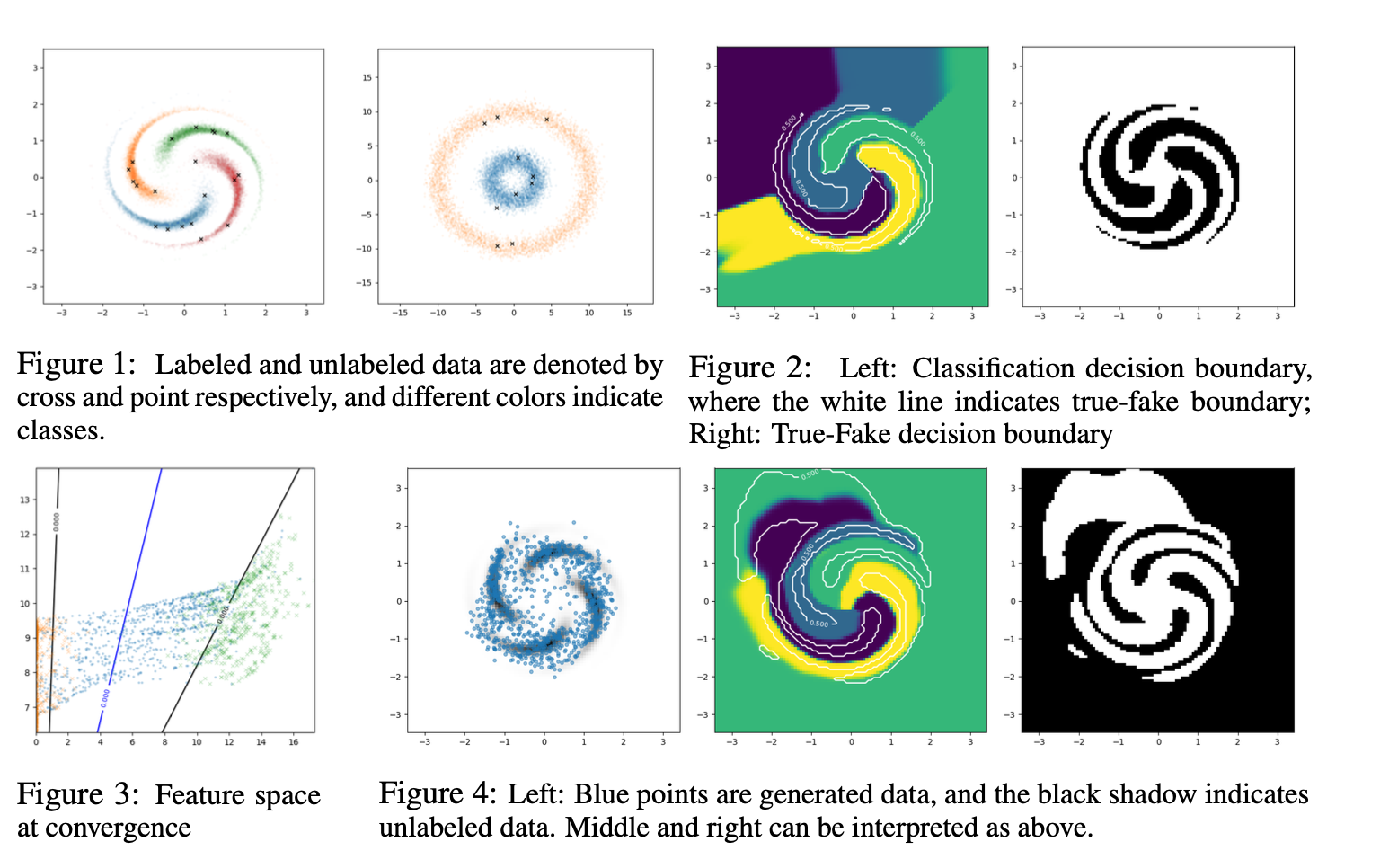
以如图所示的2D demo为例，fig 1中每种颜色代表一种流形，点代表有标签的数据。

fig 2 是 Complement Generator生成的样本点去分类之后的分类面，可以看出无论是真假样本分类还是具体类别的分类，分类面都比较完美。

fig 3是特征空间的demo 可视化，是以fig 1中第二个图为例展示的，可以看出生成的样本基本都在流形之间，并且可以找到最佳的分类面，也就是蓝色的线，将流形分开。

fig 4 是直接使用feature matching方式生成样本的结果，可以看到大多数样本其实都生成在来流形内部，右边的分类面也不完美，因此传统的feature matching方法是存在很大的问题的。

Approach

为了得到这样的生成器，本文依据feature matching GAN的不足，提出以下几点改进：

1. 使用最大熵防止collapse，并且生成流形之外的样本
2. 估计生成样本的概率并将生成的太接近流形的样本去掉

对于最大熵，本文提出两种方式实现，

第一种是通过变分推断的方式，由于生成器的熵的负值具有变分上界，即\(-\mathcal{H}(p_G(x)) \leq - \mathbb{E}_{x,z \backsim p_G}log q(z|x)\),通过限定高斯分布的方差范围从而避免任意大方差分布，这样就可以利用高斯分布的熵来达到最大化生成器熵的目的。

这样做的原因是，由于生成器的熵很难求,生成器只能得到分布中采样得到的样本，无法得到概率分布，因此通过变分推断来求解，引入变量z，\(p_G(z) = p_z(z)\)，根据定义有\(\mathcal{H}(p_G(x)) = \mathcal{H}(p_G(z)) + \mathcal{H}(p_G(x|z))-\mathcal{H}(p_G(z|x))\)，然后由于我们假定了z是服从高斯分布的，所以等式右边第一项是不需要考虑，同时还有一个假设是\(p_G(x|z)\)也是服从高斯分布的，一般GAN的任务我们都认为\(p_G(x|z)\)是服从单点分布，当然也可以理解为方差极小的高斯分布，所以这一项的熵理论上也是一定值。因此只需要考虑右边最后一项，所以很容易得到\(\mathcal{H}(p_G(x)) \geq -\mathcal{H}(p_G(z|x))\)，从而很容易推出上式了。
于是又有一个假设，就是认为q也是服从高斯分布的，只不过均值和方差不是确定的，而是网络学习得到的。这样，z的分布是有公式可以得到的，q的分布也是有公式可以得到的，就可以带入高斯分布的公式条件熵了。

第二种是通过使用pull-away term的辅助loss来实现，尽量让生成的样本之间的距离增大，从而增大生成器的熵。

为了保证生成样本都在低密度区域，必须把生成样本接近流形的点去掉。而去掉不会帮助生成器来优化生成的样本，因此可以加惩罚项惩罚接近流形的样本，继而优化生成器。

\[\mathbb{E}_{x\backsim p_G logp(x)\mathbb{I}[p(x) > \epsilon]} \]

此外，文章对无标签的数据加了个条件熵最小化的Loss，因为这类样本没有标签，可能学习到一个对所有标签均匀分布的结果，因此最小化标签的熵，可以让网络D尽量将概率分布变为一个确定的分布，最确定的情况也就是熵最小的情况，就是某一类的概率为1，其他皆为0.

复现和实验

参考官方的代码，复现了一下MNIST上的结果，没有加PT和PixelCNN，但是结果已经相当不错了，仅仅几个epoch，在每类只给5个样本下的MNIST上就能达到95%的TOP1 ACC。