[学习笔记] RBF神经网络初探

RBF神经网络初探

径向基函数

径向基函数是一种函数的取值仅仅与输入的中心点有关的函数，具有这种性质的函数就称为径向基函数。

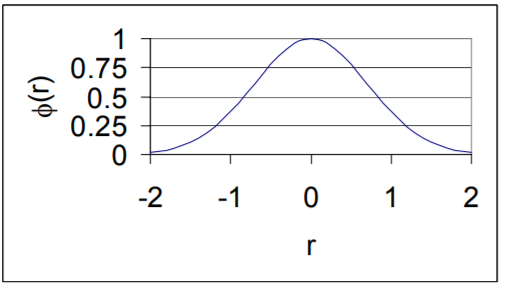
比如，高斯函数是一种径向基函数，其输出值的大小与距离中心点的距离有关，距离中心点越远，函数值越小，距离中心点越近，函数值越大。

RBF神经网络的结构

RBF神经网络一般具有两层结构，是一种前向神经网络。第一层的作用是将输入由非线性可分转变为线性可分，第二层一般是感知机类型的神经元层或ADALINE类型的神经元层。

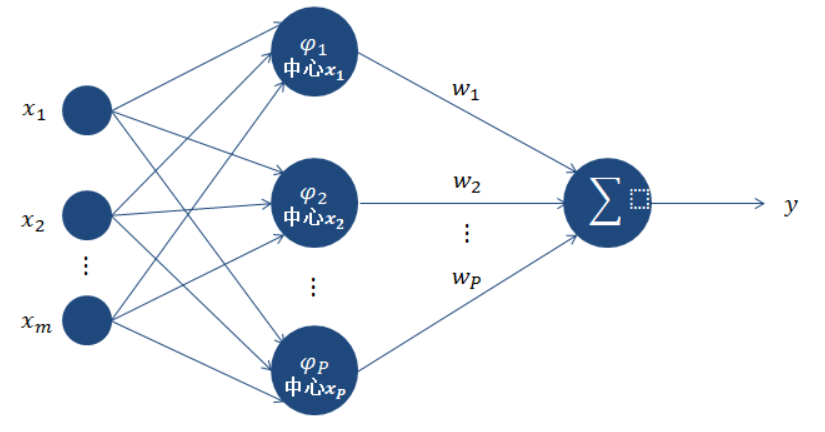
第一层计算

计算过程

对于只有一个两维的输入(p1, p2)而言，假定函数的中心点C1和C2已知(同样假设只有两个中心)，利用高斯函数作为径向基函数，如果高斯函数的标准差σ1和σ2已知，那么第一层的输出即为：

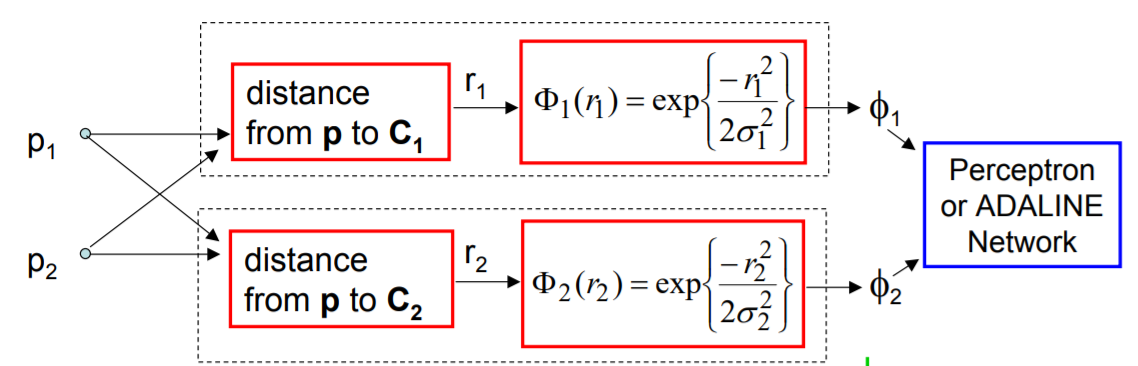
计算过程为：

1. 计算由样本(p1,p2)组成的点到中心C1的距离r1，通过高斯径向基函数投影为Φ1
2. 同理计算到到C2的距离投影到Φ2.

中心C和标准差σ的确定

上述过程假定中心C和标准差σ是已知的，实际上很多任务中是需要学习这两个量的，对于中心C，我们一般采用kmeans聚类算法来确定，因此聚类的中心点数量k也是一个超参。而σ的确定也非常简单，即以到聚类中心点的距离(平方根距离)最近的前k个样本的聚类的均值为σ，之后每个σ就都确定了。

还有一种方法来确定C和σ，就是认为C和σ是可学习的参数，利用梯度下降来更新学习C和σ。后面的代码例子中将利用梯度来学习C和σ。

第二层计算

感知机和ADALINE

对于第一层输出p(假设为5维向量)，其输出为线性映射：

\[a = hardlim(Wp + b) \]

其中W为1x5矩阵，b为1x1常量，harddim为sgn函数：

\[\begin{equation} sgn(x) = \begin{cases} 1,& x>0 \\ 0,& x=0\\ -1,& x<0 \end{cases} \end{equation} \]

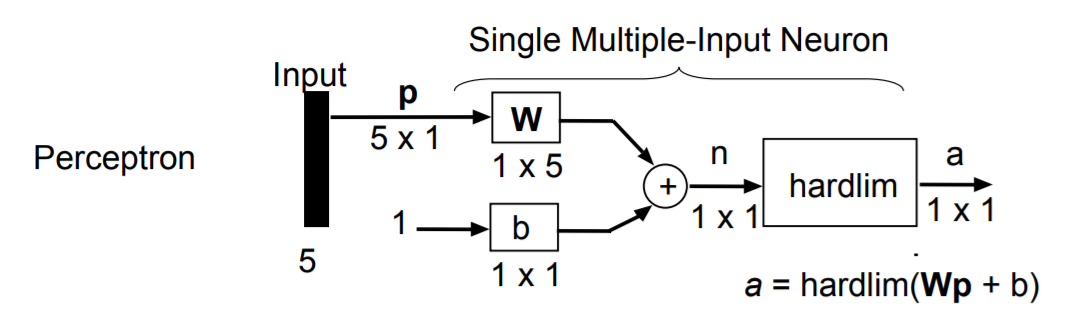
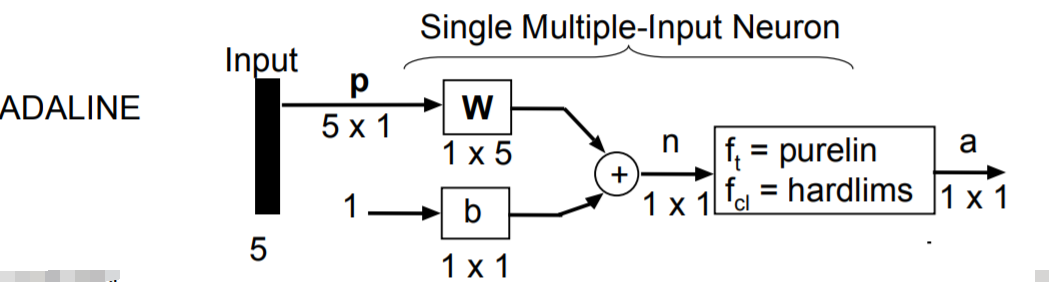
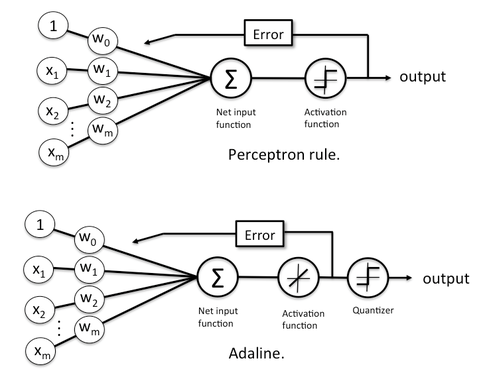
其中感知机和ADALINE其实有一些不同点，虽然前向过程的purelin恒等函数看起来没啥用(只是形式上要走个激活函数)，但两者在更新参数时使用的标签是不同的，感知机是用离散的标签作为gt来更新前面的参数，而ADALINE则是直接根据加权求和的结果，也就是连续值来更新前面的参数，具体可以见下图：

Coding

本文仅以高斯径向基函数，第二层为感知机模型，利用梯度下降算法更新参数为例来写一个RBF神经网络的Demo。（求梯度的公式感觉自己推就太麻烦了，有自动求导为啥不用.）

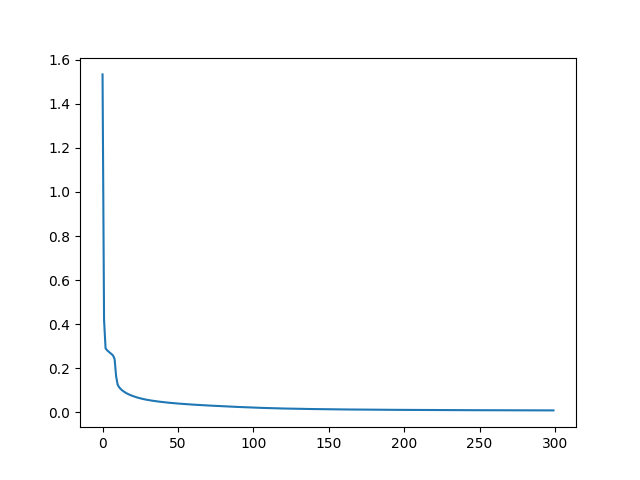
Loss:

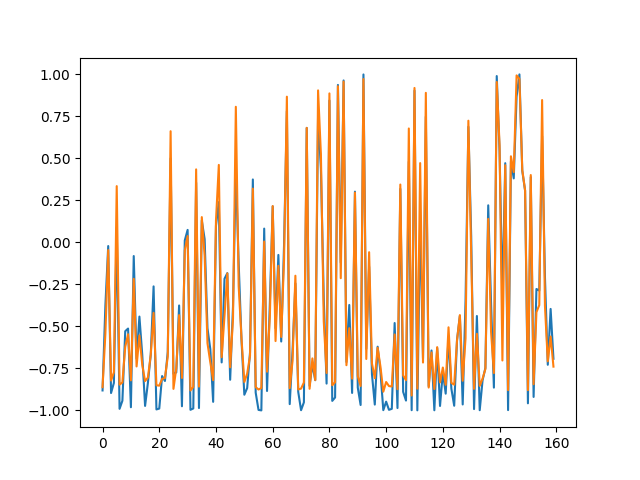
测试拟合情况：

import torch
import torch.nn as nn
import numpy as np
import torch.optim as optim
from matplotlib import pyplot as plt
class RBF(nn.Module):
    def __init__(self,input_dim = 5,k = 3):
        super(RBF,self).__init__()
        self.k = k
        self.C = nn.Parameter(torch.randn(1,k,input_dim)) # (n,k,5)
        self.sigma = nn.Parameter(torch.randn(1,k)) # (n,k)
        self.w = nn.Parameter(torch.randn(1,1,k)) # (n,1,k)
        self.b = nn.Parameter(torch.randn(1,1,1)) # (n,1,1)
        self.tanh = nn.Tanh()
    def forward(self,x):#(n,5)
        r = torch.sqrt(torch.sum((x.view(-1,1,5) - self.C)**2,dim = -1)) # (n,k)
        phi = torch.exp(-r**2/(2*self.sigma**2)).unsqueeze(-1) # (n,k,1)
        return self.tanh(self.w @ phi + self.b).squeeze(-1)



if __name__ == "__main__":
    batch_size = 4
    k = 70
    input_dim = 5
    num_epochs = 300
    x_train = torch.rand(batch_size * 160,input_dim) * 2
    y_train = torch.FloatTensor(torch.sin(torch.sum(x_train,dim = -1,keepdim=True)))
    #y_train[(x_train[:,0] > 0.5) & (x_train[:,2] < 0.5)] = 0
    
    model = RBF(input_dim,k)
    optimizer = optim.Adam(model.parameters(),lr = 1e-3)
    criterion = nn.MSELoss()
    
    loss_curve = []
    for epoch in range(num_epochs):
        running_loss = 0.
        for i in range(160):
            x = x_train[i*batch_size:(i+1)*batch_size]
            y = y_train[i*batch_size:(i+1)*batch_size]
            
            pred = model(x)
            loss = criterion(pred,y)

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            running_loss += loss
        print("loss: {}".format(running_loss / 160))
        loss_curve.append(running_loss / 160)
    x_test = torch.rand(160,input_dim)*2
    
    y_test = torch.FloatTensor(torch.sin(torch.sum(x_test,dim = -1,keepdim=True)))
    
    model.eval()
    with torch.no_grad():
        y_pred = model(x_test)
    y_test = y_test[indices]
    y_pred = y_pred[indices]
    plt.plot(y_test.squeeze(1).numpy())
    plt.plot(y_pred.squeeze(1).numpy())
    #plt.plot(loss_curve, label='train_loss')
    plt.show()