[论文理解] Convolution with even-sized kernels and symmetric padding

Convolution with even-sized kernels and symmetric padding

Intro

本文探究了偶数kernel size的卷积对网络的影响，结果表明偶数卷积在结果上并不如奇数卷积。文章从实验与原理上得出结论，偶数卷积之所以结果更差，是因为偶数卷积会使得feature map偏移，即“the shift problem”，这将导致学习到的feature不具备更强的表征能力。本文提出信息侵蚀假设，认为奇数卷积中心对称，而偶数卷积在实现时没有对称点，这将导致在实现时卷积利用的信息不能是各个方向的，只能是左上或其他方向(取决于具体实现)，因此整体将会导致feature map往一个方向偏移。为了解决这个问题，文章提出symmetric padding方法来弥补各个方向带来的损失，结果提示很明显。

The shift problem

奇数kernel size的卷积实现起来很容易，在对应位置计算当前位置和其八个邻域方向位置的feature值与权重求和即对应输出位置一个值，而偶数kernel size的卷积要如何实现呢？在tensorflow里，偶数kernel size的卷积如2×2卷积是利用当前点和其左上、上方、左方一共四个点与对应权值相乘求和得到的，正因如此，在实现过程，输出feature map的感受野其实是有缺陷的，他只能对应与其左上方的区域，多层卷积之后暴露出来的问题就是feature map的偏移。

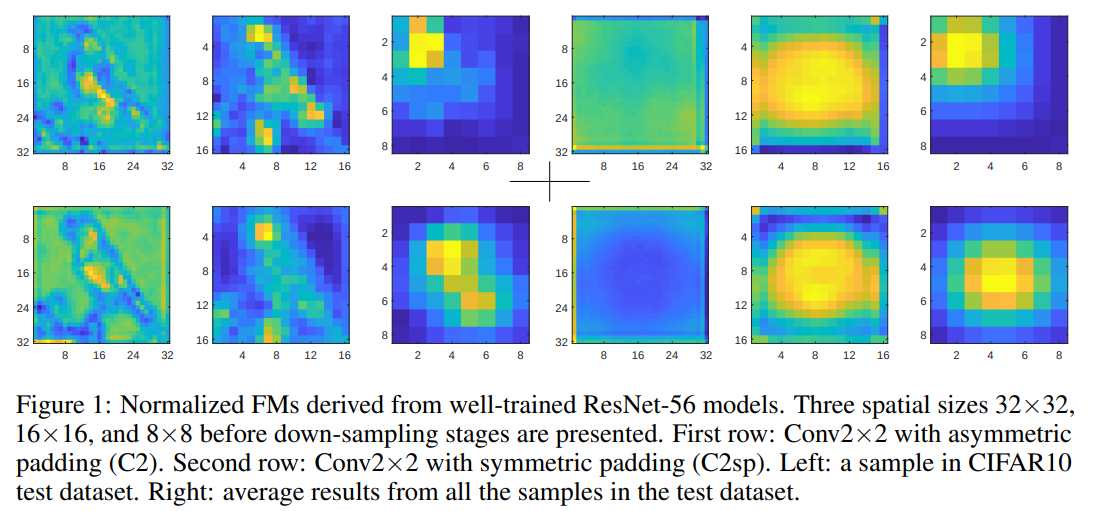
如上图所示，第一行是没使用本文方法padding的conv2x2的结果，第二行是本文方法的结果。

输出的feature map和输入feature map的关系可以表述为：

\[F^o(p) = \sum_{i=1}^{c_i}\sum_{\delta \in \mathcal{R}}\omega_i(\delta) \cdot F^i(p+\delta) \]

其中p表示位置坐标，\(F^i\)和\(F^o\)分别表示输入feature和输出feature，\(\delta\)表示卷积核内的位置，\(\omega_i\)表示卷积核的权重。

对于奇数kernel size卷积，其中\(\mathcal{R}\)可以写成：

\[\mathcal{R} = \{(-\kappa,-\kappa),(-\kappa,-\kappa+1),\cdots,(\kappa,\kappa)\},\kappa = \lceil \frac{k-1}{2}\rceil \]

以kernel的中心为原点，各个方向的偏移值就是上面的表示。对于奇数卷积，显然上式是中心对称的，而对于偶数kernel size卷积，对应的\(\mathcal{R}\)定义为：

\[\mathcal{R} = \{(1-\kappa,1-\kappa),(1-\kappa,2-\kappa) ,\cdots,(\kappa,\kappa) \} \]

上式并没有利用各个方向的信息，并且卷积核并不是中心对称的。

The information erosion hypothesis

对于输入位置p，经过n次偶数卷积之后对应的位置为：

\[F_n[p - (\frac{n}{2},\frac{n}{2})] \gets F_0(p) \]

因而网络越深，shift现象越严重。

为了说明偶数卷积对信息的侵蚀作用，文章定义feature的L1范数为该feature map信息量的度量。

\[Q_n = \frac{1}{hw} \sum_{p\in h \times w} |F_n(p)|,Q_n < Q_{n-1} \]

基于这个定义，文章实验了不同kernel size的信息量，得到如图所示结果：

可以看到C3和C5整体信息量锐减的比C2和C4慢的多。

Symmetric padding

为了解决shift带来的影响，本文提出了一种padding方式，具体的操作如图所示：

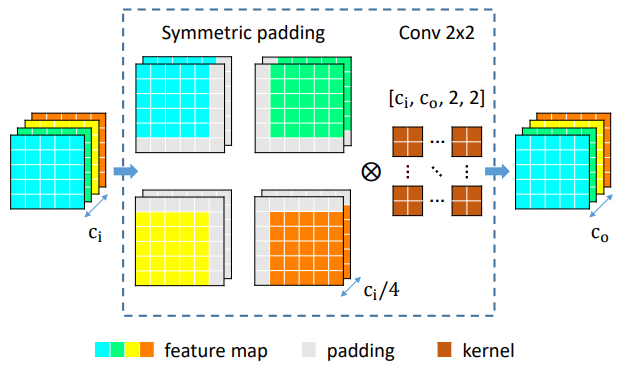
即先将feature map分成四个group，每个group在不同方向上按如图所示的方式进行padding，最后不用padding直接conv2x2即可。

这样做的好处就是使得网络的某些channel能利用到特定方向的信息，从宏观上看网络利用到了各个方向的信息，一定程度上缓解了shift带来的问题。

Codding

import torch
import torch.nn as nn
import torch.nn.functional as F

class SpConv2d(nn.Module):
    def __init__(self,in_channels,out_channels,kernel_size,stride,padding,*args,**kwargs):
        super(SpConv2d,self).__init__()
        self.conv = nn.Conv2d(in_channels,out_channels,kernel_size,stride,padding)
    def forward(self,x):
        n,c,h,w = x.size()
        assert c % 4 == 0
        x1 = x[:,:c//4,:,:]
        x2 = x[:,c//4:c//2,:,:]
        x3 = x[:,c//2:c//4*3,:,:]
        x4 = x[:,c//4*3:c,:,:]
        x1 = nn.functional.pad(x1,(1,0,1,0),mode = "constant",value = 0) # left top
        x2 = nn.functional.pad(x2,(0,1,1,0),mode = "constant",value = 0) # right top
        x3 = nn.functional.pad(x3,(1,0,0,1),mode = "constant",value = 0) # left bottom
        x4 = nn.functional.pad(x4,(0,1,0,1),mode = "constant",value = 0) # right bottom
        x = torch.cat([x1,x2,x3,x4],dim = 1)
        return self.conv(x)

class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.conv = SpConv2d(4,16,2,1,0)
    def forward(self,x):
        return self.conv(x)
if __name__ == "__main__":
    x = torch.randn(2,4,14,14)
    net = Net()
    print(net(x))