[图像处理] 直方图均衡化原理 - 数学推导

直方图均衡化

效果

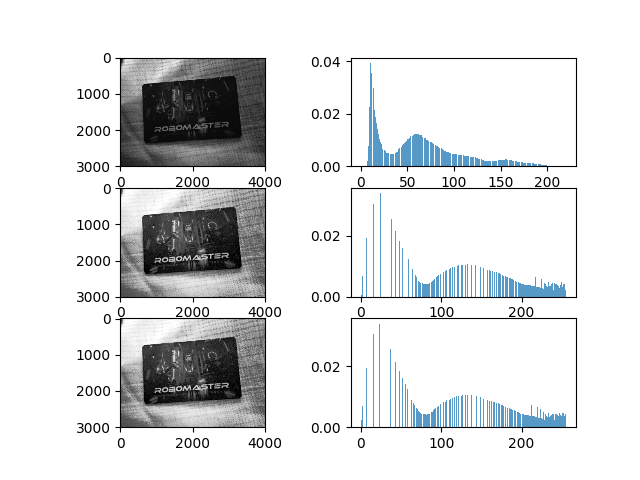
代码

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

src = cv.imread("/home/xueaoru/下载/IMG_20190326_232636.jpg")
gray = cv.cvtColor(src,cv.COLOR_BGR2GRAY)
# 原图
arr = gray.flatten()
eq = [np.sum(arr == i) for i in range(256)]
eq = np.array(eq)
eq = eq / eq.sum()
fg = plt.figure(1)
plt.subplot(3,2,1)
plt.imshow(gray,cmap='gray')
plt.subplot(3,2,2)
plt.hist(arr,bins = 256,density=1,alpha = 0.75)
# opencv 直方图均值化
plt.subplot(3,2,3)
out = cv.equalizeHist(gray)
plt.imshow(out,cmap='gray')
plt.subplot(3,2,4)
arr_2 = out.flatten()
plt.hist(arr_2,bins = 256,density=1,alpha = 0.75)
# 自己实现直方图均值化
fx = []
fx.append(eq[0])
for i in range(1,256):
    fx.append(fx[i-1]+eq[i])
val = np.array([255*fx[a] for a in arr])
val = val.reshape(gray.shape)
plt.subplot(3,2,5)
plt.imshow(val,cmap="gray")
plt.subplot(3,2,6)
arr_3 = val.flatten()
plt.hist(arr_3,bins=256,density=1,alpha = 0.75)
plt.show()

原理

图像直方图的原始分布：

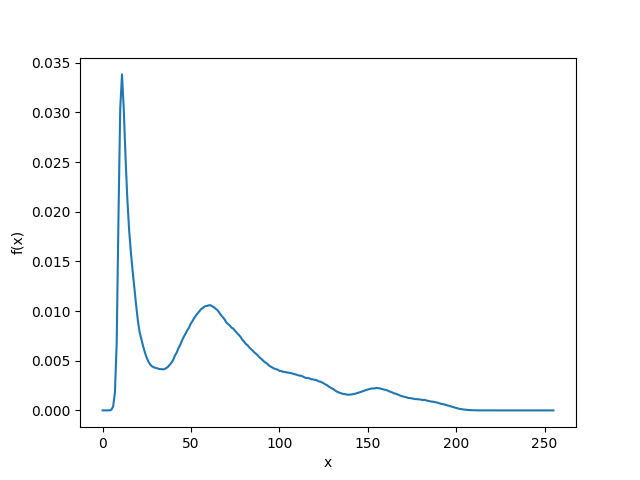
目标分布：

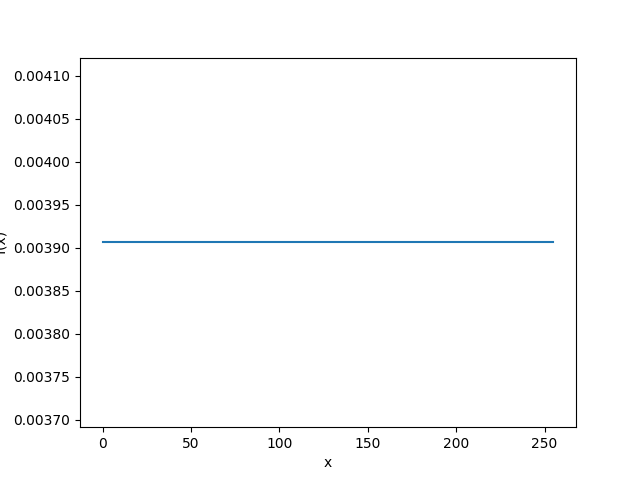
\[F_Y(y) = P\lbrace Y\leq y \rbrace = P \lbrace T(X) \leq y \rbrace = P \lbrace X \leq T^{-1}(y) \rbrace = F_X(T^{-1}(y)) \tag{1} \]

那么这个公式是如何得来的呢？

\[P \lbrace T(X) \leq y \rbrace = P \lbrace X \leq T^{-1}(y) \rbrace \tag{2} \]

\[例如，有Y=3X,也即T(X) = 3X,那么P \lbrace 3X \leq y \rbrace = P \lbrace X \leq \frac{y}{3} \rbrace =P \lbrace X \leq T^{-1}(y) \rbrace\\， 若T(X) = -3X,很明显上面的公式符号方向会改变。 \]

由于我们要求的变换函数在变换后仍然要保持在变换之前变换亮度相对高的变换之后相对亮度仍然要高，所以变换函数必须是单调递增的，所以上式不变号。

\[由(1)继续推，两边同时求导，那么有\\ f_Y(y) = \frac{dT^{-1}(y)}{dy}*f_x(T^{-1}(y))=\frac{dx}{dy}*f_x(X) \tag{3} \]

\[化简一下有\\ \frac{1}{255}dy = f_x(x)dx\\ 两边同时求积分有\\ y = 255*\int^{x}_0f_x(x)dx\\\tag{4} \]

\[离散化上式则有\\ y = \sum_{i=0}^{x} f_x(i) \]

根据上面的推导，我们写出了上面的代码。但是，由图我们看到，直方图均衡化之后的图像的概率分布好像并不是完全均匀分布的呀？怎么回事？

我们仔细查阅了相关资料，在《冈萨雷斯数字图像处理》这本书中查到了相关的语句。

然而，我们还是不理解，为什么有的灰度值没有对应的变换后的值？

继续往后看，直到看到了这个图，恍然大悟！

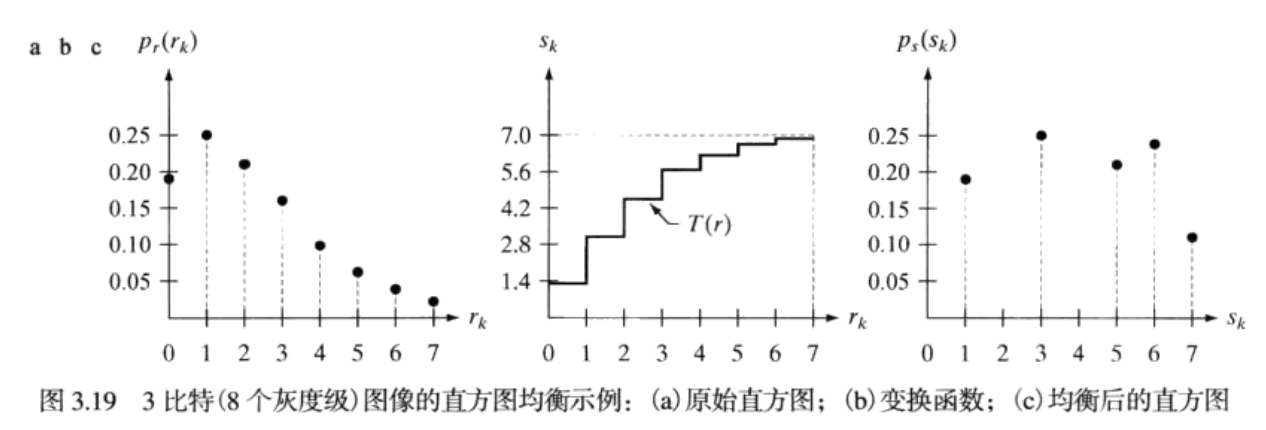
可以看到，均衡后的直方图中，灰度值为2的点，在变换函数中并没有一个合适的sk值与之对应，因此这些点的值就这么消失了！