PAT 甲级 1064 Complete Binary Search Tree解题思路（全网最清晰之一）
网上看了很多关于这题的解答，基本上都没讲的太清楚，关于解题思路很多都是一笔带过，然后给出大段的代码，这种解题文章没意思。
本文只讲解题思路，不给出代码，但求尽量把解题思路讲清晰。
做本题所必需的前置知识条件
-
二叉排序树的中序遍历序列是一个递增序列，这个是做这道题必须知道的前置知识。
-
二叉树的中序遍历方式，是本题所需的第二个知识，最简单的方法就是用递归的方式。注意这里的中序遍历方式是对所有二叉树都有用的，而并不是单单针对二叉排序树。后面两个知识也不只是针对二叉排序树的，而是对所有的完全二叉树都适用。
-
完全二叉树的存储方式，可以直接用一维数组存储，这是做本题所需的第三个知识。其中，假设父结点在数组中的编号为i，那么它左子结点的编号就为2i，右子结点的编号就为2i+1。
-
使用一维数组存储完全二叉树时，将数组从头到尾按顺序输出的结果，就是该完全二叉树的层次遍历序列。
解题思路
最终目的：生成一棵完全的二叉排序树，并按层次遍历顺序输出所有结点。
由于二叉树中元素的个数已经由第一个参数n给出，且要求是完全二叉树，那么我们就可以直接创建一个长度为n的一维数组tree，用来存储最后生成的完全二叉排序树。这个时候我们的数组中已经预留了每个结点的位置，但还没有添上值，相对应的完全二叉排序树也只有各个结点的位置，而每个结点的值还未知。假设结点个数为6，如图所示：
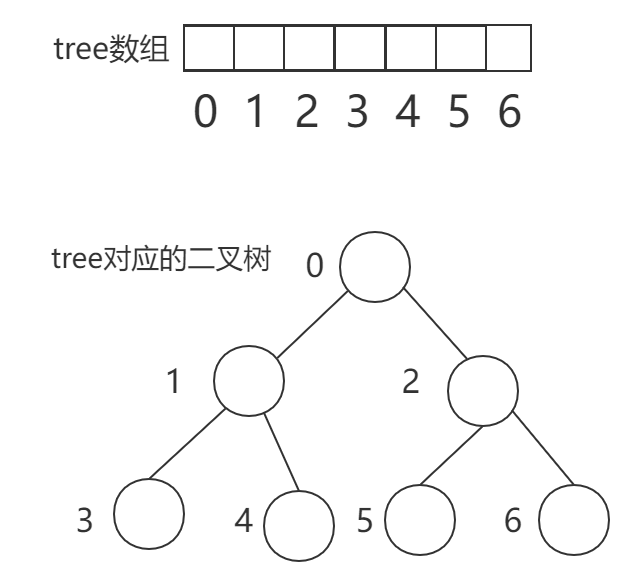
我们可以对题目中给出的所有数字进行从小到大的排序，得到数组nums，这样我们就得到了tree作为二叉排序树时的中序遍历序列。
之后我们可以对tree这颗完全二叉树用递归的方式进行中序遍历，对于用一维数组存储的完全二叉树，中序遍历的递归函数如下：
void inOrder(int root) {
if (root >= n) return ;
inOrder(root * 2 + 1);
... // 遍历到结点时的操作方法
inOrder(root * 2 + 2);
}
对于一棵已经存在值的二叉树，遍历到结点时的操作方法通常是取出该结点的值输出或是存储。而目前tree这棵树是没有值的，我们需要的是让它能填上值，因此只要将取出本结点的值操作改为为本结点填入值的操作即可为tree填上完整的数据。即每次都将中序遍历数组nums的下个数填入到当前遍历到的tree的结点对应的位置。
当中序遍历完毕后，tree的值也已经全部填满了，最后只要将数组下标从0开始按序输入即可得到tree作为完全二叉树的层次遍历序列
