假设检验
假设检验
| 名称 | 说明 | 假设检验 | 统计量 | 参考 | 函数 |
| Kolmogorov-Smirnov(K检验) |
以样本数据的累计频数分布与特定理论分布比较,若两者间的差距很小,则推论该样本取自某特定分布族。 |
H0:数据集符合正态分布,H1:样本所来自的总体分布不符合正态分布。 令F0(x)表示预先假设的理论分布,Fn(x)表示随机样本的累计概率(频率)函数 |
D=max|F0(x) - Fn(x)| |
D值越小,越接近0,表示样本数据越接近正态分布 p值,如果p-value小于显著性水平α(0.05),则拒绝H0 |
ks.test(S, "pgamma", 1) ks.test(S, "pexp") |
| Shapiro-Wilk(W检验) | 检验是否数据符合正态分布,类似于线性回归的方法一样,是检验其于回归曲线的残差。样本量在3到5000之间。 | H0:数据集符合正态分布 | 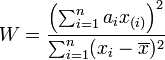 |
统计量W 最大值是1,越接近1,表示样本与正态分布匹配 p值,如果p-value小于显著性水平α(0.05),则拒绝H0 |
shapiro.test(S) |
| binomial Test | 二项分布总体的假设检验 (检验样本是否服从概率等于[大于或小于]某种数值) | 原假设:p=p0,p<p0,p<p0 计算结果p-值很小,表示拒绝假设,否则为接受假设. | binom.test(x,n,p=0.5, # x是成功次数,n是试验总数,p是原假设,默认概率为0.5 alternative=c(“two.side”,”less”,”greater”), conf.level=.95) |
- | |
| Jarque-Bera Test | 基于峰度和偏度检验分布的正态性 | The skewness and the excess kurotsis of samples are zero. |
jarque.bera.test (tseries包) |
||
| 名称 | 说明 | 假设检验 | 统计量 | 参考 | 函数 |
| Fisher精确的独立检验 | 原假设:X,Y相关。 | fisher.test(x, y = NULL, workspace = 200000, hybrid = FALSE,control = list(), or = 1, alternative = "two.sided",conf.int = TRUE, conf.level = 0.95) | |||
| Wilcoxon秩检验 | 原假设:中位数大于,小于,不等于mu. | wilcox.test(x, y = NULL,alternative = c("two.sided", "less", "greater"),mu = 0, paired = FALSE, exact = NULL, correct = TRUE,conf.int = FALSE, conf.level = 0.95, ...) | |||
| 相关性检验(cor) |
原假设:x,y不相关. |
cor.test(x, y,alternative = c("two.sided", "less", "greater"),method = "spearman", conf.level = 0.95, ...) |
如果p值很小,则拒绝原假设,认为x,y是相关的。否则认为是不相关的。 | ||
| t检验 |
正态总体均值的假设检验 单个总体情况(检验样本是否符合等于某个均值) |
t.test(x,y=Null, #只提供x为单个正态总体均值检验,否则为两个总体均值检验alternative=c(“two.side”,”less”,”greater”),#双边检验 单边检验 mu=0,#原假设:uo=0,均值为某个具体数字 paired=FALSE,var.equal=FALSE, #方差齐性选项 conf.level=.95)# 置信水平95% |
两个总体情况(检验两个总体数据是否一致u1=u2) t.test(x,y) 同上 成对数据t-检验(检验两个总体数据是否一致) t.test(X-Y,…..) |
P值小于显著性水平时拒绝原假设,否则,接受原假设。具体的假设要看所选择的是双边假设还是单边假设(又分小于和大于) | |
| F检验 | 正态总体方差检验 | 单个总体情况(方差是否为某一值) 两个样本情况(两个样本方差是否相同) |
var.test(x,y,ratio=1, #方差比原假设,默认为1 alternative=c(“two.side”,”less”,”greater”), conf.level=.95) |
P值小于显著性水平时拒绝原假设,否则,接受原假设。具体的假设要看所选择的是双边假设还是单边假设(又分小于和大于) |
|
| McNemar检验 | 原假设:两组数据的频数没有区别。 | mcnemar.test(x, y = NULL, correct = TRUE) | |||
| Pearson 拟合优度χ2检验 | 原假设H0:X符合F分布。 | chisq.test(x, y = NULL, correct = TRUE,p = rep(1/length(x), length(x)), rescale.p = FALSE,simulate.p.value = FALSE, B = 2000) |
p-值小于某个显著性水平,则表示拒绝原假设,否则接受原假设。 | ||
| kappa检验 | 检验多重共线性 | xtx<-cor(newdata[2:10]) kappa(xtx,exact=T) |
多重共线性检验,<100 不存在多重共线性 | ||
| vif 检验(方差膨胀因子) | 检验多重共线性 | library(car) round(vif(lm3),2) |
vif值小于10,多重共线性的问题不严重 | ||
| 线性模型假设综合检验 | library(gvlma) gvlm1<-gvlma(lm1) |
||||
| 相关计算相关矩阵和显著性水平 | orr.test()函数可以一次做很多事情,可以为Pearson、Spearman或Kendall相关计算相关矩阵和显著性水平 | psych包 | |||
| 偏相关 | pcor(u,s)偏相关是指在控制一个或多个定量变量时,另外两个定量变量之间的相互关系,其中u是一个数值向量,前两个数值表示要计算相关系数的变量下标,其余的数值为条件变量(既要排除影响的变量)的下标;S为变量的协方差阵 | pcor()函数计算偏相关系数 | ggm包 | ||
| Durbin-Watson Test | 计量经济学 | The autocorrelationof the disturbance is 0. | durbinWatsonTest(car) | dwtest(Lmtest) | |
| ljung-Box | 计量经济学 | Thedata are independently distributed,i.e. the autocorrelation coefficients are all zero. | Box.test(stats) | AutocorTest(FinTS) | |
| lagrange multiplier Test | 计量经济学 | No ARCH effect. | ArchTest |
参考:豆瓣



 浙公网安备 33010602011771号
浙公网安备 33010602011771号