数据处理
数据处理
研究数据的增长率分布存在一定规律的模型
Box-Cox变换是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。比如在使用线性回归的时候,由于残差 epsilon 不符合正态分布而不满足建模的条件,这时候要对响应变量Y进行变换,把数据变成正态的。
R里边的相关函数的函数很多,一般可以分成两类,针对(线性)模型的和针对数据的变换。
1.forecast package
函数:BoxCox.lambda和BoxCox
BoxCox.lambda这个函数用于数值向量或时间序列,可以得到\lambda的估计精确值。
forecast package的Boxcox方法是先用BoxCox.lambda函数自动筛选出最合适的lambda,然后用Boxcox进行普通的Box-cox变换,BoxCox.lambda这个函数用于数值向量或时间序列,可以得到lambda的估计精确值
> BoxCox.lambda(trees$Volume, method = "loglik")
[1] -0.05
>
> volume.f <- BoxCox(trees$Volume, lambda = -0.05)
> trees.f <- cbind(trees, volume.f) #重新拟合模型
> l.f <- lm(volume.f ~ log(Height) + log(Girth), data = trees.f) #建立线性模型
> pander(l.f)
---------------------------------------------------------------
Estimate Std. Error t value Pr(>|t|)
----------------- ---------- ------------ --------- -----------
**(Intercept)** -5.454 0.6731 -8.103 8.013e-09
**log(Height)** 0.965 0.172 5.609 5.269e-06
**log(Girth)** 1.678 0.06313 26.58 2.073e-21
---------------------------------------------------------------
Table: Fitting linear model: volume.f ~ log(Height) + log(Girth)
> pander(anova(l.f))
----------------------------------------------------------------
Df Sum Sq Mean Sq F value Pr(>F)
----------------- ---- -------- ---------- --------- -----------
**log(Height)** 1 2.534 2.534 540.1 7.646e-20
**log(Girth)** 1 3.315 3.315 706.7 2.073e-21
**Residuals** 28 0.1314 0.004691 NA NA
----------------------------------------------------------------
Table: Analysis of Variance Table
2.car package
powerTransform要更复杂一些,这个函数是针对线性模型计算一个最优的lambda ,采取的方法是最大似然估计。 使用这个函数的问题是只能对模型l寻找最优lambda,而且还得不到 lambda的估计的精确值。
> summary(p1<-powerTransform(trees$Height))
bcPower Transformation to Normality
Est Power Rounded Pwr Wald Lwr bnd Wald Upr Bnd
trees$Height 2.9353 1 -1.1299 7.0004
Likelihood ratio tests about transformation parameters
LRT df pval
LR test, lambda = (0) 2.0440099 1 0.1528064
LR test, lambda = (1) 0.8837162 1 0.3471858
> hist(bcPower(trees$Height,p1$roundlam))
> hist(trees$Height)
> p1$roundlam
trees$Height
1
3.MASS包
函数:boxcox
这个函数是针对线性模型计算一个最优的\lambda ,采取的方法是最大似然估计。在关于\lambda的对数最大似然图像上找估计值的95%置信区间。对\lambda的搜索的默认范围是[-2,2],步长0.1。结果会输出一张表示似然结果的图。当然可以自定义搜索的范围或者步长。 使用这个函数的问题是只能对模型(lm和aov寻找最优\lambda,而且还得不到 \lambda的估计的精确值。
> boxcox(Volume ~ log(Height) + log(Girth), data = trees) #找lambda > boxcox(Volume ~ log(Height) + log(Girth), data = trees, lambda = seq(-0.08, + 0, length = 10))# 缩小寻找的范围,大约是-0.065(中间的线) > volume <- (trees$Volume^(-0.065) - 1)/(-0.065) #变换 > trees.t <- cbind(trees, volume) #重新拟合模型 > l.t <- lm(volume ~ log(Height) + log(Girth), data = trees.t) #建立线性模型 > qqPlot(l.t) #残差可认为是正态了
1.回归模型中,Box-Cox变换是对因变量Y作如下变换:
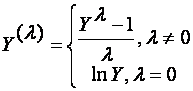
这里 是一个待定变换参数。对不同的
是一个待定变换参数。对不同的 ,所做的变换自然就不同,所以是一个变换族。它包括了对数变换(
,所做的变换自然就不同,所以是一个变换族。它包括了对数变换( =0),平方根变换(
=0),平方根变换( )和倒数变换(
)和倒数变换(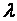 =-1)等常用变换。
=-1)等常用变换。
对因变量的n个观测值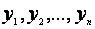 ,应用上述变换,得到变换后的向量
,应用上述变换,得到变换后的向量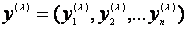 (1.2)
(1.2)
即要确定变换参数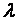 ,使得
,使得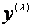 满足
满足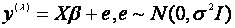 (1.3)
(1.3)
即通过对因变量的变换,使得变换过的向量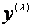 与回归自变量具有线性相依关系,误差也服从正态分布,误差各分量是等方差且相互独立。
与回归自变量具有线性相依关系,误差也服从正态分布,误差各分量是等方差且相互独立。
以极大似然法来确定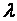 。因为
。因为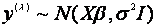 ,所以对固定的
,所以对固定的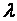 ,
, ,
,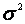 的似然函数为
的似然函数为
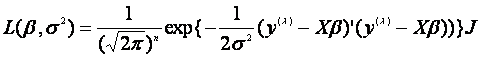 (1.4)
(1.4)
这里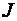 为变换Jacobi的行列式
为变换Jacobi的行列式
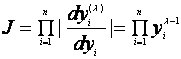 (1.5)
(1.5)
当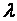 固定时,
固定时, 是不依赖于参数
是不依赖于参数 和
和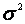 的常数因子。
的常数因子。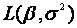 的其余部分关于
的其余部分关于 和
和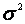 求导数,令其等于0,可以求得
求导数,令其等于0,可以求得 和
和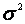 的极大似然估计
的极大似然估计
 (1.6)
(1.6)
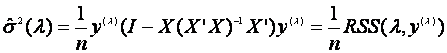 (1.7)
(1.7)
为了求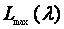 的最大值,考虑到lnx是x的单调函数,对
的最大值,考虑到lnx是x的单调函数,对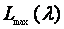 求对数。略去与
求对数。略去与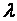 无关的常数项,得到
无关的常数项,得到
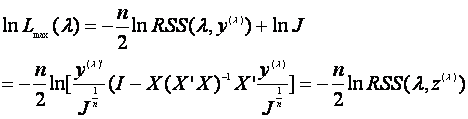 (1.8)
(1.8)
其中
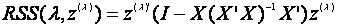 (1.9)
(1.9)
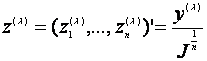 (1.10)
(1.10)
 (1.11)
(1.11)
1.9)式对Box-Cox变换带来很大方便,因为为了求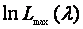 的最大值,只需求残差平方和的
的最大值,只需求残差平方和的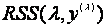 最小值。
最小值。
2 单变量的Box-Cox变换
设变量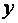 经变换后,
经变换后,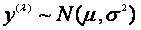 (2.1)
(2.1)
对固定的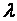 ,
, ,
,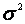 的似然函数为
的似然函数为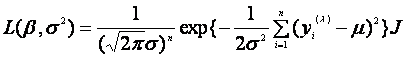 (2.2)
(2.2)
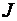 同为变换Jacobi的行列式
同为变换Jacobi的行列式
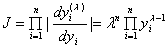 (2.3)
(2.3)
求得 和
和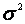 的极大似然估计为
的极大似然估计为
 (2.4)
(2.4)
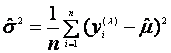 (2.5)
(2.5)
对极大似然函数作对数变换
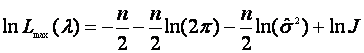 (2.6)
(2.6)
化简得
 (2.7)
(2.7)
其中
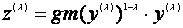 (2.8)
(2.8)
 (2.9)
(2.9)
(2.9)亦即为几何平均值。
为了简单起见,重新将Box-Cox变换定义为
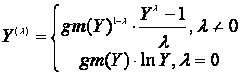 (2.10)
(2.10)
为了最大化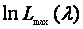 ,只须最小化
,只须最小化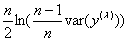 。
。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号