数据结构
1、绪论
1.1、数据结构在学什么?
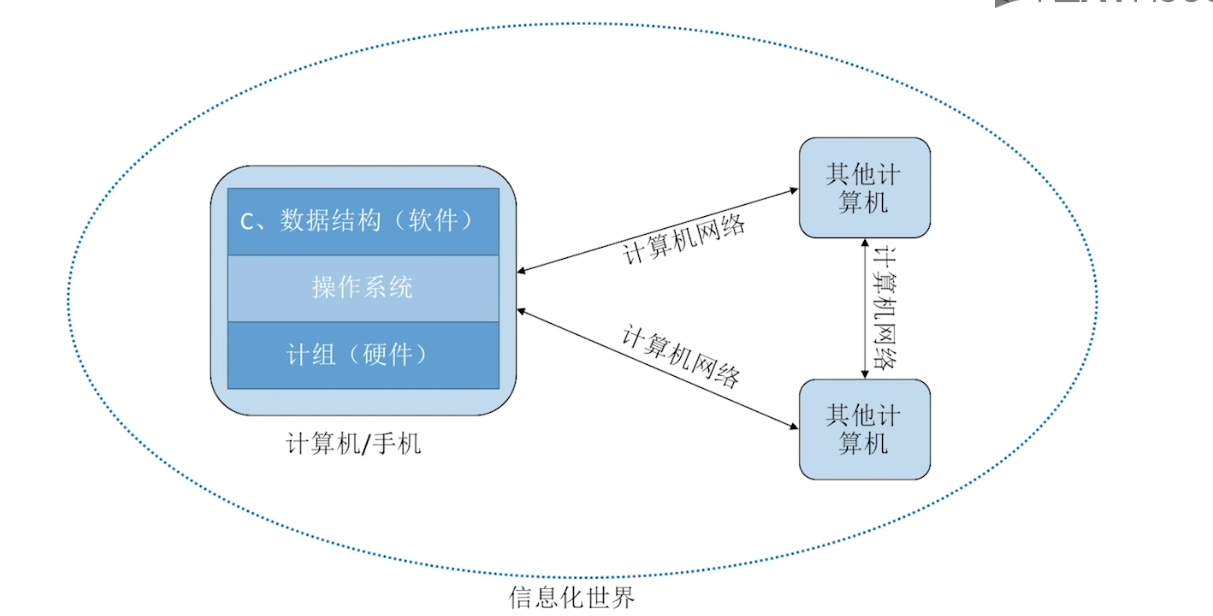

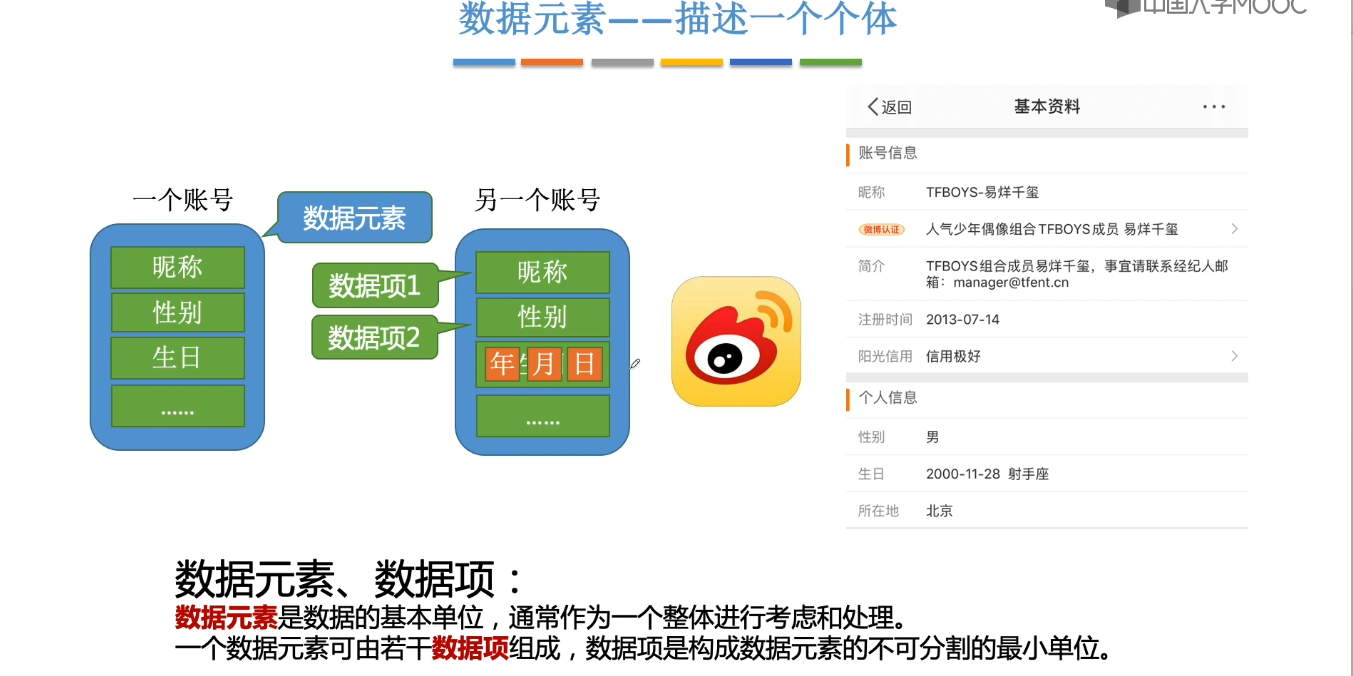
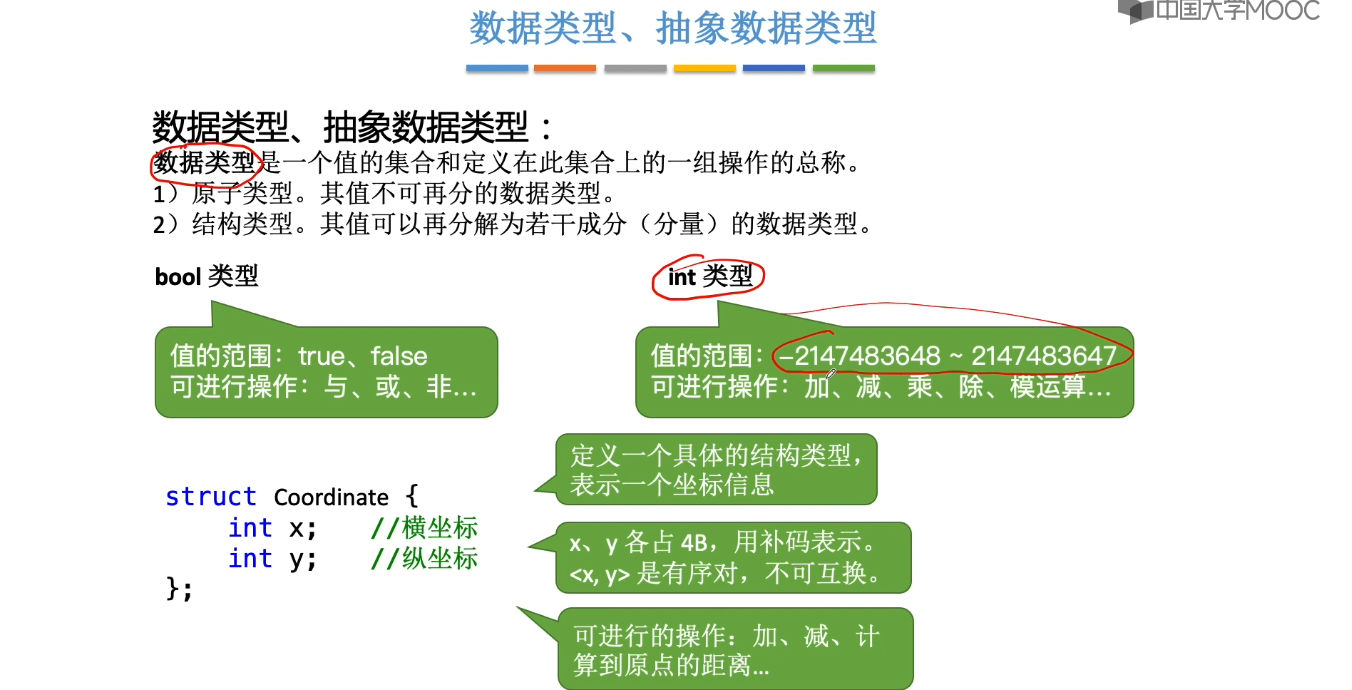
1.2、基本概念和术语
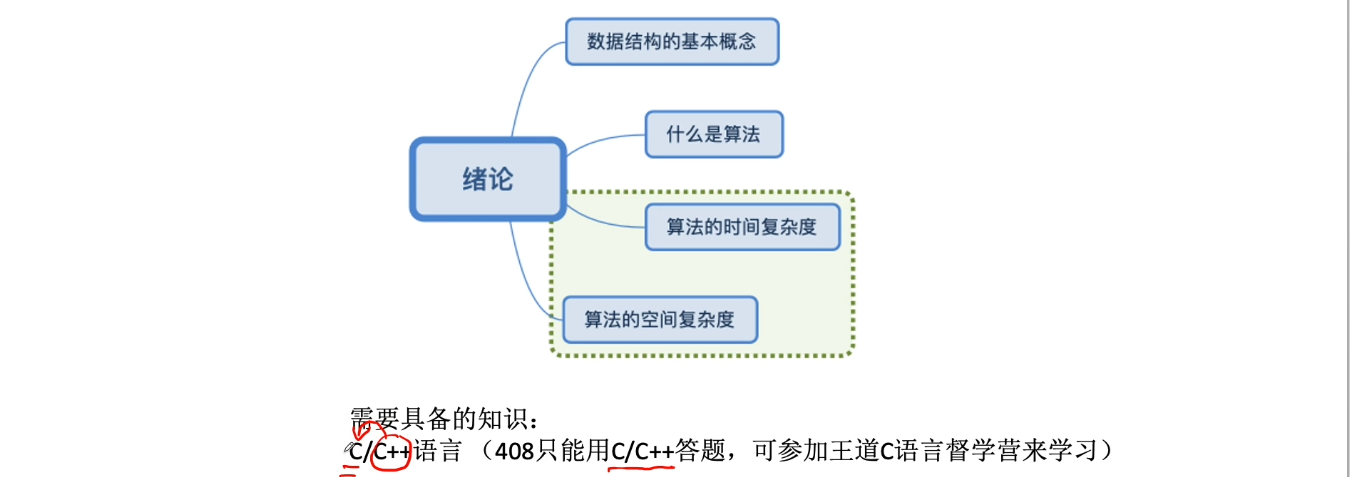
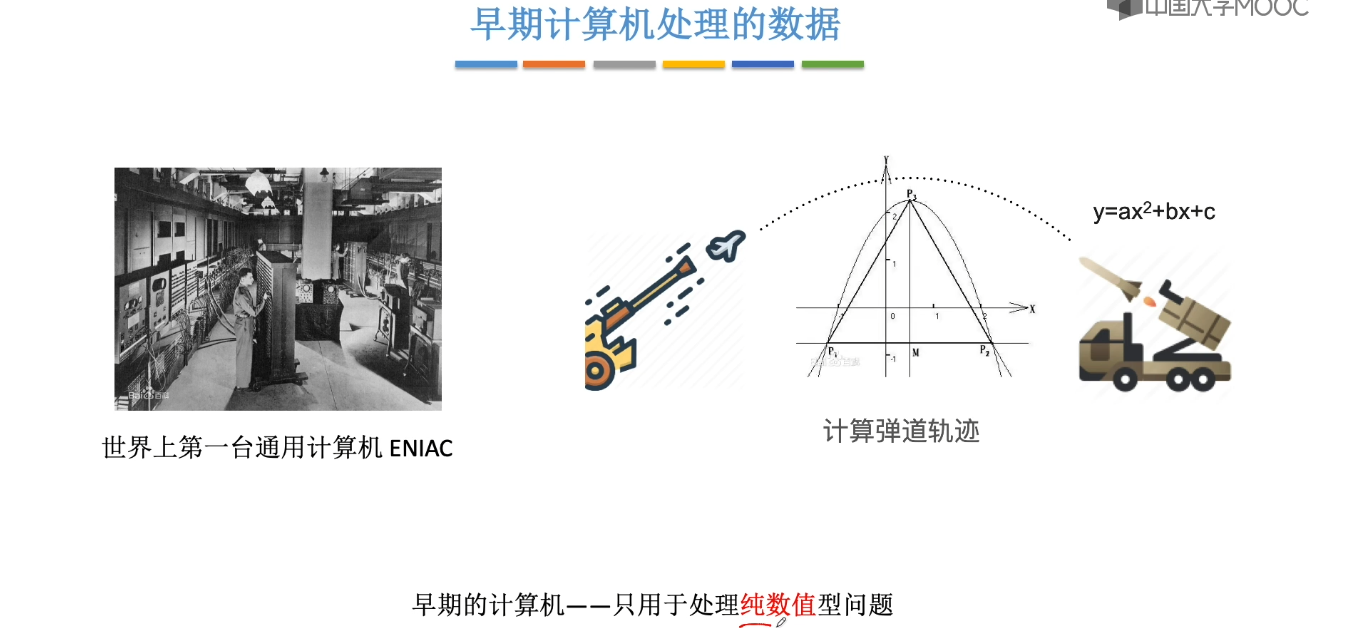



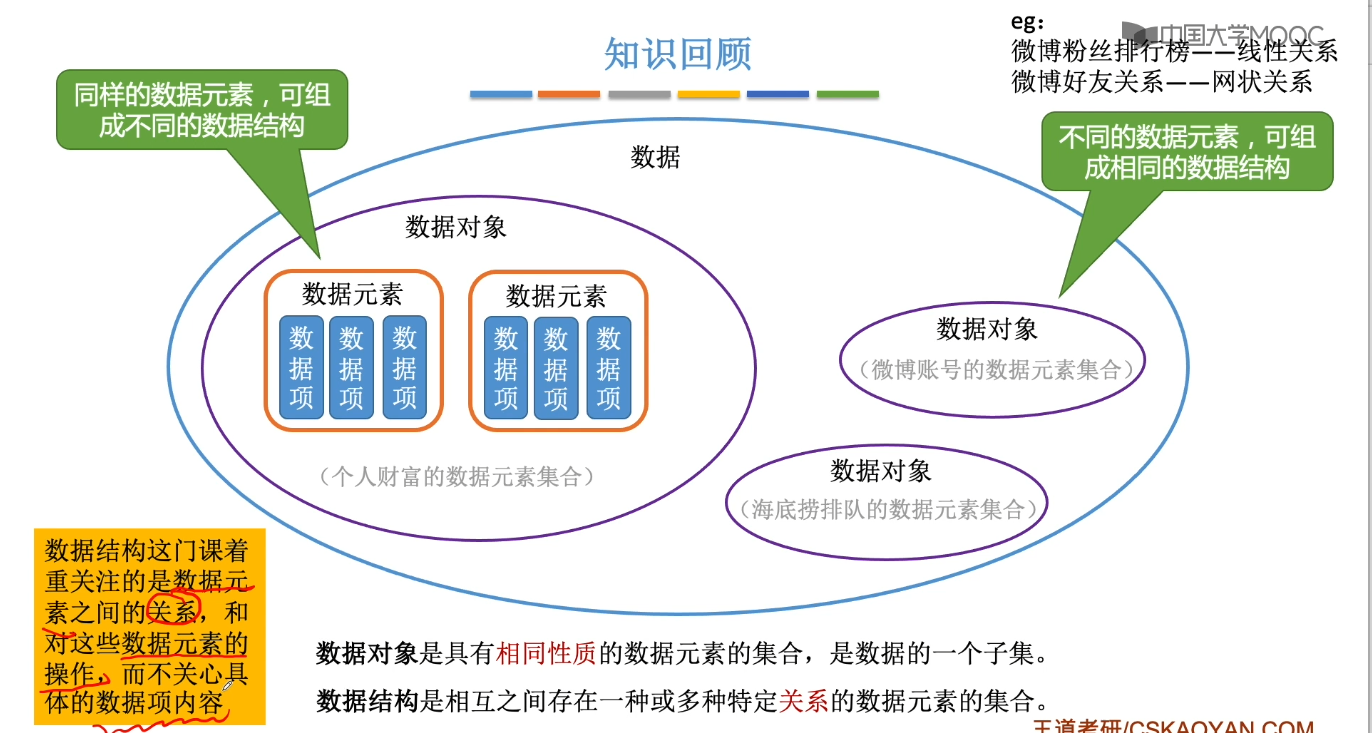
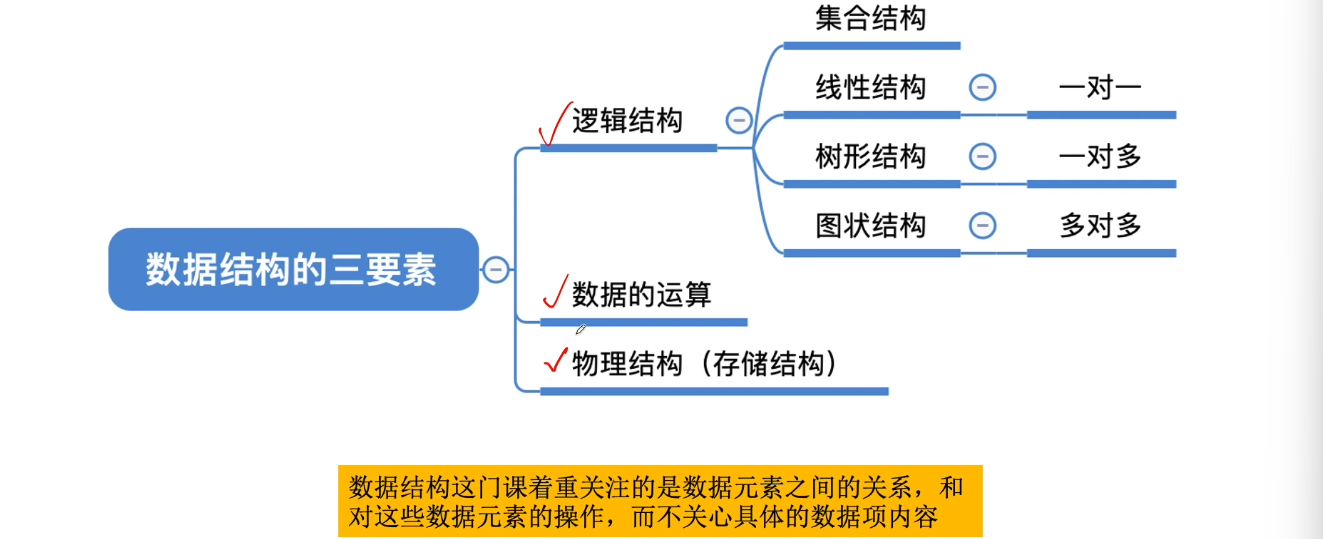
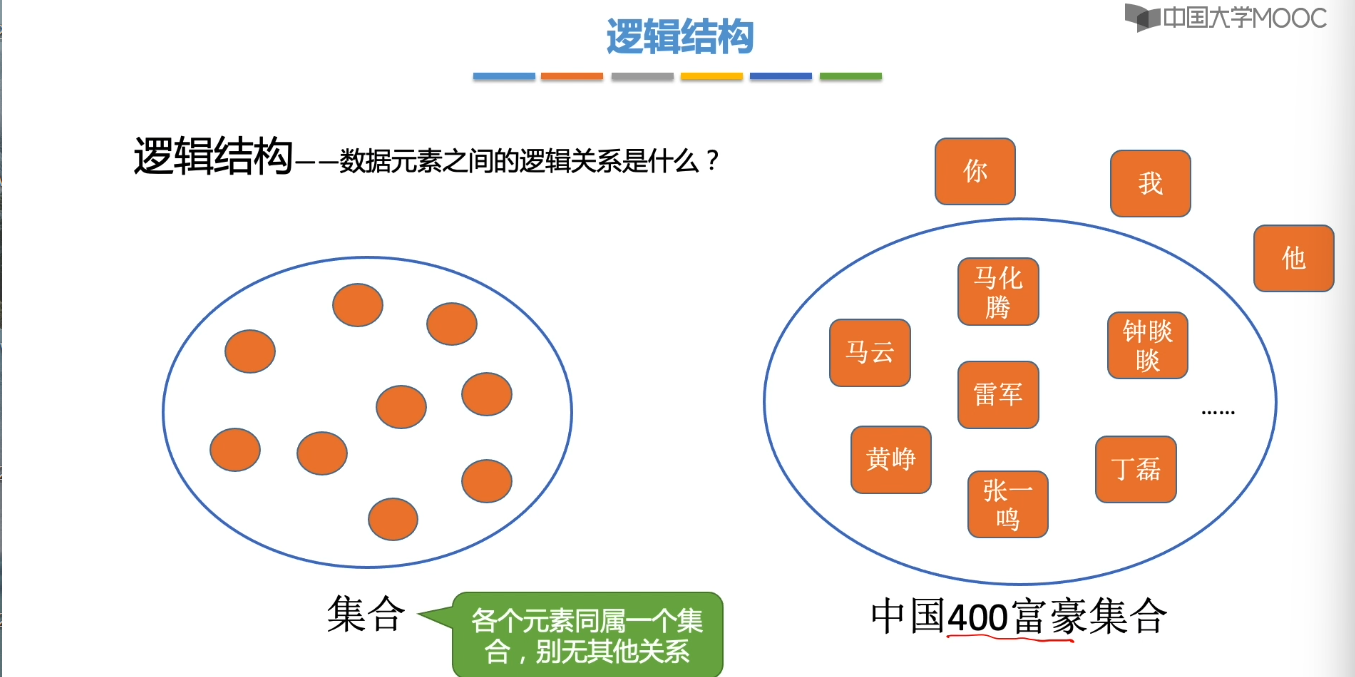
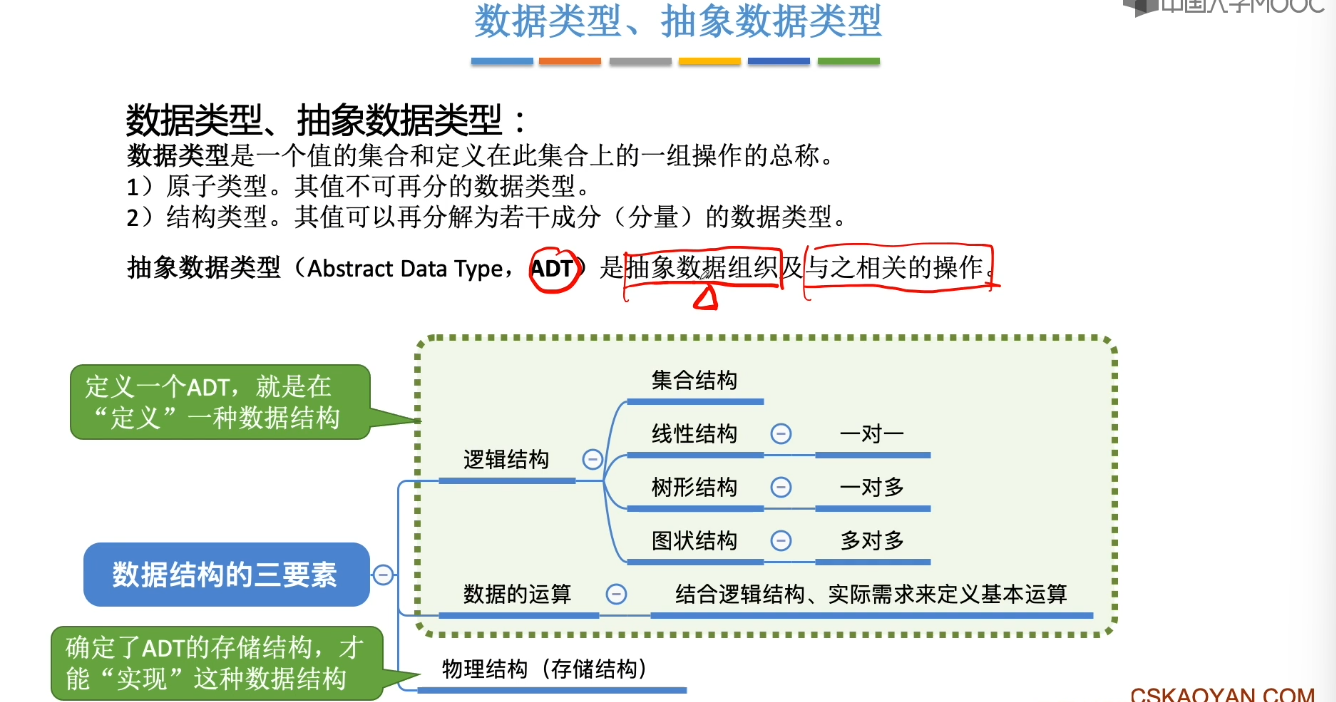
1.3、数据结构三要素
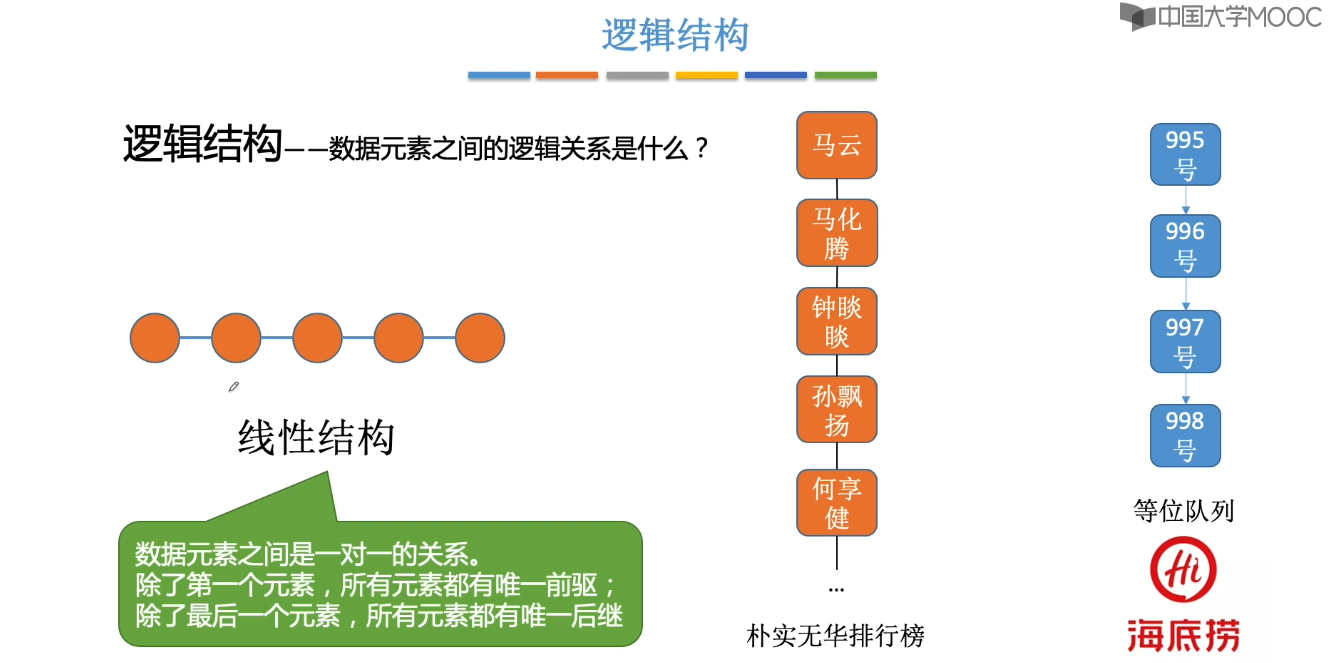
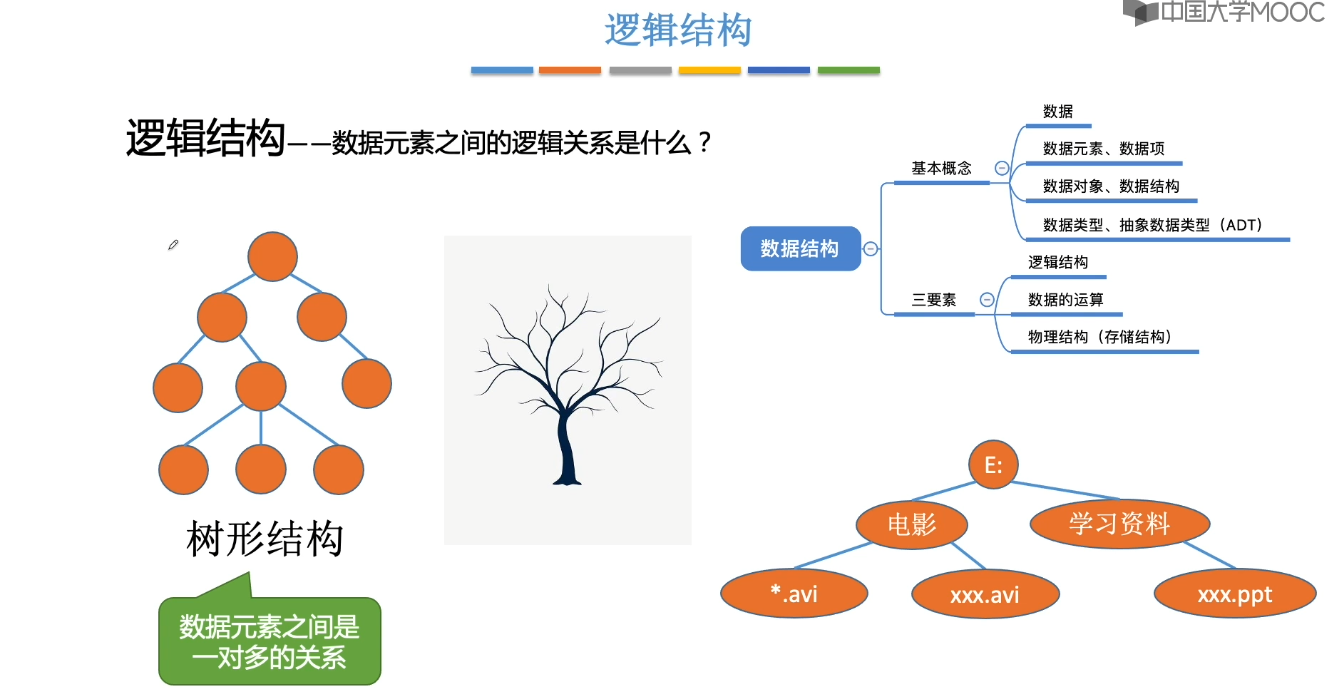
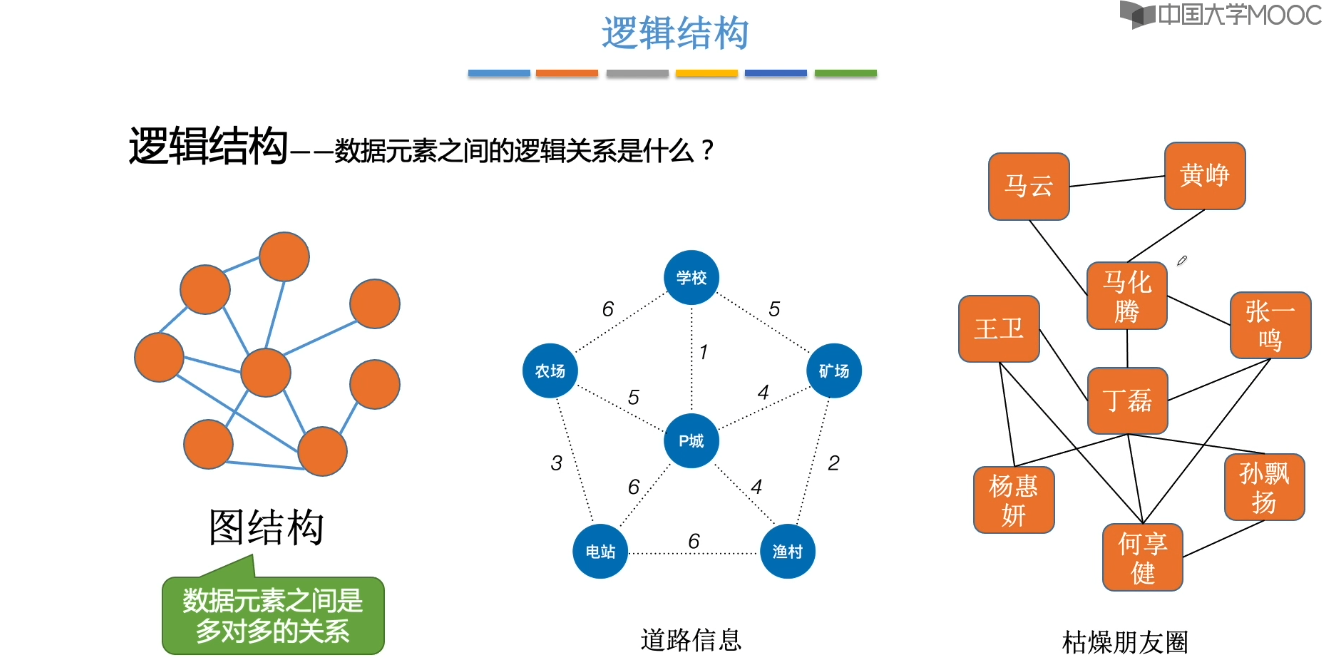
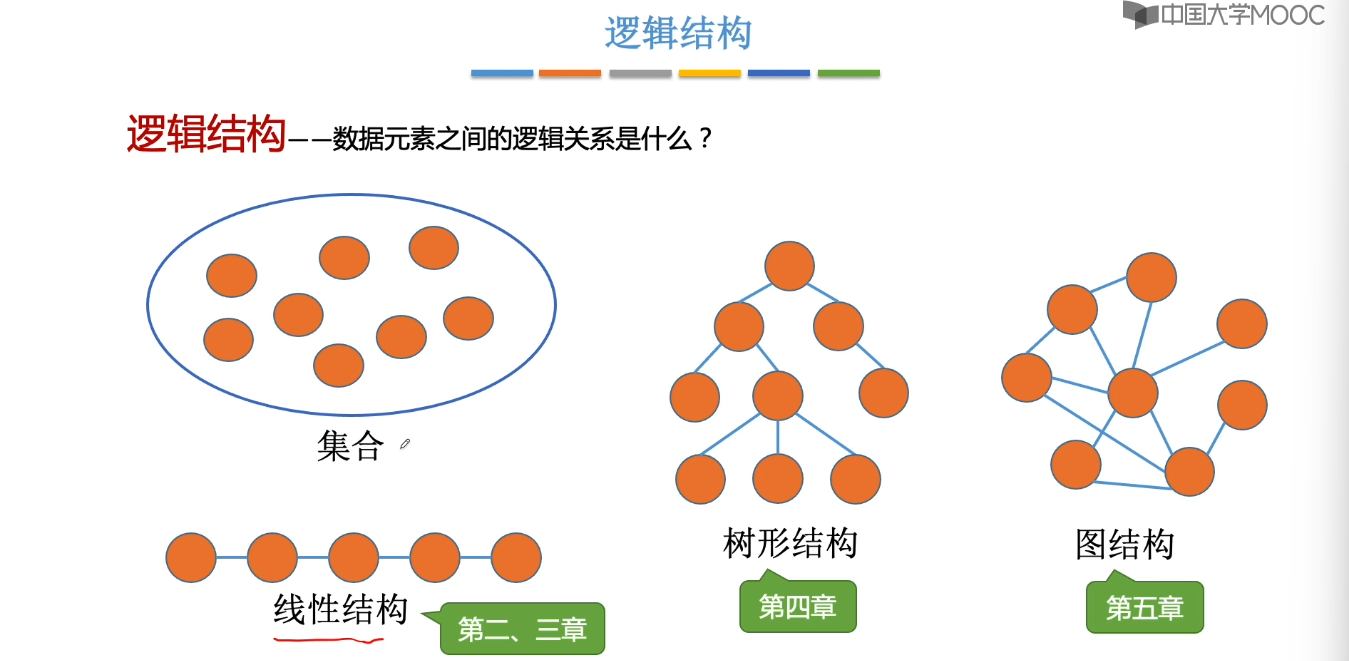

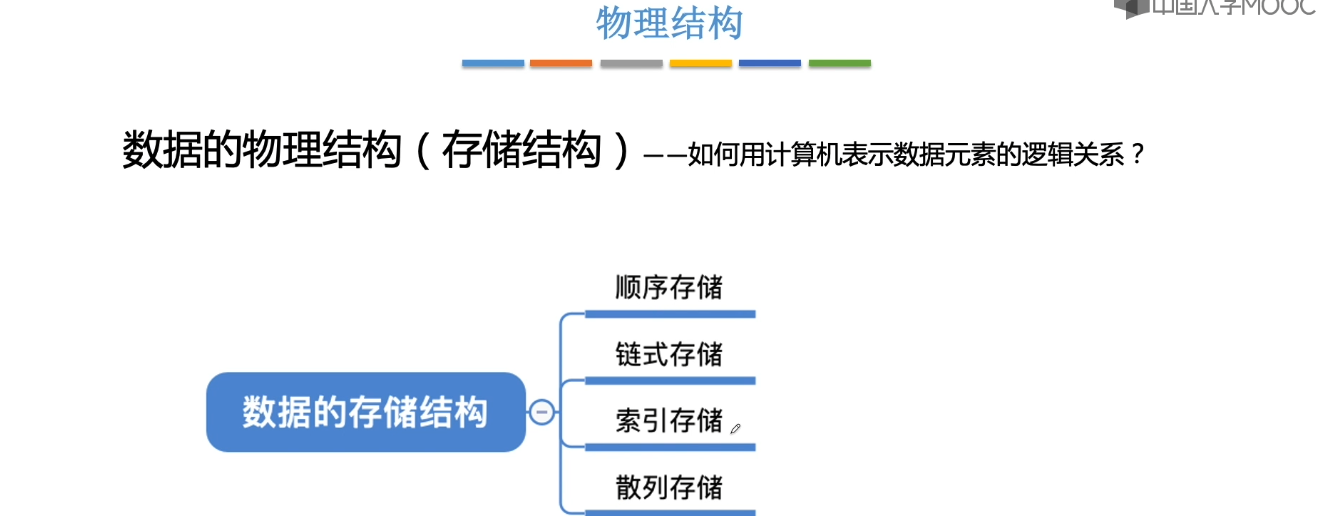
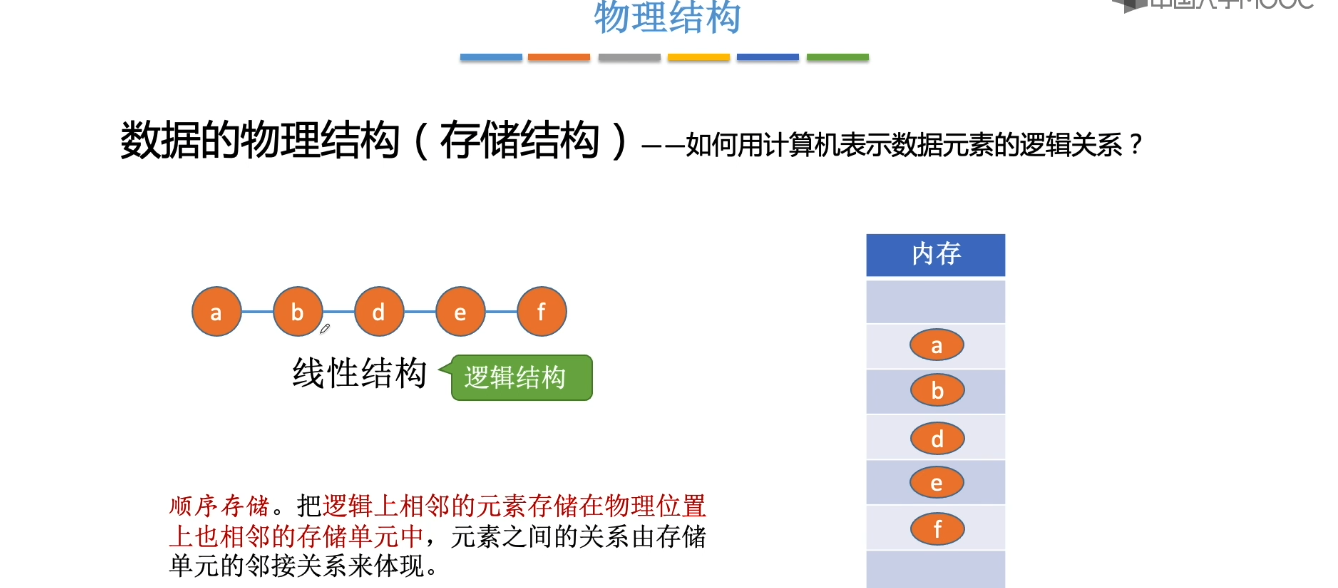
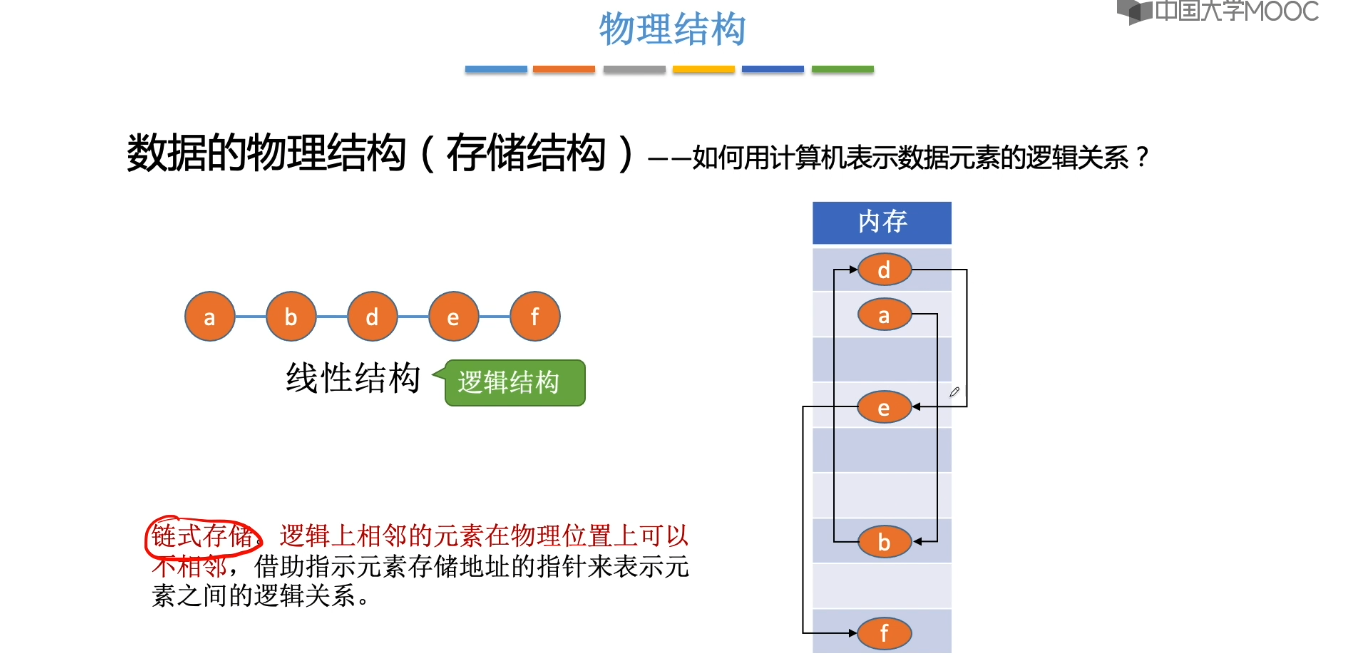
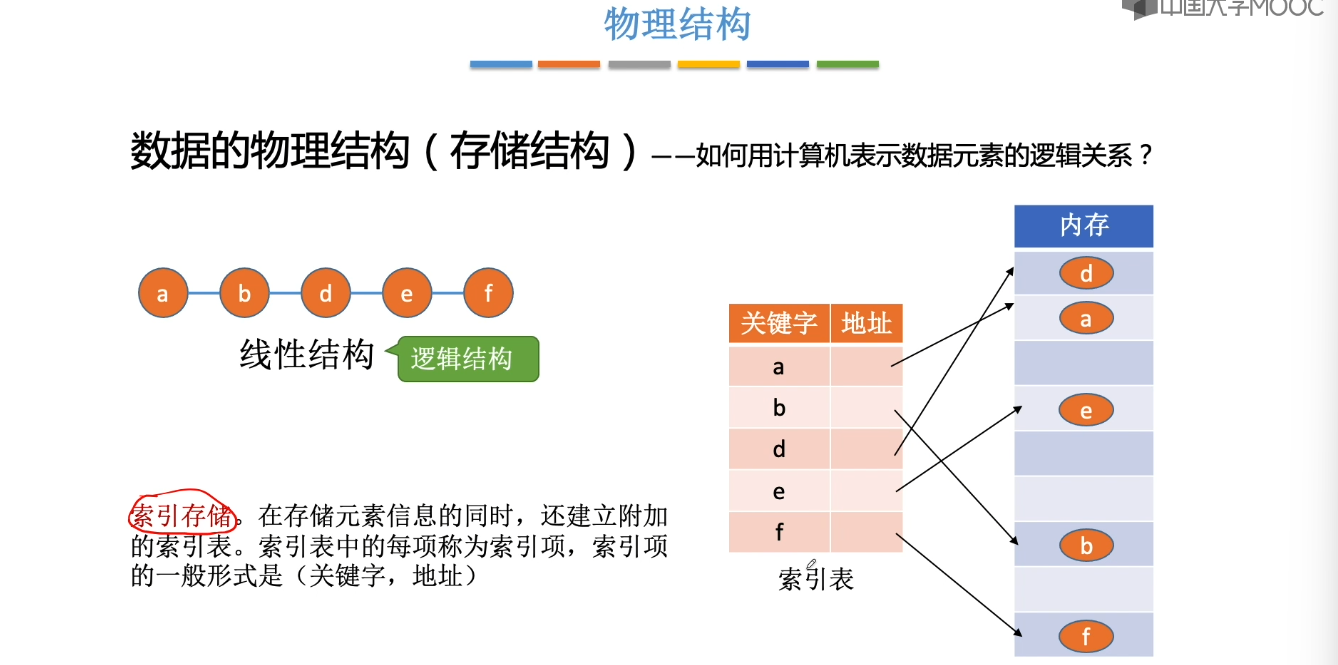
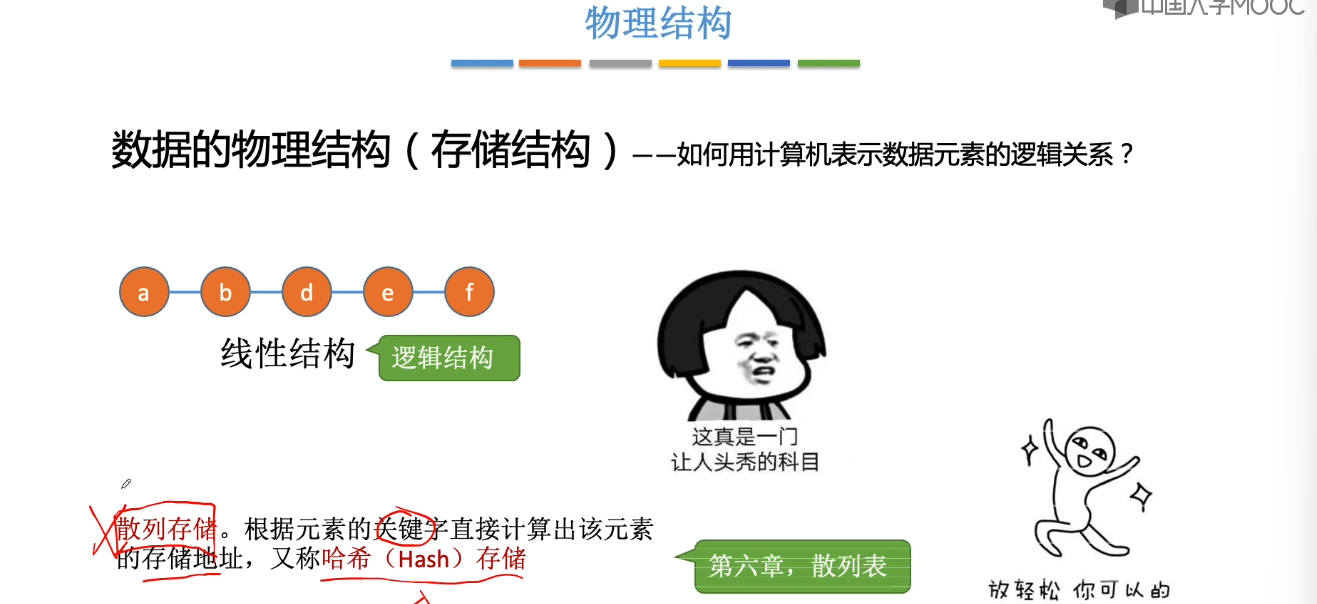
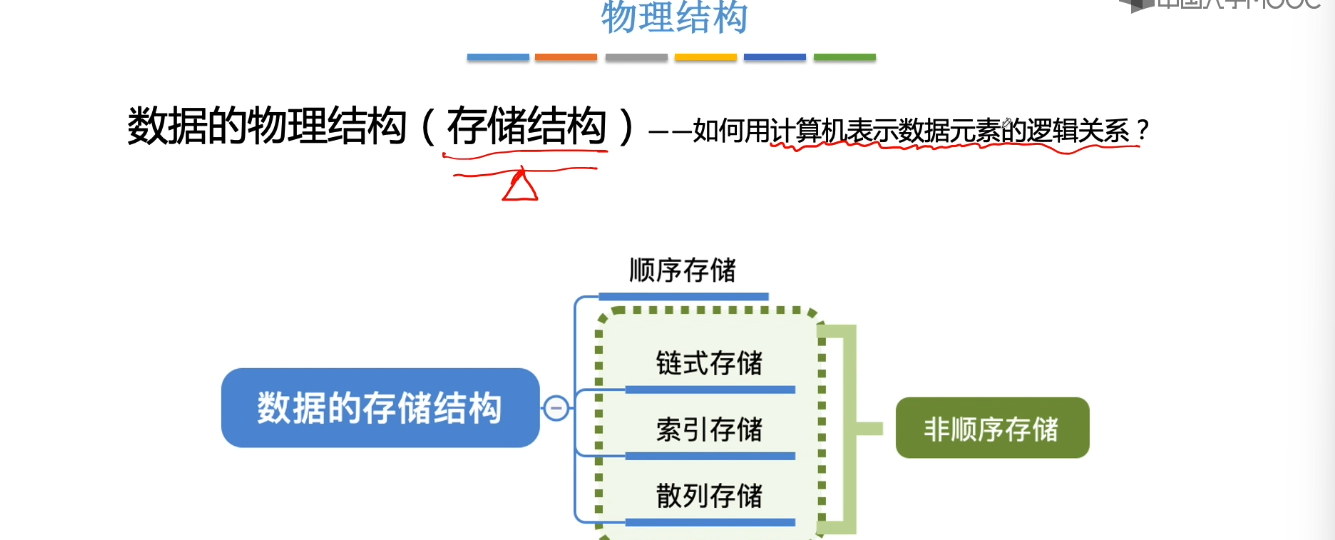
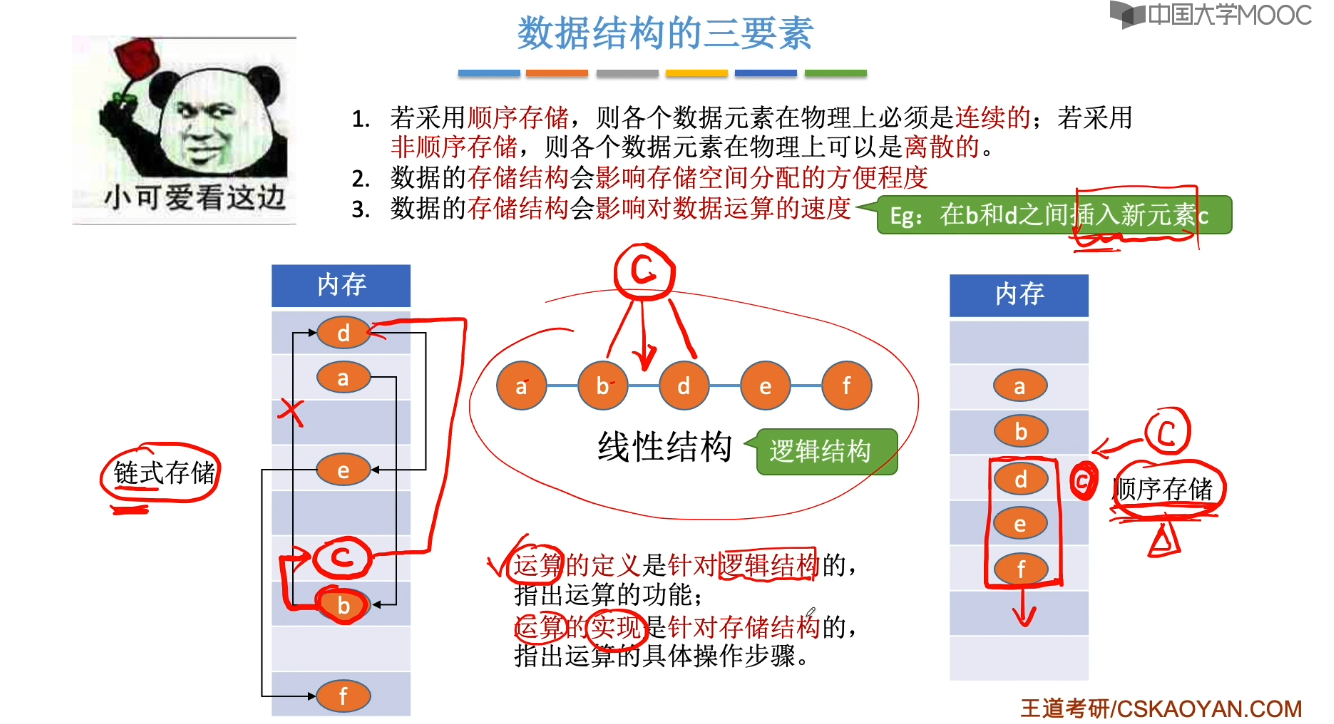
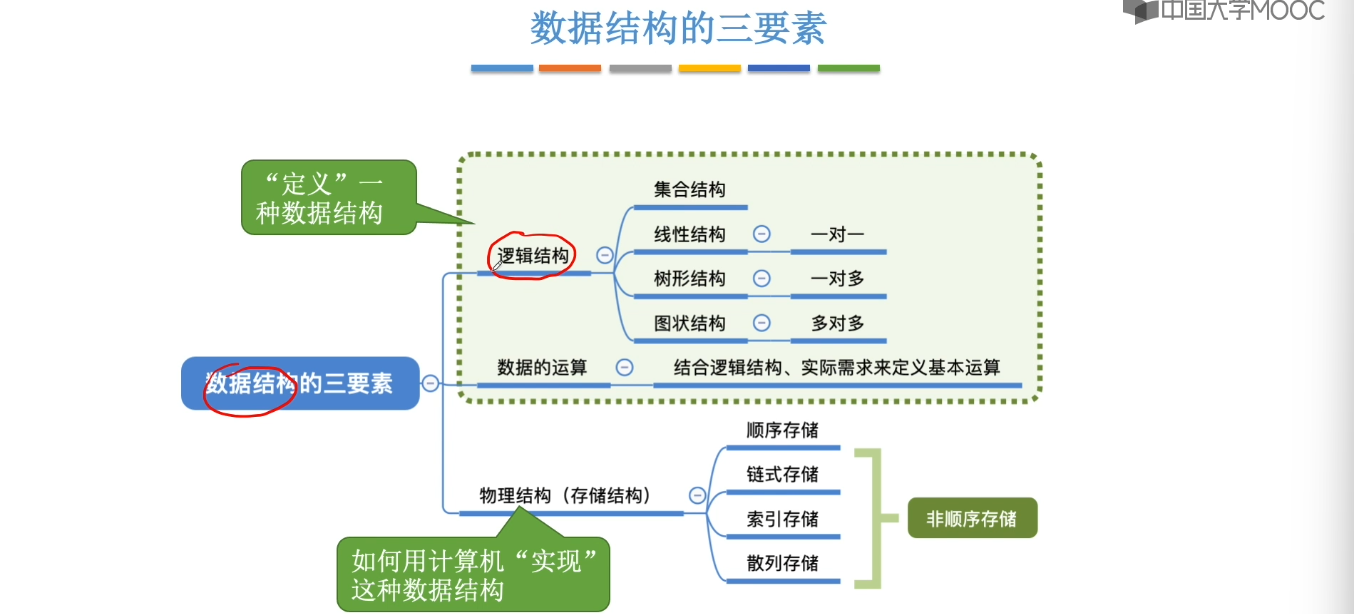
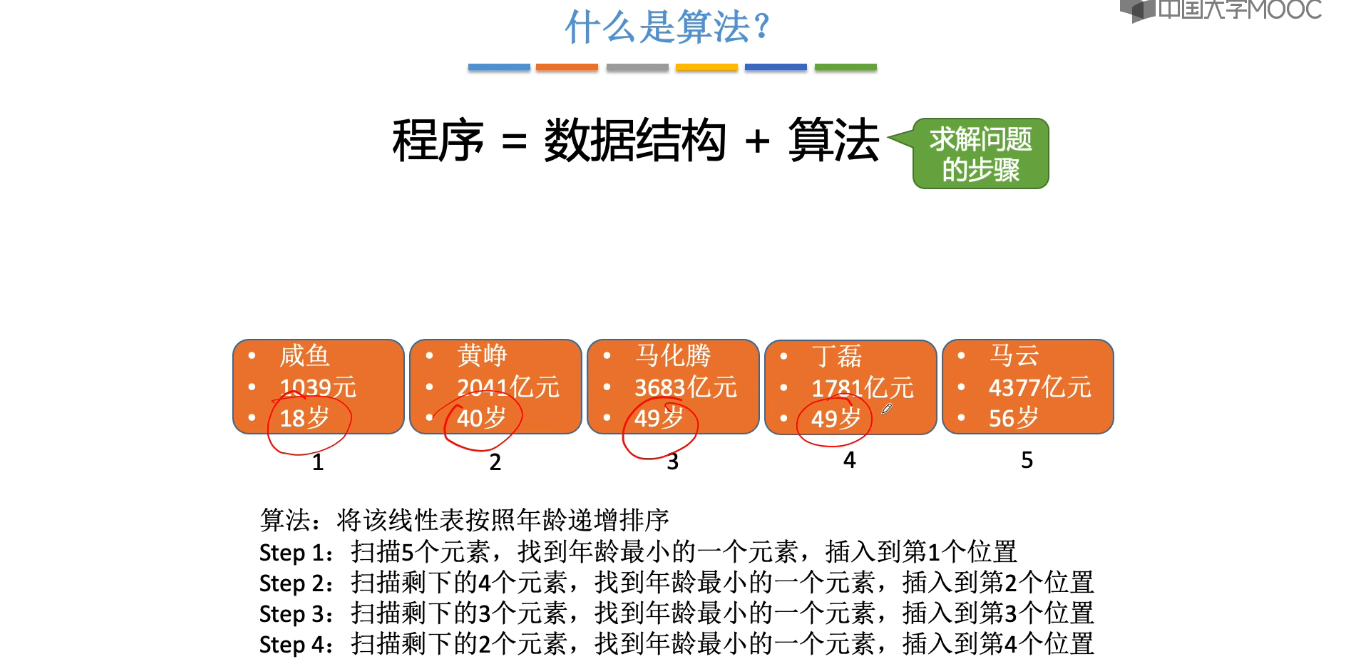
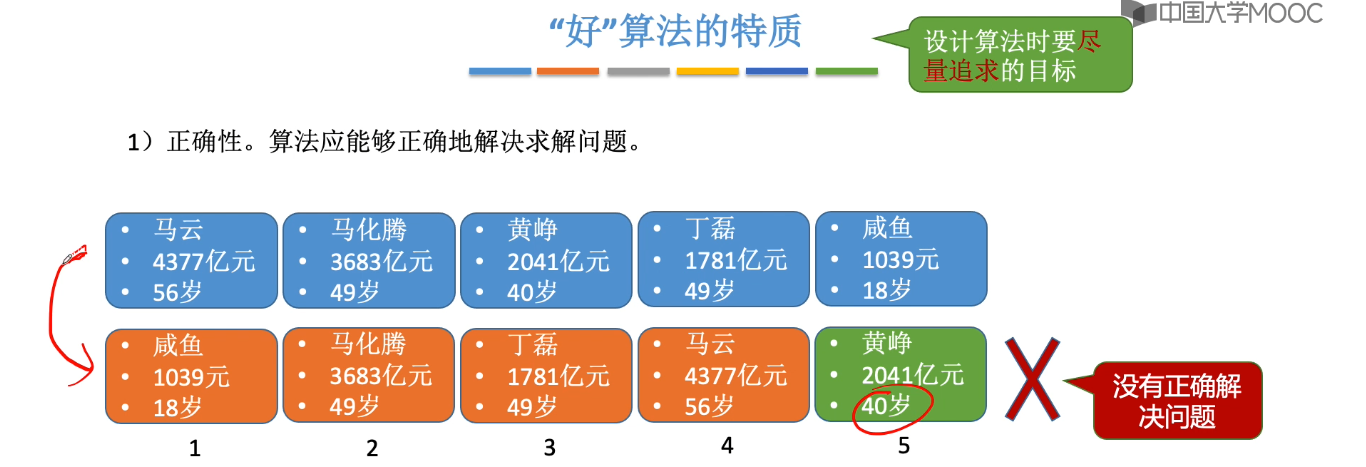
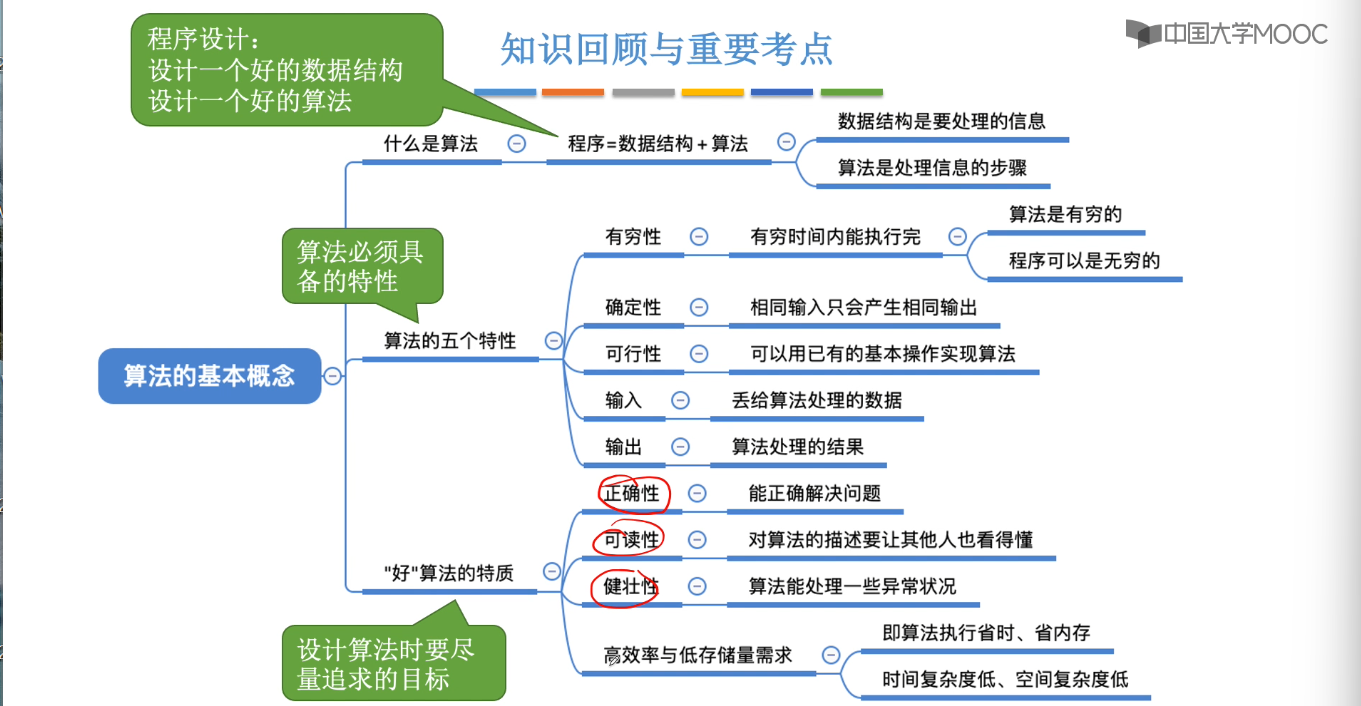
1.4、算法的基本概念






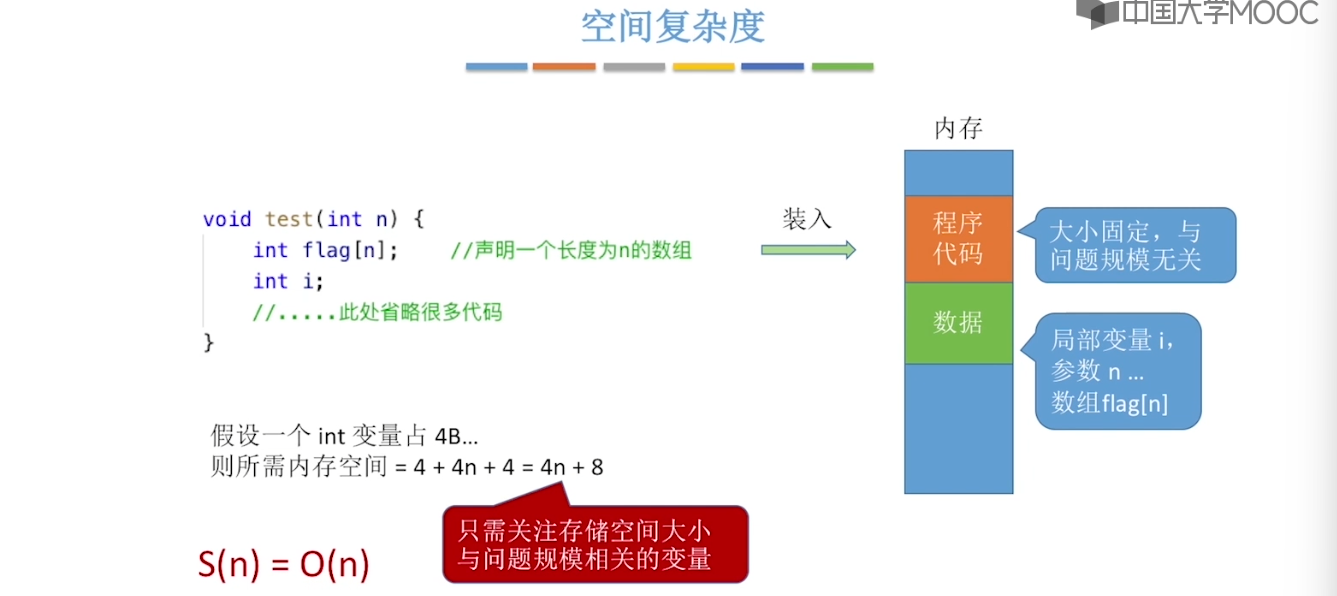
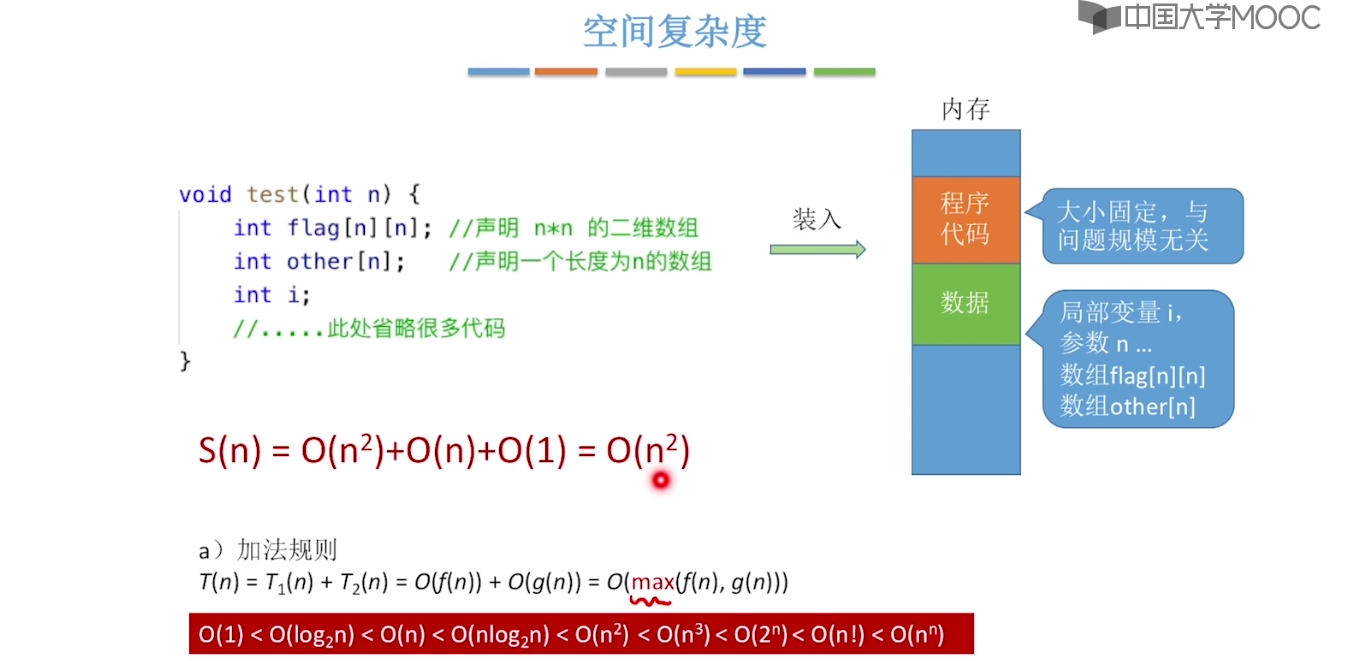
1.5、算法的空间复杂度

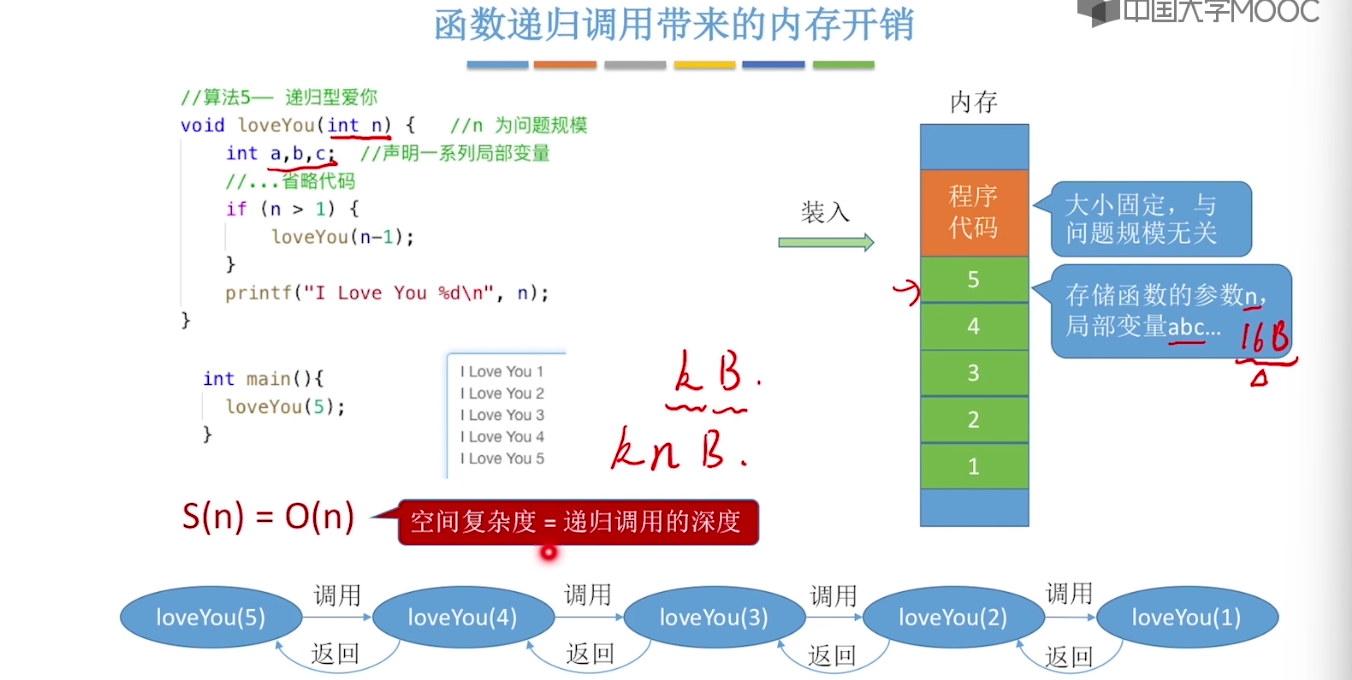
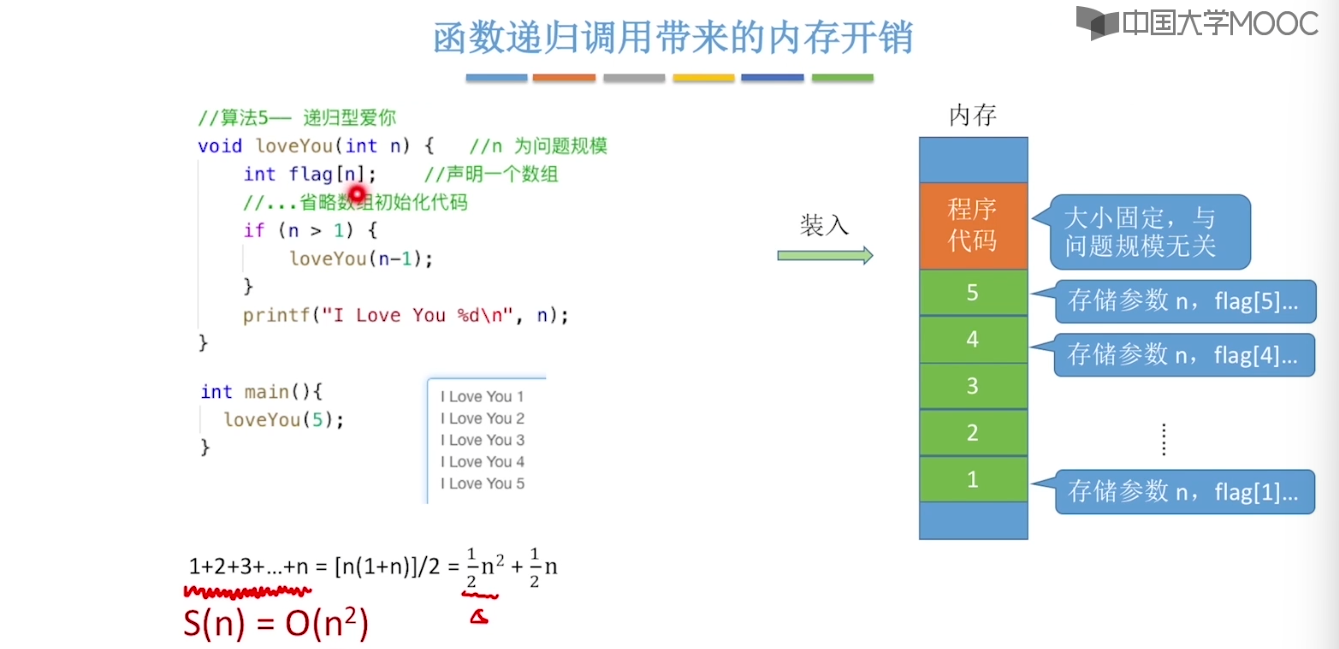

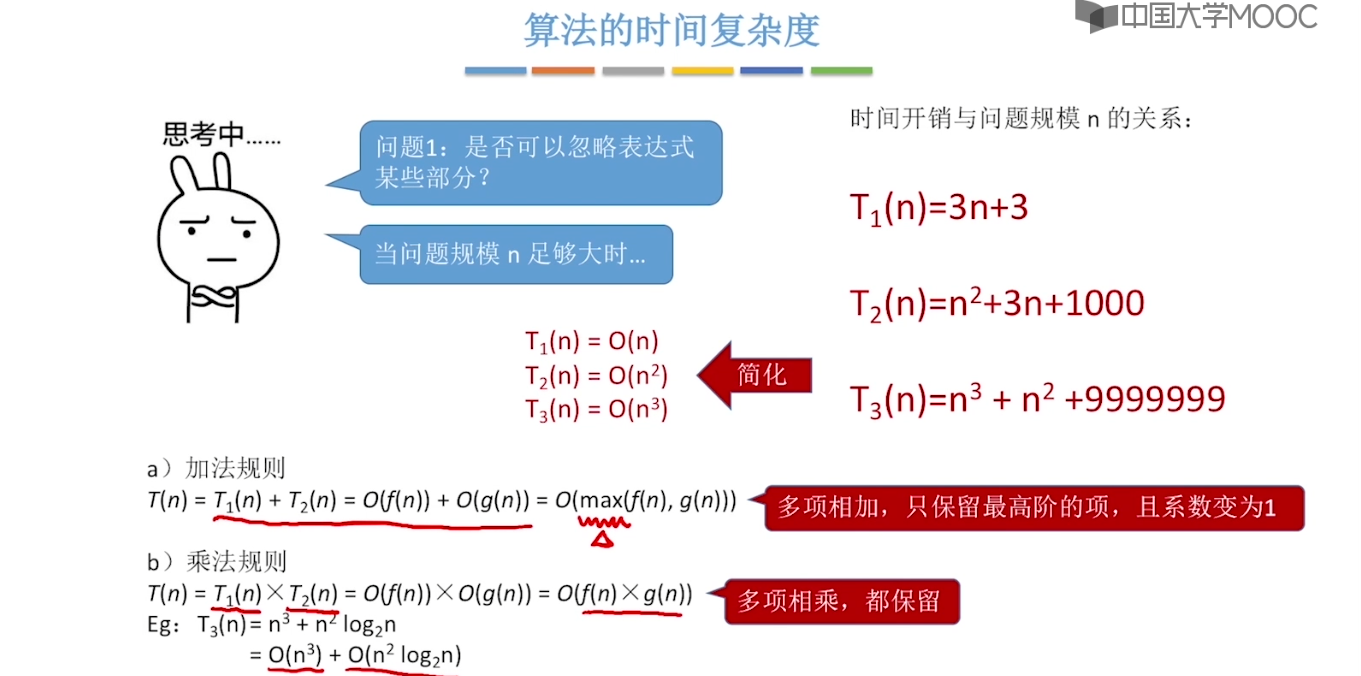
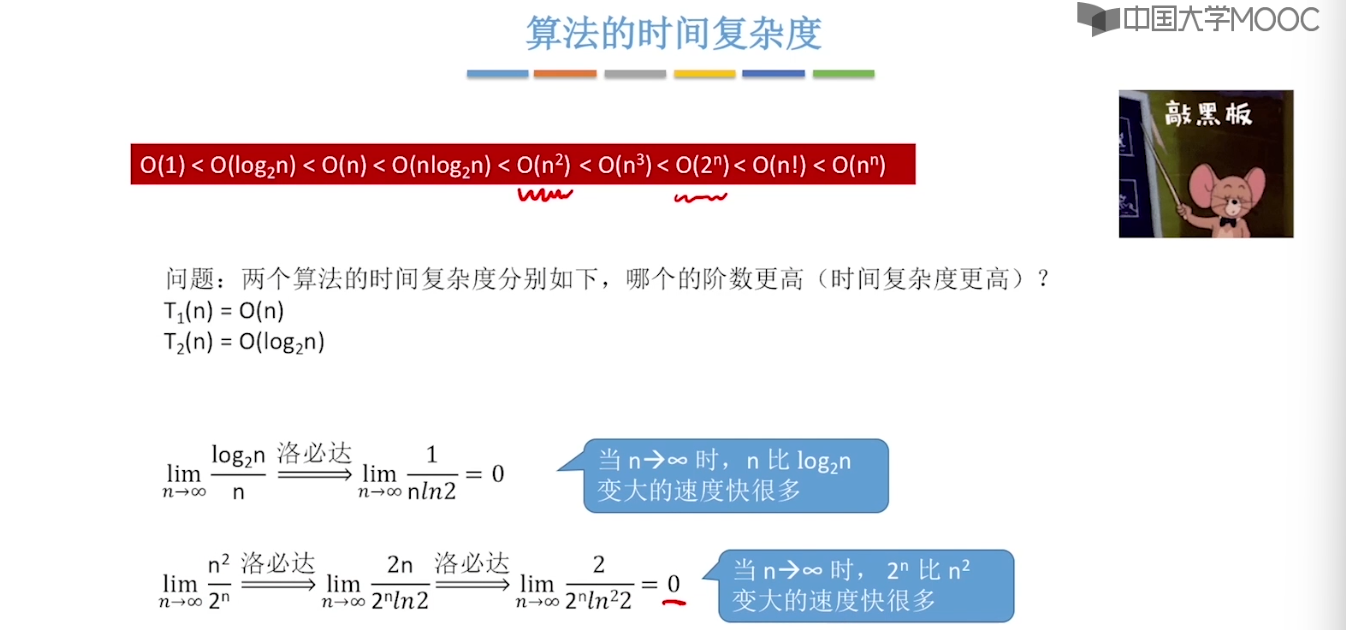
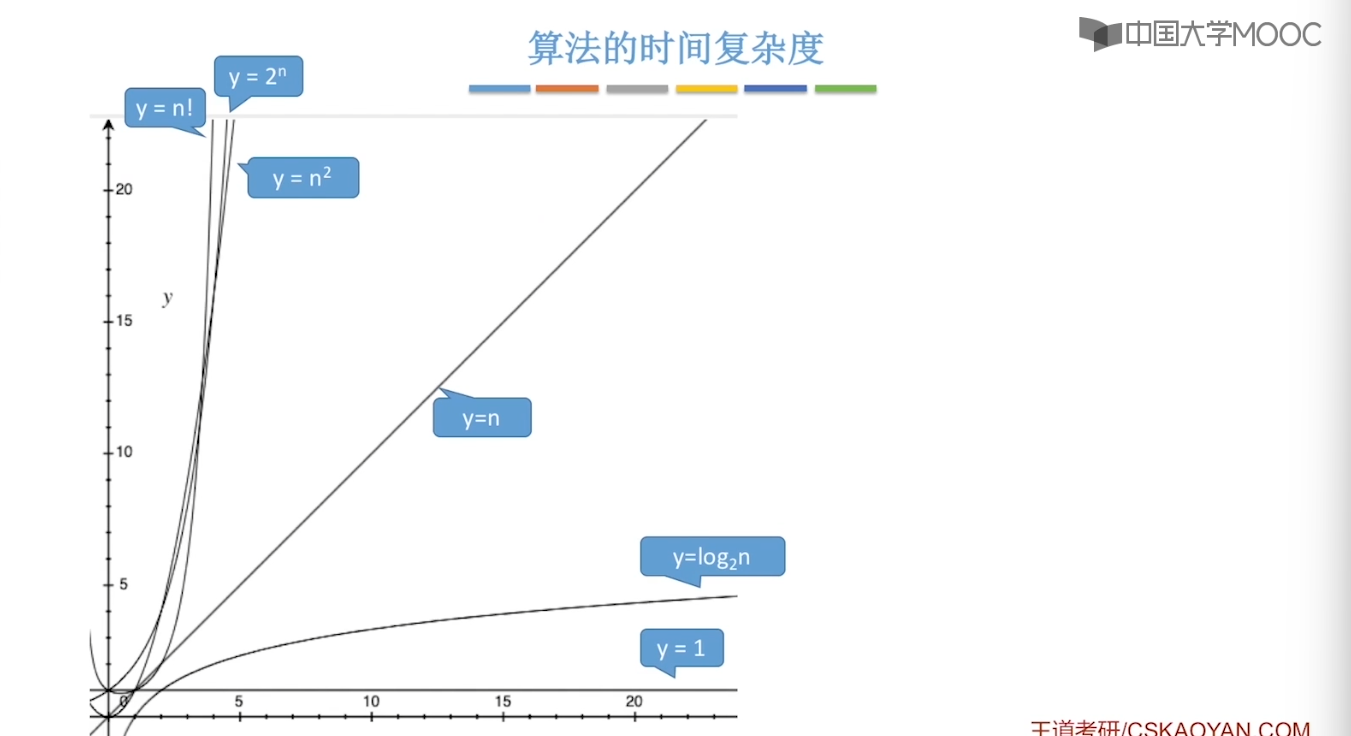
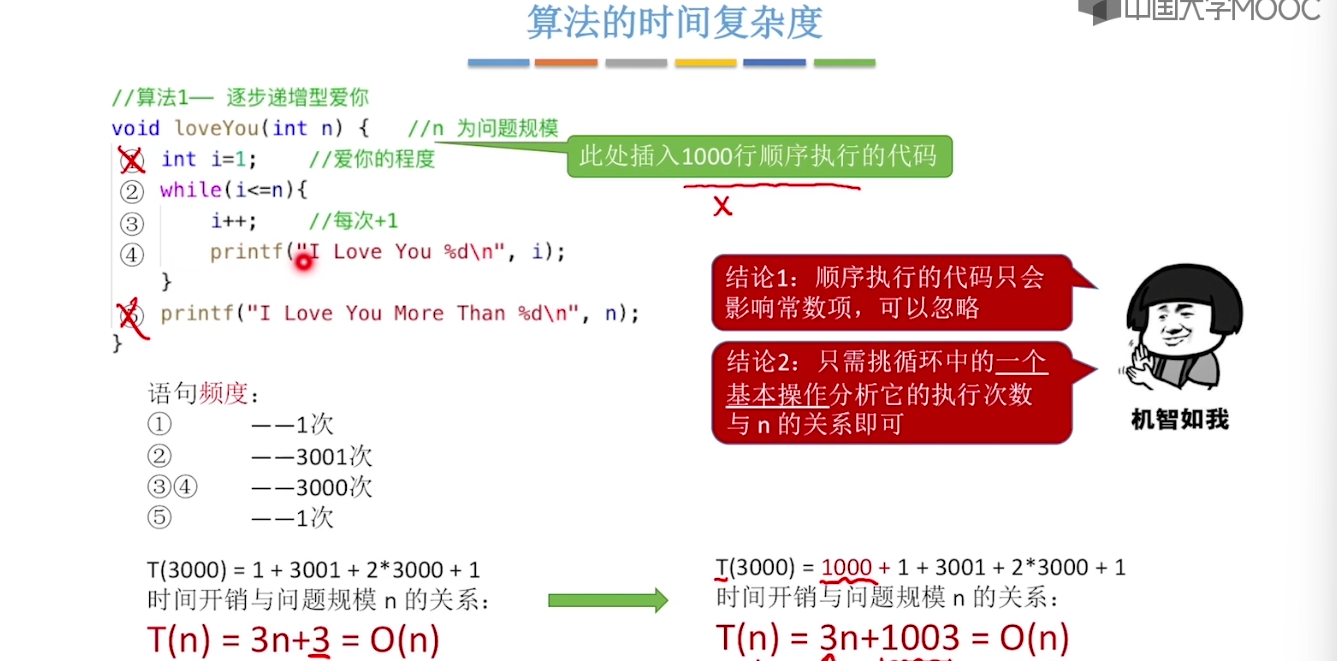
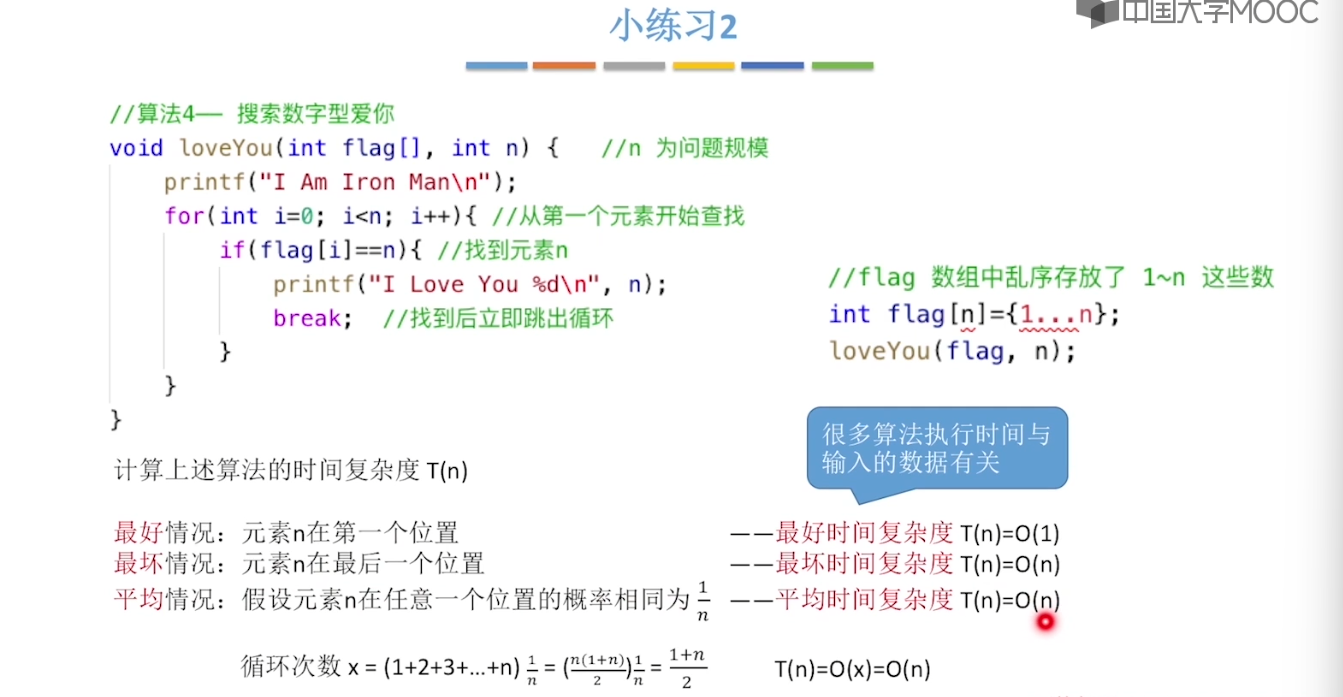
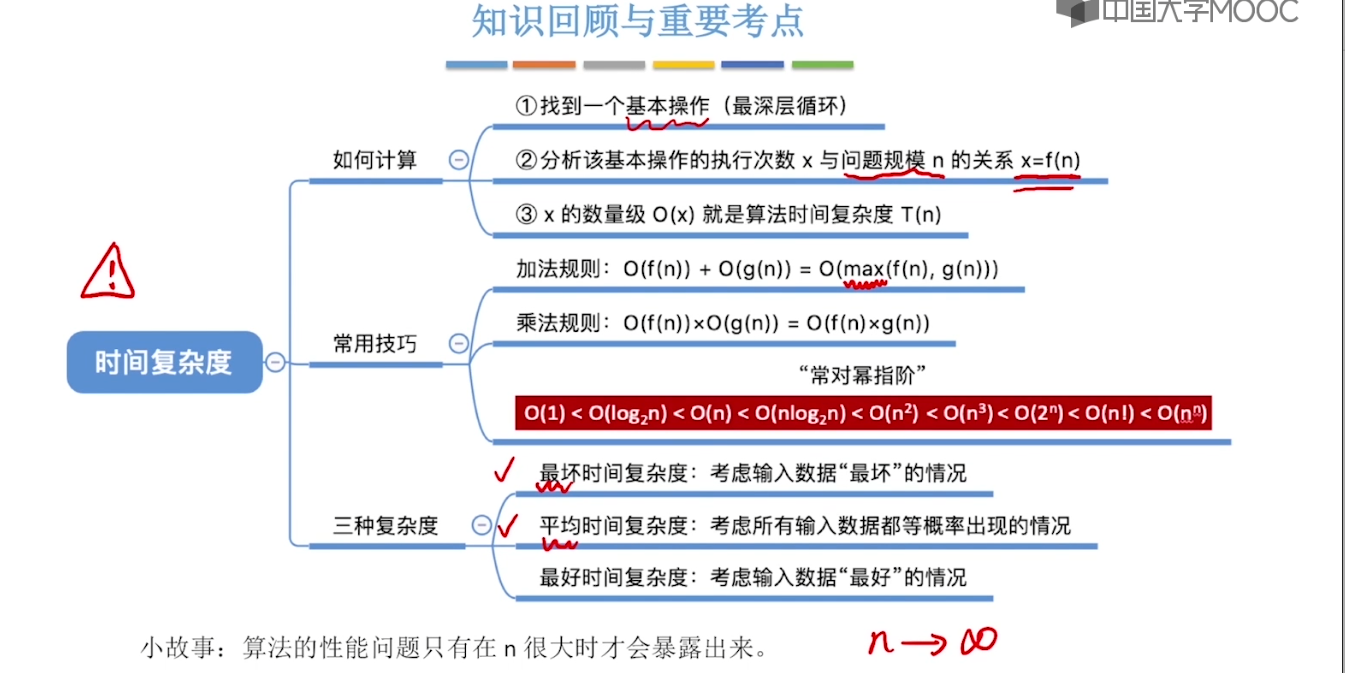
1.6、算法的时间复杂度







2、线性表
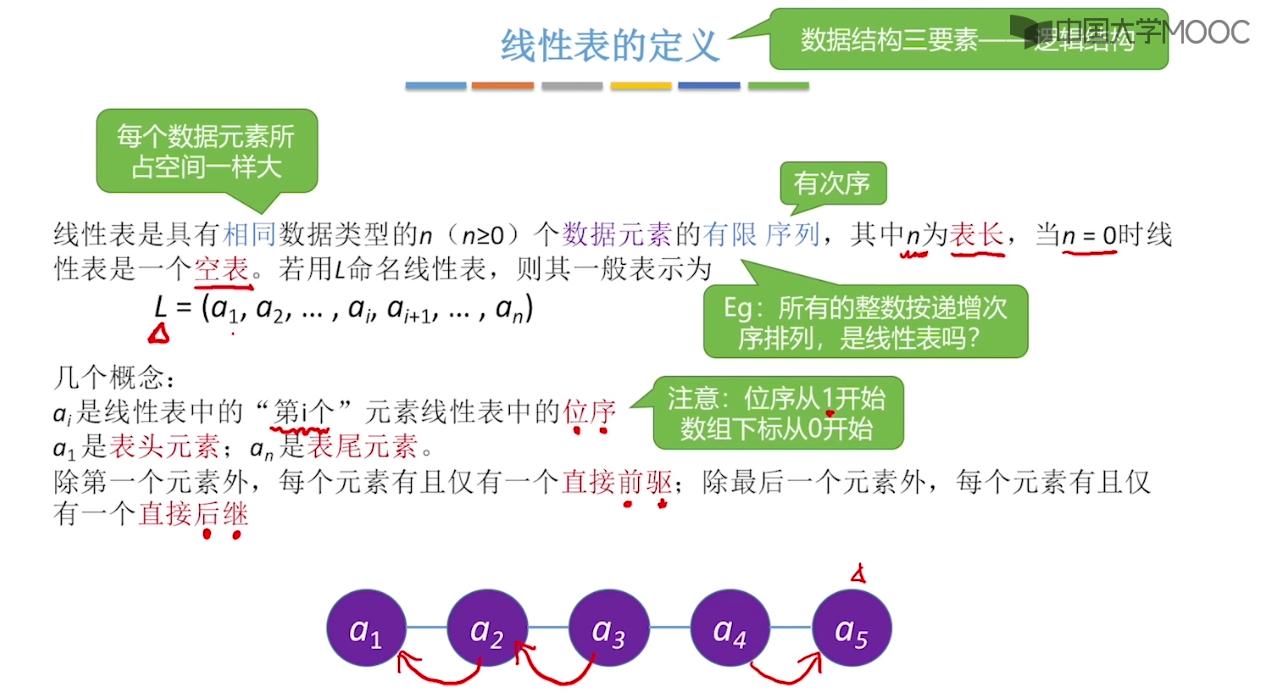
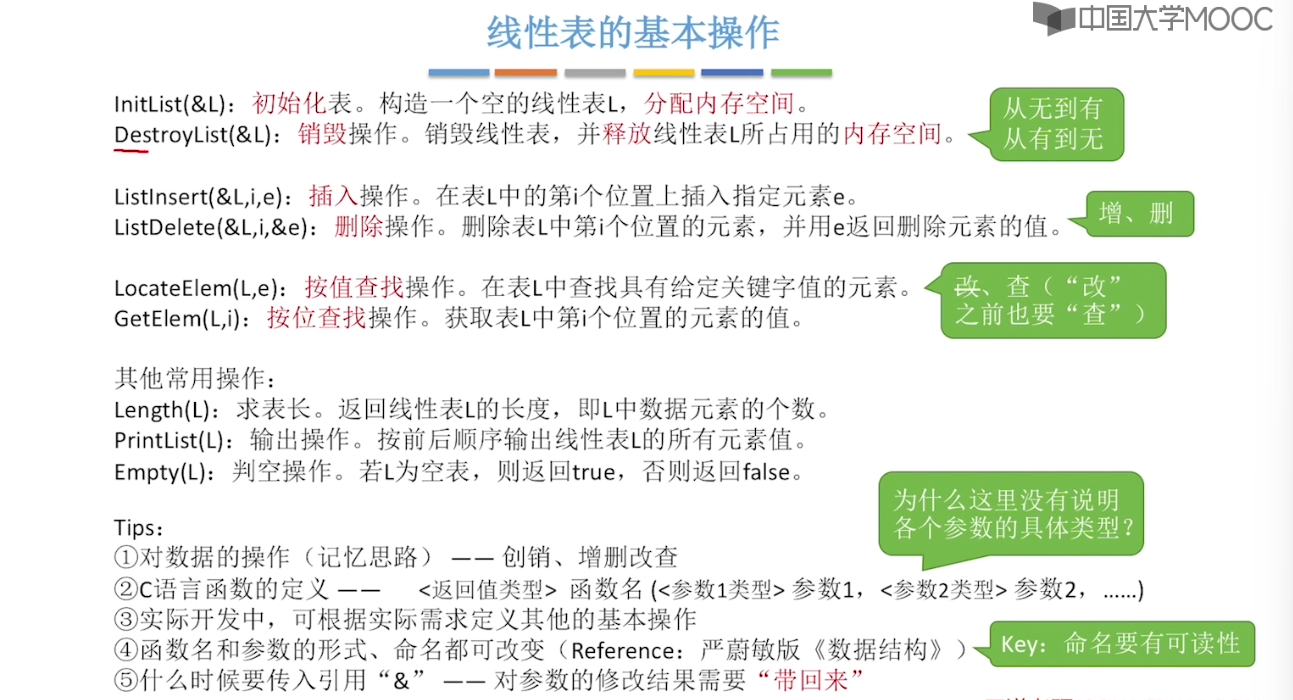
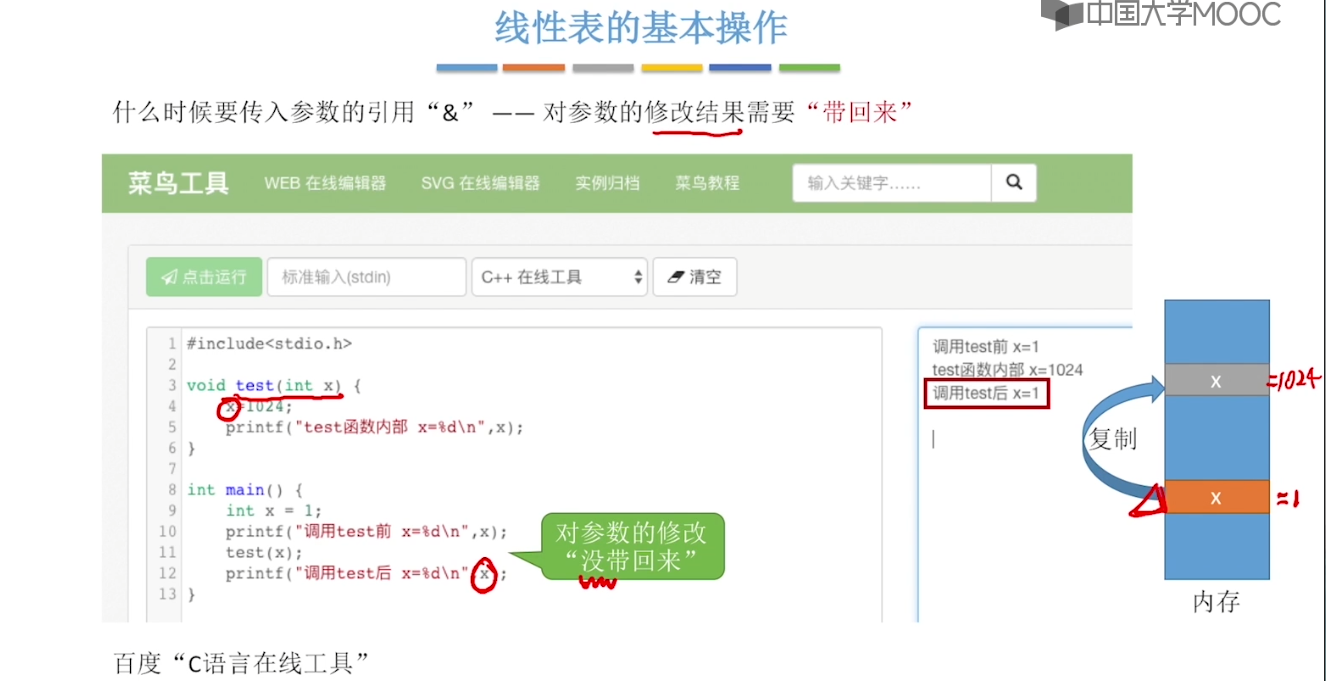
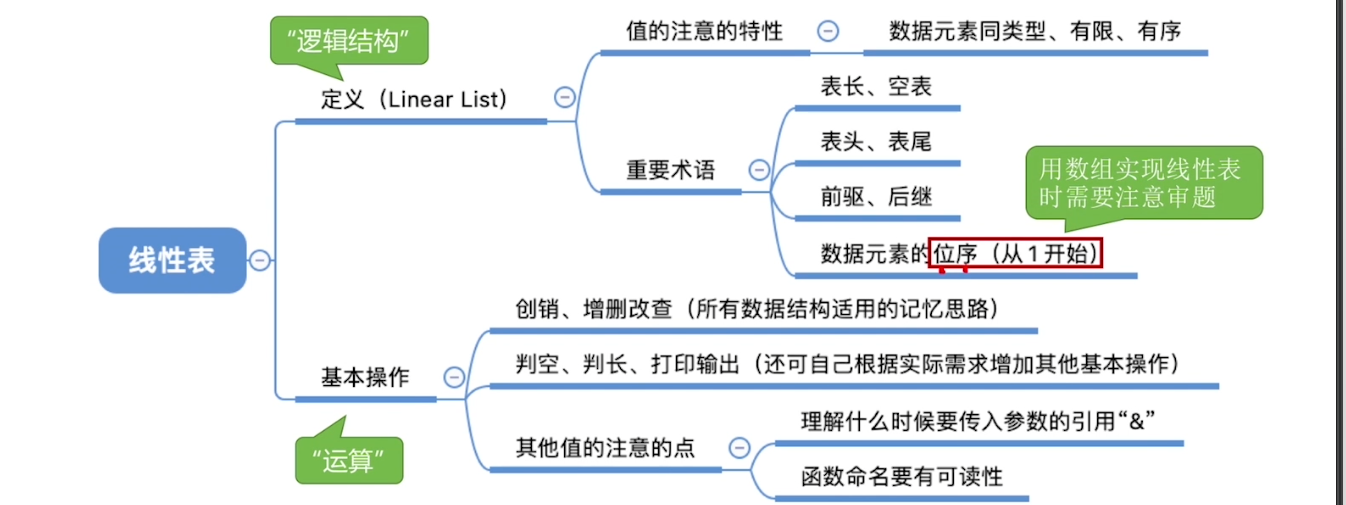
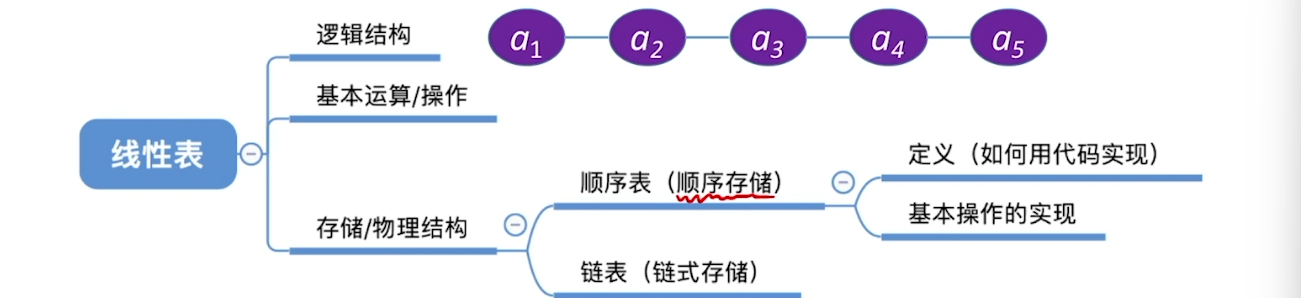
2.1、线性表的定义和基本操作
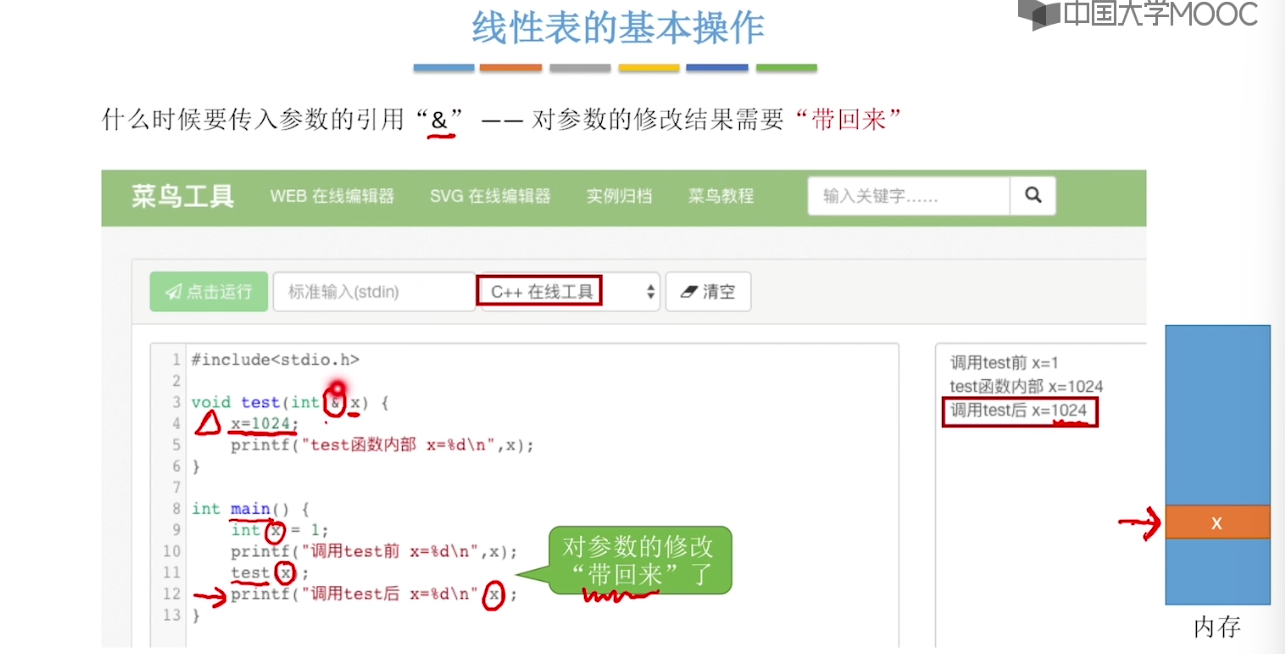
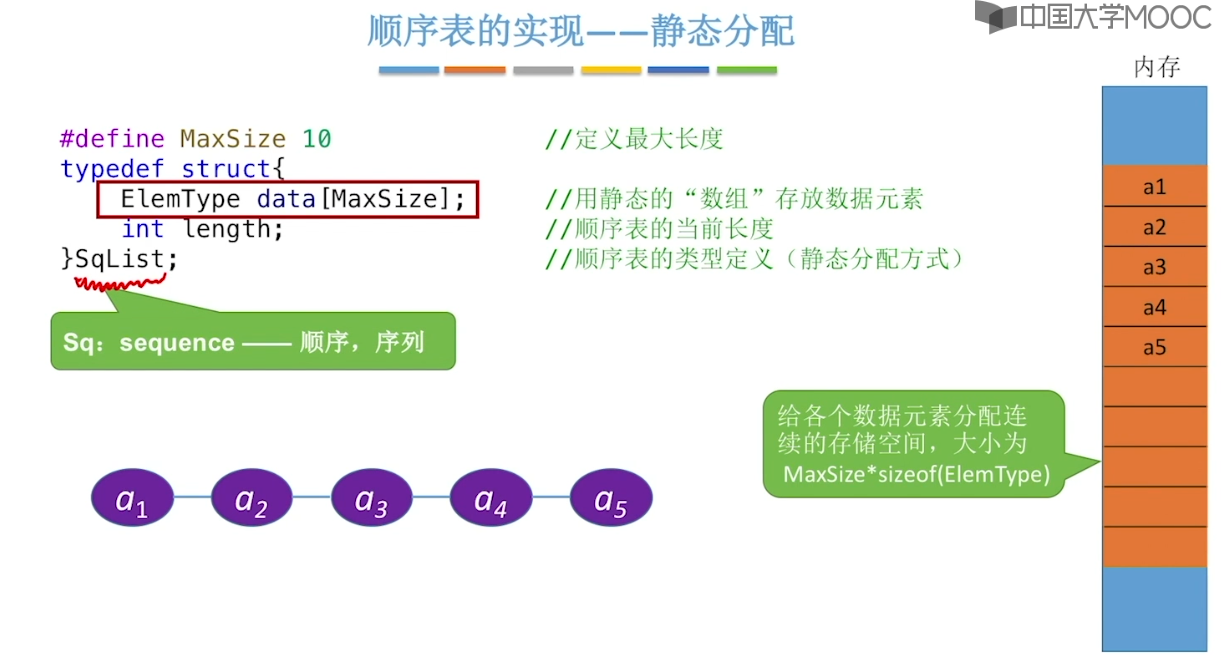
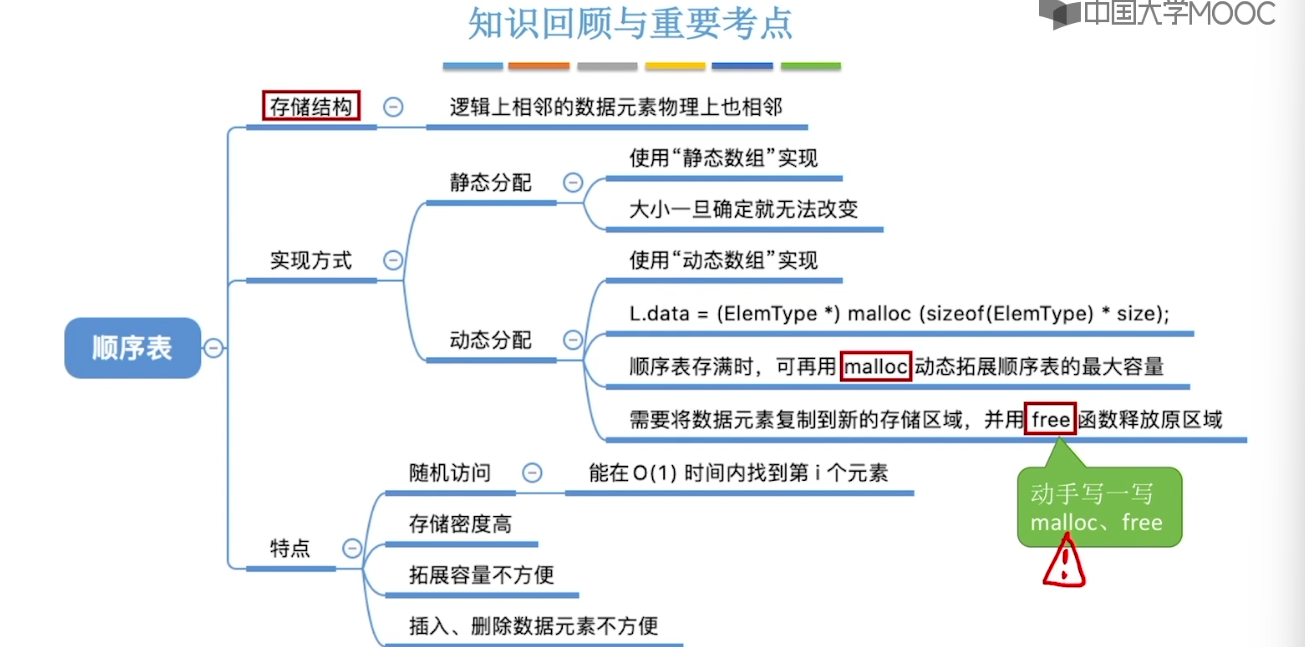
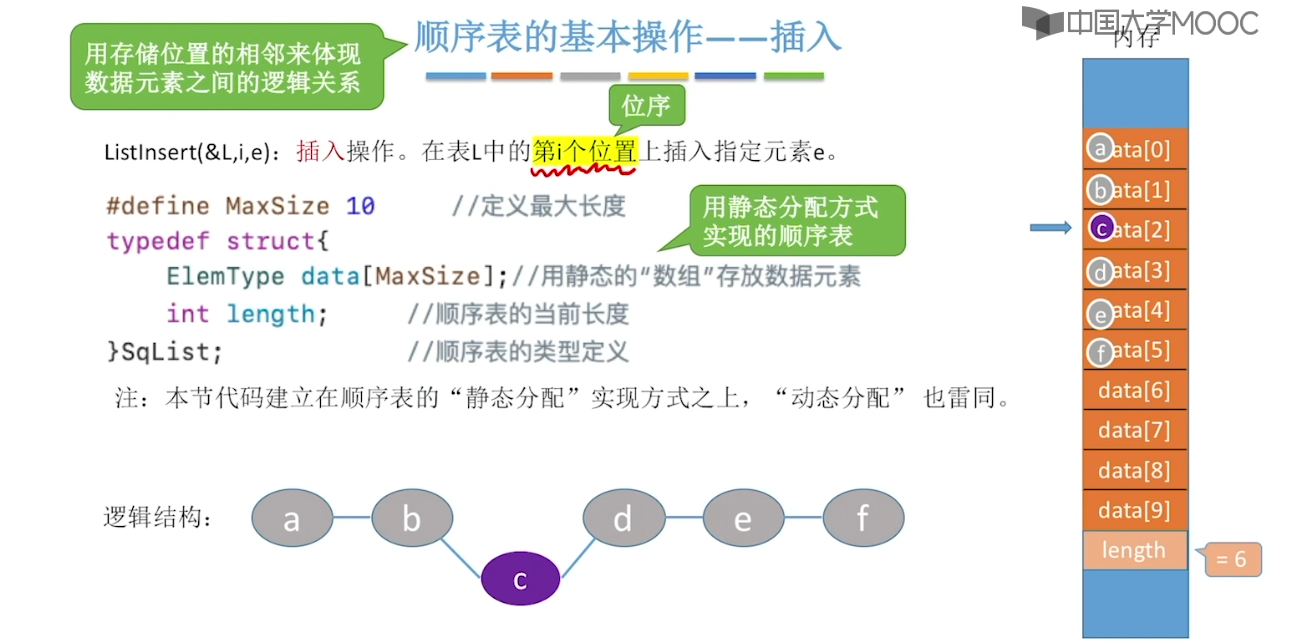
2.2、顺序表的定义 & 插入删除
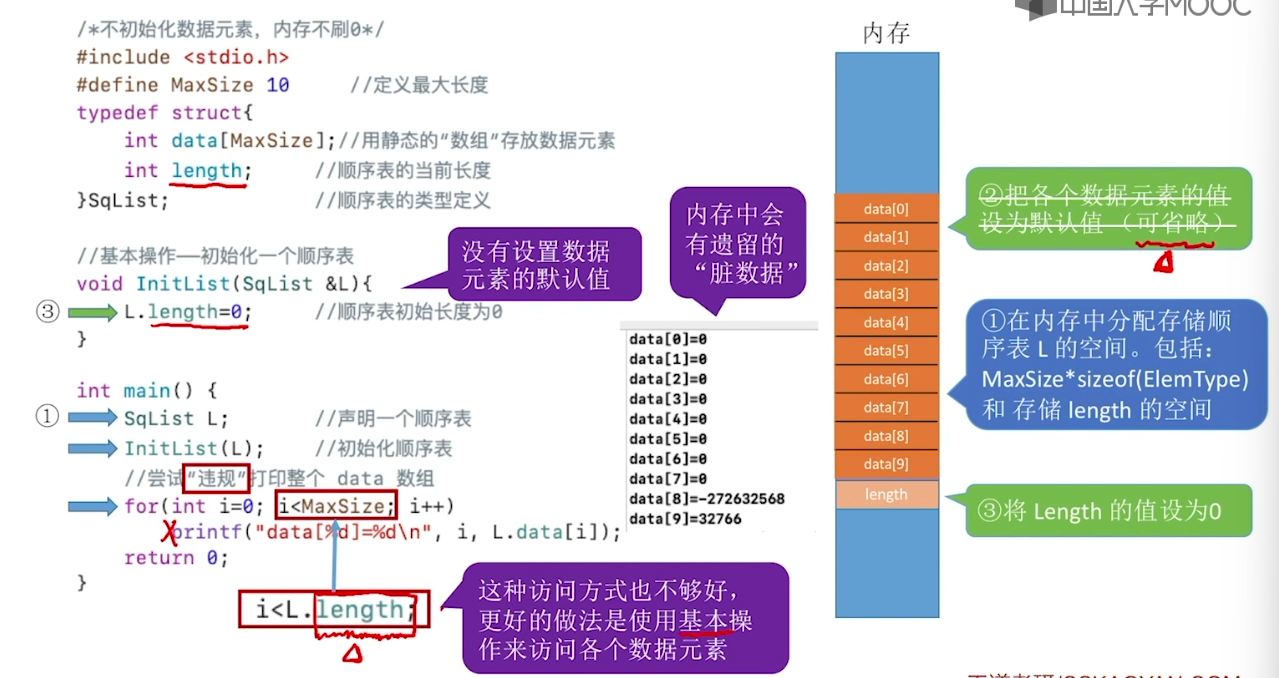
#include<stdio.h>
#include<string.h>
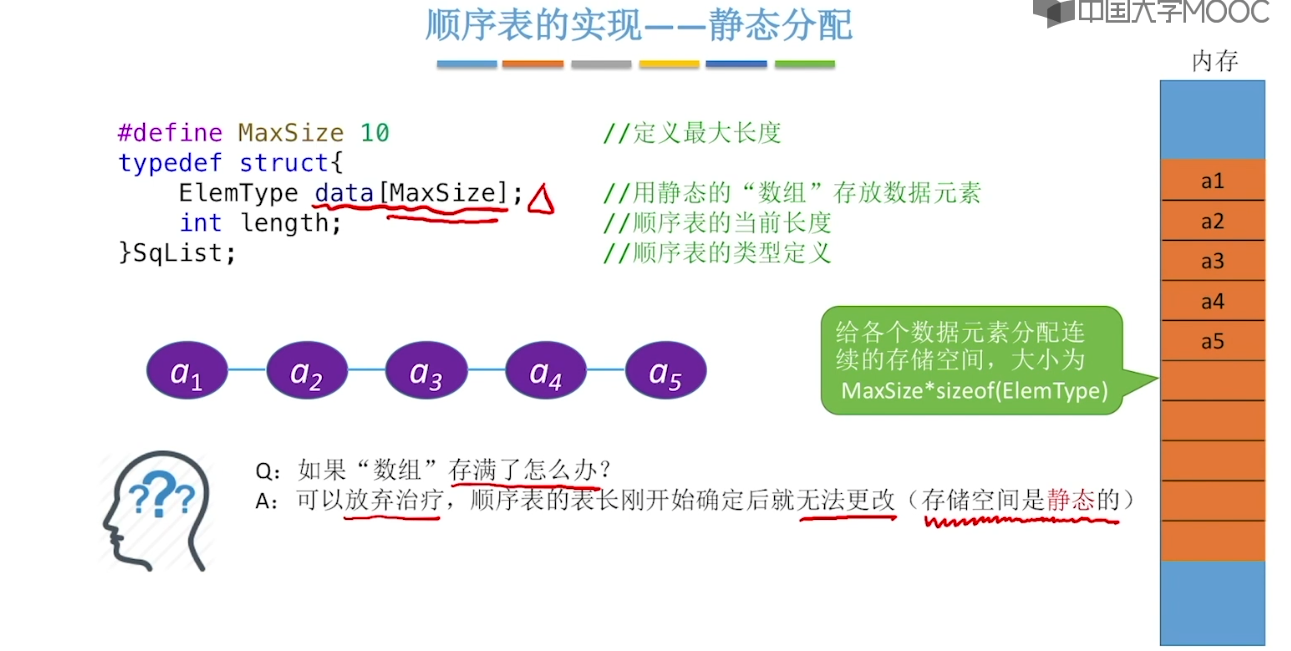
#define MaxSize 10 // 定义最大长度
#define ElemType int // 定义元素类型为 int
// 静态顺序表的类型定义(静态分配方式)
typedef struct {
ElemType data[MaxSize]; // 用静态的”数组“存放数据元素
int length; // 顺序表的当前长度
}StaticSeqList;
// 基本操作——初始化一个顺序表
void initList(StaticSeqList& list) {
for (int i = 0; i < MaxSize; i++) {
list.data[i] = 0; // 将所有数据元素设置为默认初始值
}
list.length = 0; // 顺序表初识长度为0
}
int main() {
StaticSeqList list; // 声明一个顺序表
initList(list); // 初始化顺序表
return 0;
}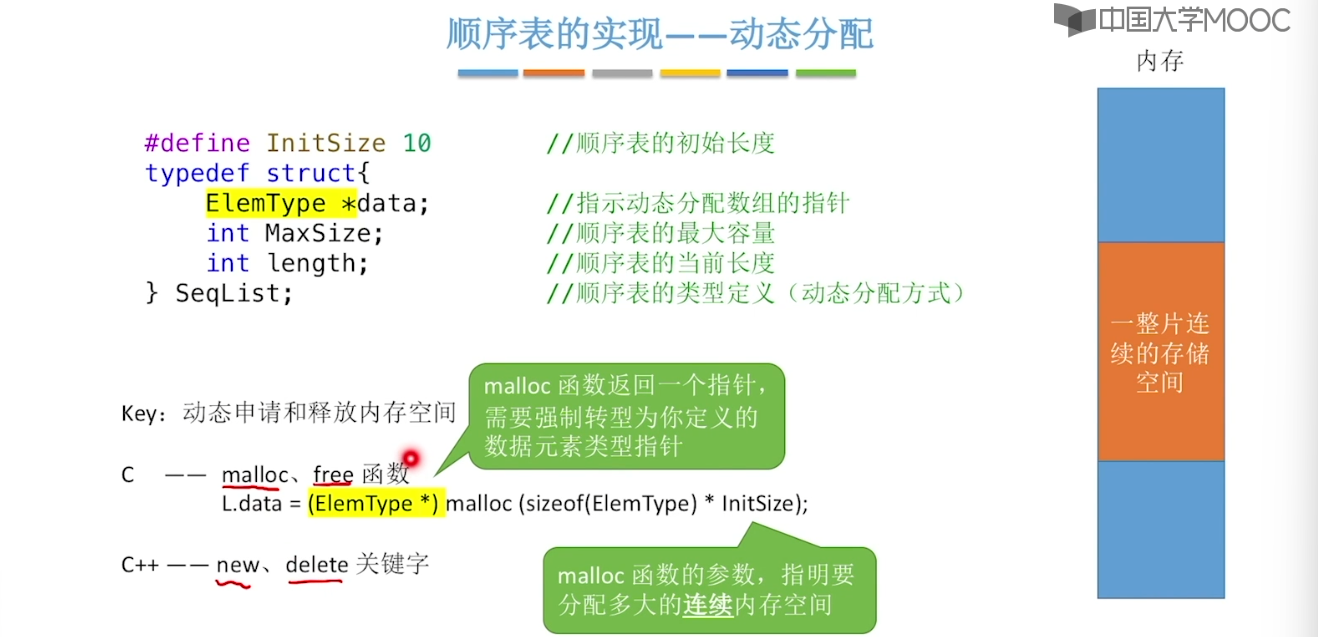


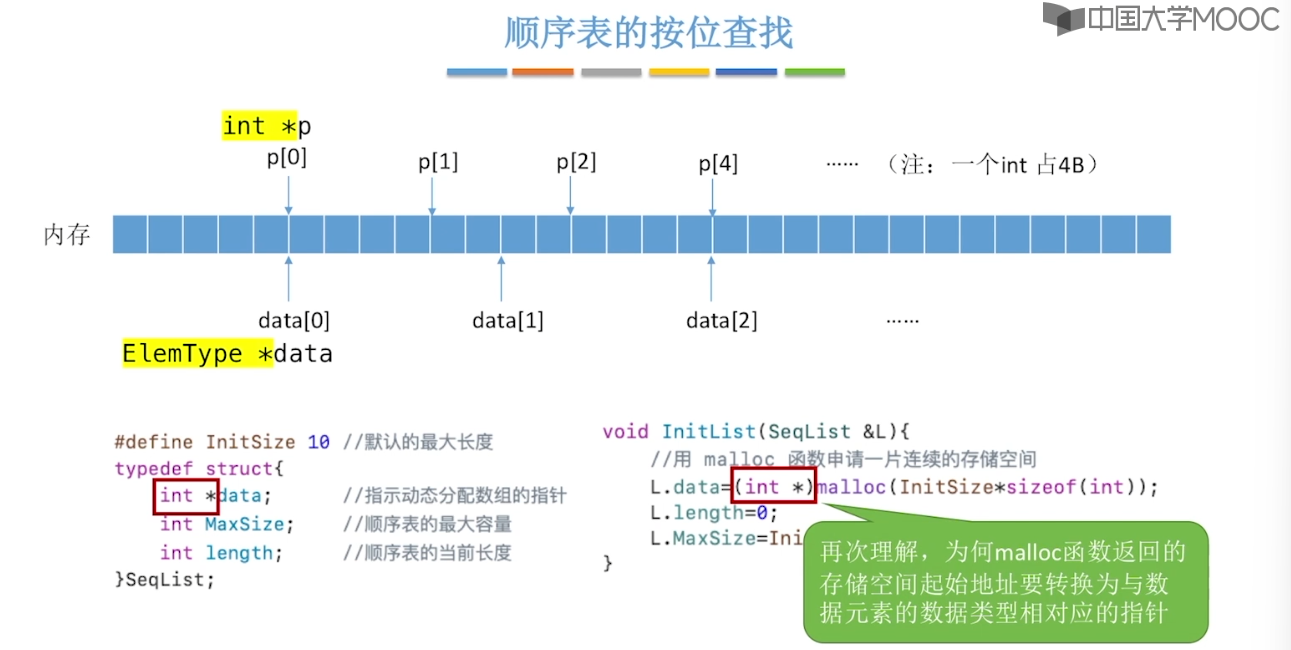
#include<stdio.h>
#include<stdlib.h>
#define InitSize 10 // 顺序表的初始长度
typedef struct {
int* data; // 指示动态分配数组的指针
int length; // 顺序表的当前长度
int maxSize; // 顺序表的最大容量
}DynaSeqList;
void initList(DynaSeqList& list) {
// 用 malloc 函数申请一片连续的存储空间
list.data = (int*)malloc(InitSize * sizeof(int));
list.length = 0;
list.maxSize = InitSize;
}
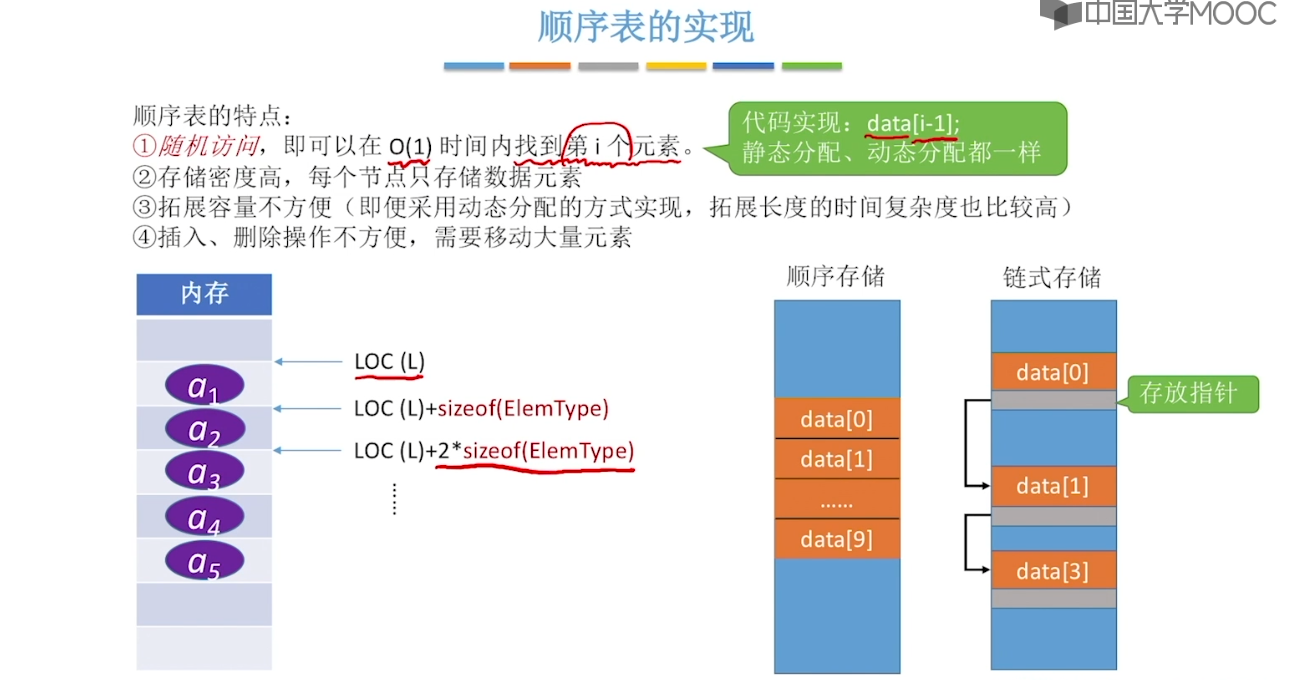
// 增加动态数组的长度
void increaseSize(DynaSeqList& list, int len) {
int* p = list.data;
list.data = (int*) malloc((list.maxSize + len) * sizeof(int));
for (int i = 0; i < list.length; i++) {
list.data[i] = p[i]; // 将数据复制到新区域
}
list.maxSize = list.maxSize + len; // 顺序表最大长度增加len
free(p); // 释放原来的内存空间
}


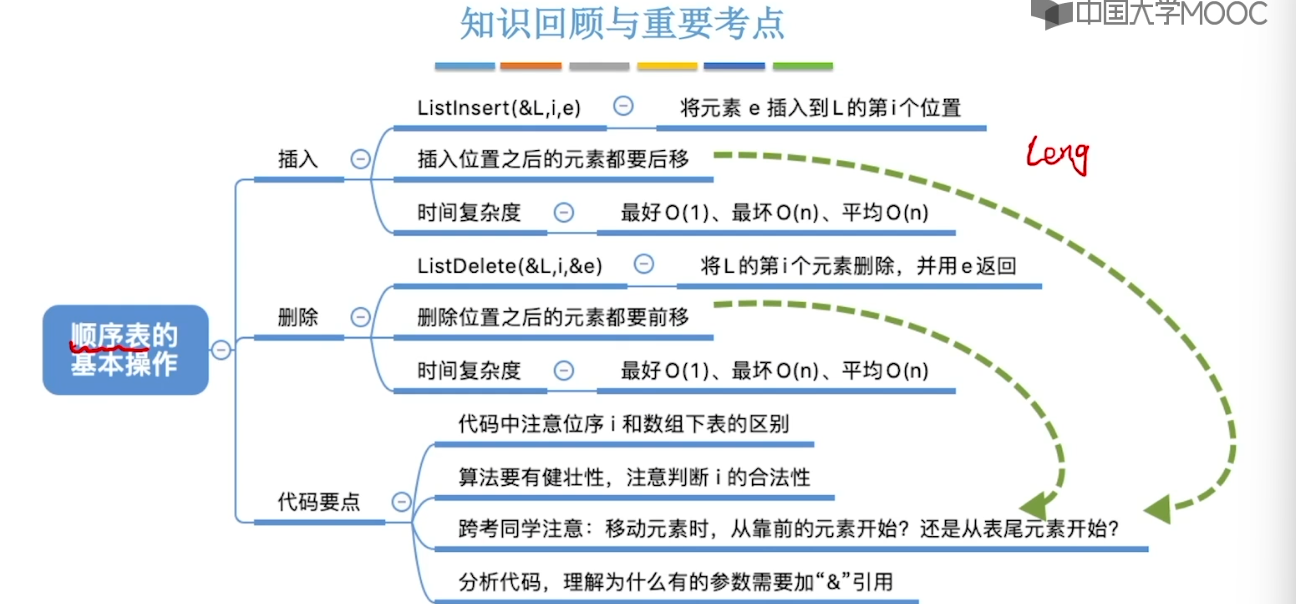
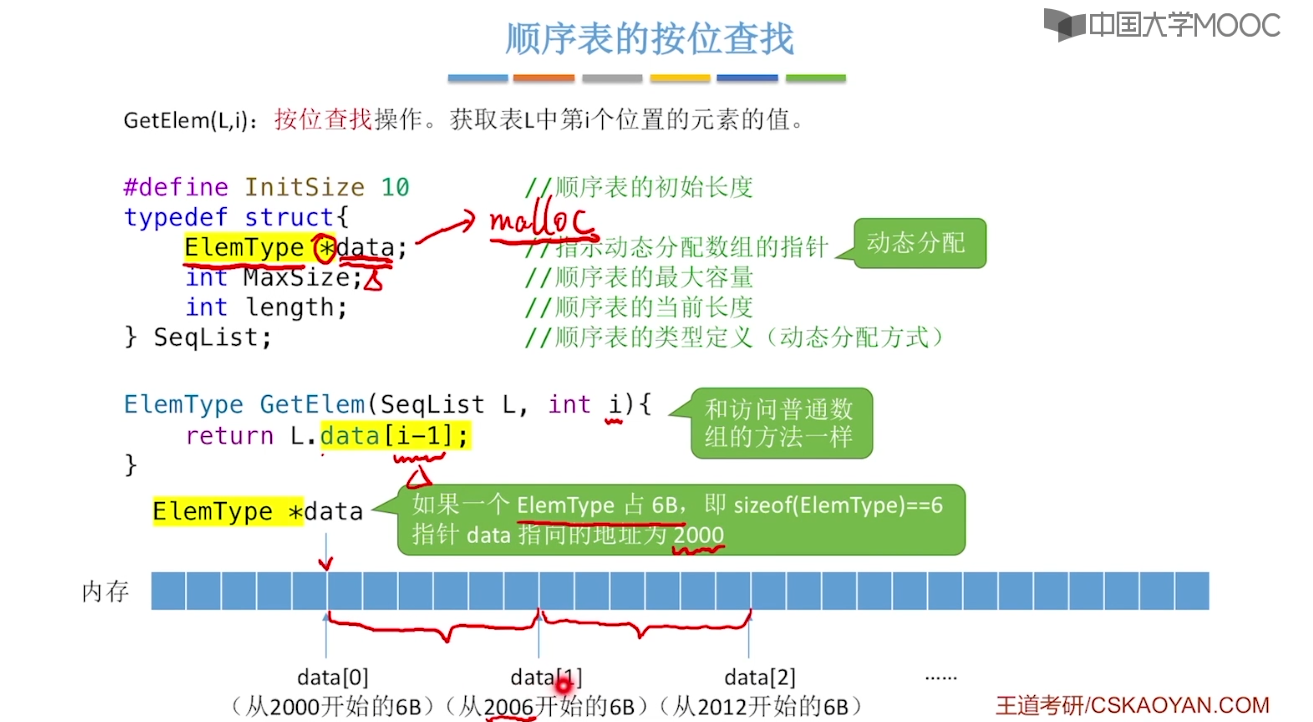
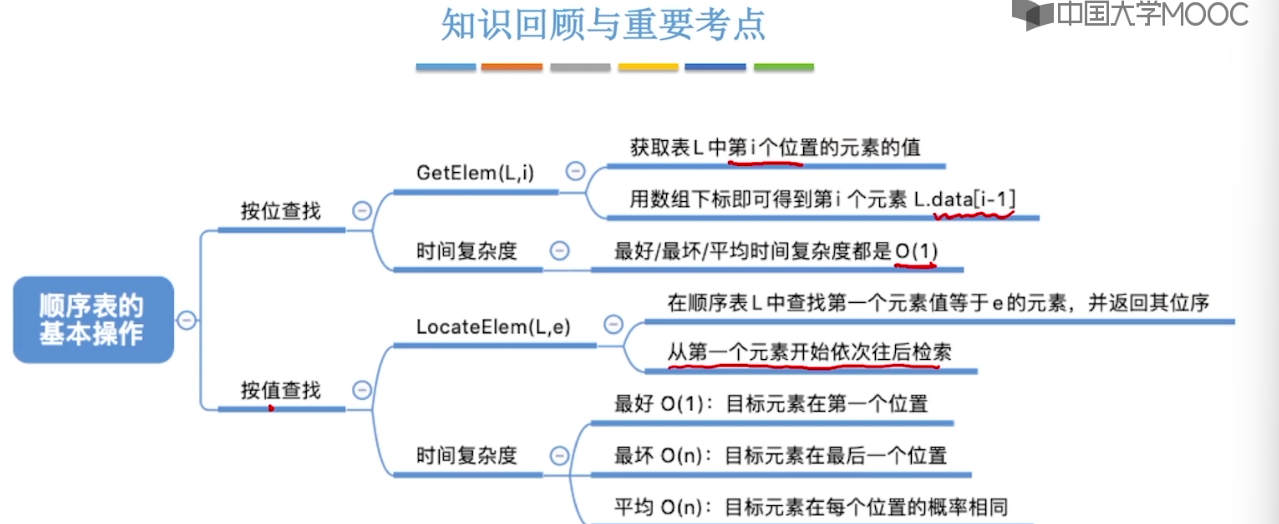
2.2、顺序表的查找







#include<stdio.h>
#include<string.h>
#define MaxSize 100 // 定义最大长度
// 静态顺序表的类型定义(静态分配方式)
typedef struct {
int data[MaxSize]; // 用静态的”数组“存放数据元素
int length; // 顺序表的当前长度
}StaticSeqList;
// 基本操作——初始化一个顺序表
bool initList(StaticSeqList& list) {
for (int i = 0; i < MaxSize; i++) {
list.data[i] = 0; // 将所有数据元素设置为默认初始值
}
list.length = 0; // 顺序表初识长度为0
return true;
}
bool isFullList(StaticSeqList& list) {
return list.length >= MaxSize;
}
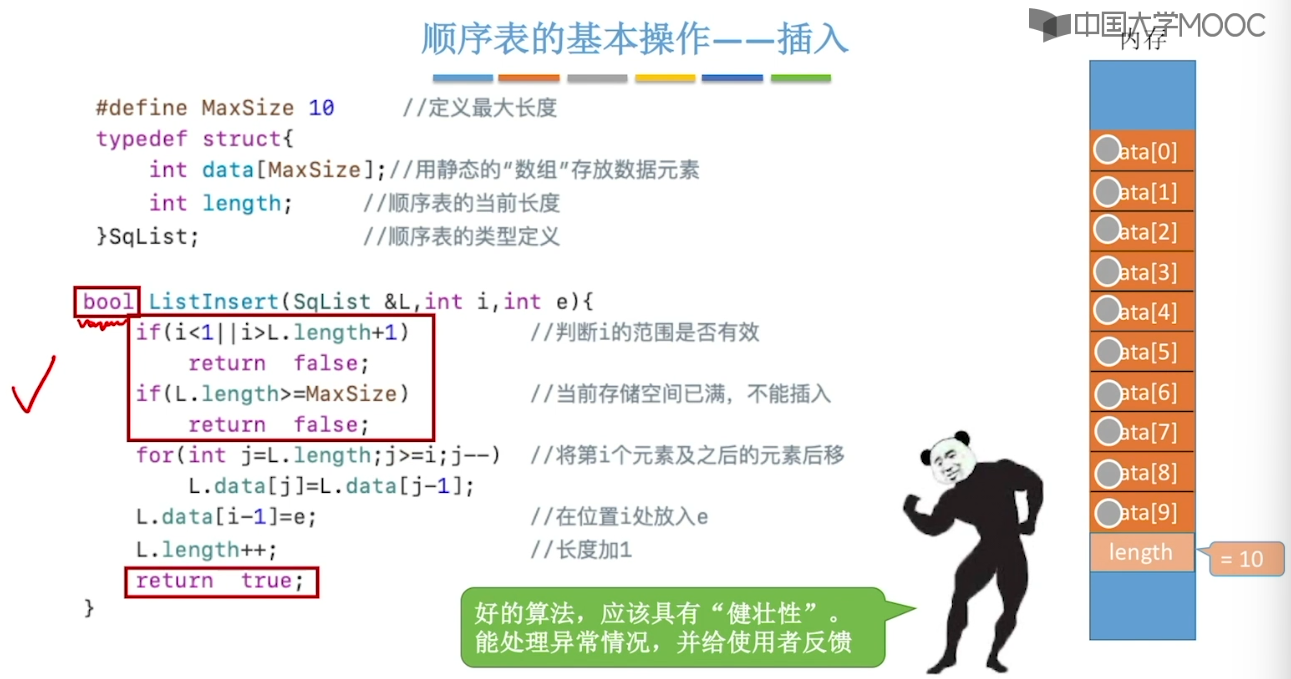
// 顺序表的插入,时间复杂度为O(n)
bool insertList(StaticSeqList& list, int index, int e) {
if (index < 0 || index >= list.length + 1) {
printf("[插入元素%d出错:元素的插入不能出现间断]\n", e);
return false;
}
if (isFullList(list)) {
printf("[表的容量已满,插入失败!]\n");
return false;
}
for (int i = list.length - 1; i >= index; i--) {
list.data[i + 1] = list.data[i];
}
list.data[index] = e;
list.length++;
}
// 判断是否为空
bool isEmptyList(StaticSeqList& list) {
return list.length == 0;
}
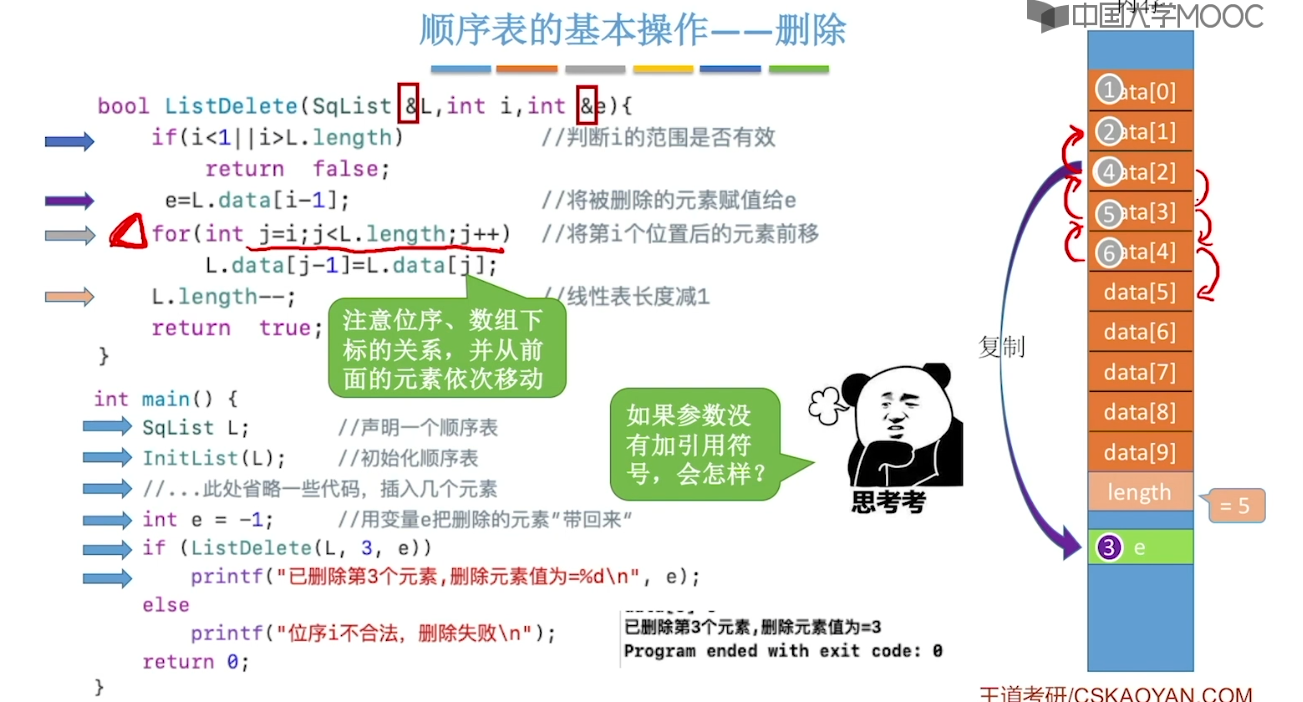
// 顺序表的删除
int deleteList(StaticSeqList& list, int index) {
// 判断i的范围是否有效
if (index < 0 || index > list.length - 1) {
printf("[超出顺序表边界的索引:%d]", index);
return -1;
}
// 将被删除的元素赋值给e
int e = list.data[index];
for (int i = index; i < list.length; i++) {
// 将第i个位置后的元素前移
list.data[i] = list.data[i + 1];
}
list.length--; // 线性表长度减1
return e;
}
// 顺序表按位查找
int getElem(StaticSeqList& list, int index) {
if (index < 0 || index >= list.length) {
return -1;
}
return list.data[index];
}
// 顺序表的按值查找
int indexOfElem(StaticSeqList& list, int e) {
for (int i = 0; i < list.length; i++) {
if (list.data[i] == e) {
return i;
}
}
return -1;
}
void printList(StaticSeqList& list) {
printf("当前线性表为:[");
for (int i = 0; i < list.length; i++) {
printf(" (%d)%d", i, list.data[i]);
}
printf(" ]\n");
}
int main() {
StaticSeqList list; // 声明一个顺序表
initList(list); // 初始化顺序表
printf("在索引为0的位置插入元素1,");
insertList(list, 0, 1); printList(list);
printf("在索引为1的位置插入元素2,");
insertList(list, 1, 2); printList(list);
printf("在索引为0的位置插入元素3,");
insertList(list, 0, 3); printList(list);
printf("在索引为2的位置插入元素4,");
insertList(list, 2, 4); printList(list);
int deletedElem = deleteList(list, 1);
printf("删除索引为1的元素:%d, ", deletedElem); printList(list);
int elem = getElem(list, 1);
printf("索引为1的元素为:%d,", elem); printList(list);
int index = indexOfElem(list, 4);
printf("元素为4的索引为:%d,", index); printList(list);
return 0;
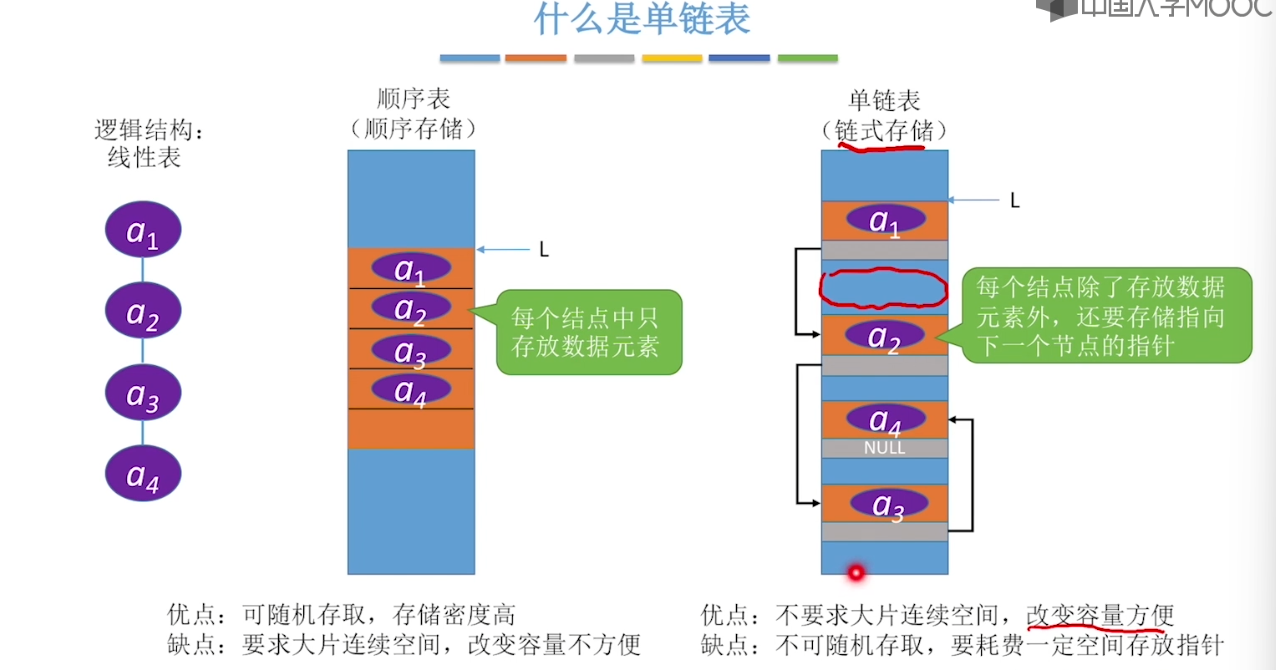
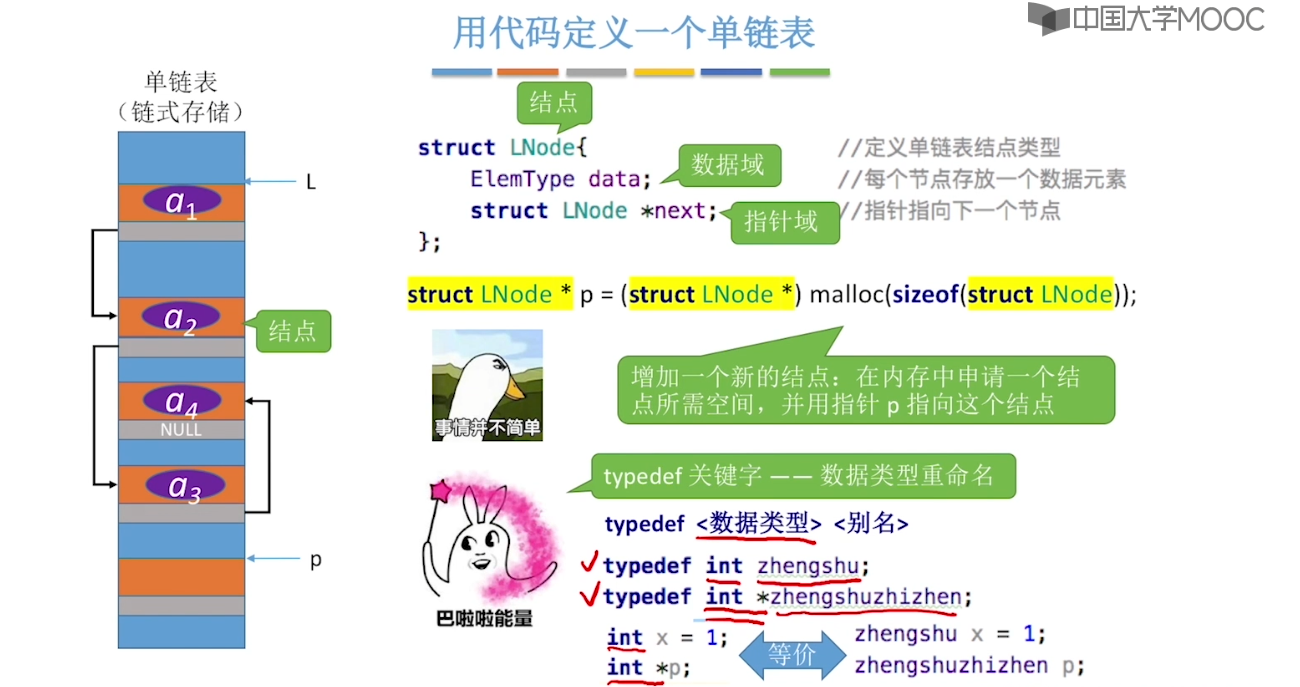
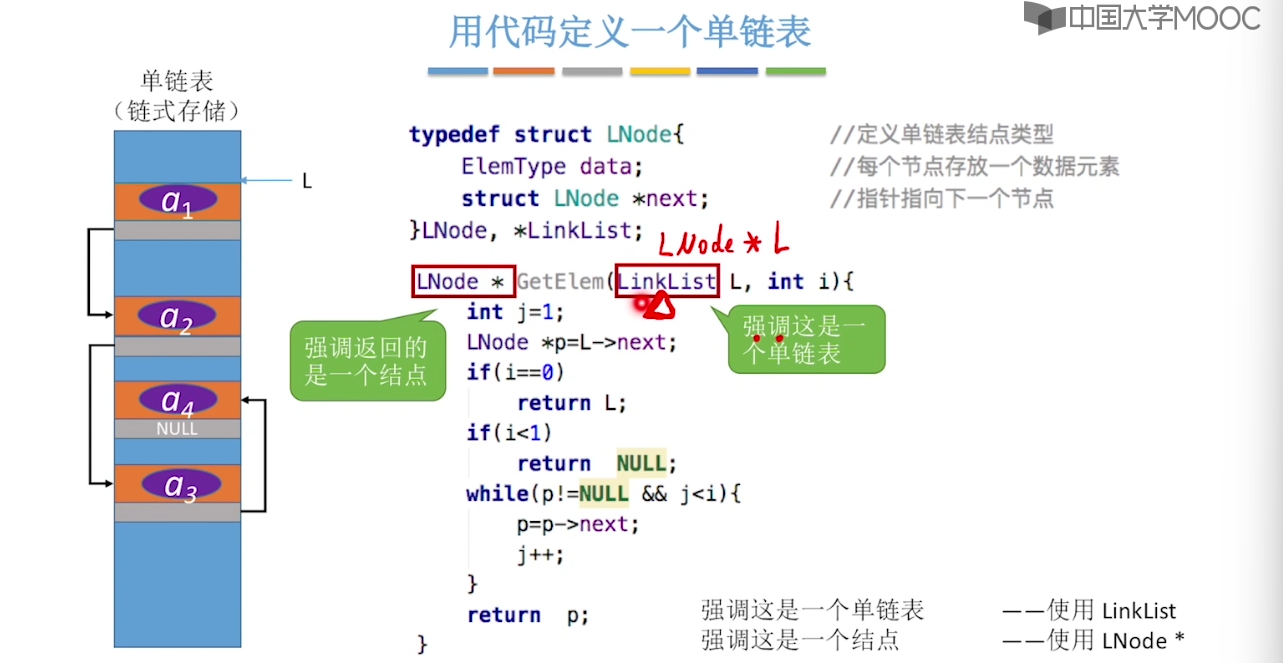
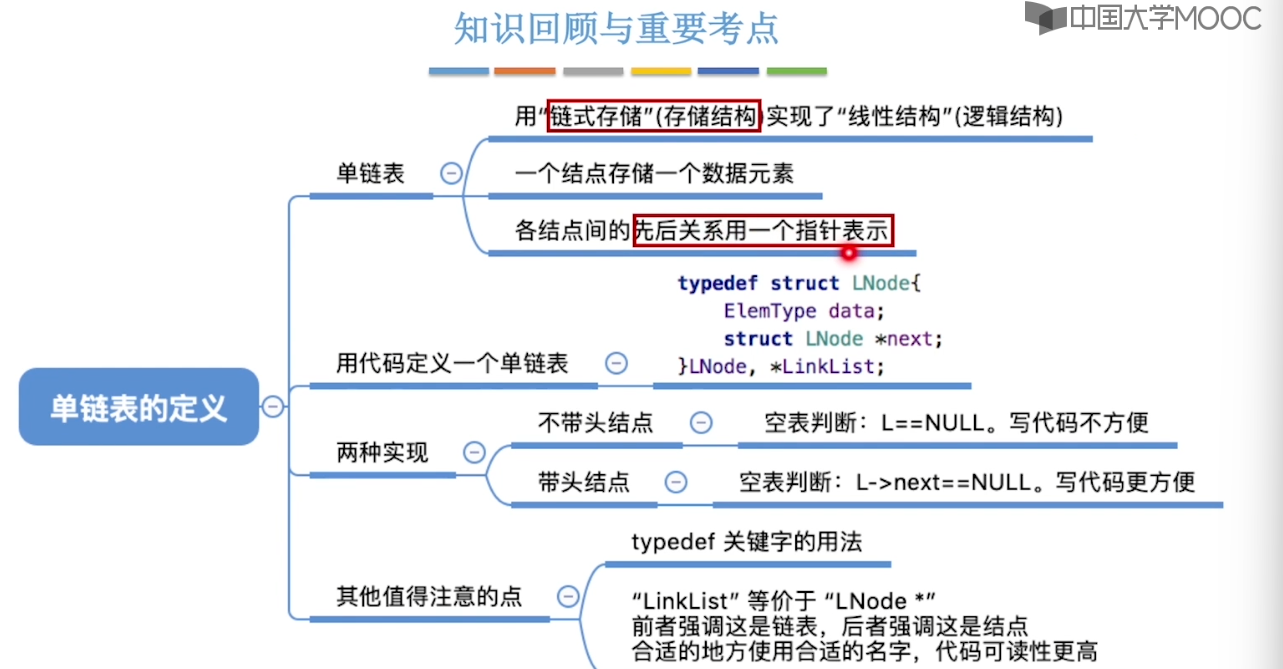
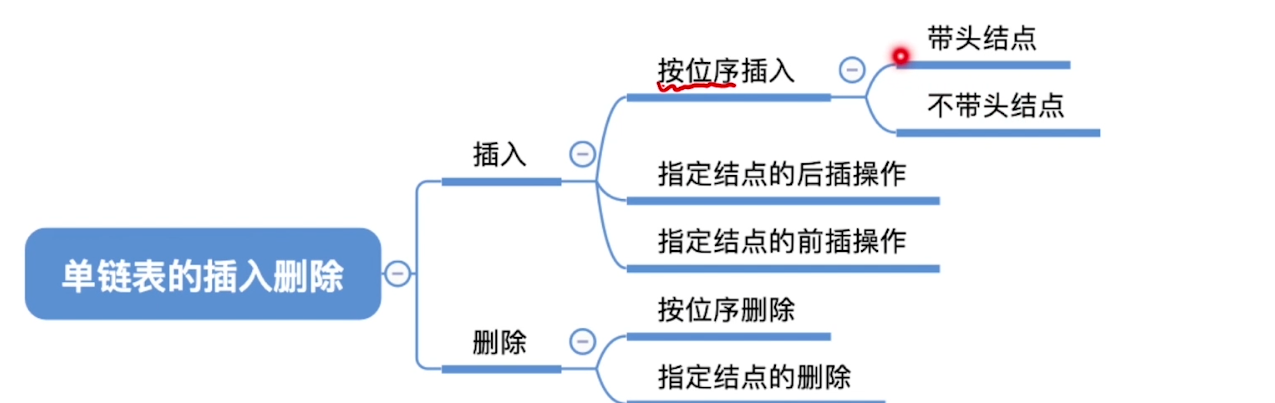
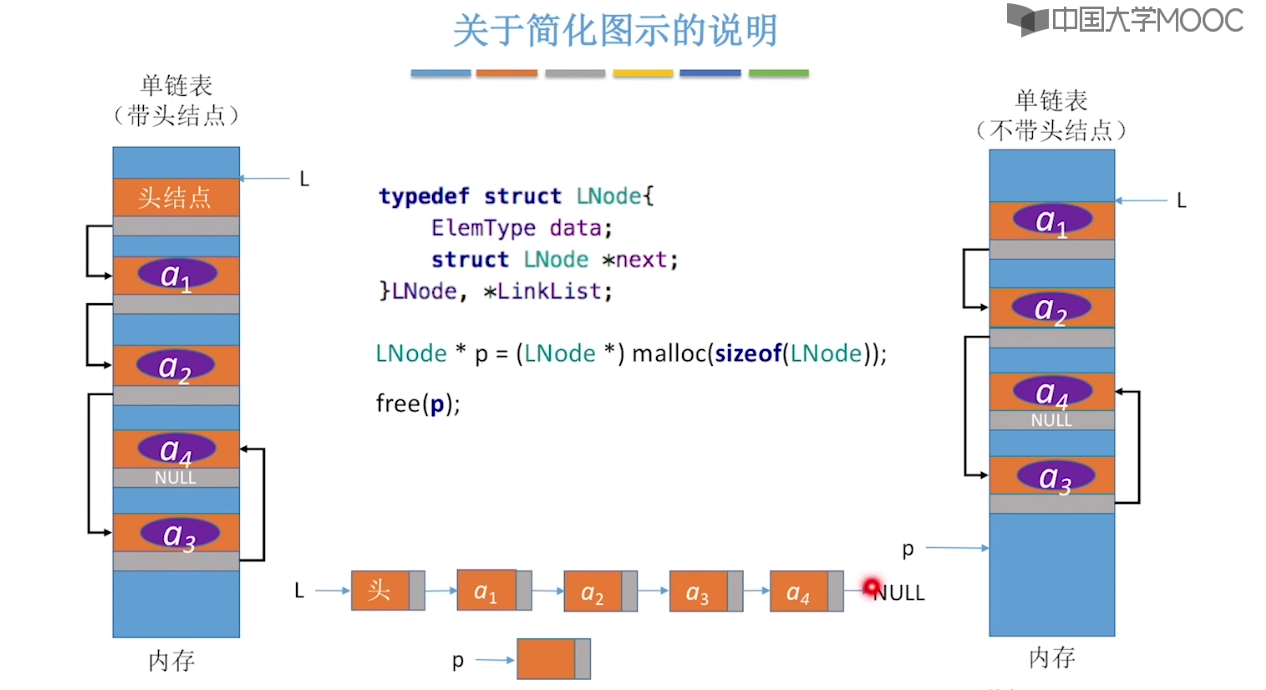
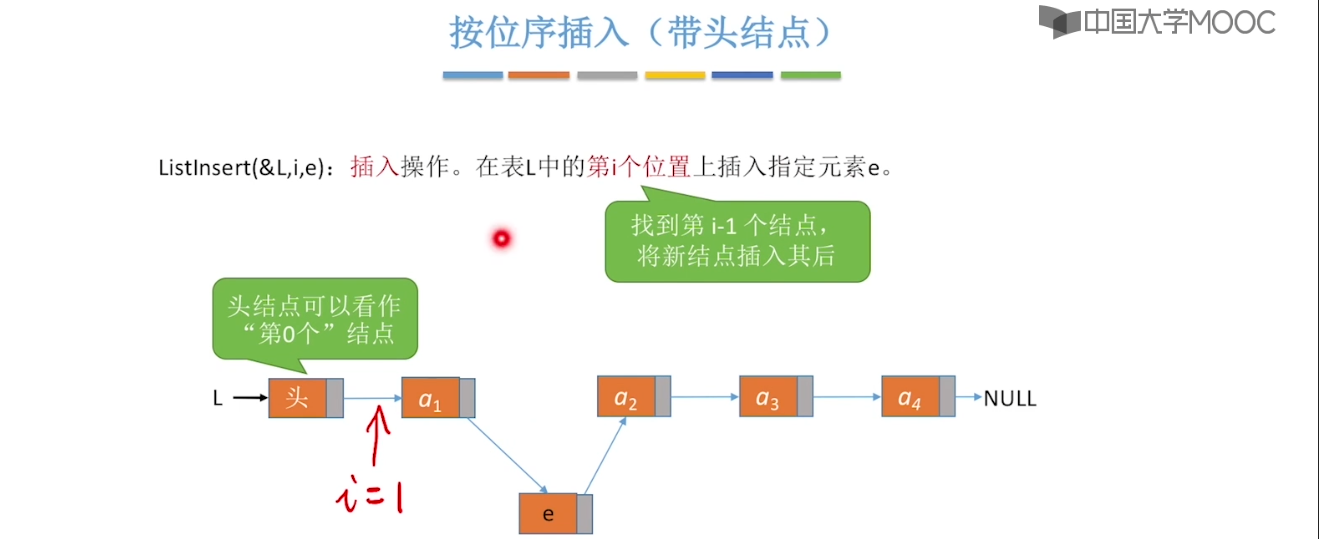
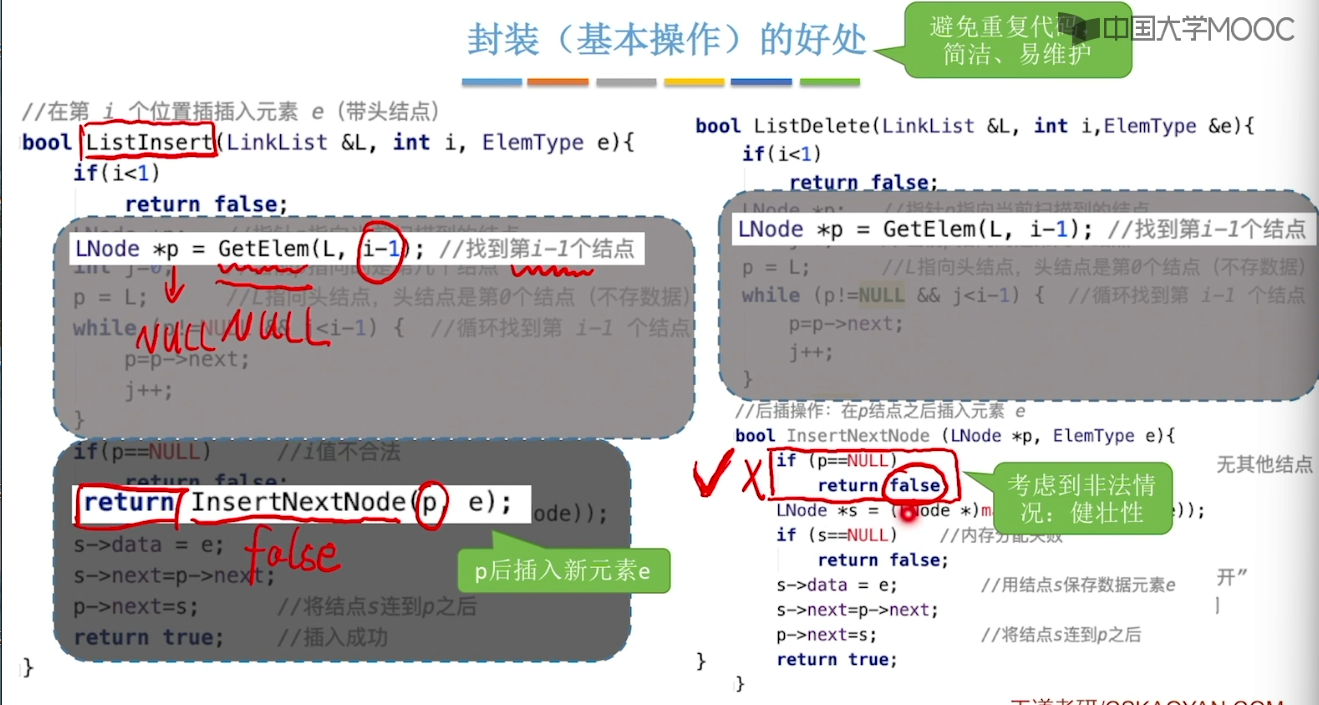
}2.3、单链表的定义

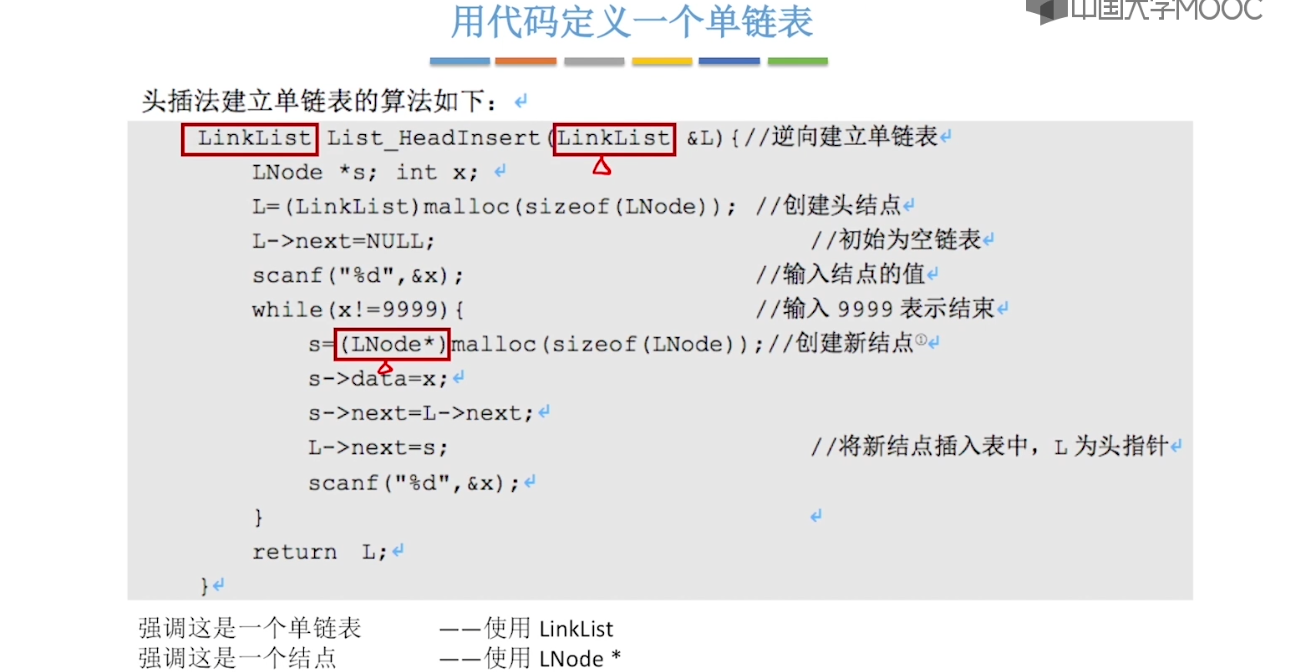
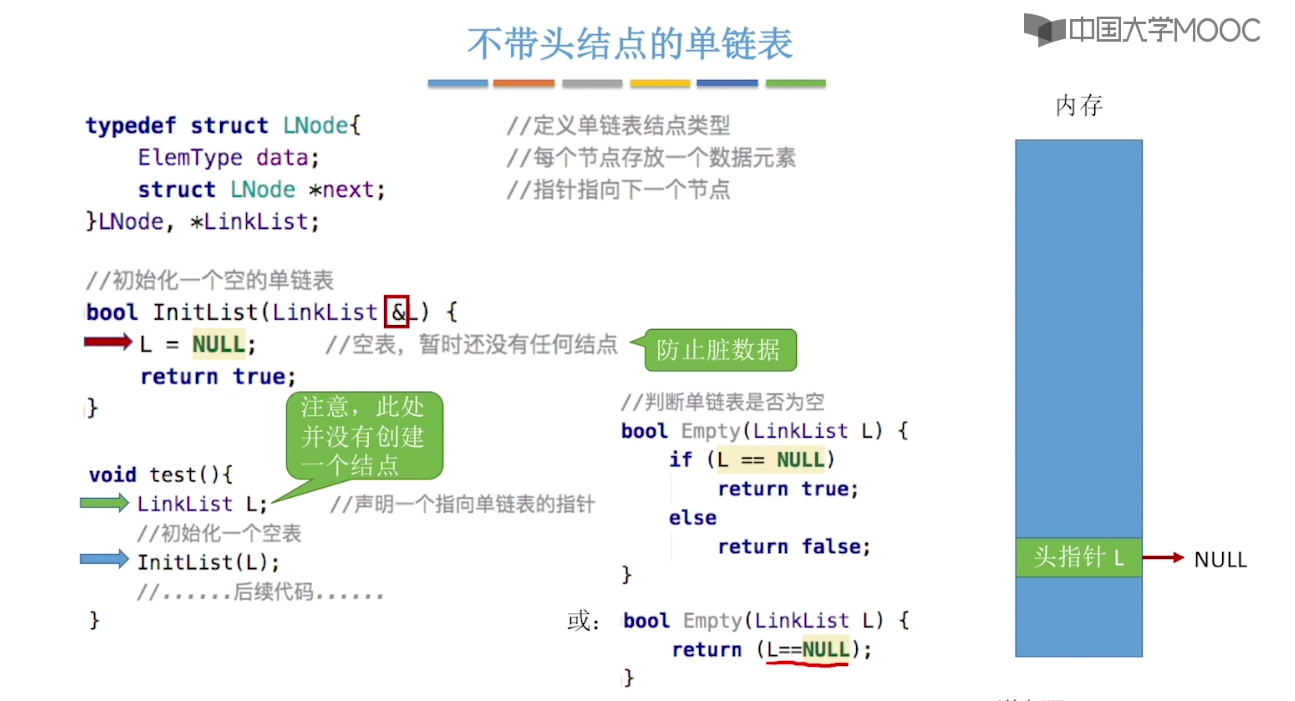
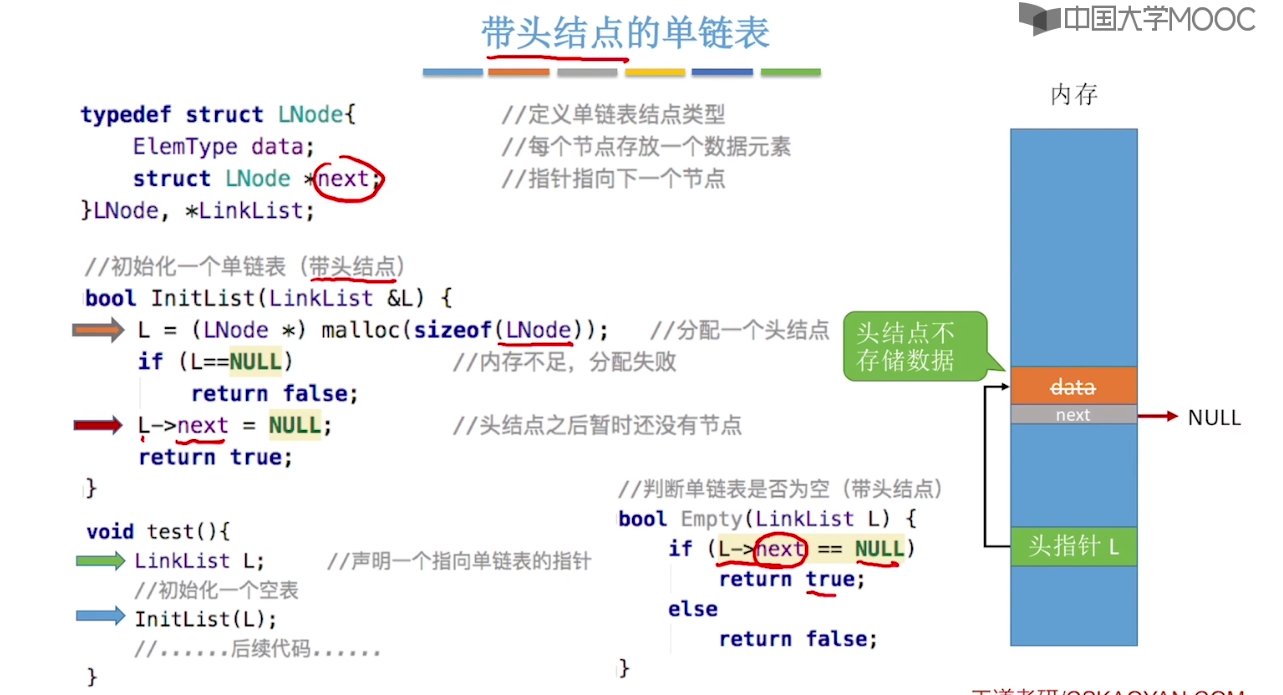
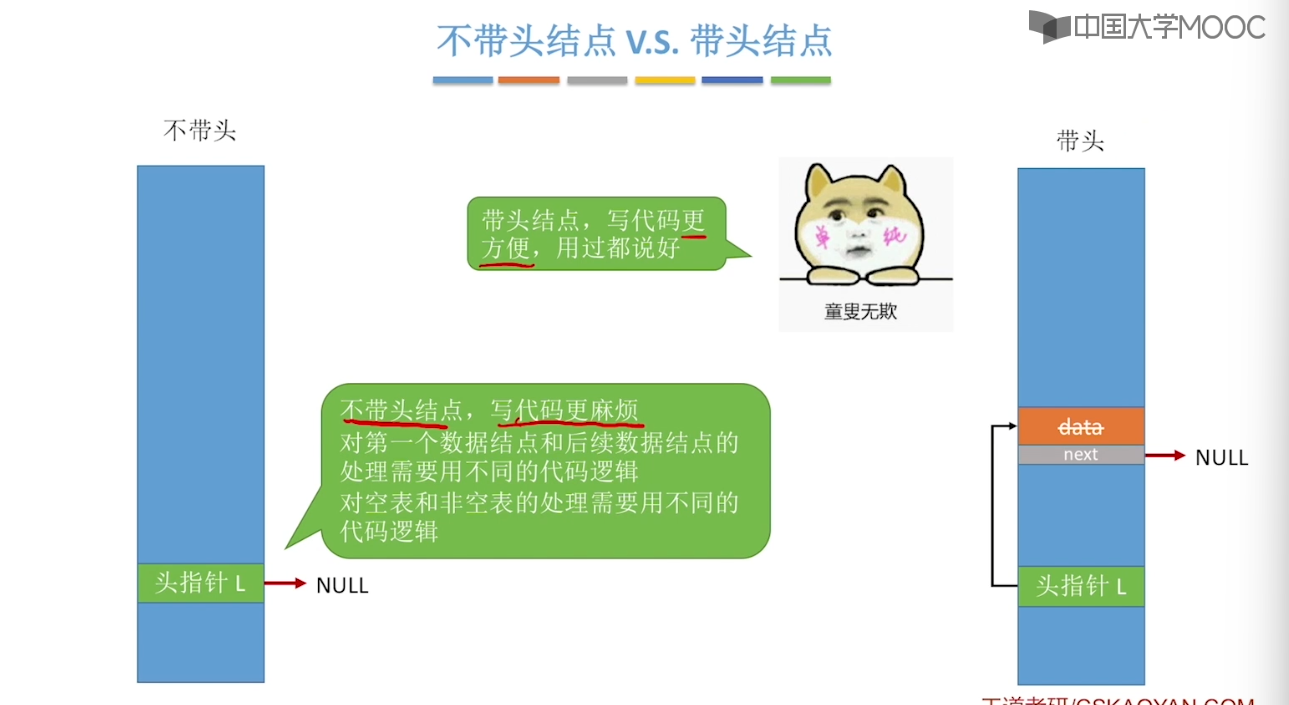


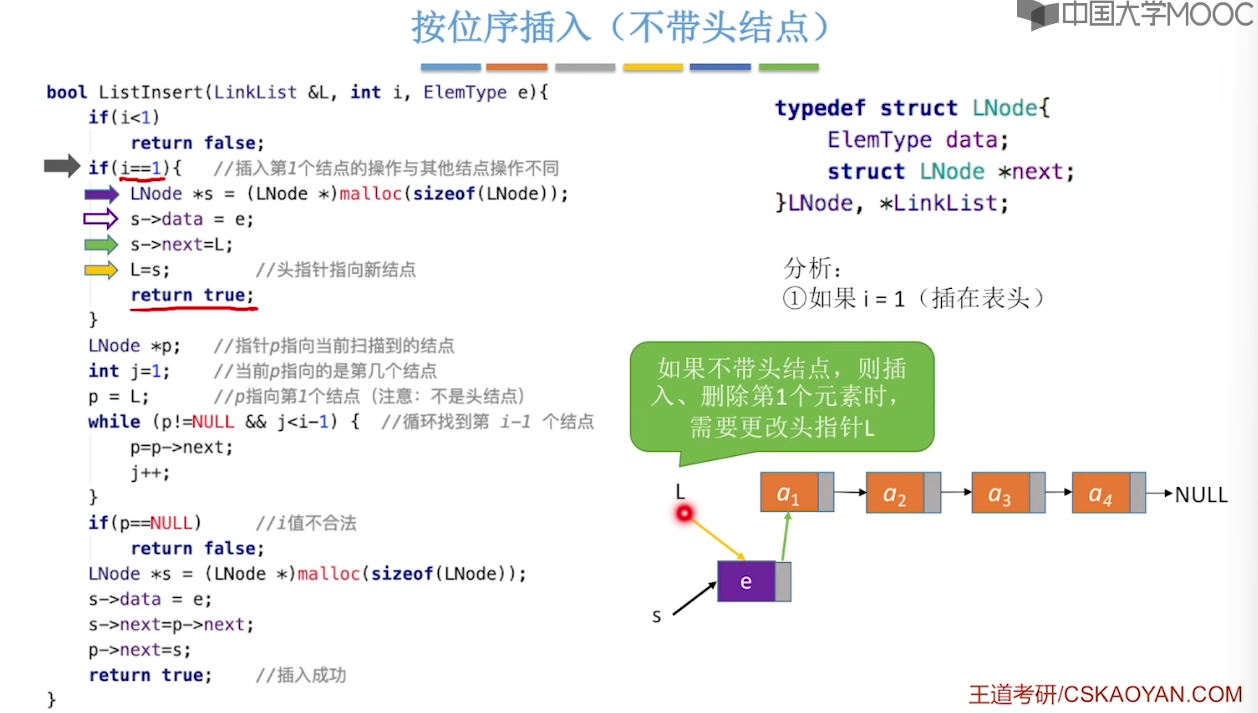
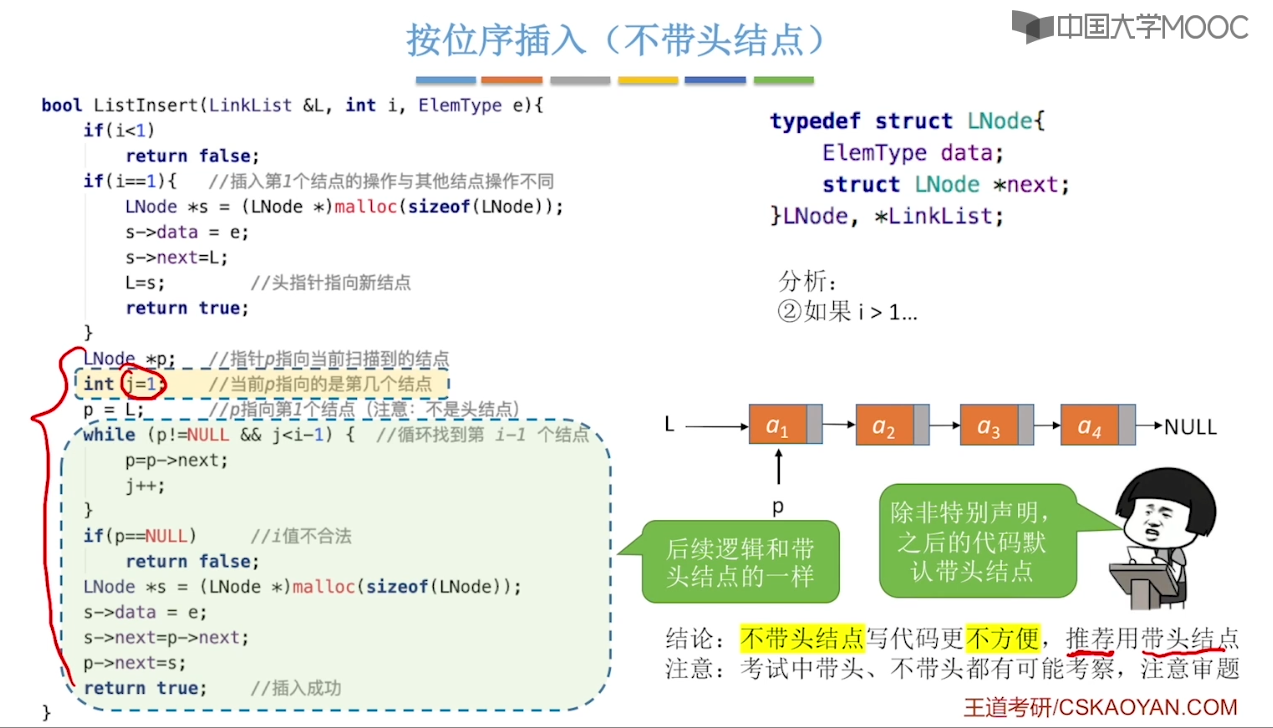

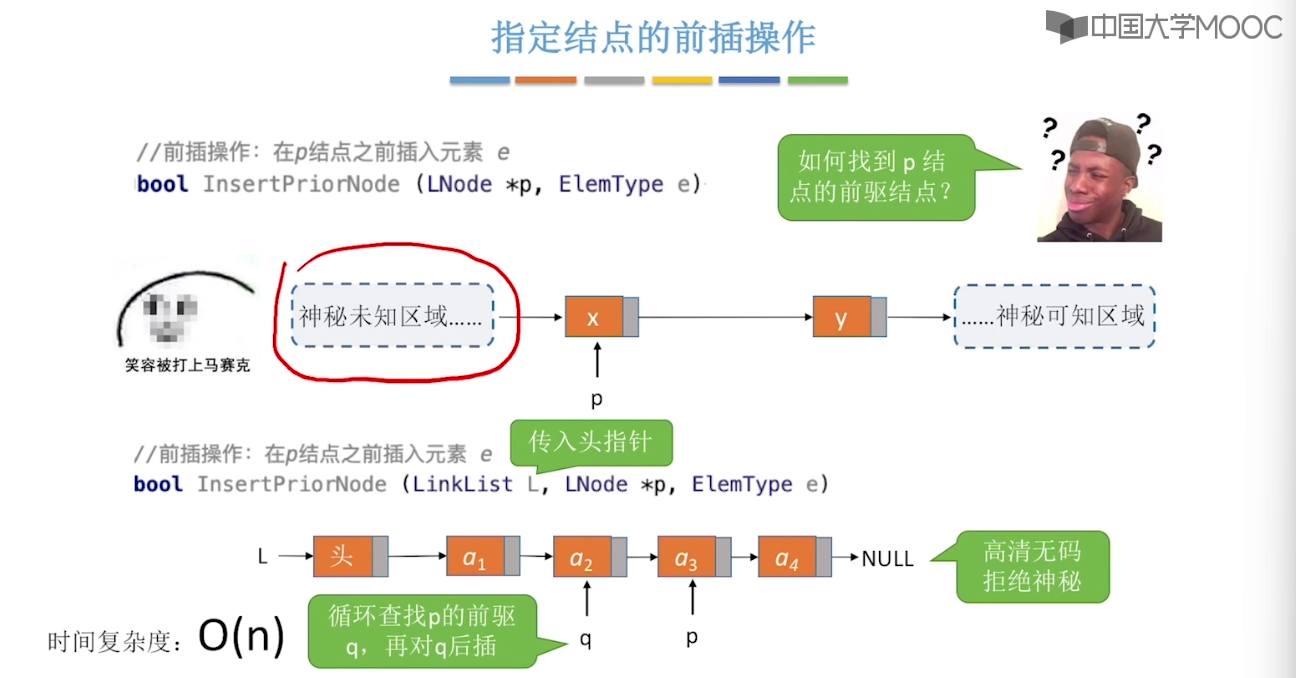
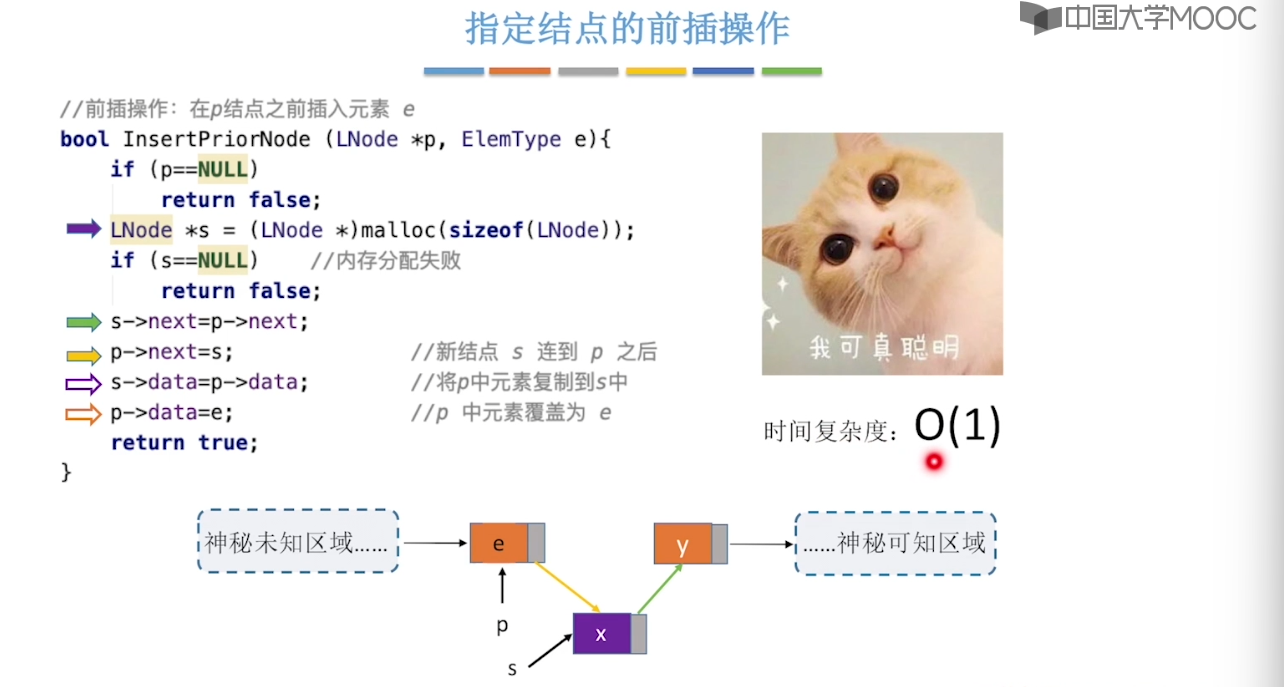
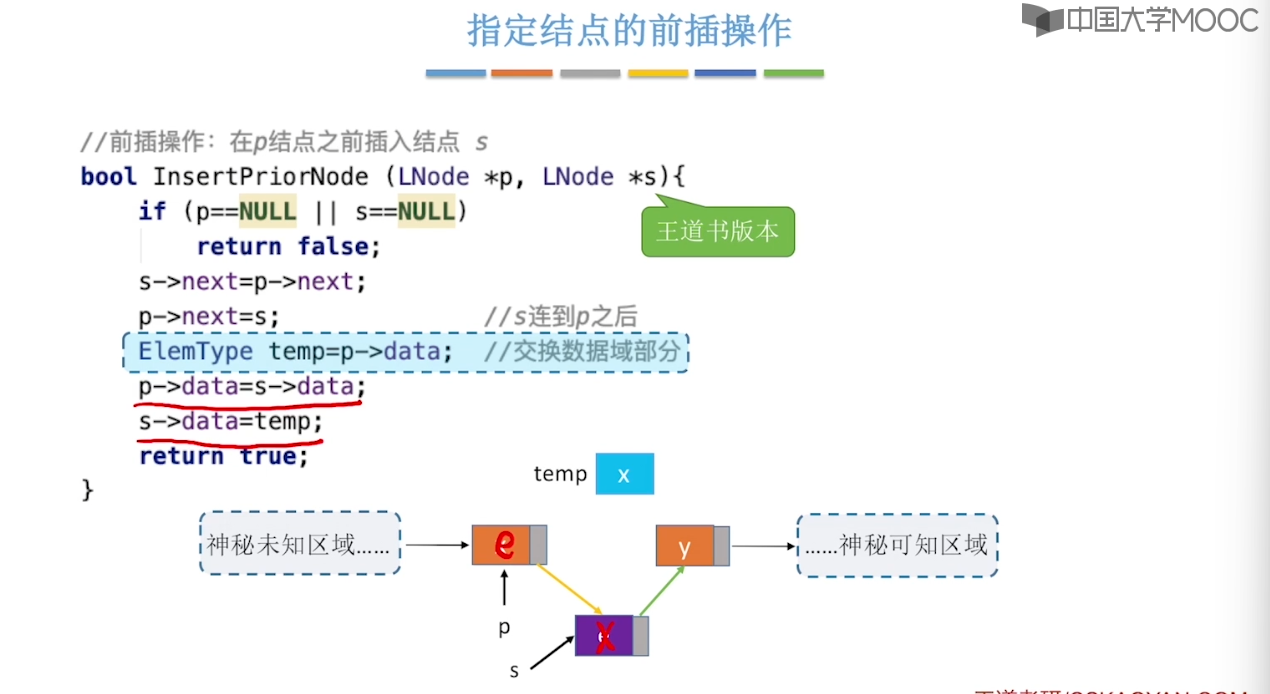
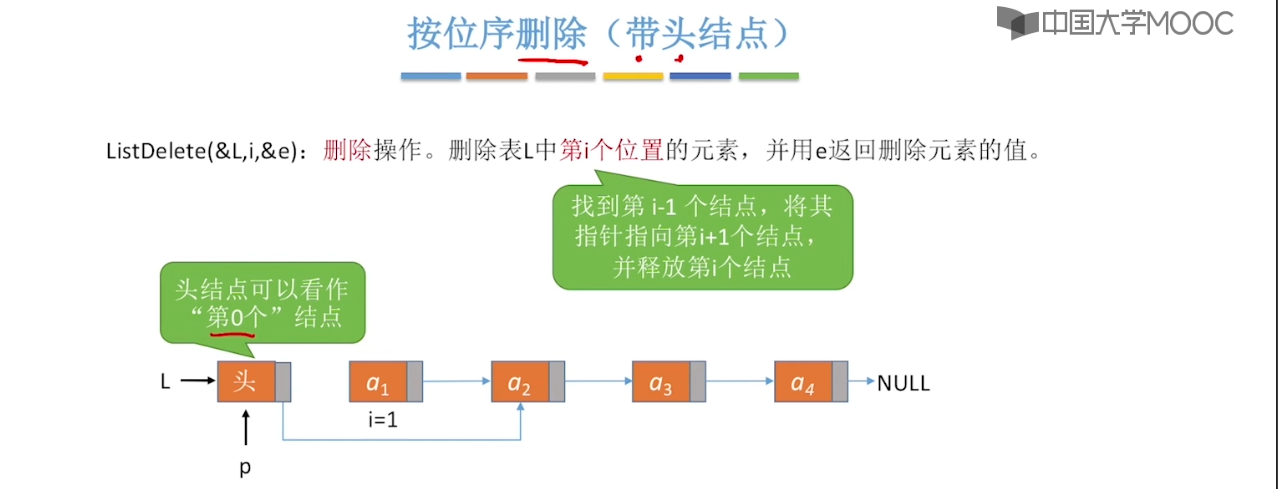
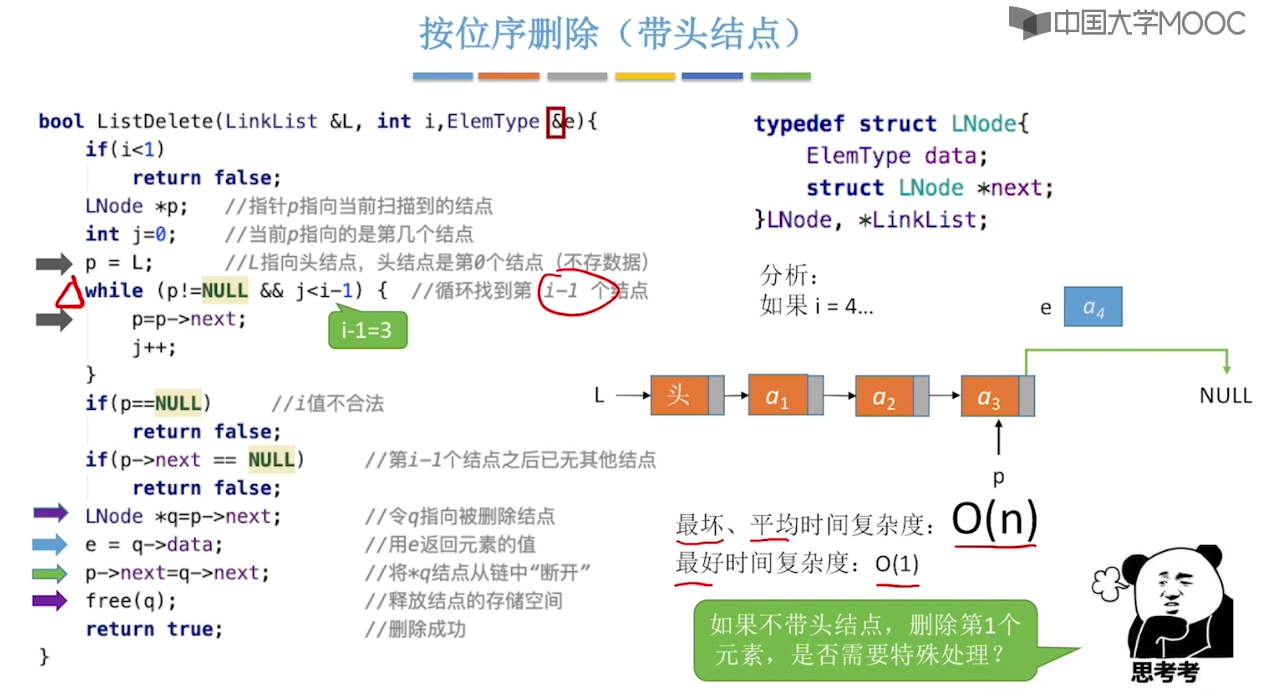
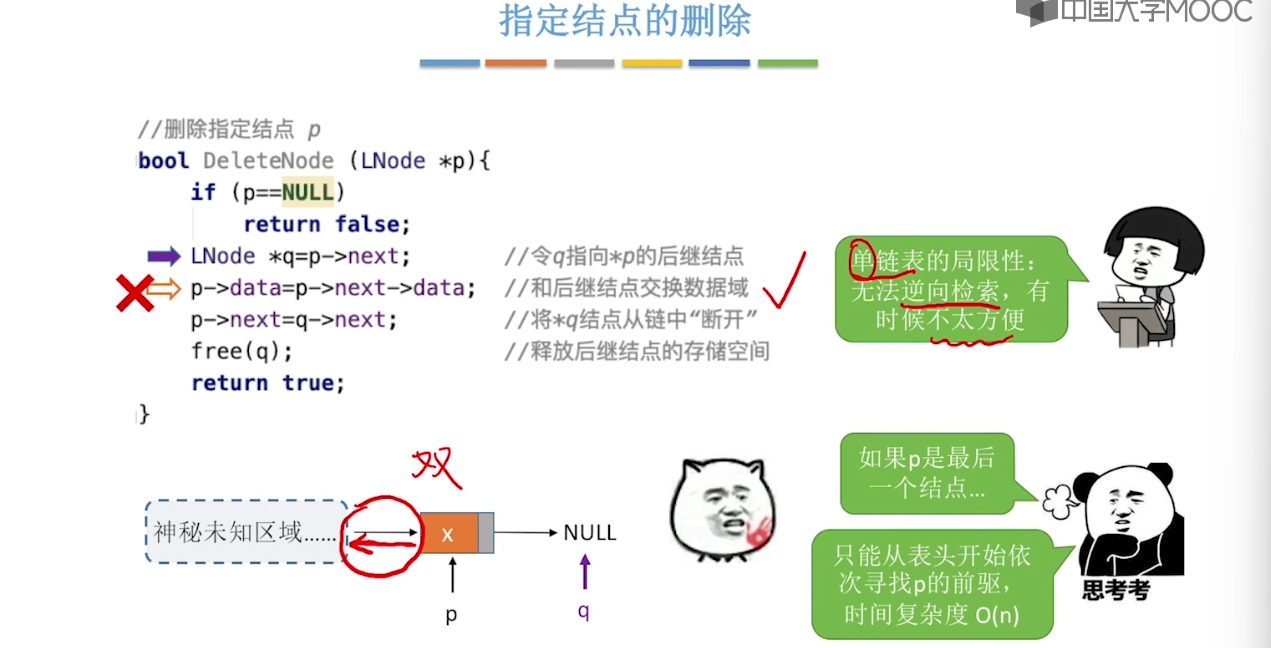
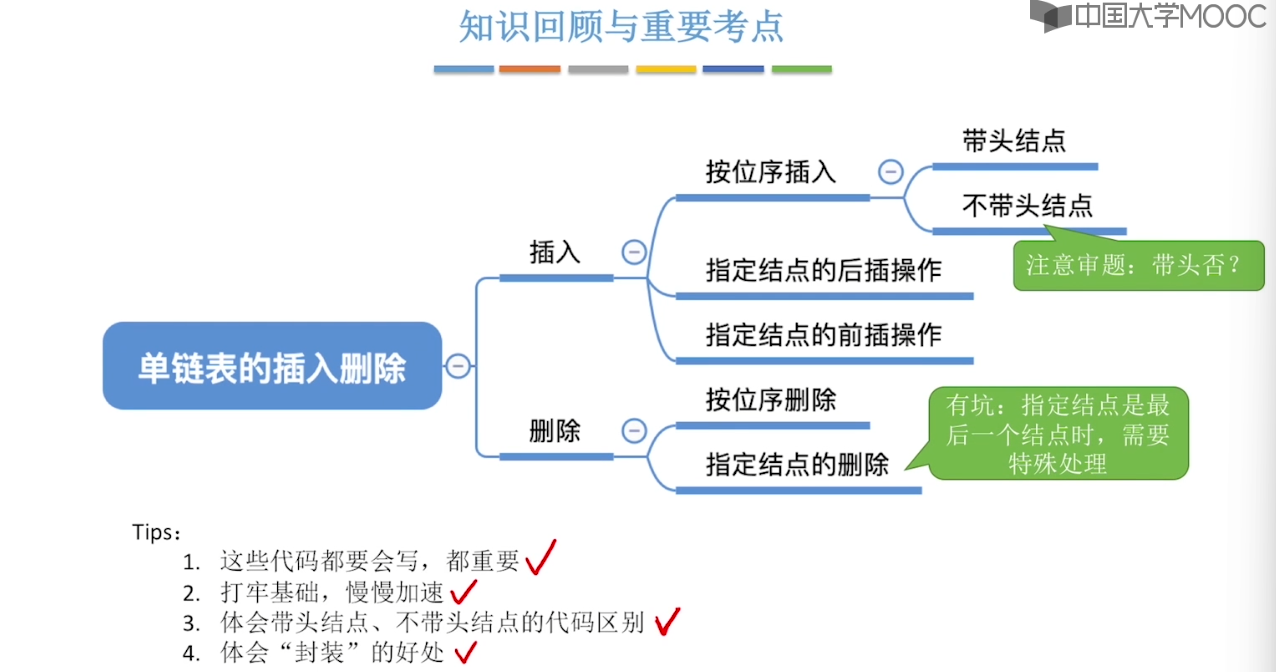
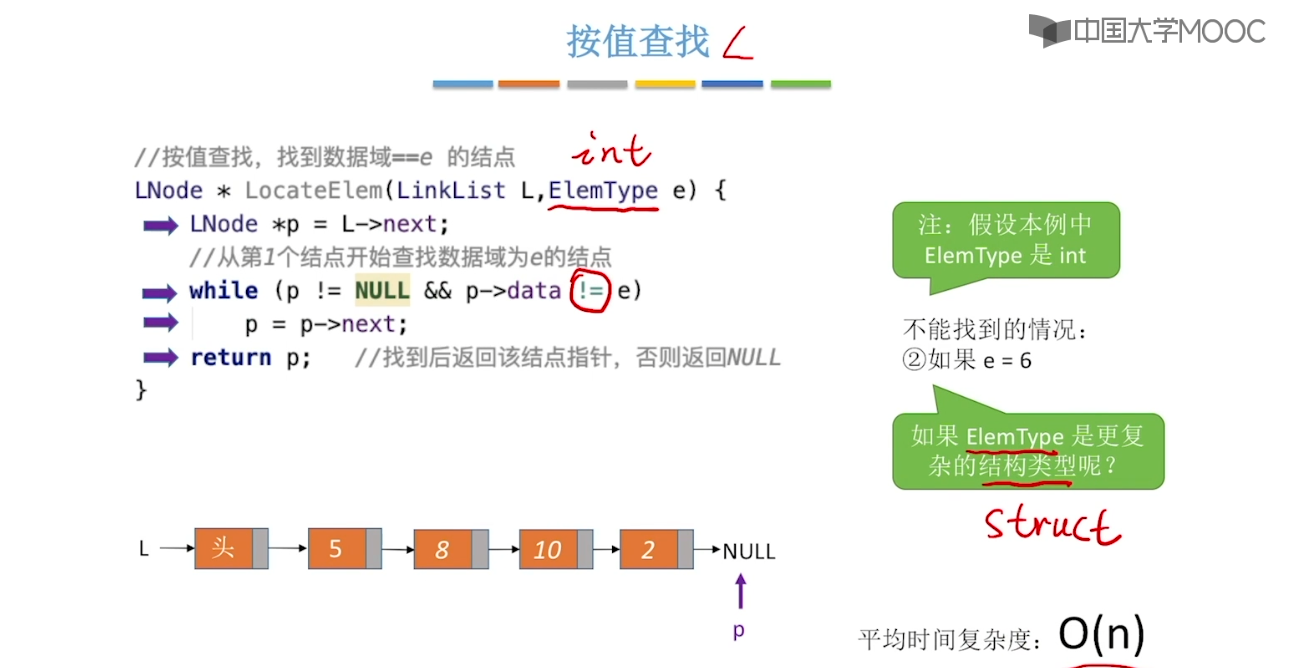
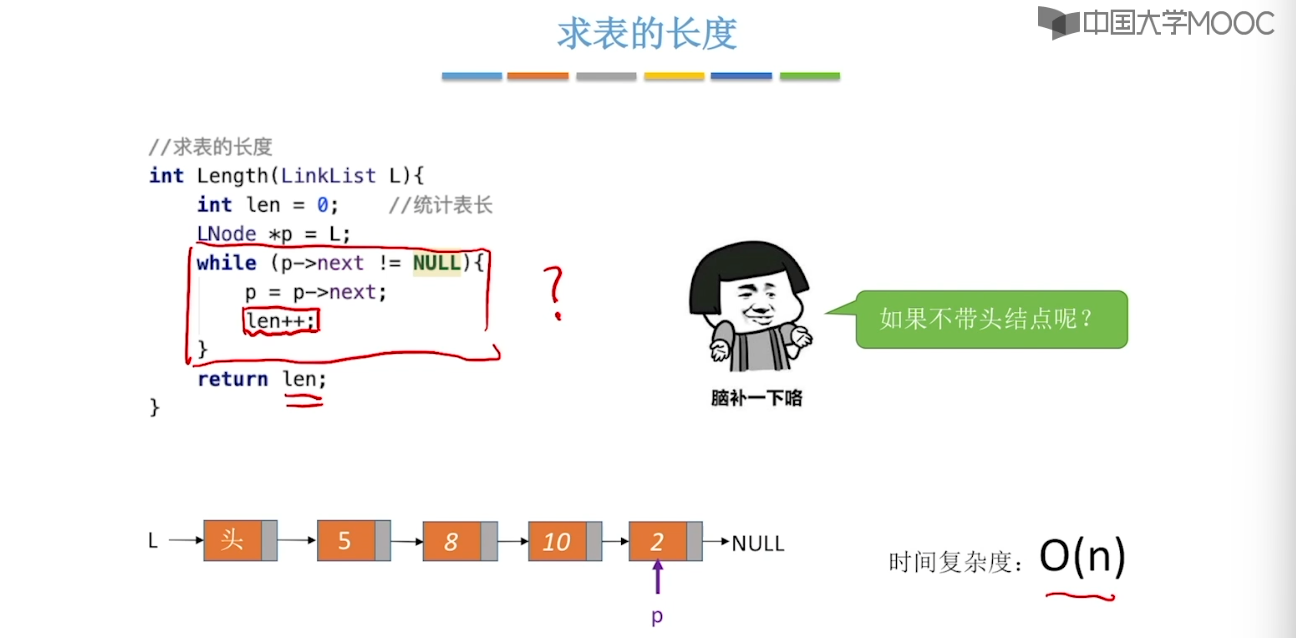
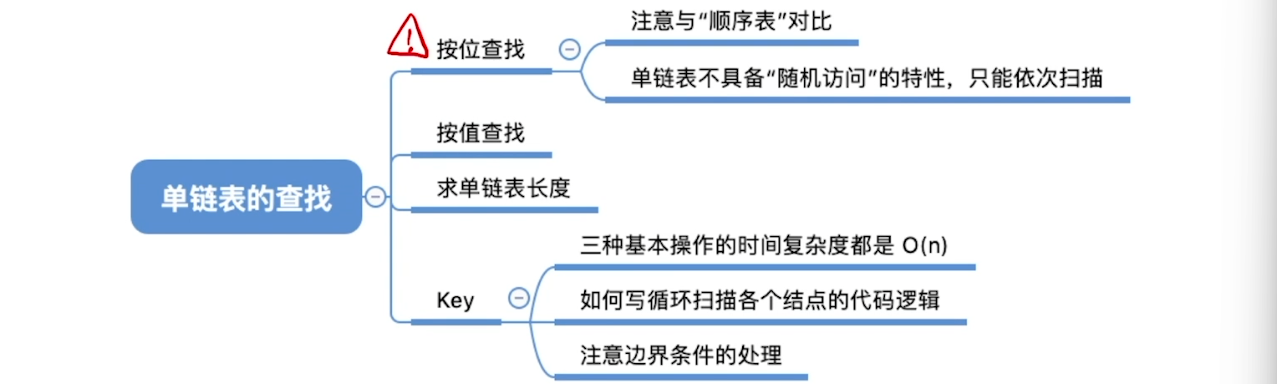
2.4、单链表的查找
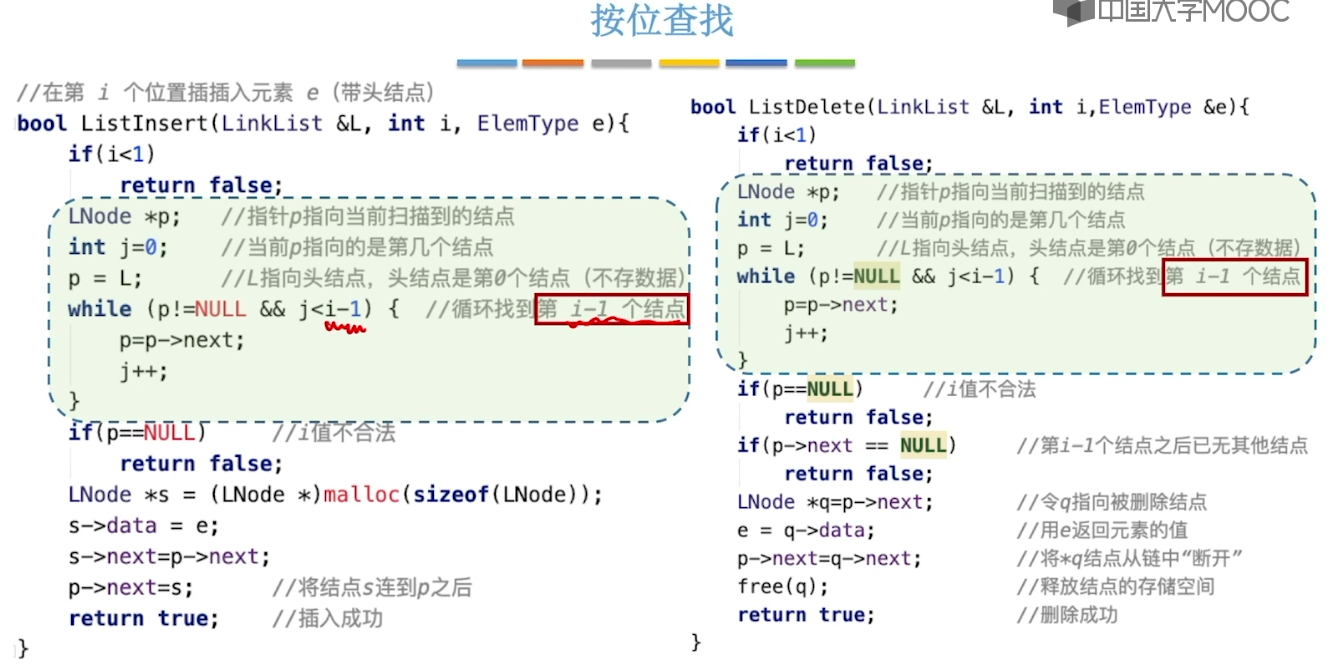
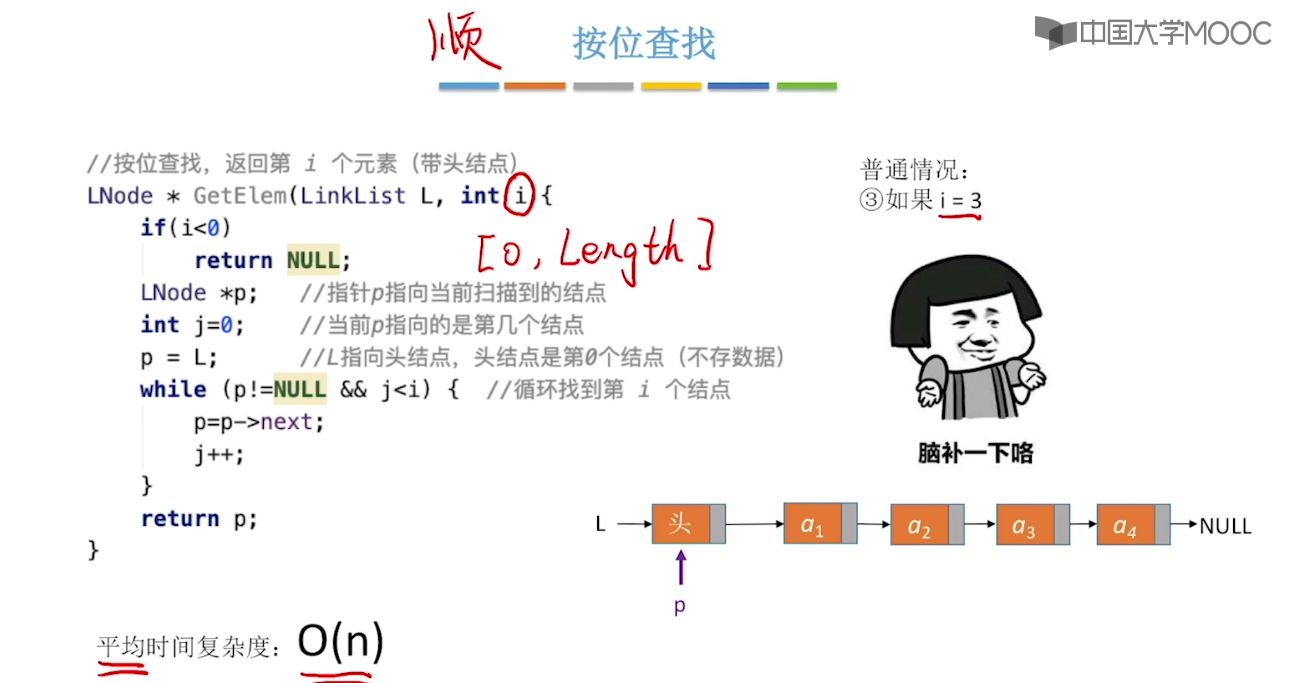
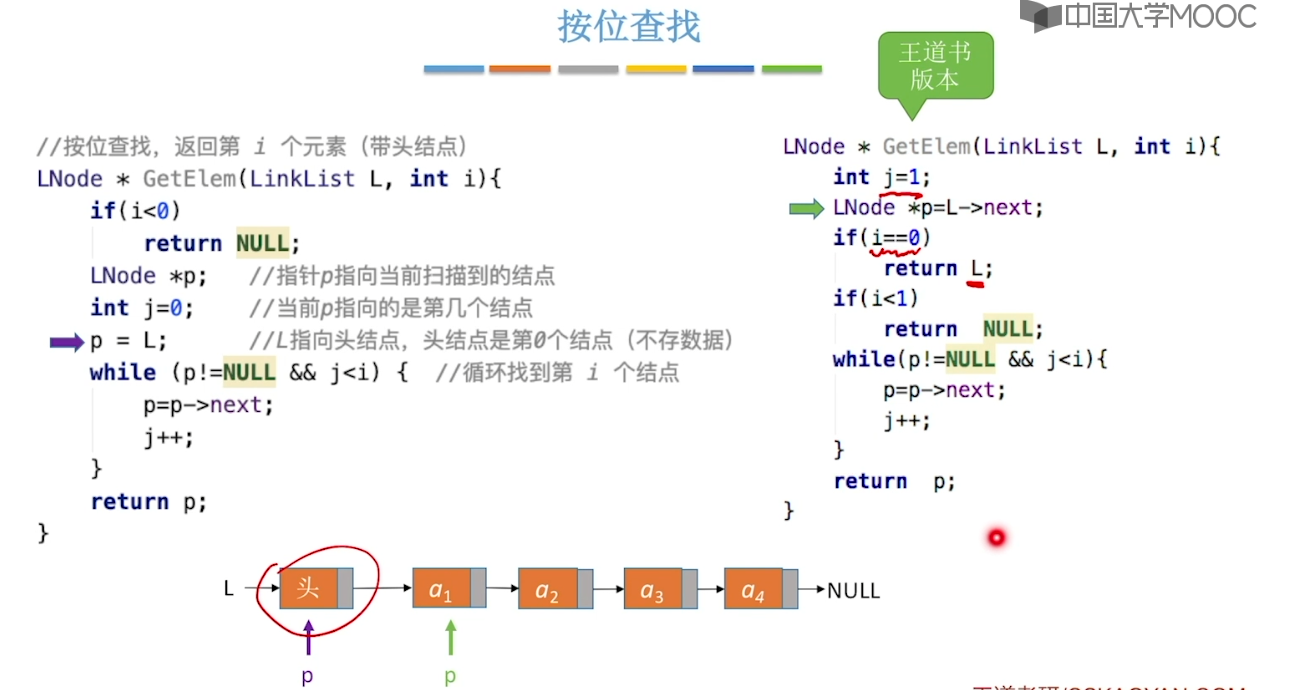

2.5、单链表的建立
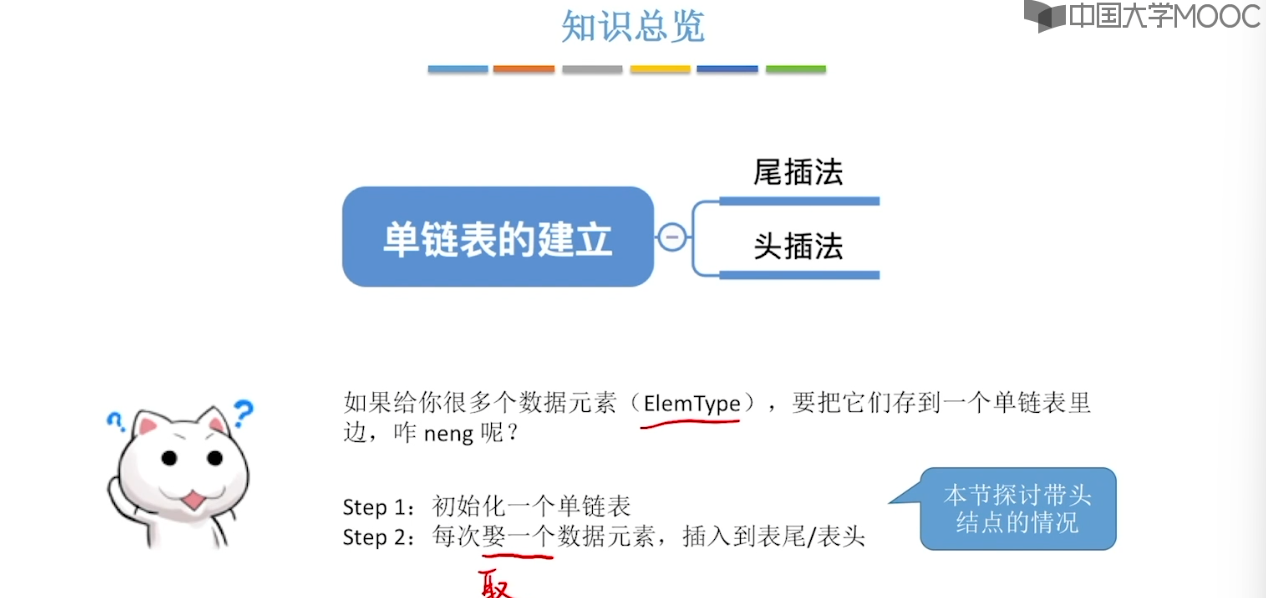
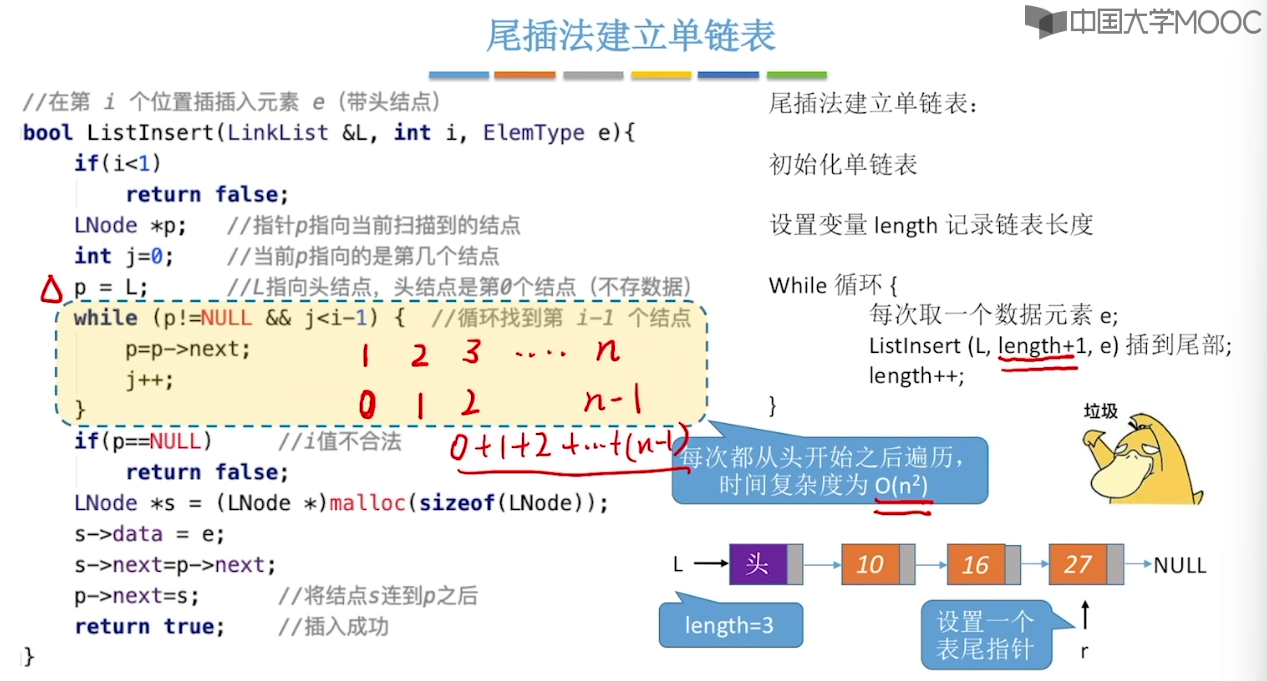
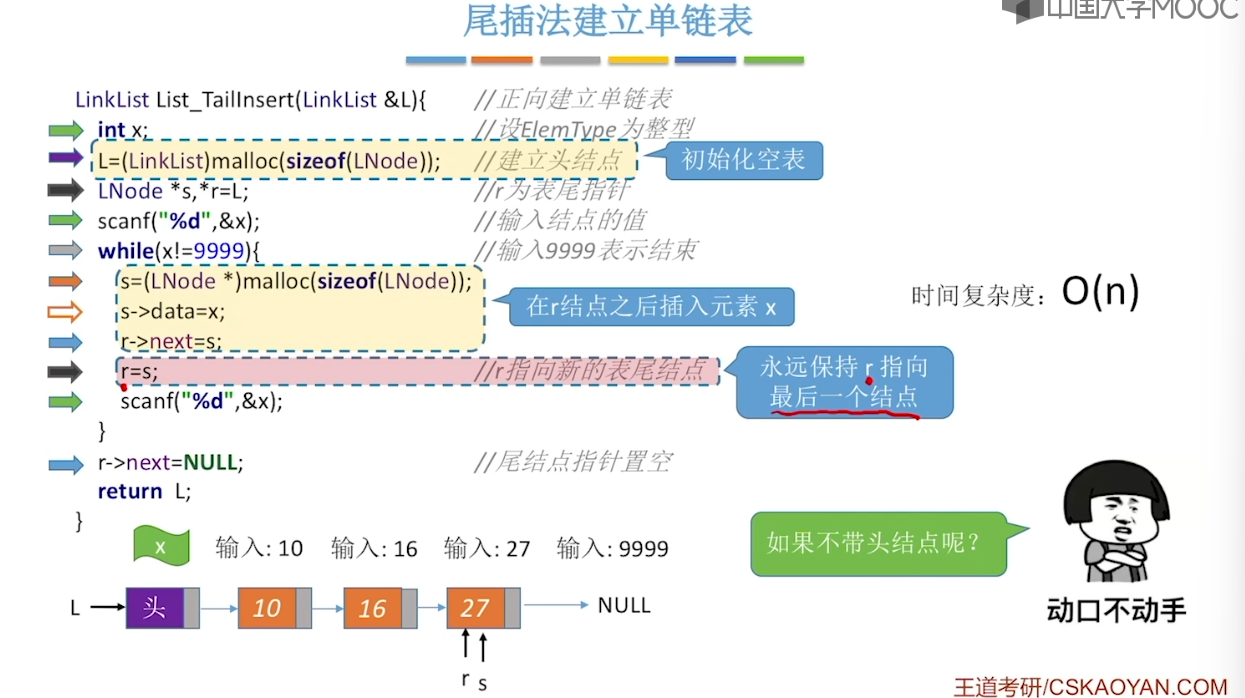

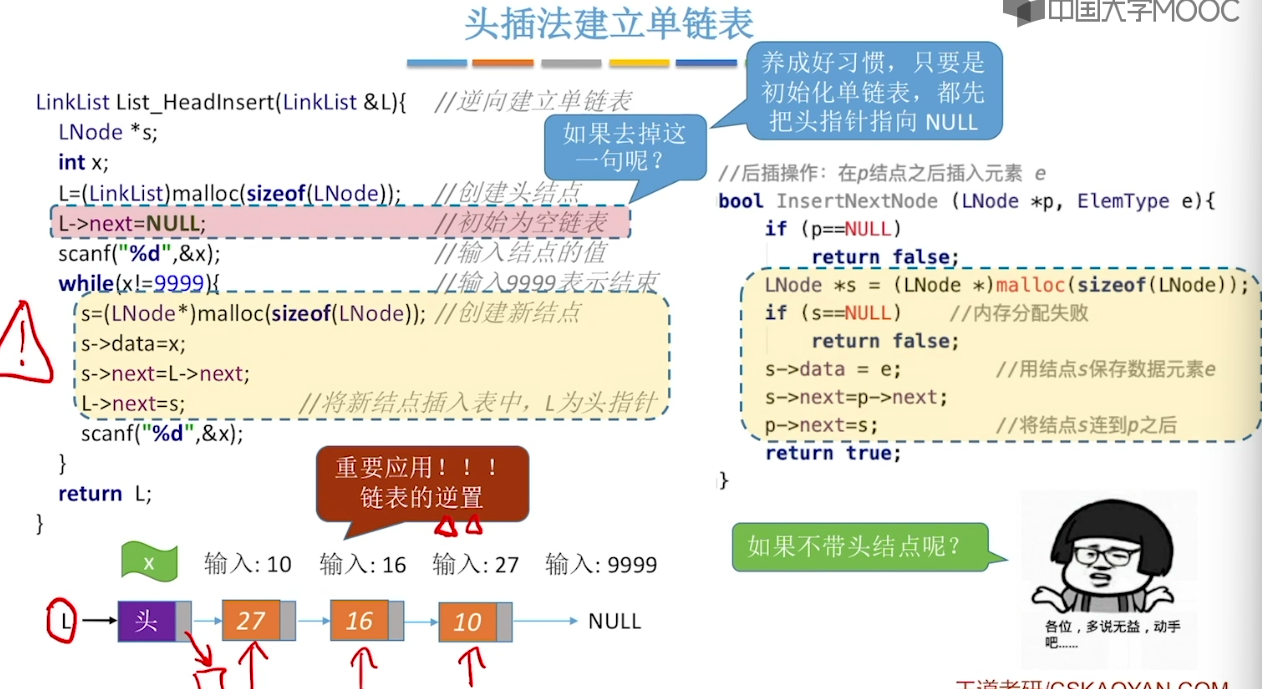
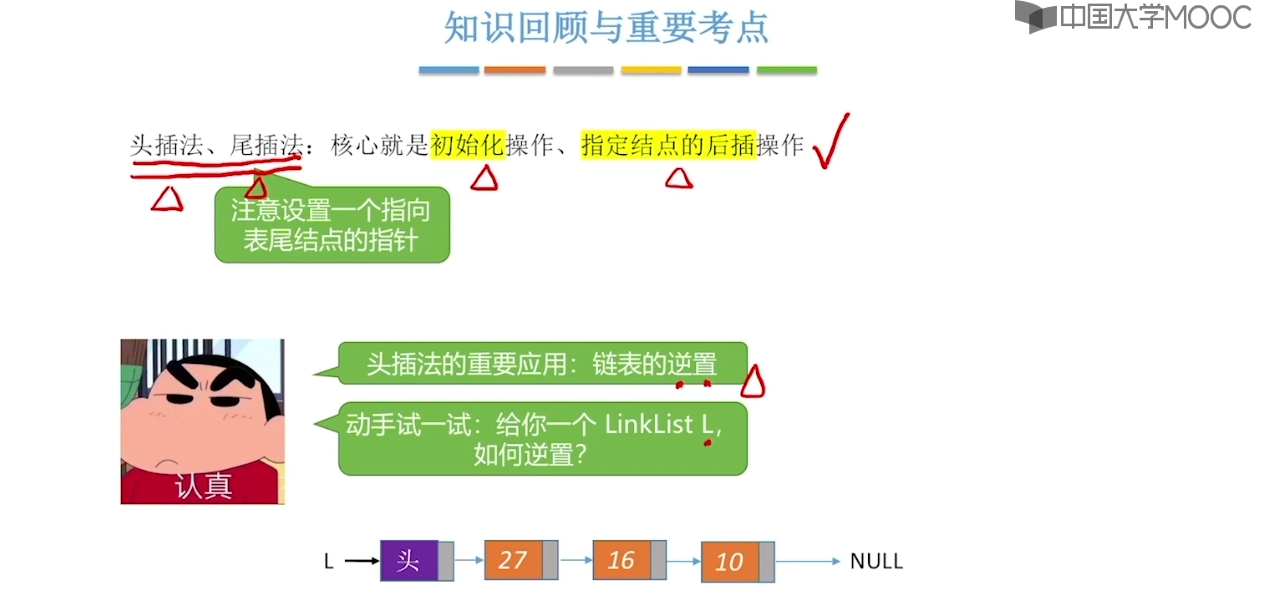
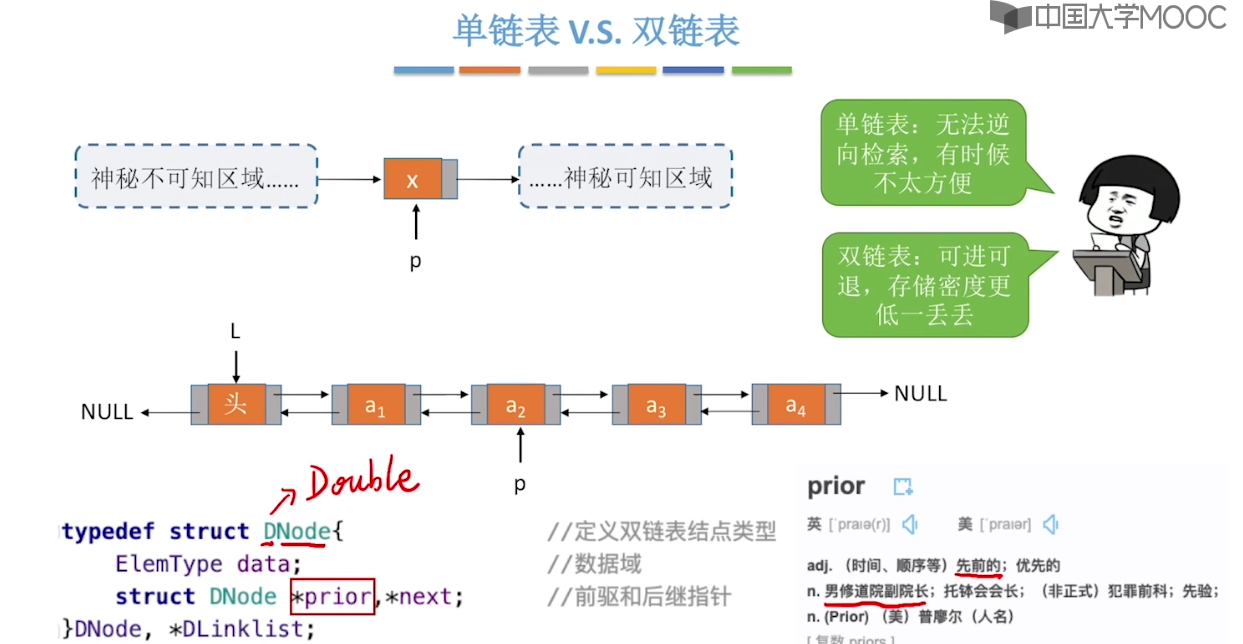
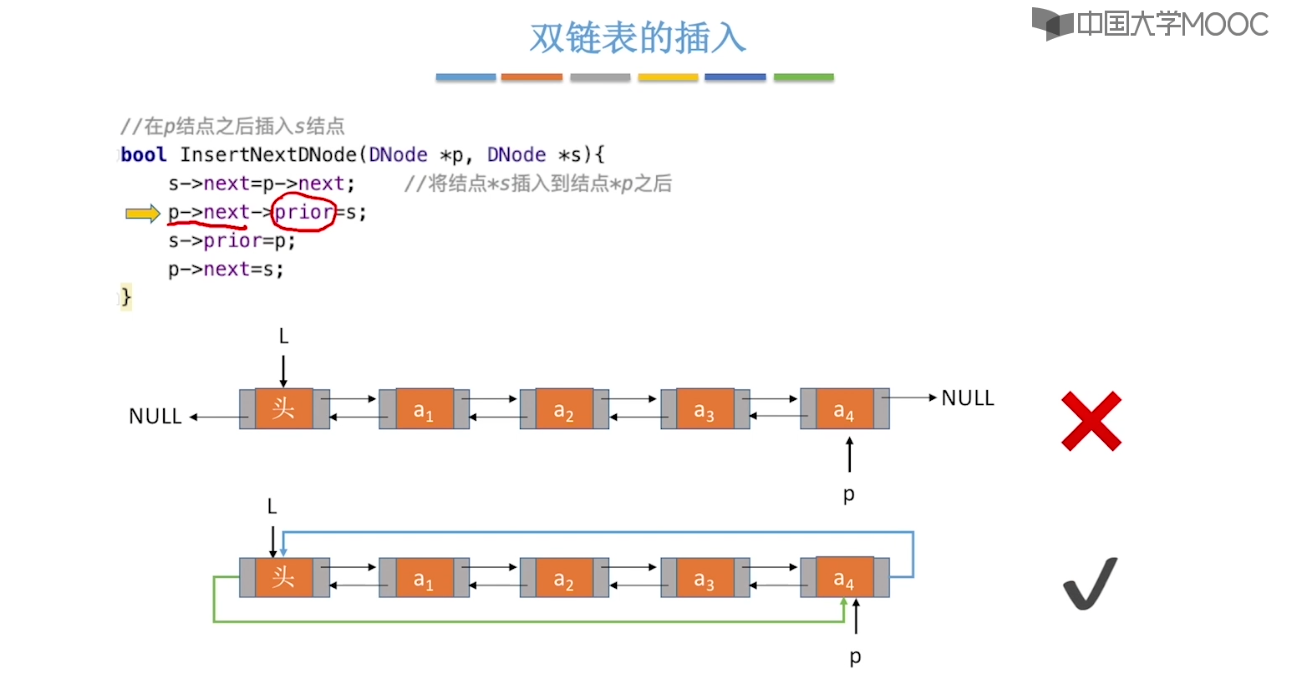
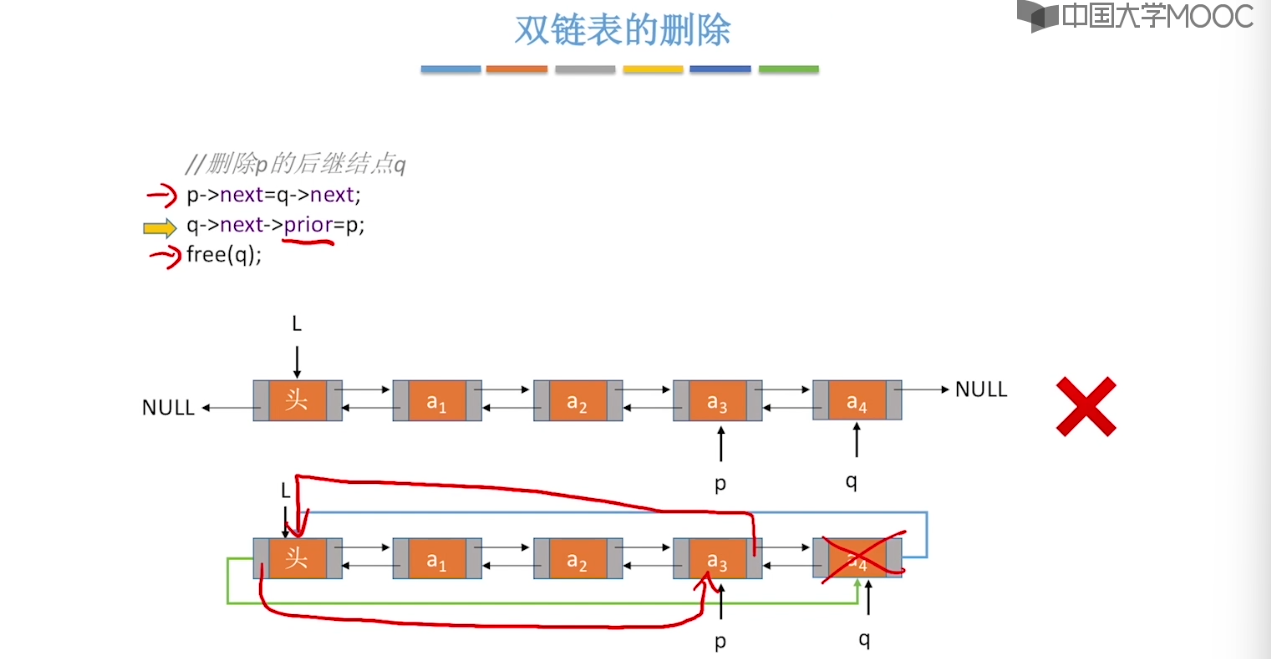
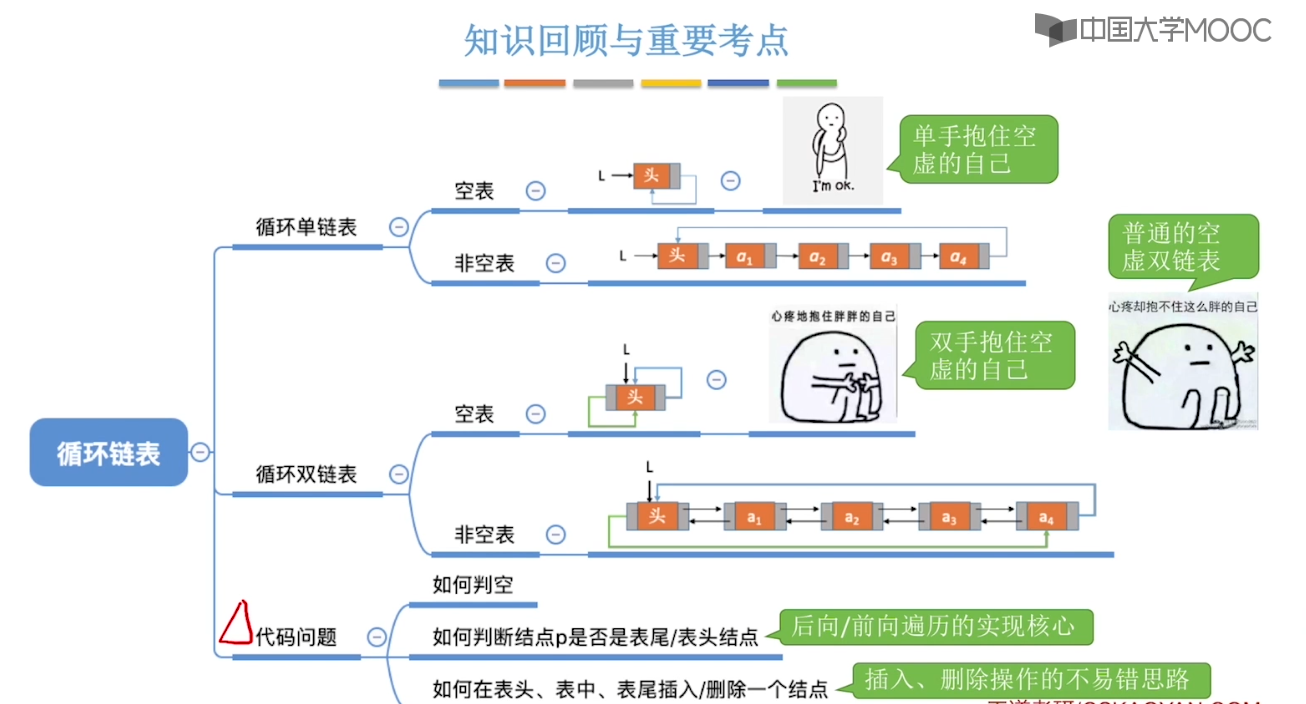
2.6、双链表

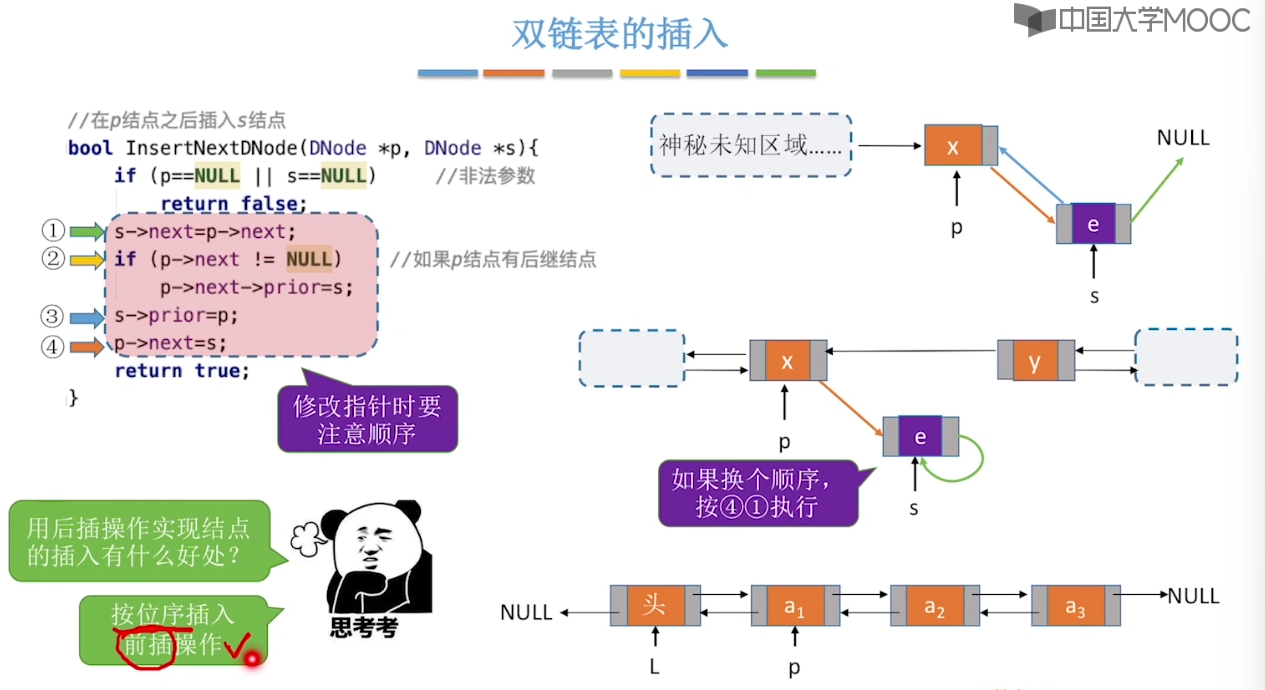
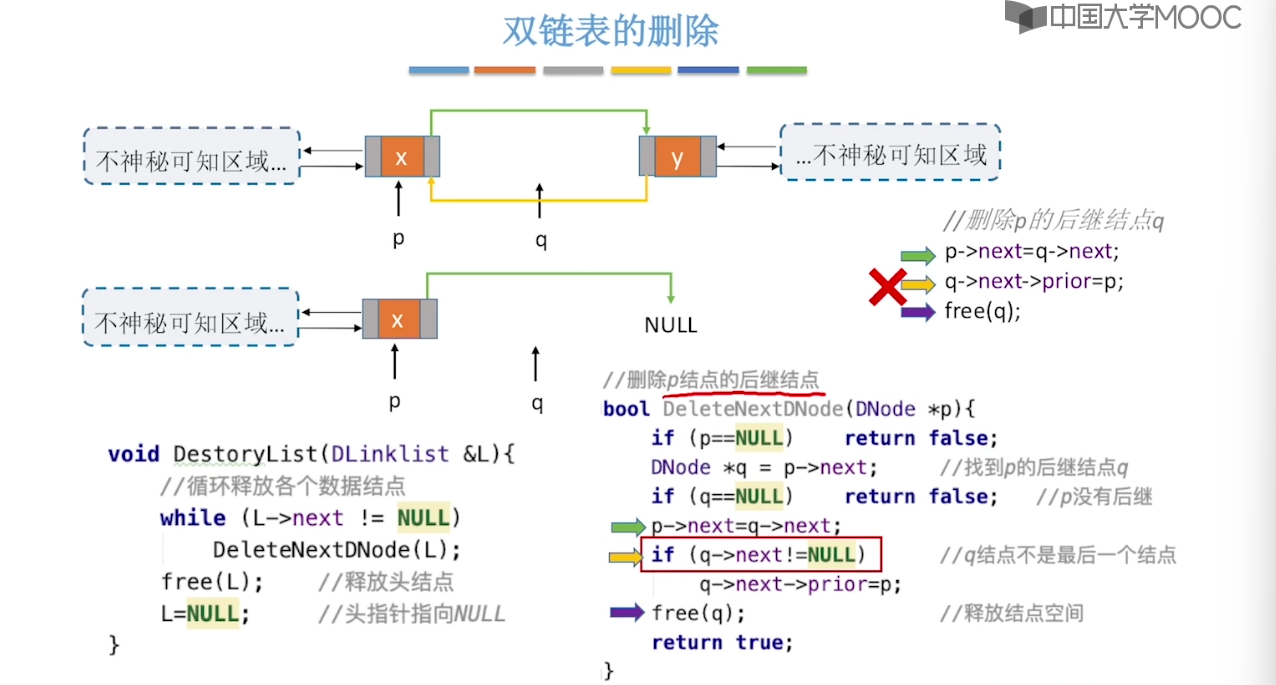


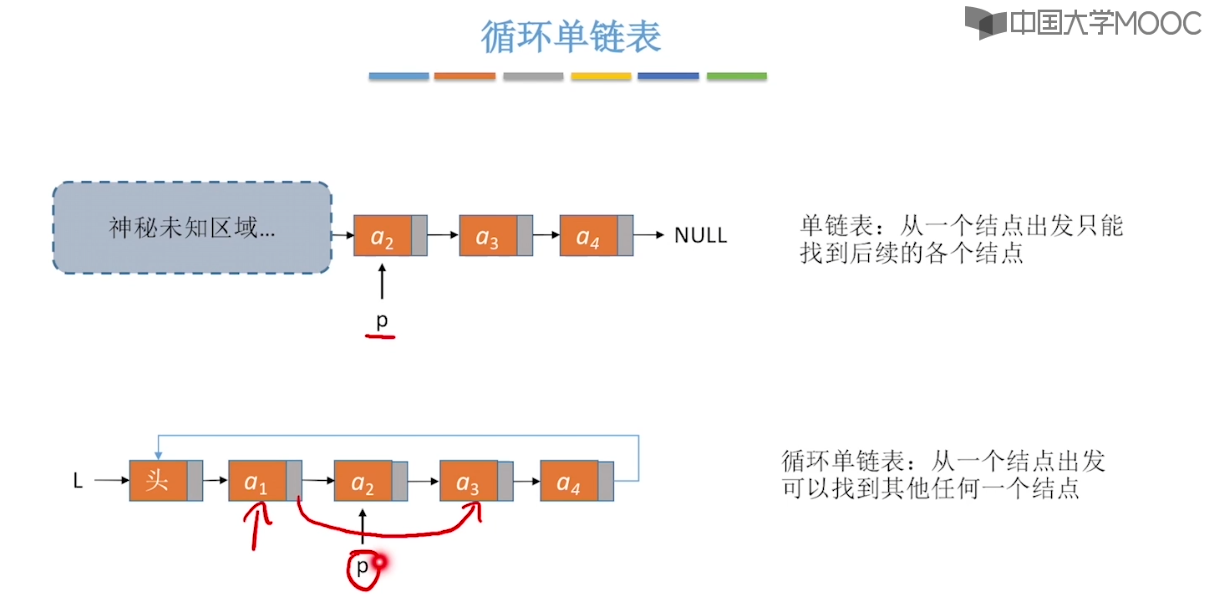
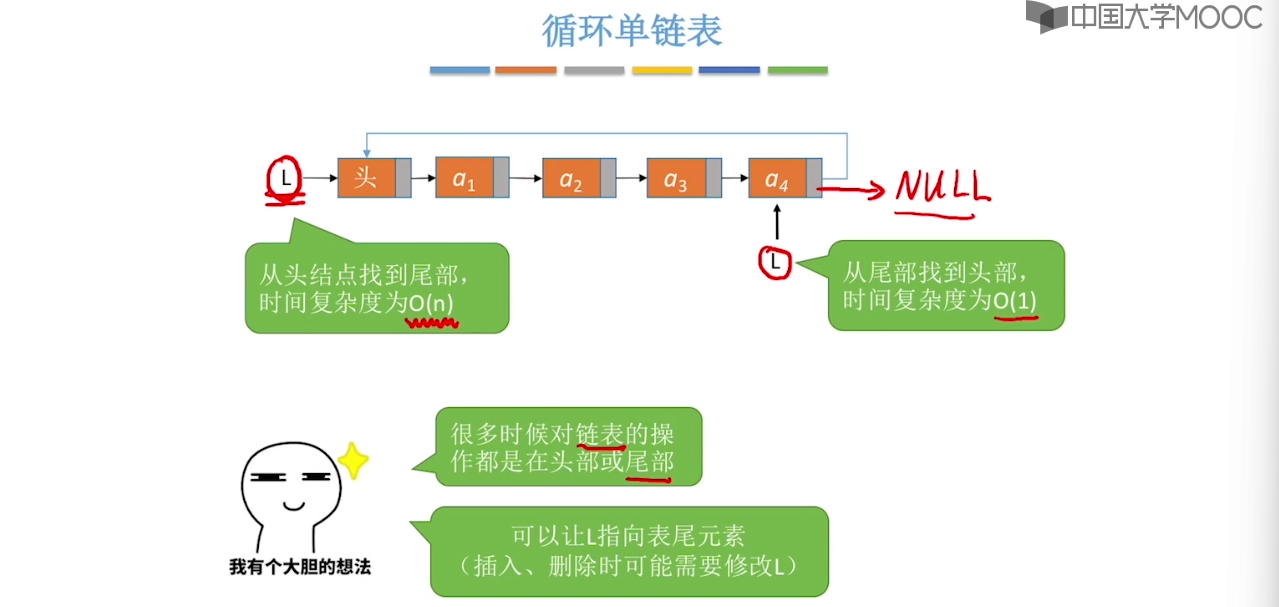
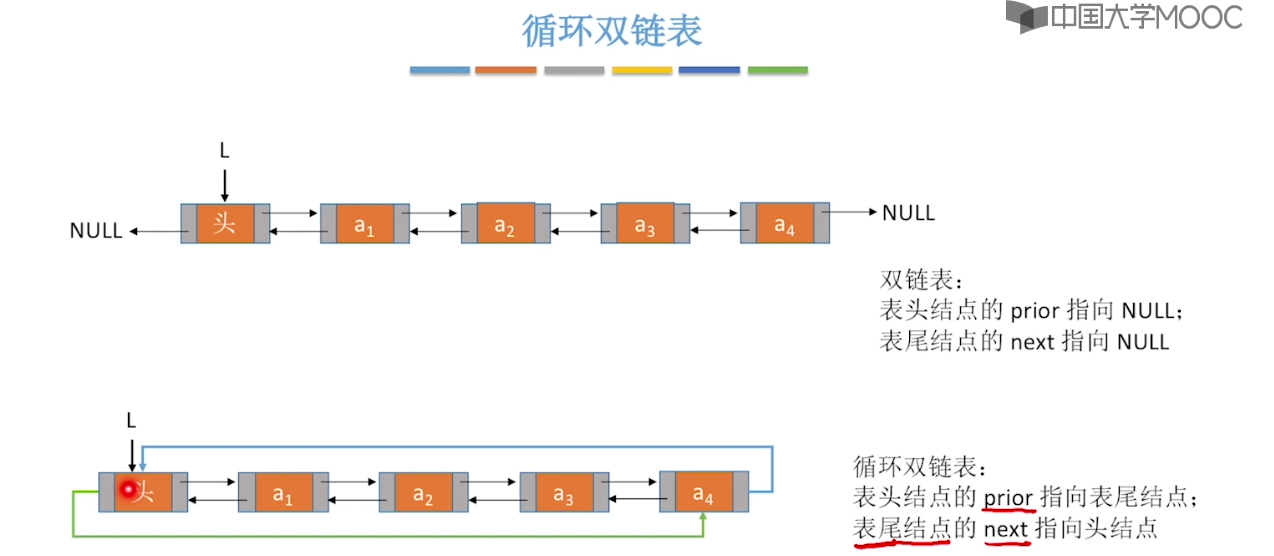
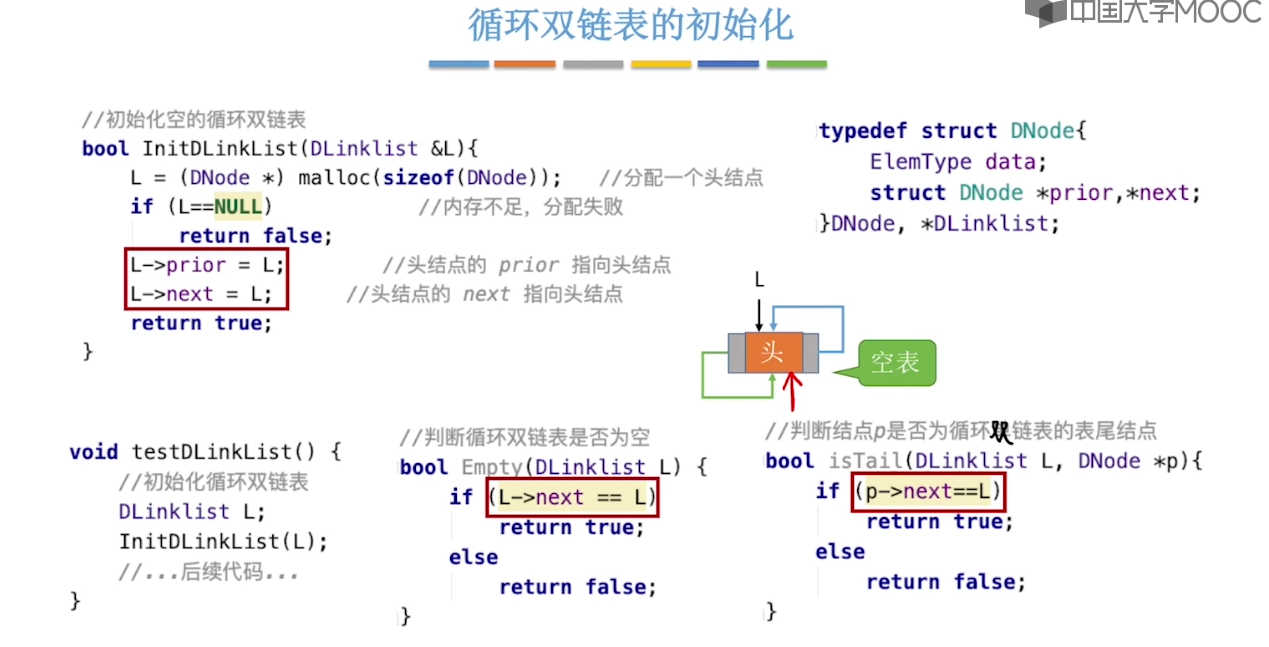
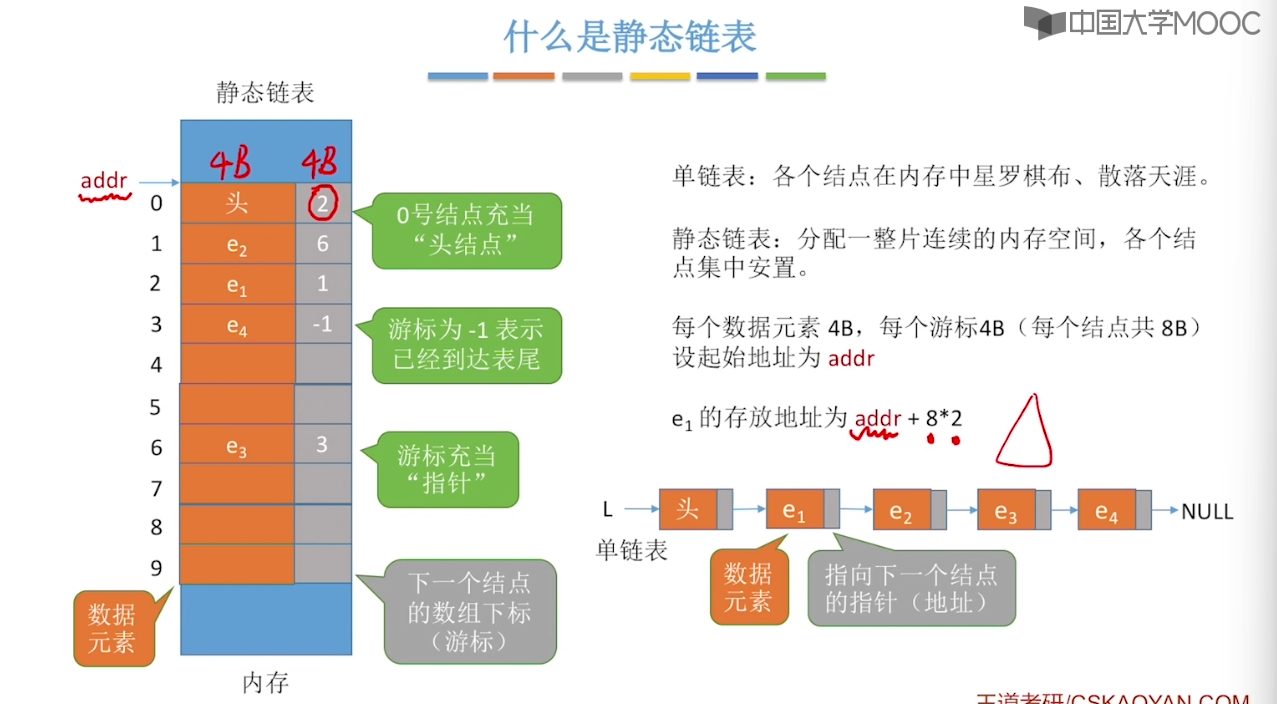
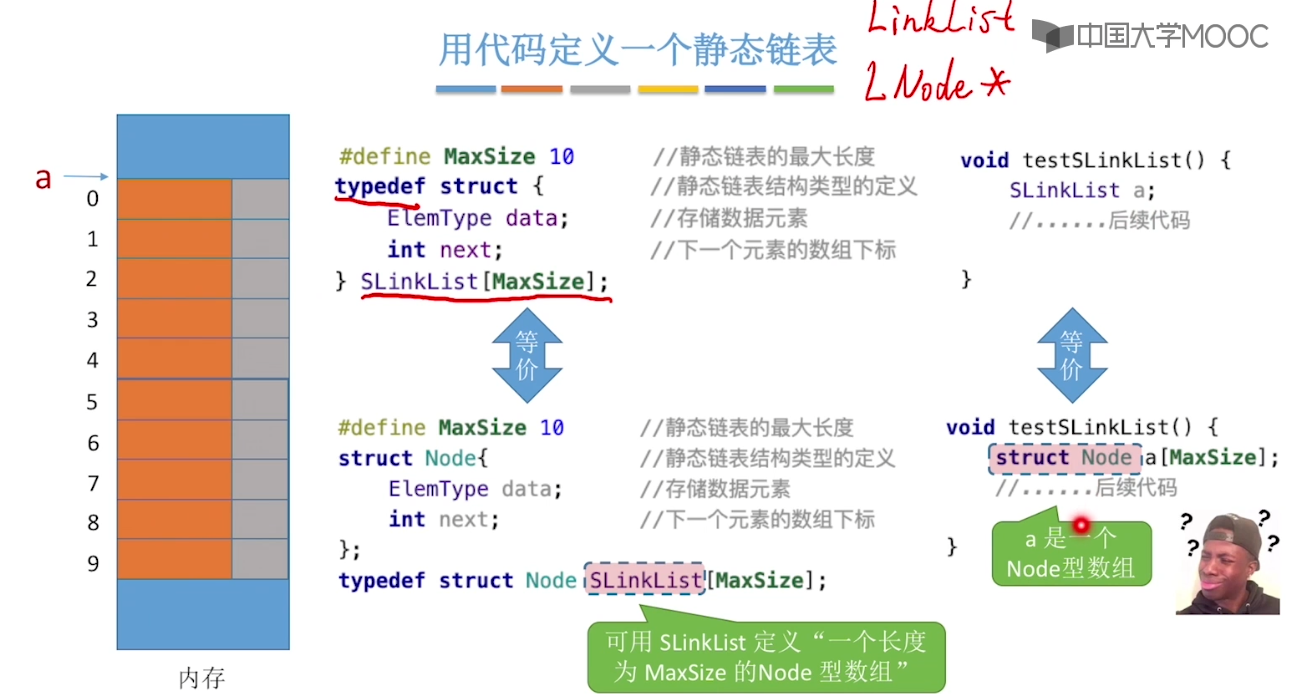
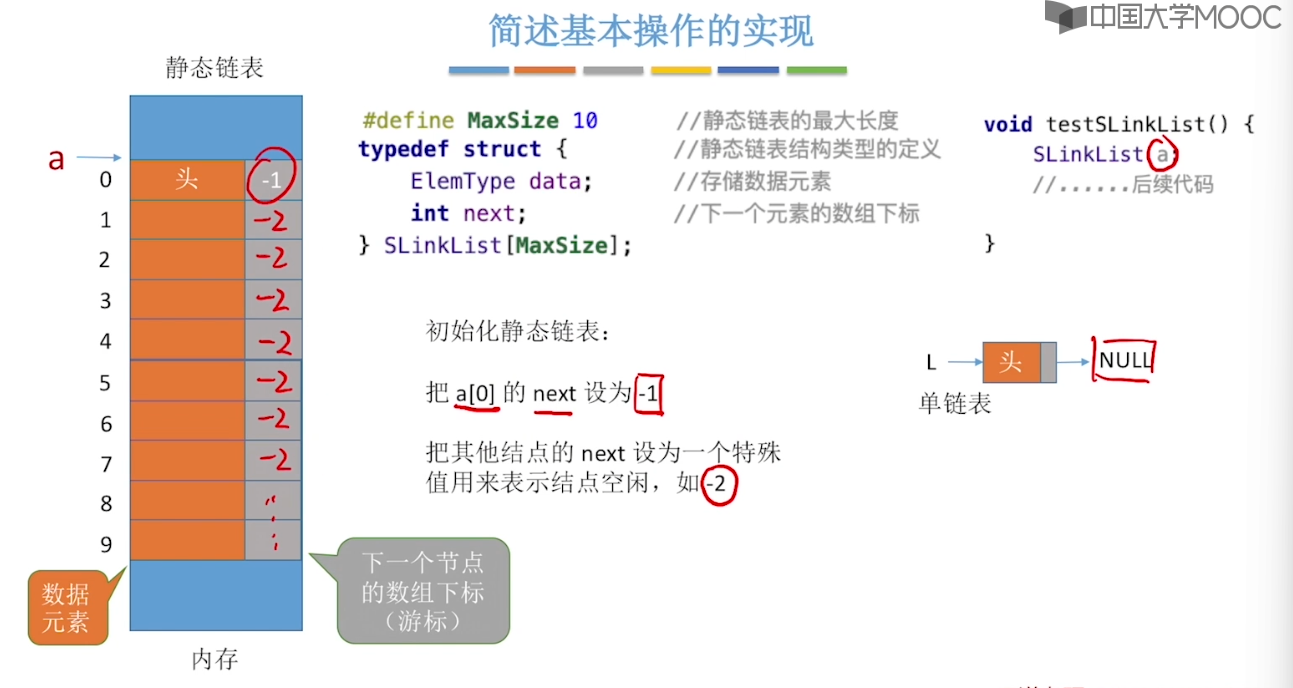
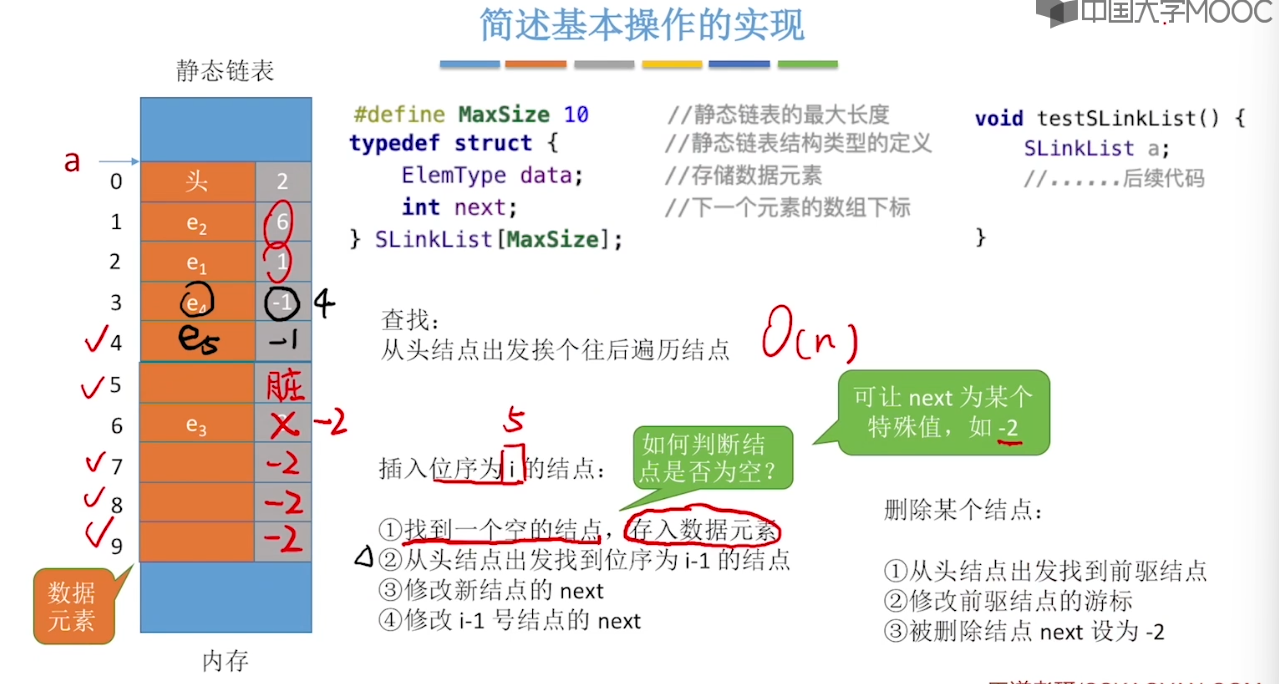
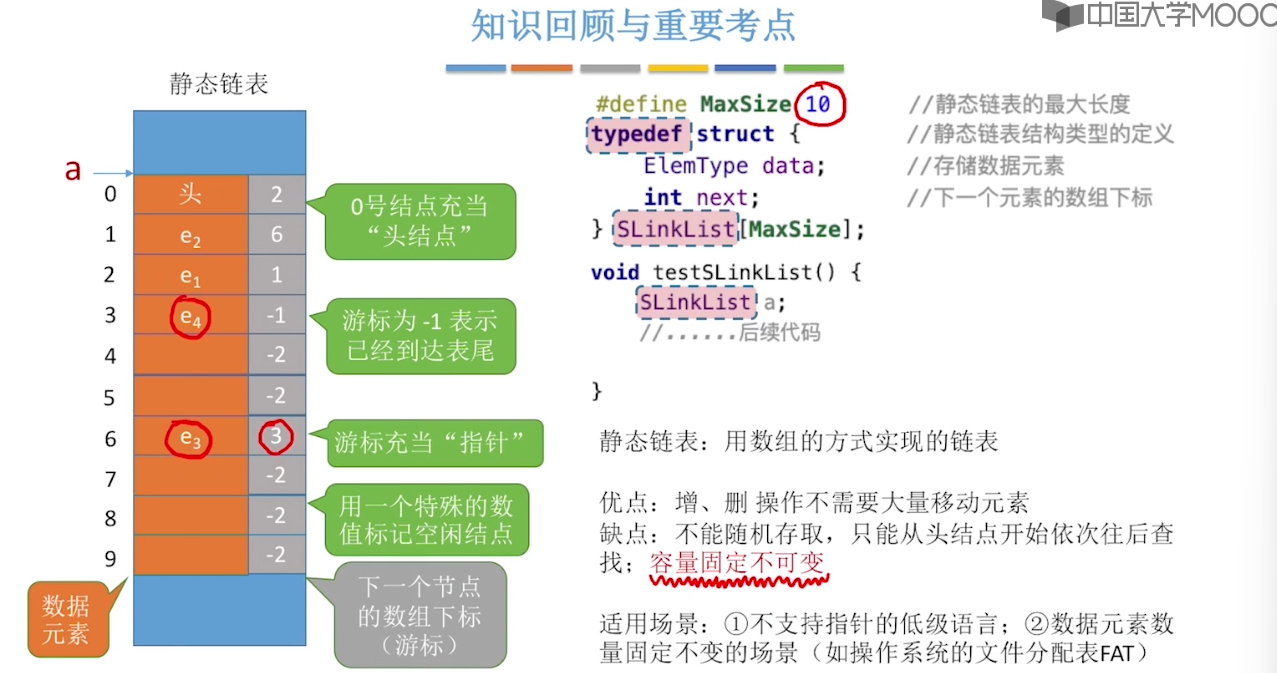
2.7、静态链表

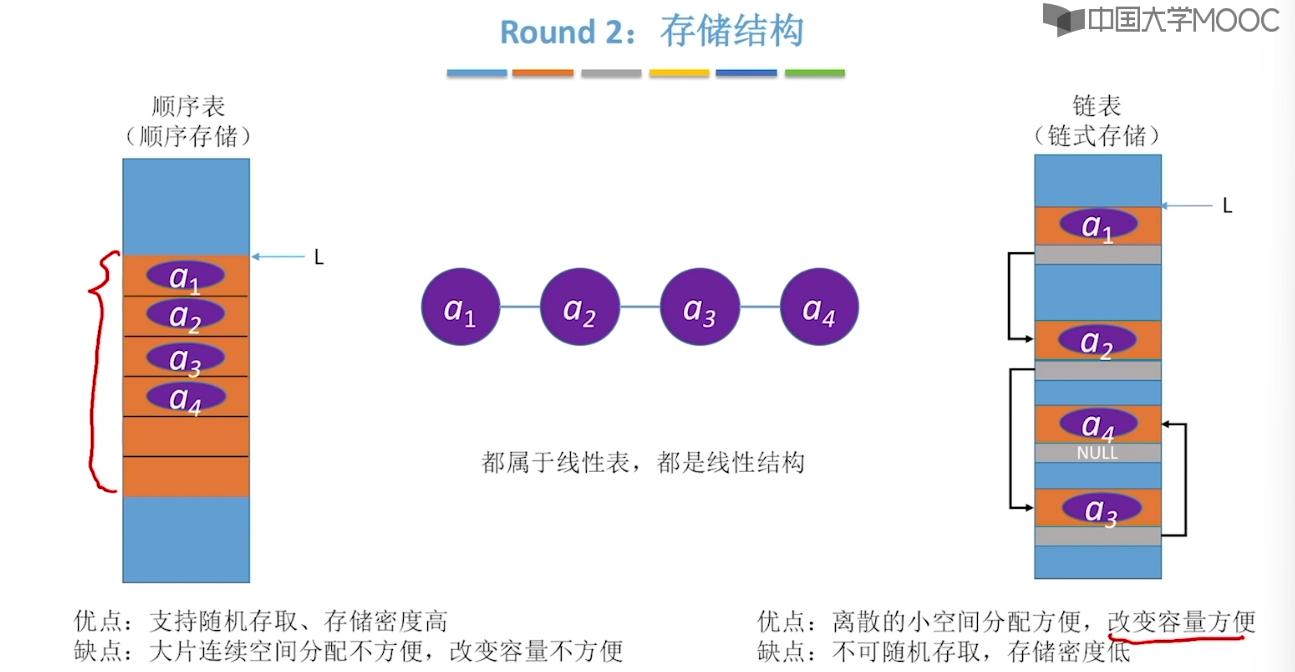
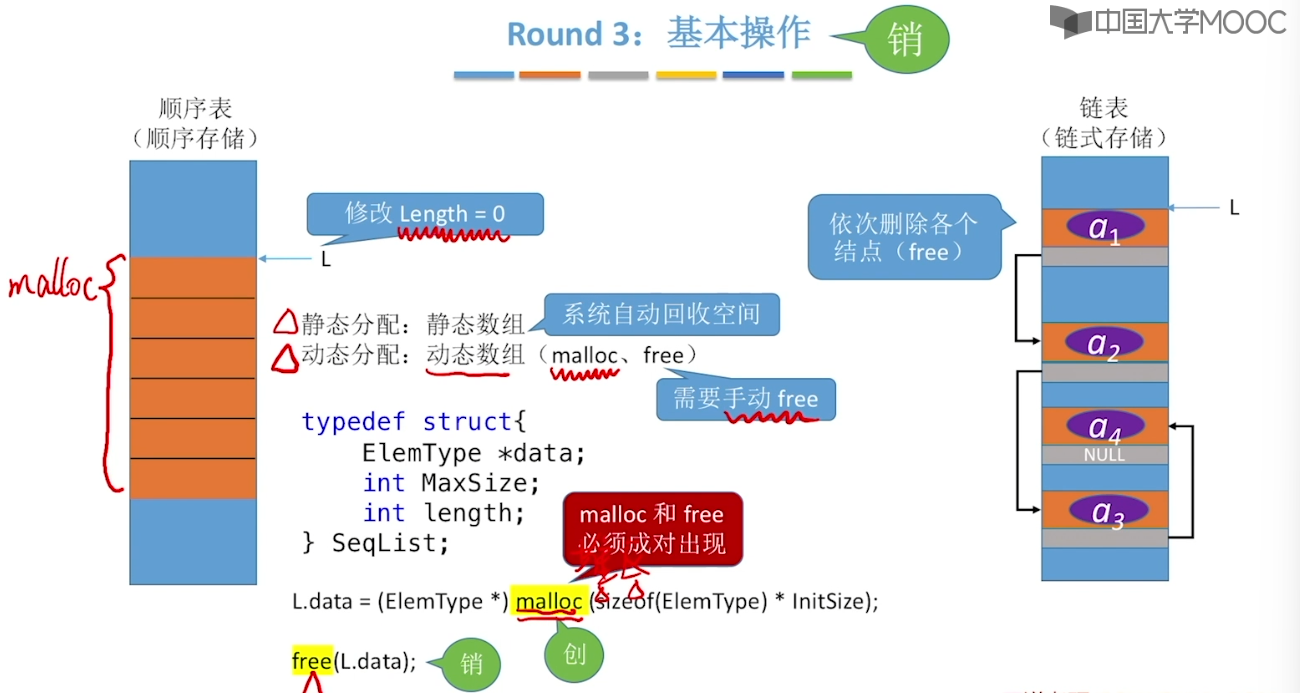
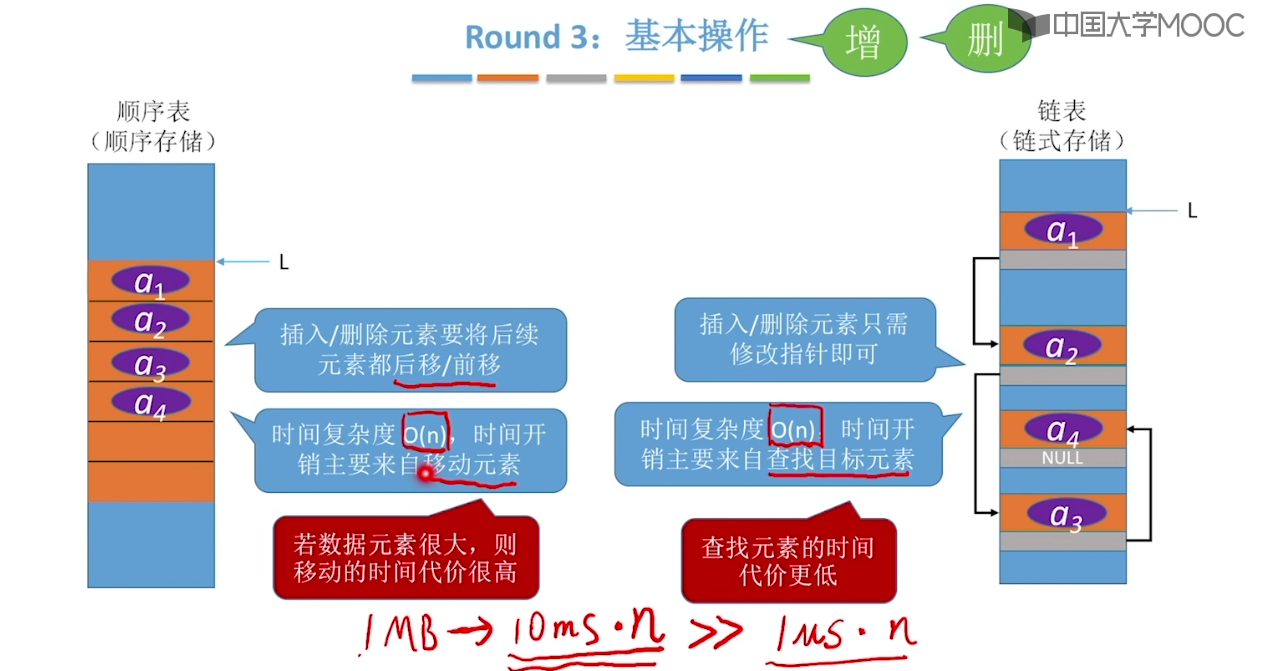
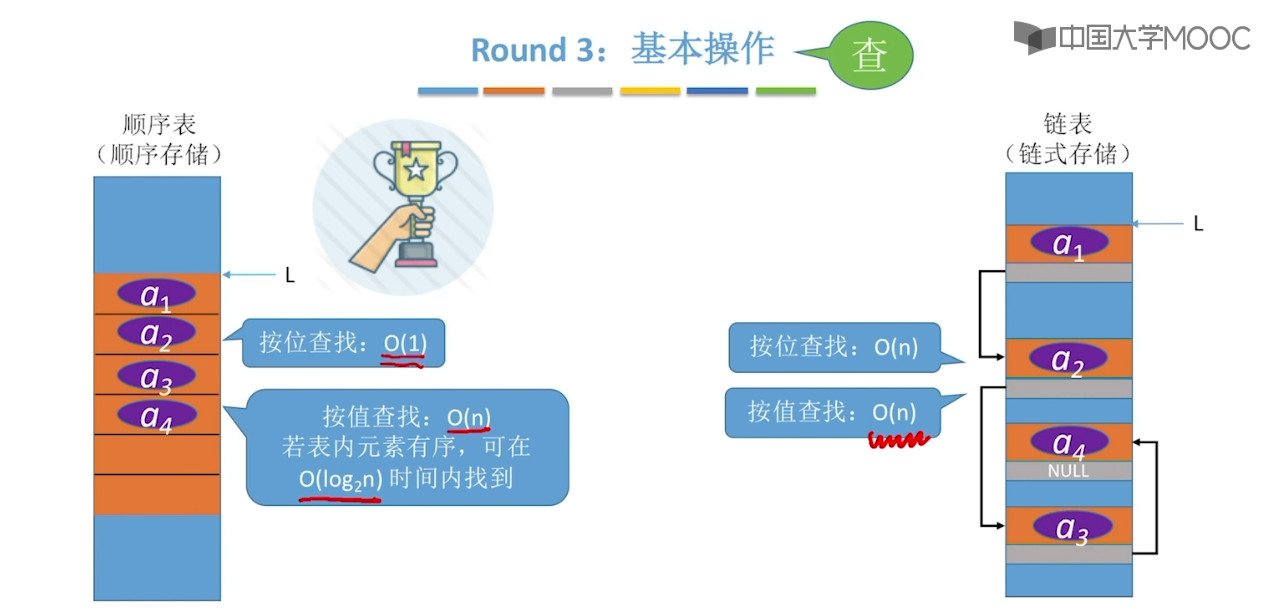
2.8、顺序表 & 链表




3、栈、队列和数组
3.1、栈的基本概念
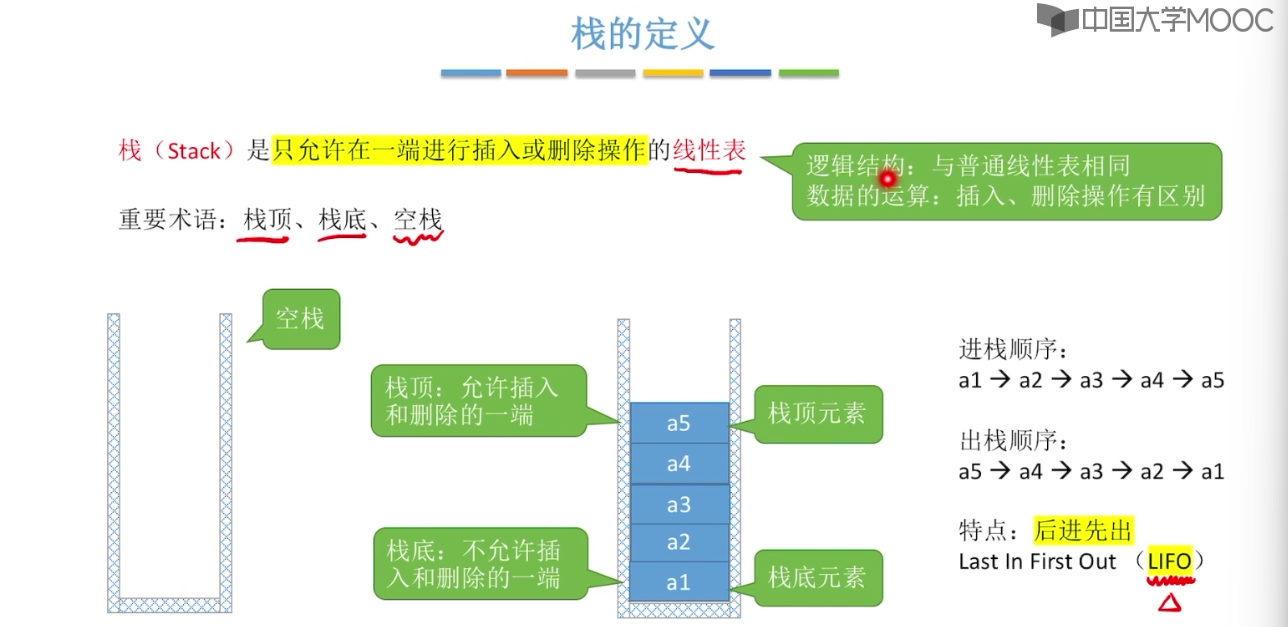

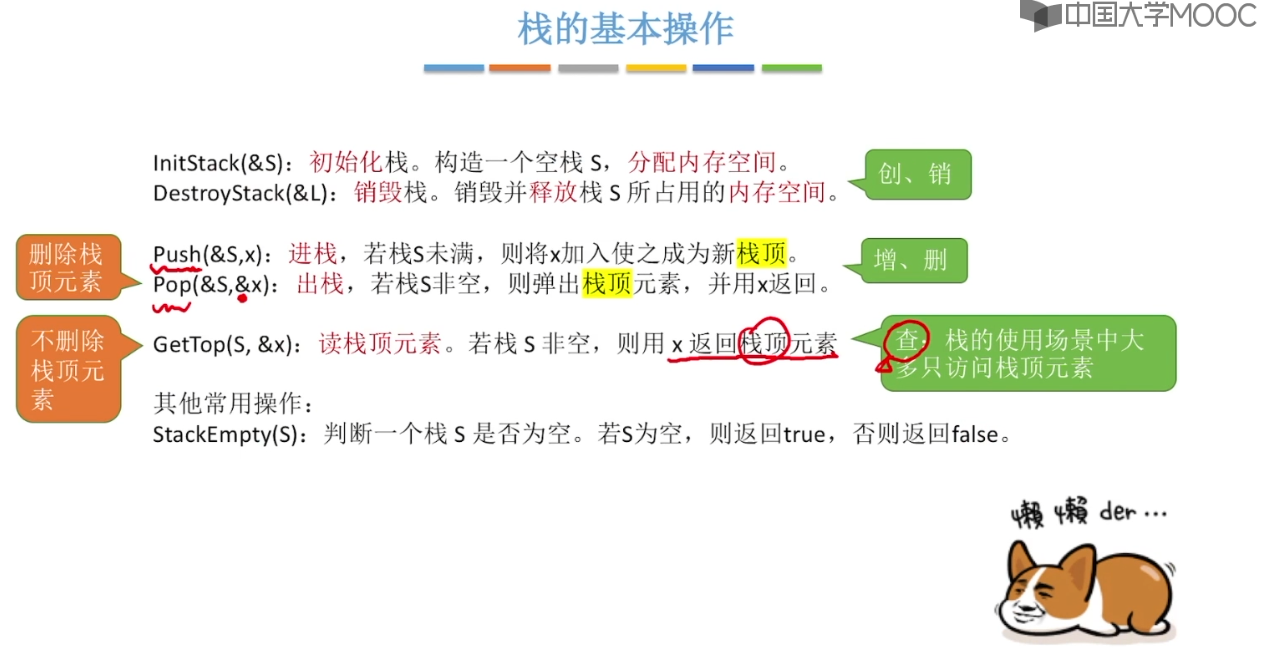

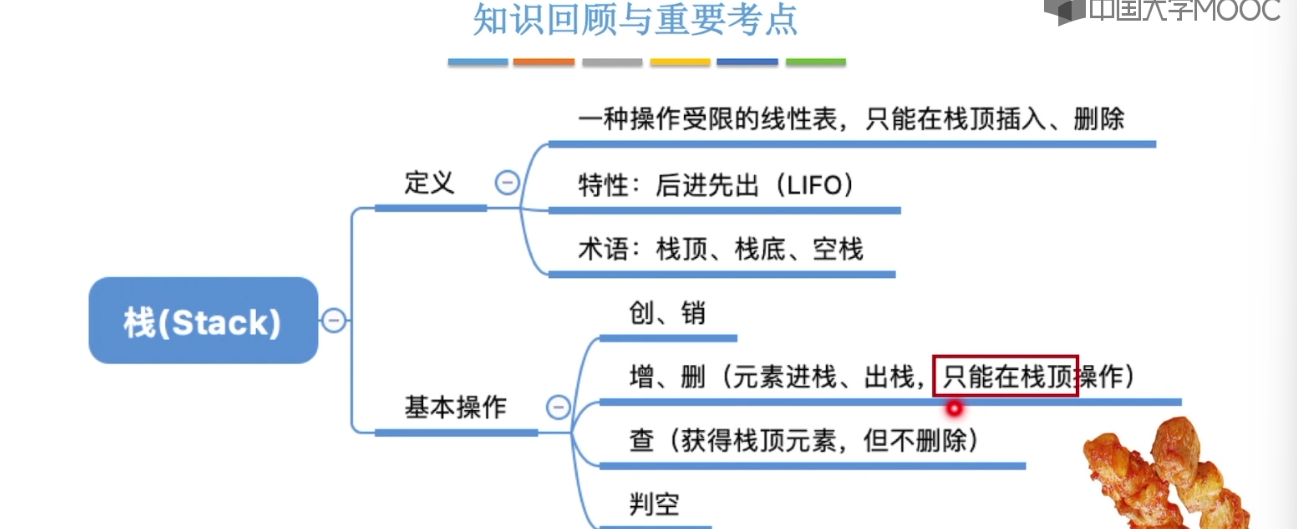
3.2、栈的顺序存储实现
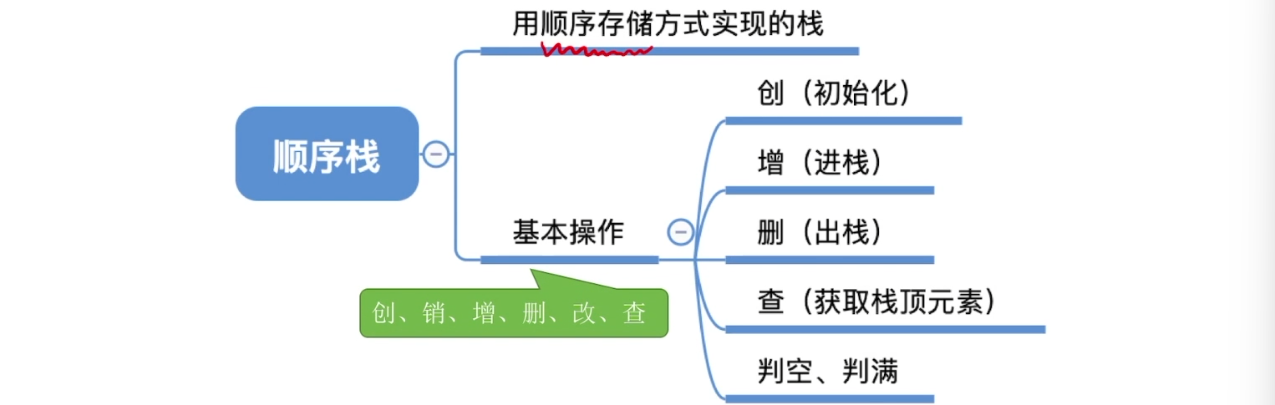
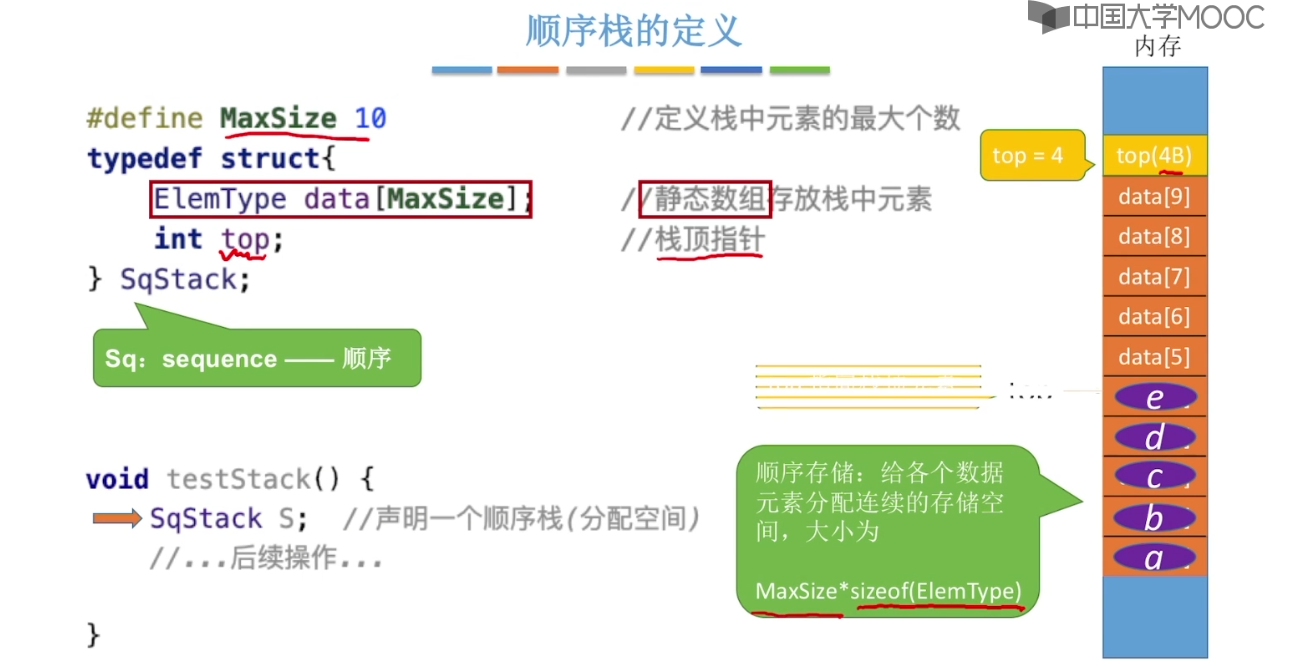
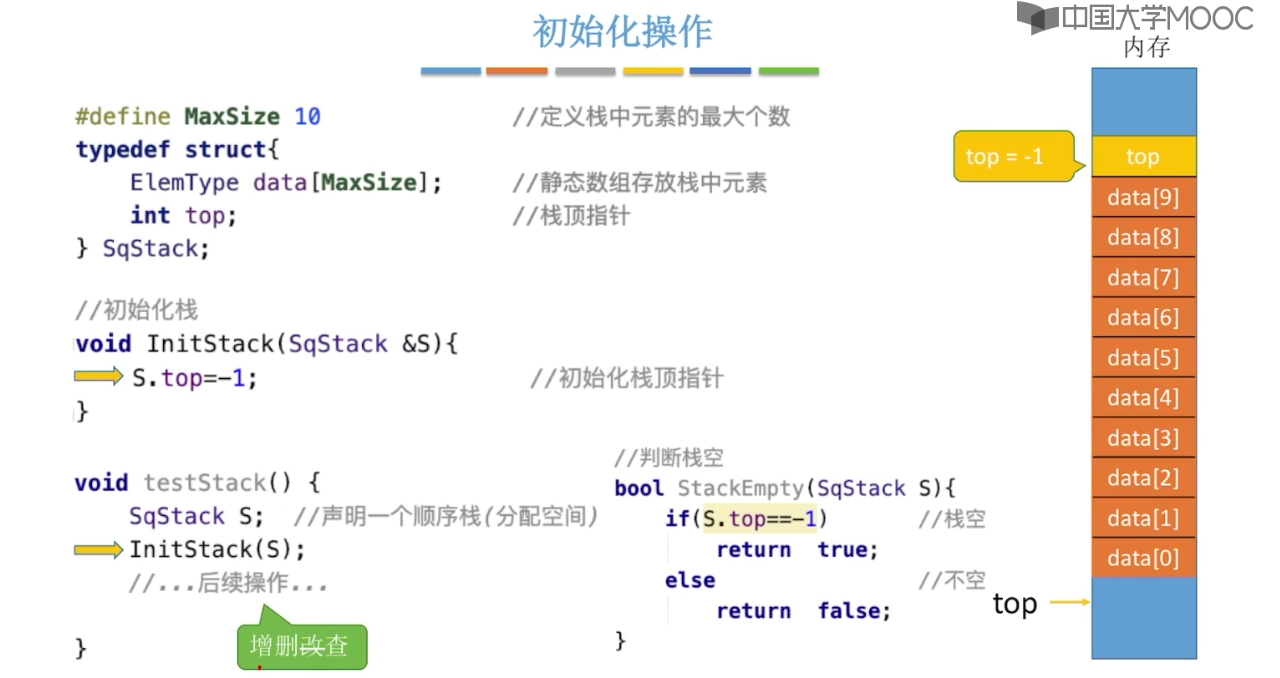
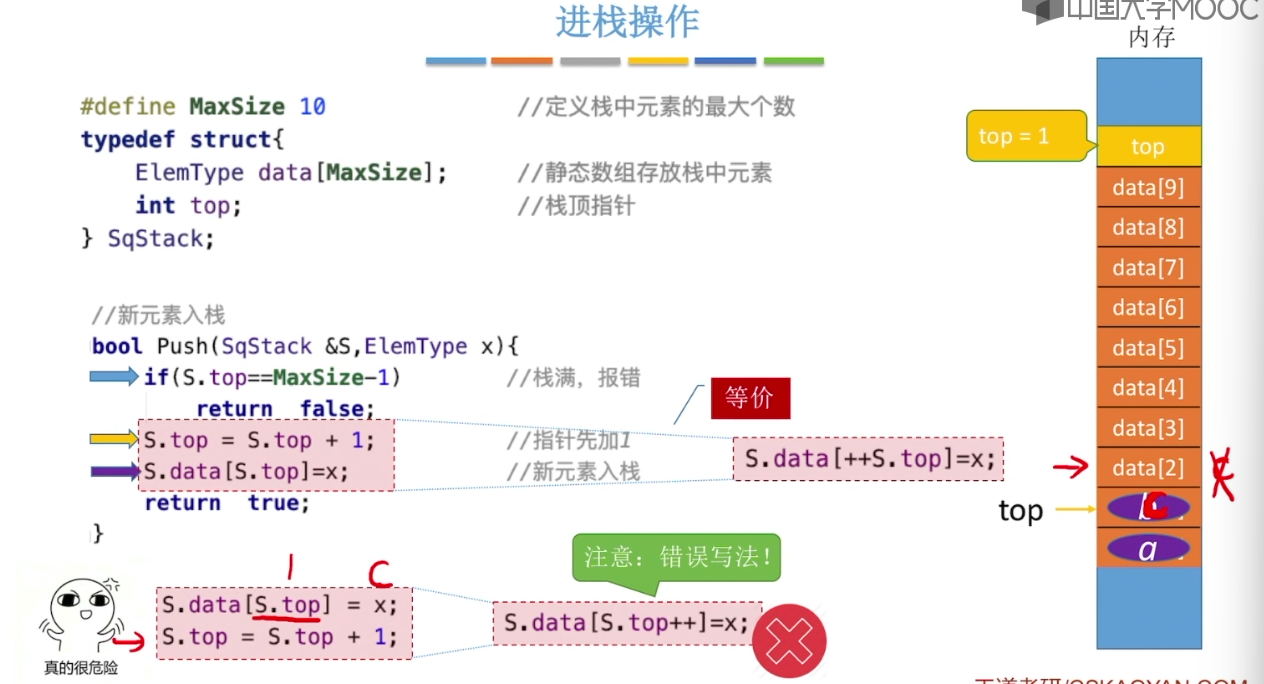
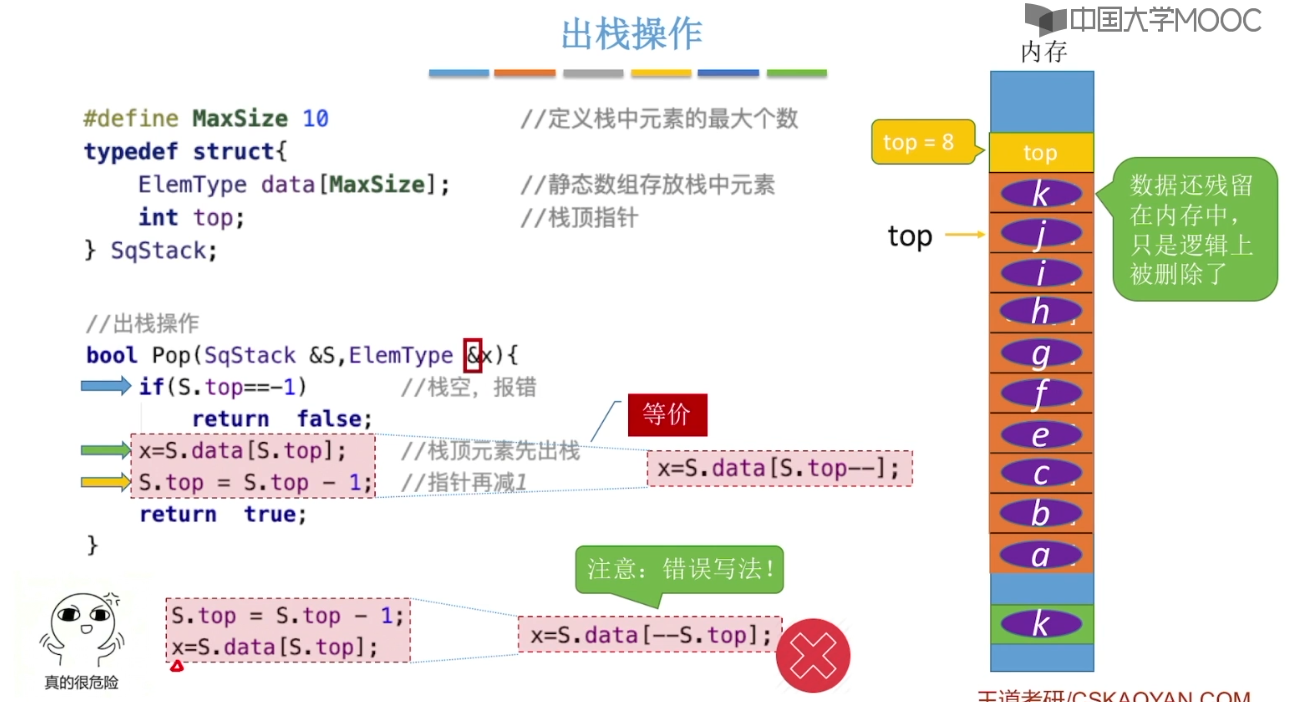
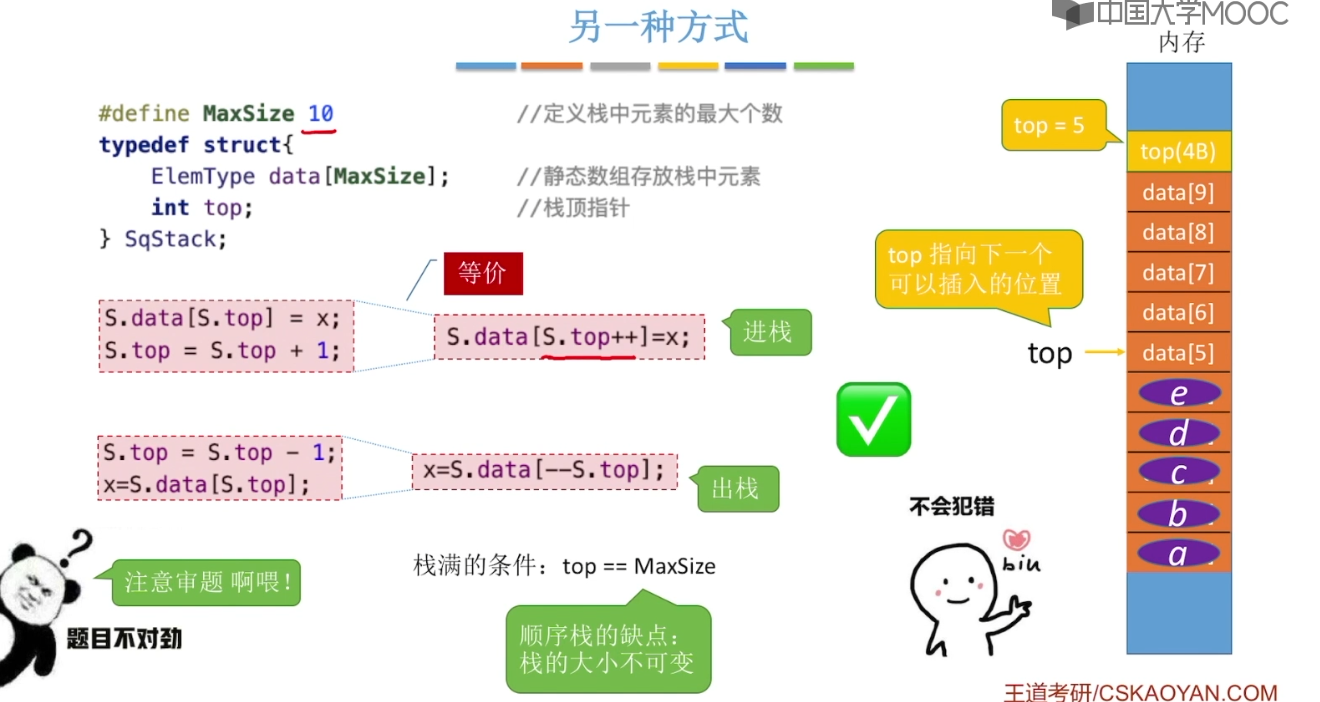

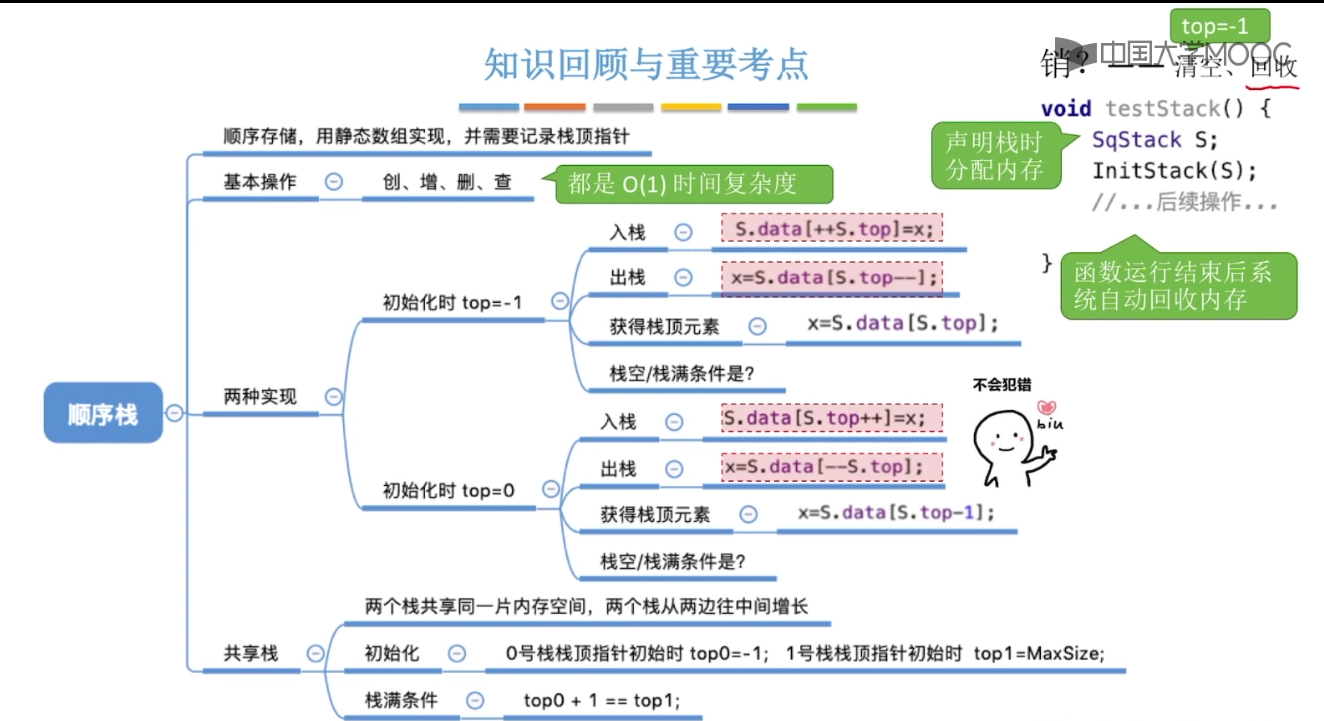
3.3、栈的链式存储实现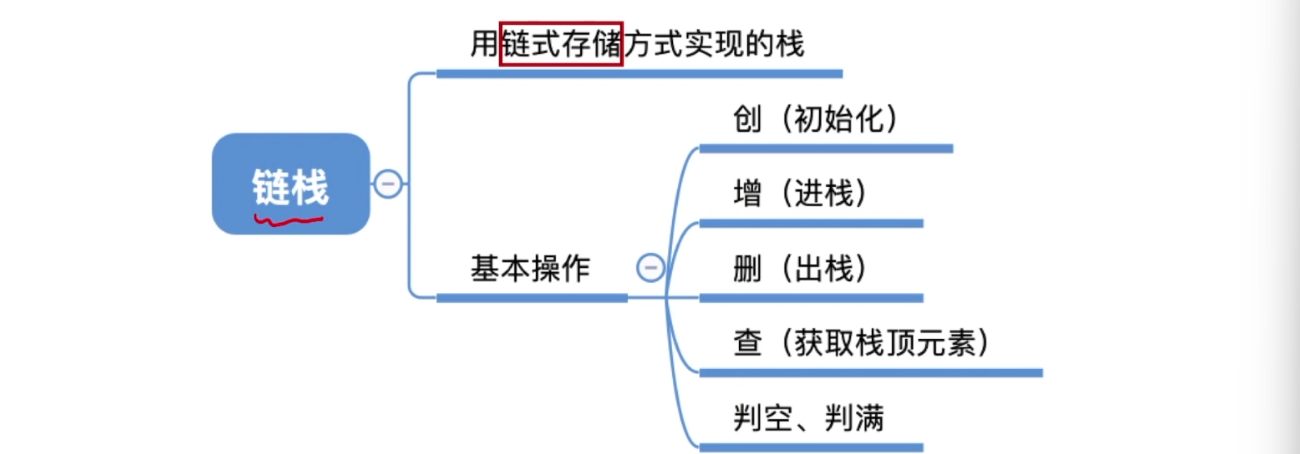
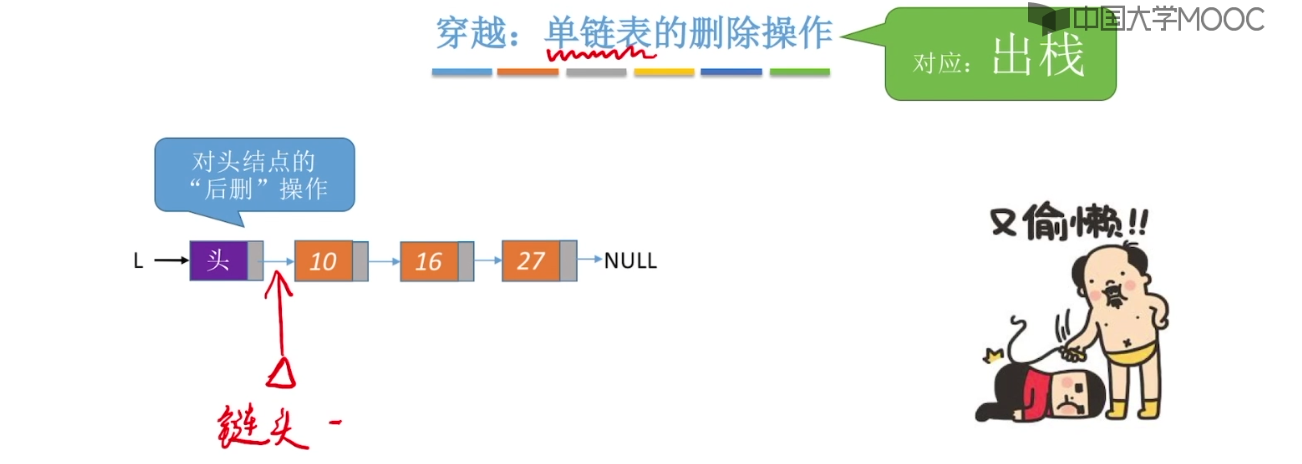
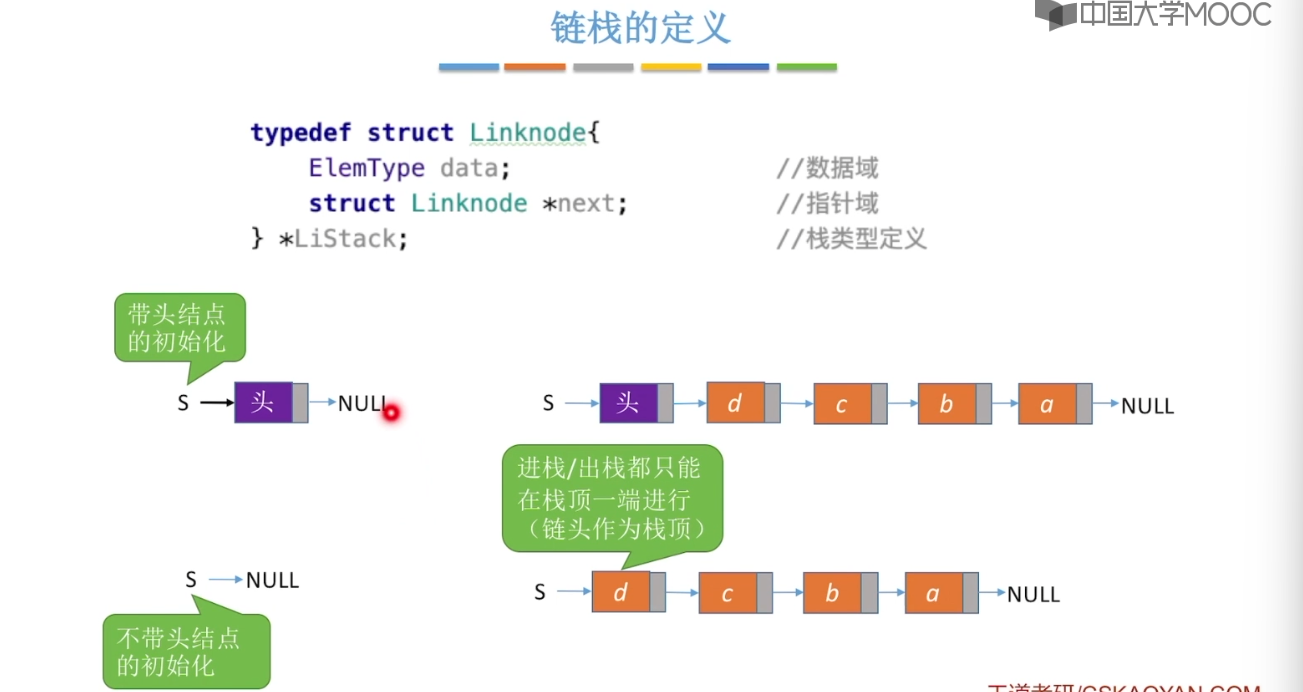
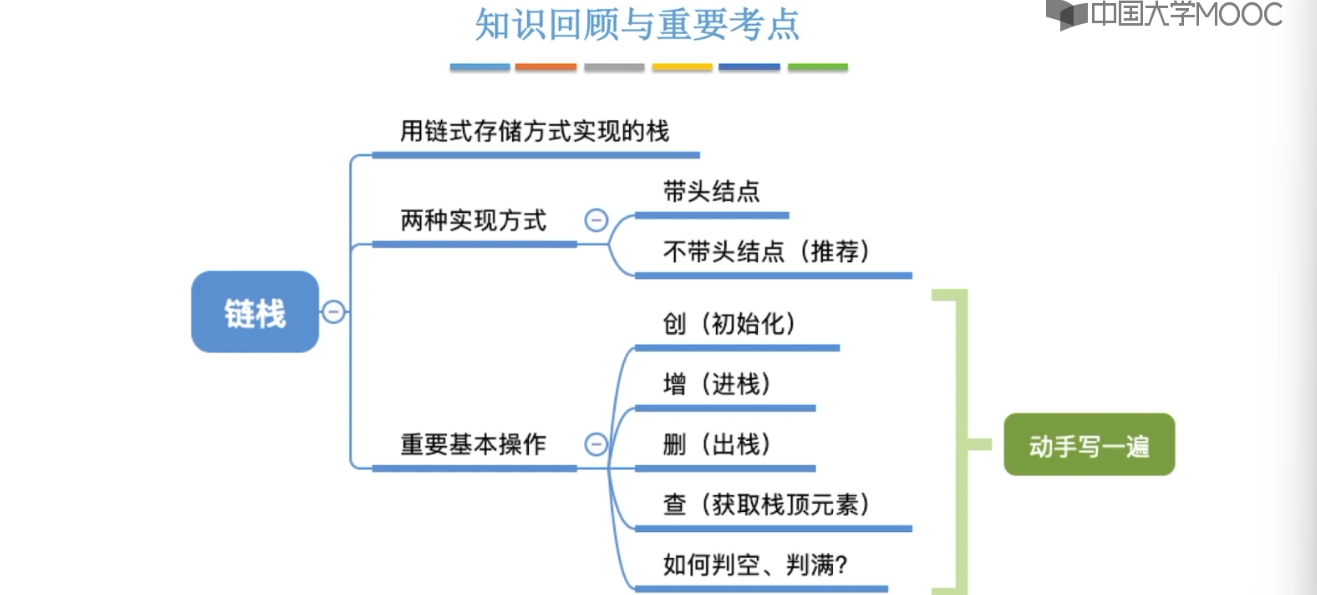
3.4、队列的基本概念


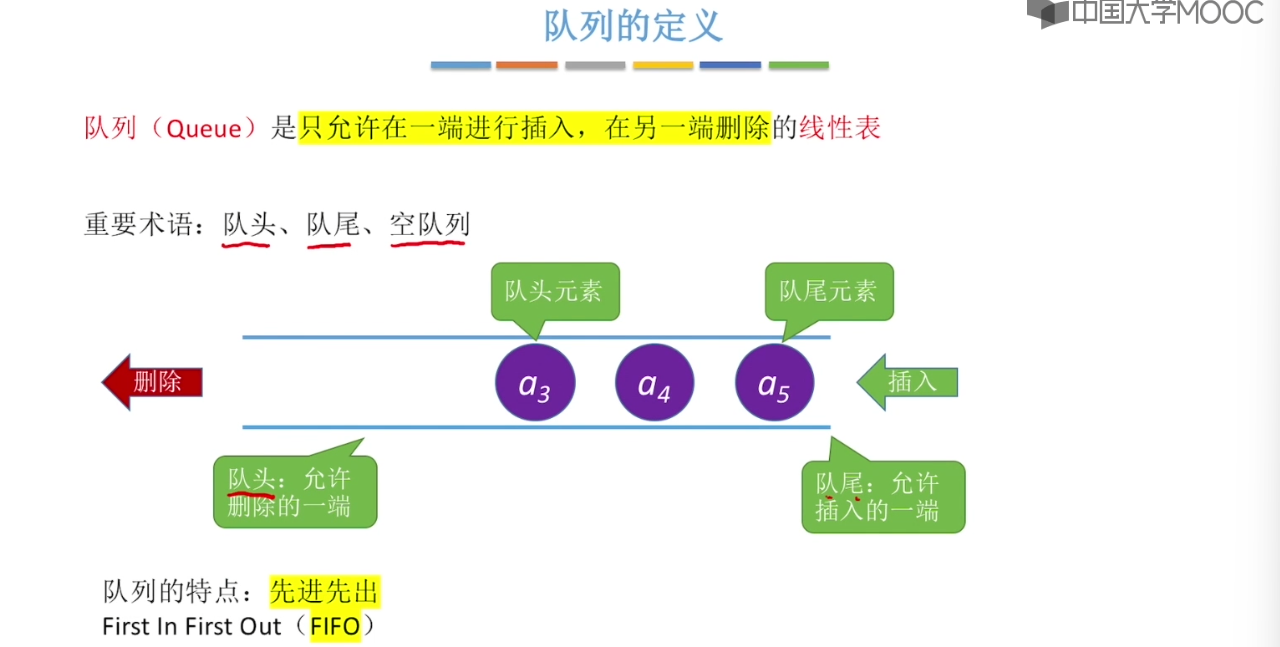

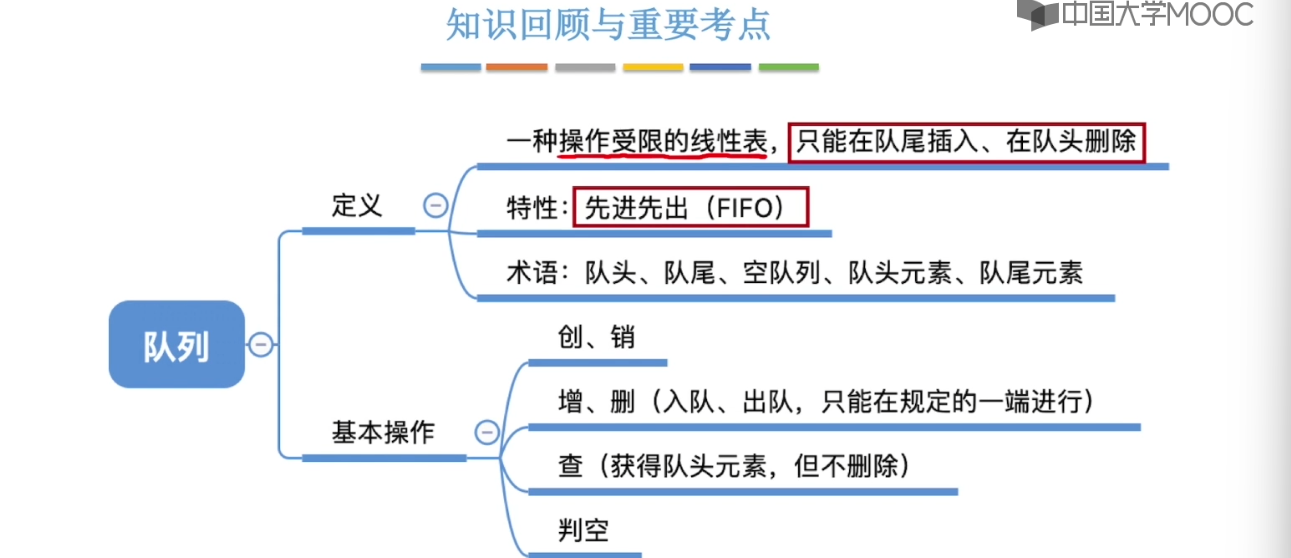
3.5、队列的顺序实现
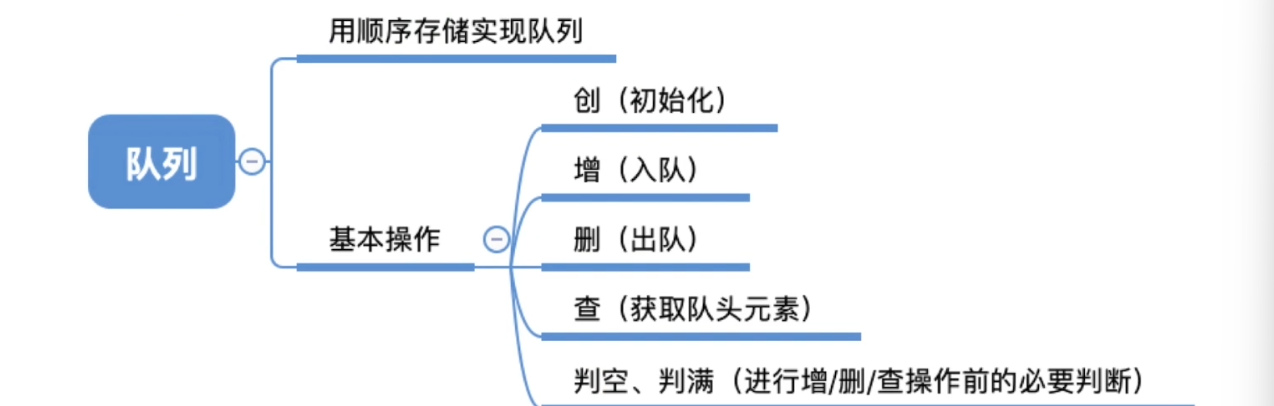


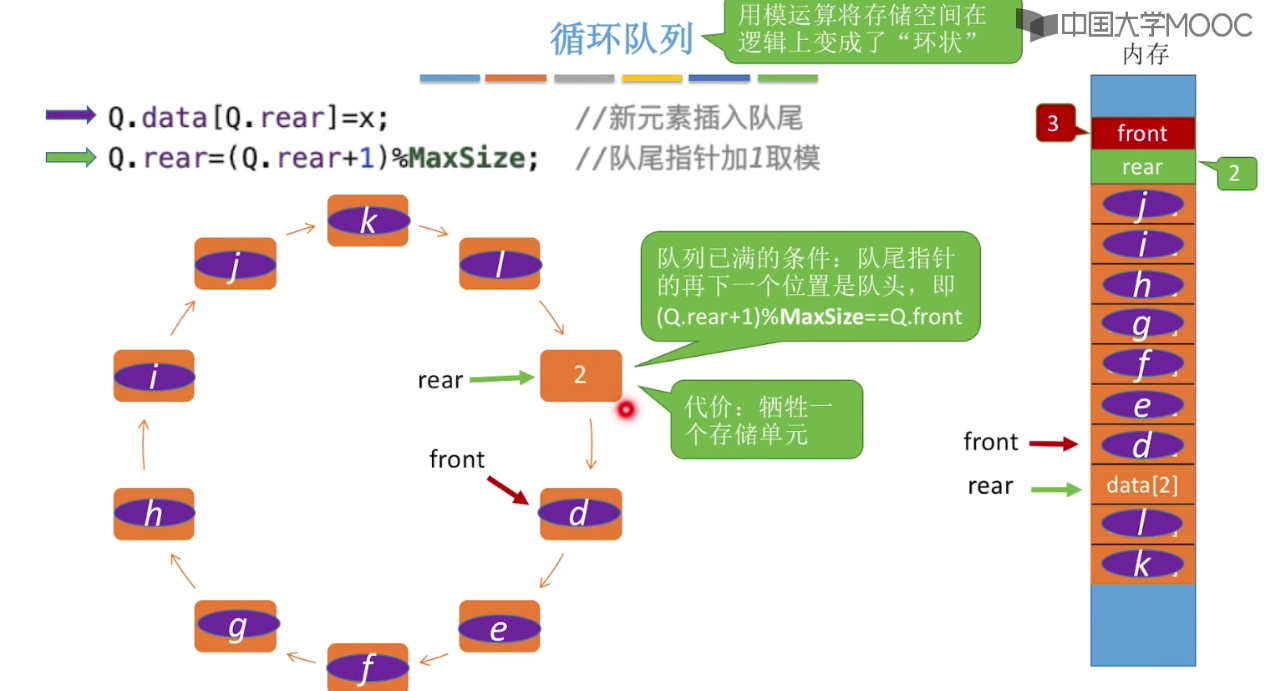
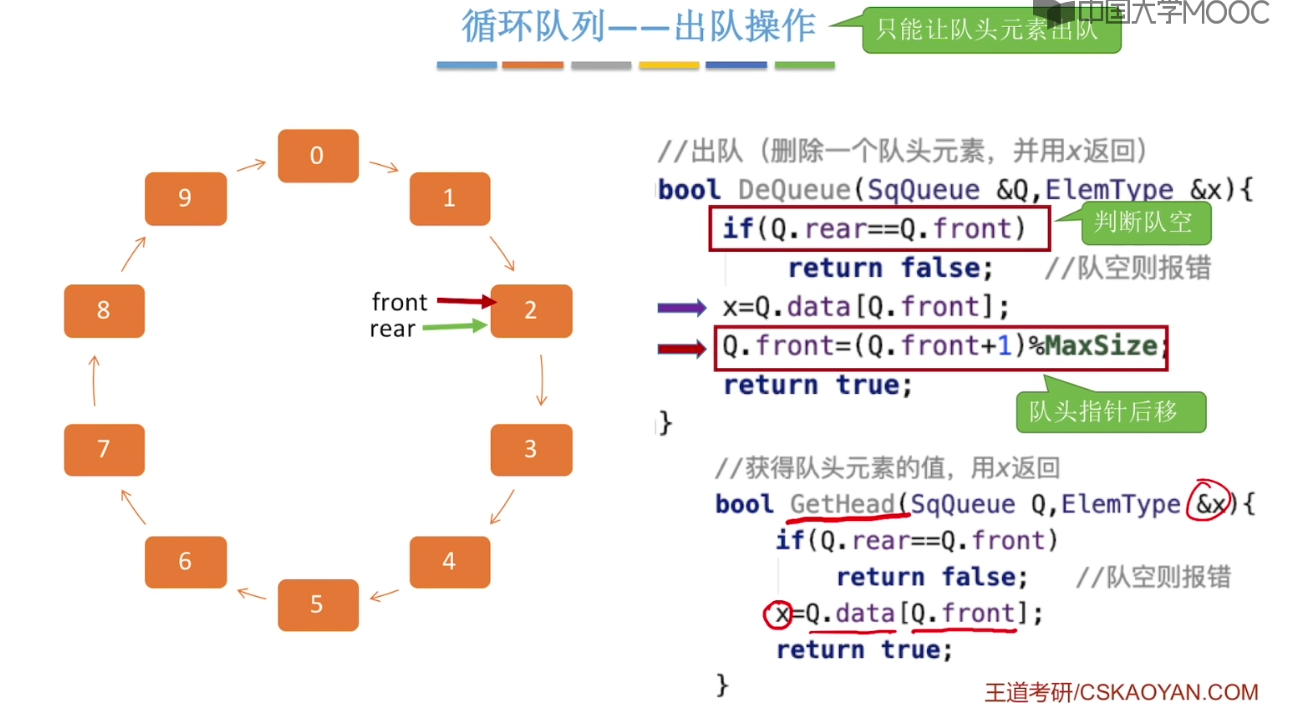
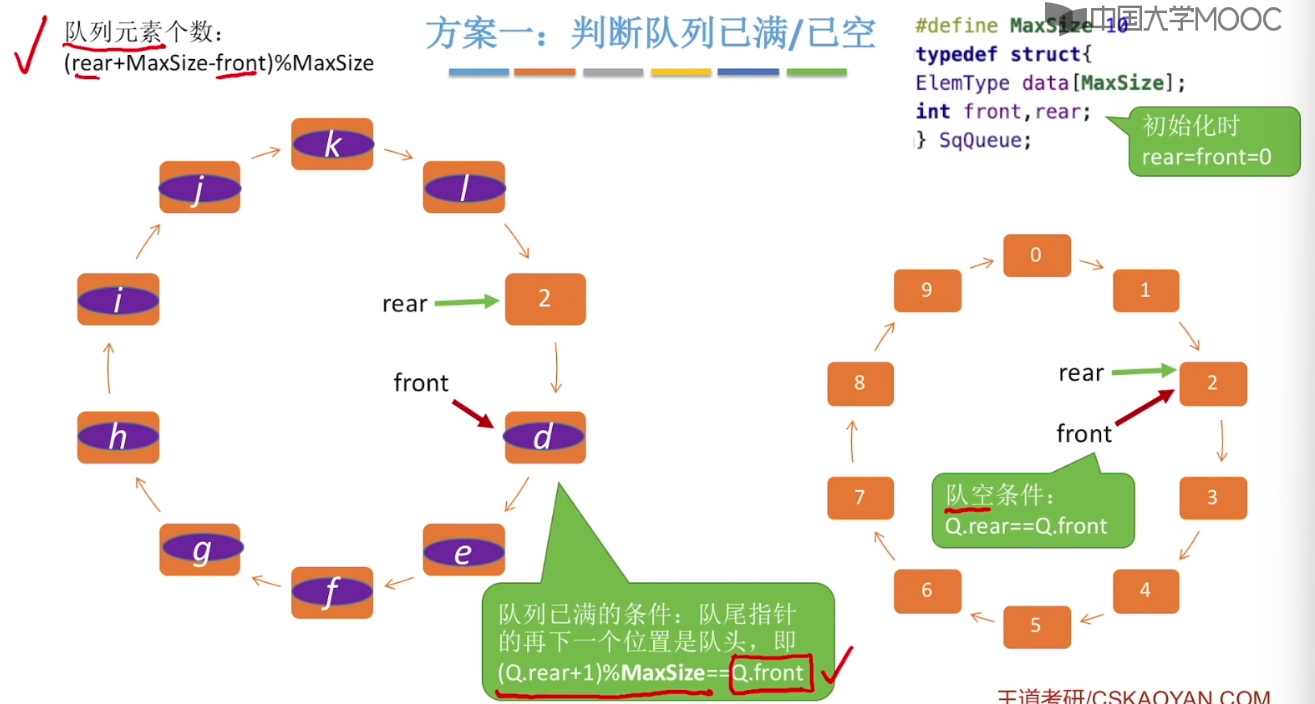
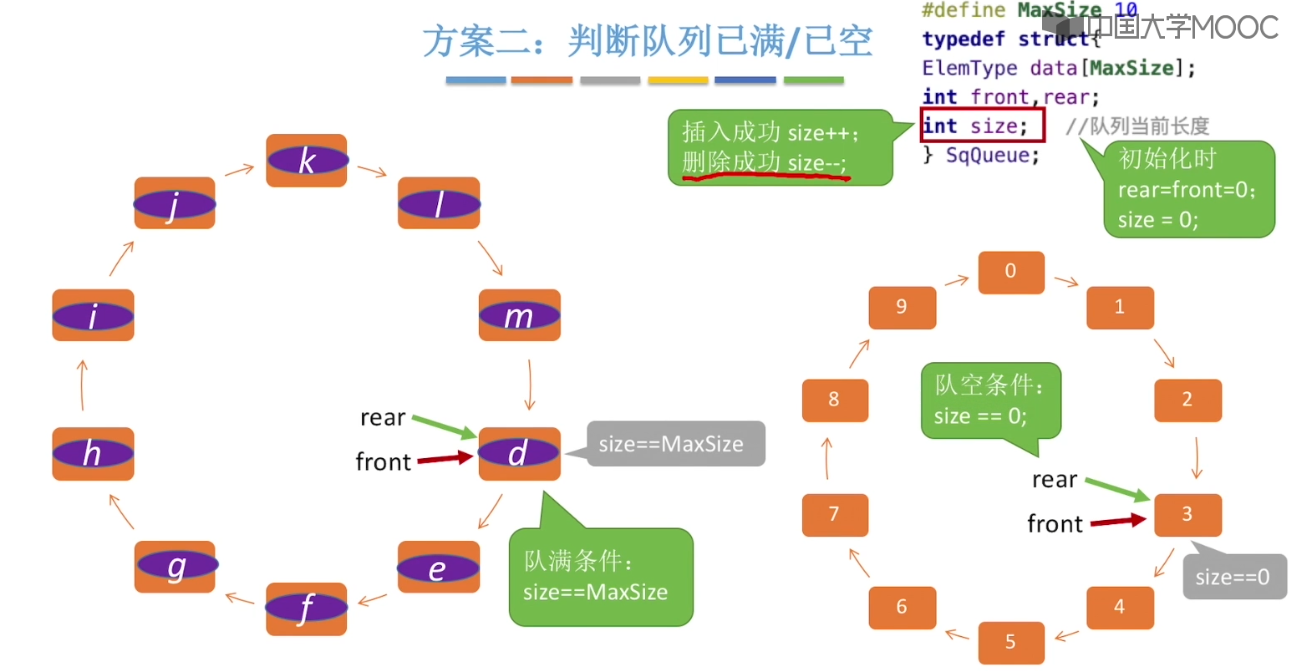
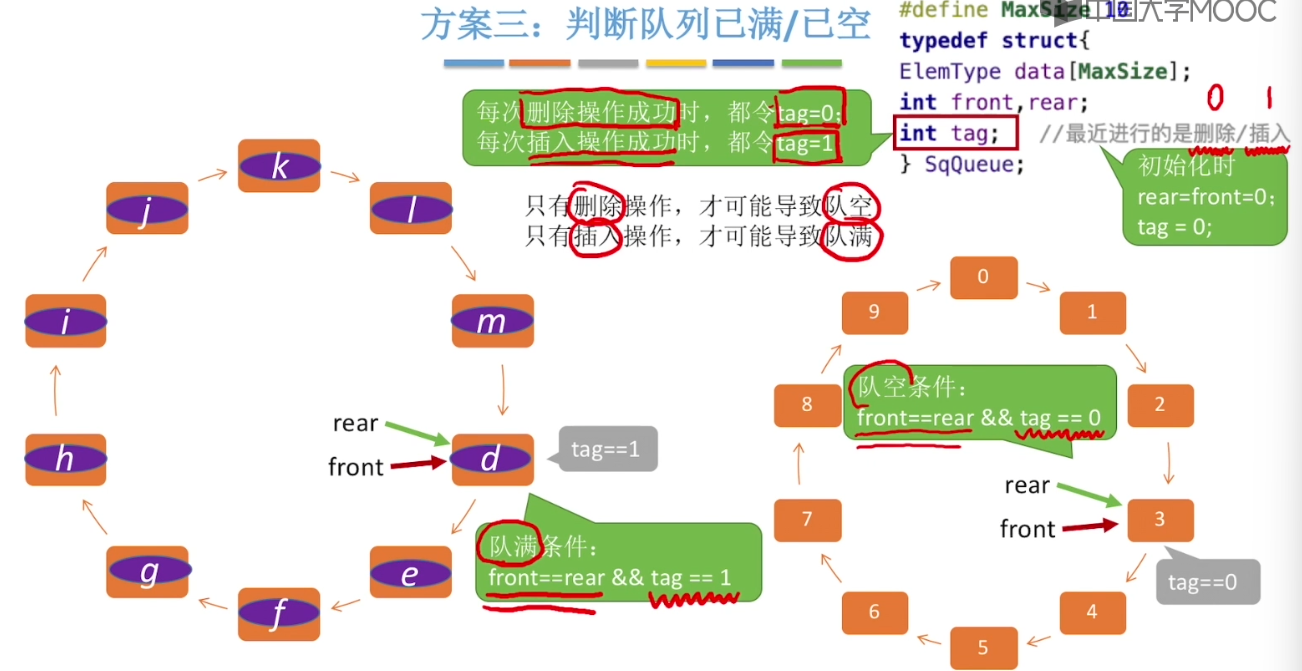
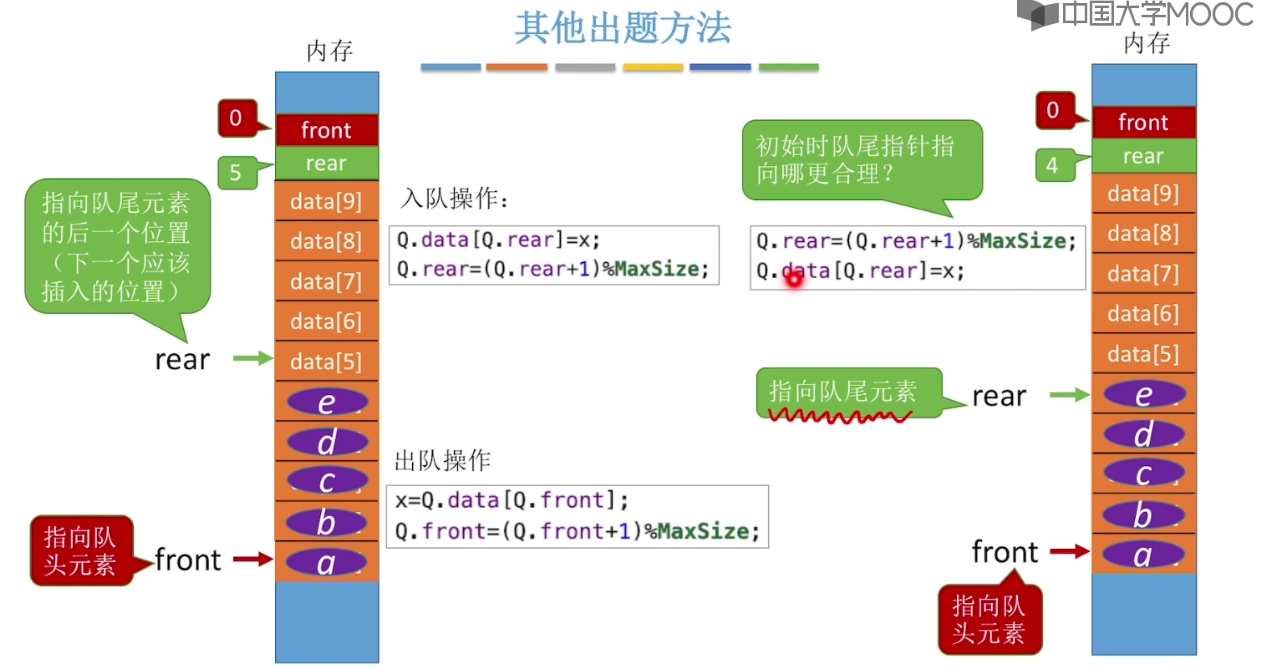
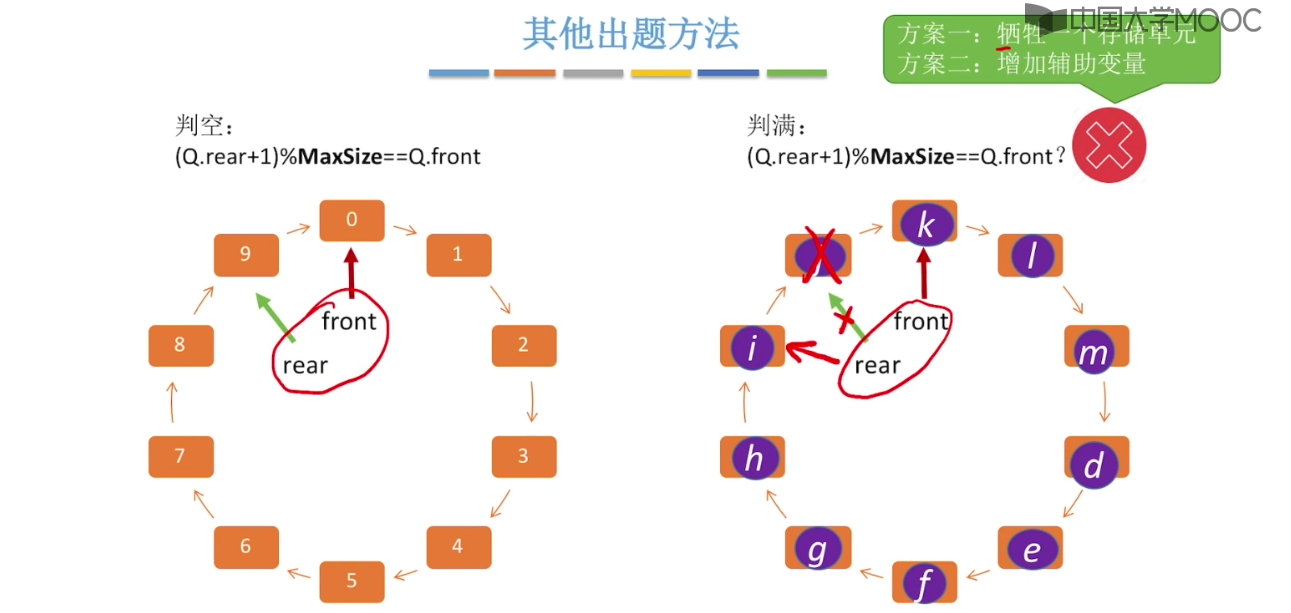
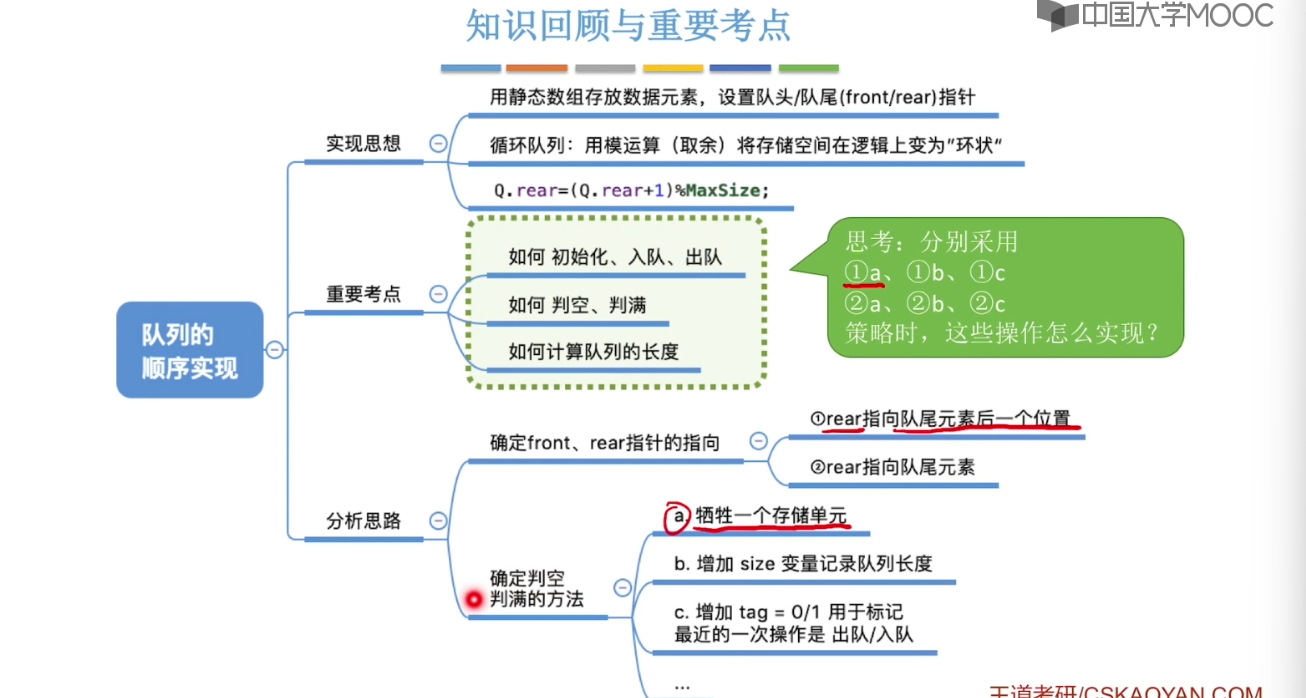
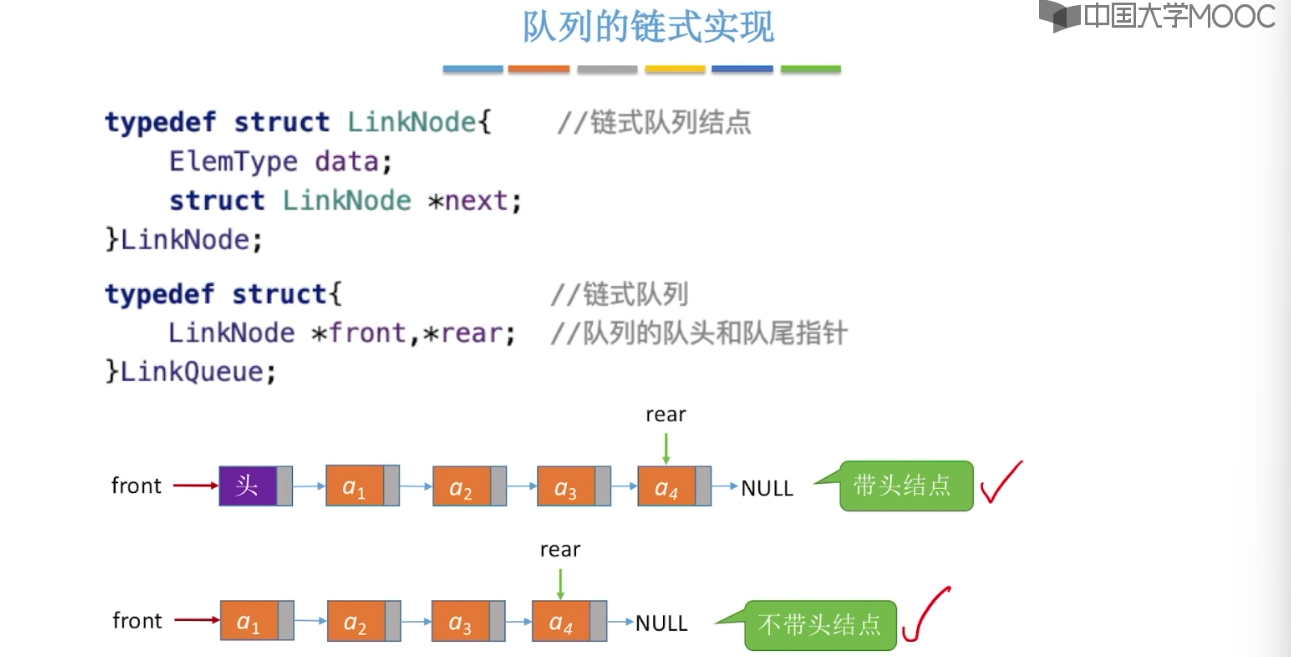
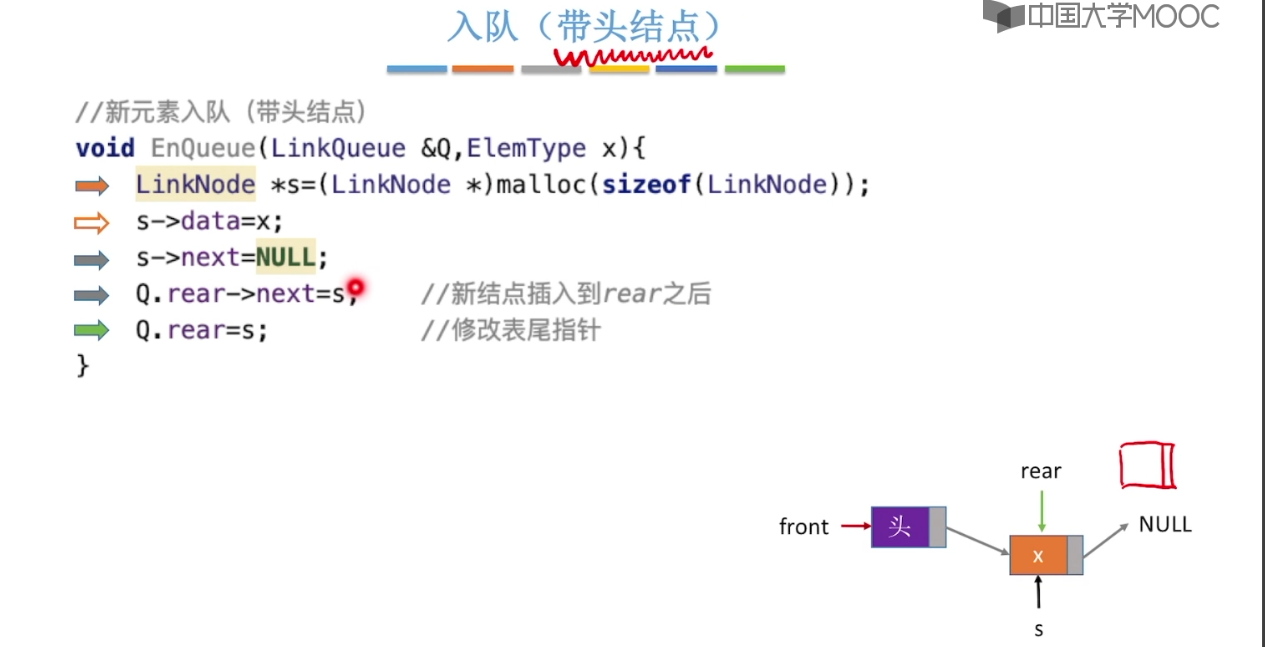
3.6、队列的链式实现
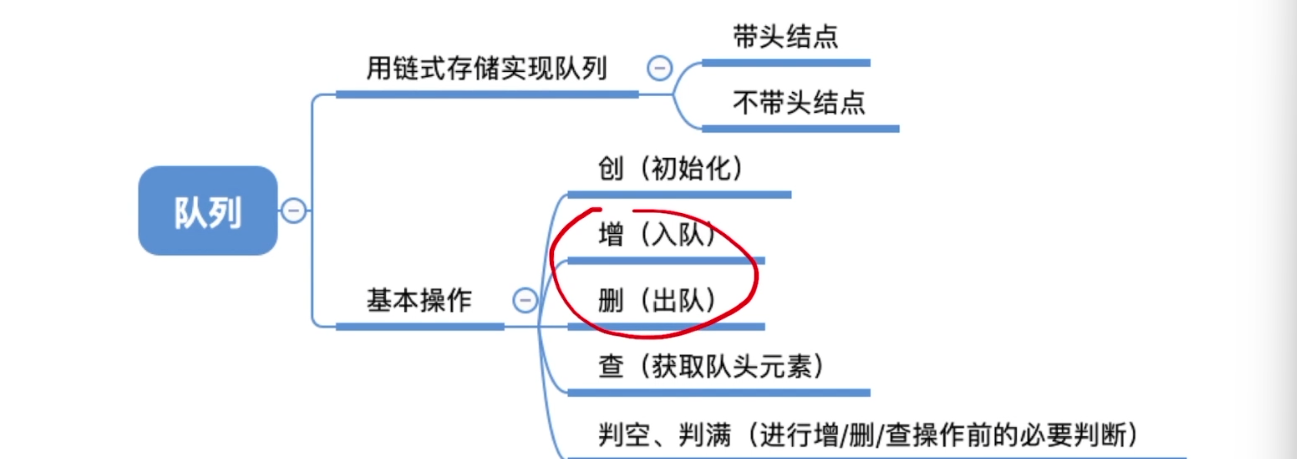

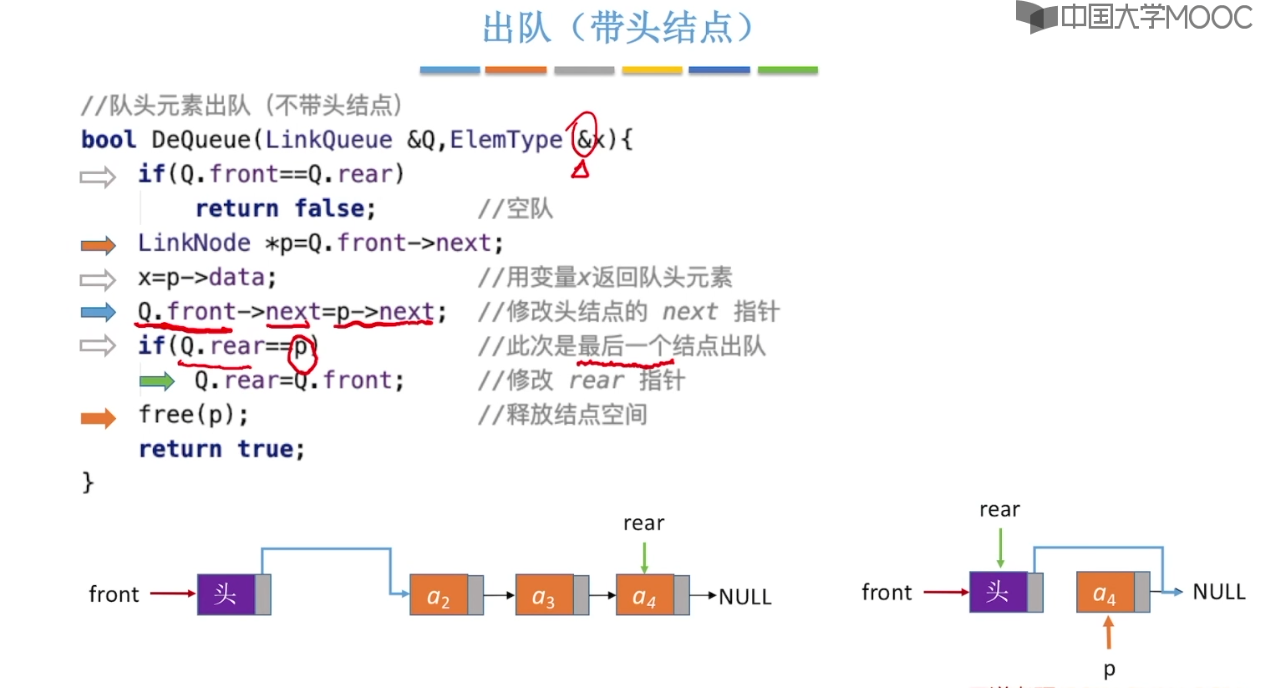
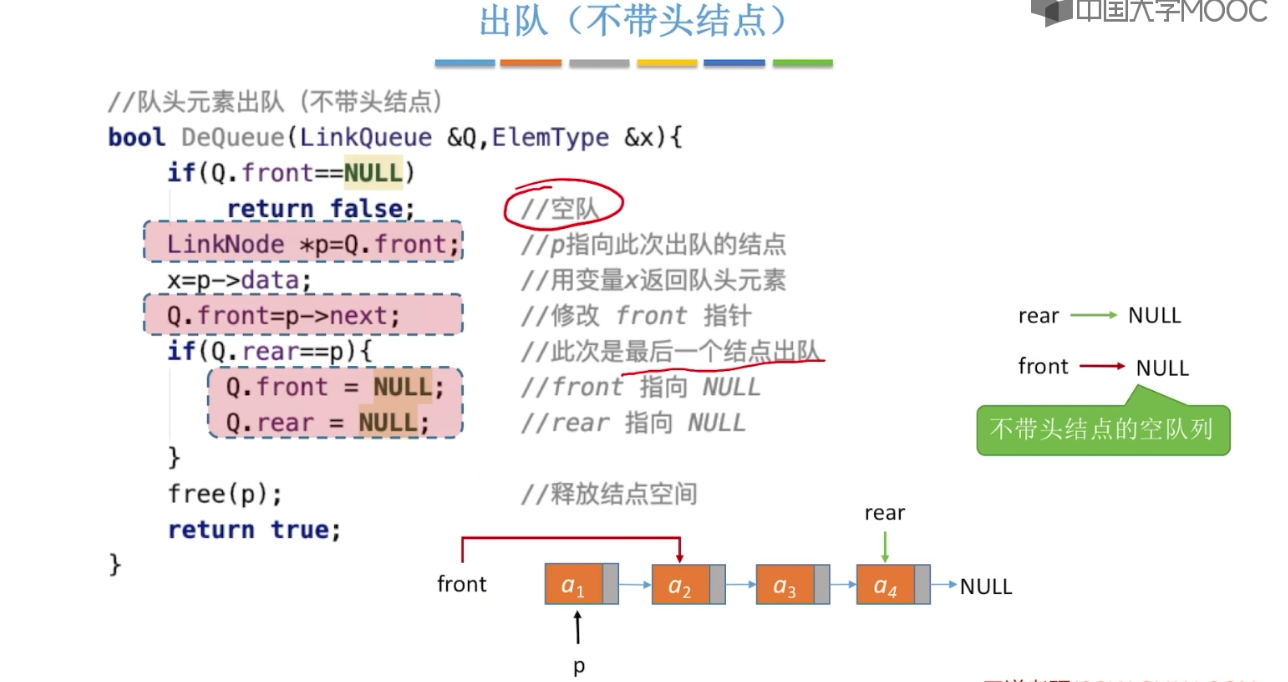
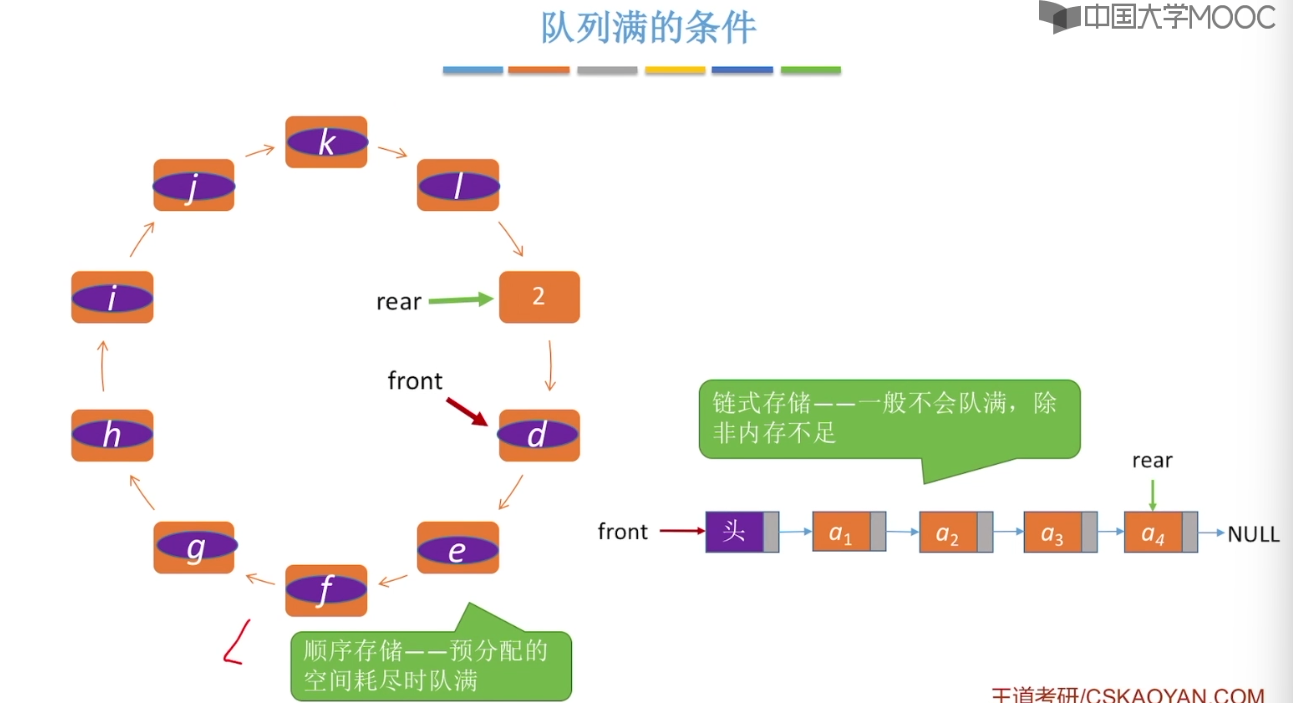
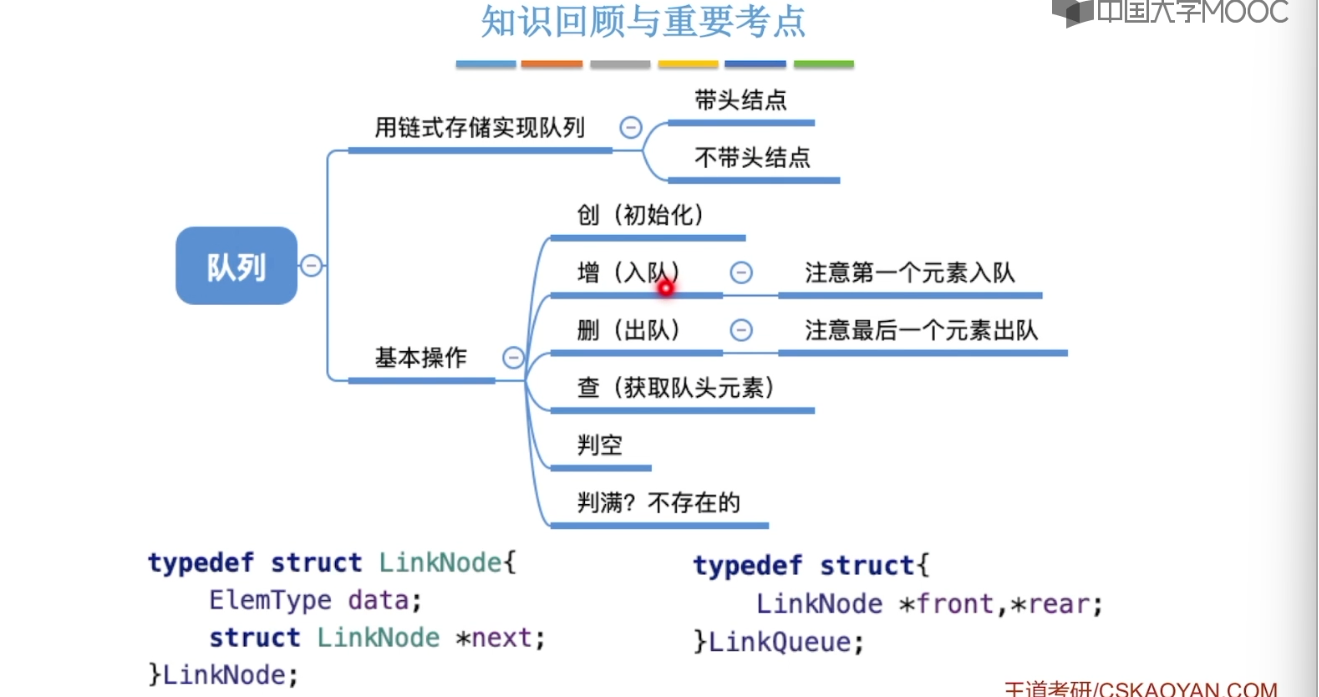
3.7、双端队列
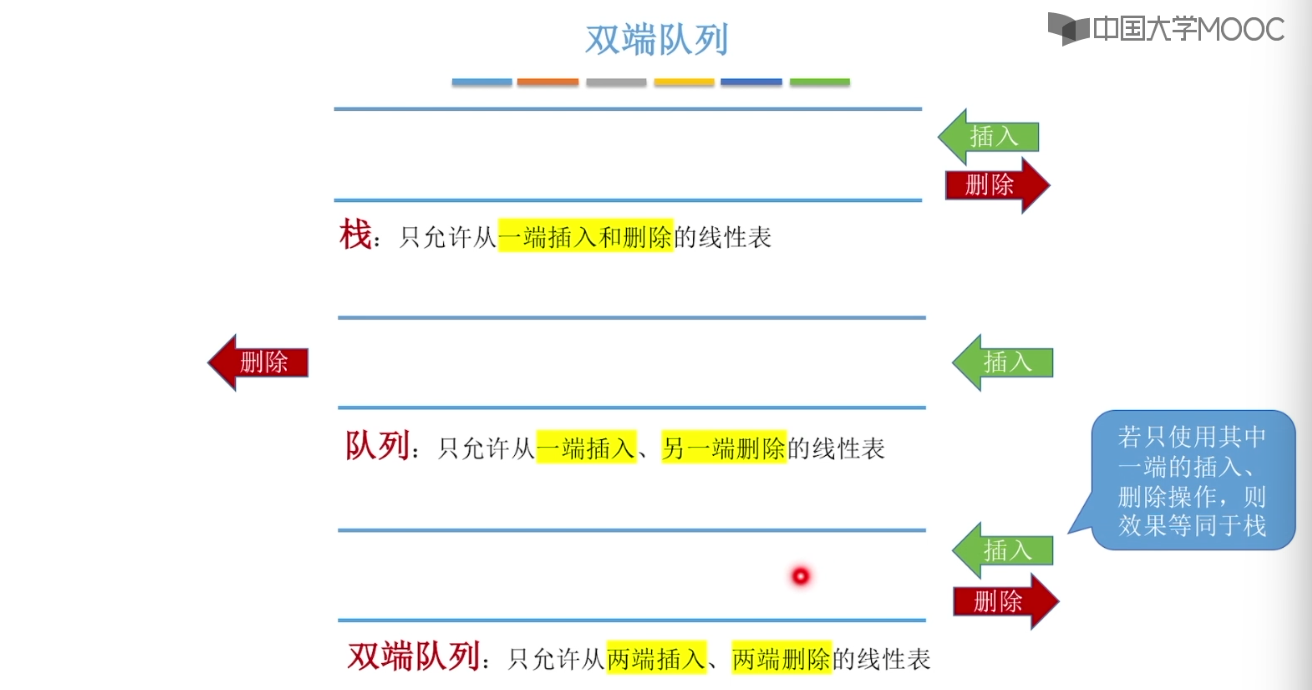
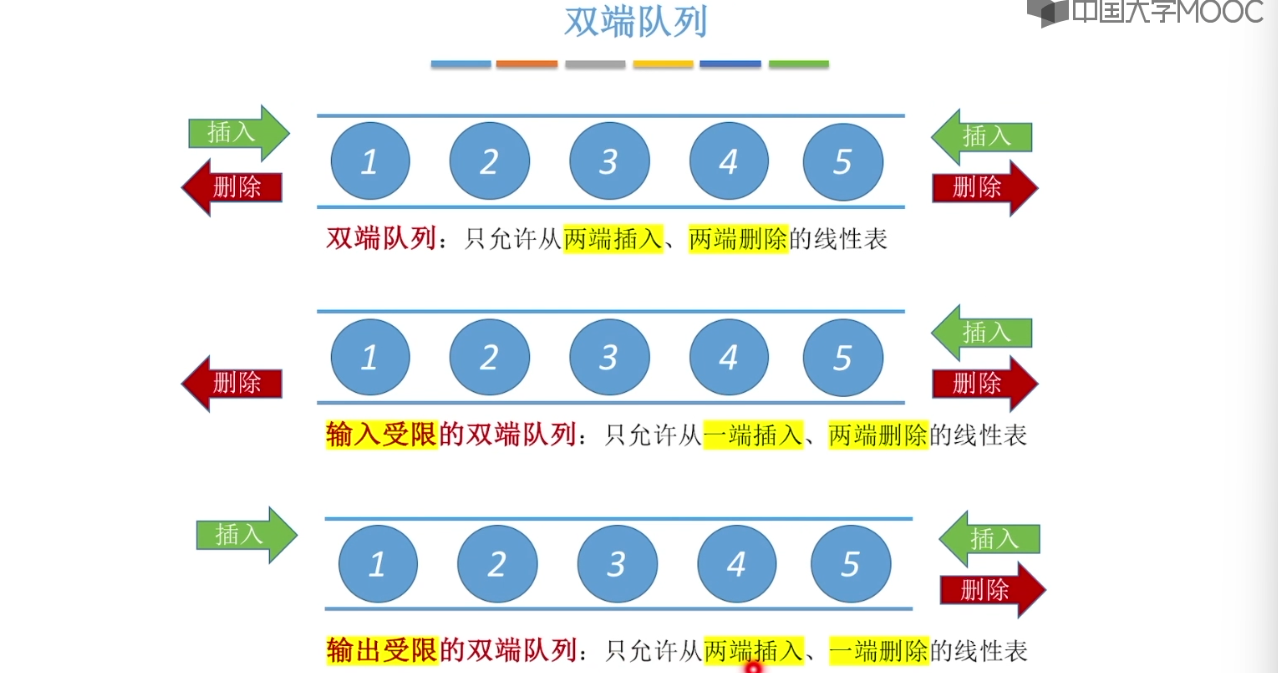
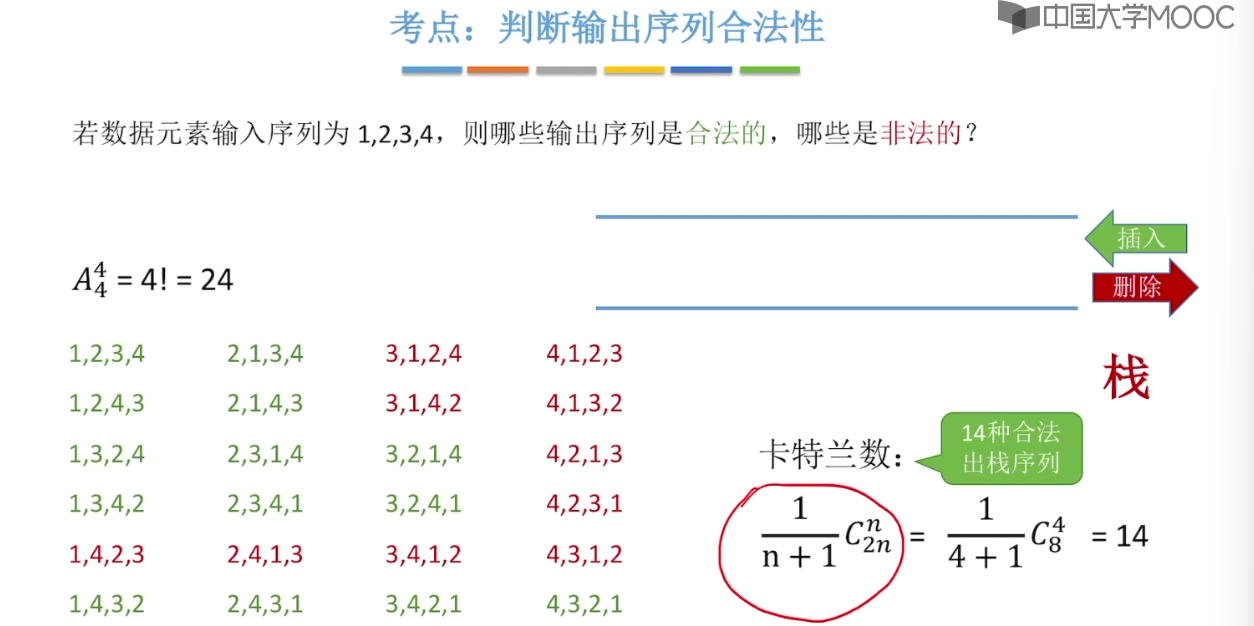
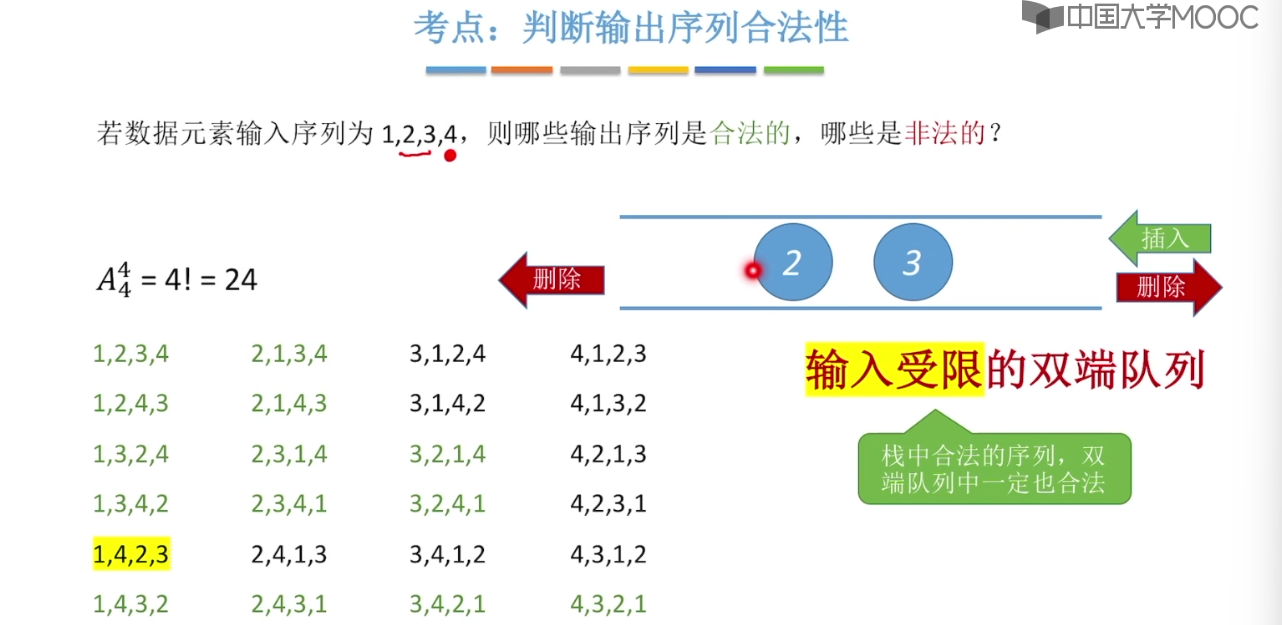
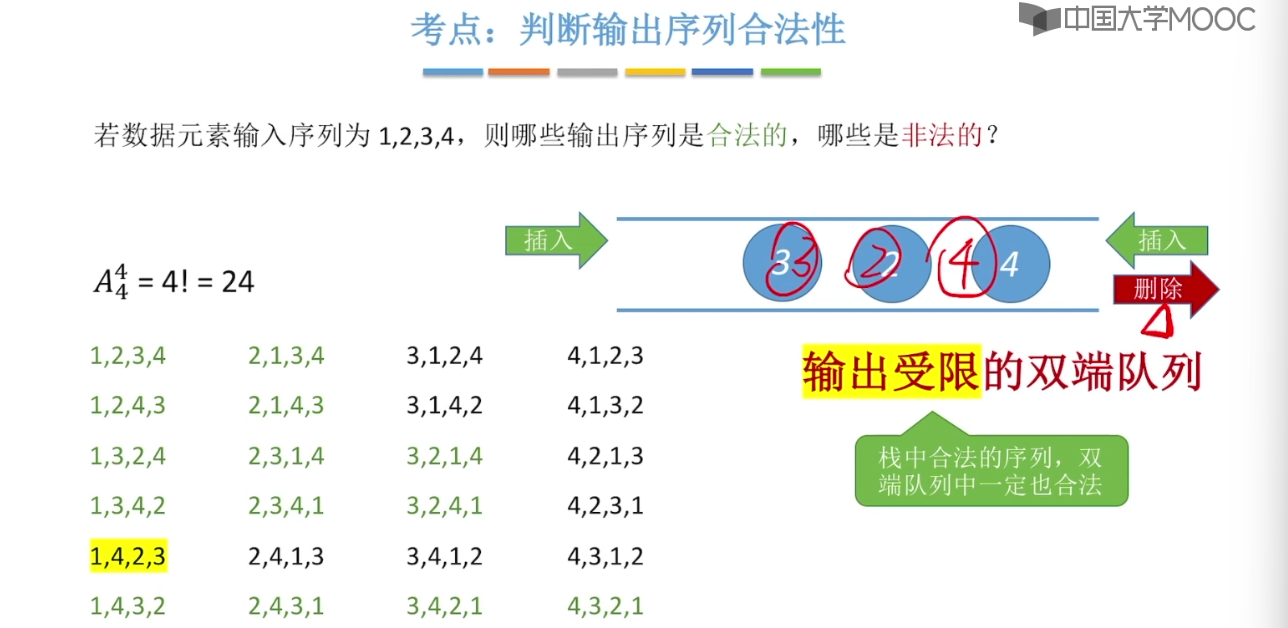
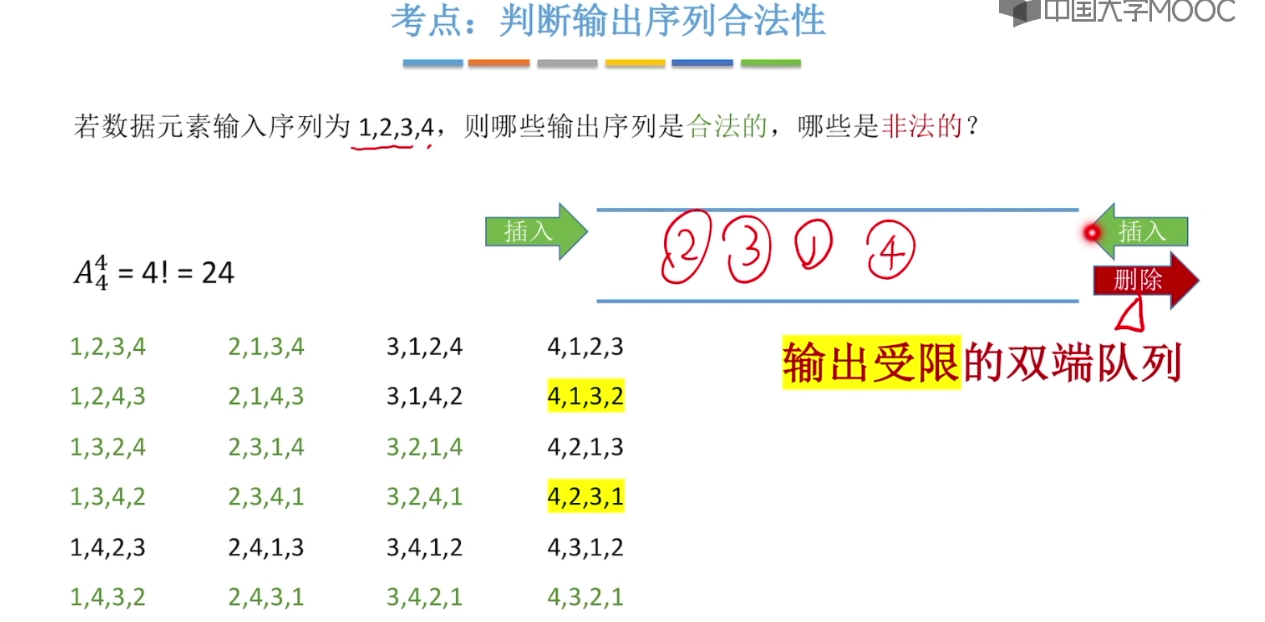
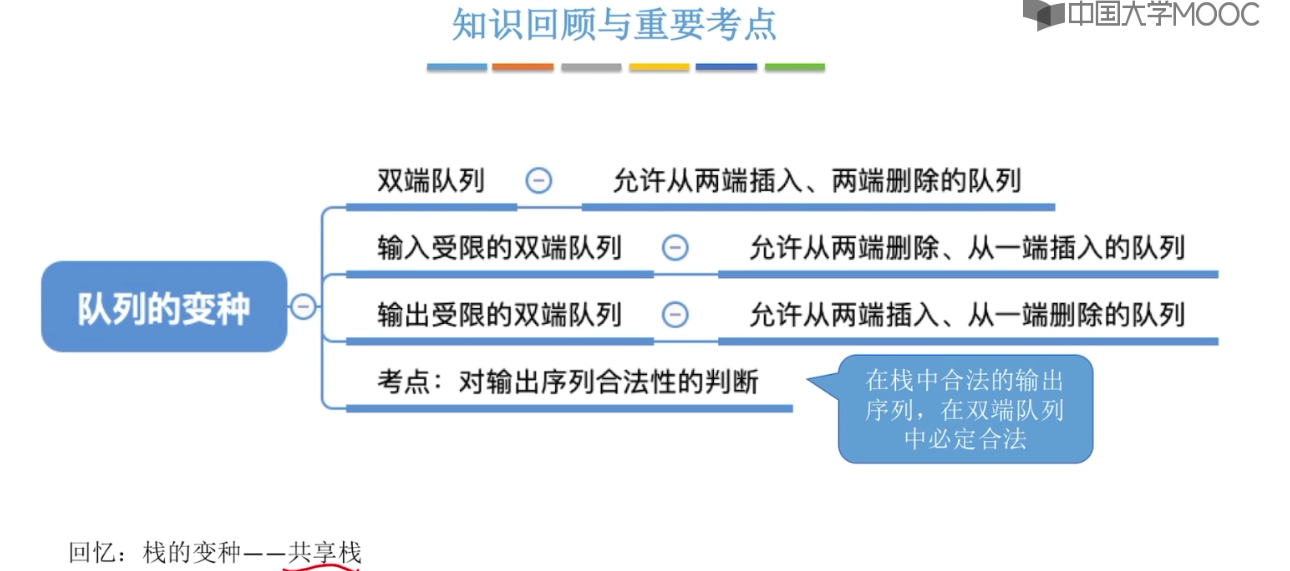
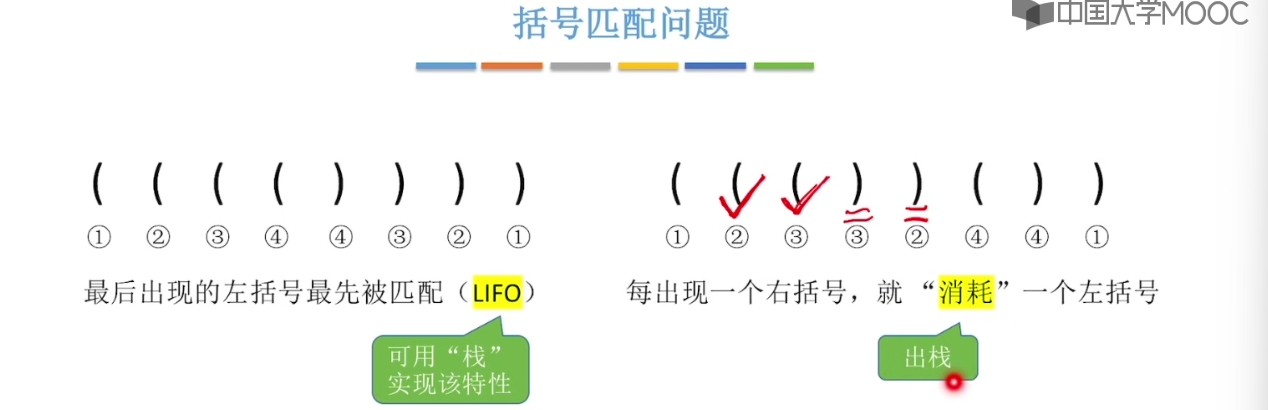
3.8、栈在括号匹配中的应用

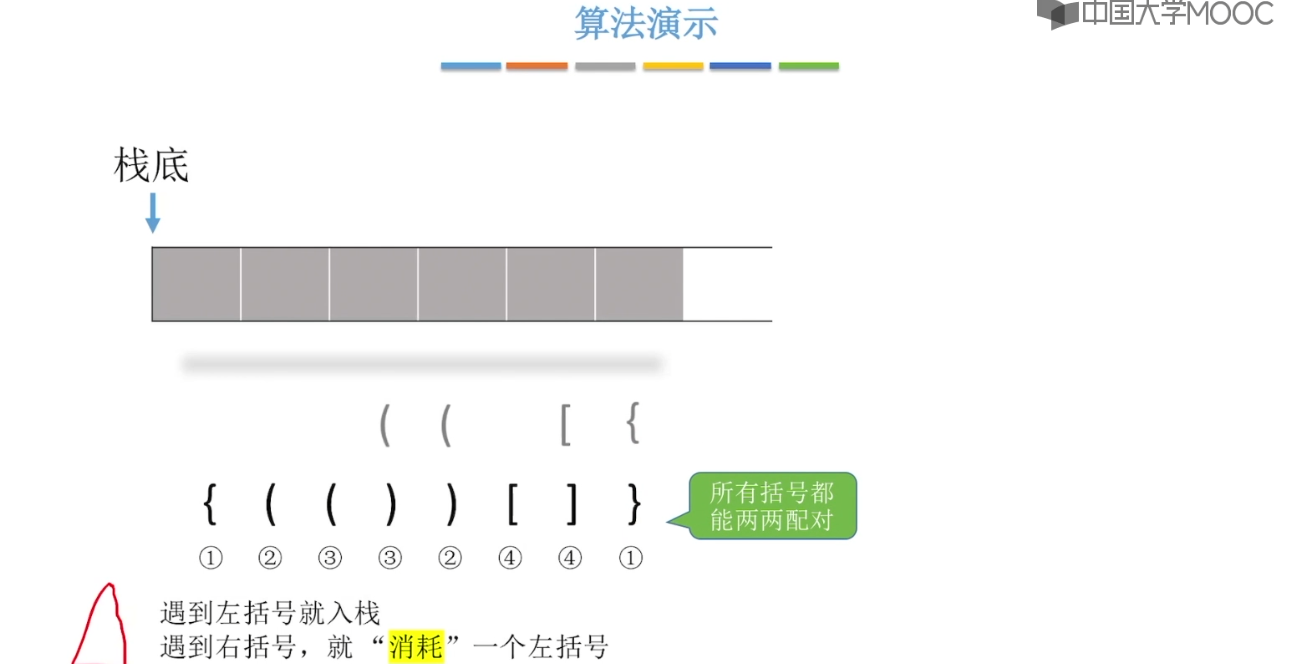
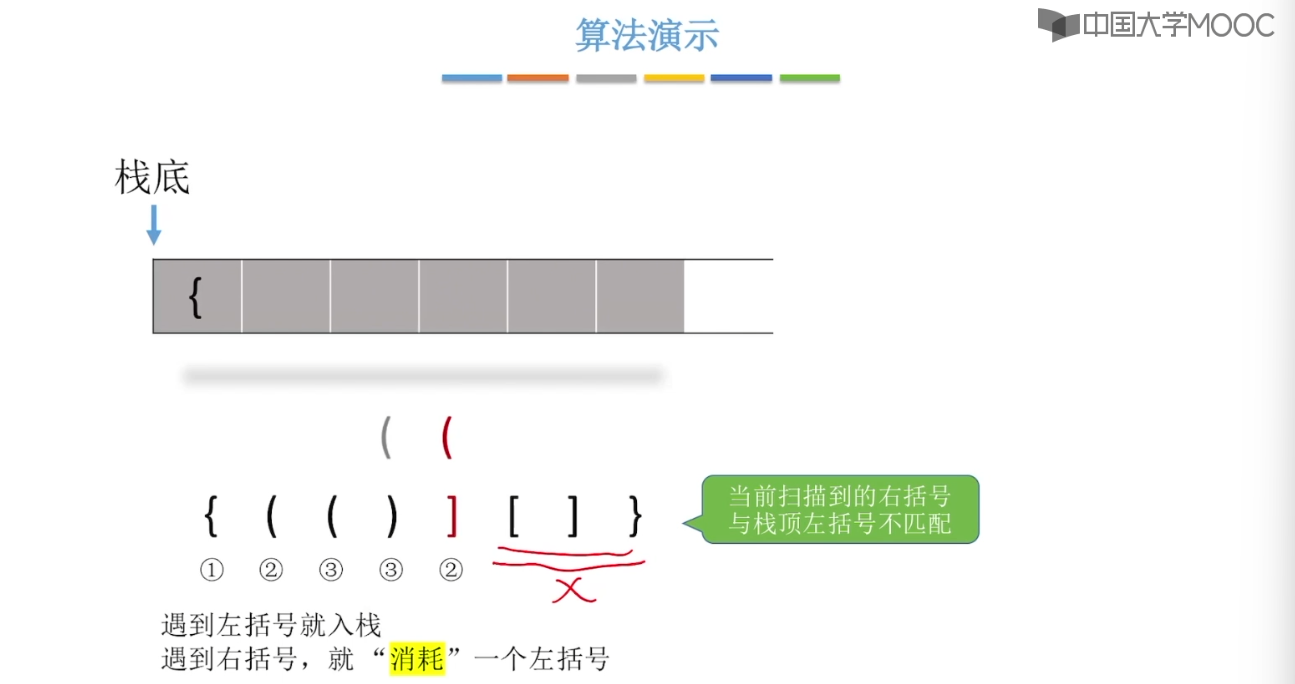
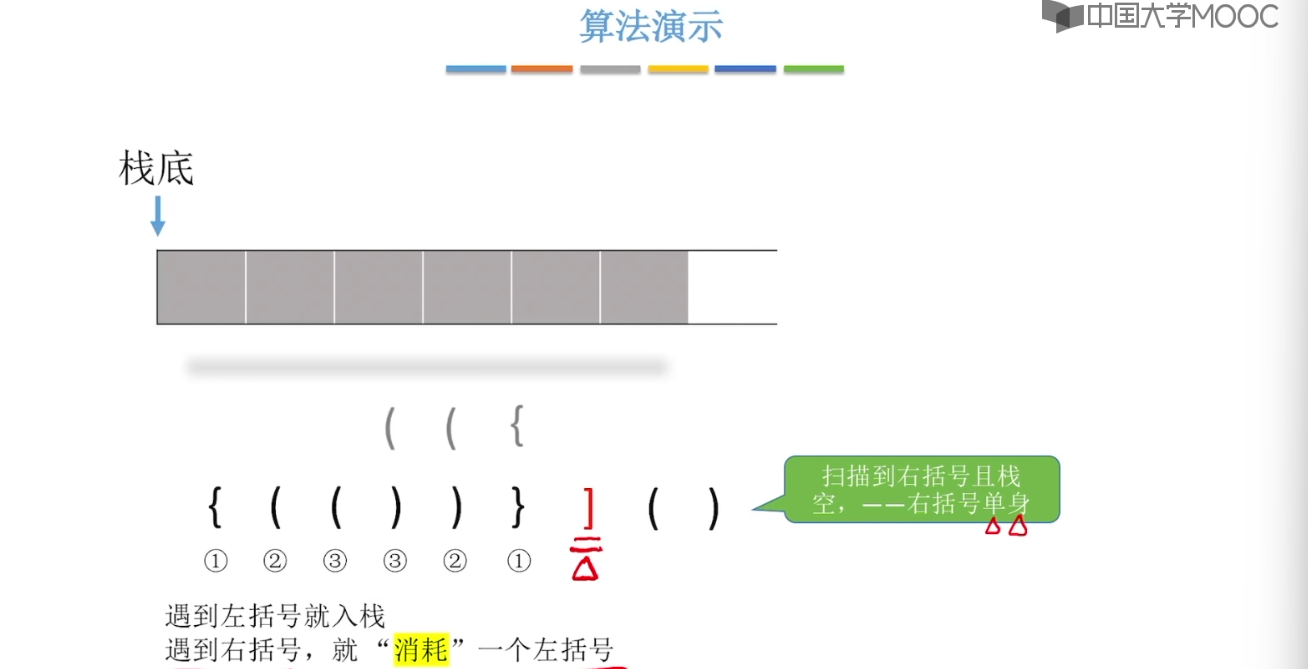
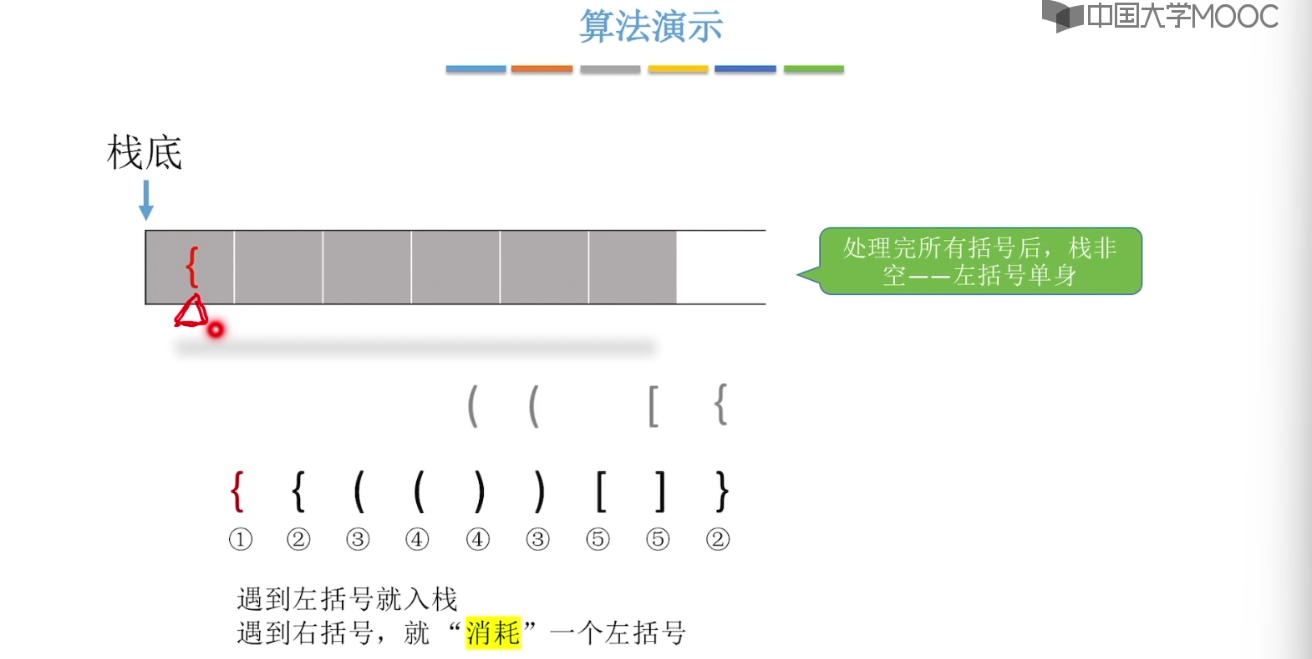
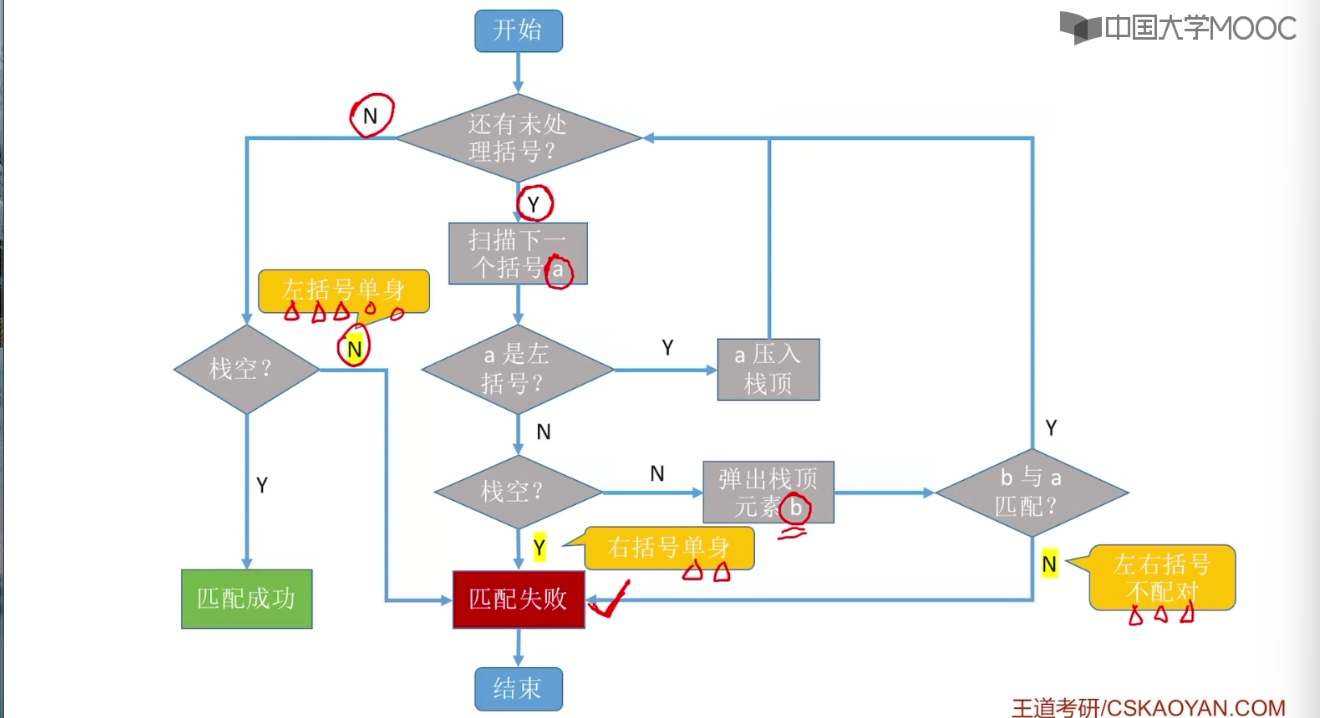

3.9、栈在表达式中的应用

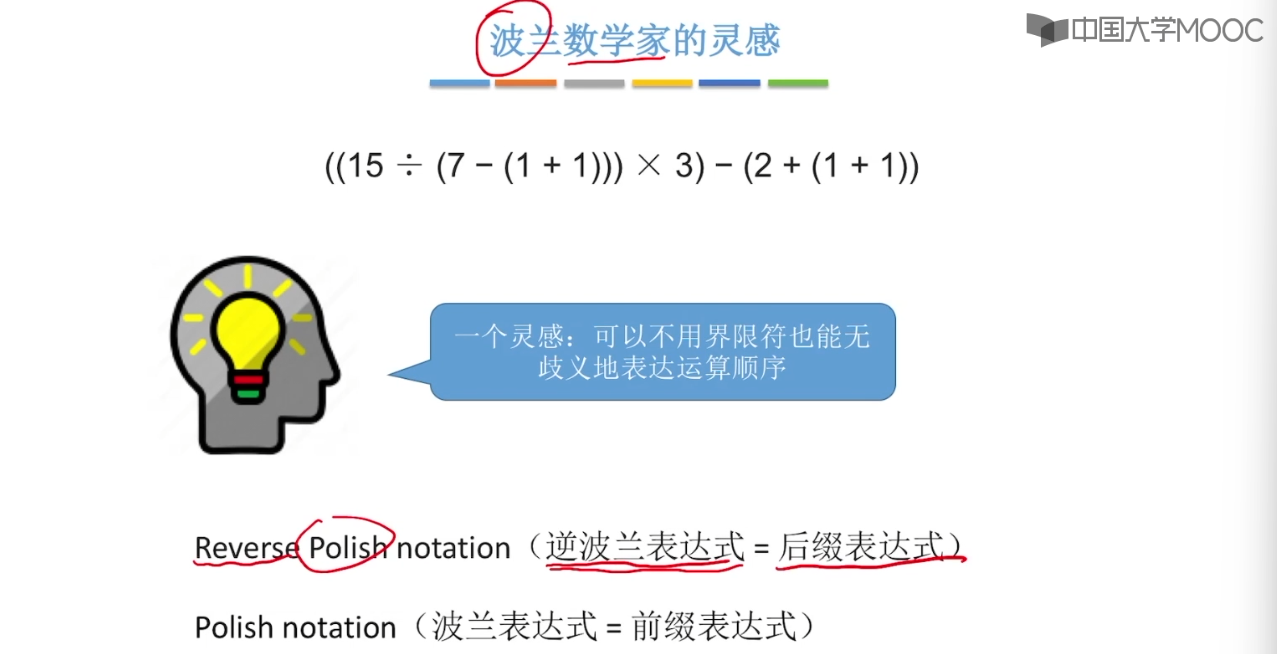
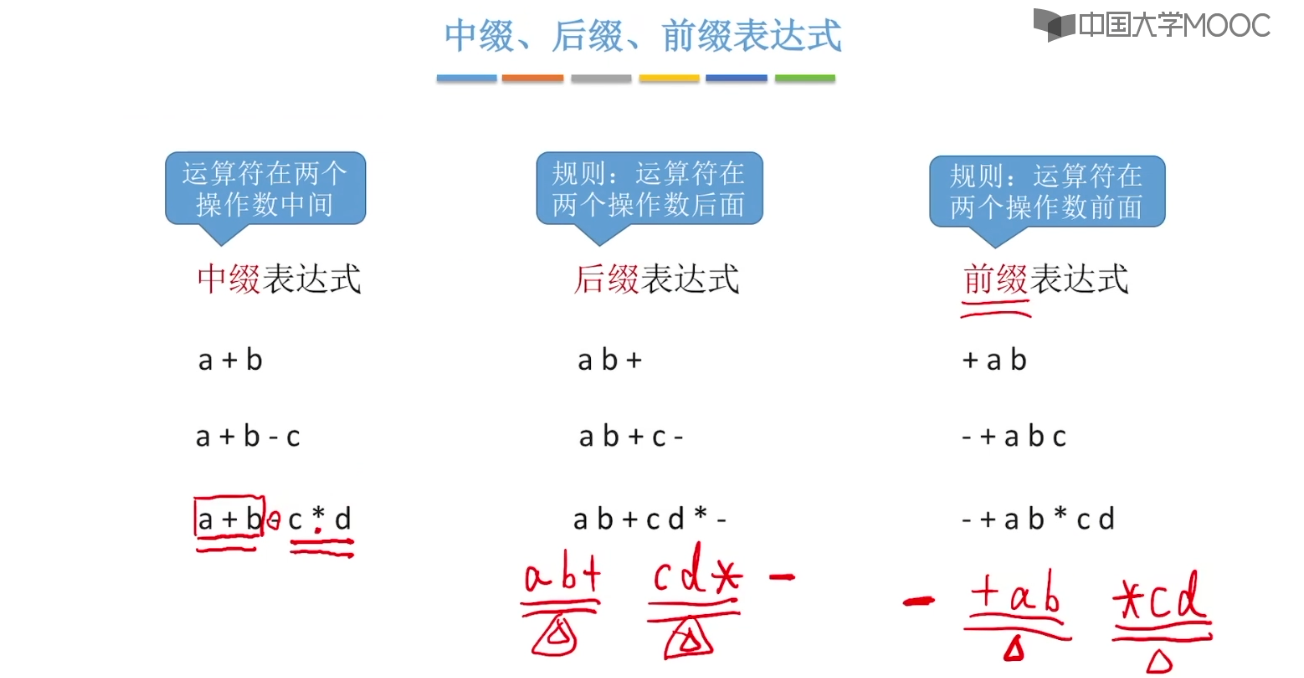

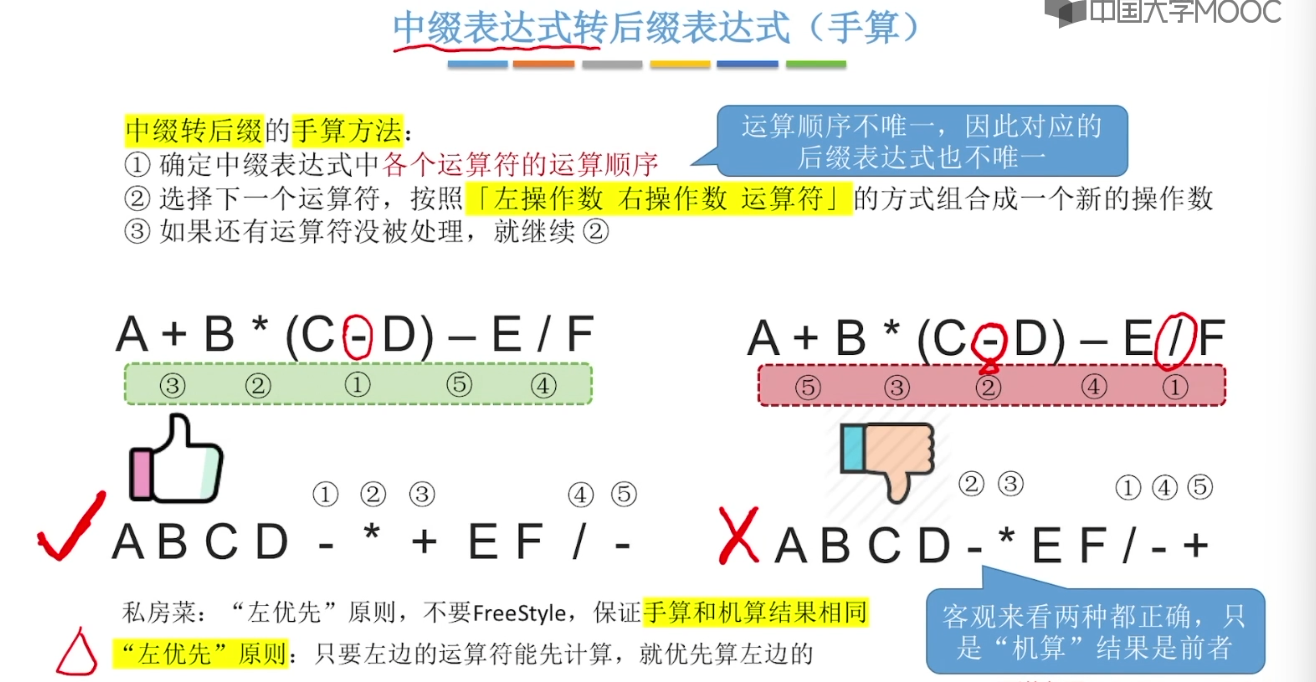


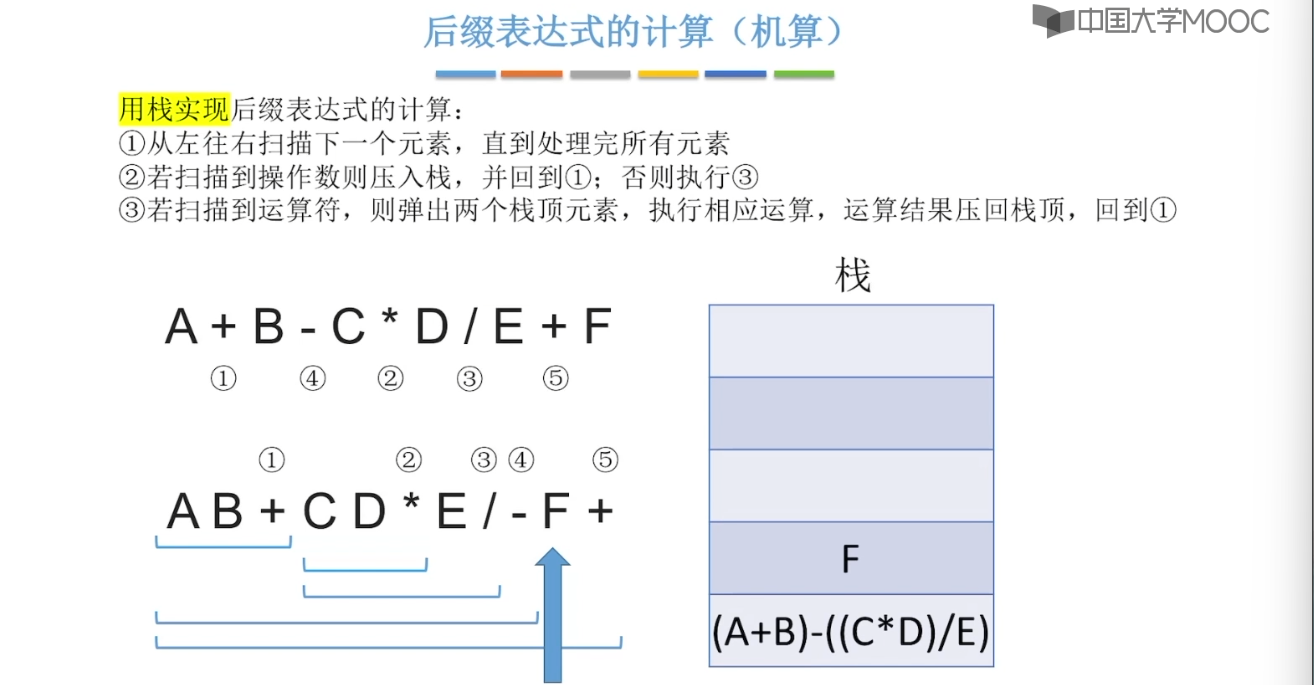





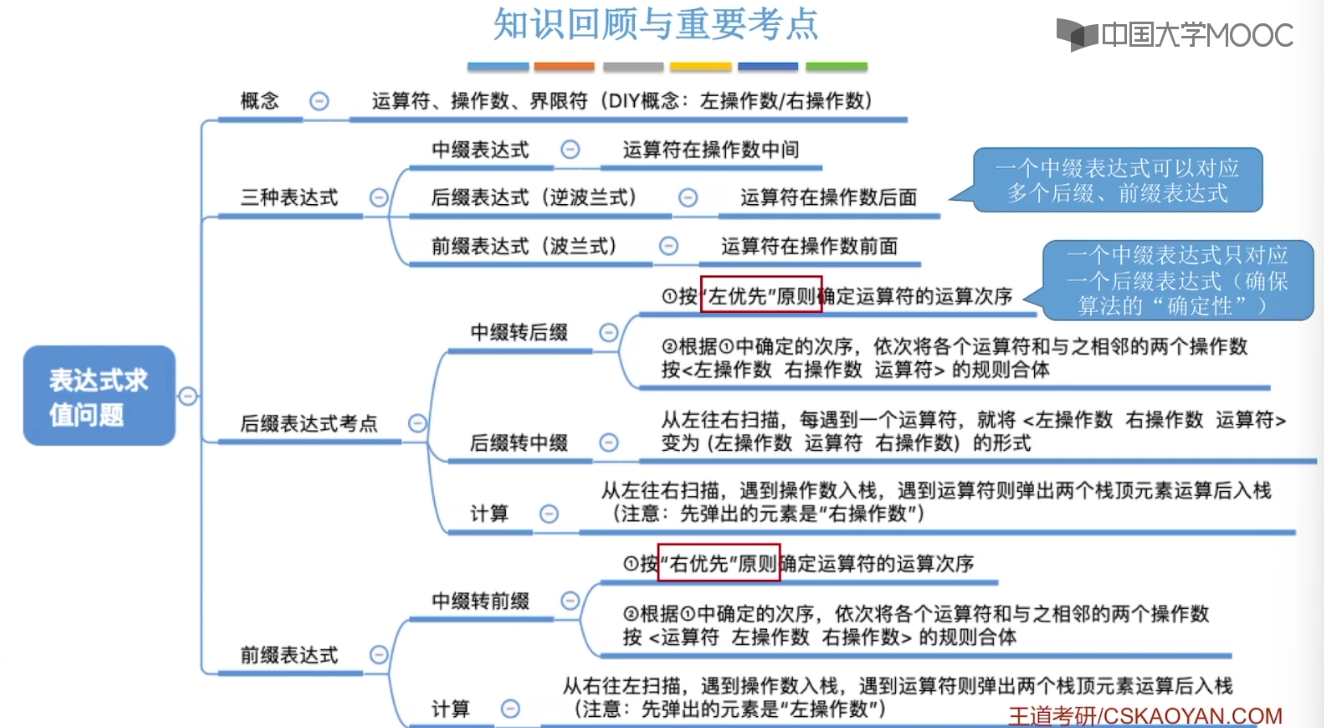




3.10、栈在递归的中的作用

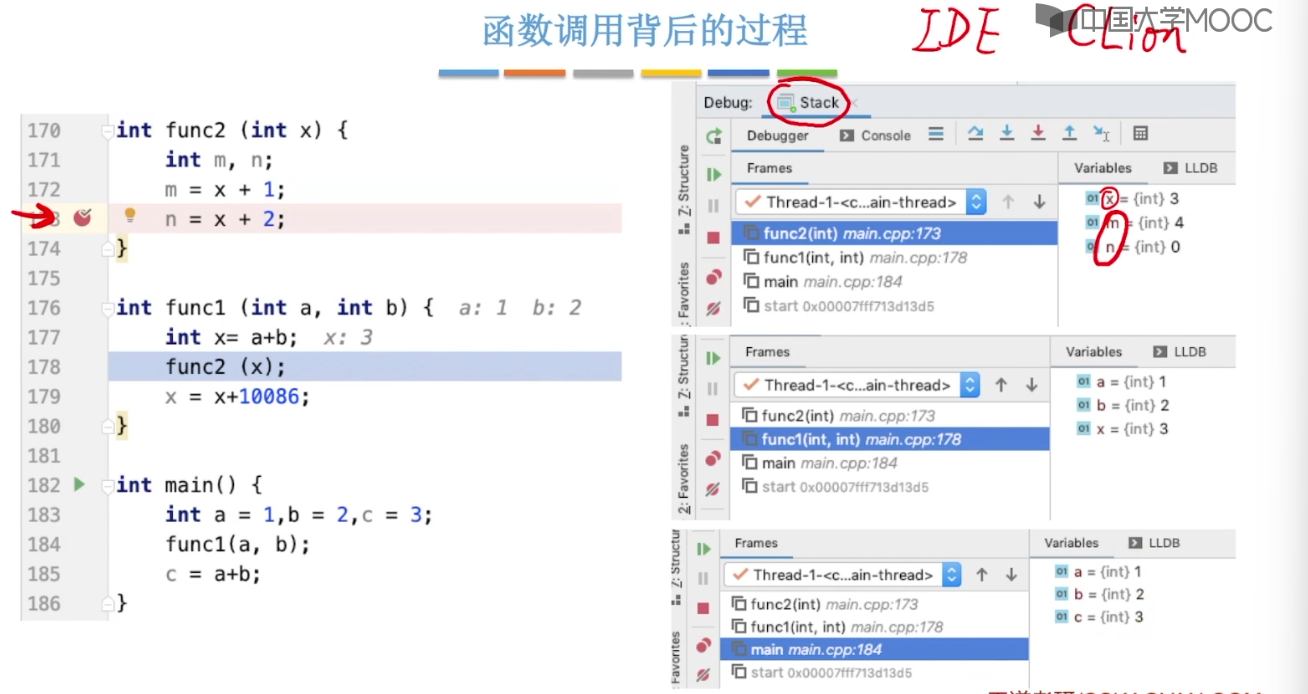


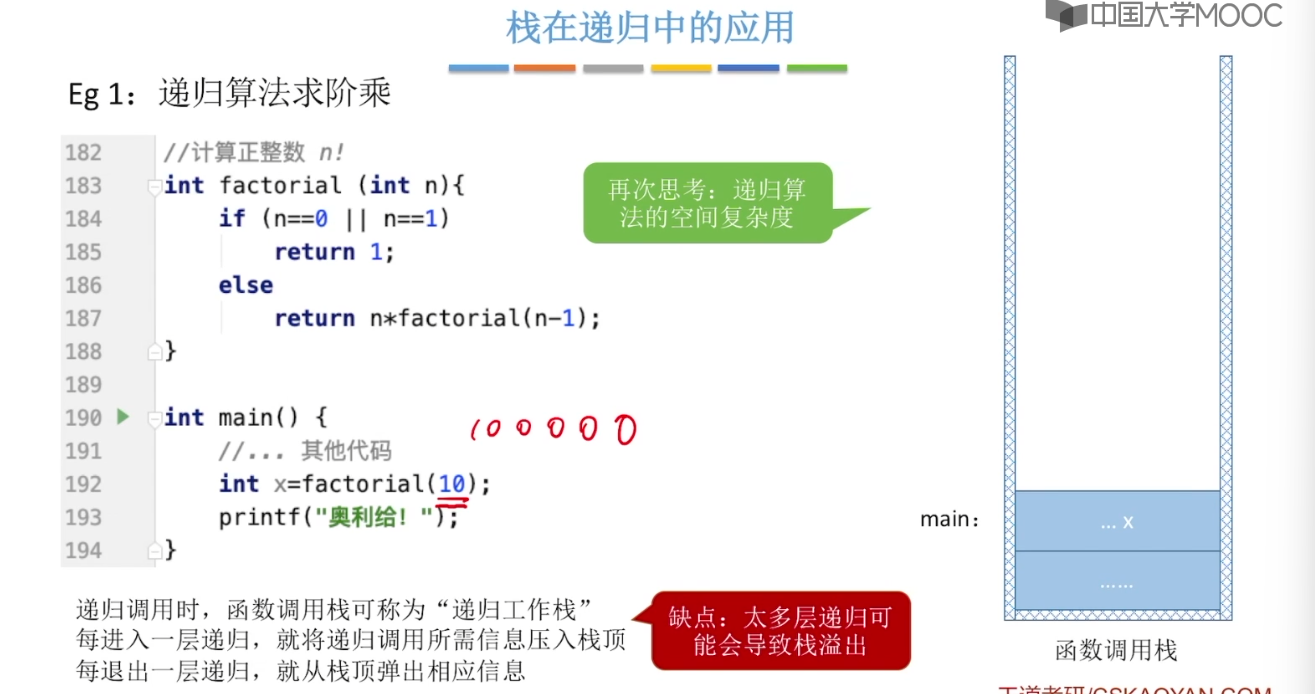
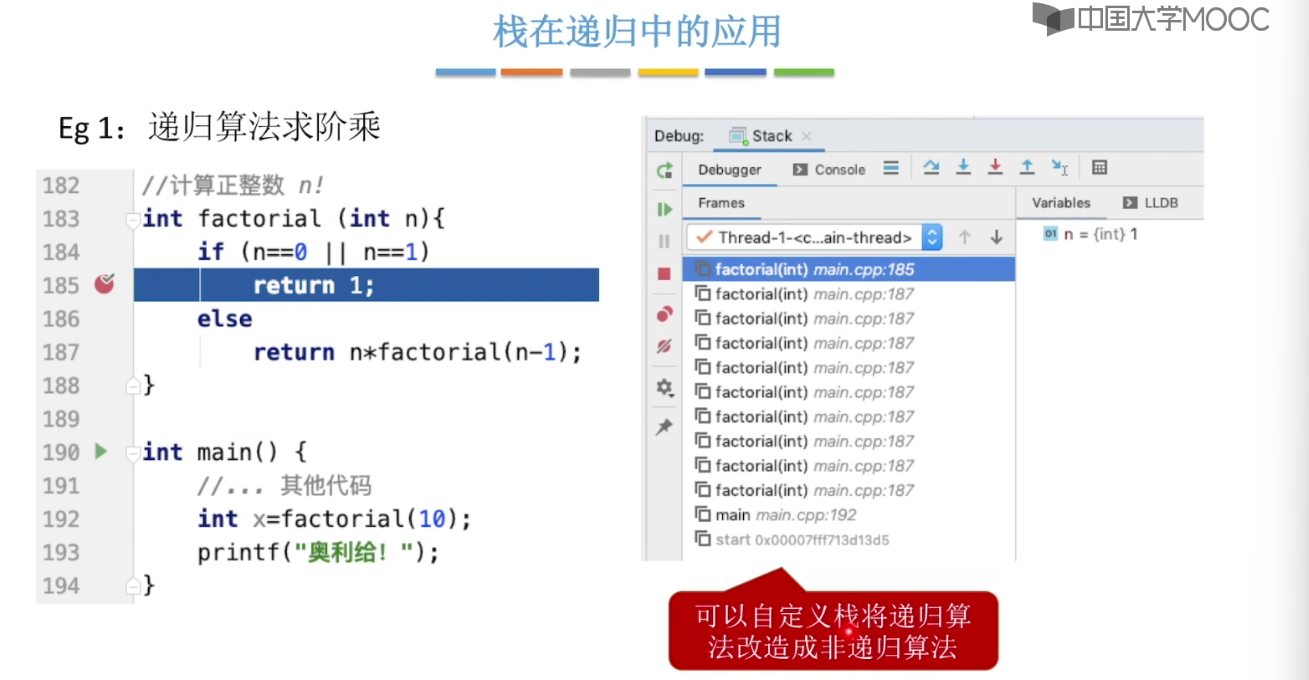
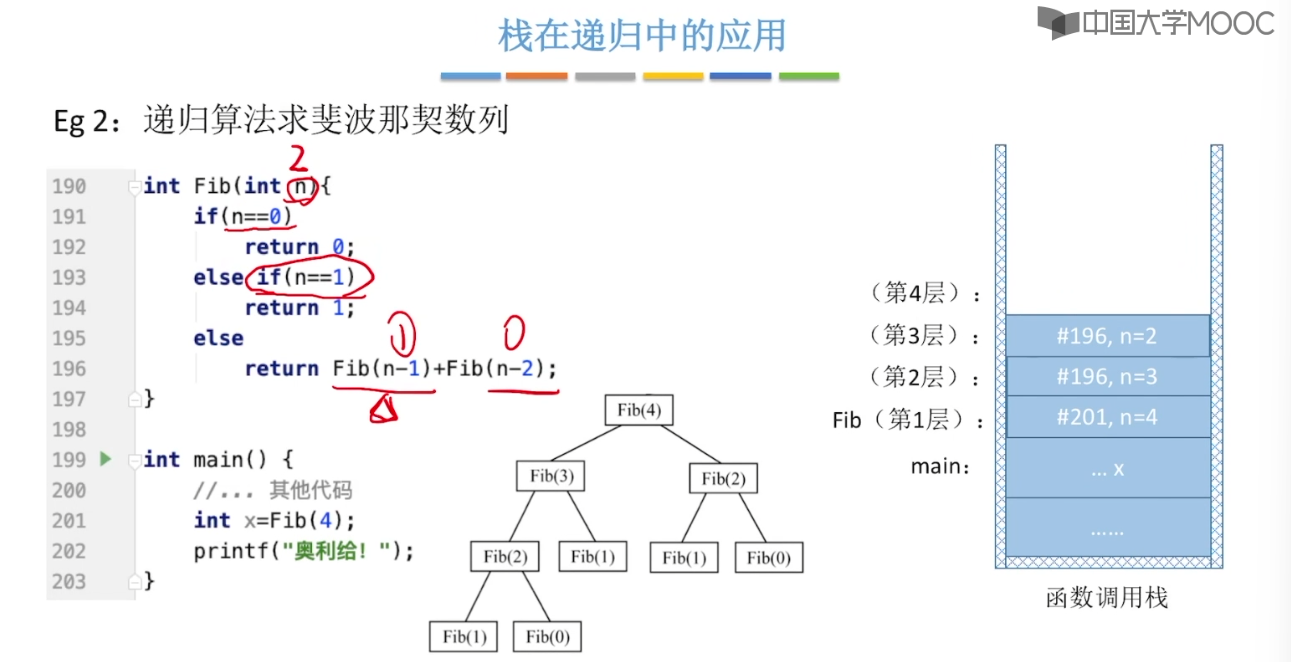
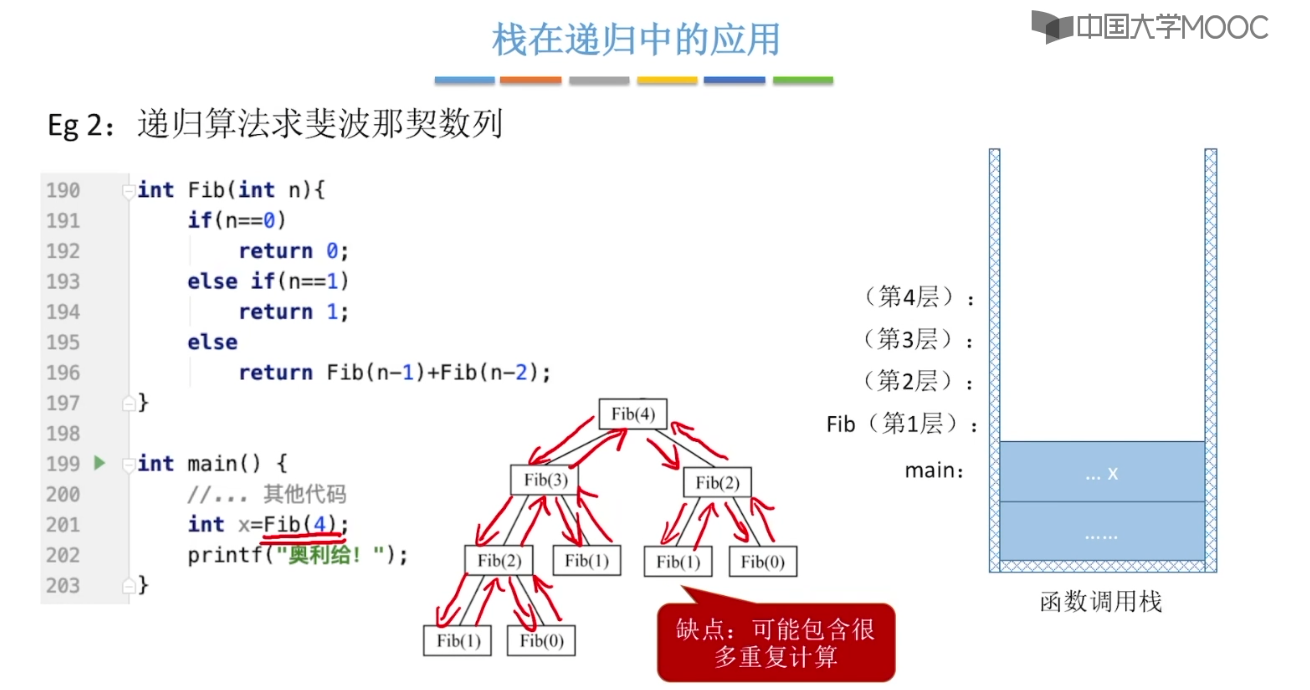

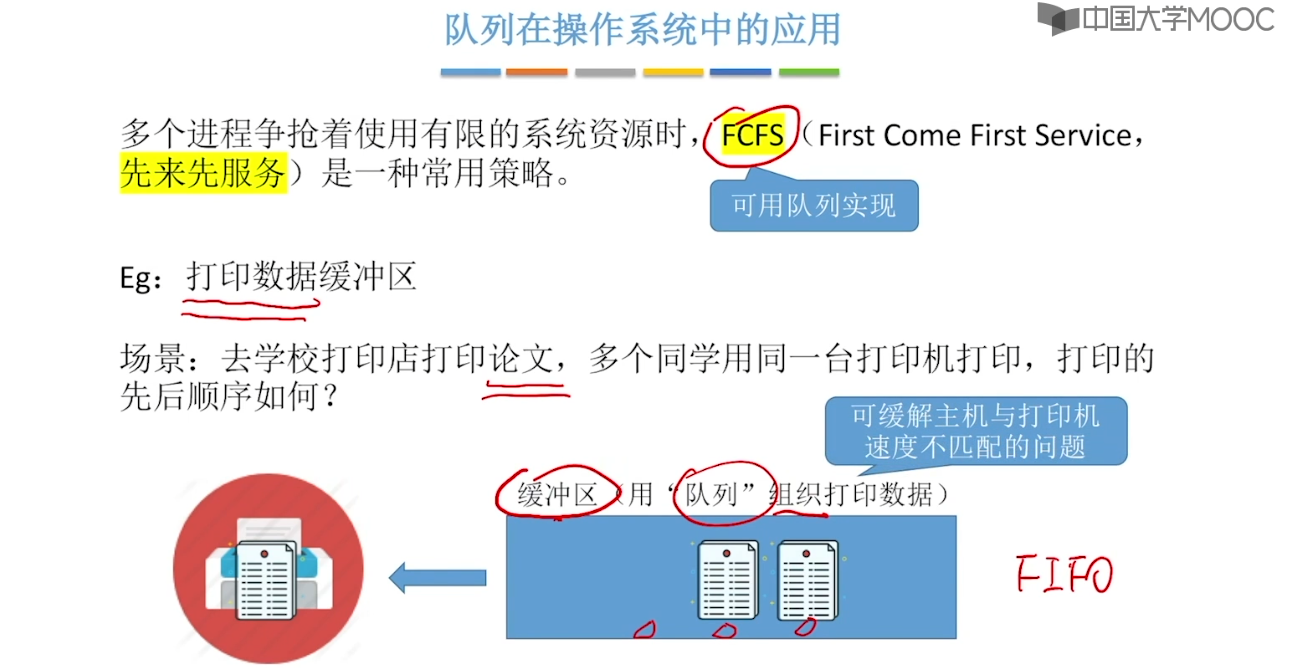
3.11、队列的应用

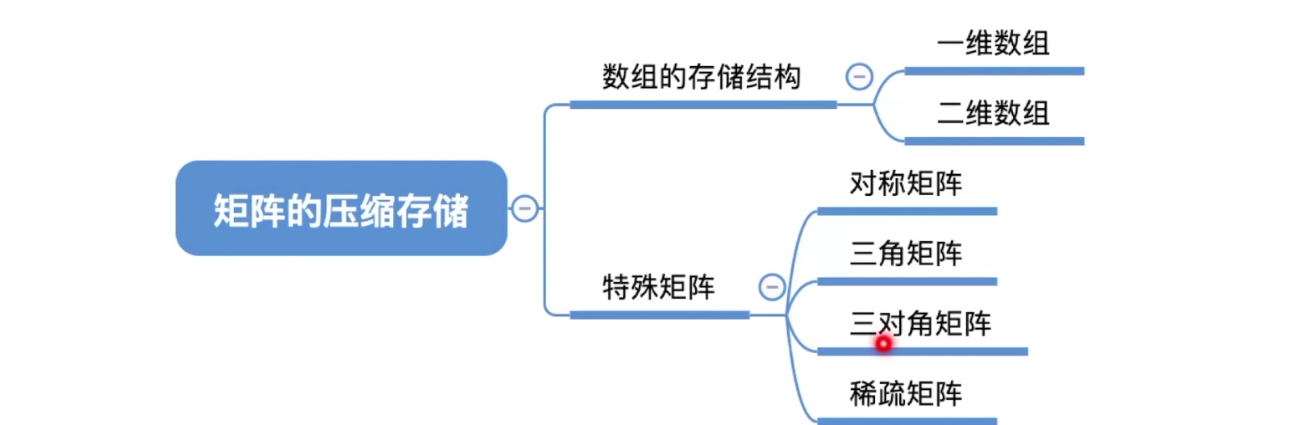
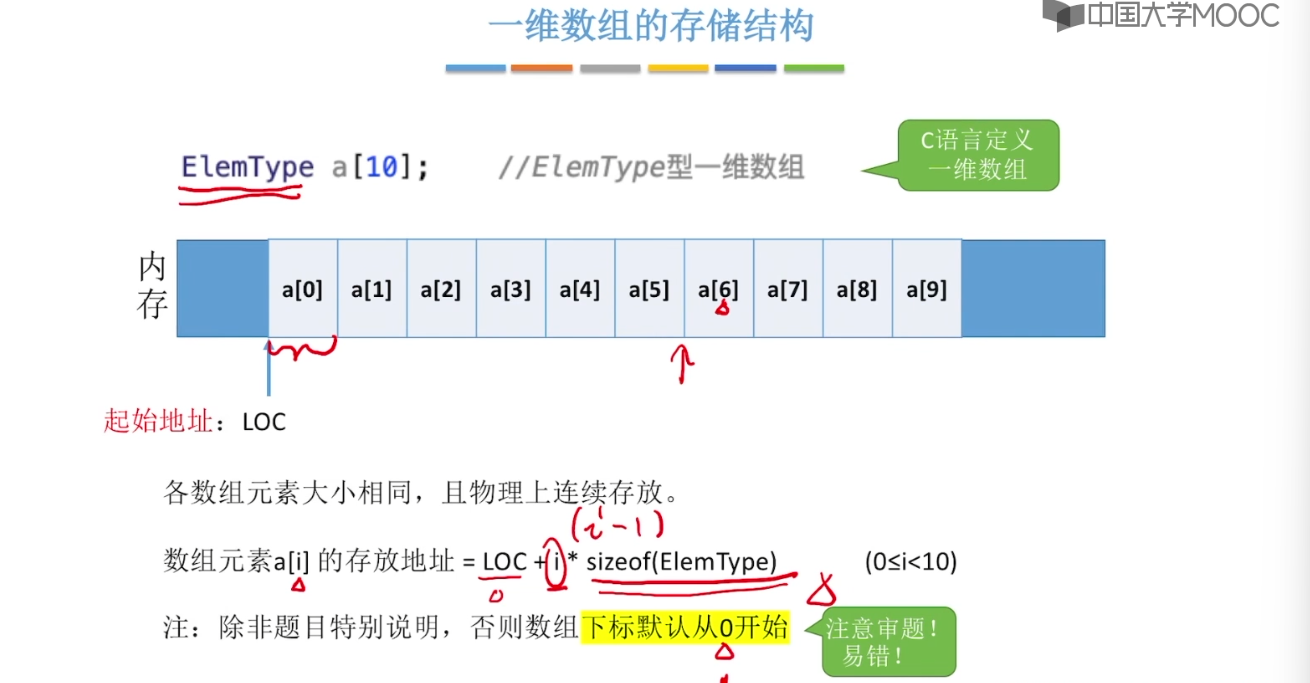
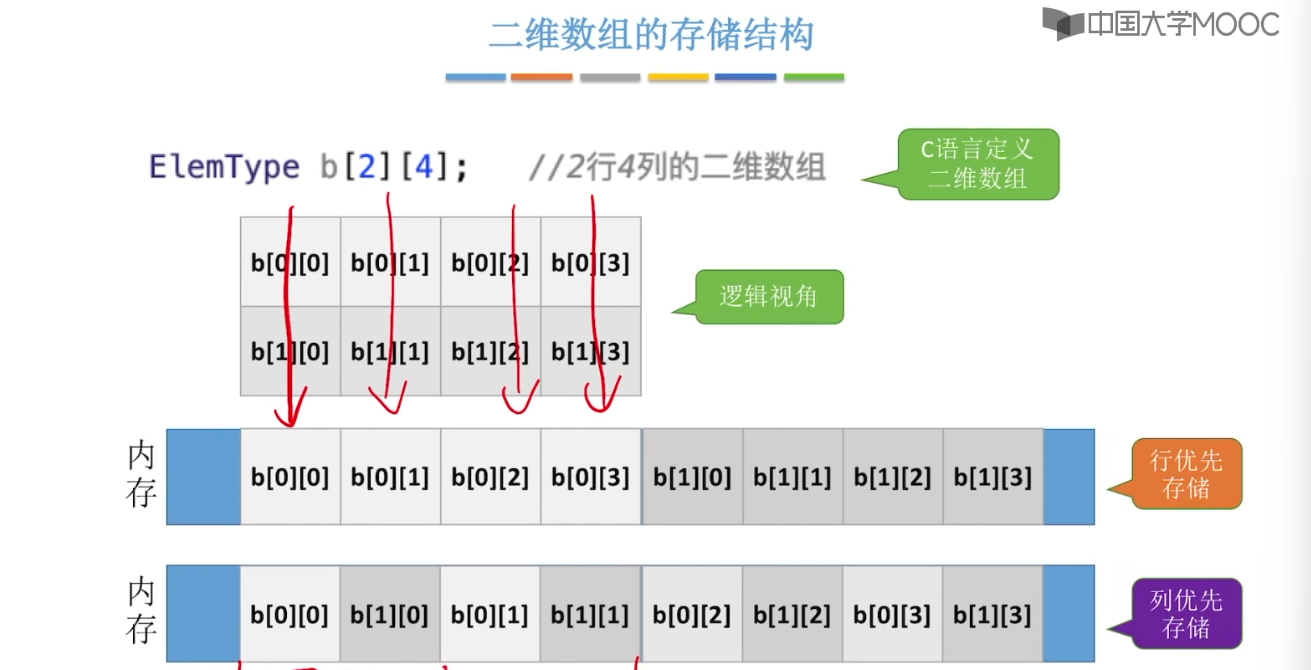
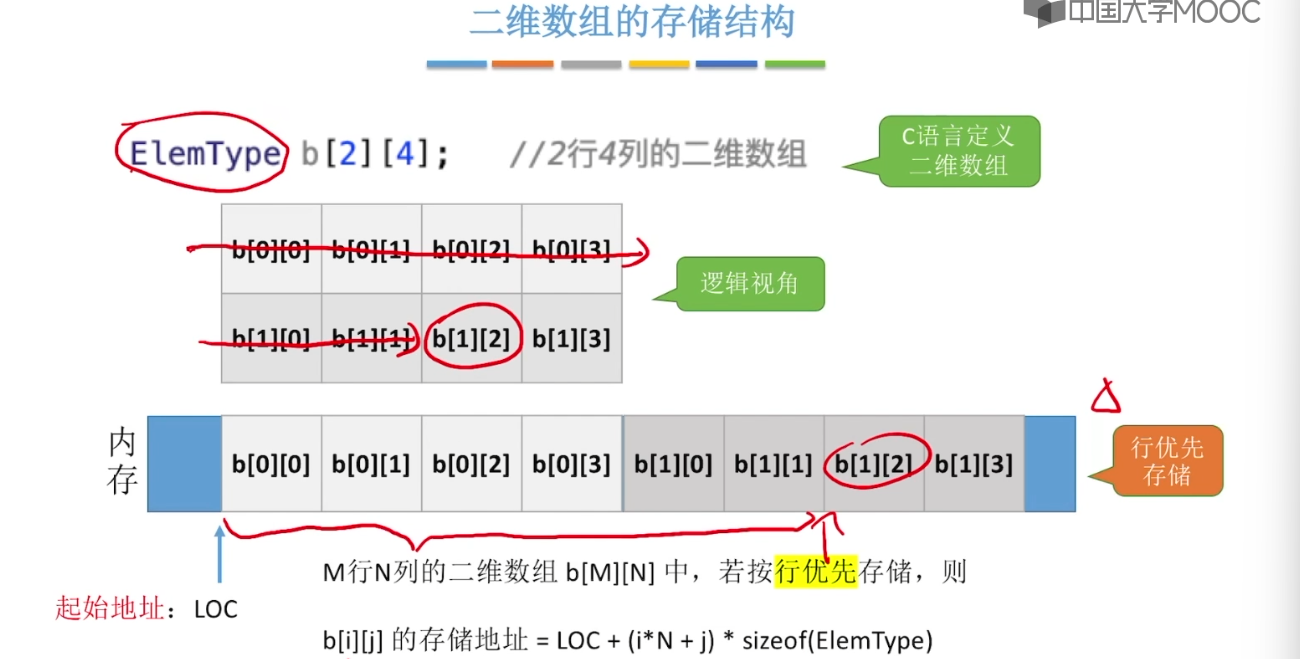
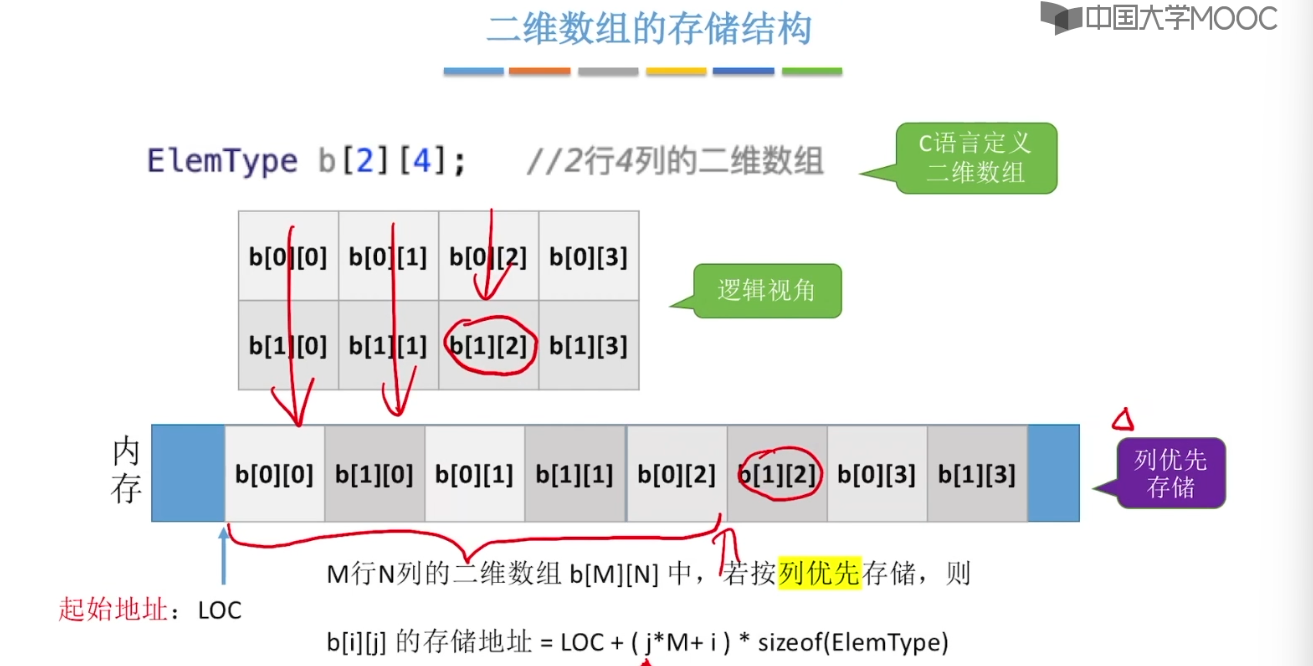
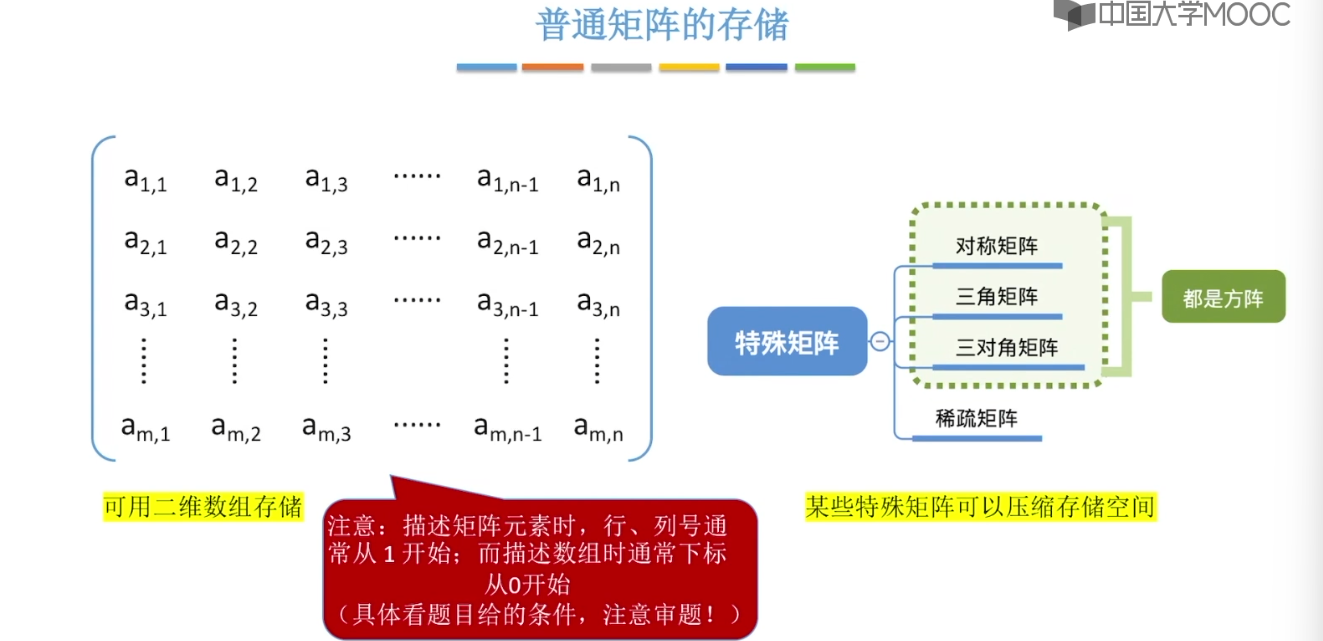
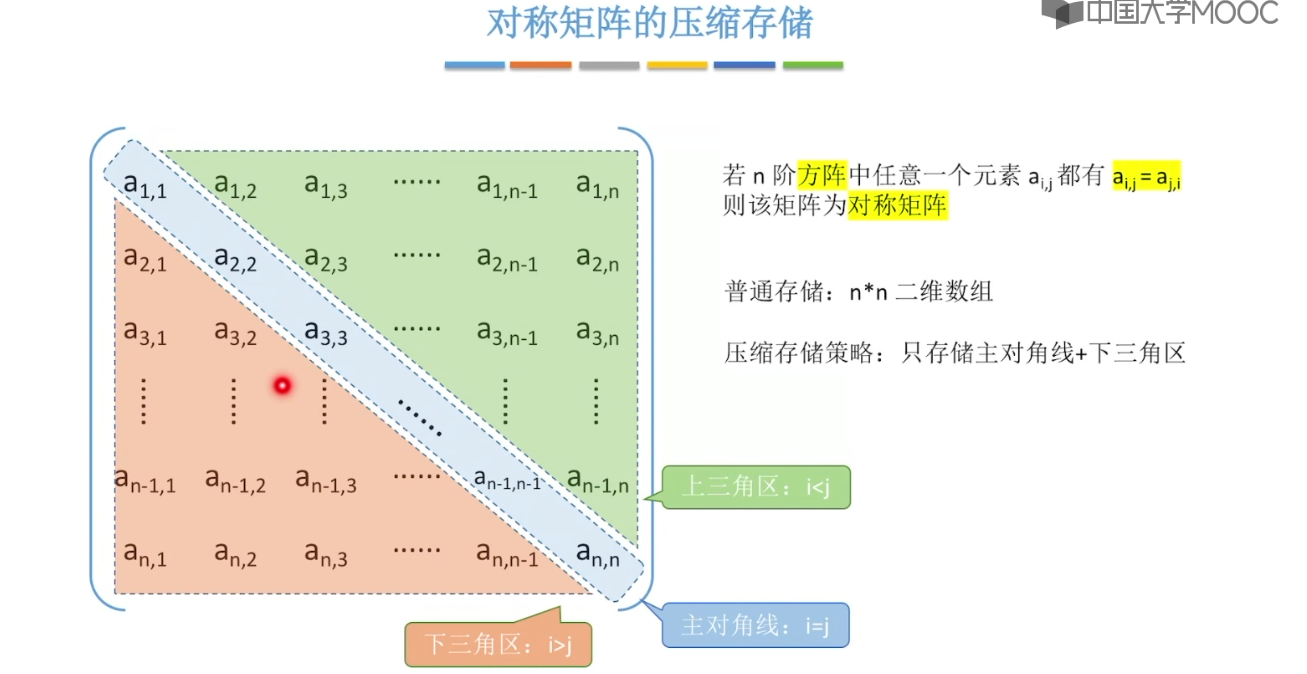
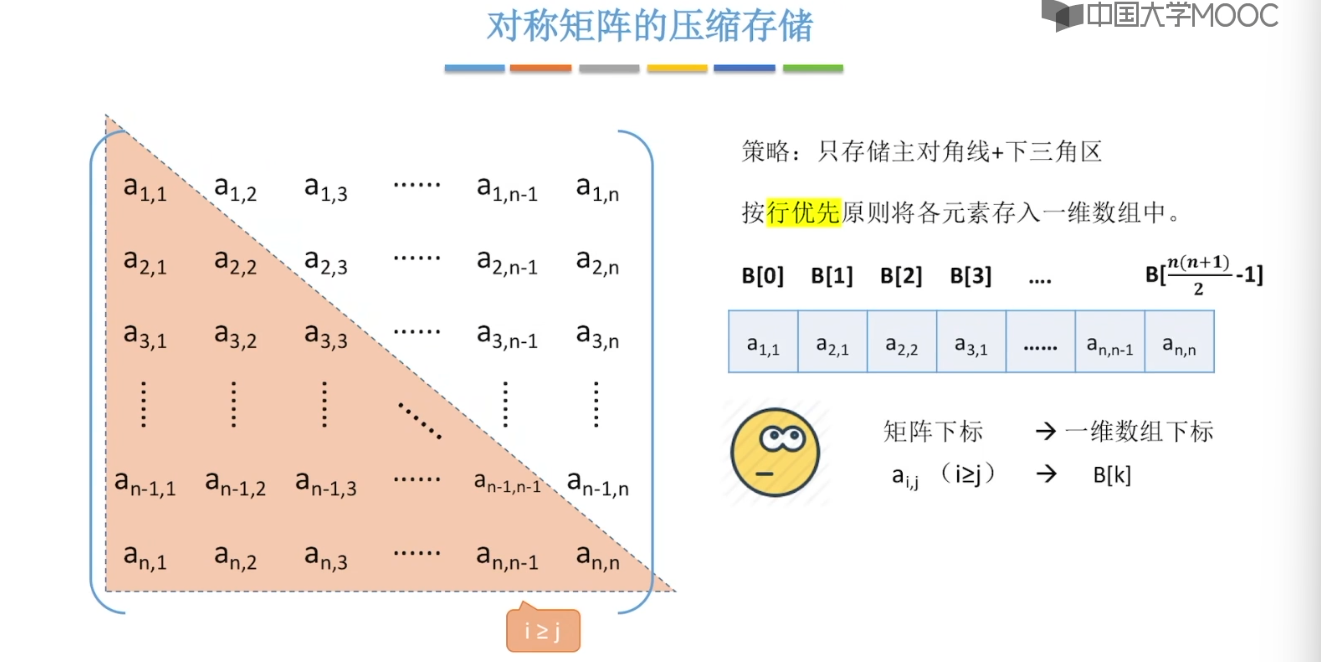
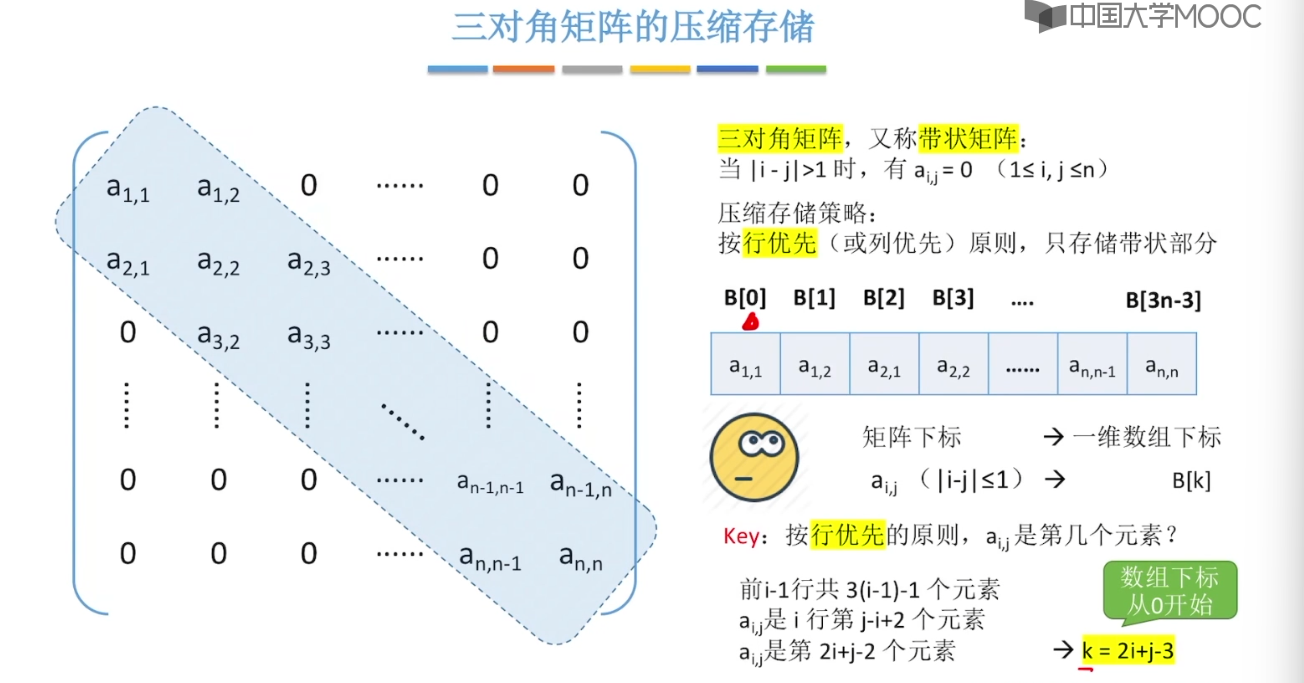
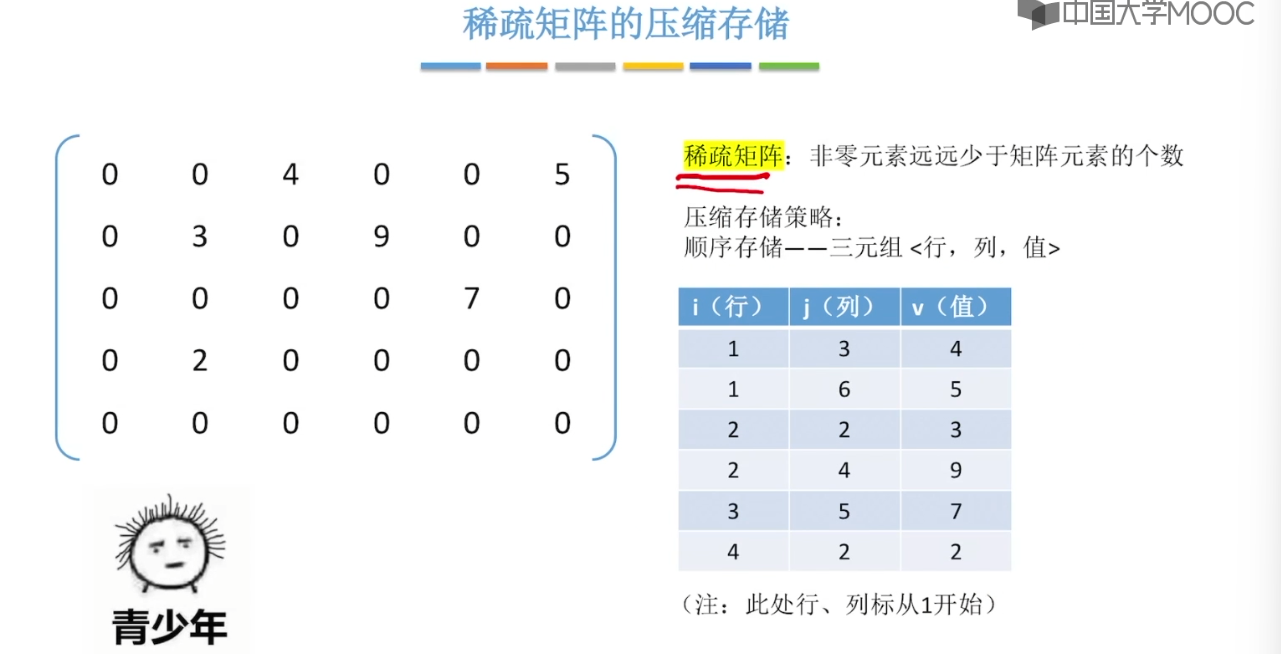
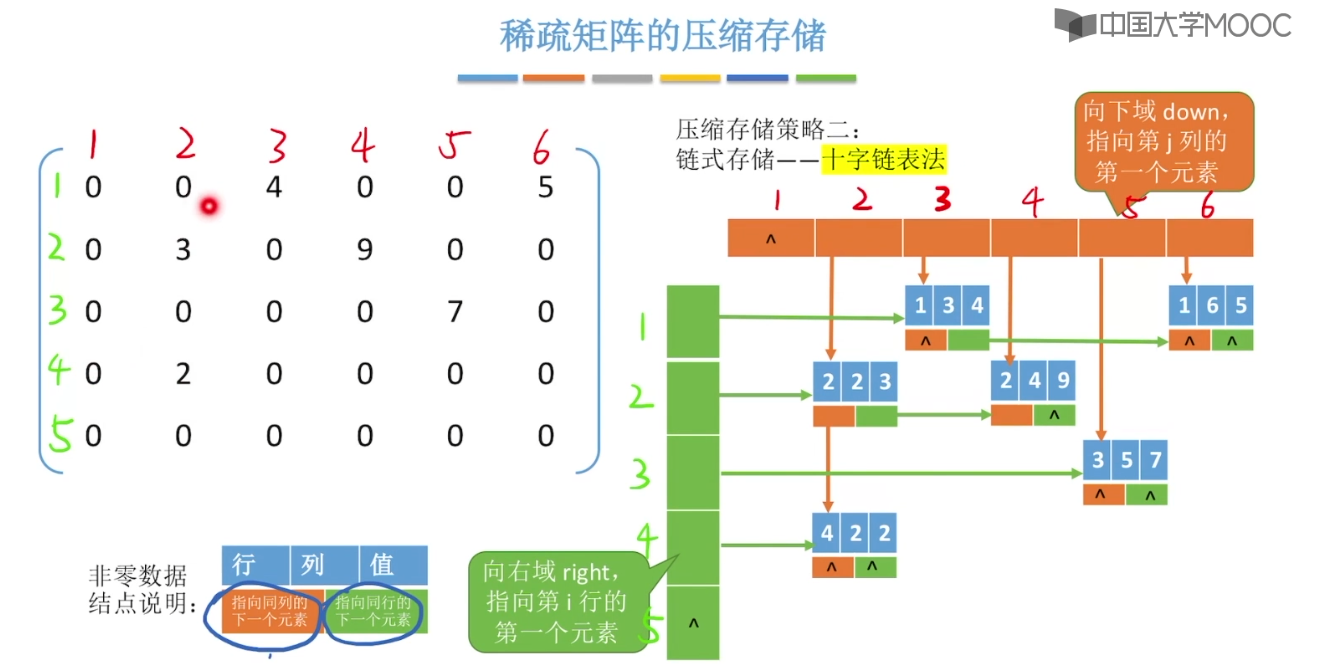
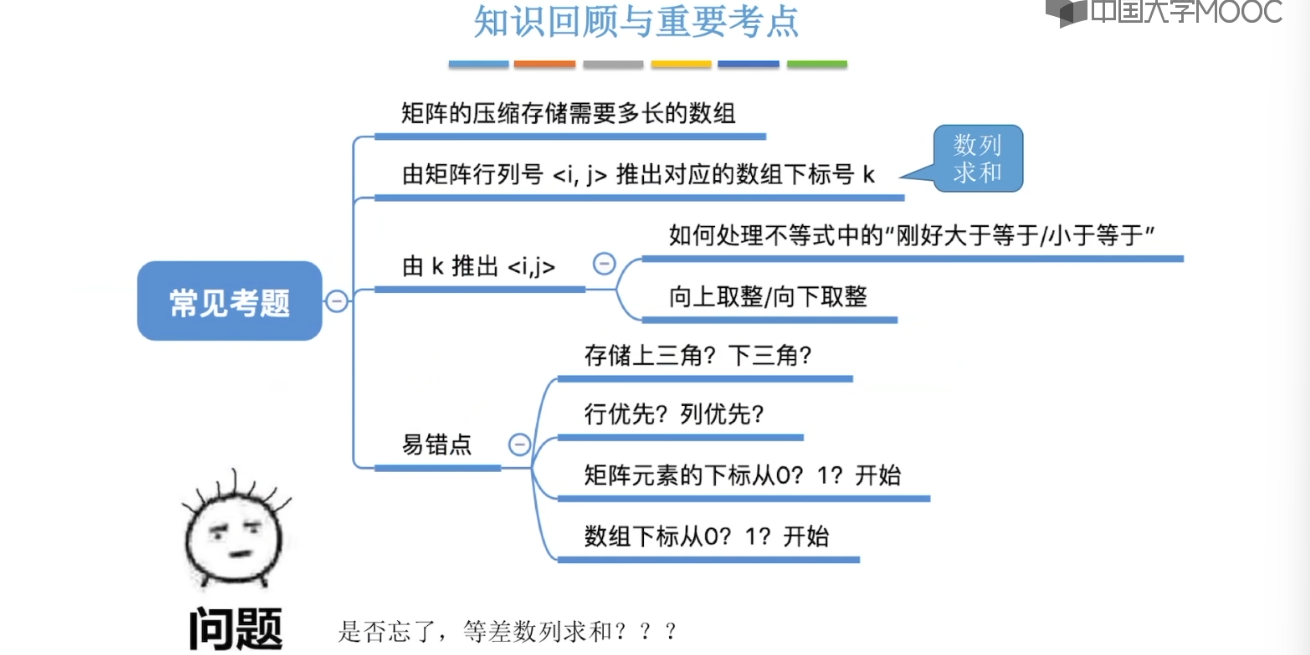
3.12、特殊矩阵的压缩存储
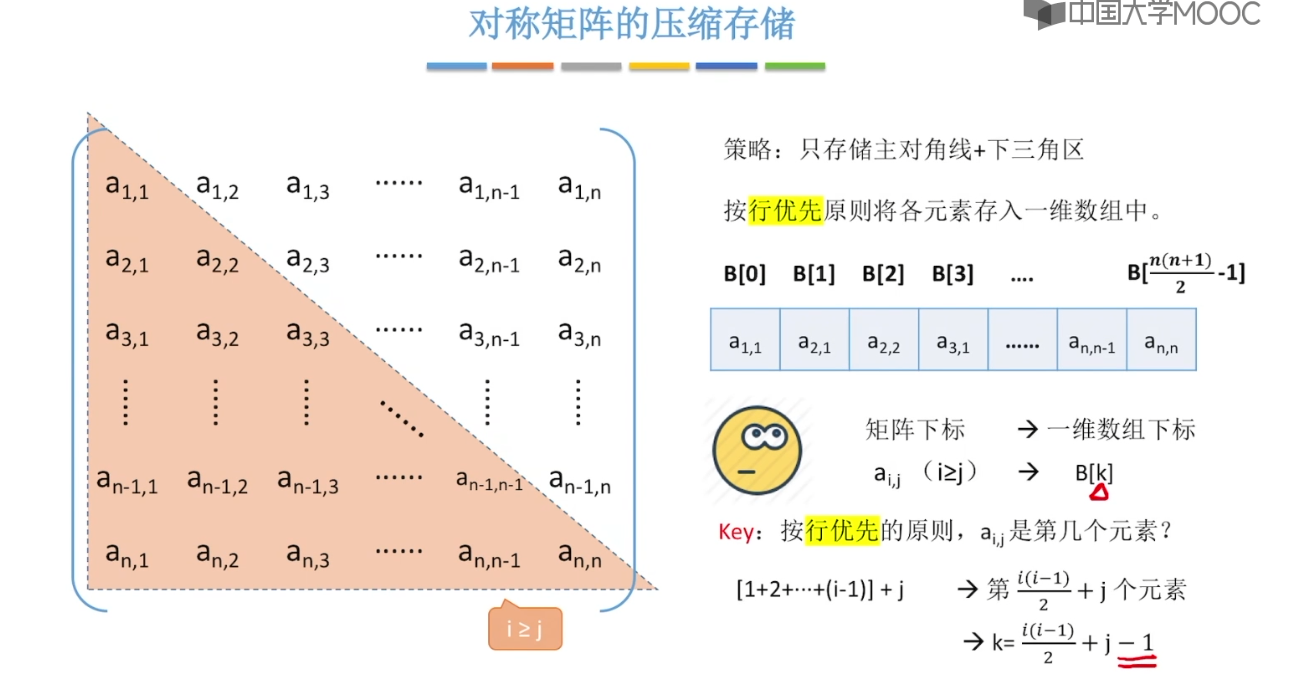

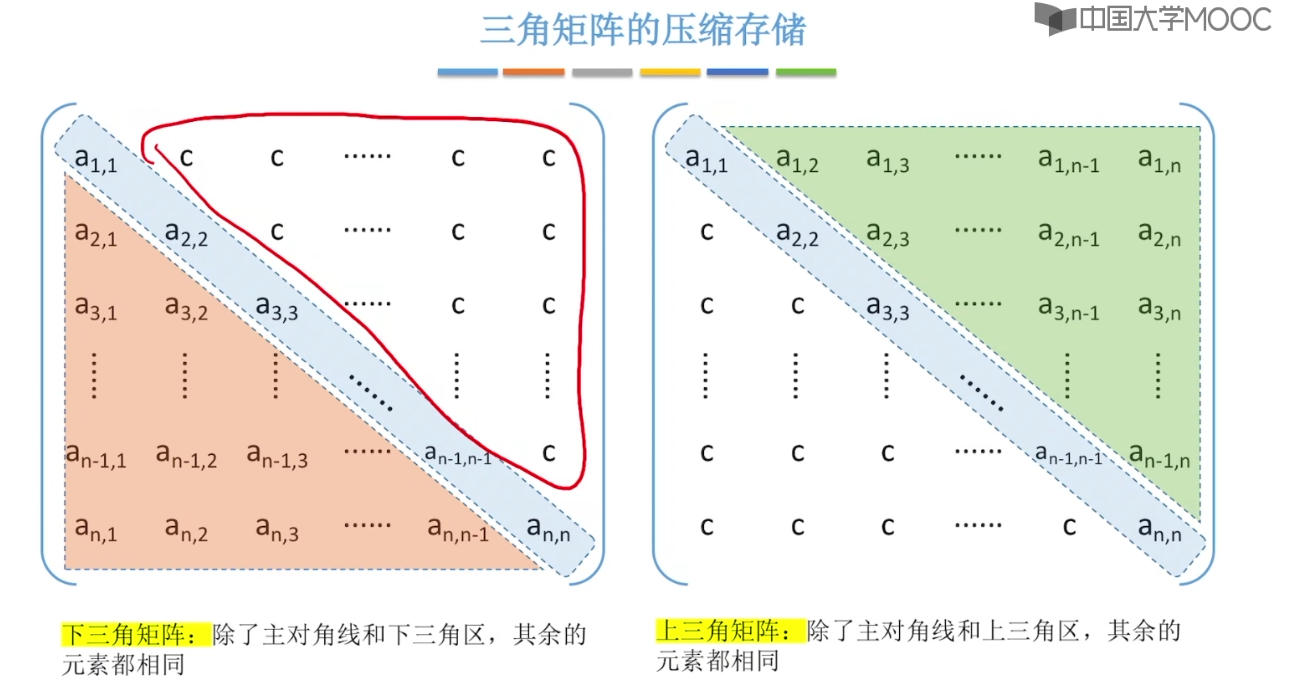
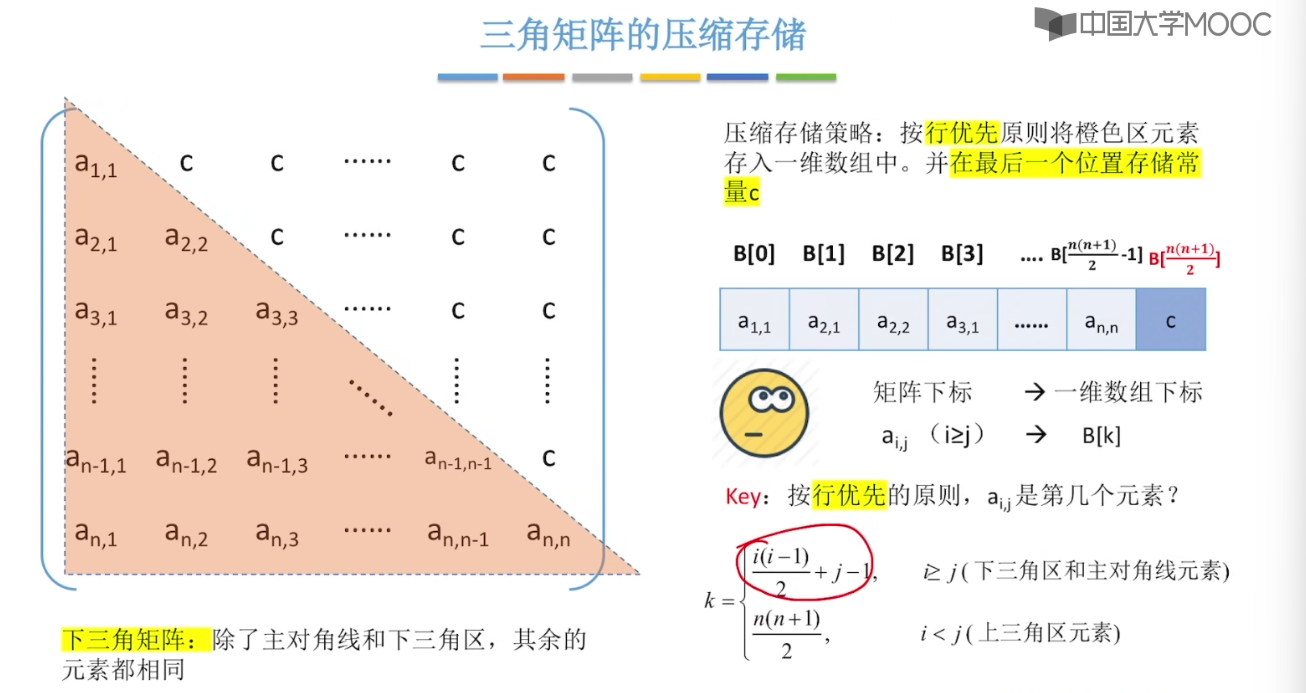
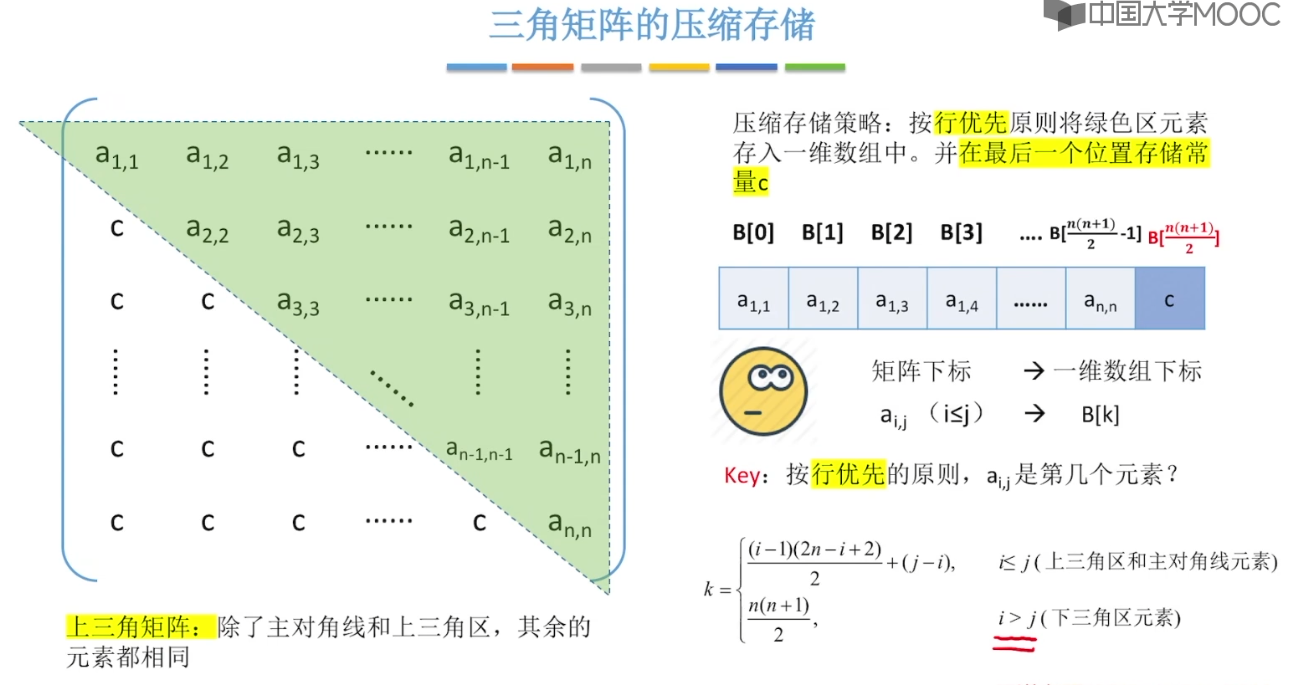

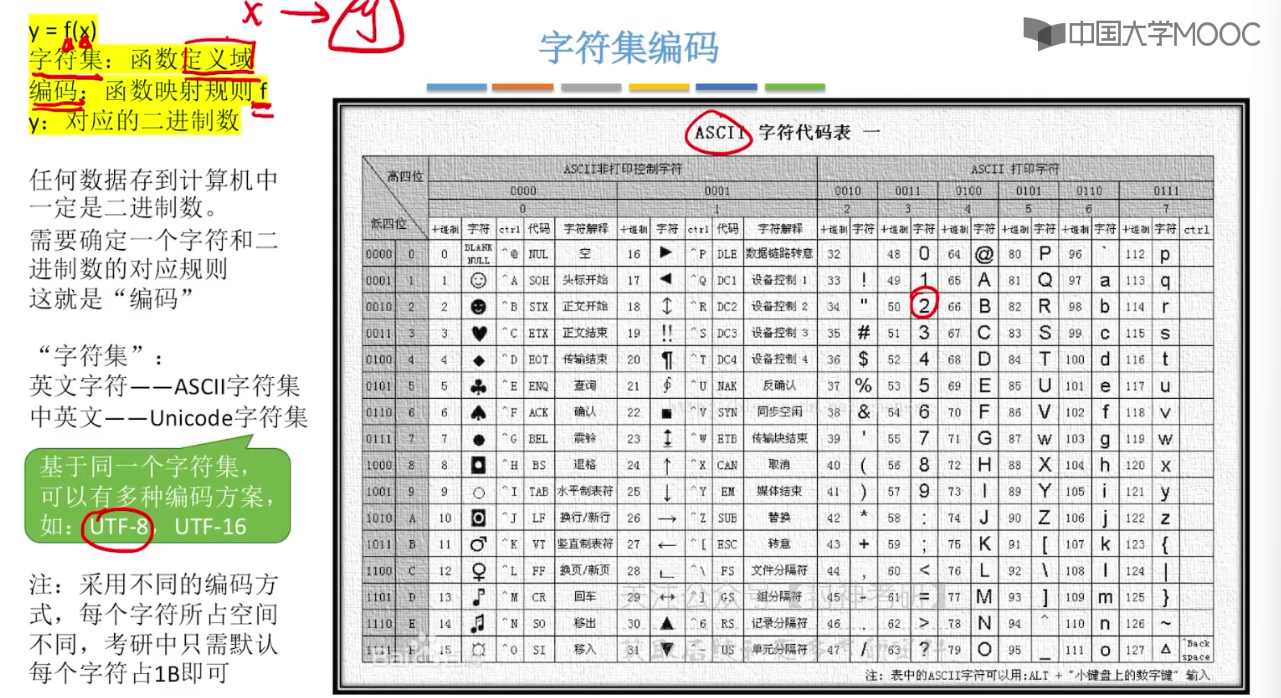
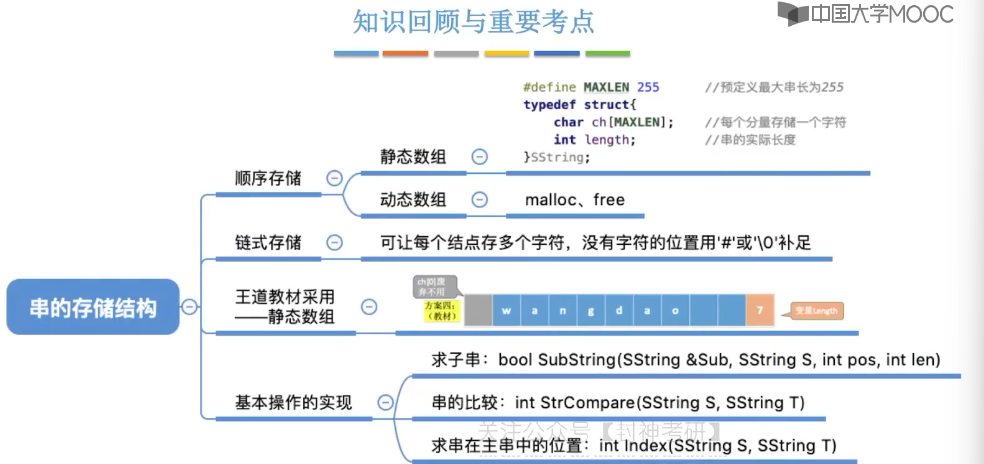
4、串
4.1、串的定义和基本操作
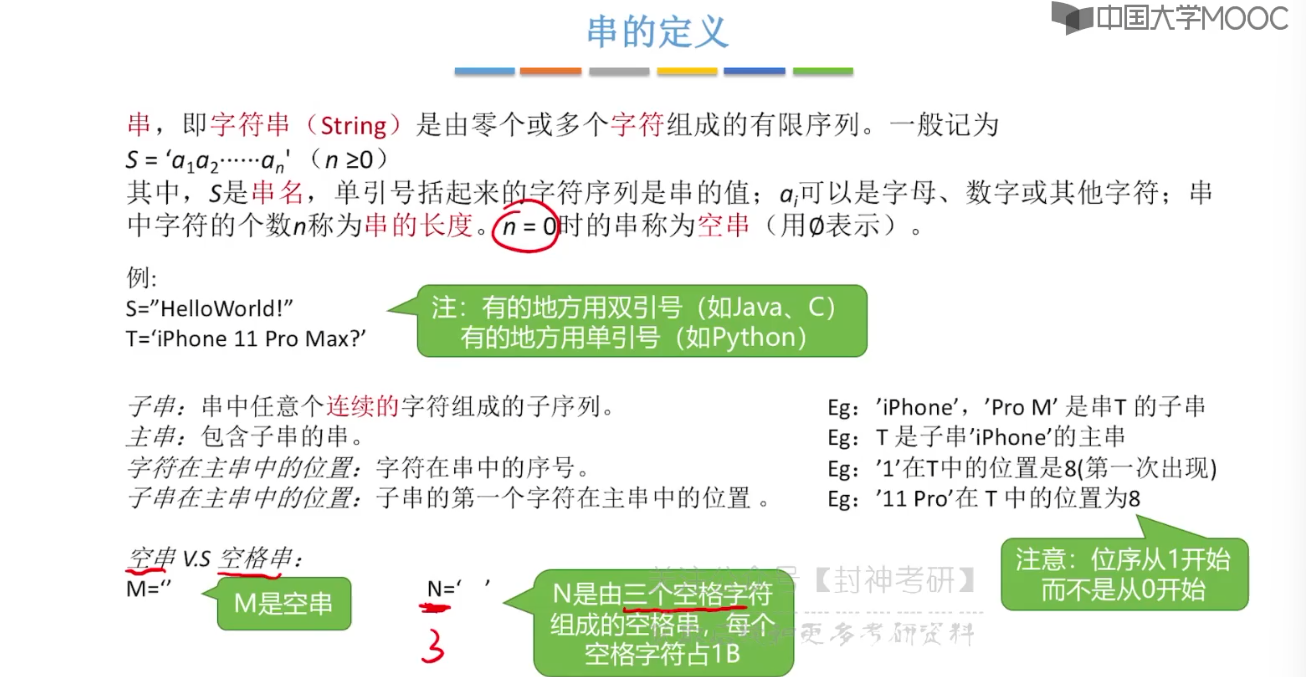
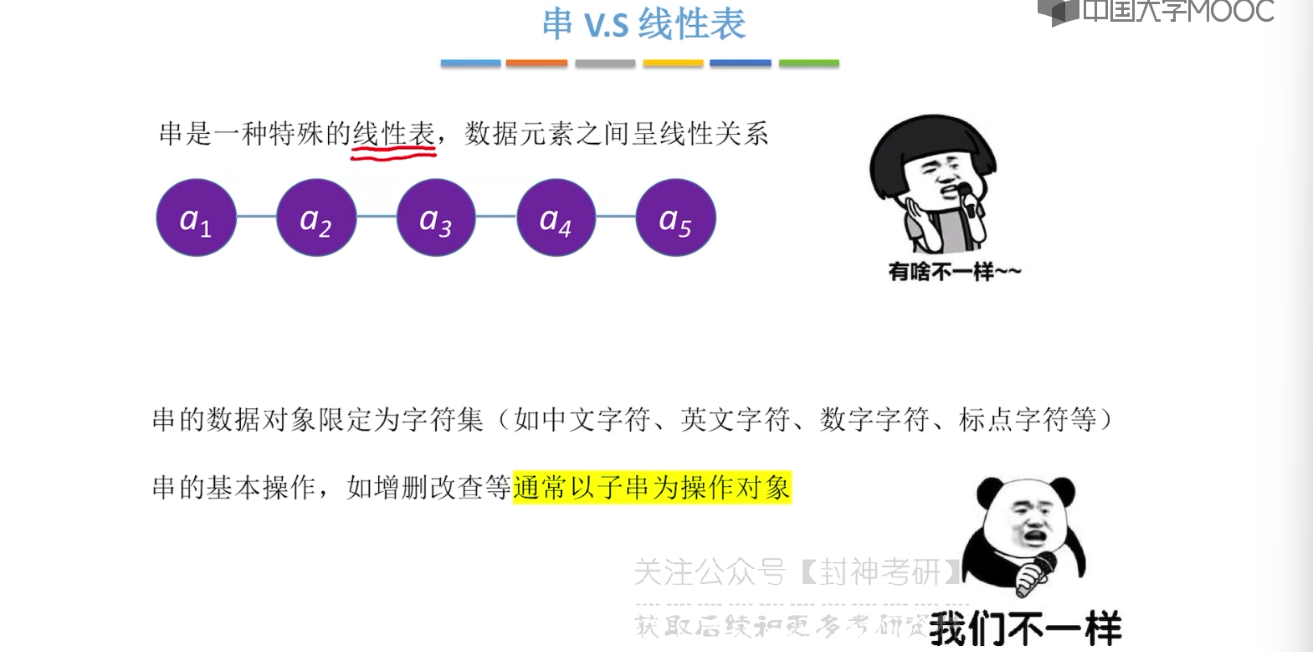

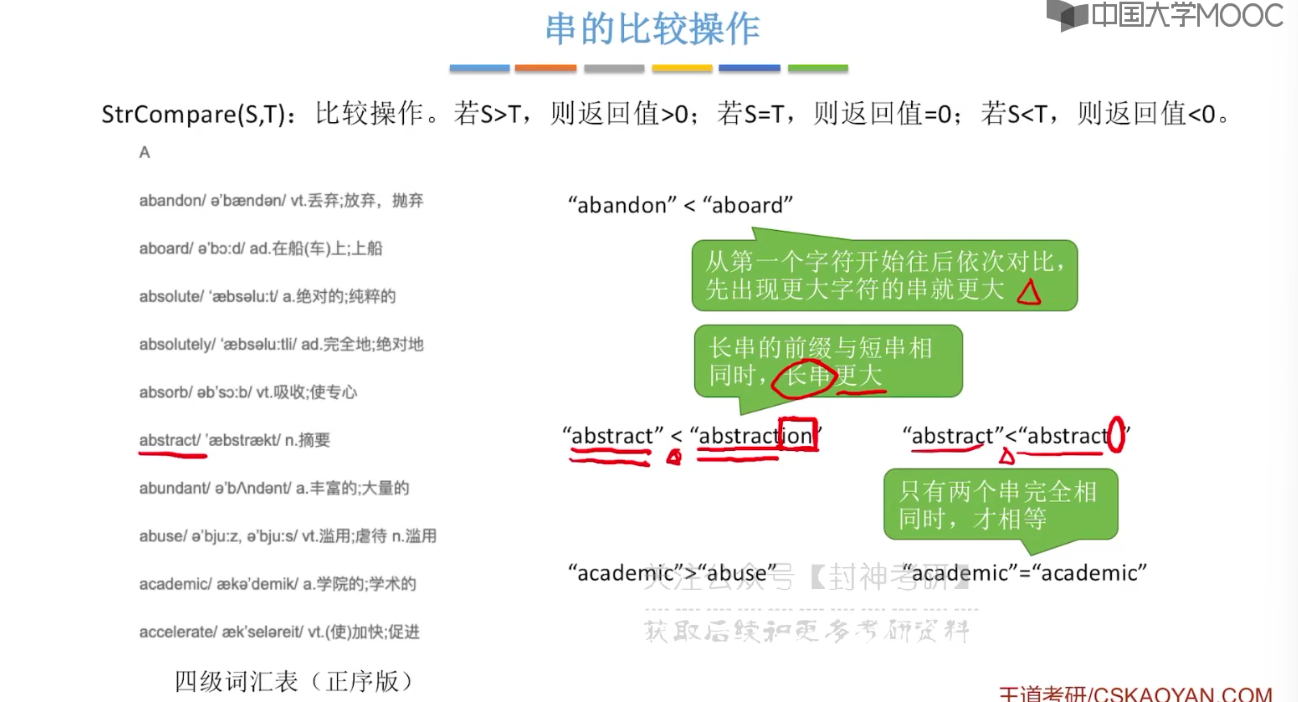


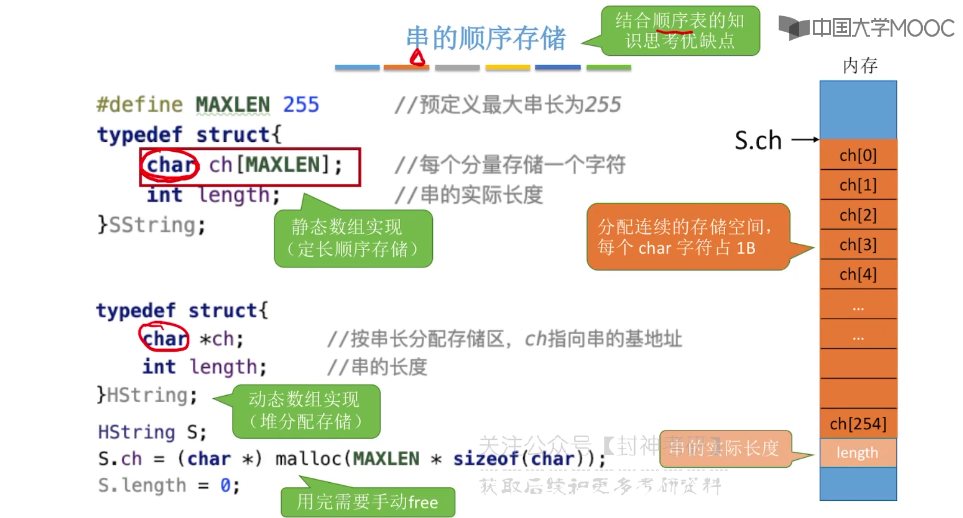
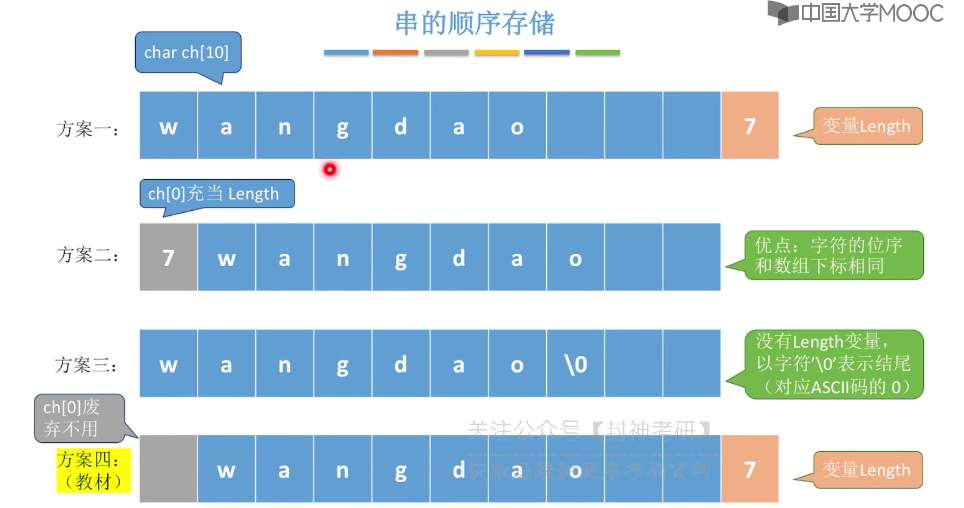
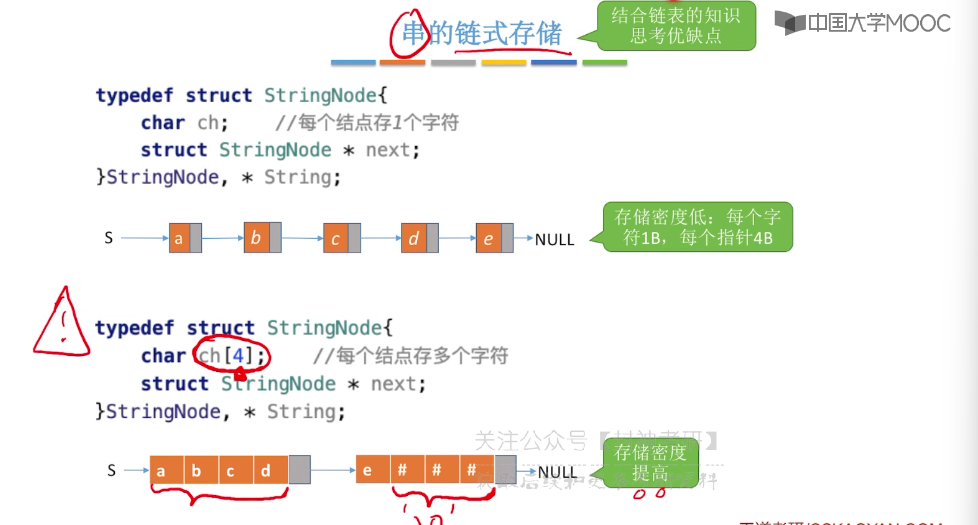
4.2、串的存储结构

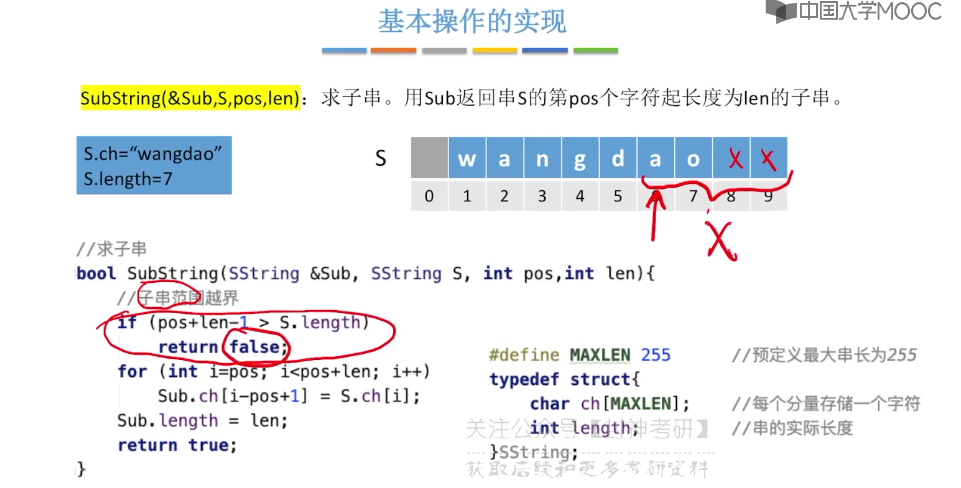
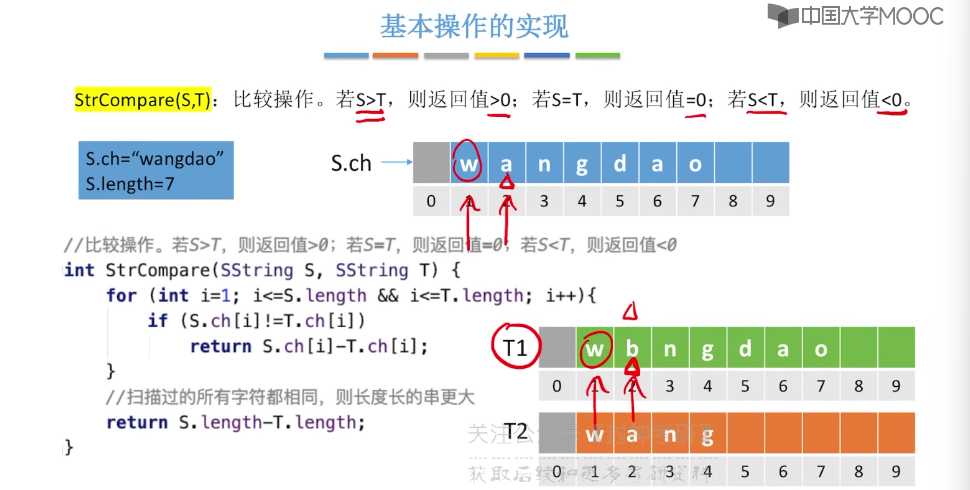

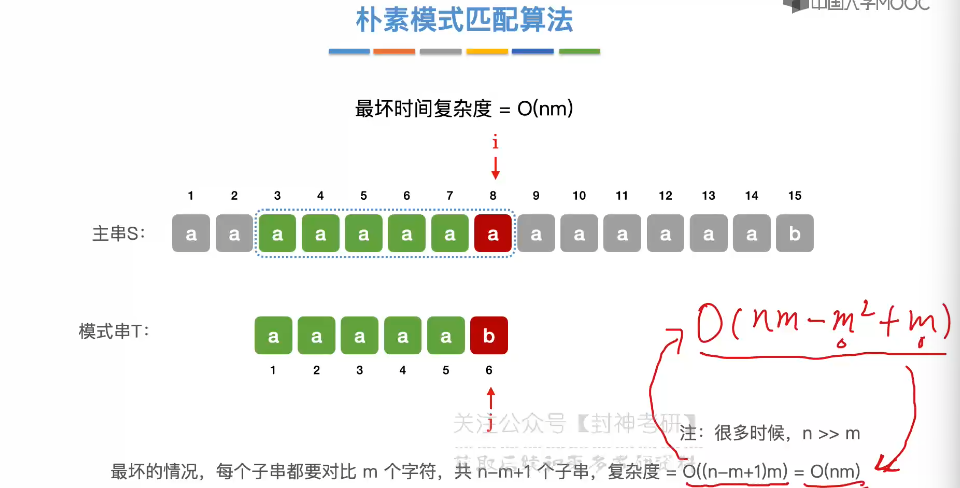
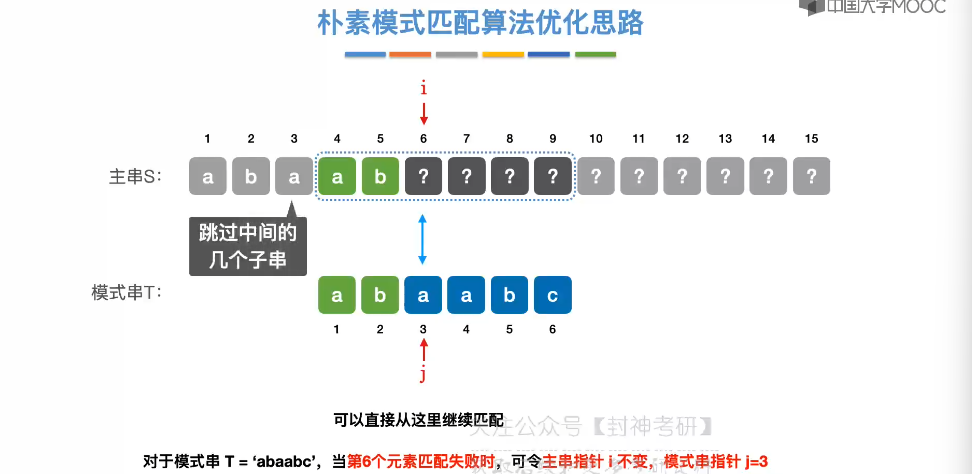
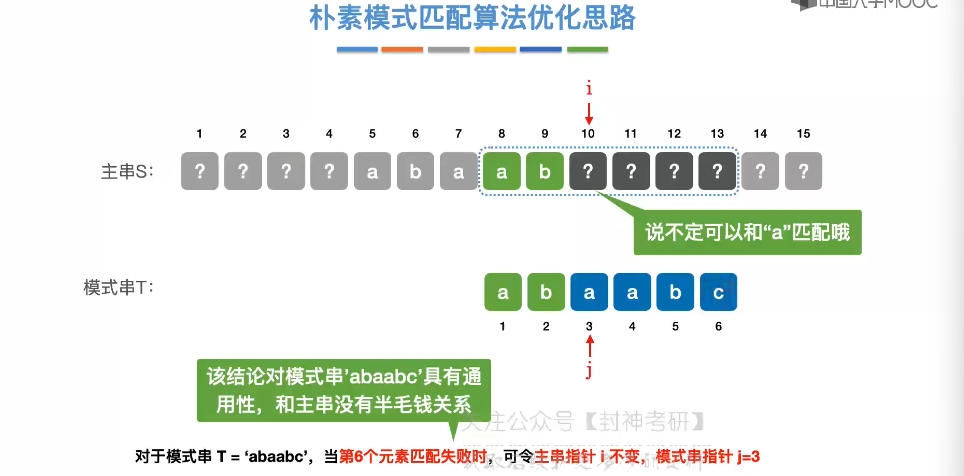
4.3、朴素模式匹配算法

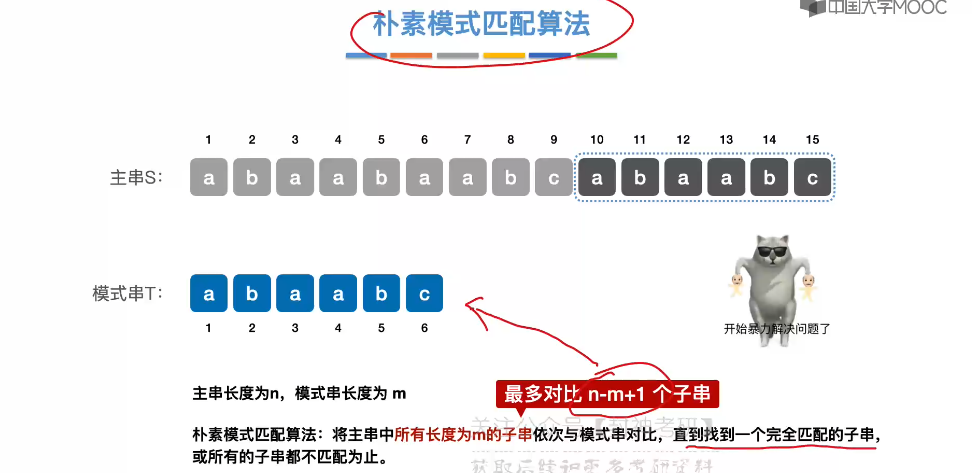

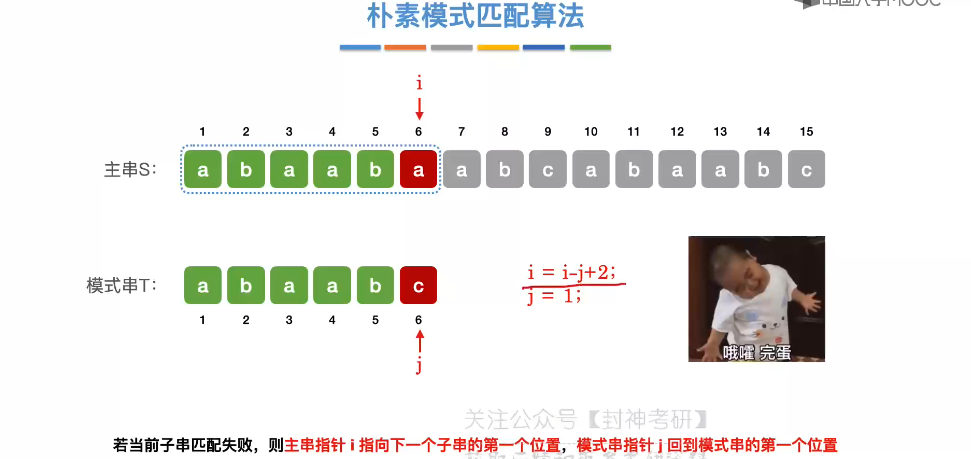
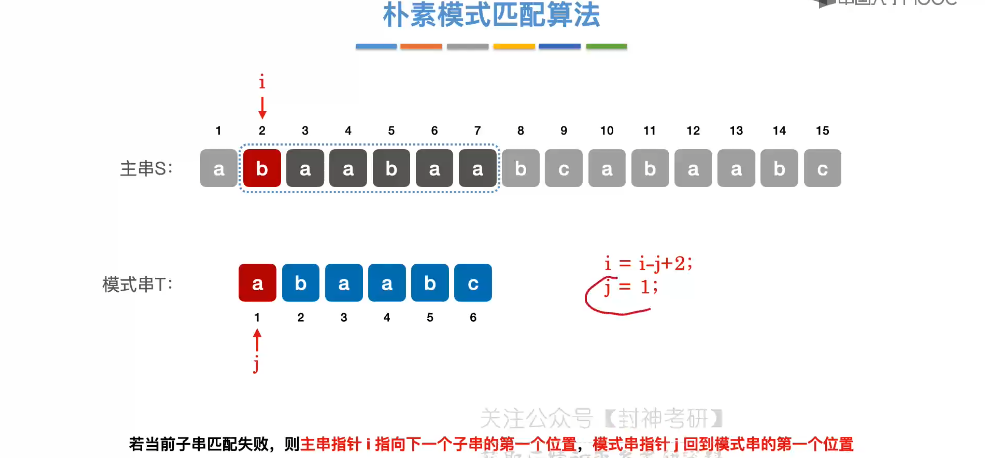
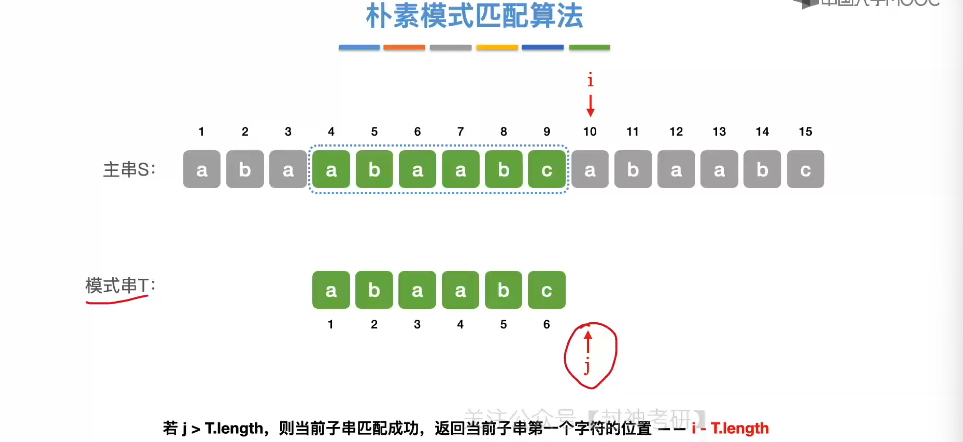

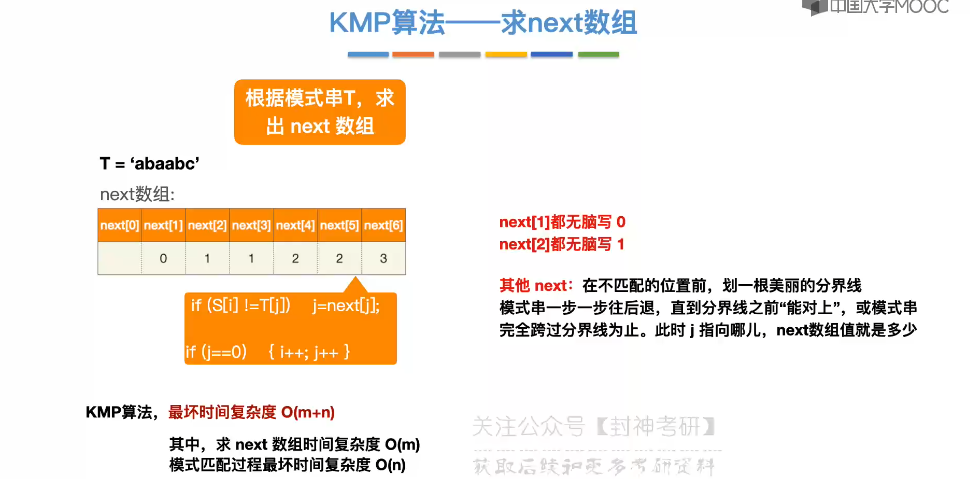
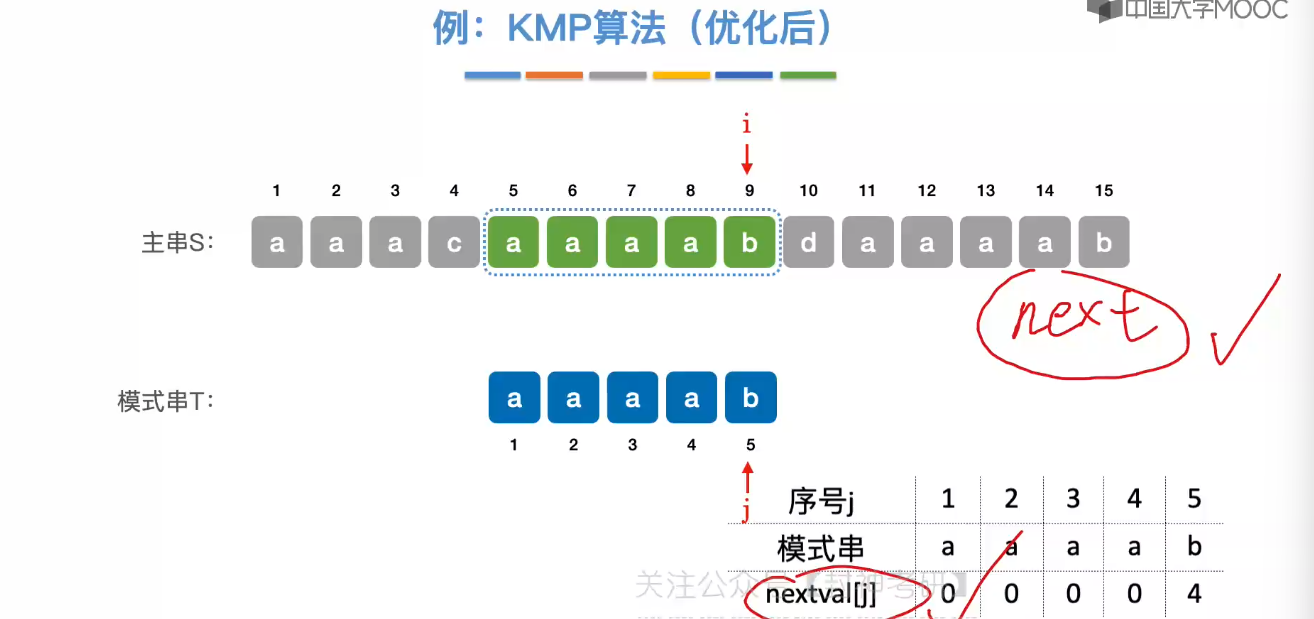
4.4、KMP 算法
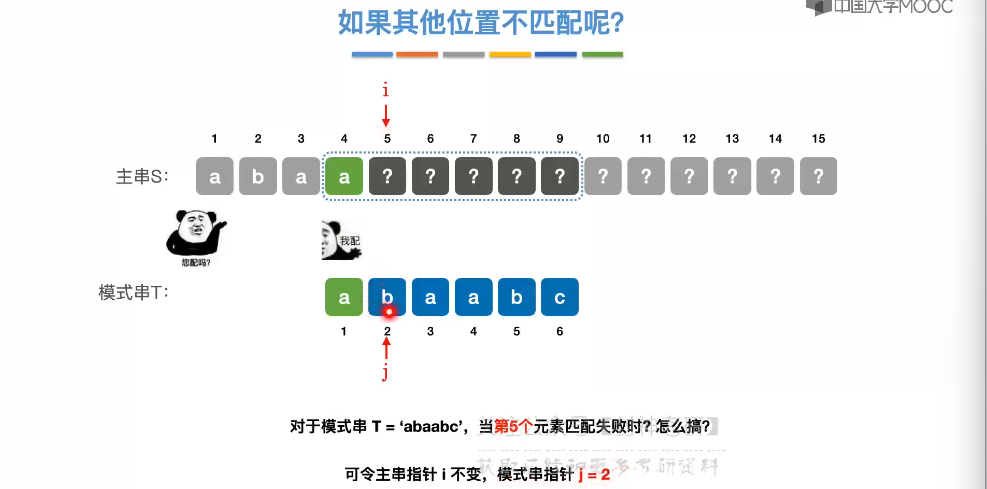
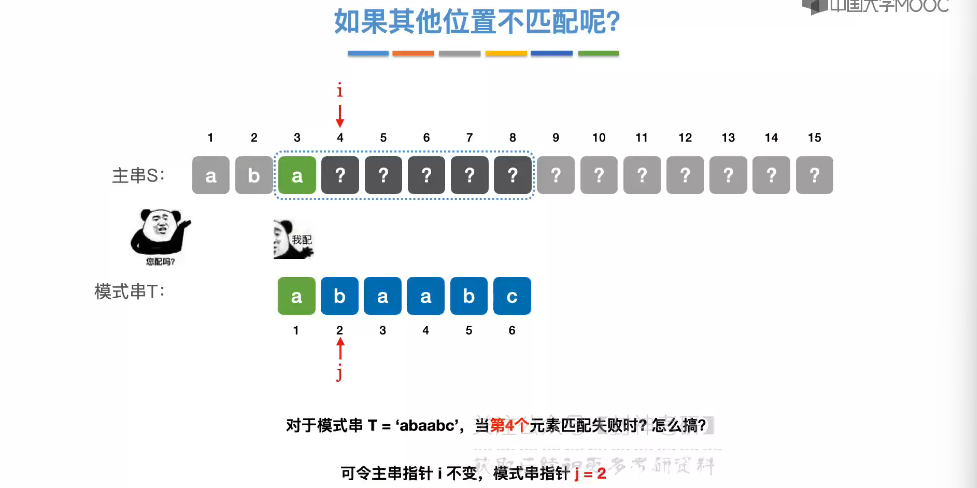
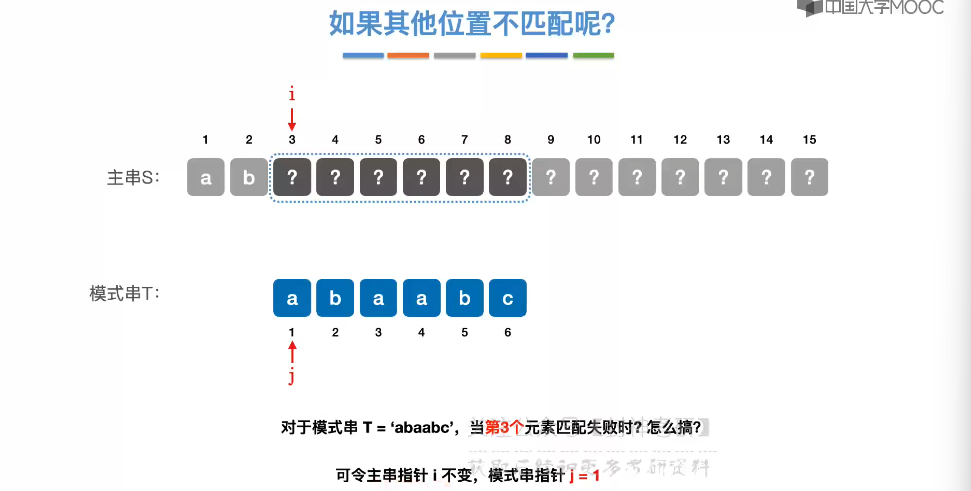
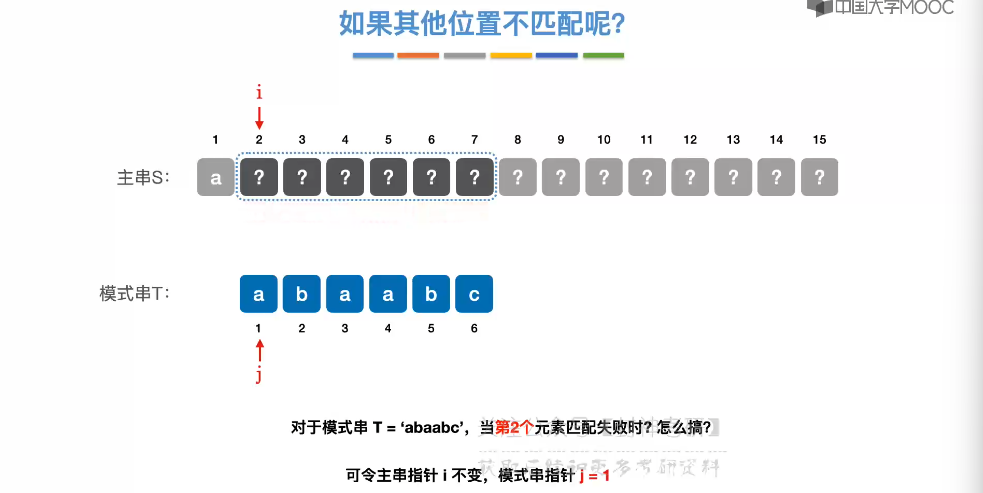
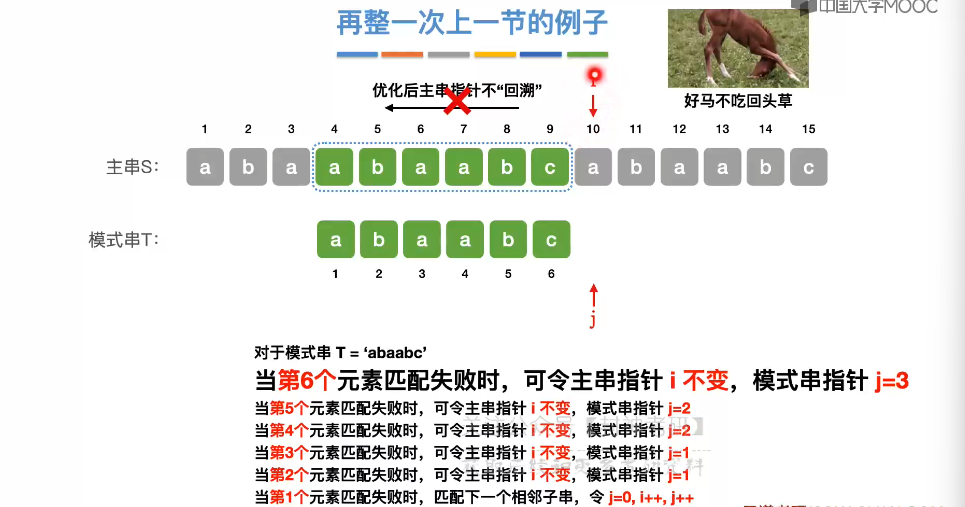
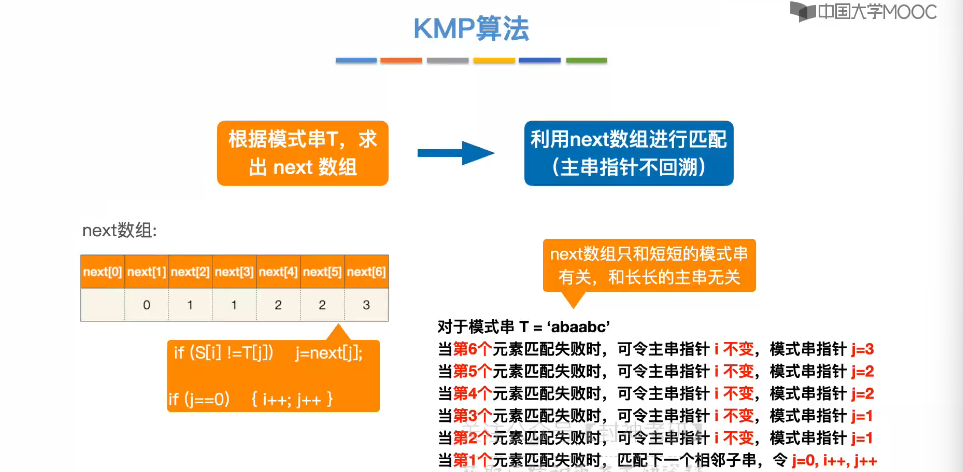

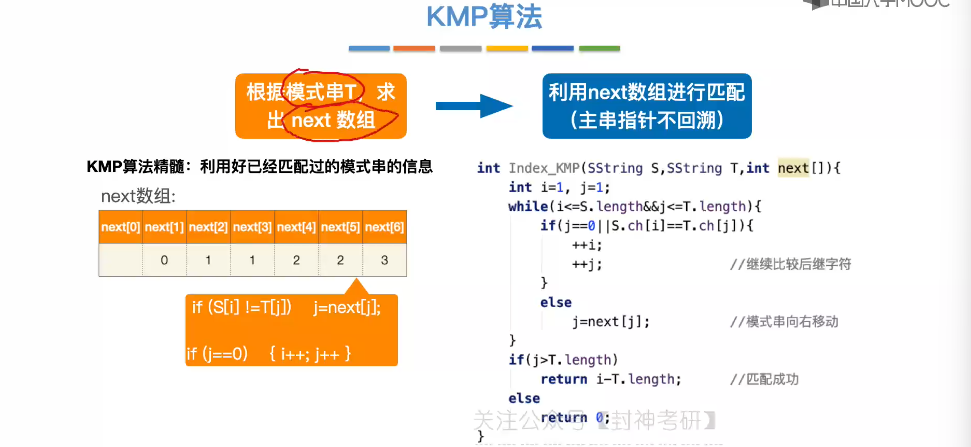
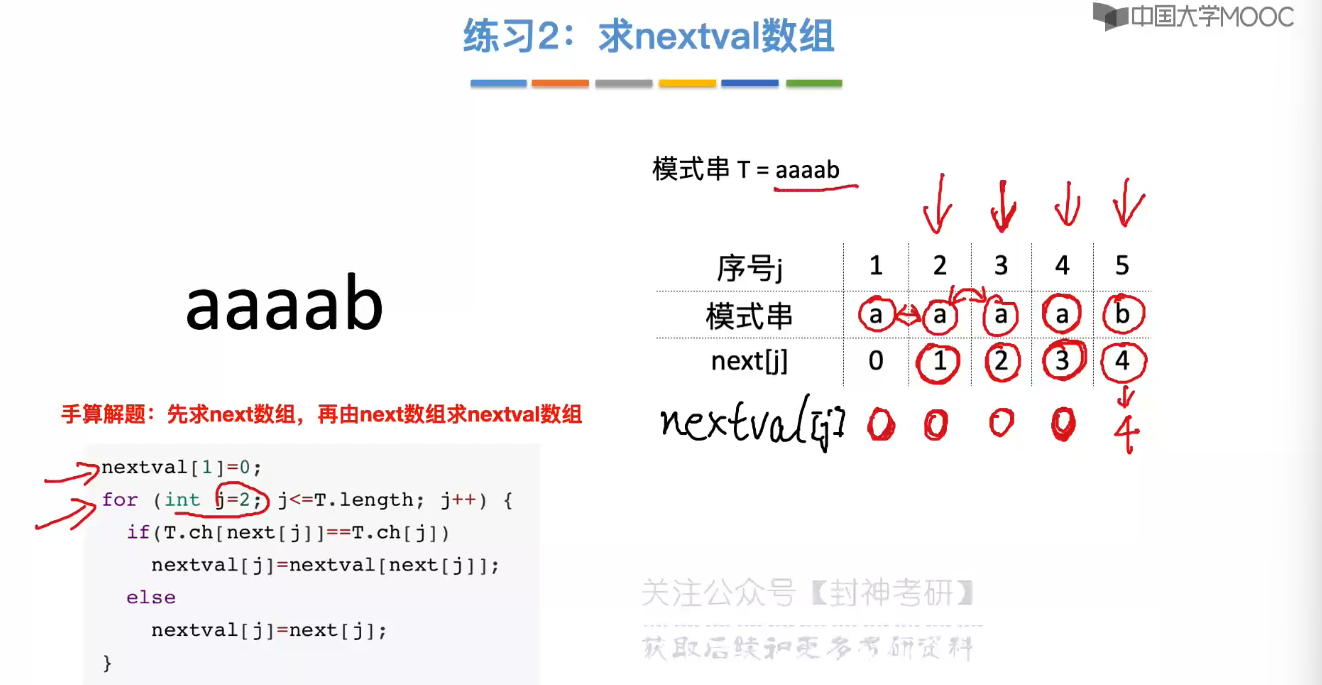
4.5、求 next 数组

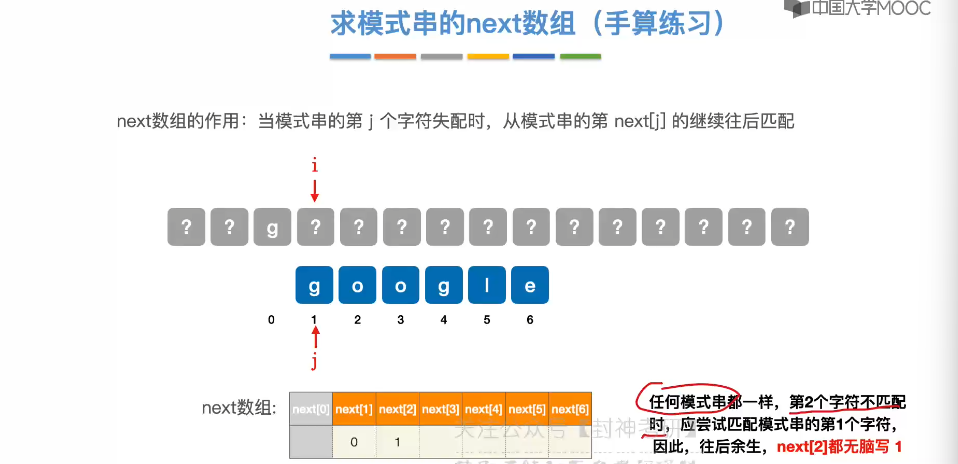
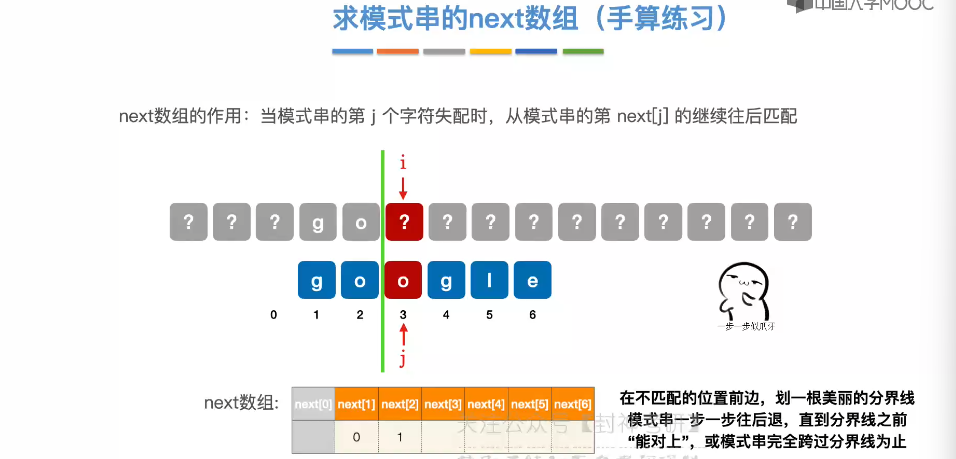

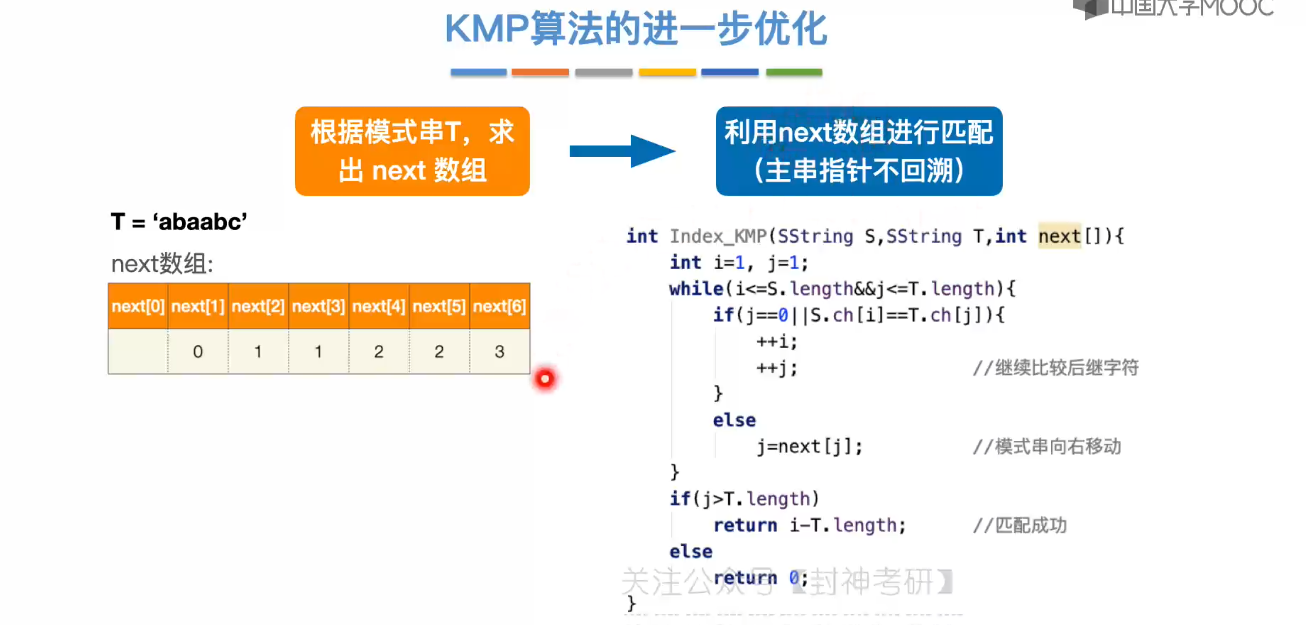
4.6、KMP 算法的进一步优化


5、树与二叉树
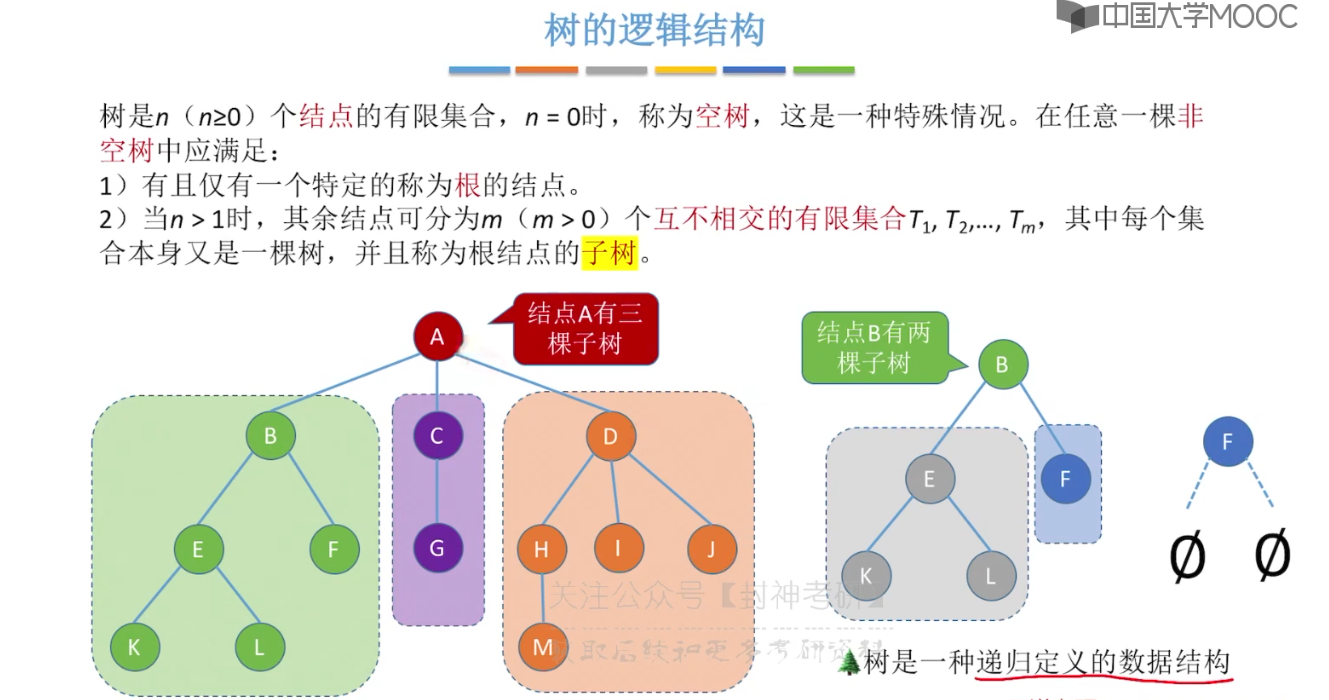
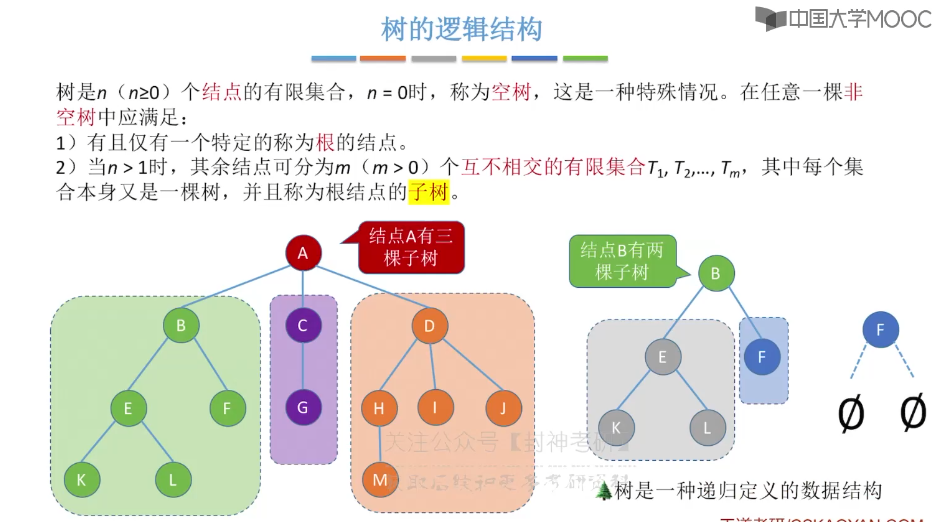
5.1、树的定义和基本术语
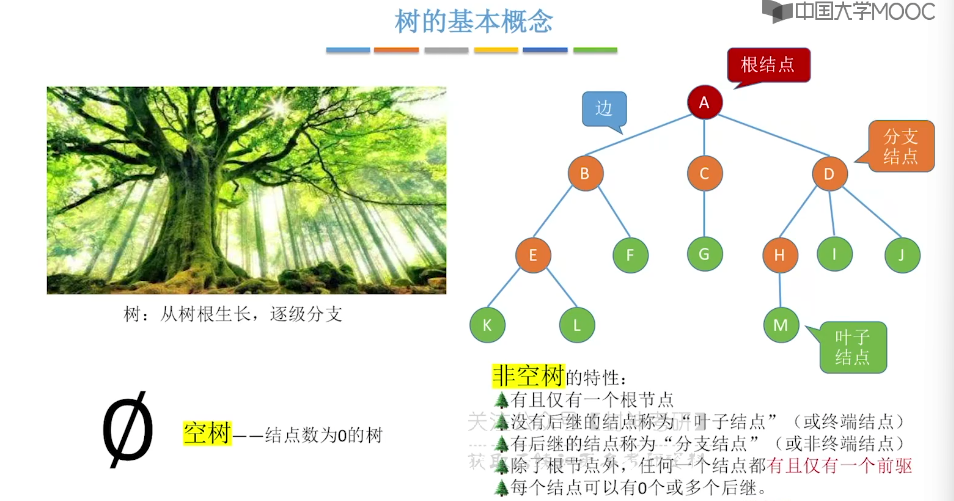
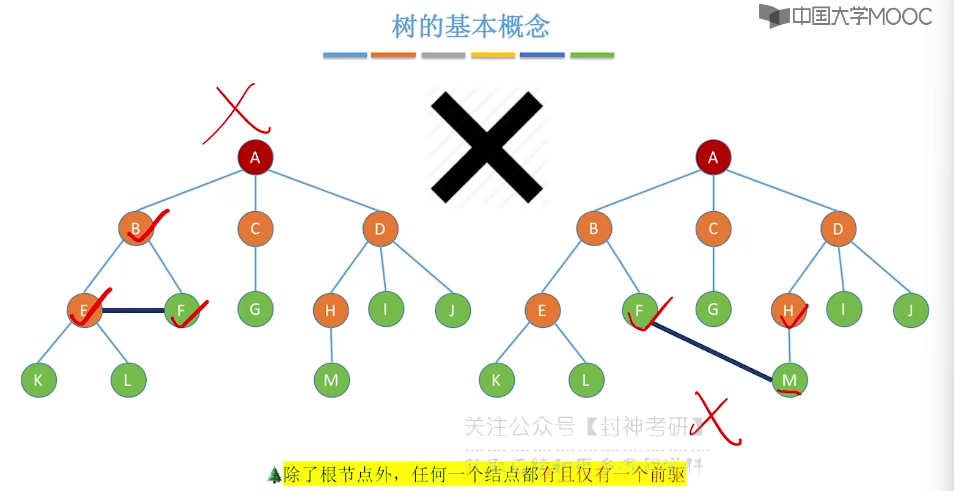
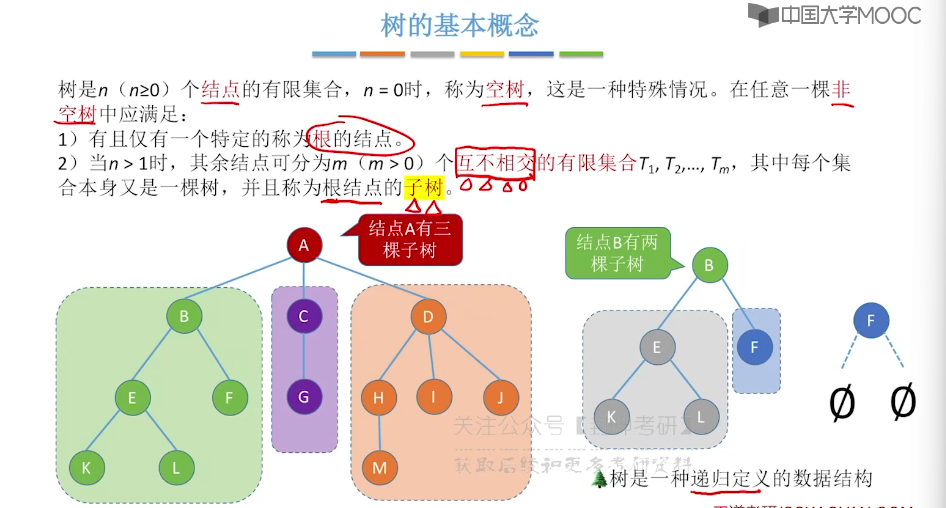
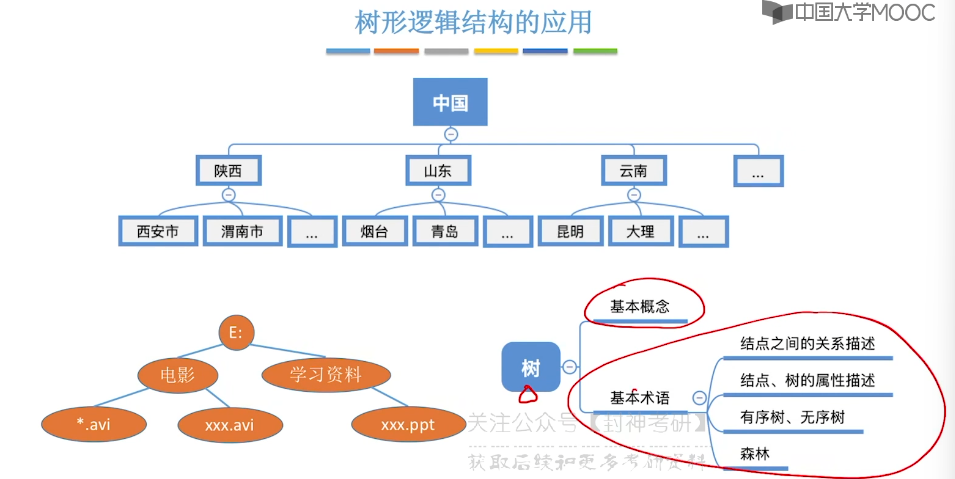
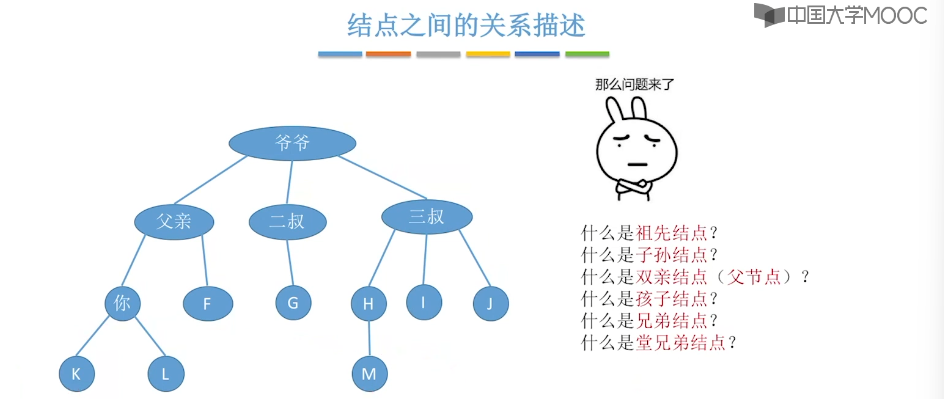
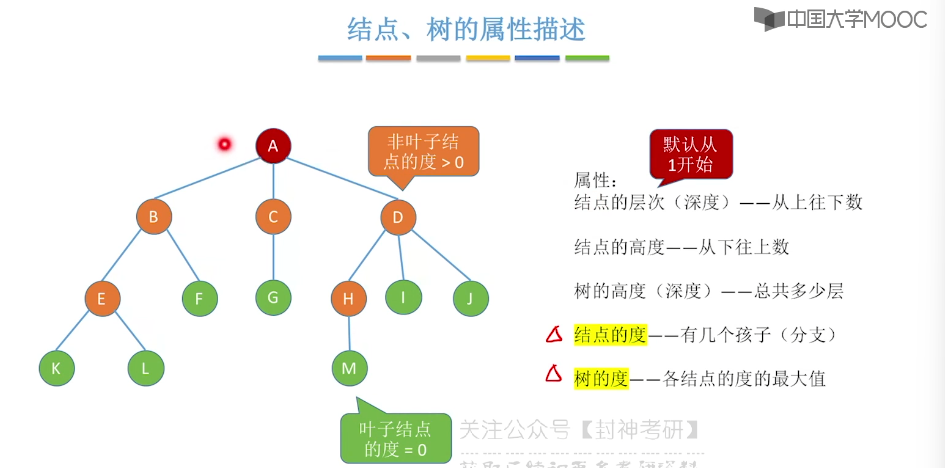
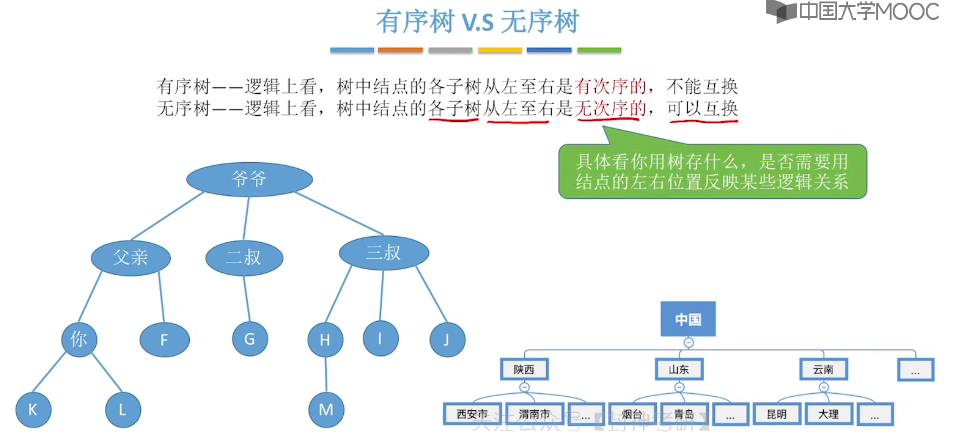
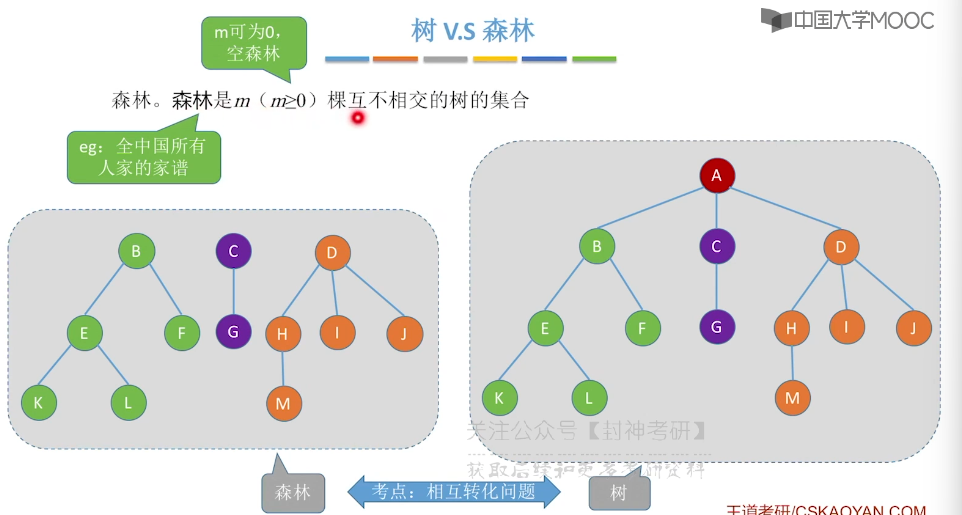
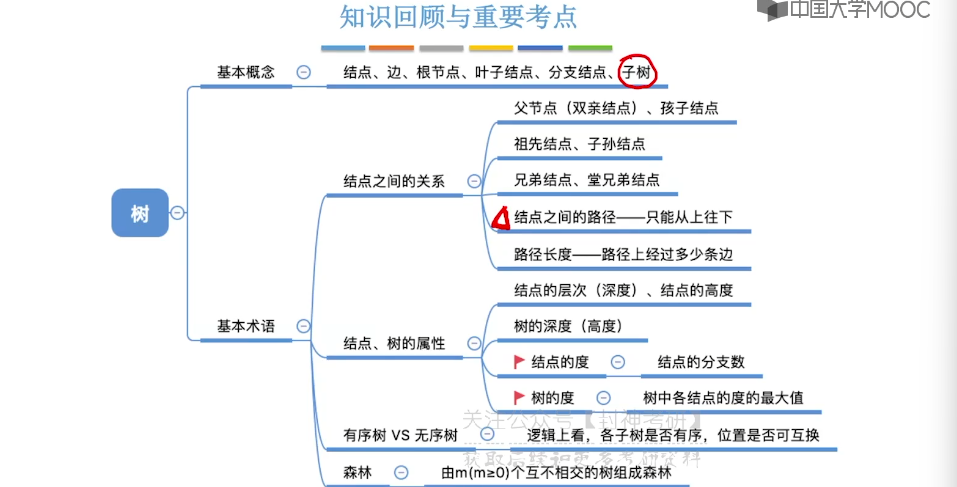
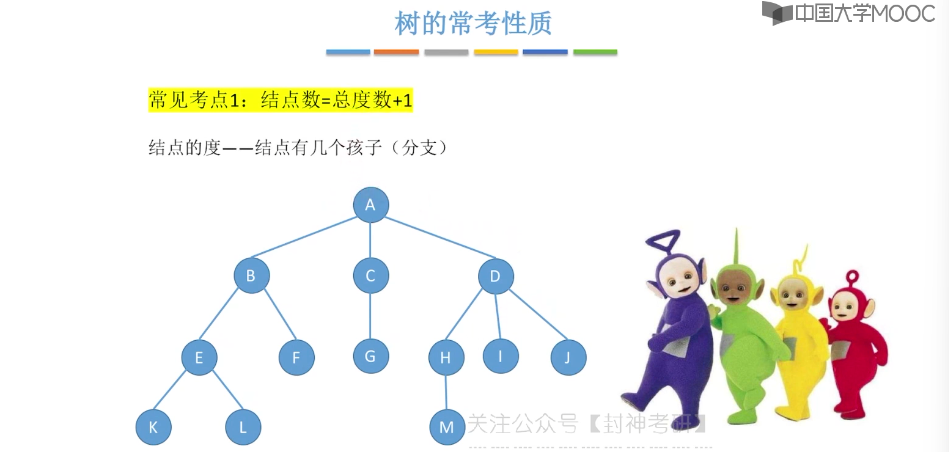
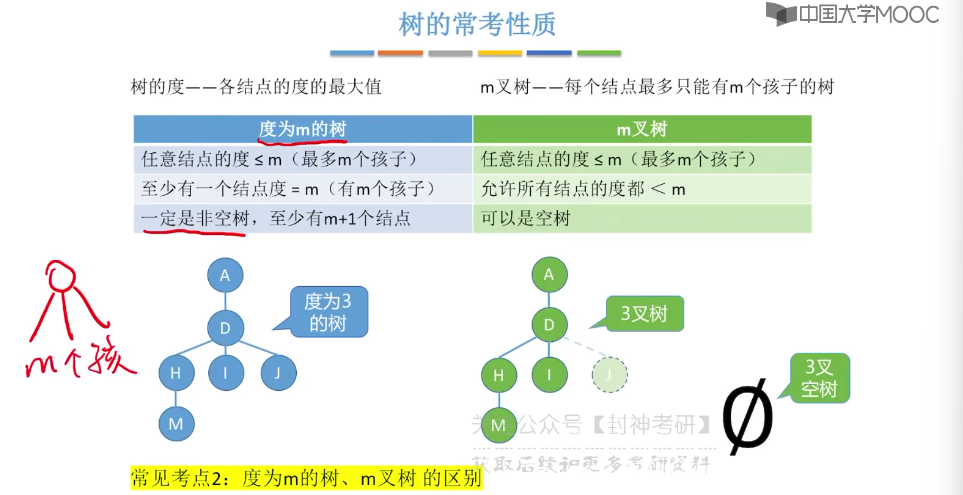
5.2、树的性质
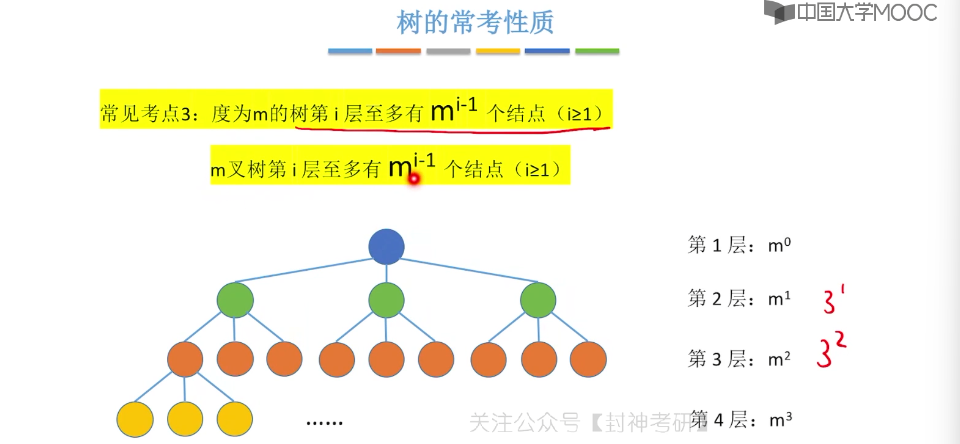
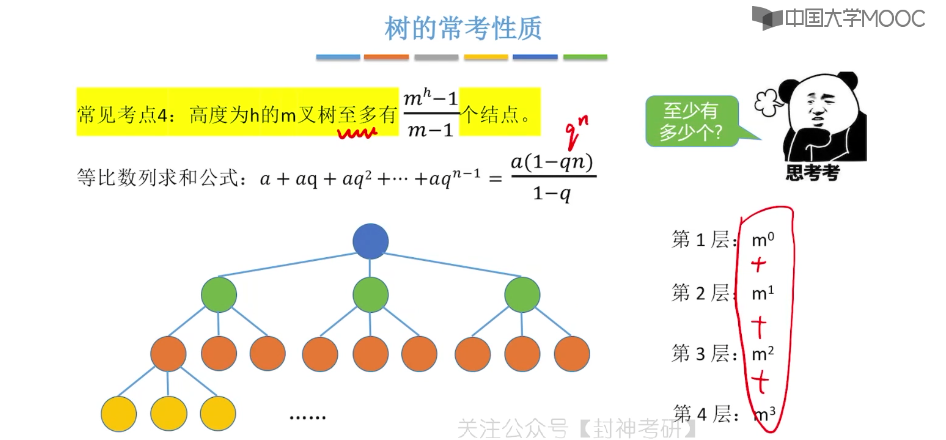


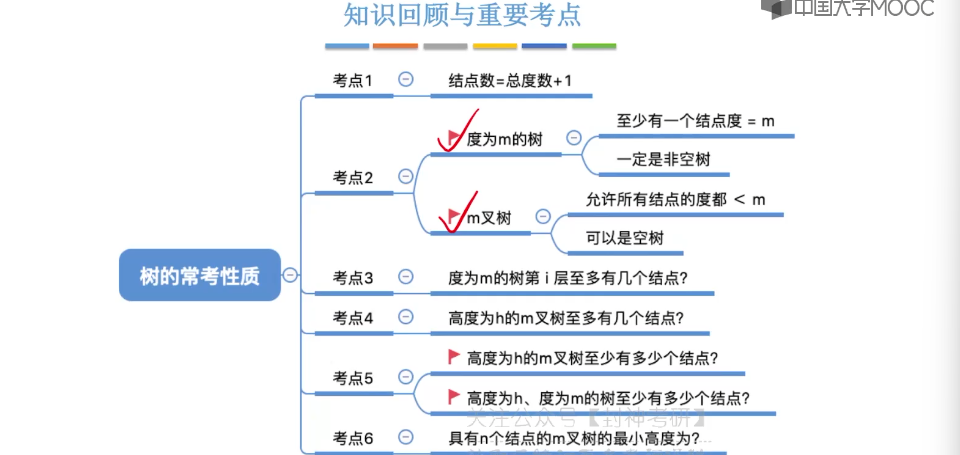
5.3、二叉树的定义和基本术语
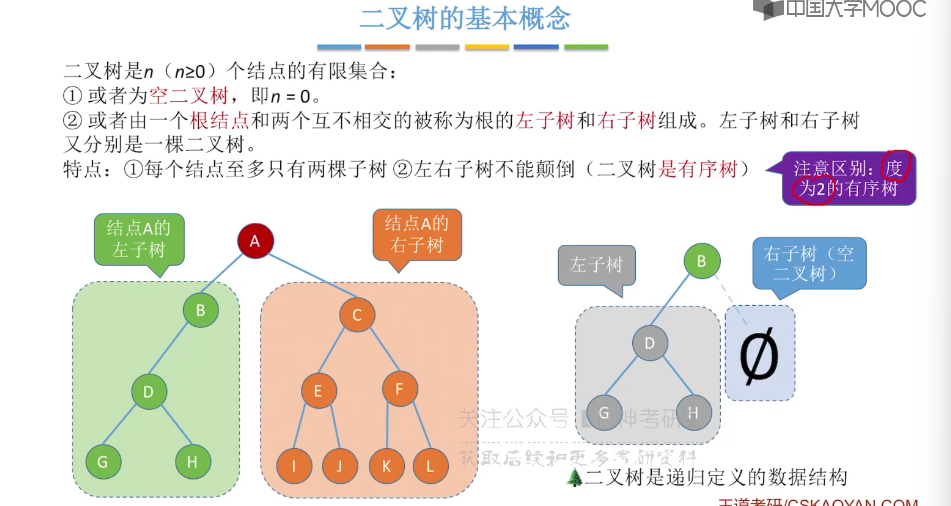
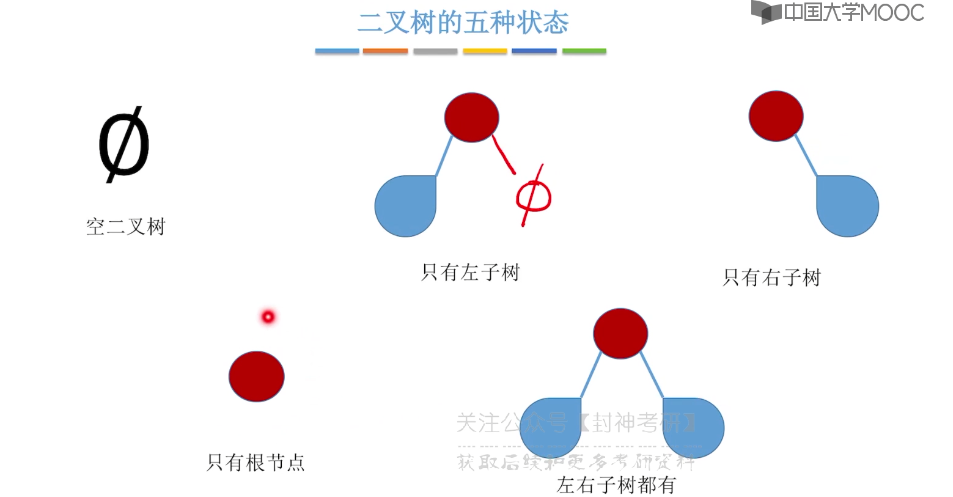
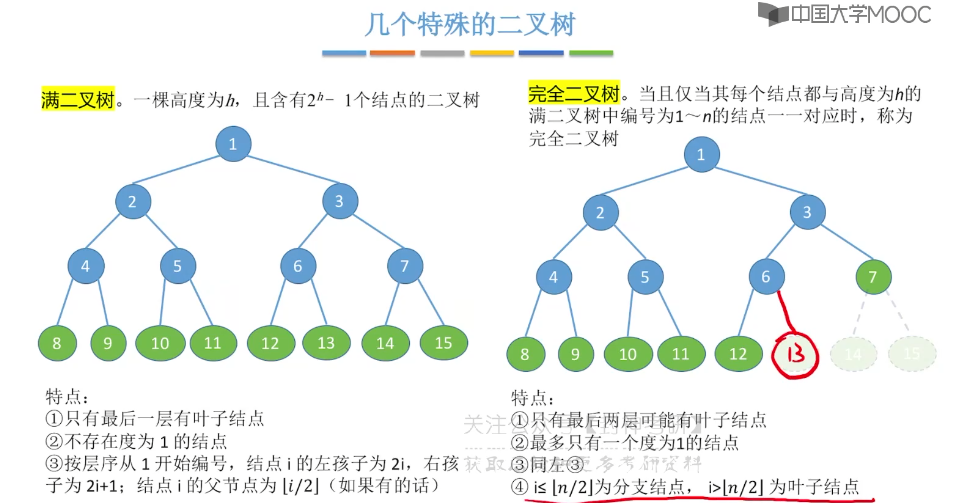
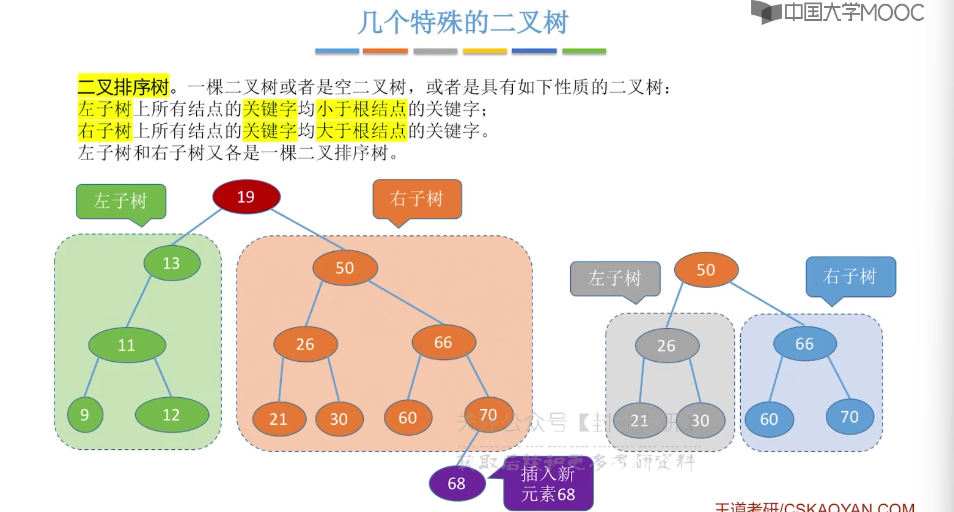
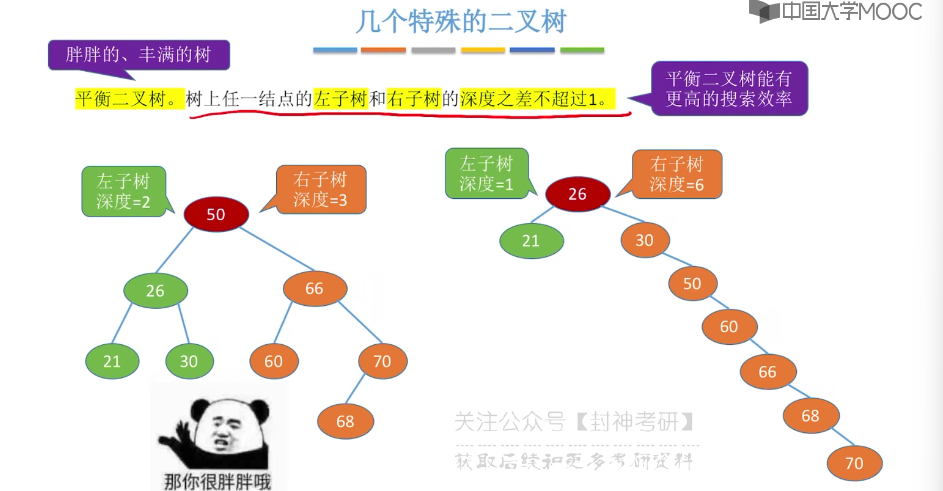
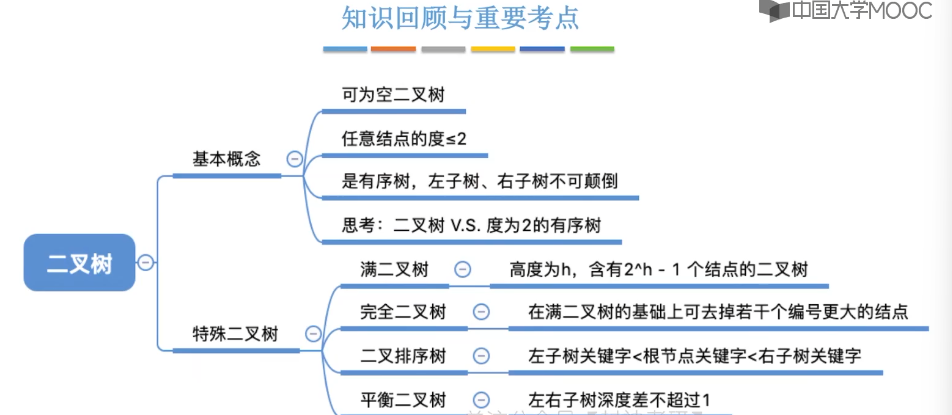
5.4、二叉树的性质
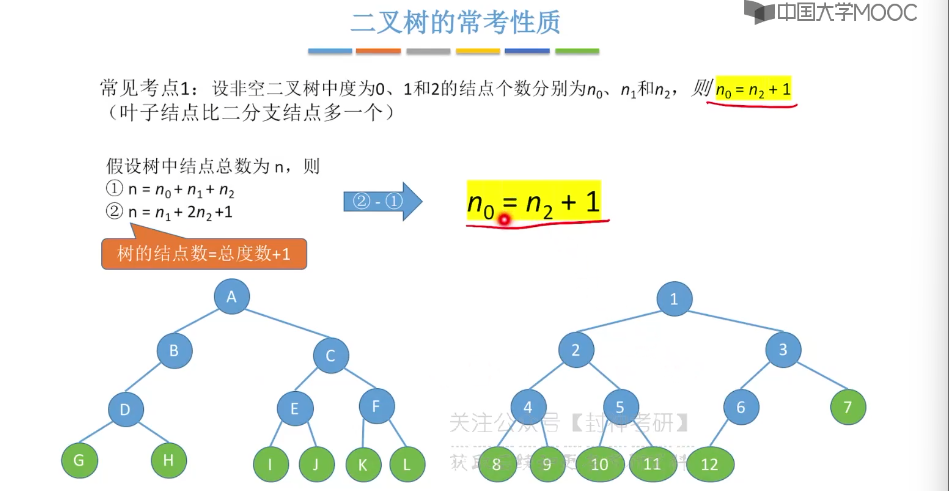
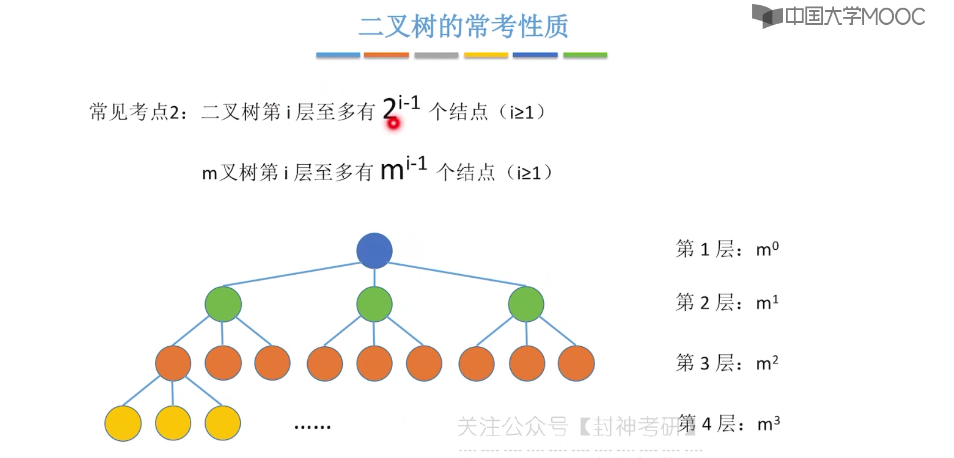
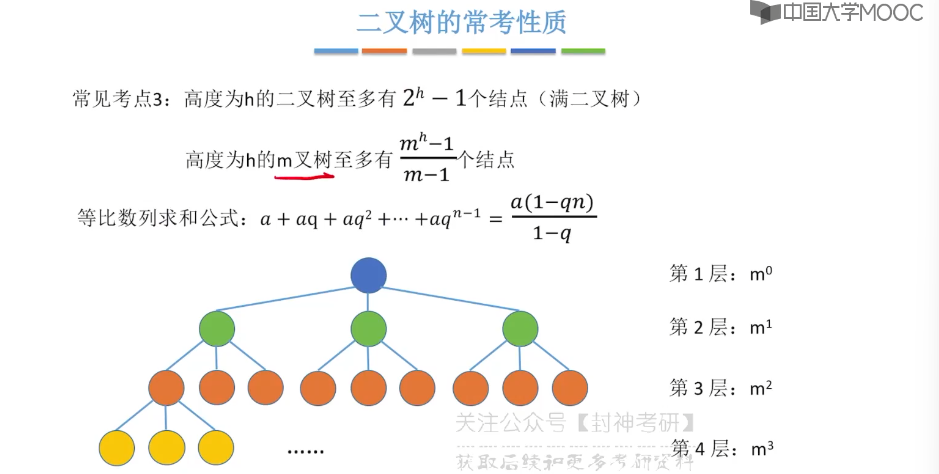
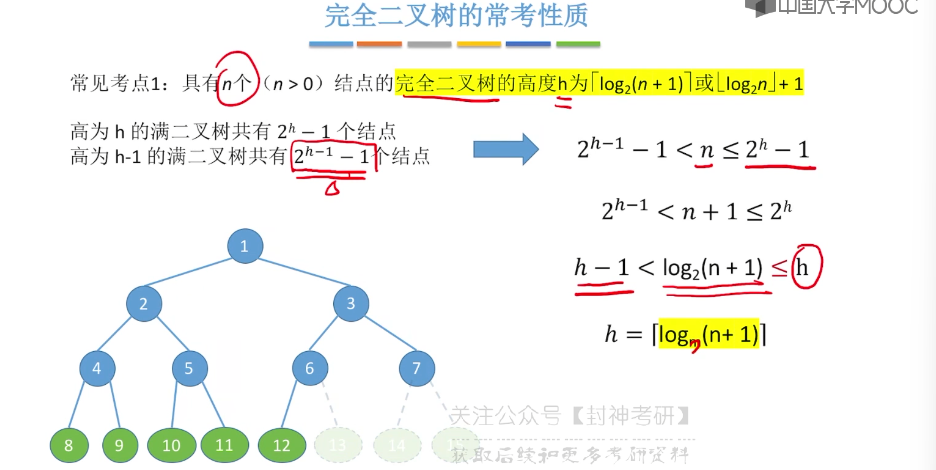
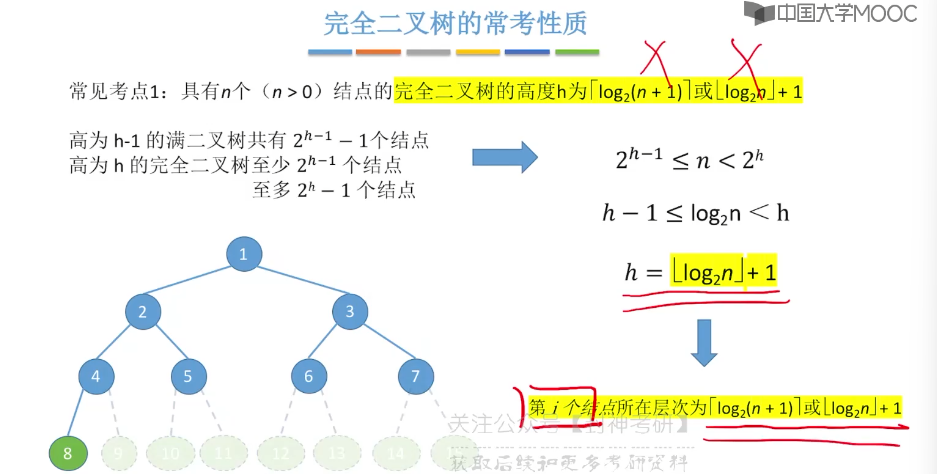
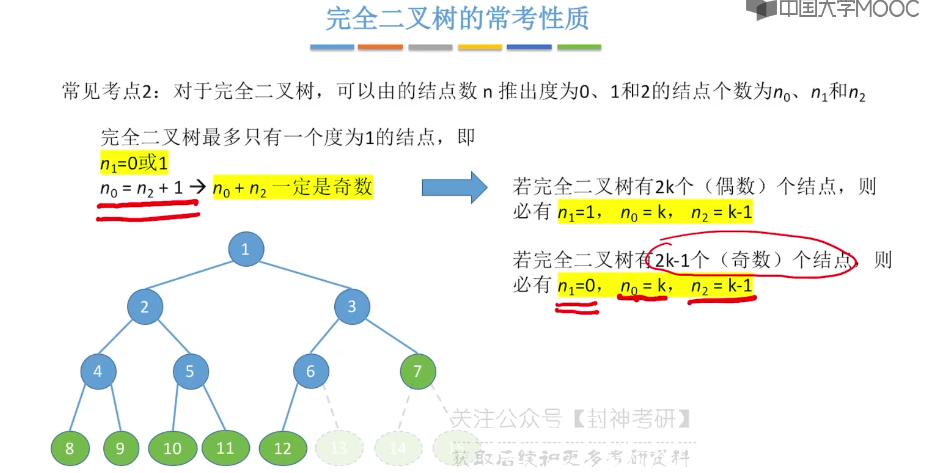

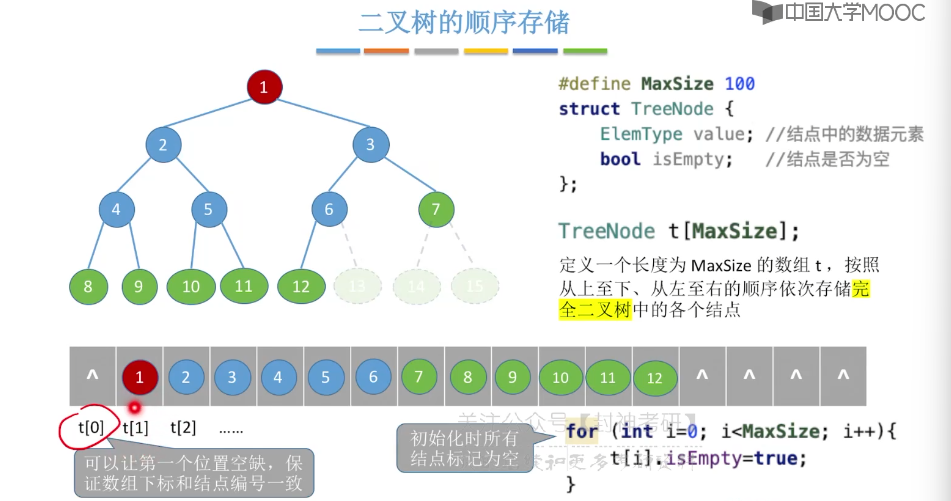
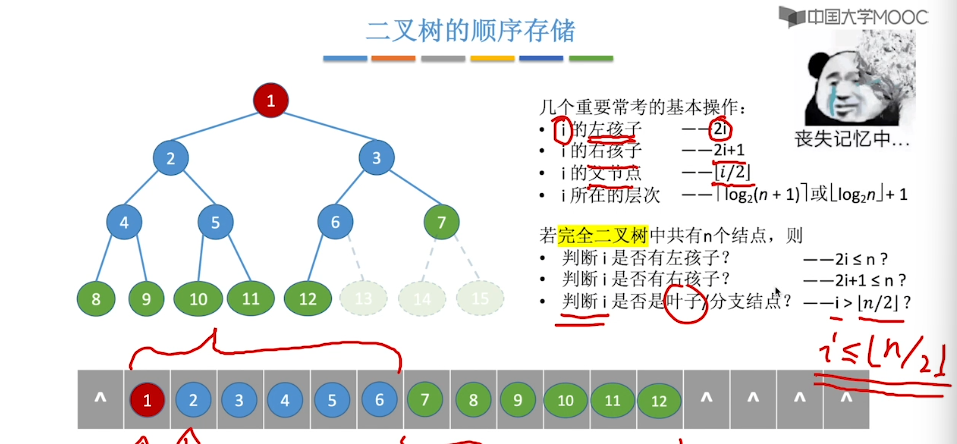
5.5、二叉树的存储结构
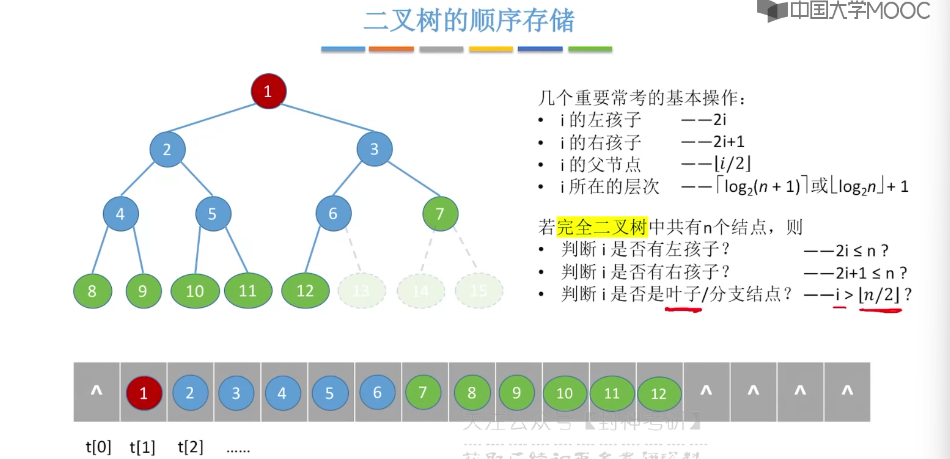
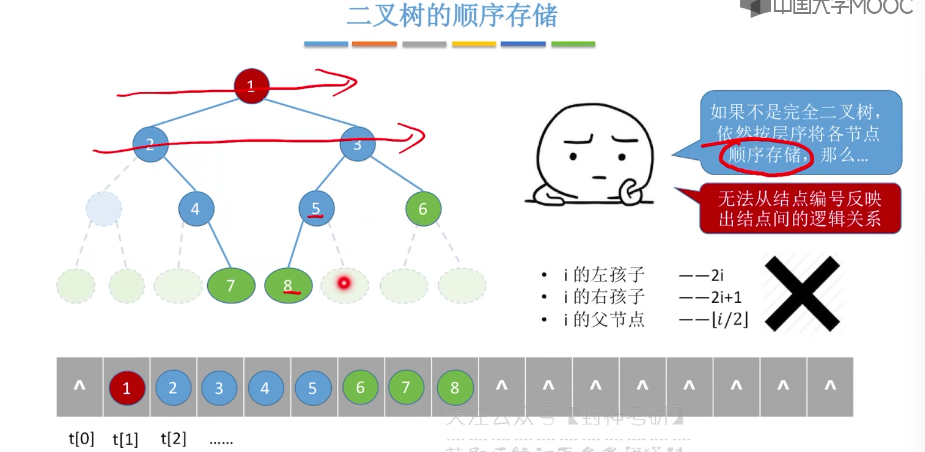
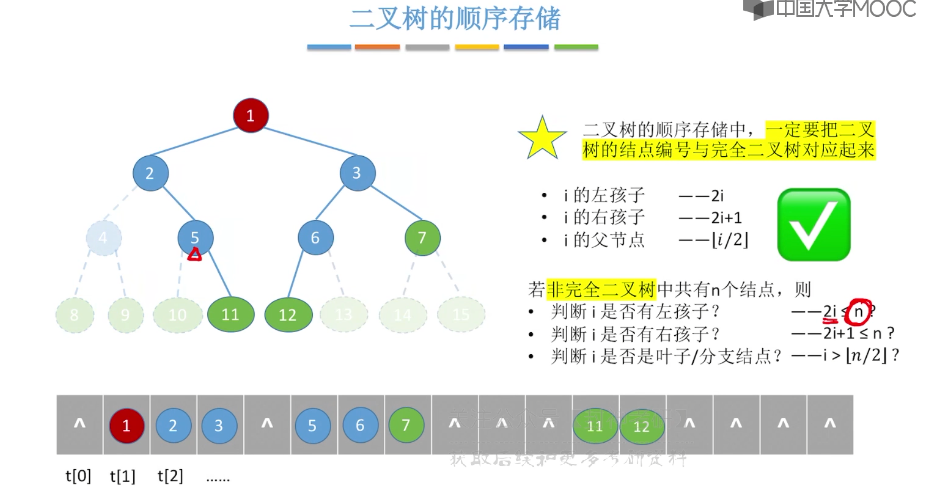
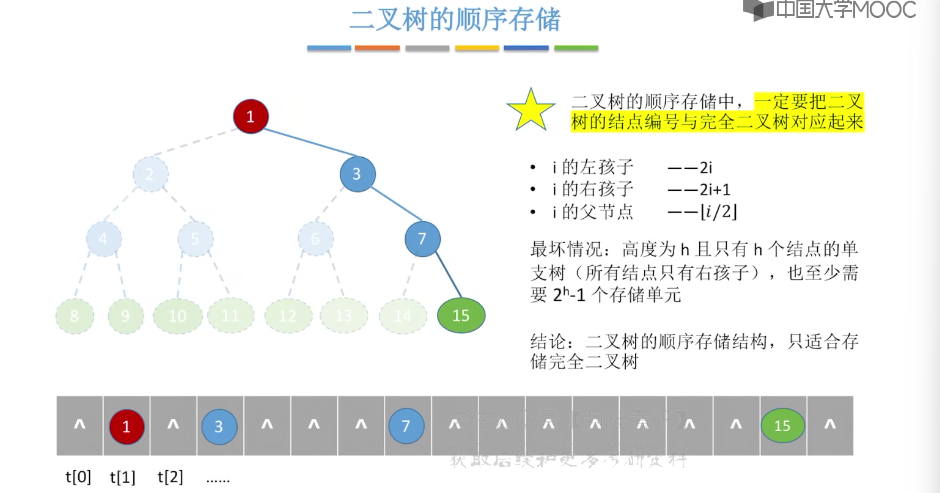
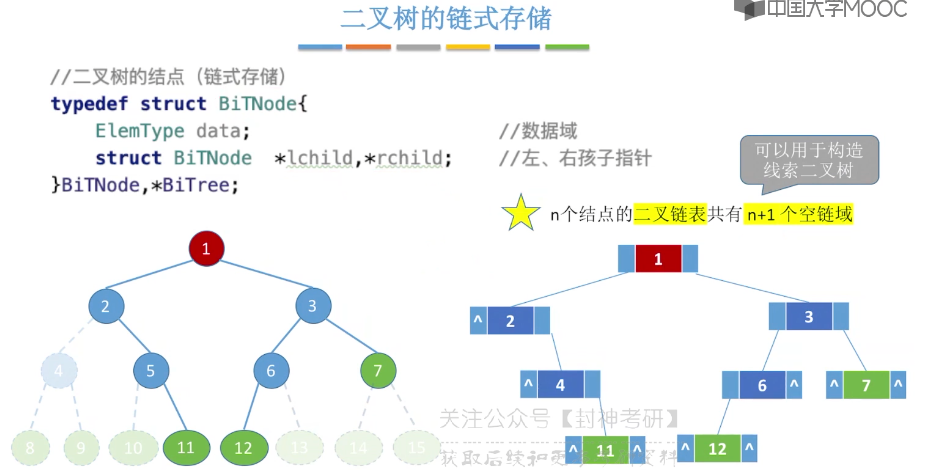
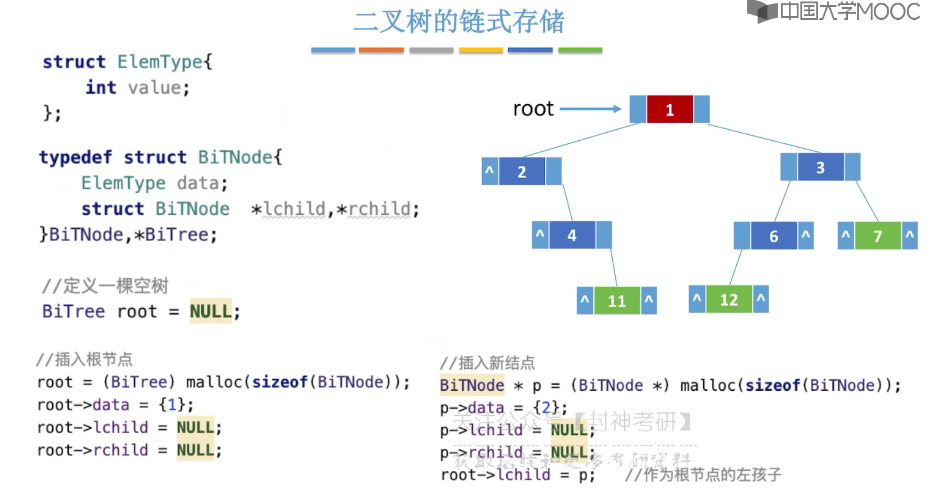
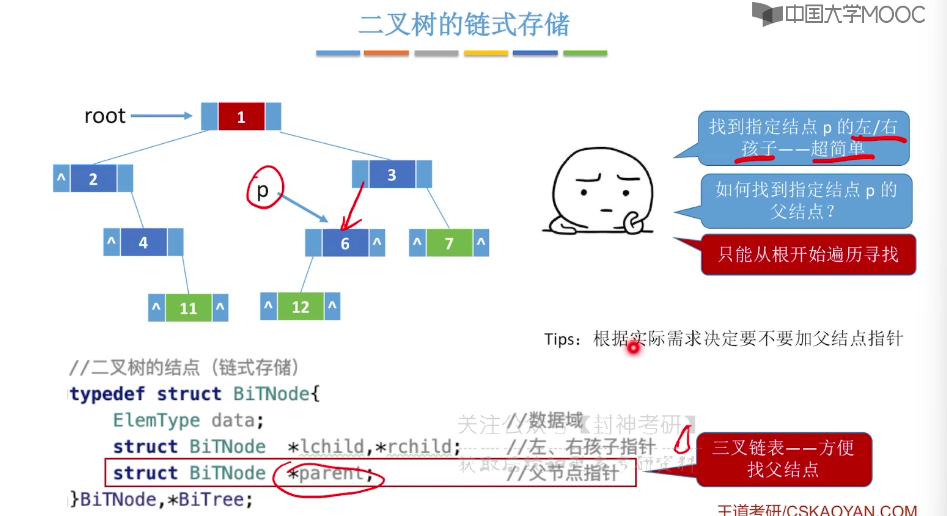
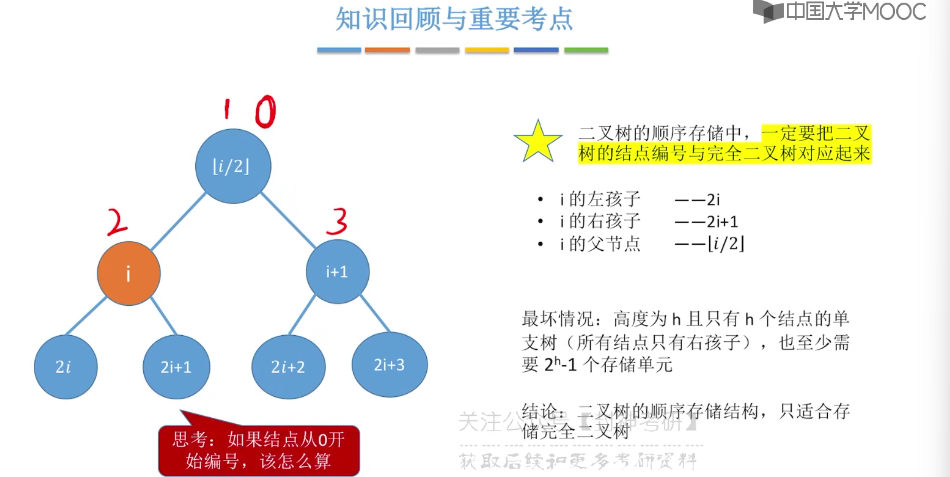
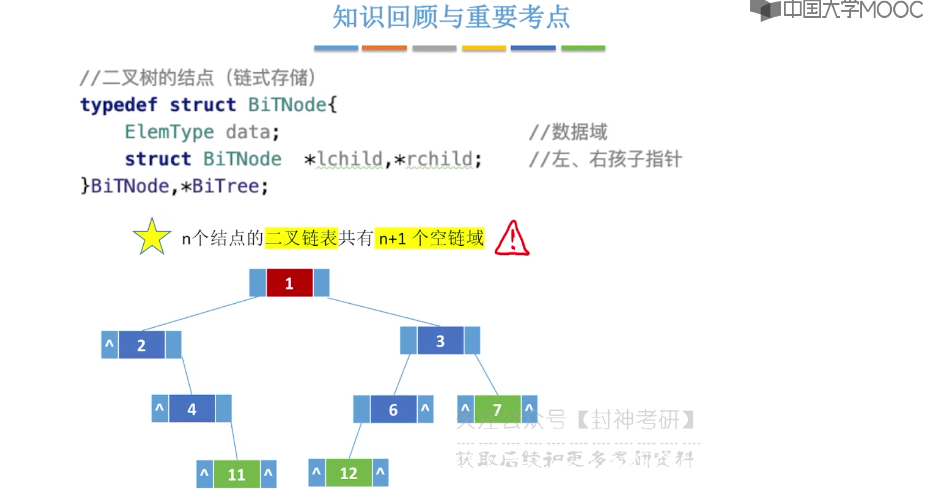
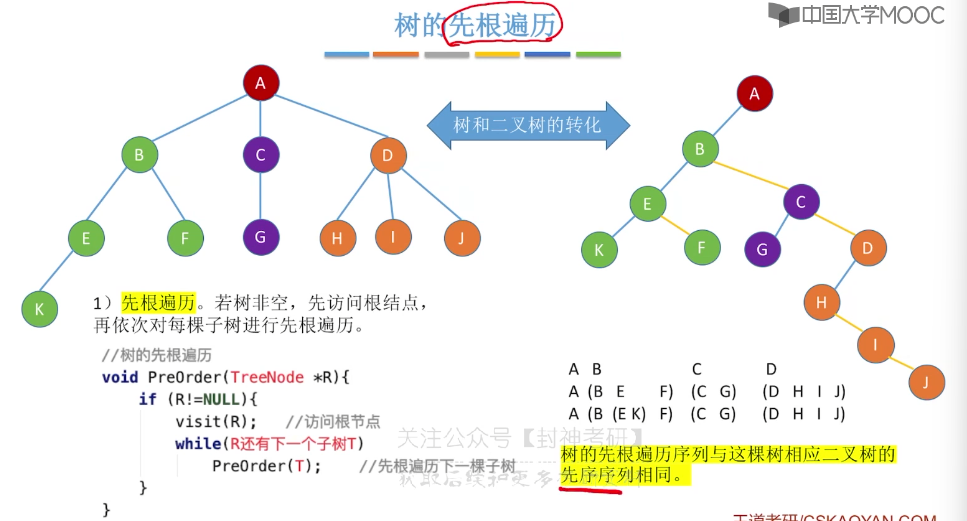
5.6、二叉树的先中后序遍历
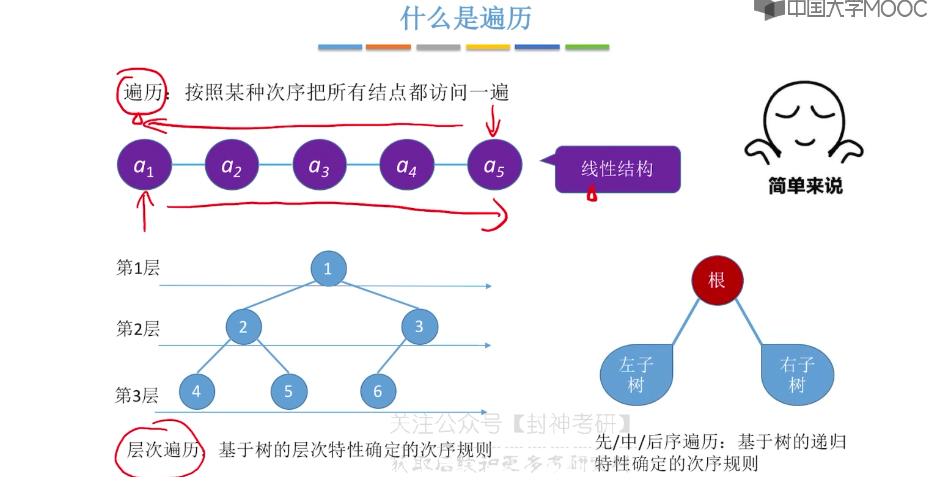
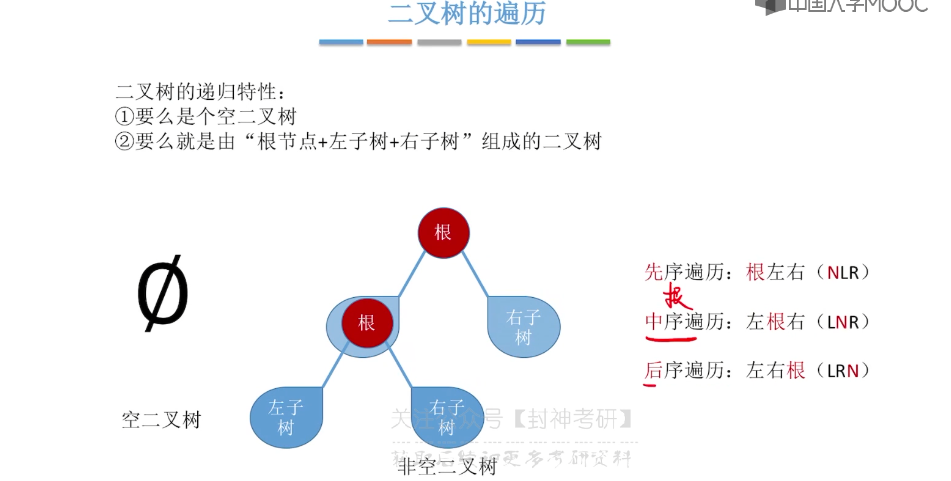
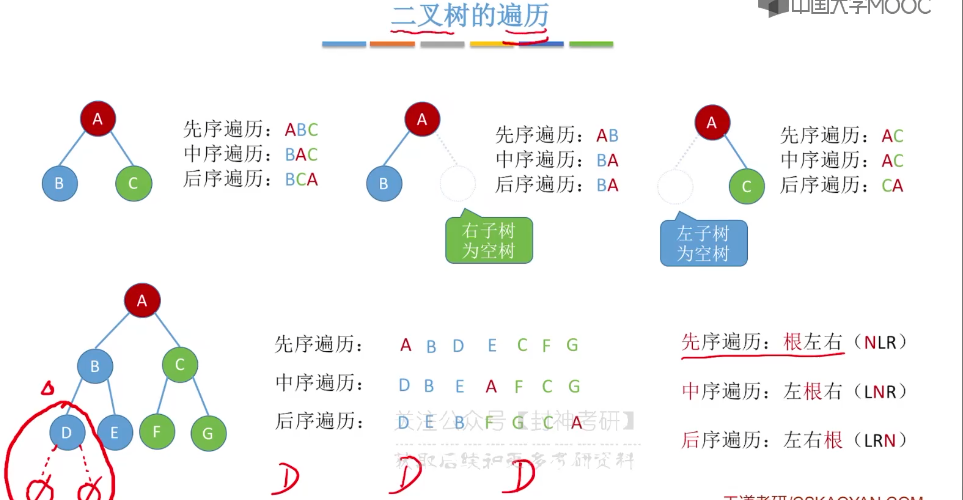
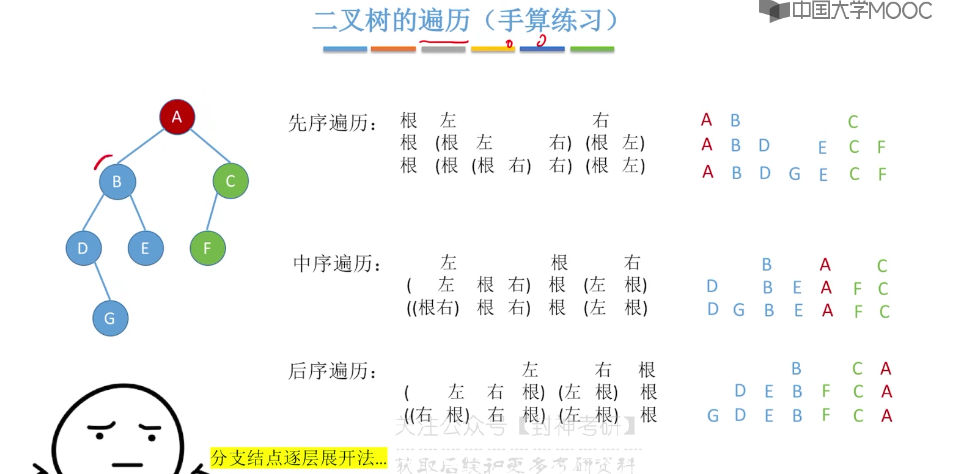
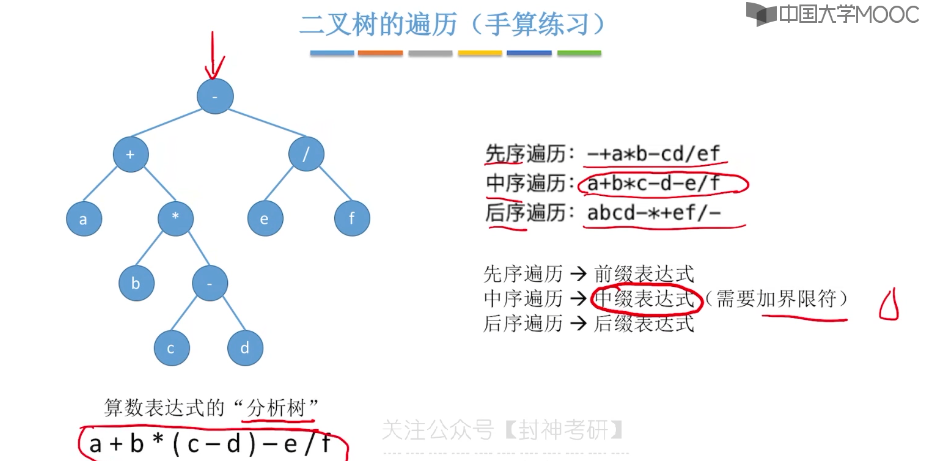
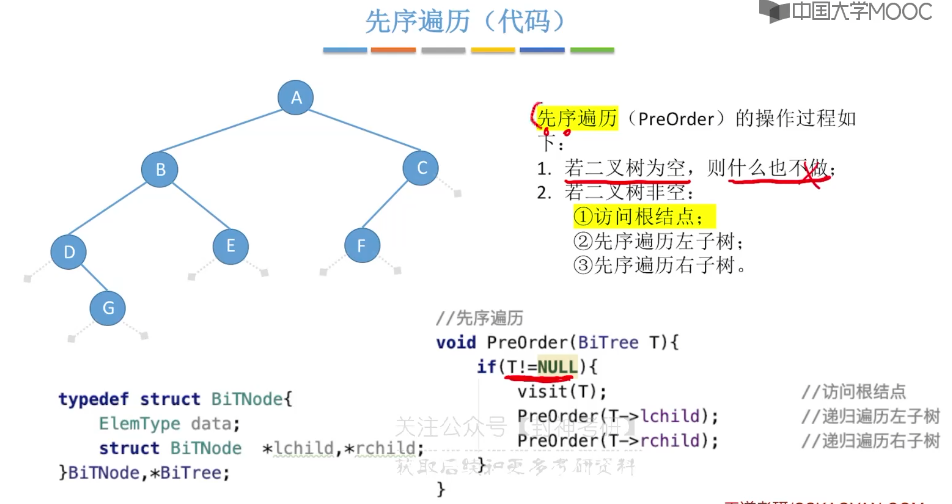
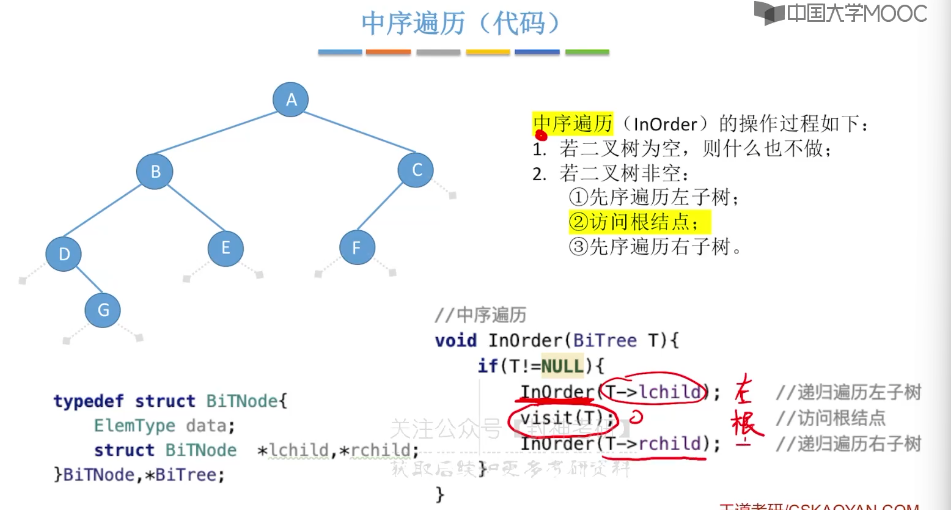
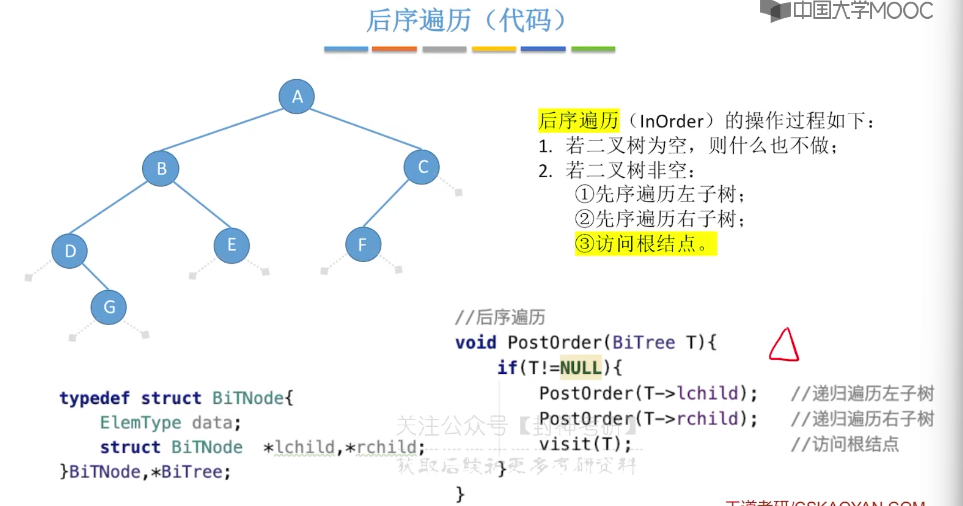
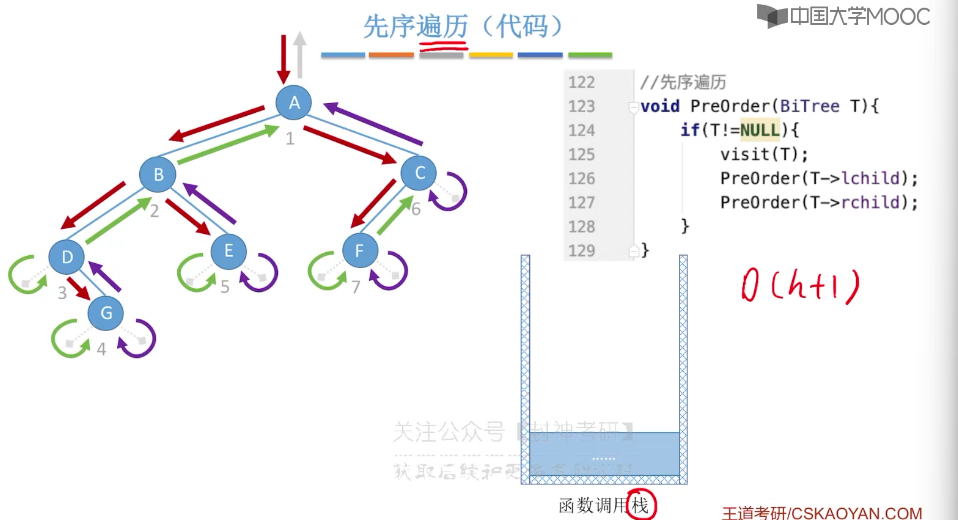
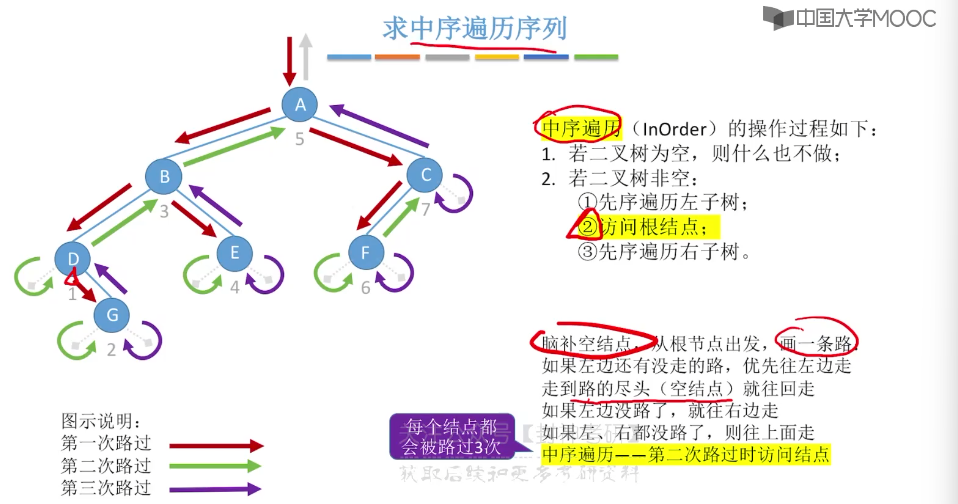
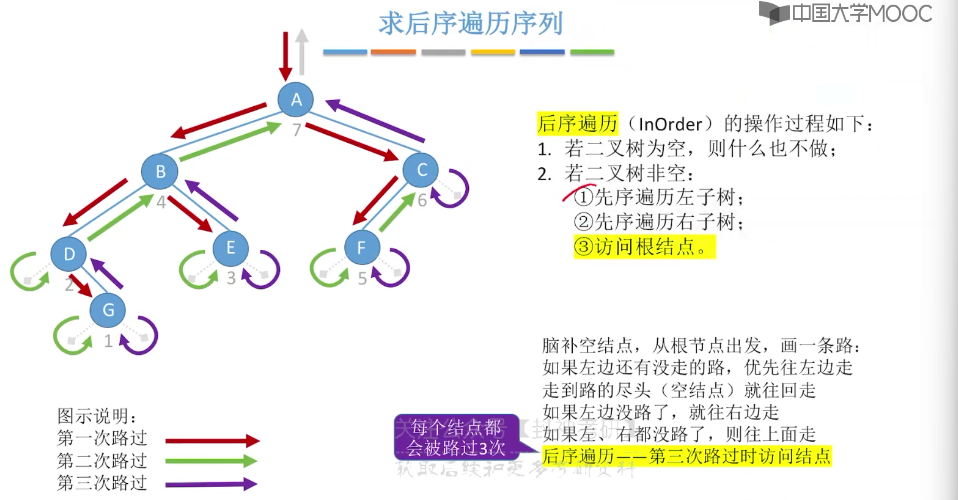
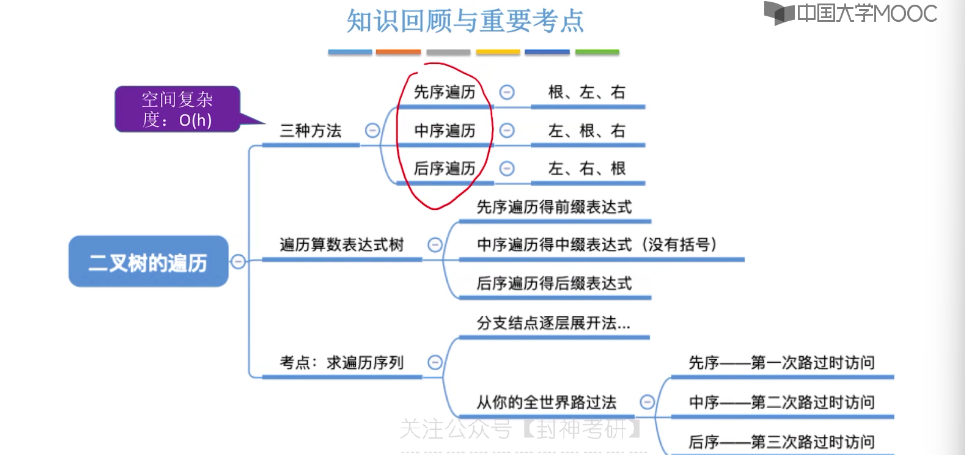
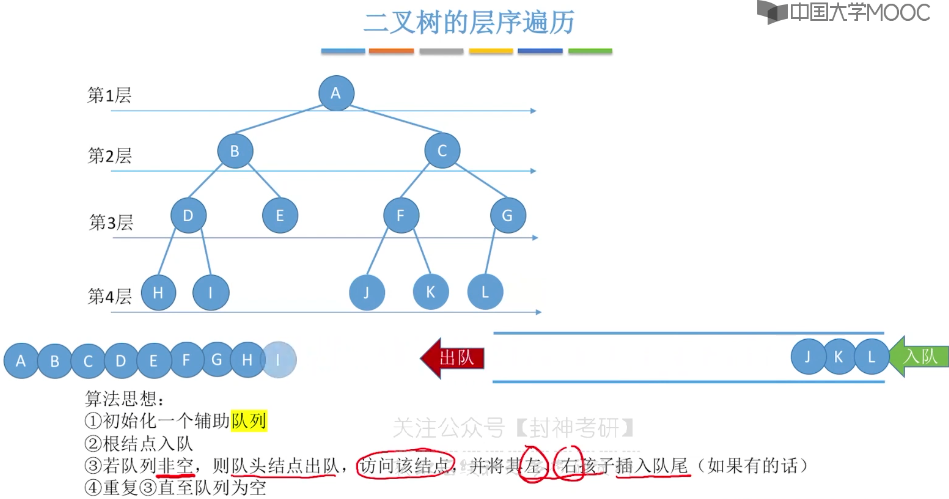
5.7、二叉树的层序遍历


#include<stdio.h>
#include<stdlib.h>
// 链队列
typedef struct LNode {
char data;
LNode* next;
}LNode;
typedef struct LinkQueue {
LNode* front, * rear;
}LinkQueue;
// 初始化链队列
bool initQueue(LinkQueue& queue) {
queue.front = (LNode*)malloc(sizeof(LNode));
queue.front->next = NULL;
queue.rear = queue.front;
return true;
}
// 入队
bool enQueue(LinkQueue& queue, char e) {
LNode* s = (LNode*)malloc(sizeof(LNode));
s->data = e;
// 插入
s->next = queue.rear->next;
queue.rear->next = s;
queue.rear = s;
return true;
}
// 判断是否队空
bool isEmptyQueue(LinkQueue& queue) {
return queue.front == queue.rear;
}
// 出队
bool deQueue(LinkQueue& queue, char& e) {
if (isEmptyQueue(queue)) return false;
LNode* s = queue.front->next;
e = s->data;
queue.front->next = s->next;
if (s == queue.rear) {
queue.rear = queue.front;
}
free(s);
return true;
}
// 销毁
bool releaseQueue(LinkQueue& queue) {
LNode* ptr;
while (queue.front != NULL) {
ptr = queue.front;
queue.front = ptr->next;
free(ptr);
}
return true;
}
// 打印队列
void printQueue(LinkQueue& queue) {
printf("当前队列元素为:队头 ");
LNode* ptr = queue.front->next;
while (ptr != NULL) {
printf(" <%c", ptr->data);
ptr = ptr->next;
}
}
// 二叉树的结点(链式存储)
typedef struct BiTNode {
char data;
BiTNode* lChild, * rChild;
}BiTNode, * BiTree;
// 二叉树的初始化
bool initTree(BiTree& tree) {
tree = NULL;
return true;
}
// 访问节点
void visit(BiTNode node) {
printf("%c", node.data);
}
// 先序遍历
void preOrder(BiTree& tree) {
if (tree == NULL) return;
visit(*tree);
preOrder(tree->lChild);
preOrder(tree->rChild);
}
// 中序遍历
void inOrder(BiTree& tree) {
if (tree == NULL) return;
inOrder(tree->lChild);
visit(*tree);
inOrder(tree->rChild);
}
// 后序遍历
void postOrder(BiTree& tree) {
if (tree == NULL) return;
postOrder(tree->lChild);
postOrder(tree->rChild);
visit(*tree);
}
// 求树的高度
int treeDepth(BiTree& tree) {
if (tree == NULL) return 0;
int lDepth = treeDepth(tree->lChild);
int rDepth = treeDepth(tree->rChild);
return lDepth > rDepth ? lDepth + 1 : rDepth + 1;
}
int main() {
LinkQueue queue; initQueue(queue);
enQueue(queue, 'a');
enQueue(queue, 'b');
enQueue(queue, 'c');
printQueue(queue);
//BiTree tree; initTree(tree);
releaseQueue(queue);
}5.8、由遍历序列构造二叉树
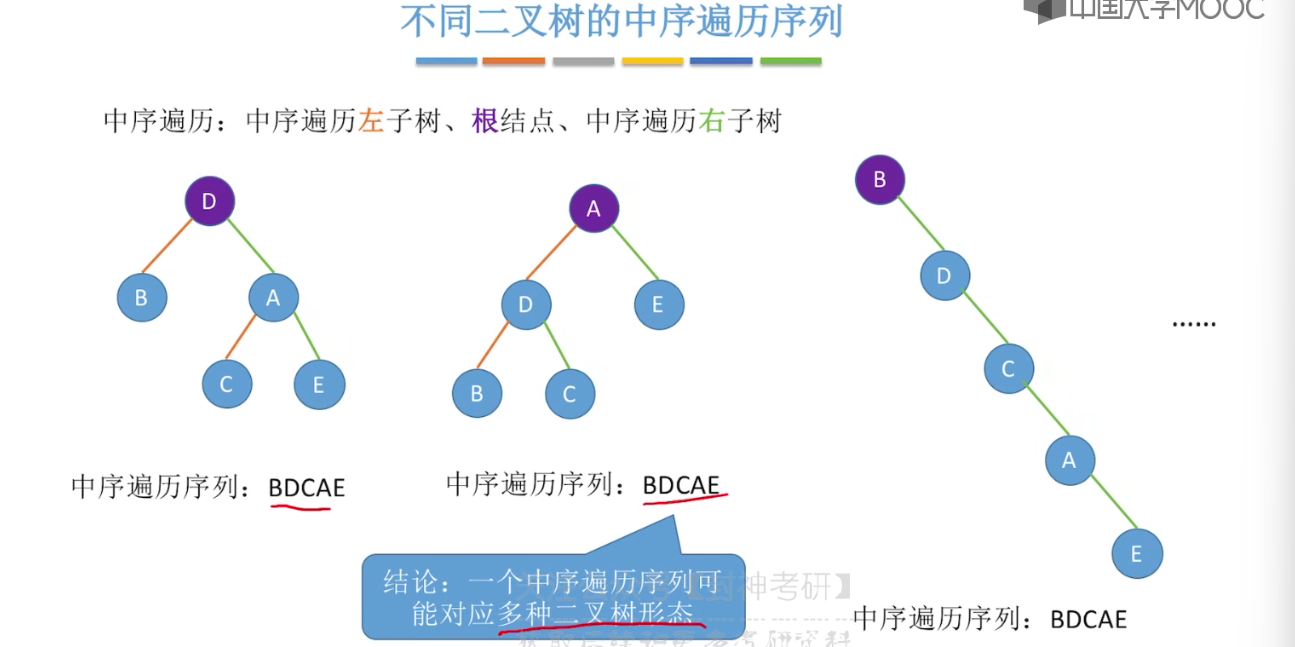
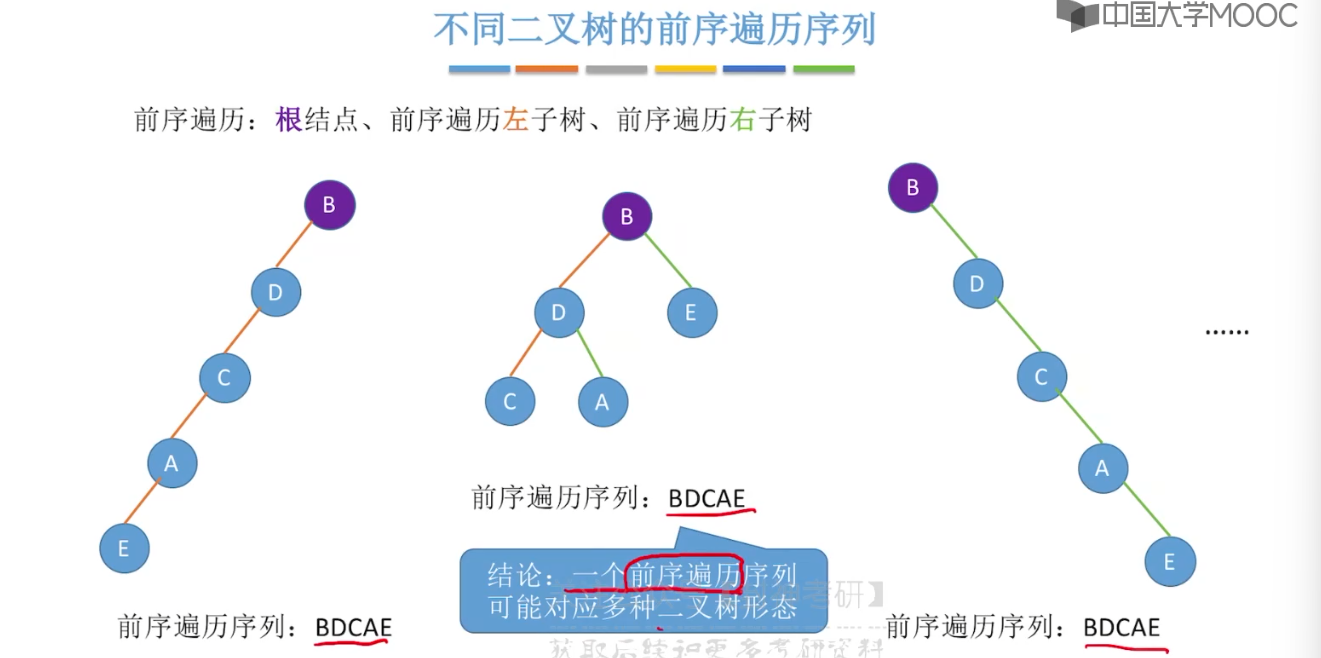

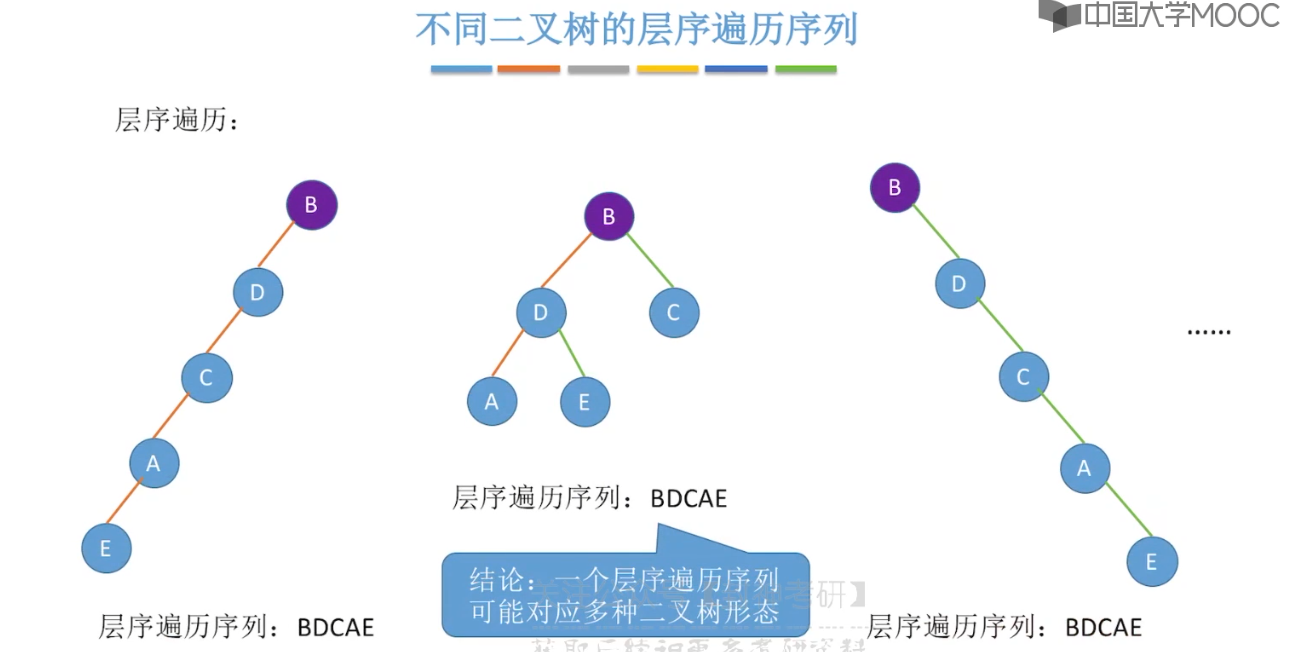

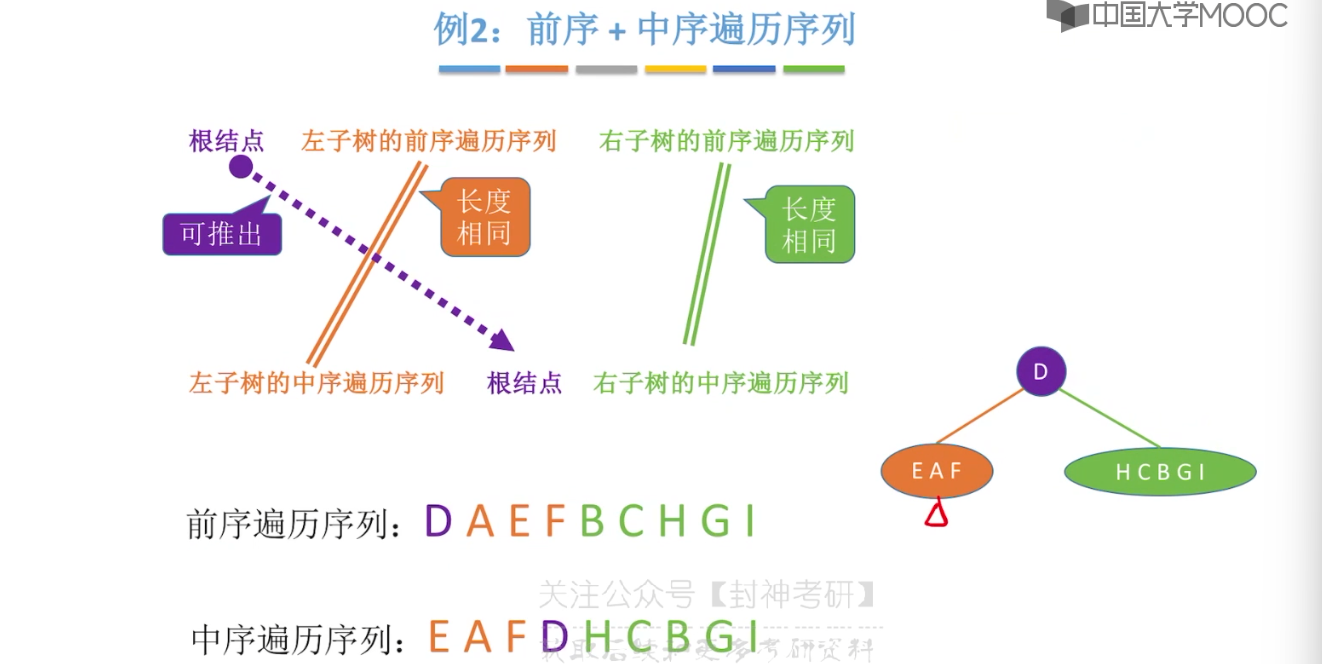
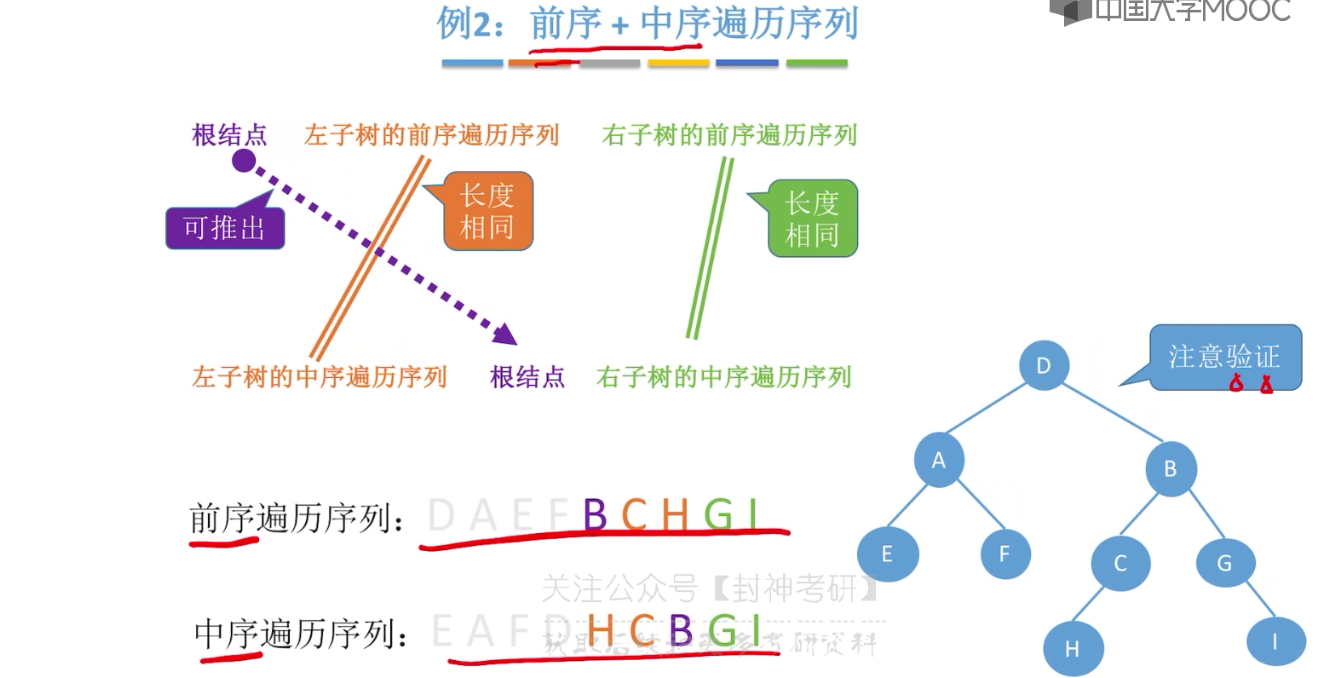
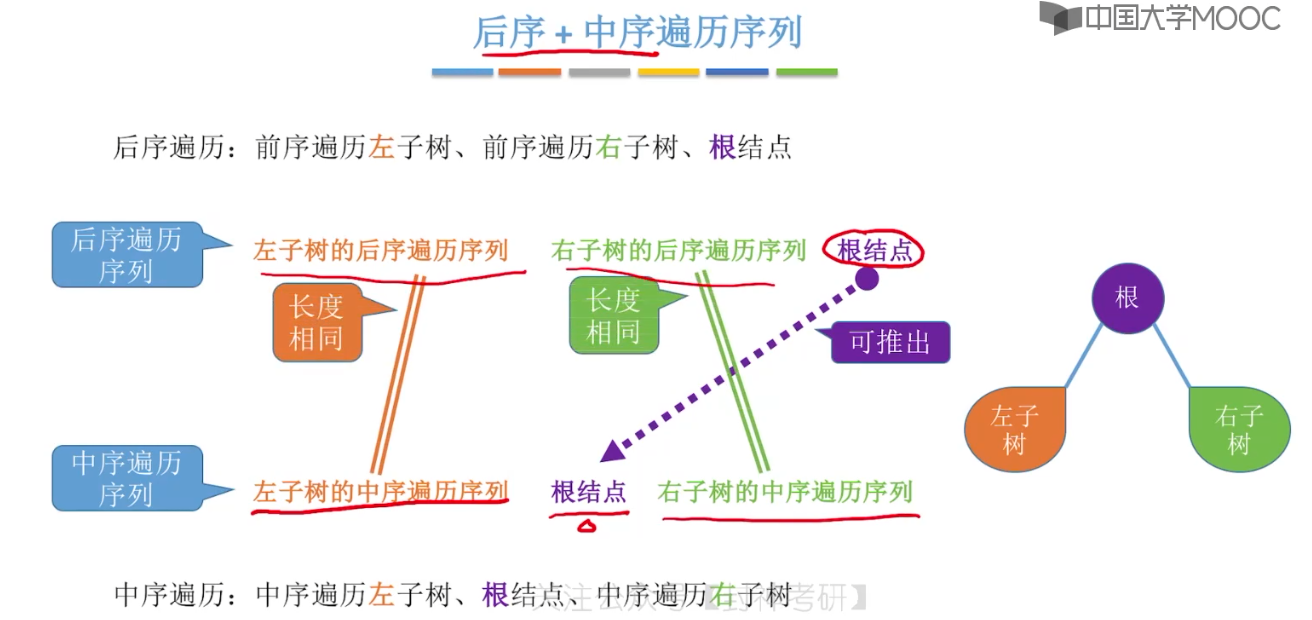
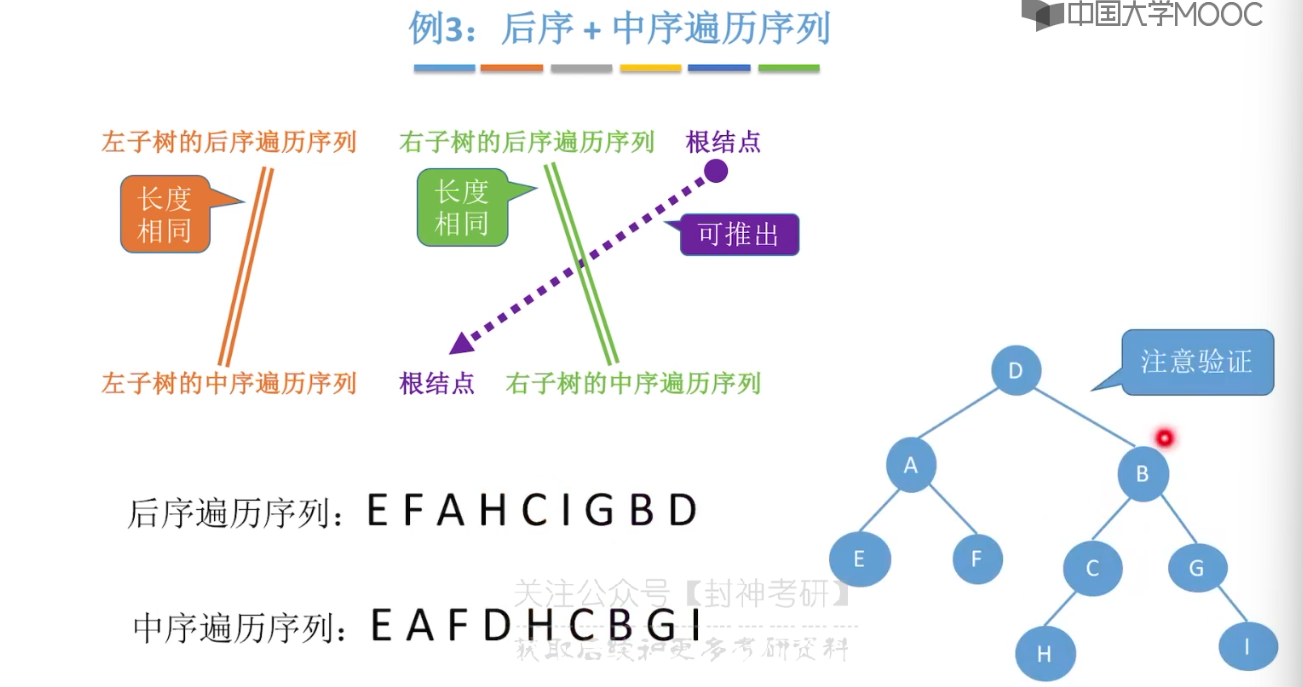
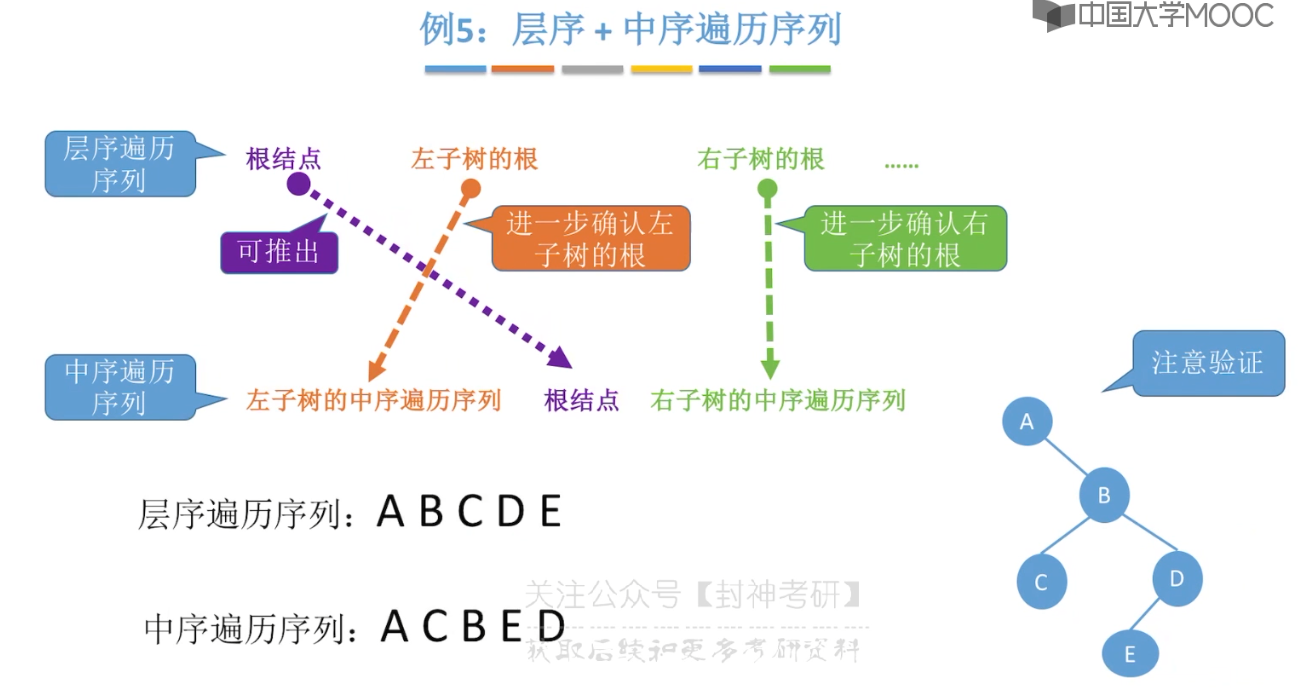
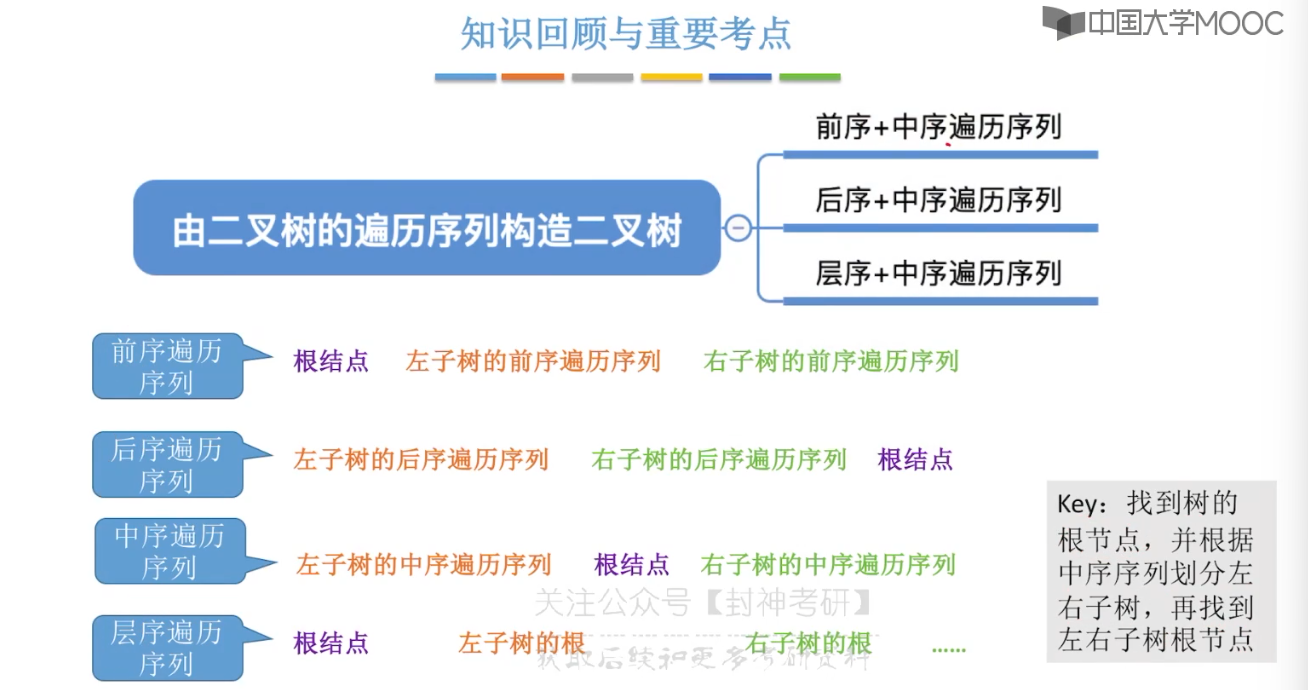
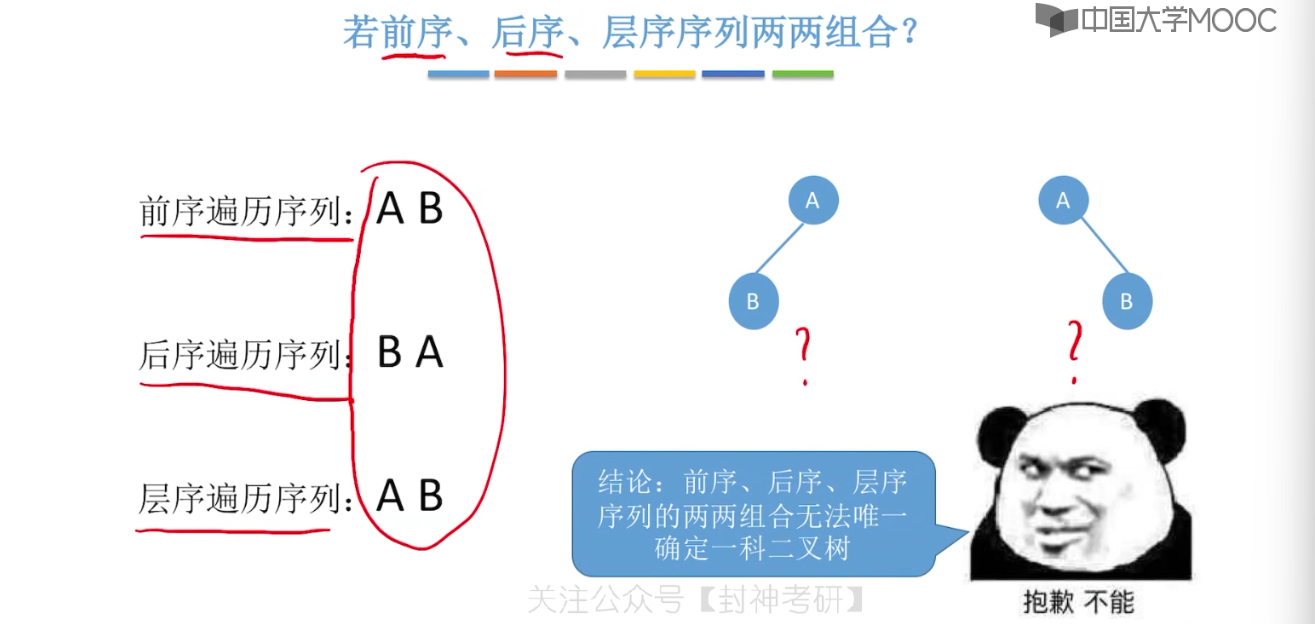
5.9、线索二叉树的概念
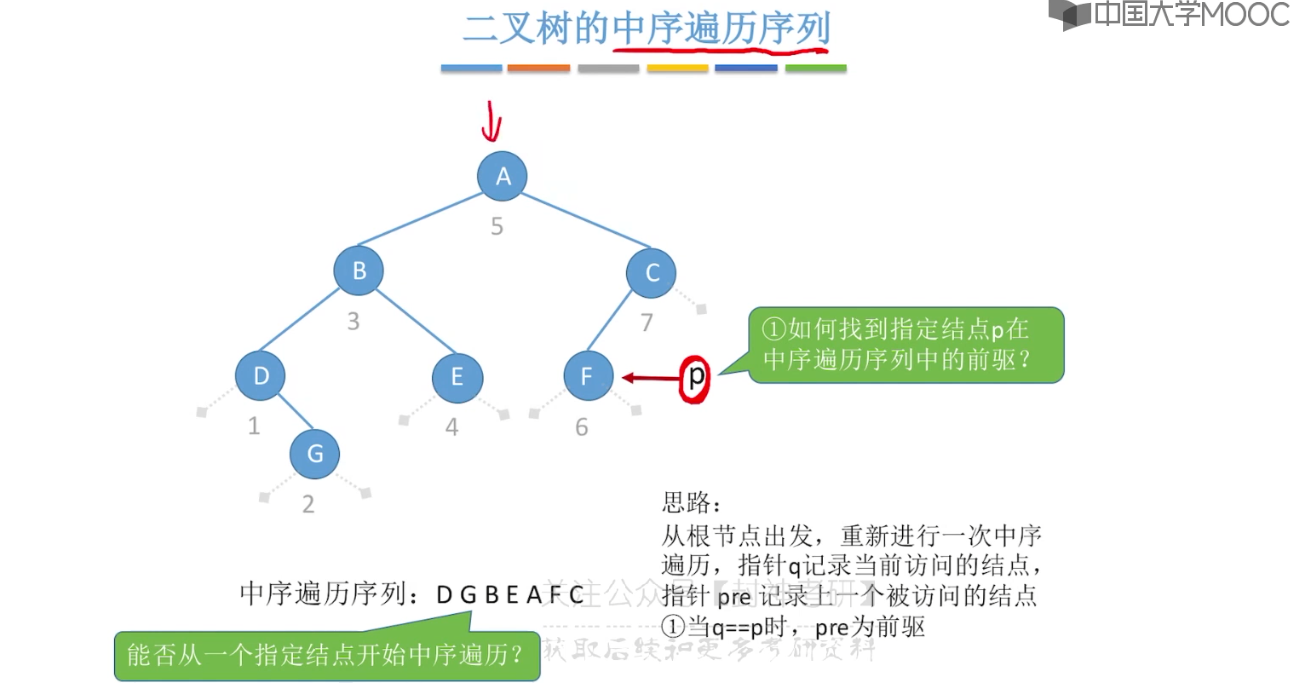
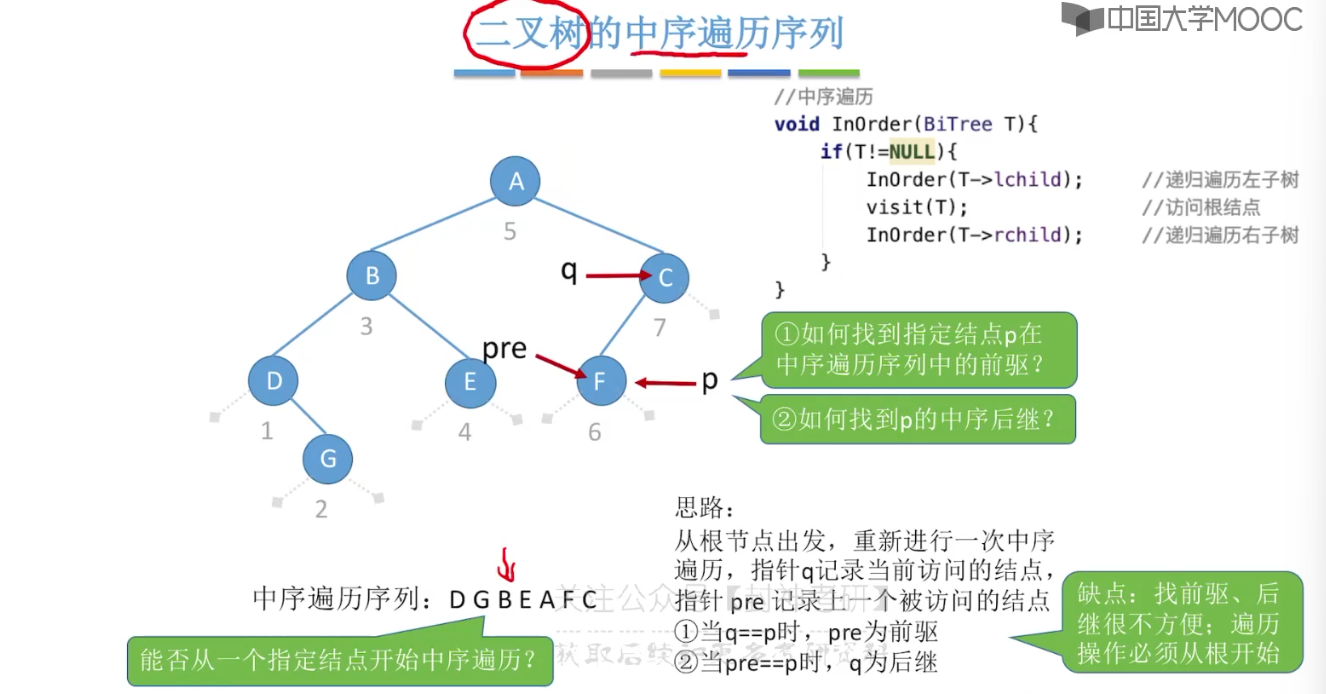
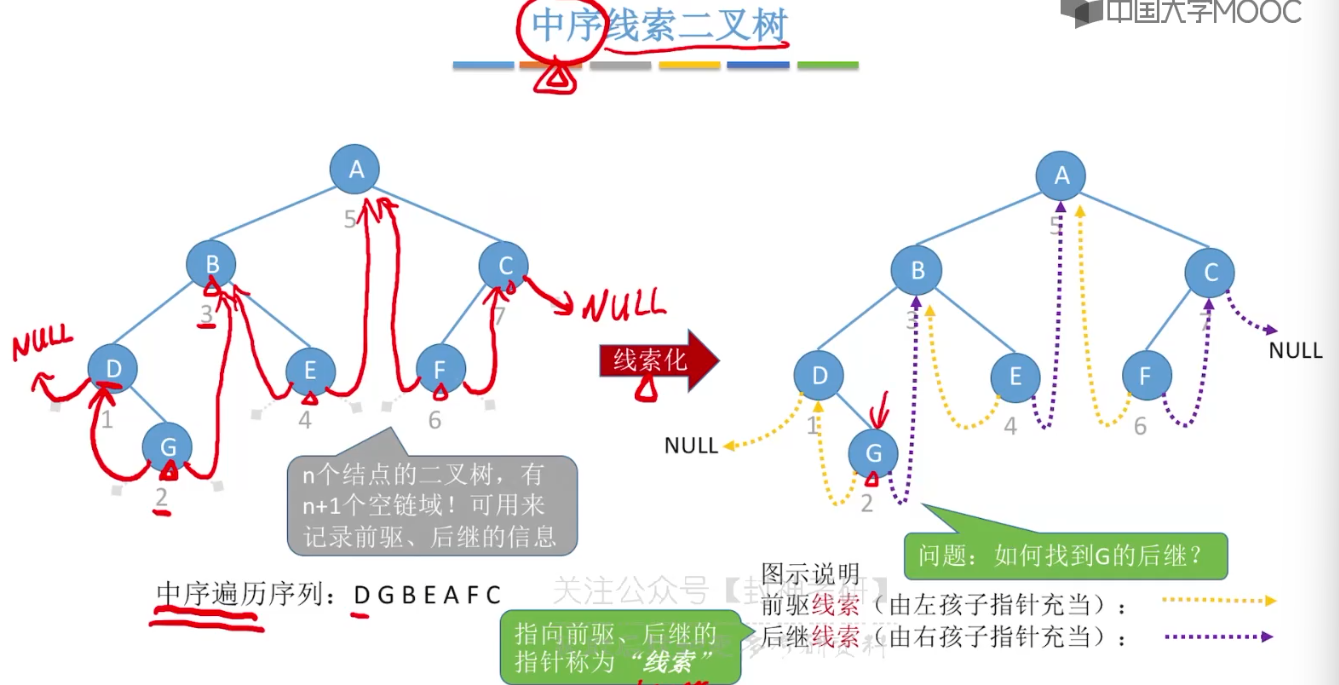
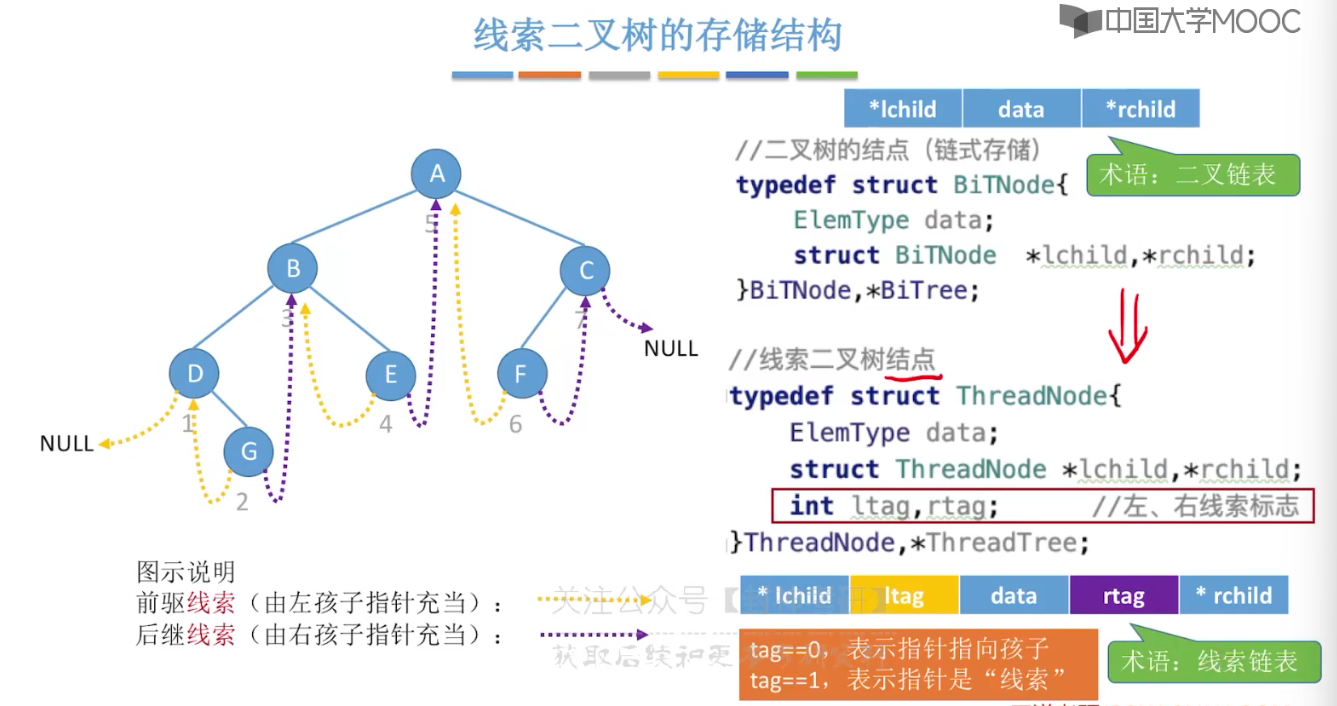
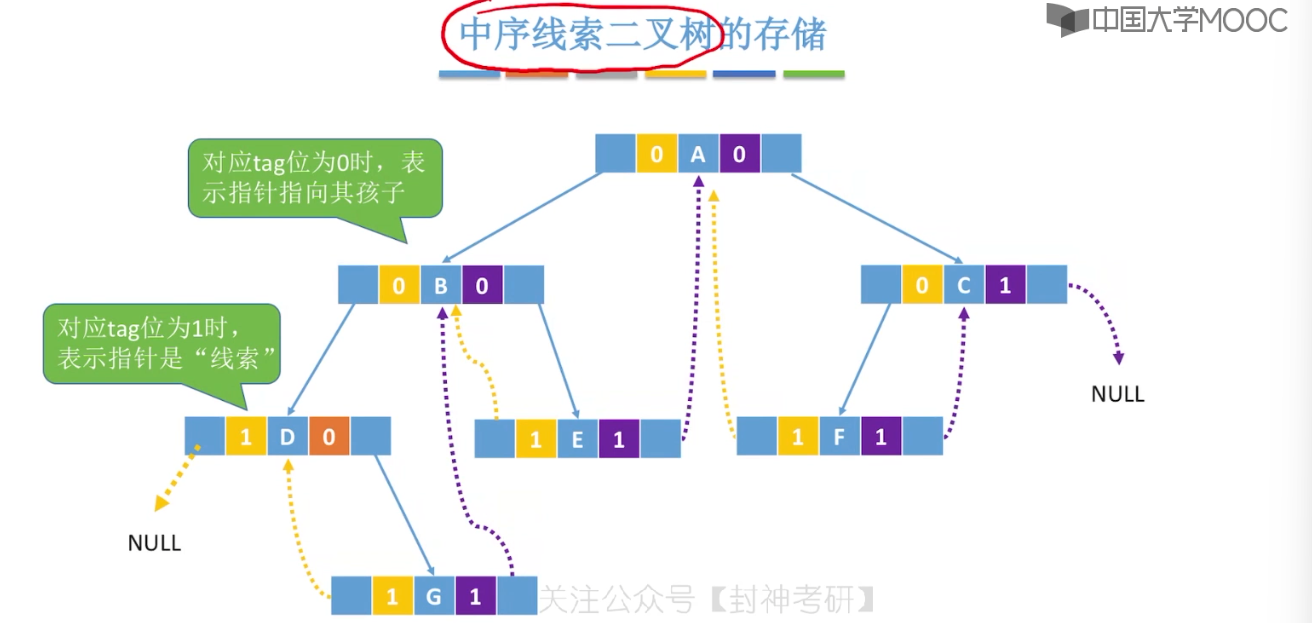
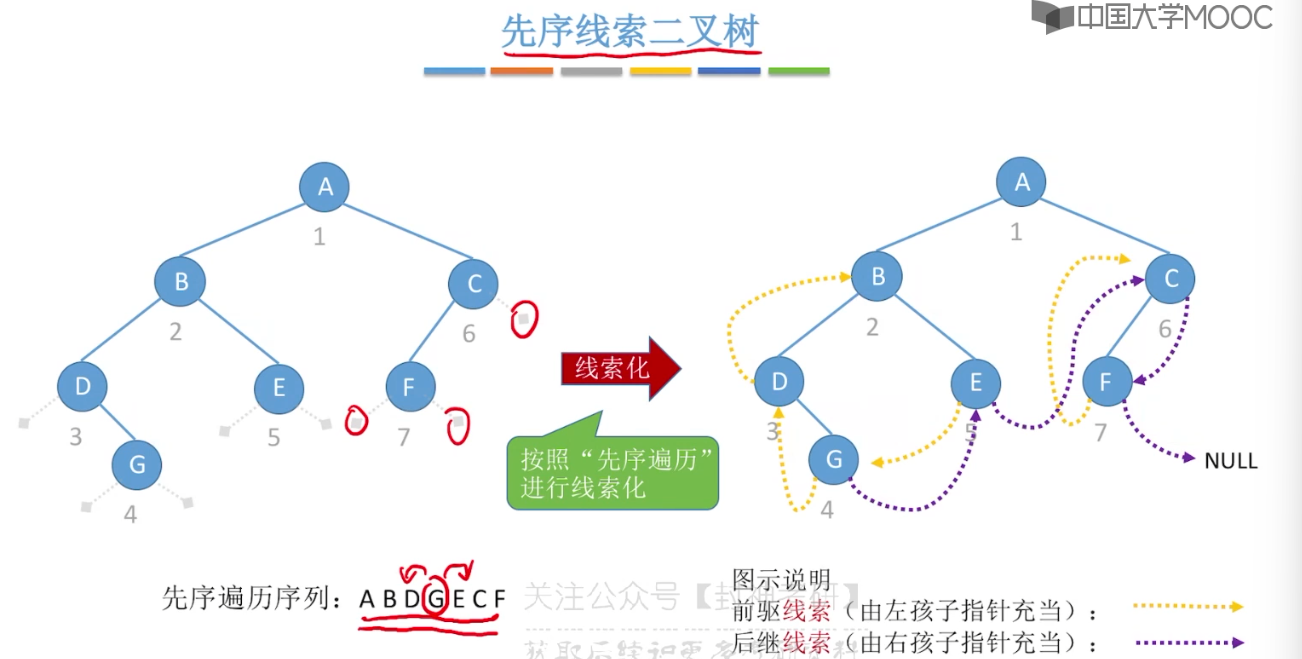
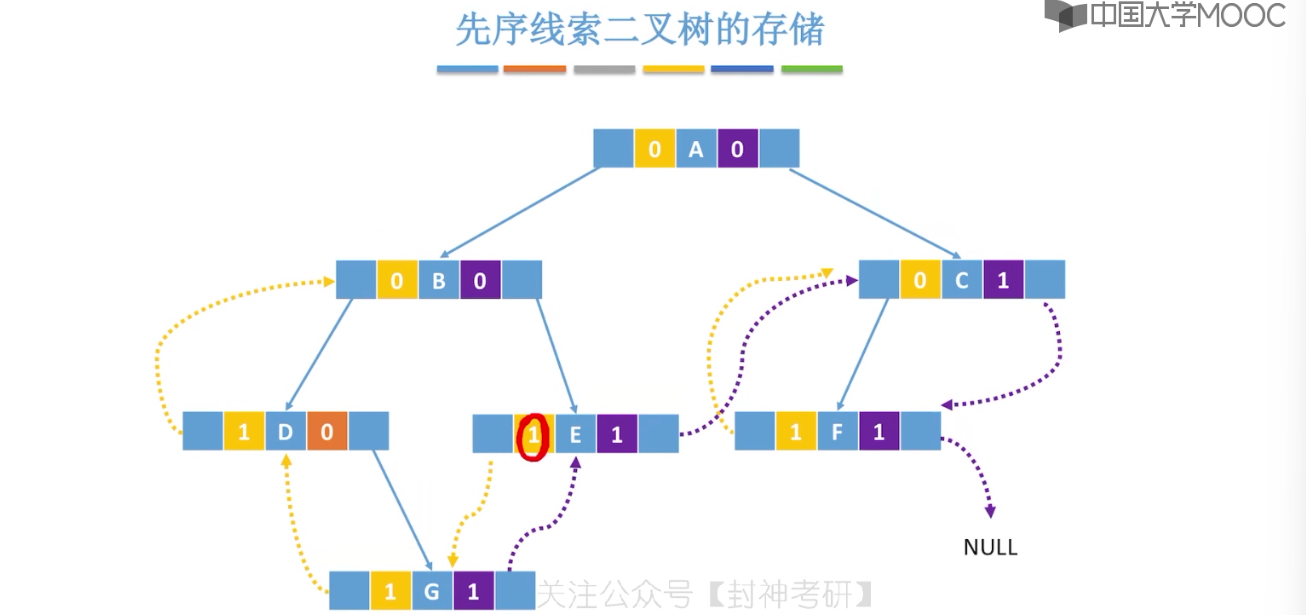
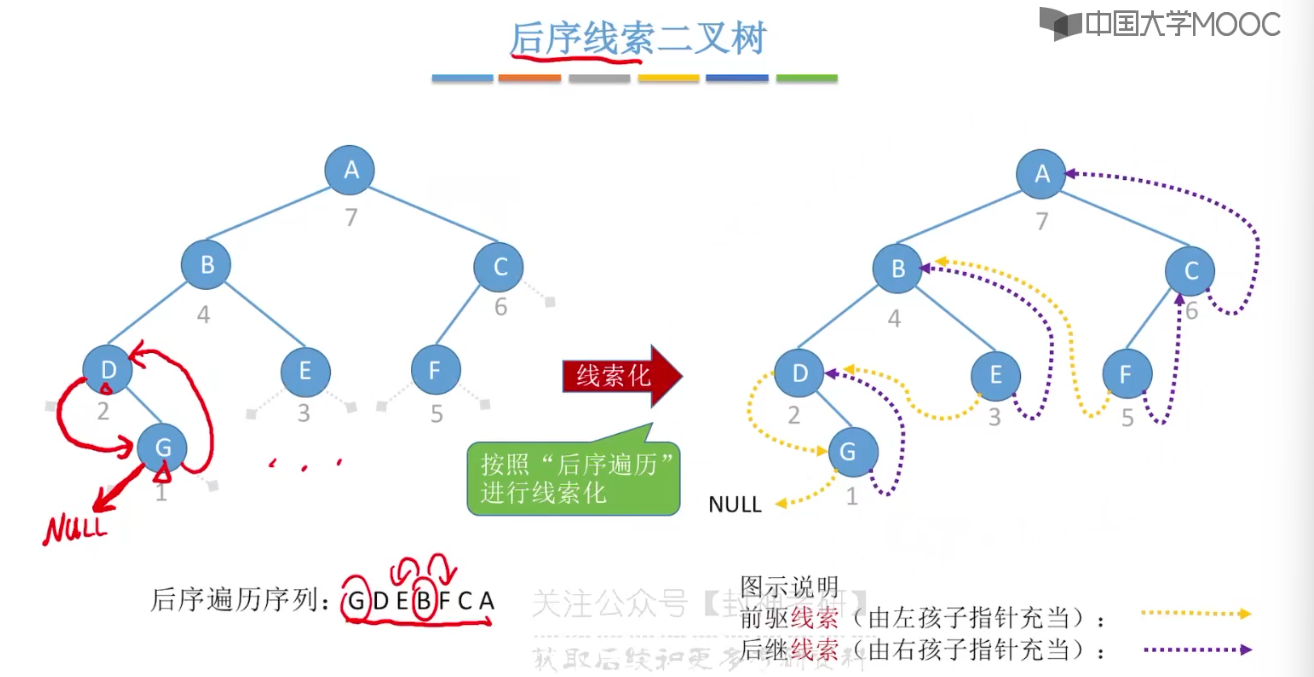
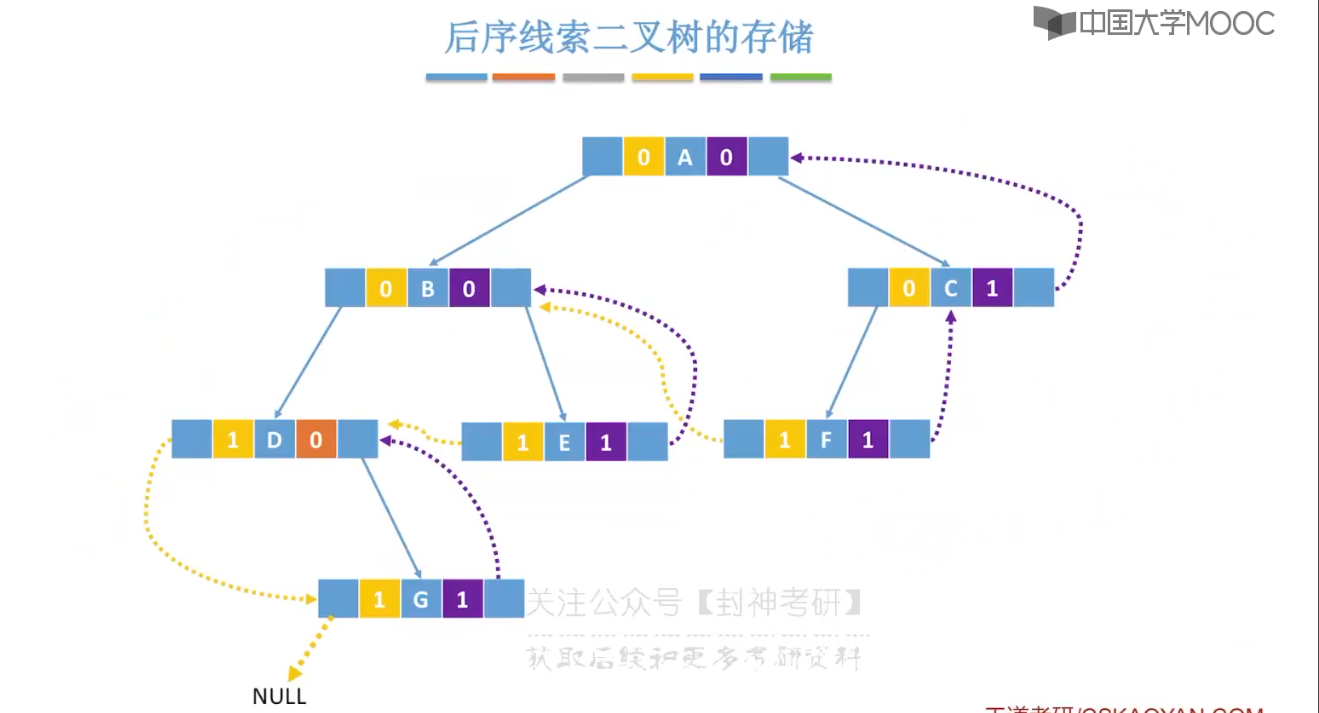
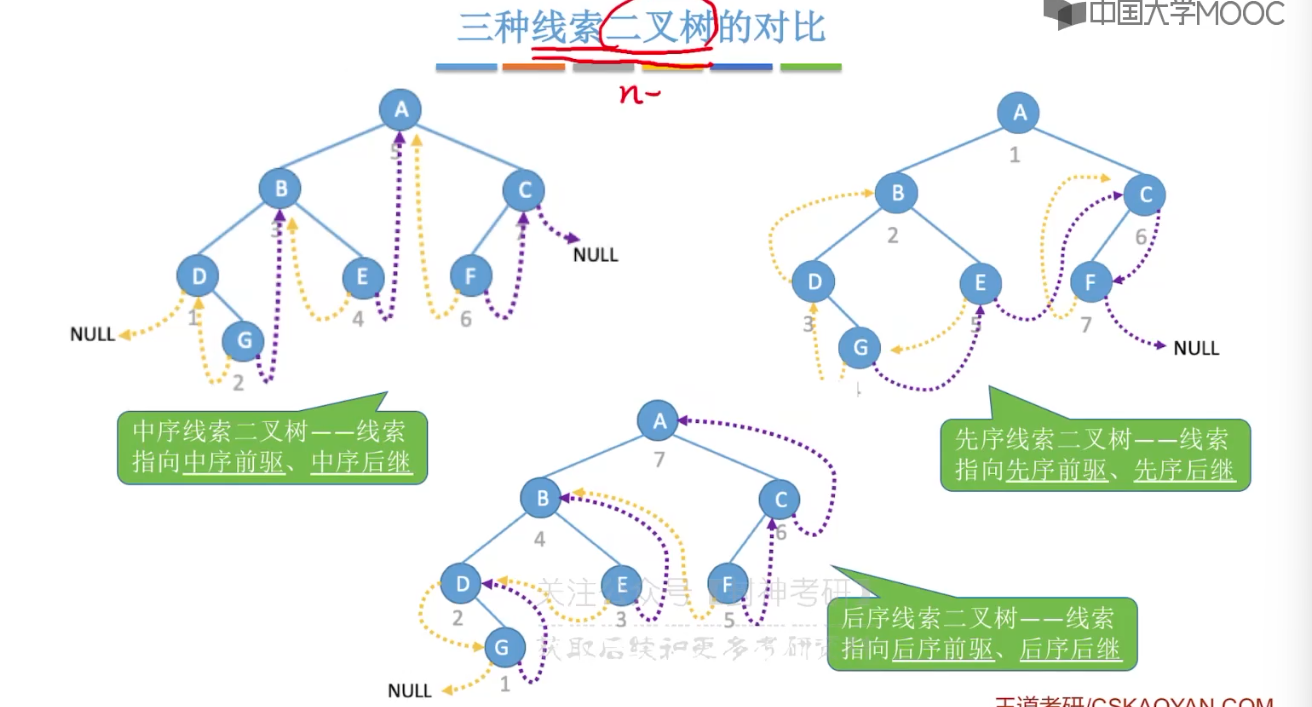
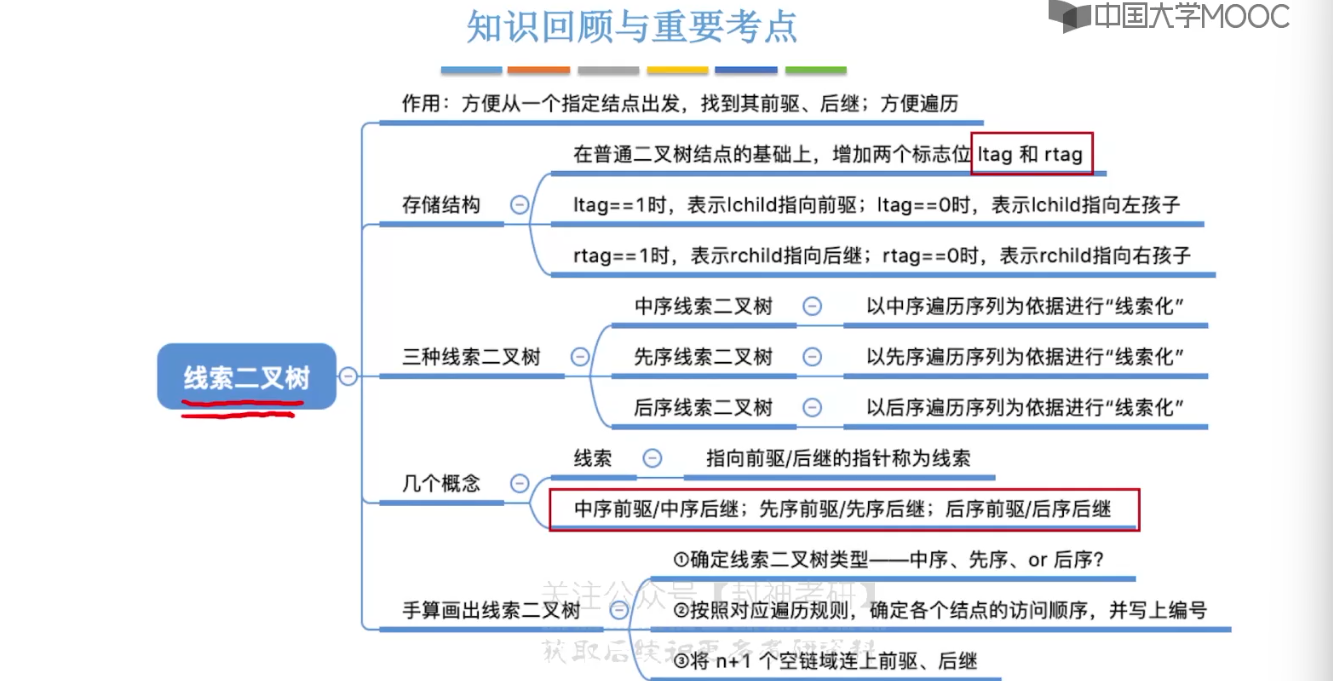
5.10、二叉树的线索化

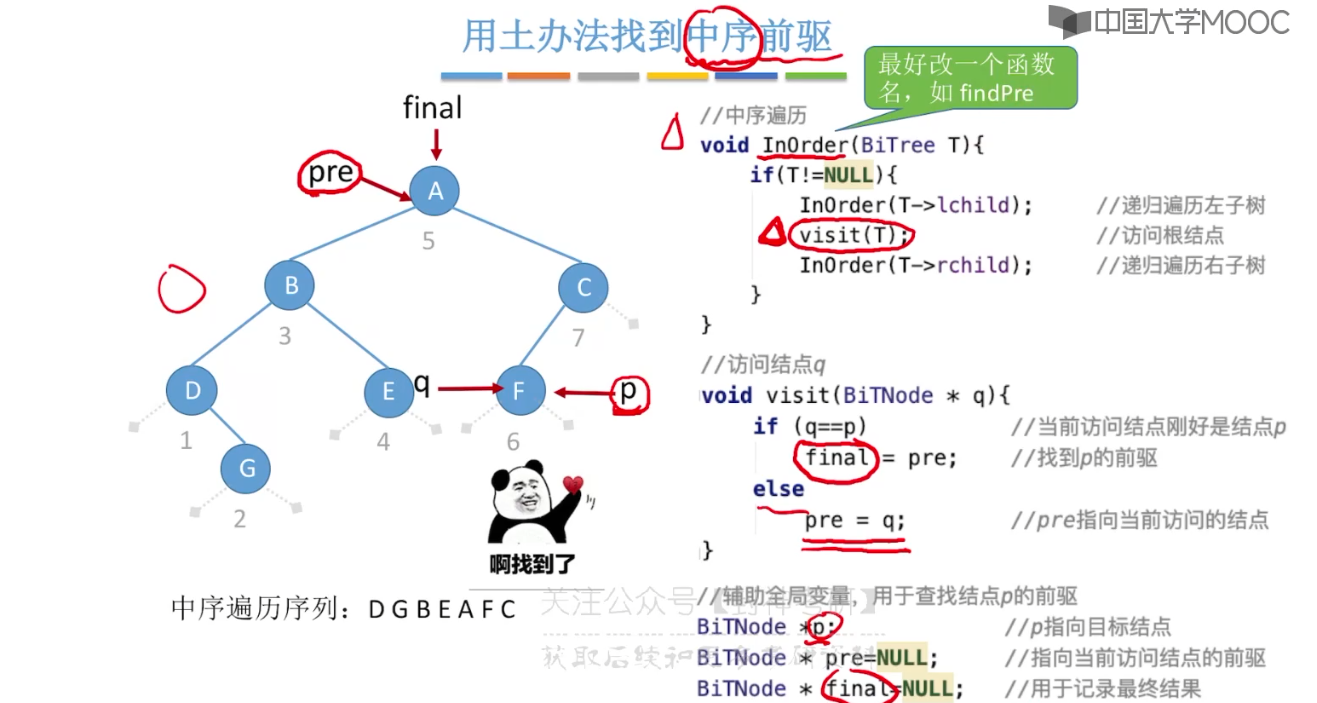
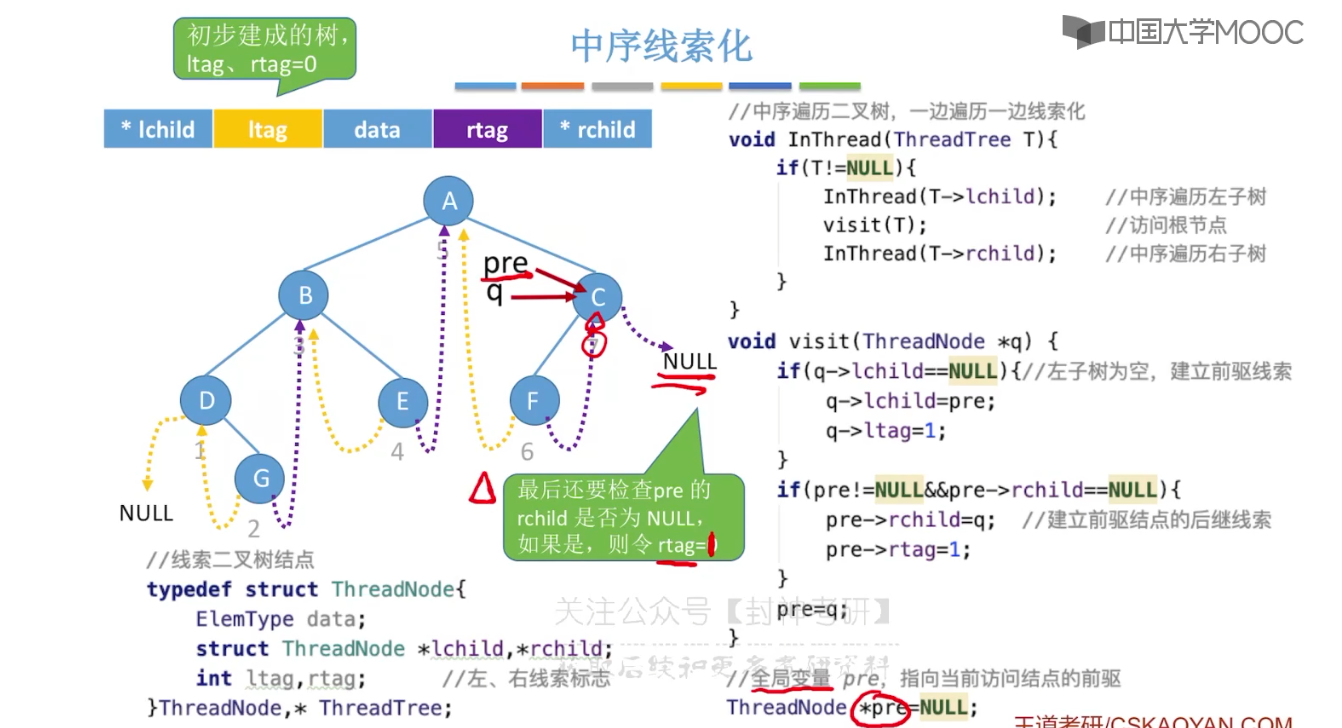

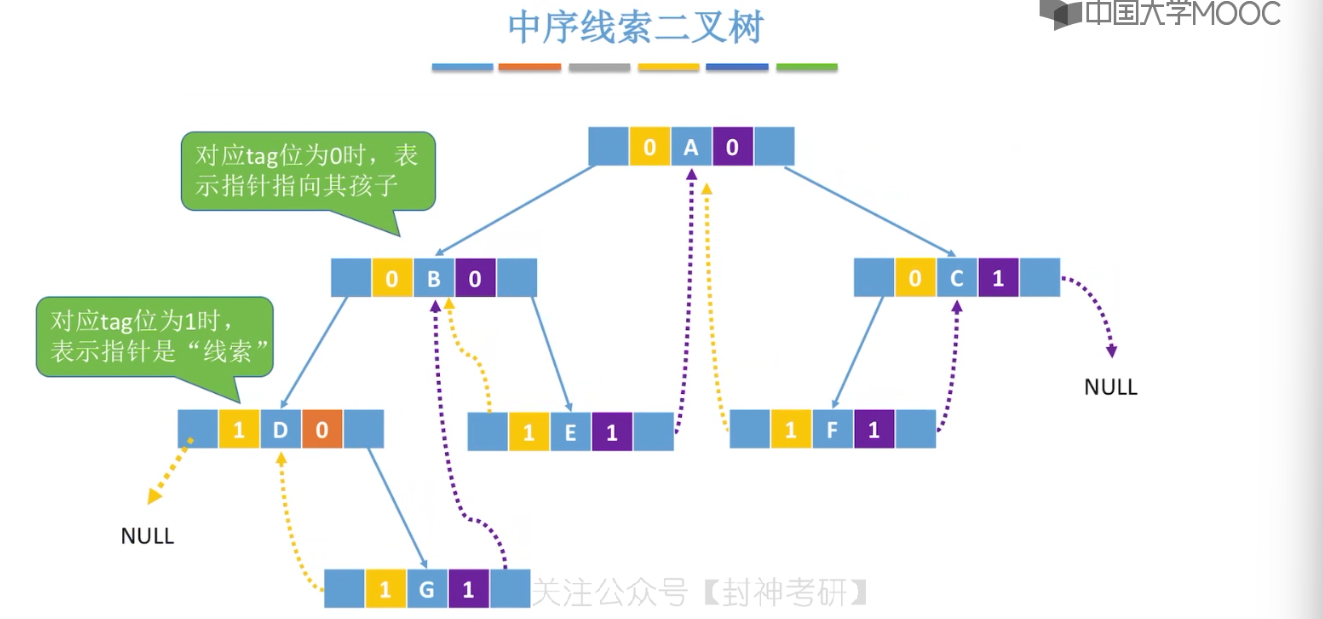


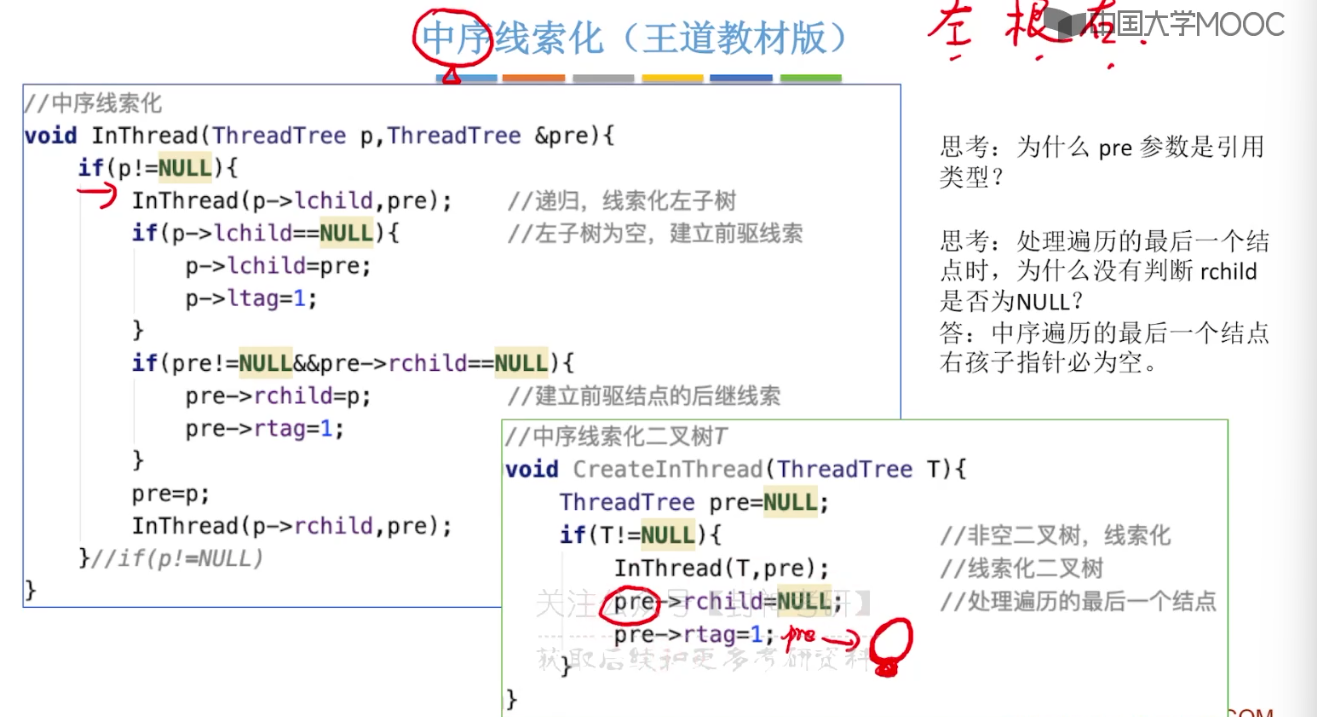
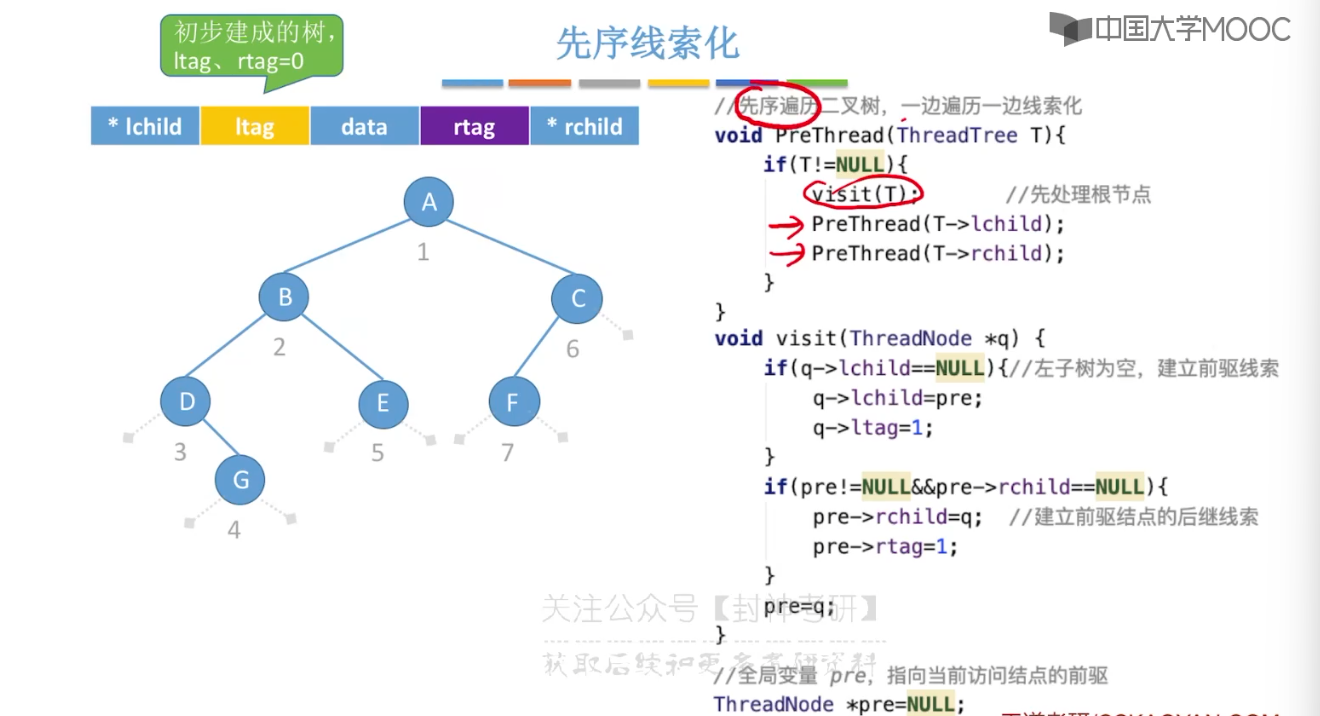
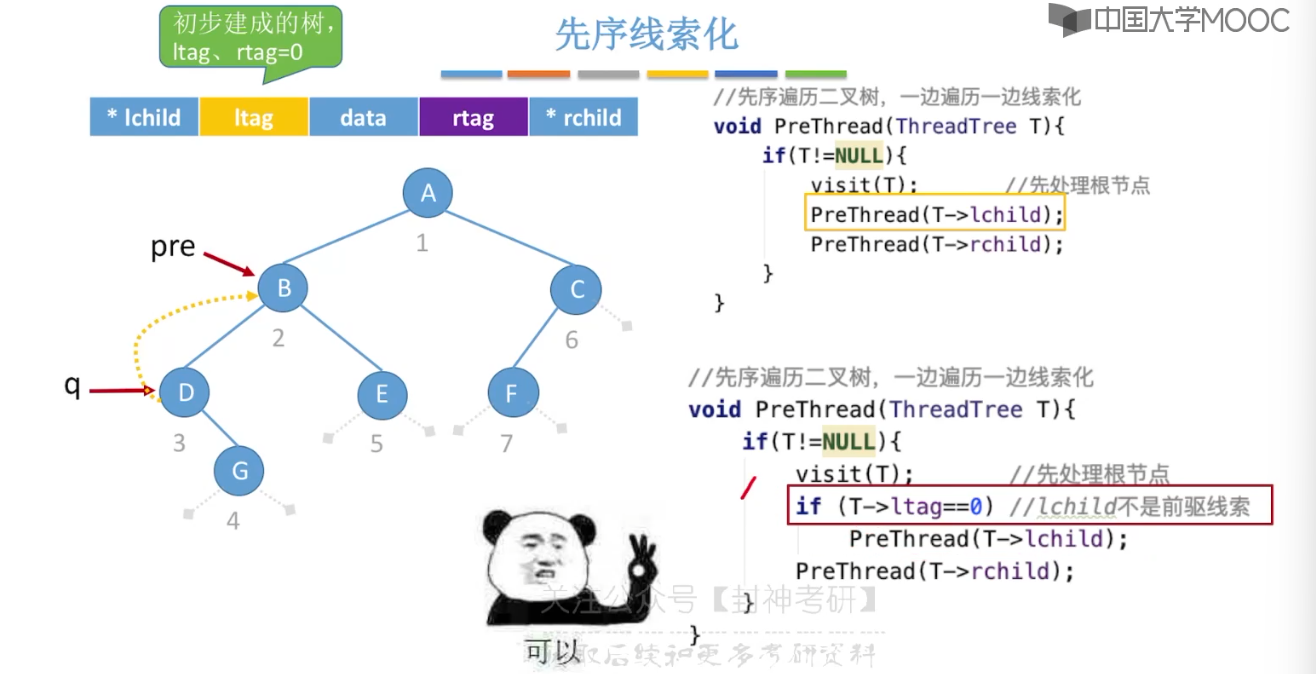



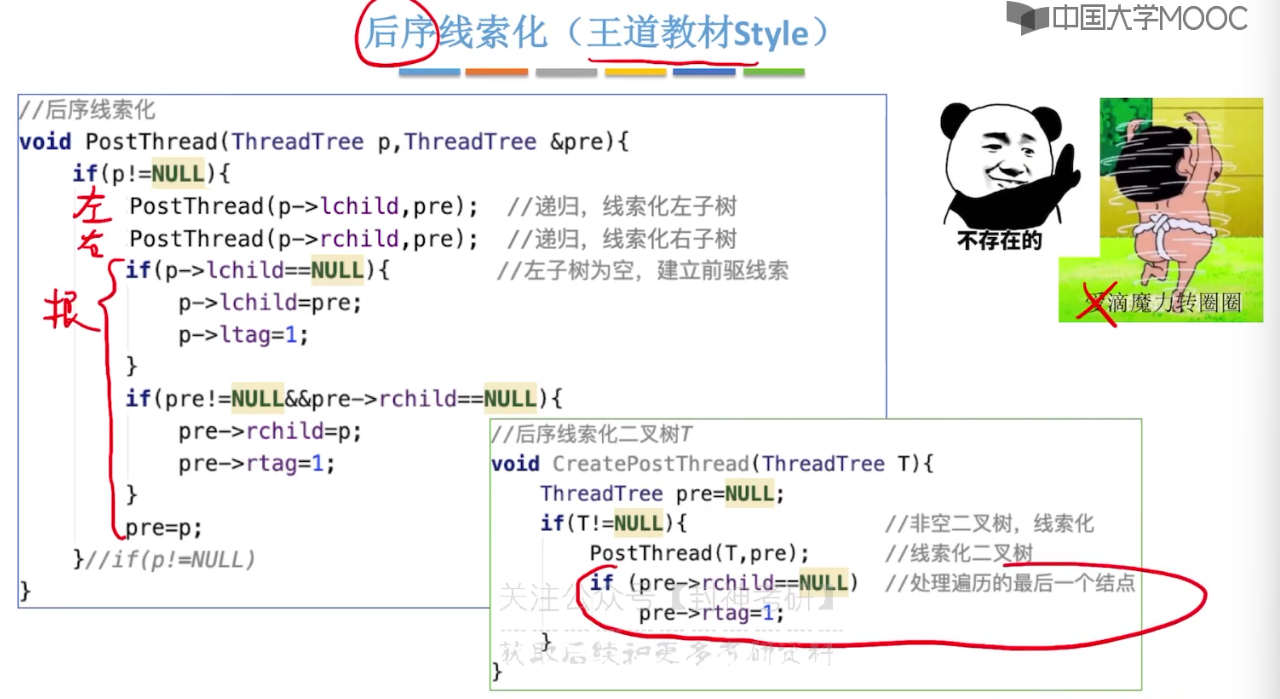
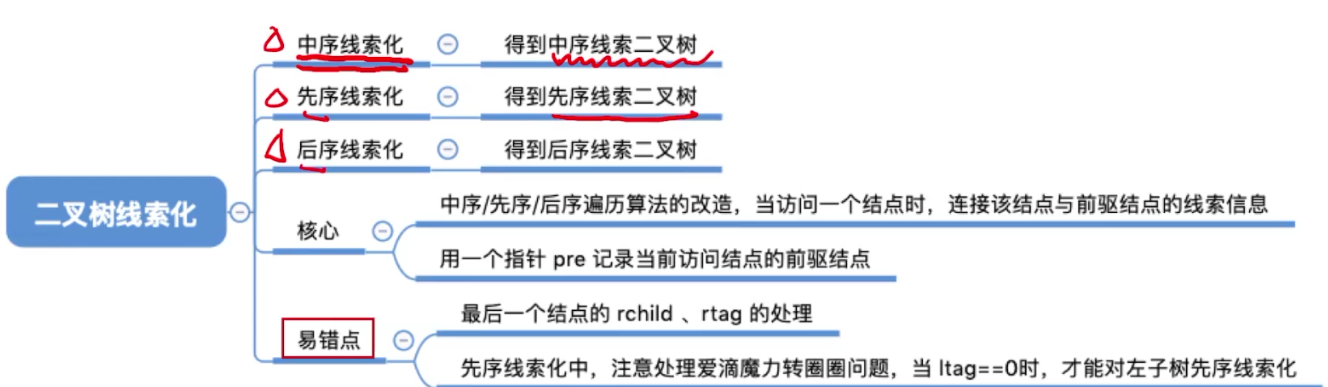
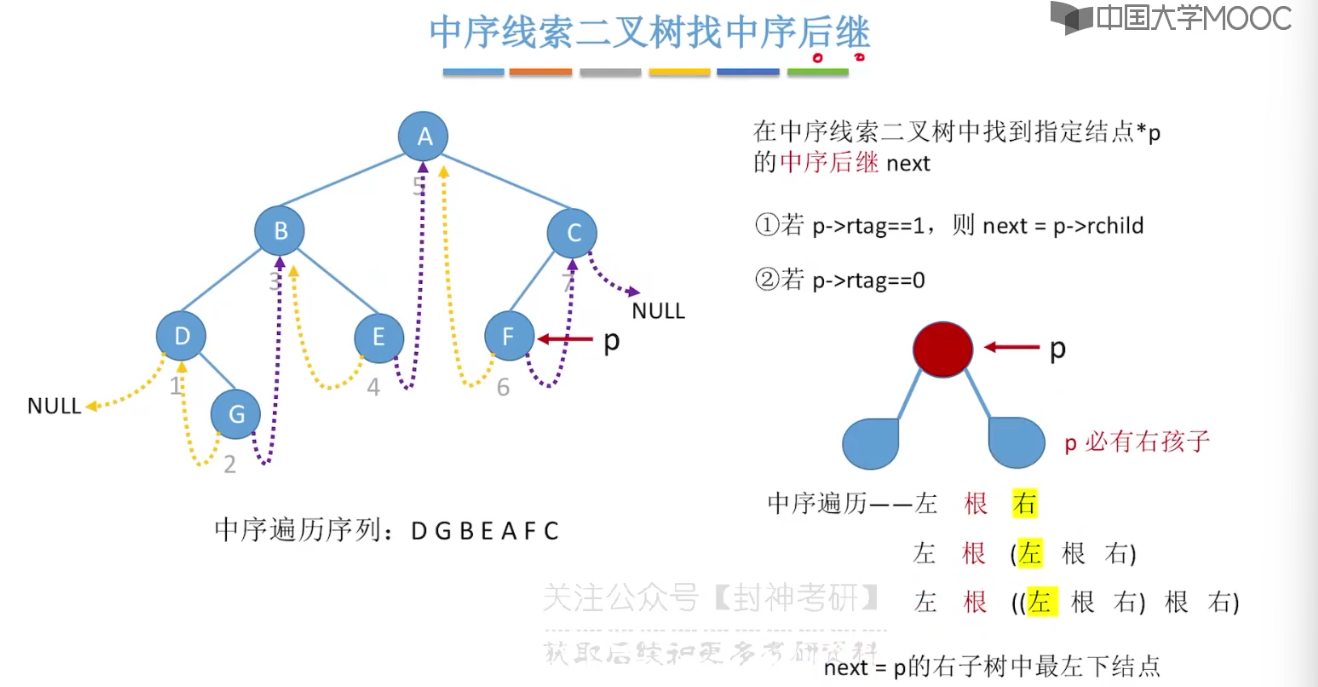
5.11、在线索二叉树中找前驱后继
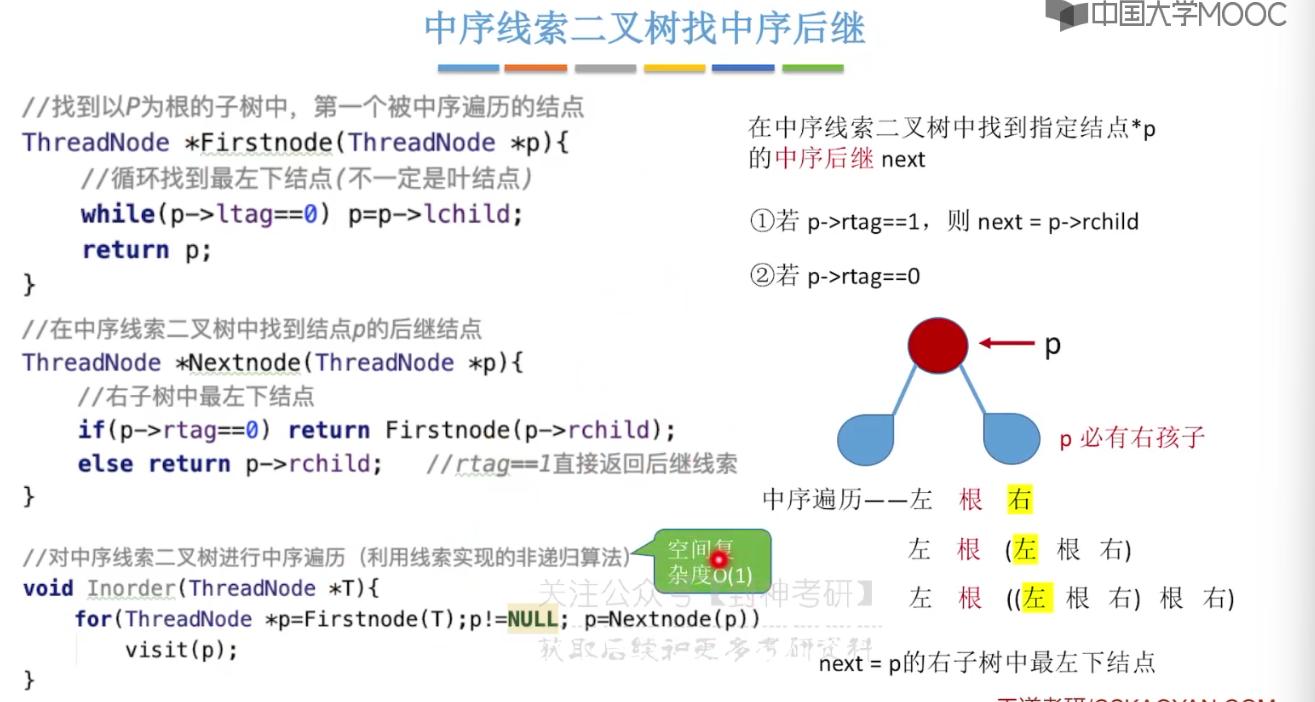
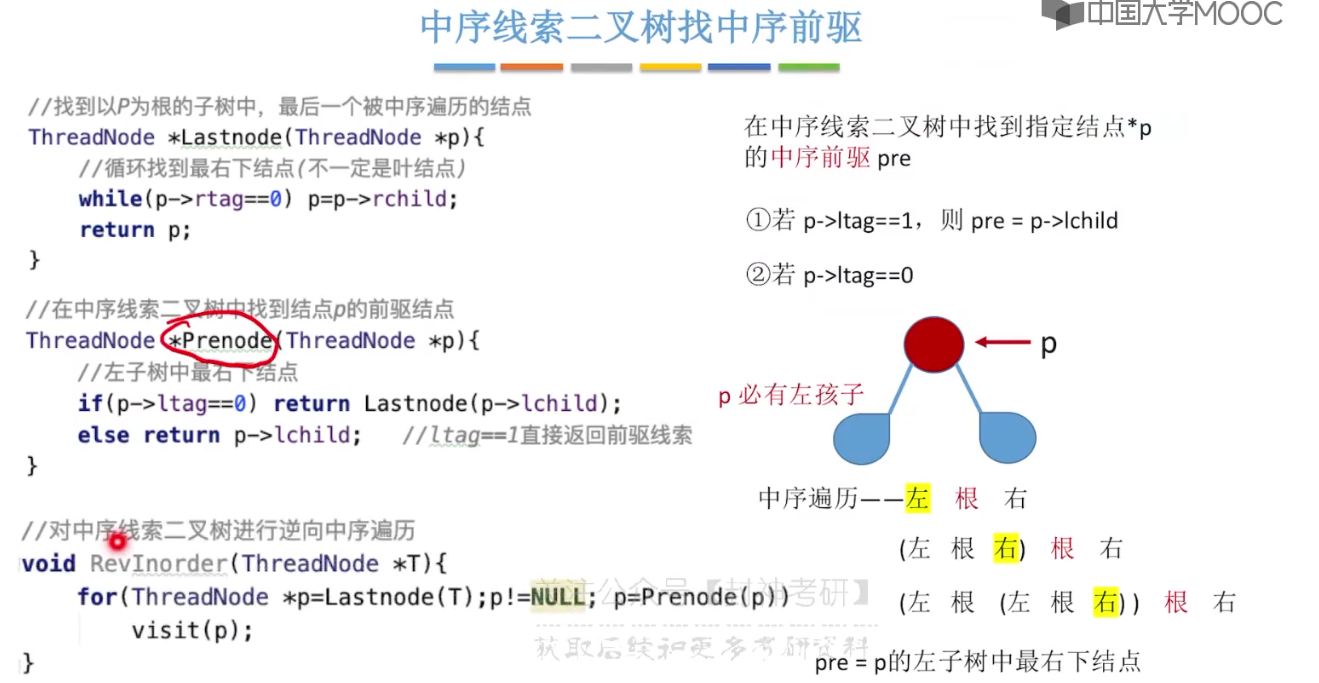
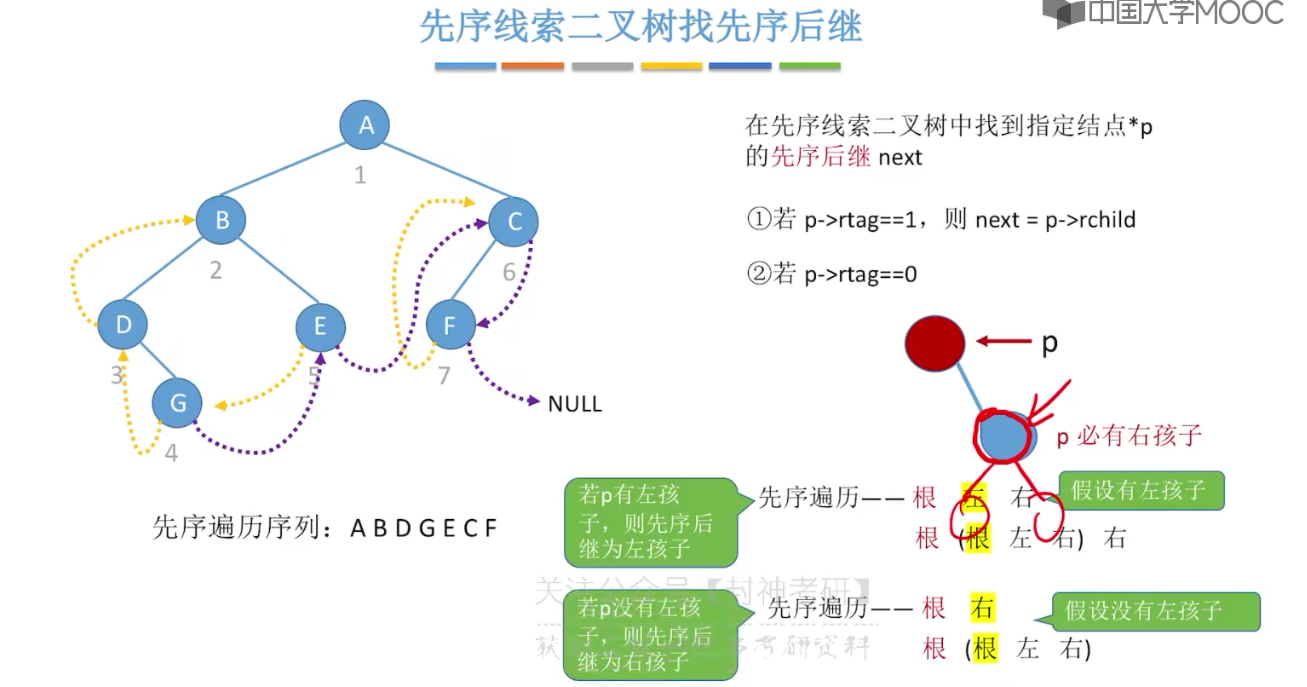
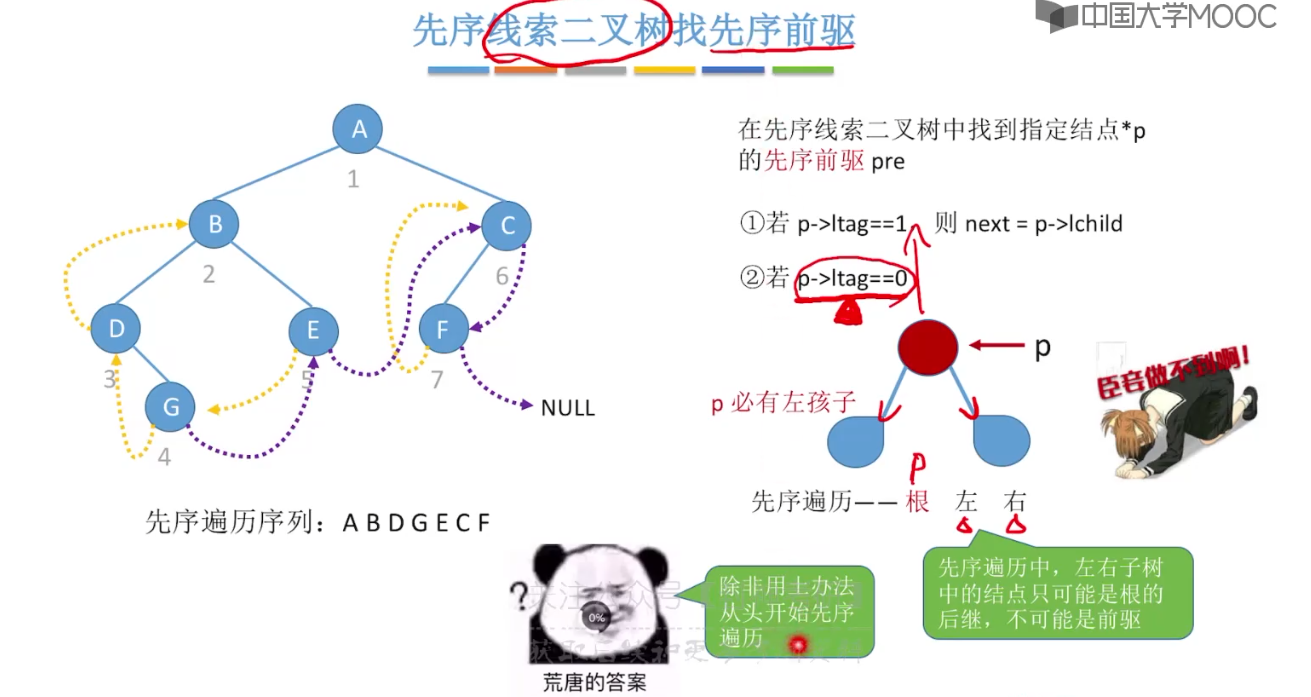
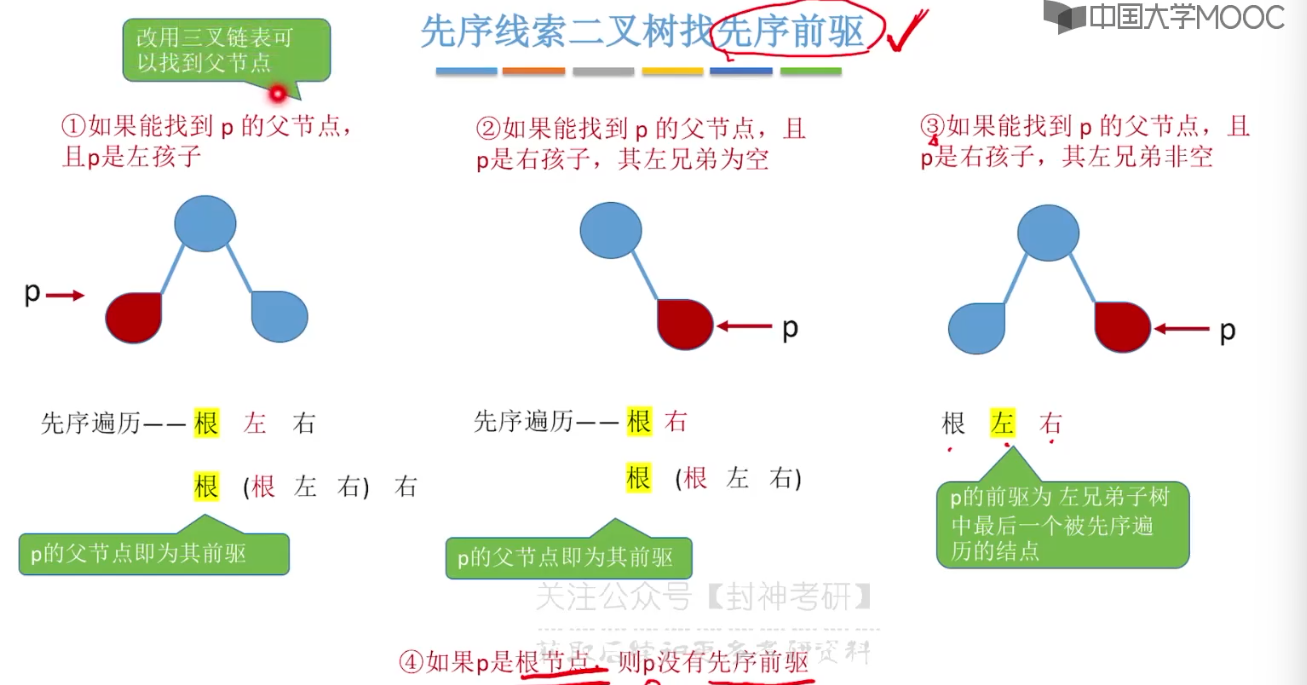
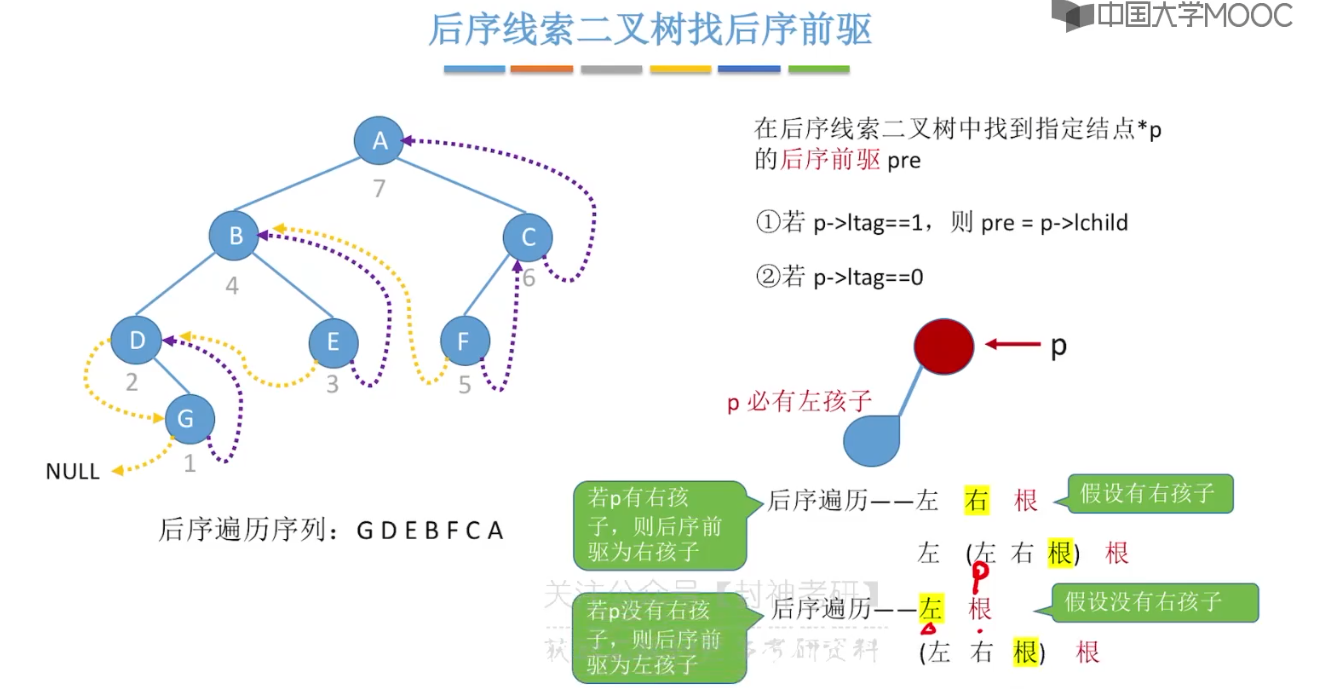
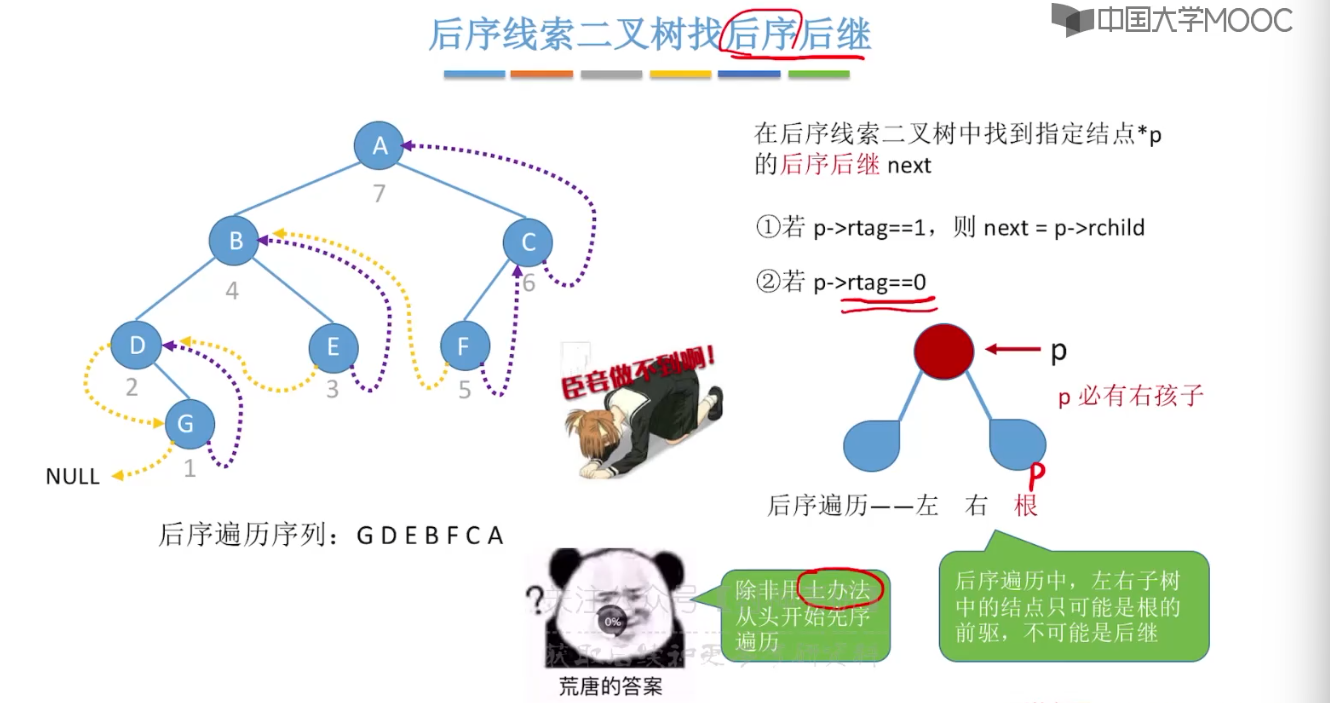
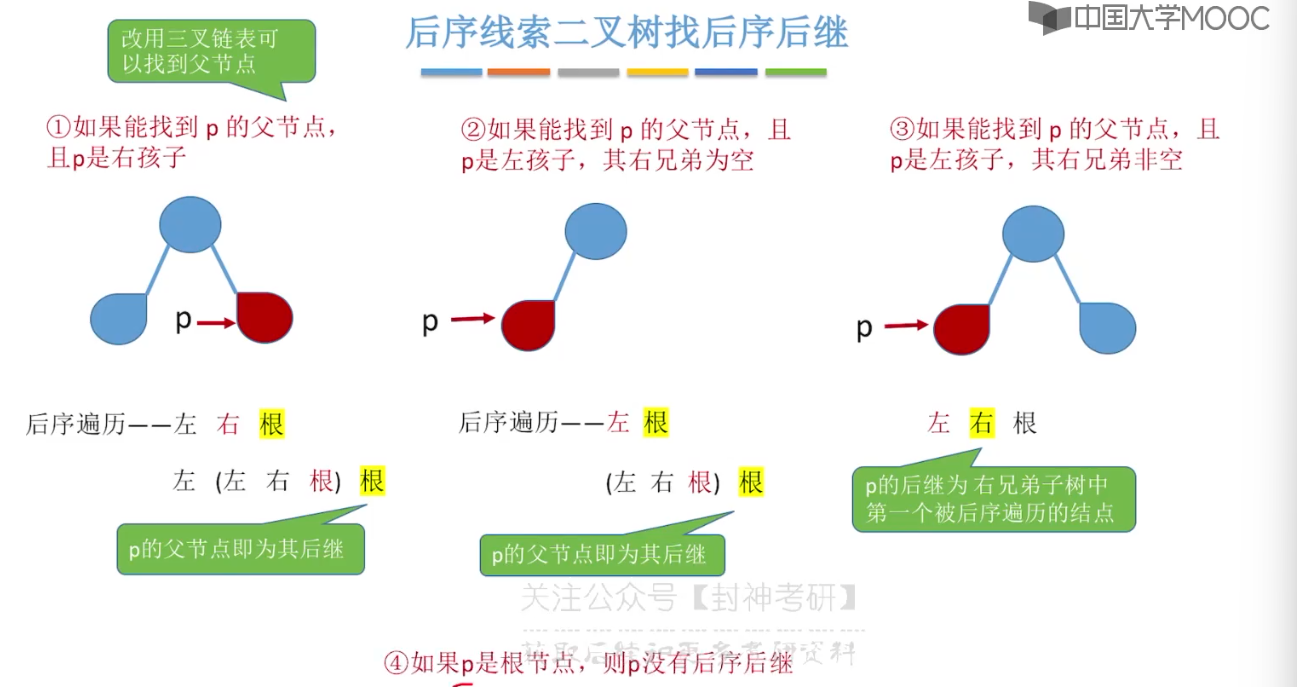
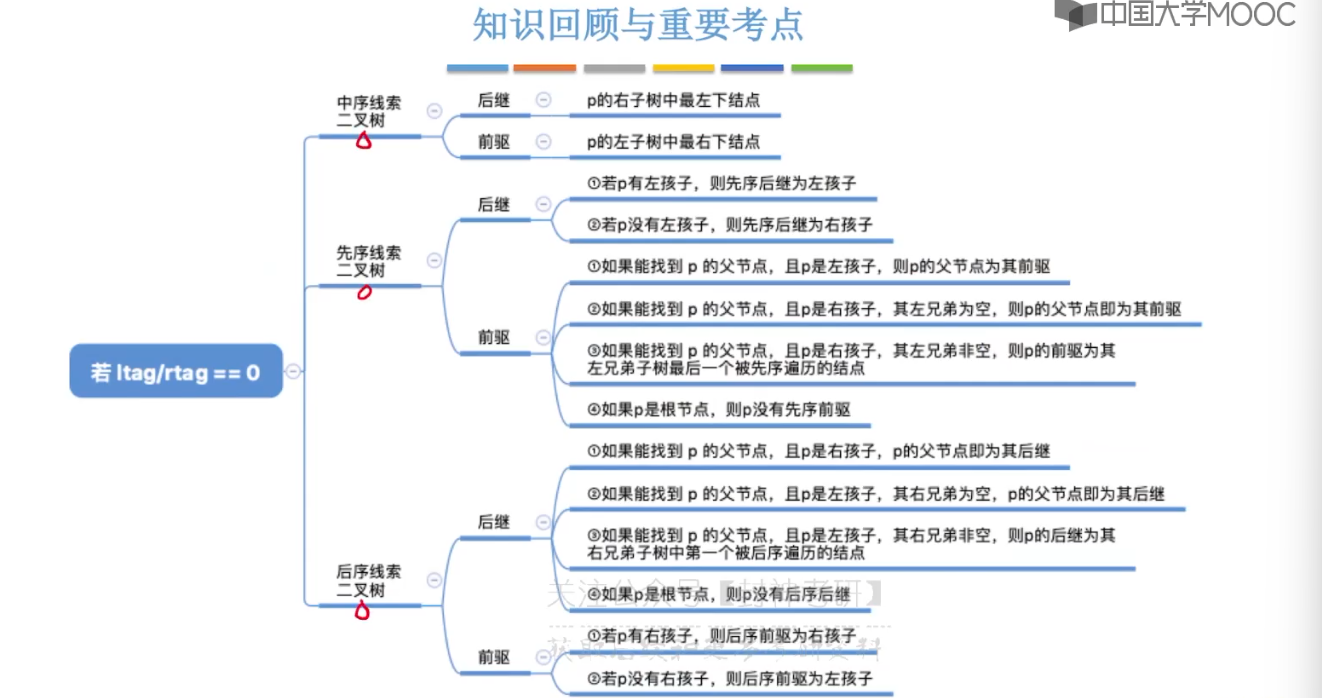

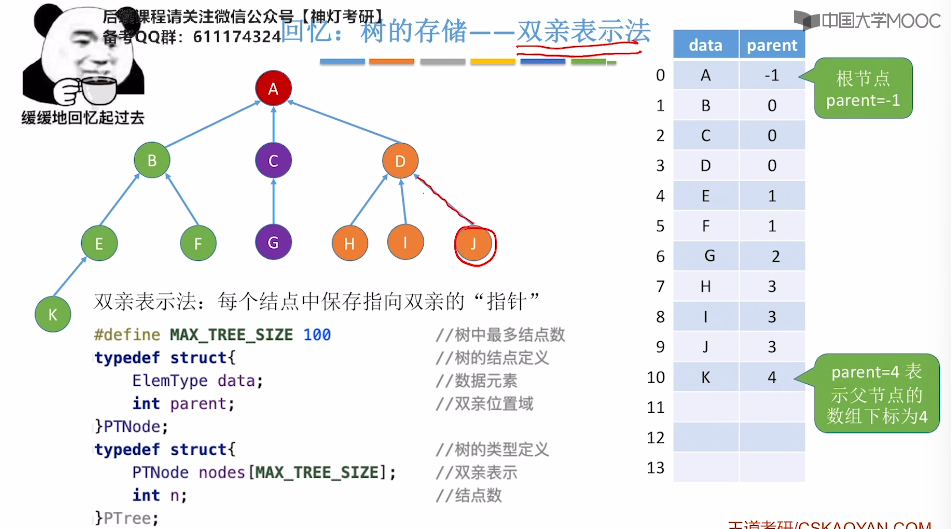
5.12、树的存储结构

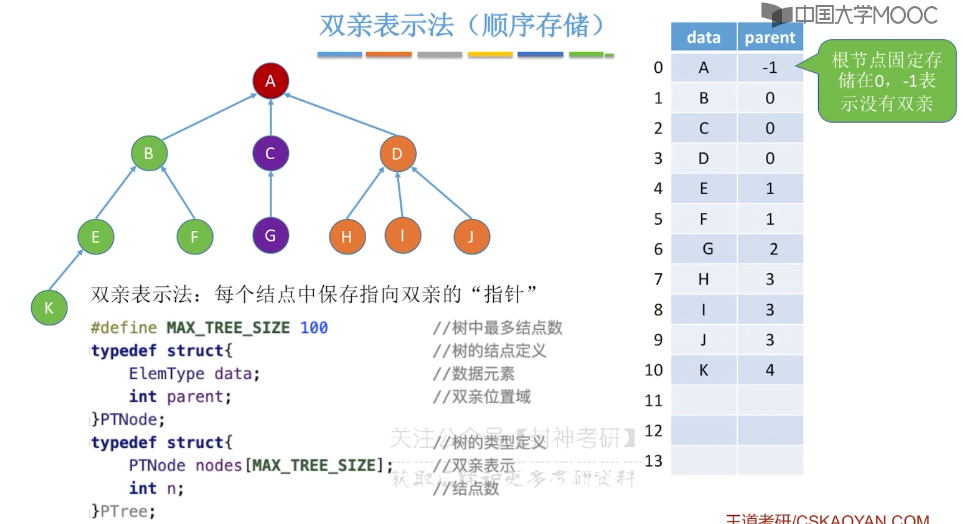
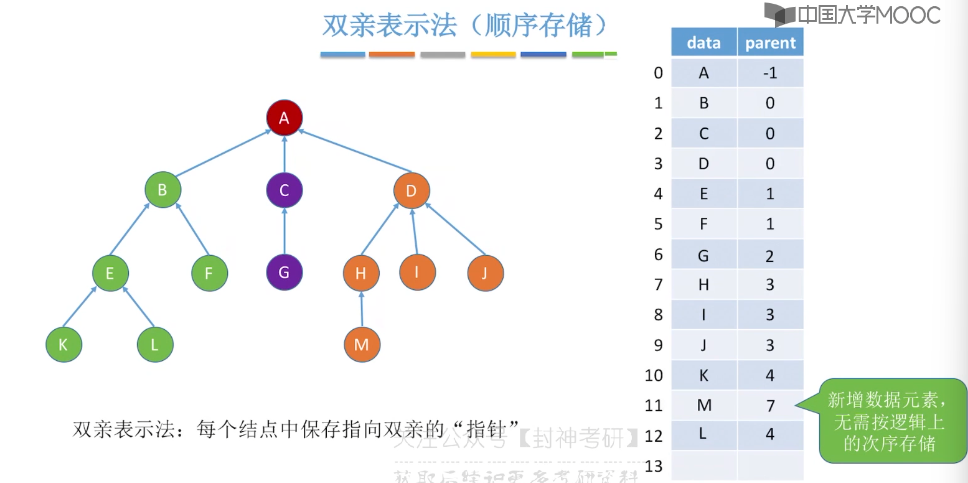
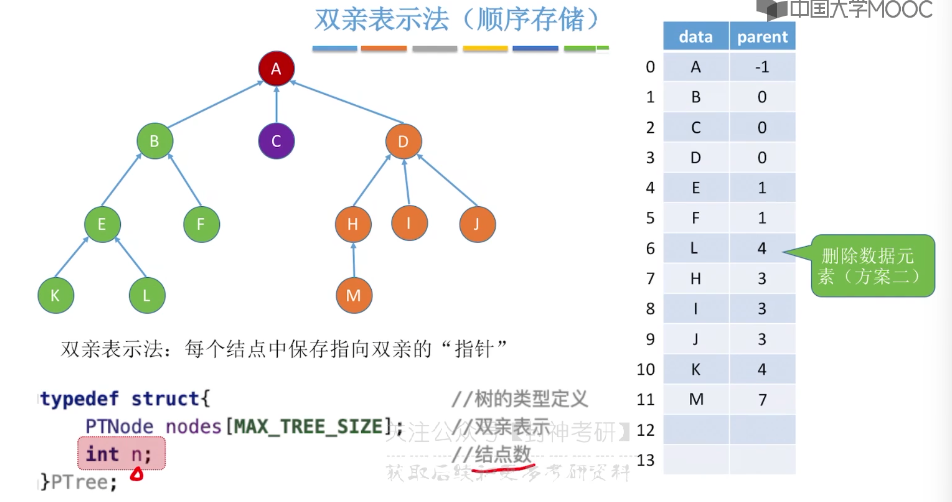
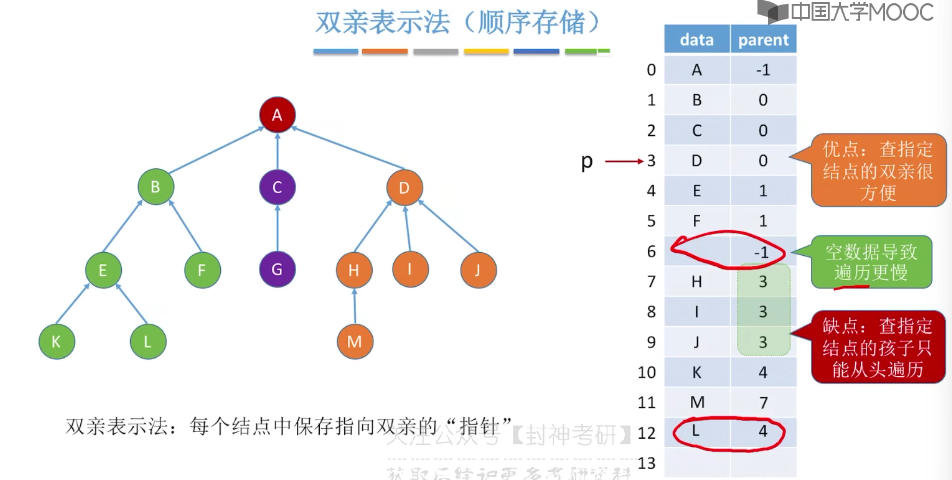
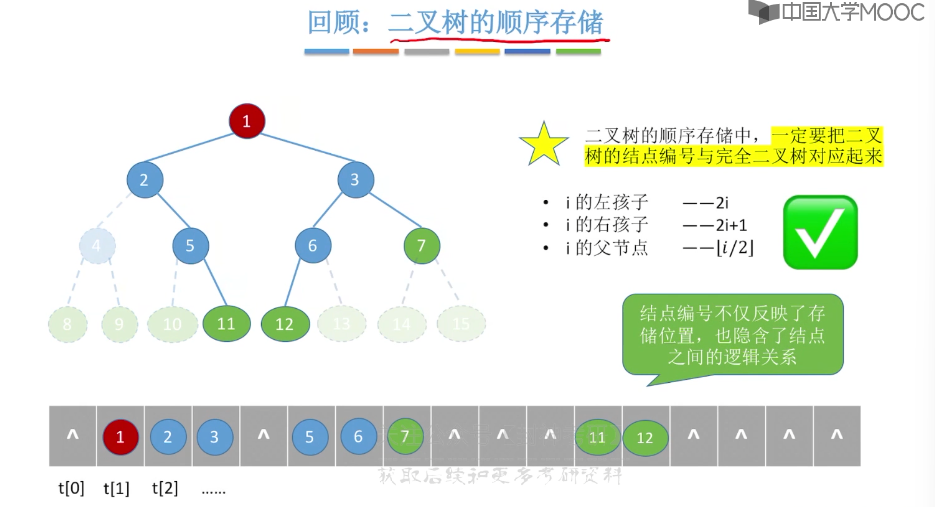
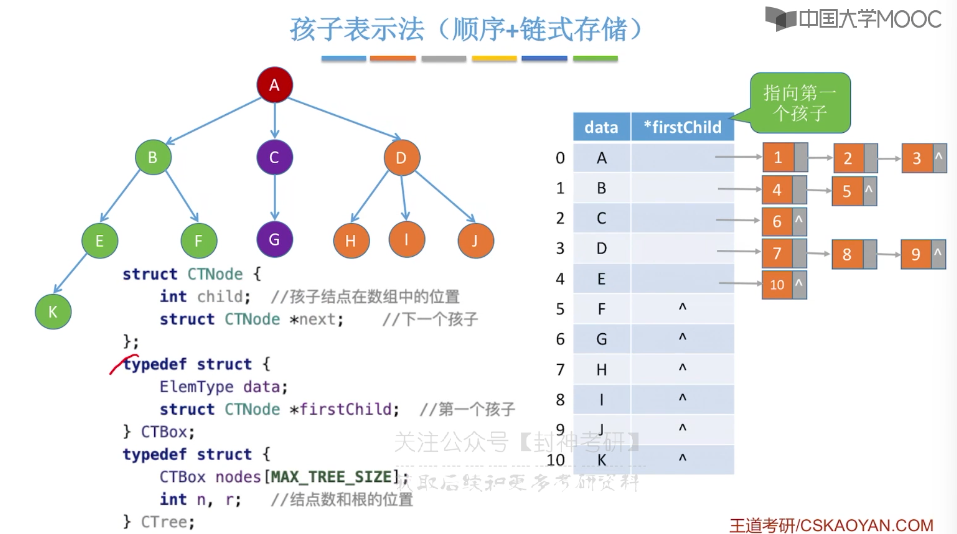
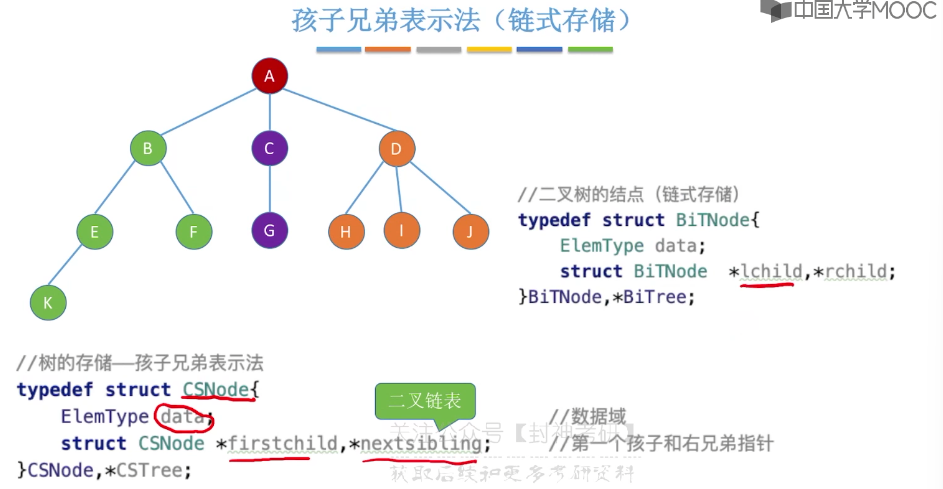
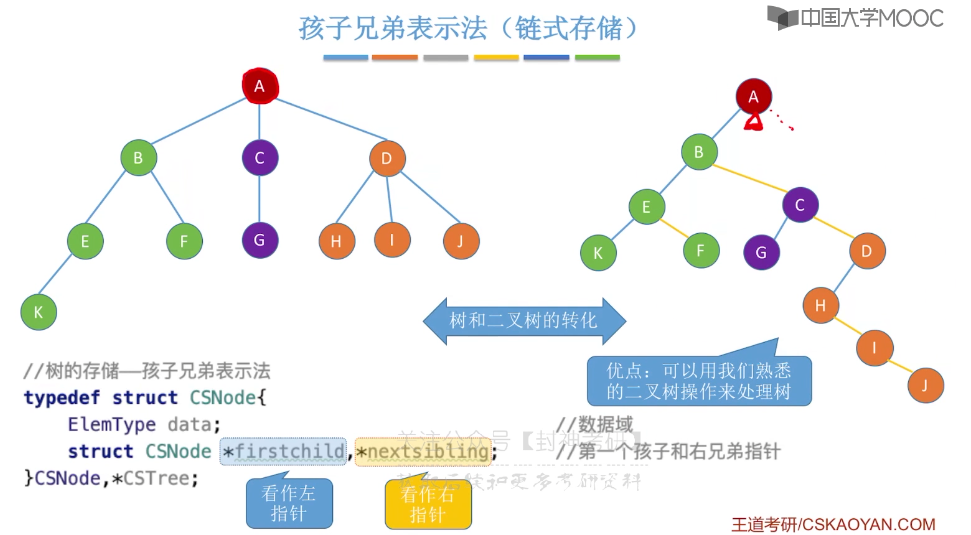
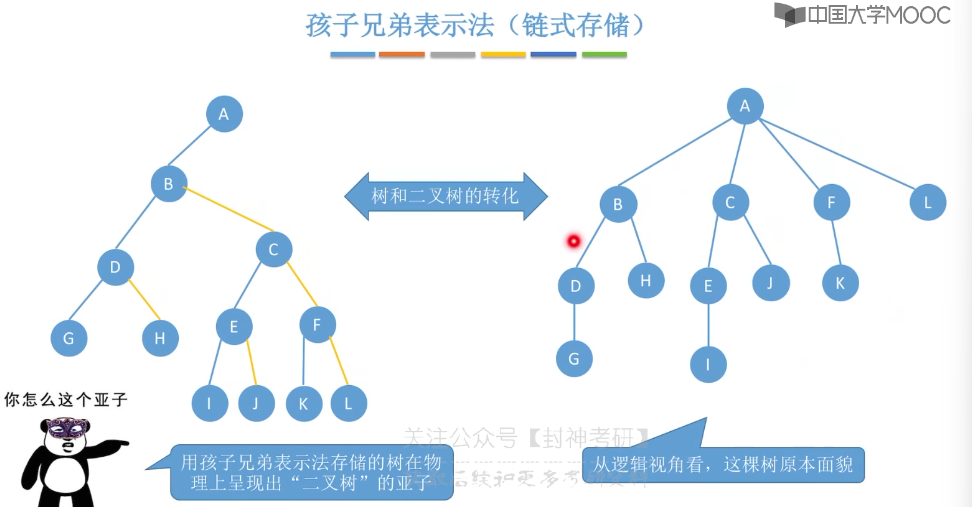
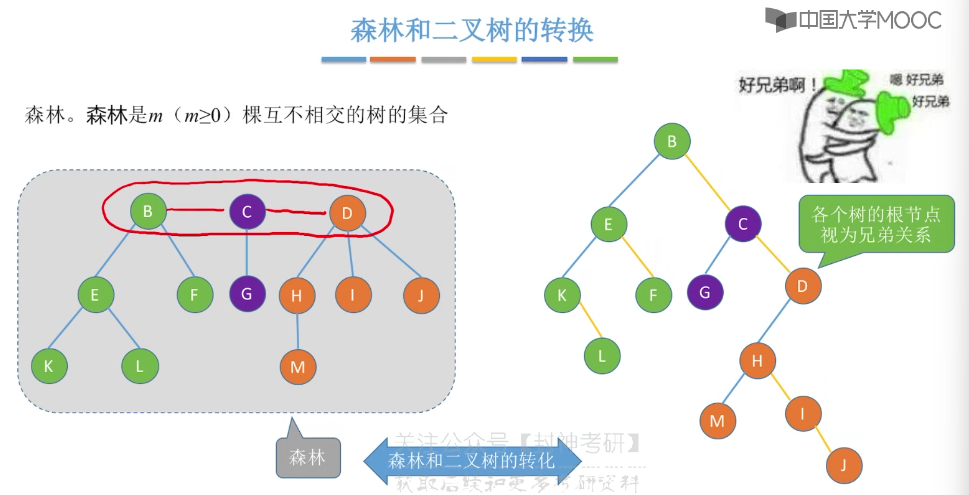
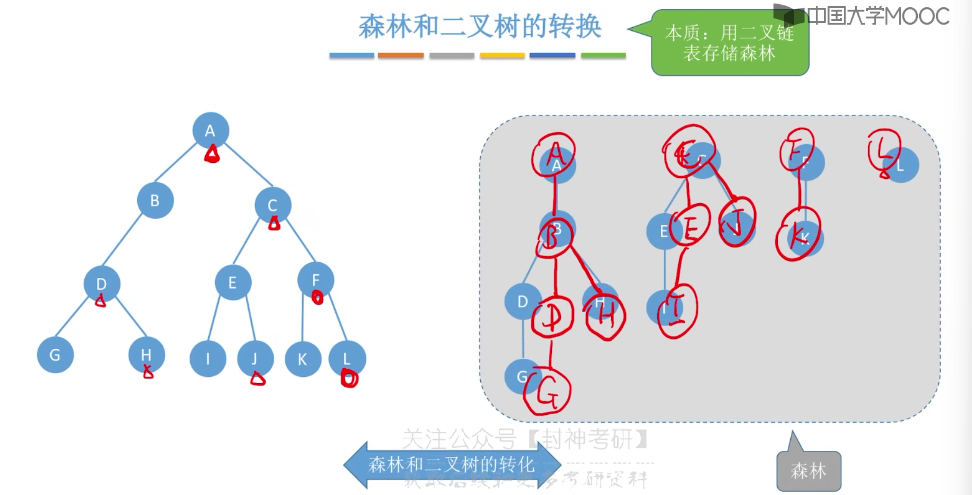
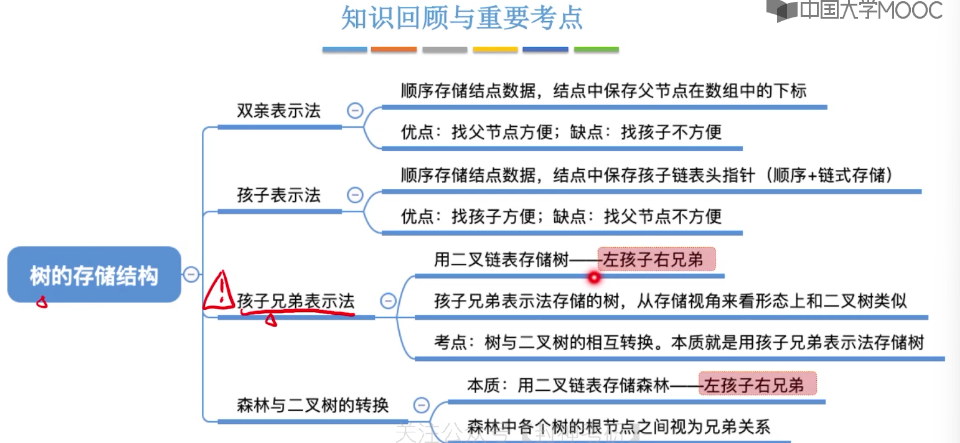
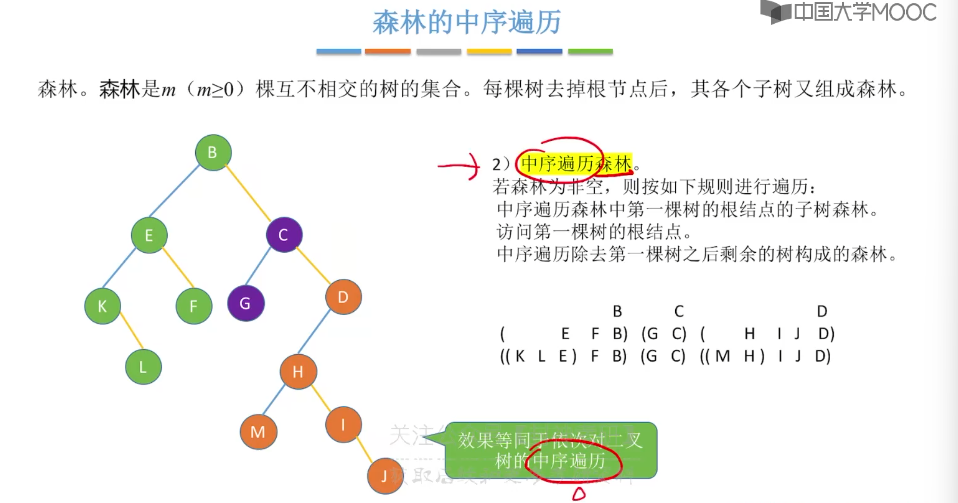
5.13、树和森林的遍历

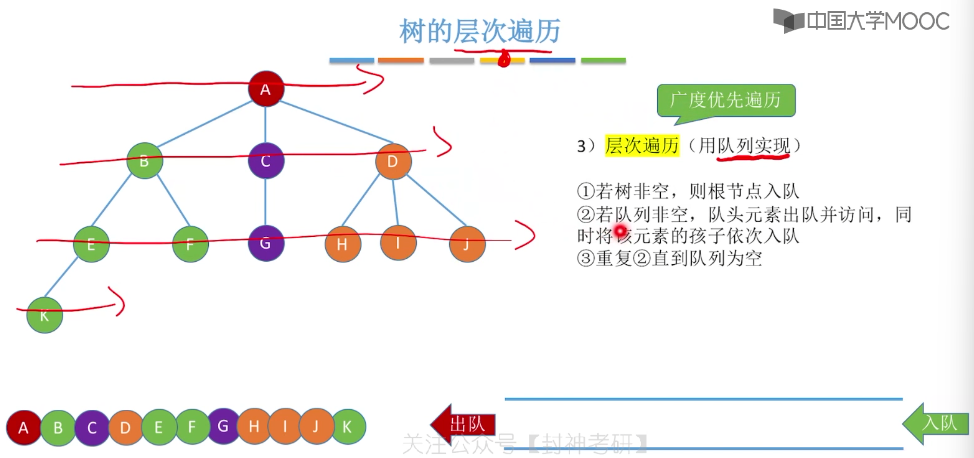
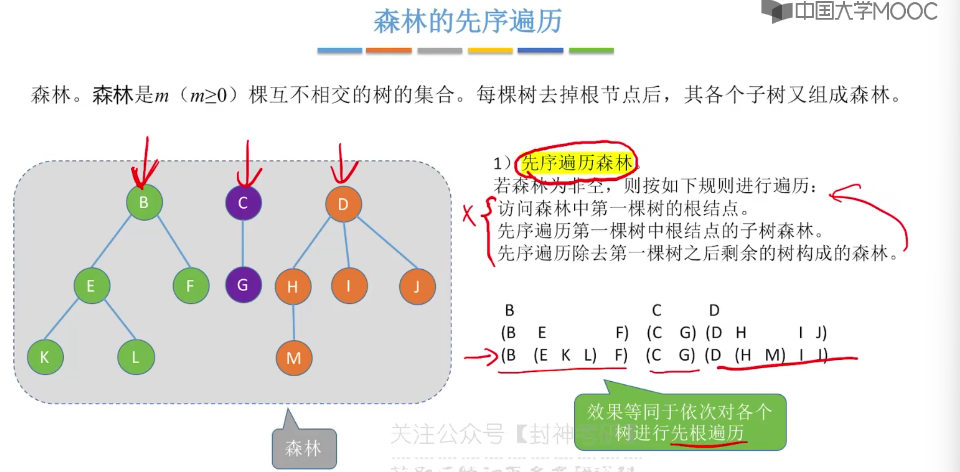
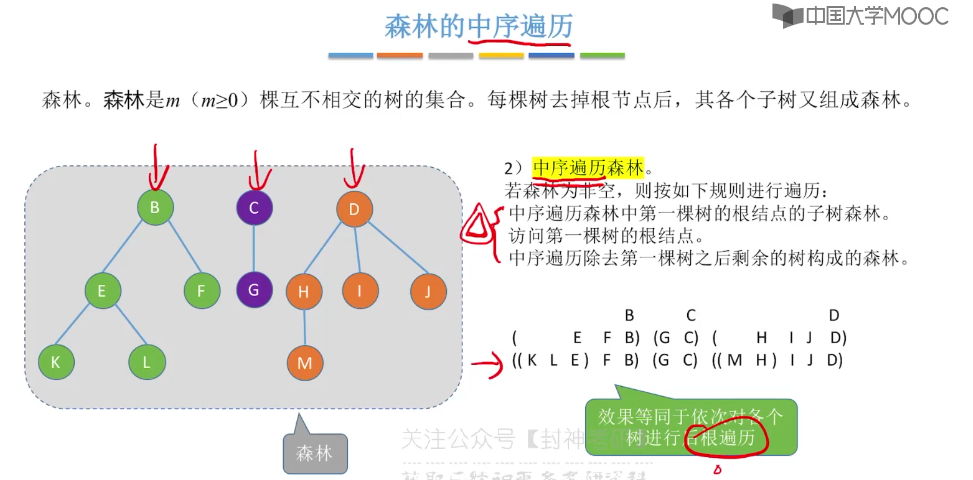
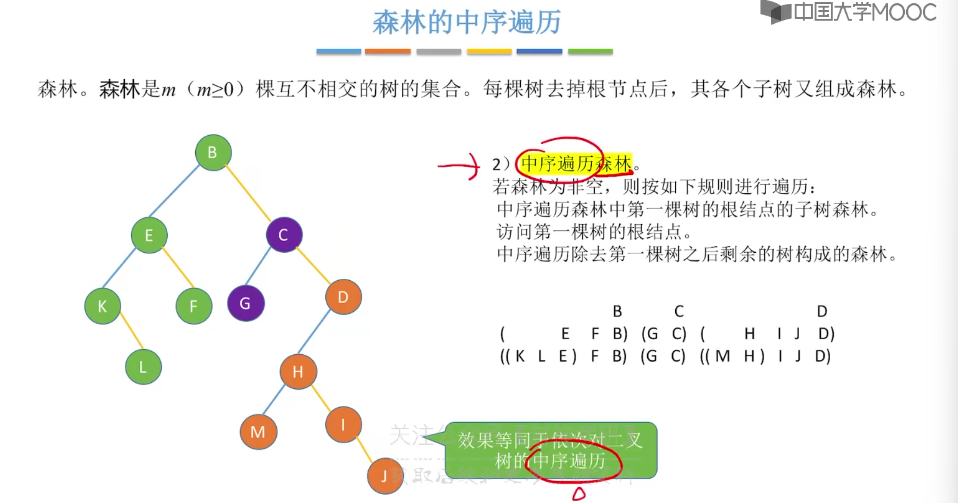
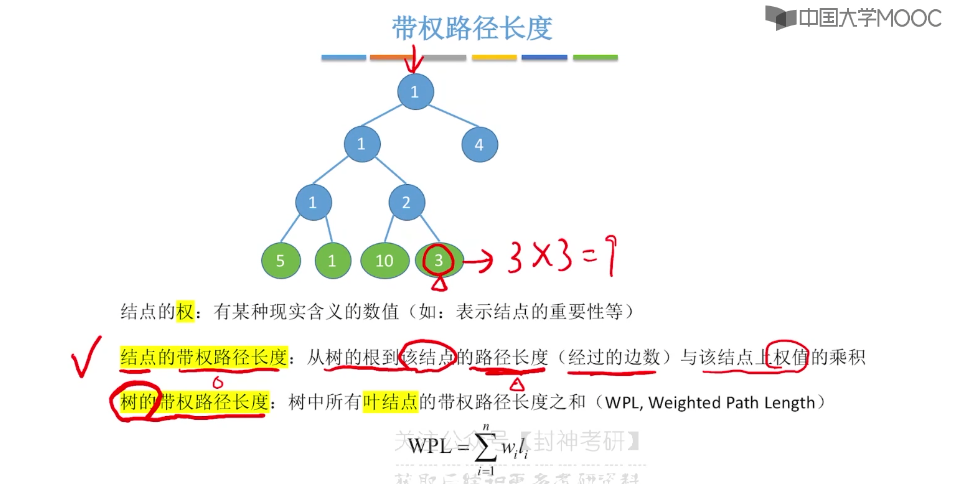
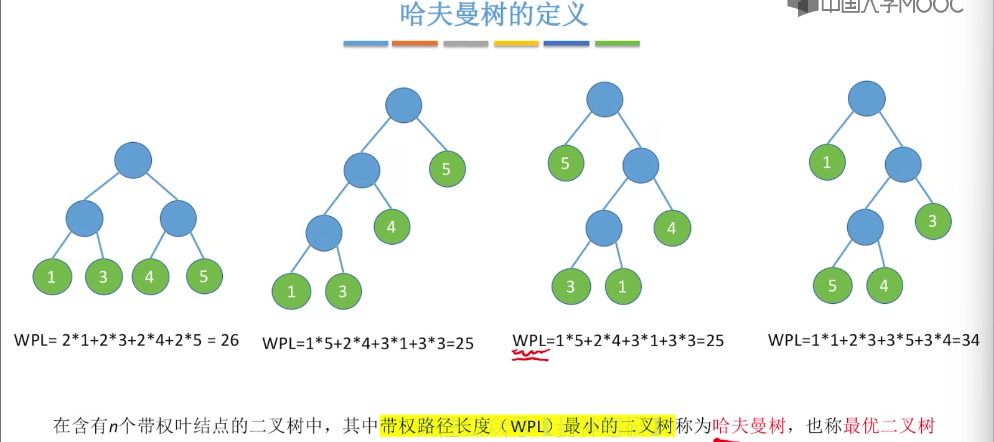
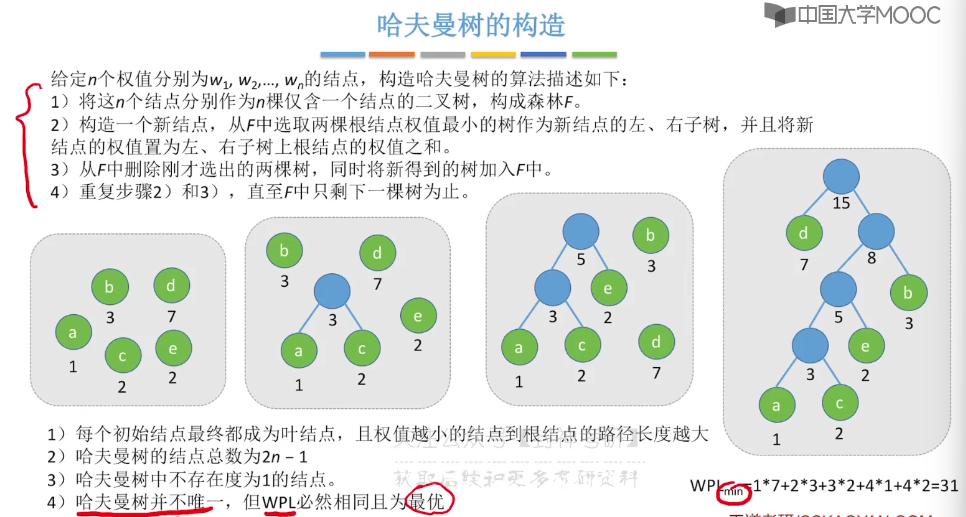
5.15、哈夫曼树
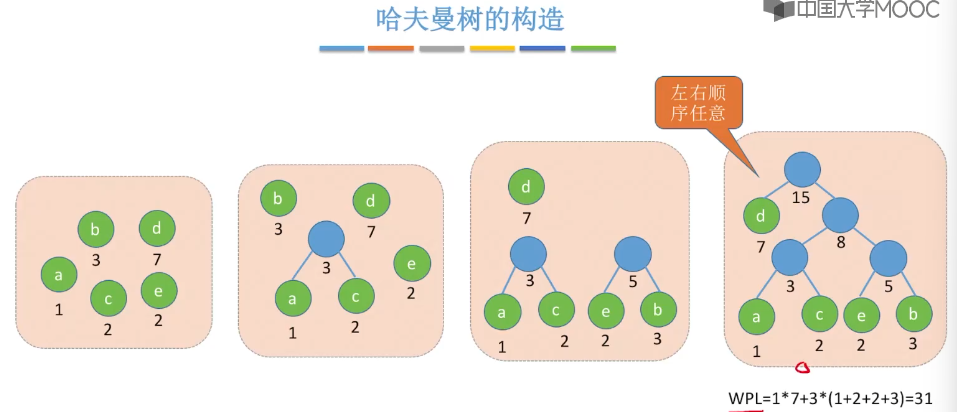

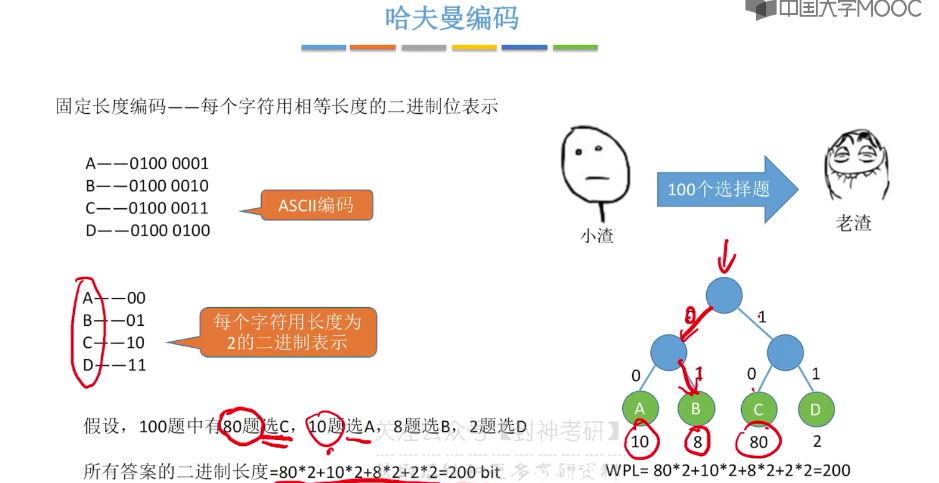
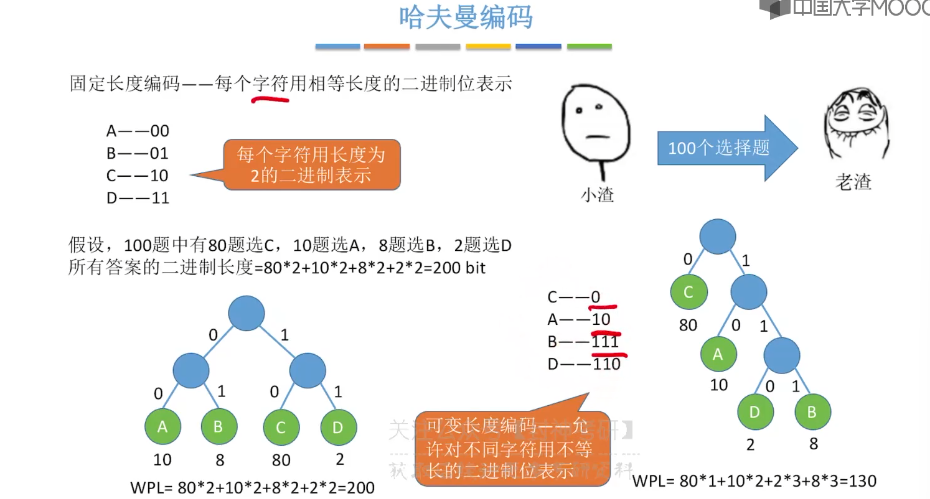
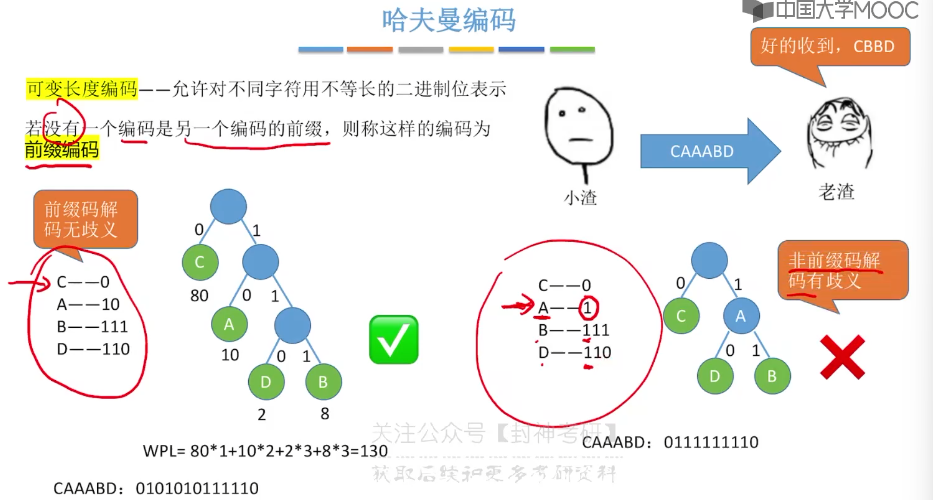
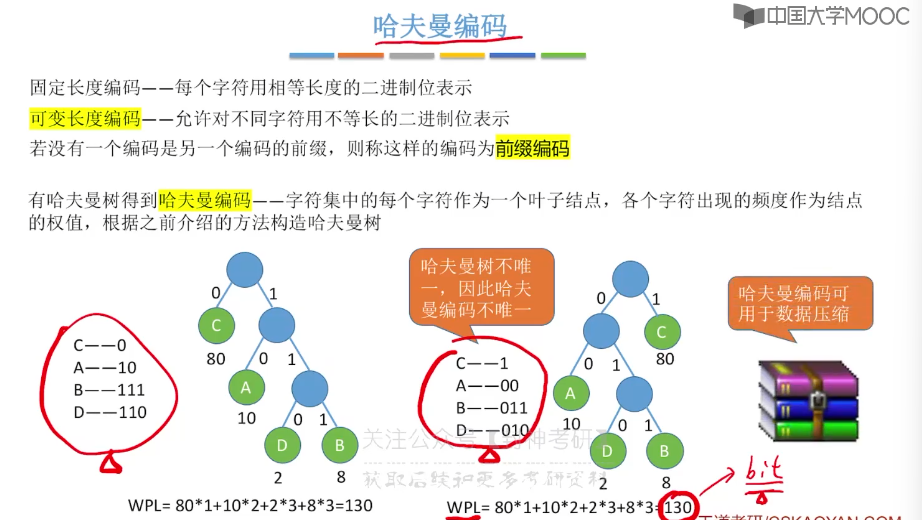
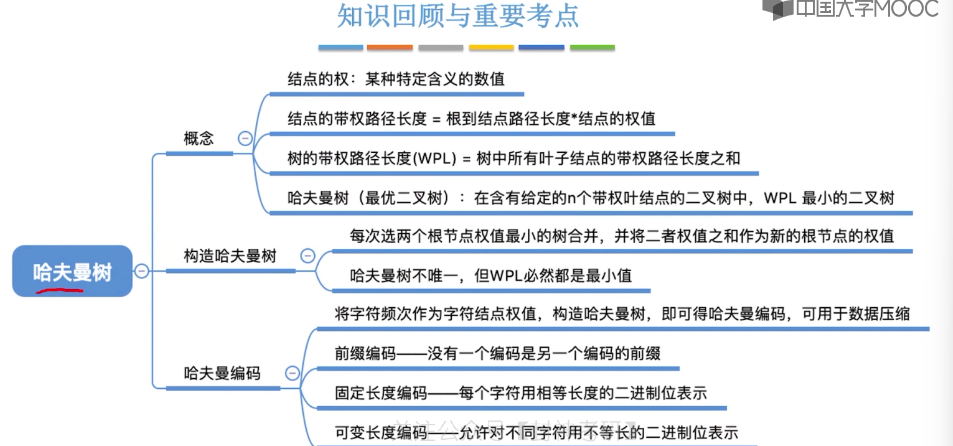
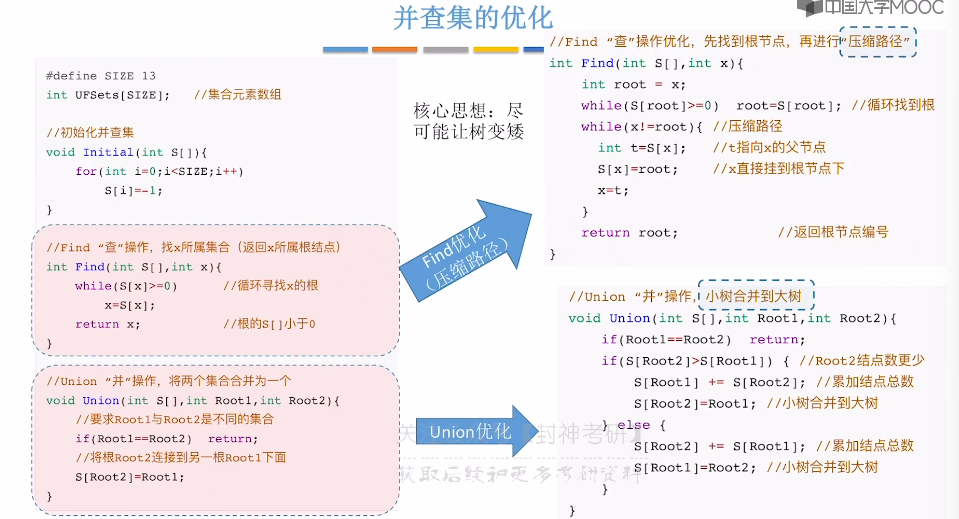
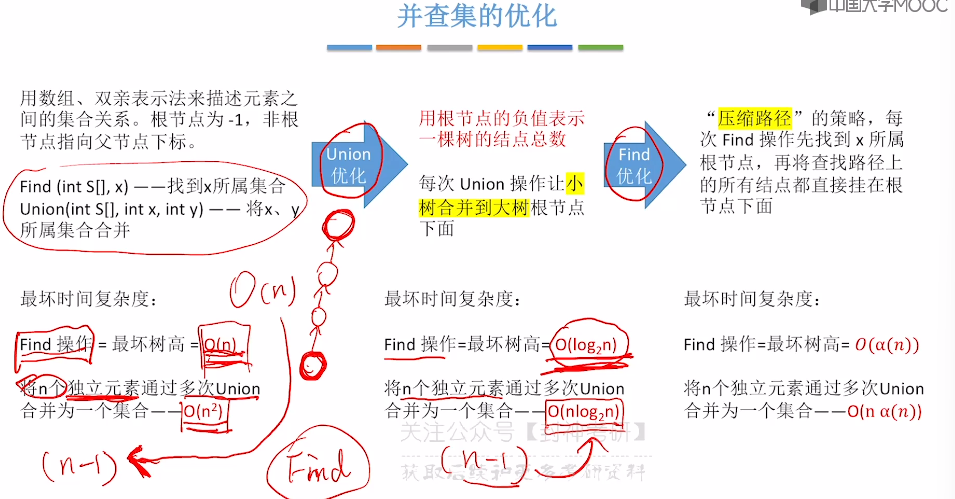
5.16、并查集
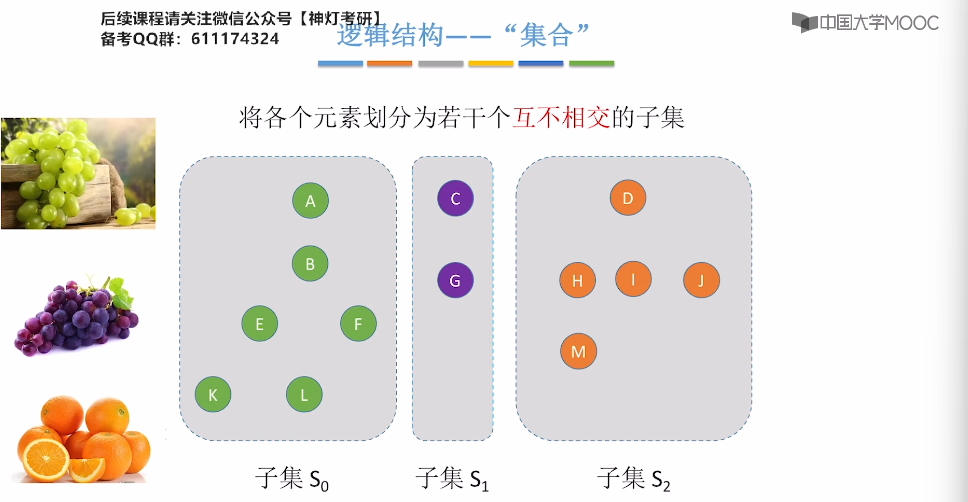
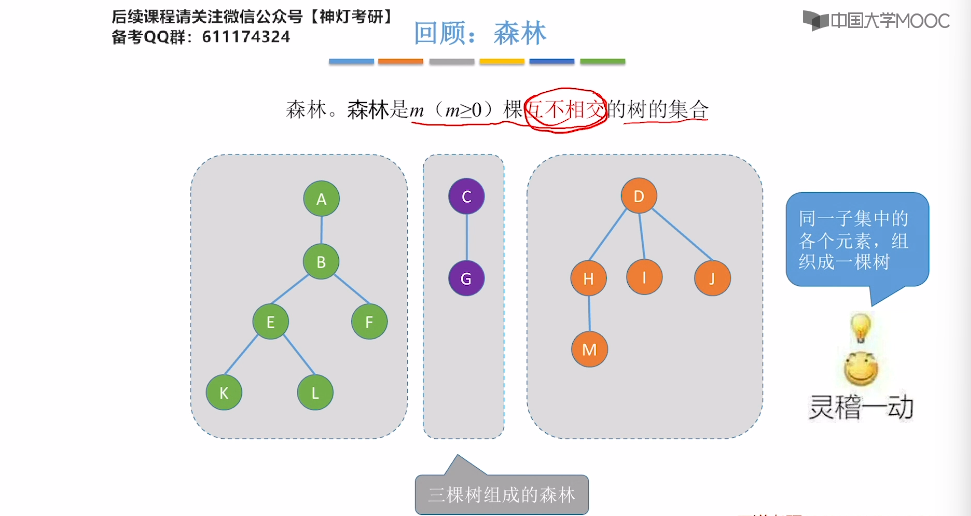
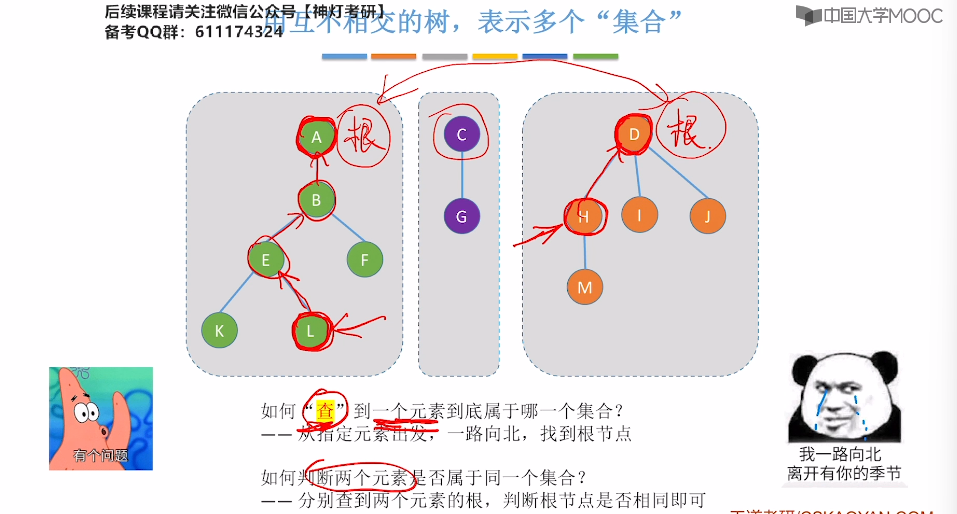

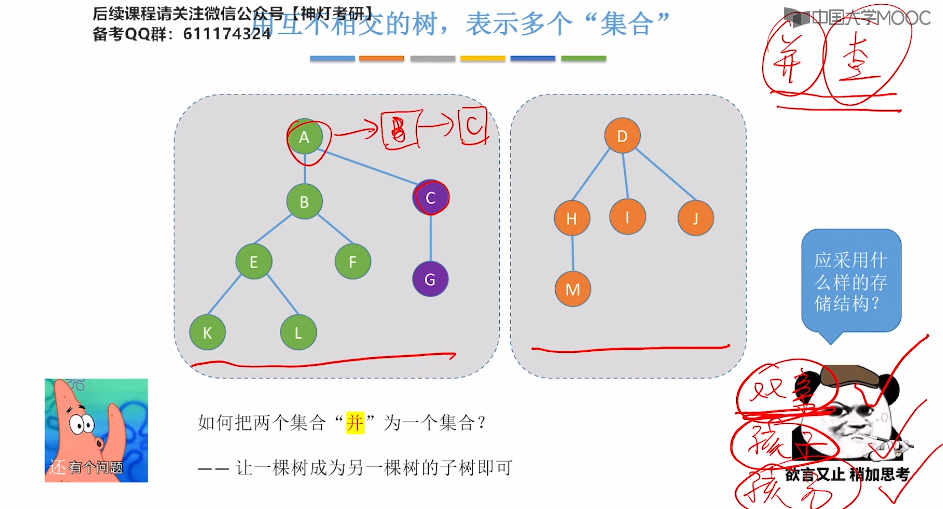
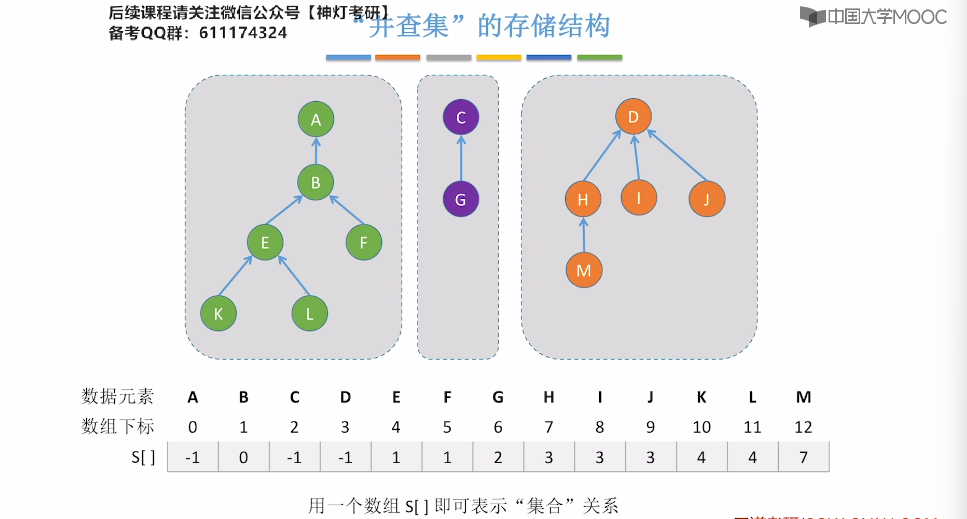
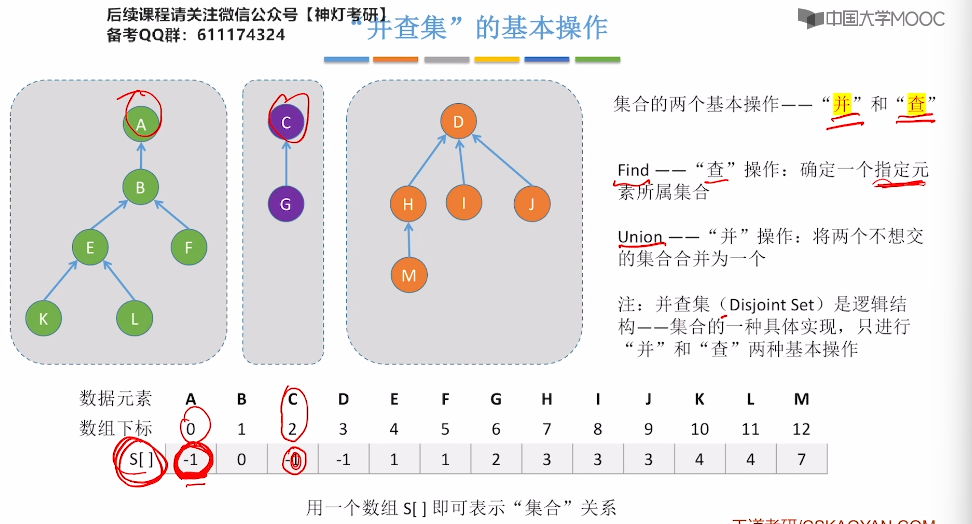
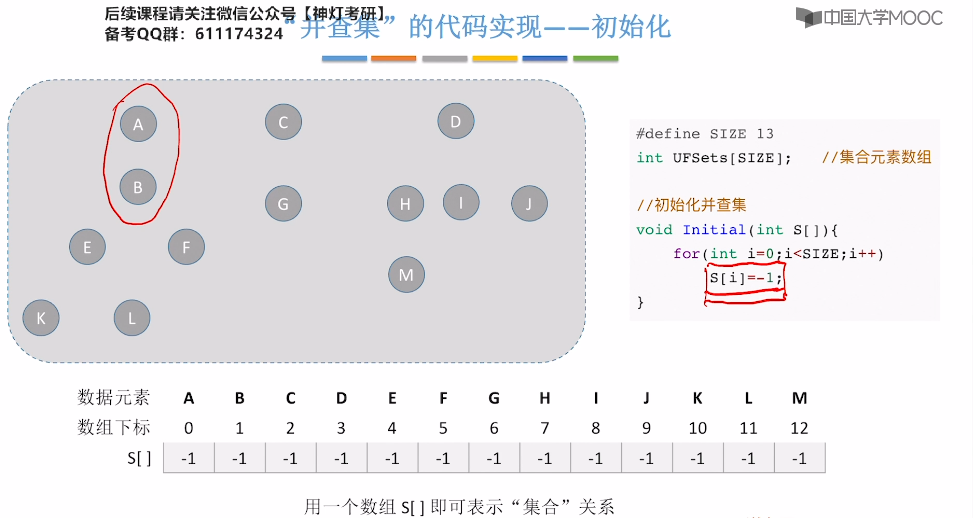
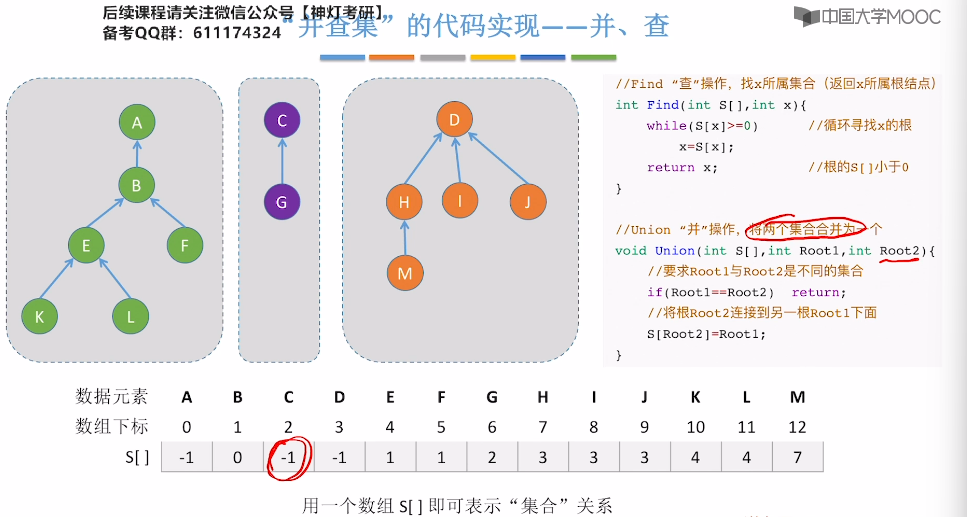
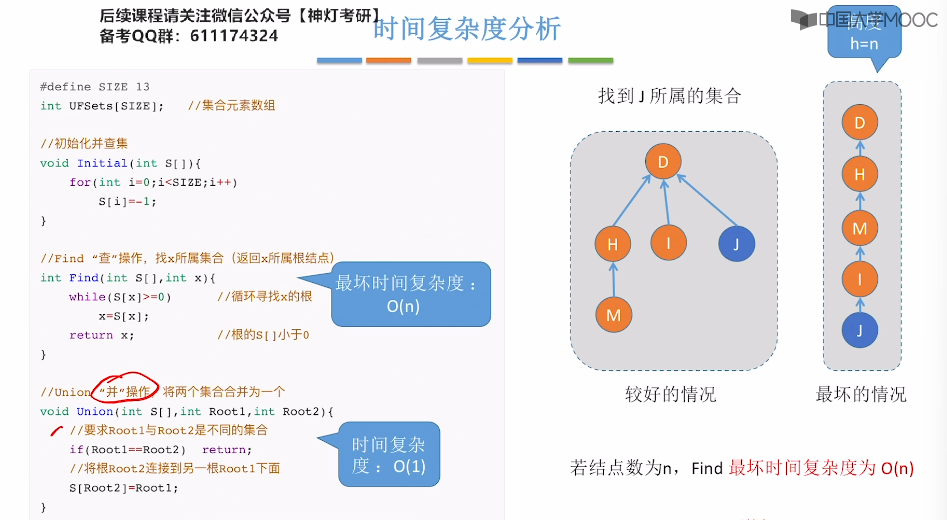
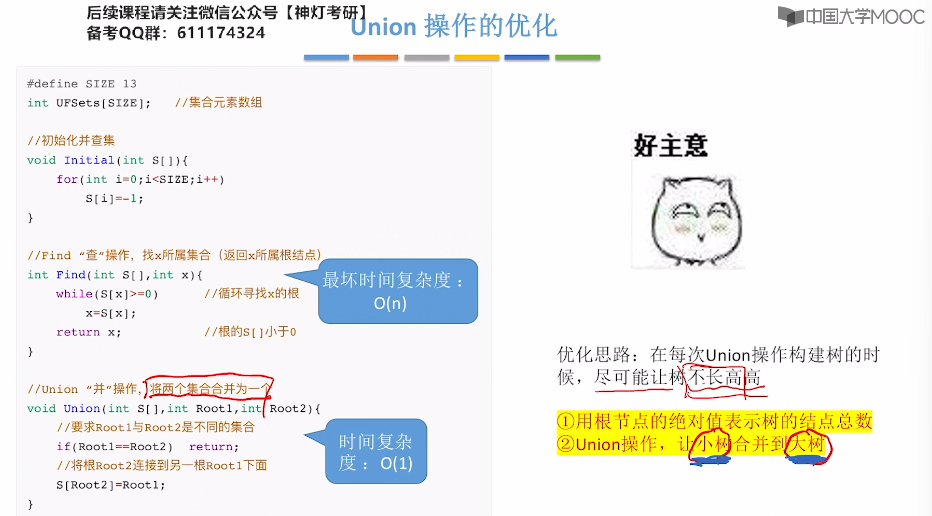
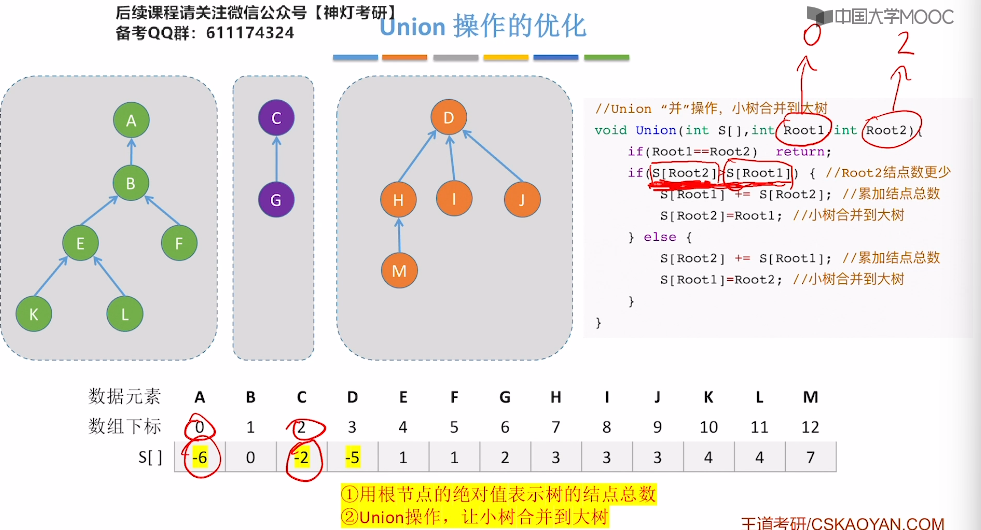
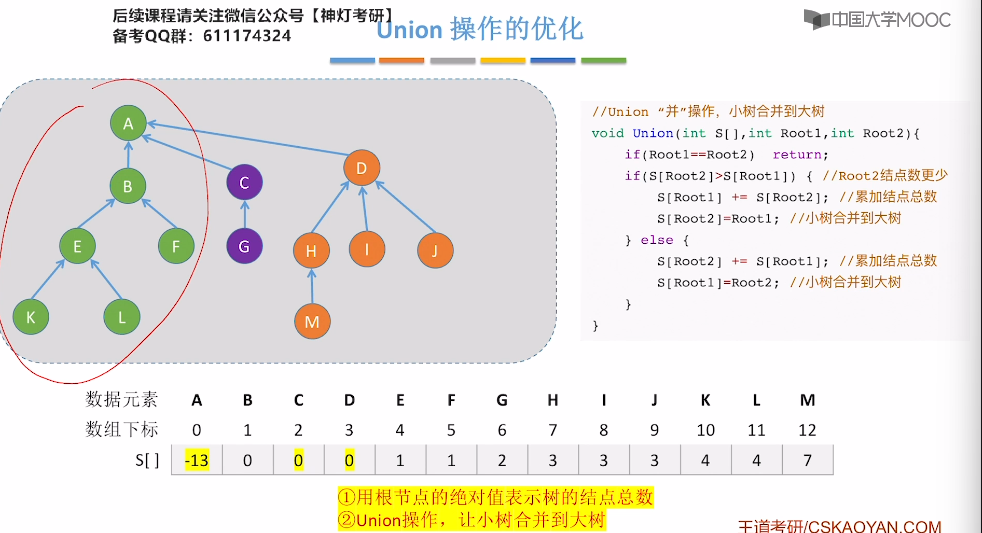
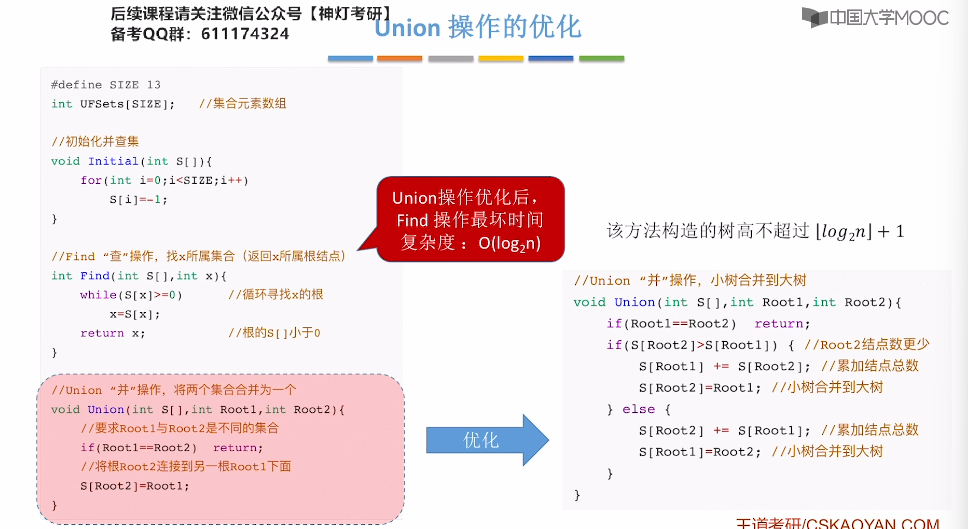
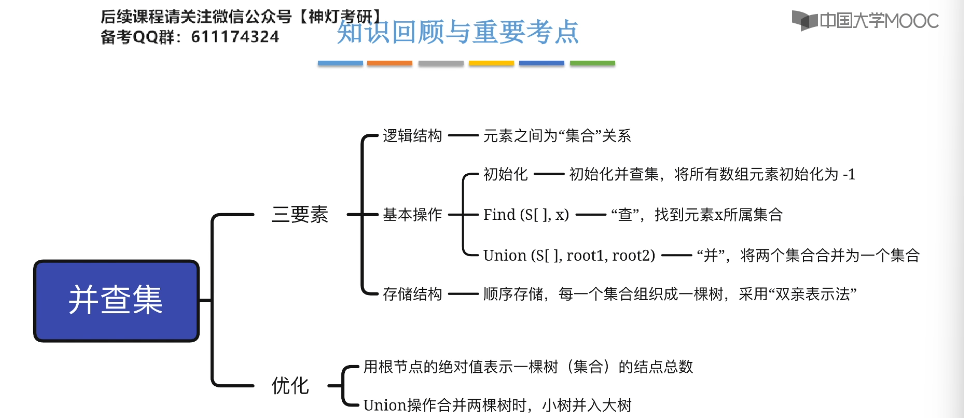
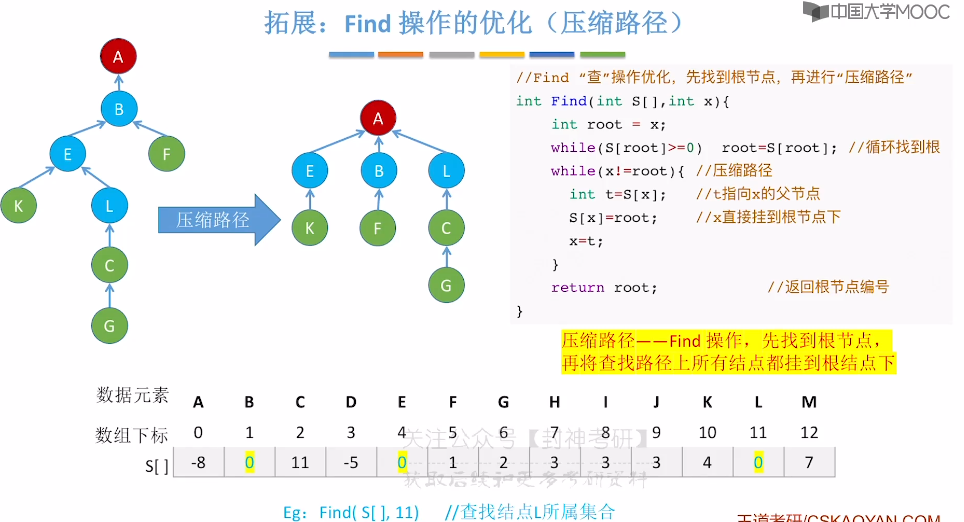
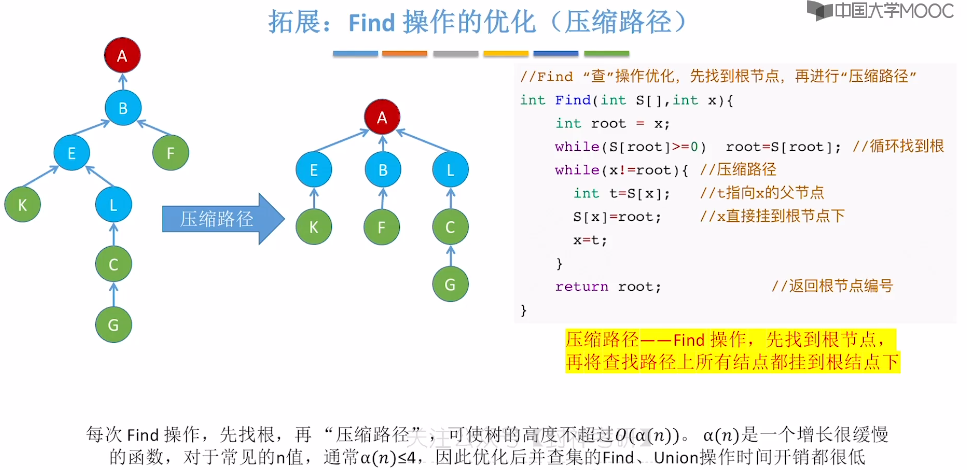
5.17、并查集的进一步优化

6、图
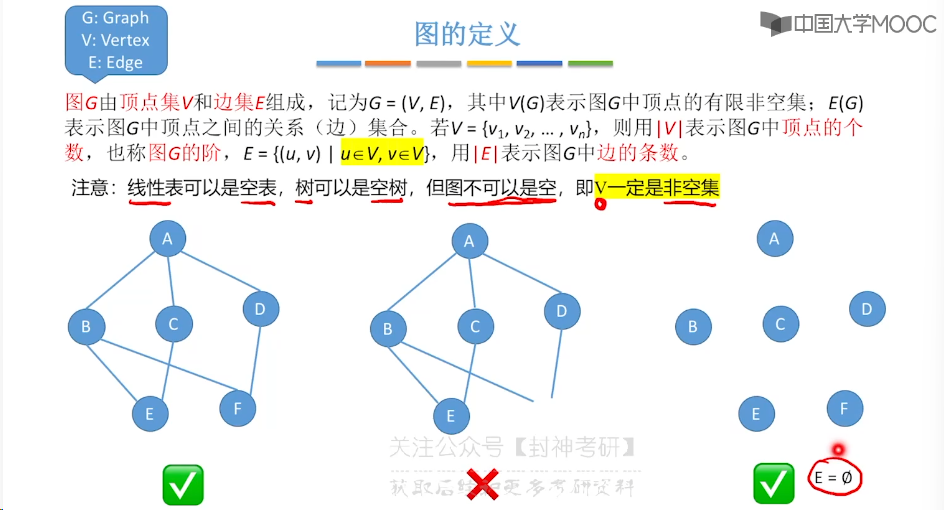
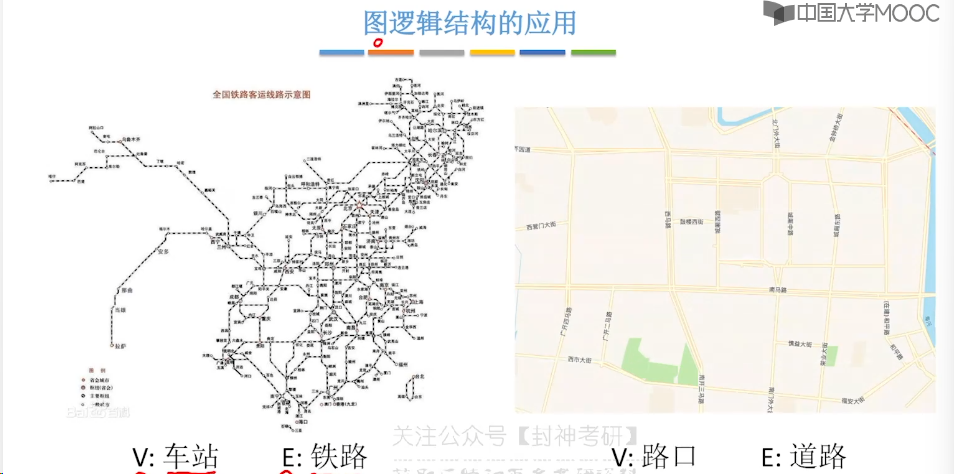
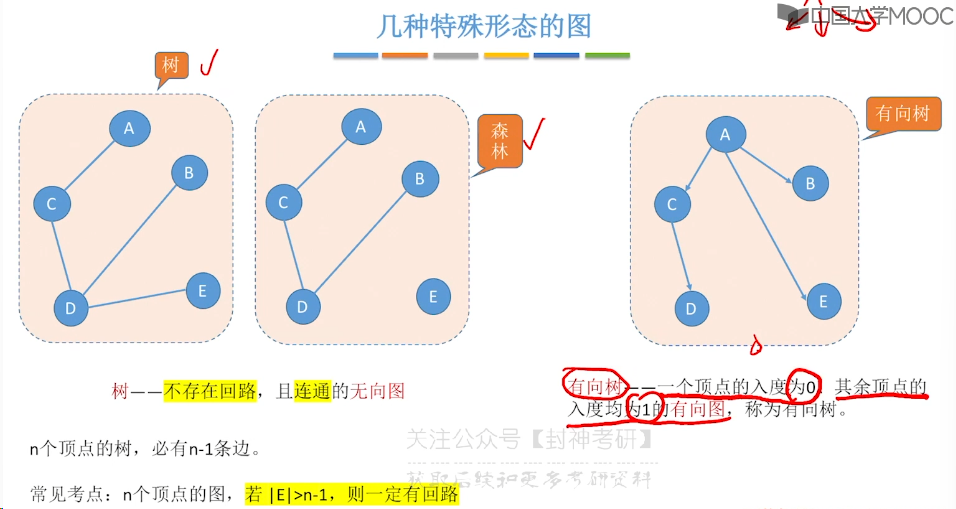
6.1、图的基本概念
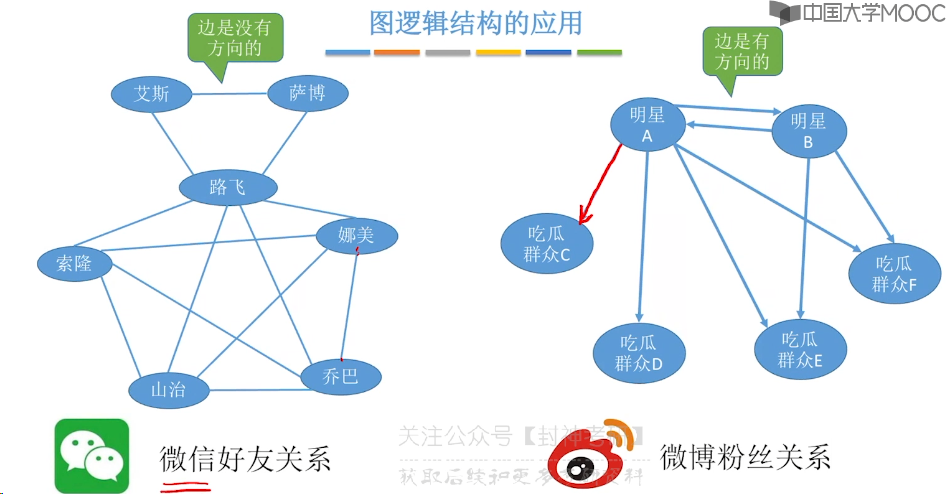
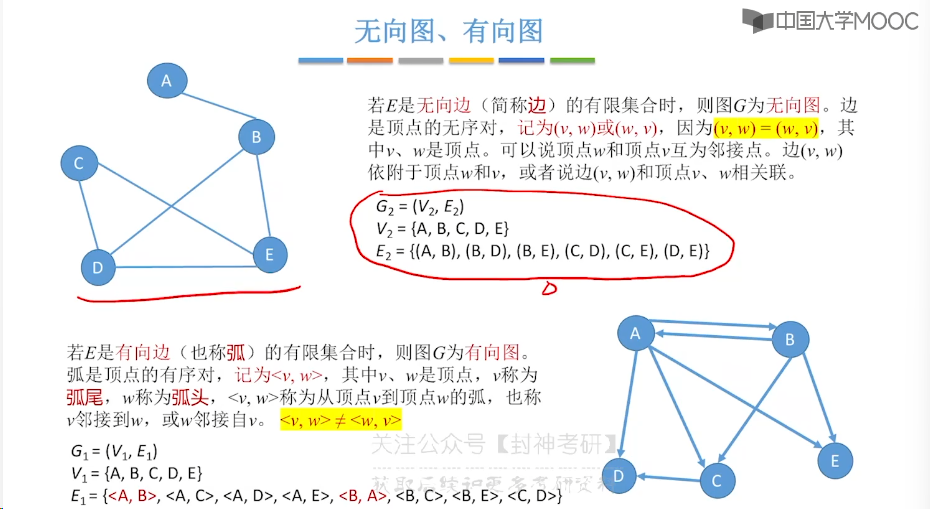
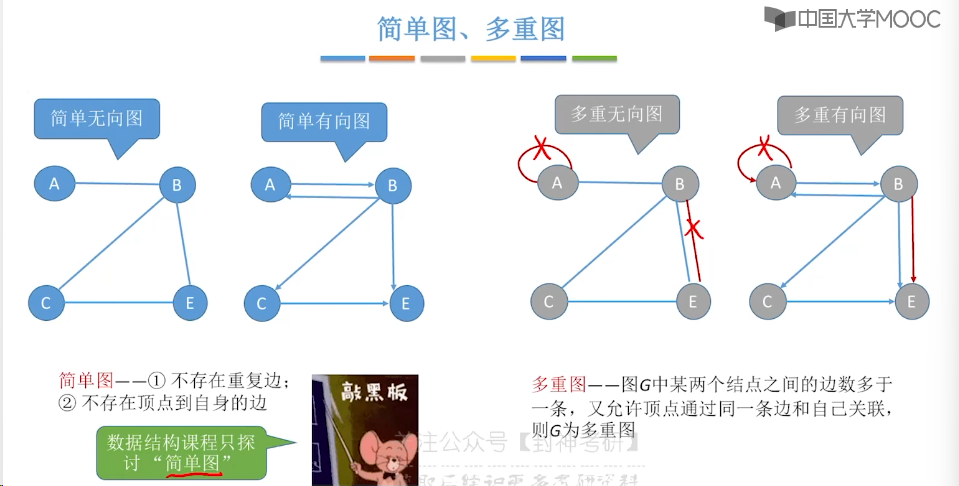
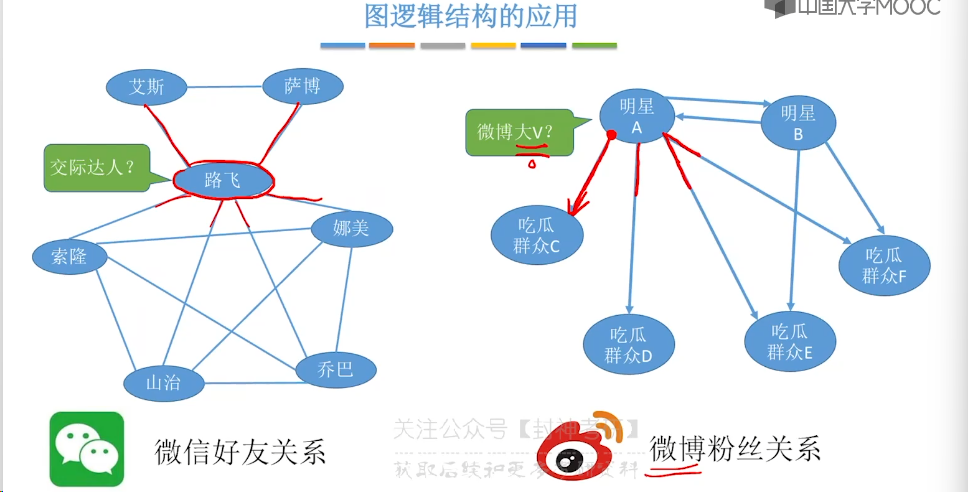
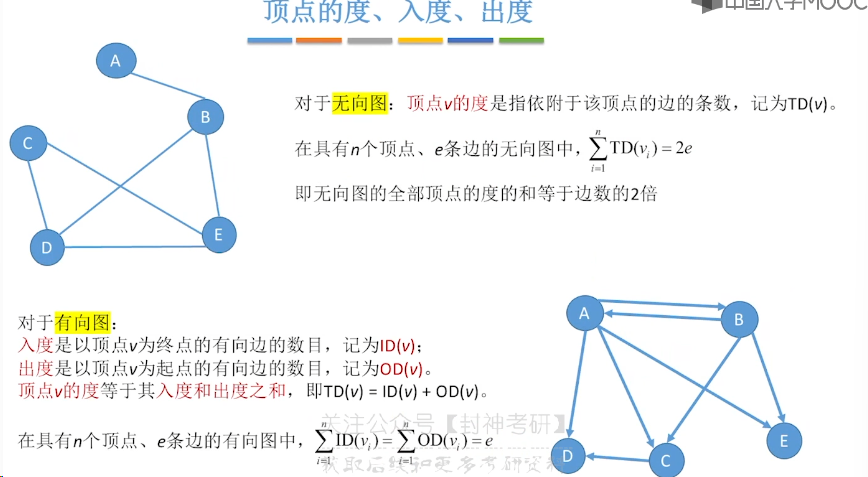
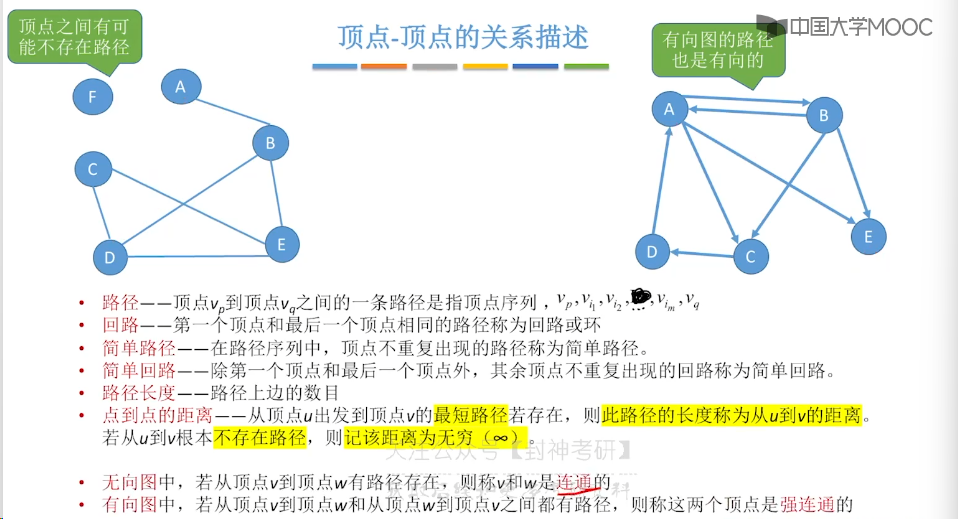
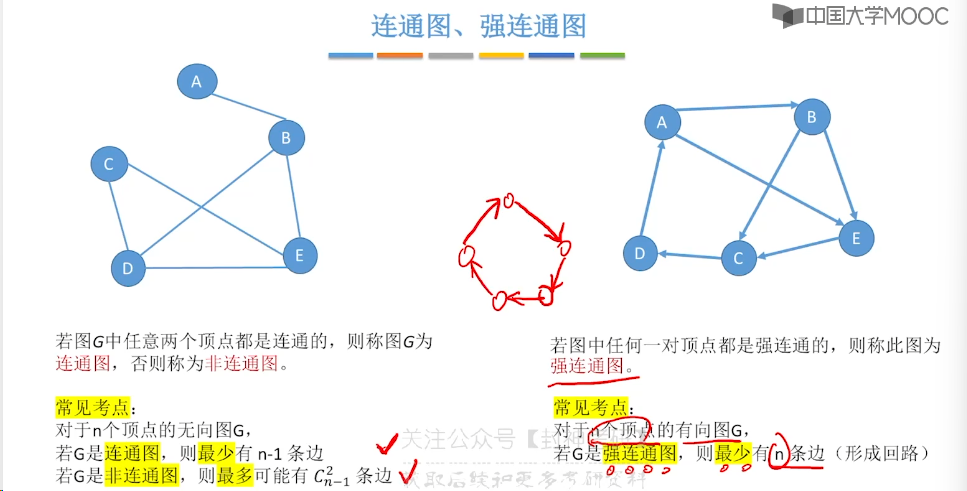
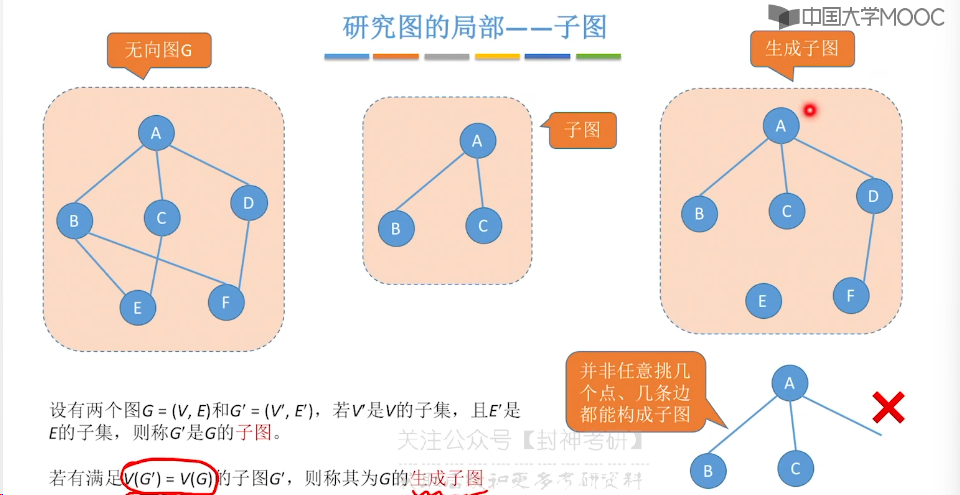
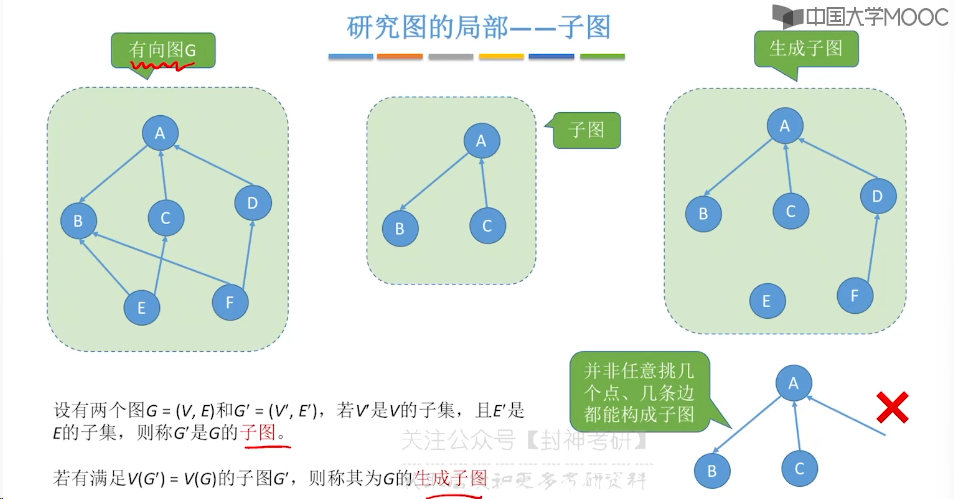
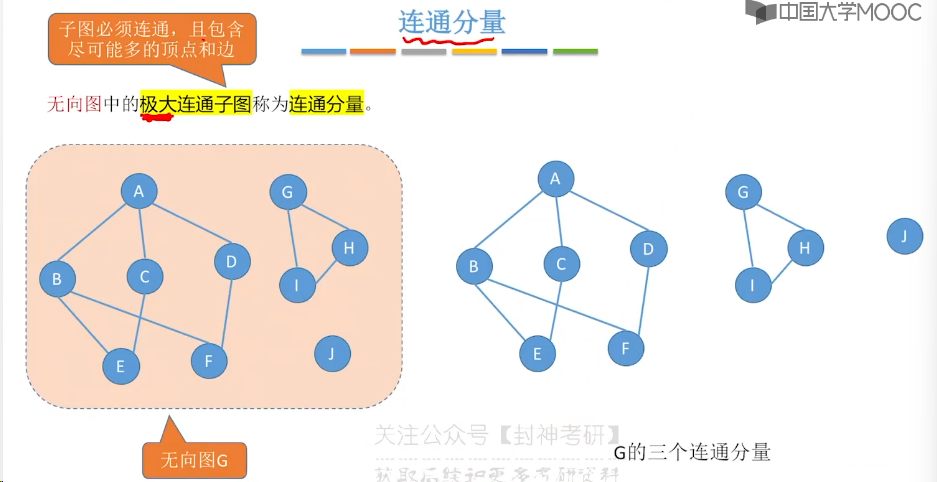
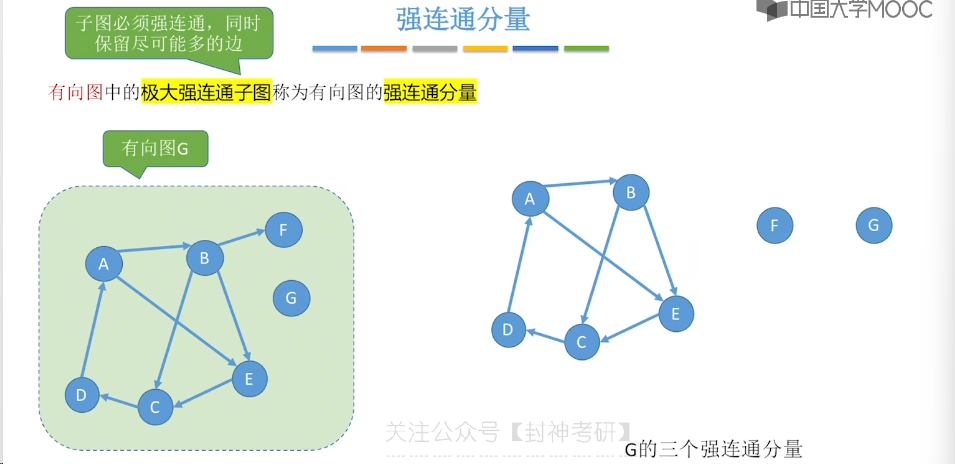
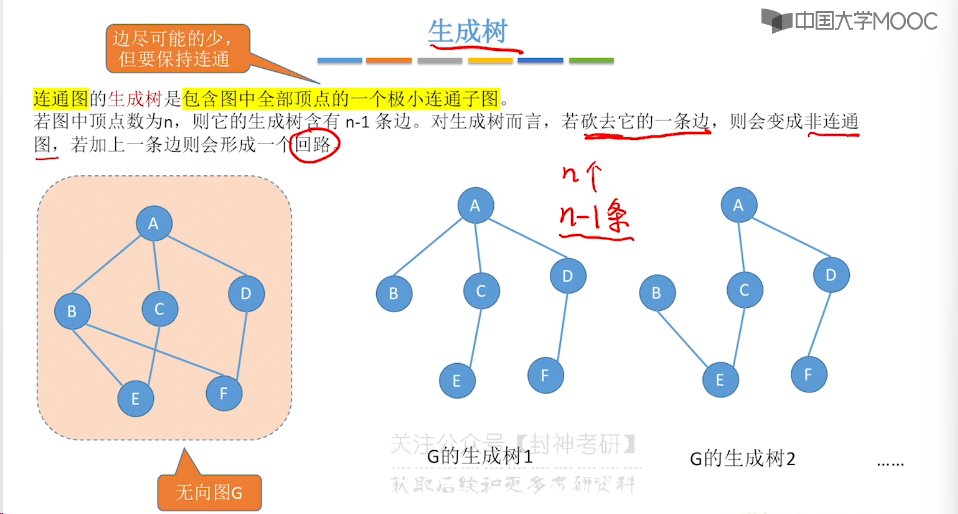
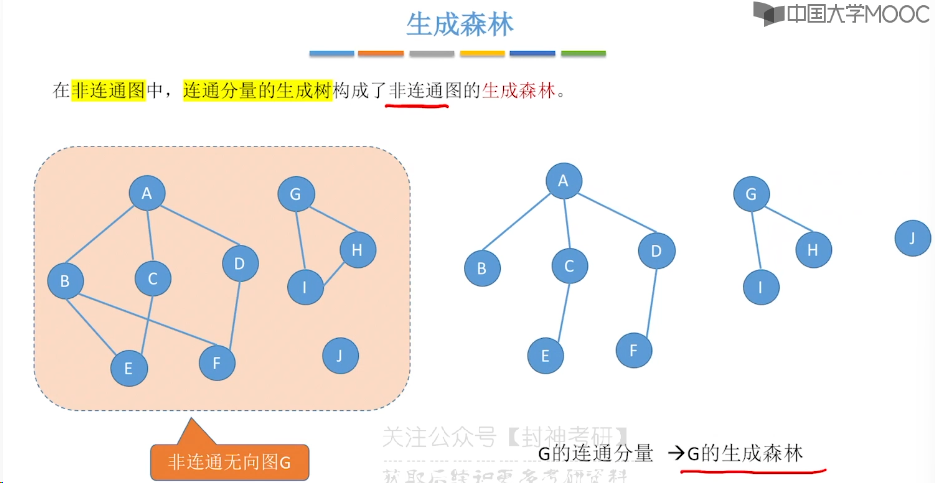
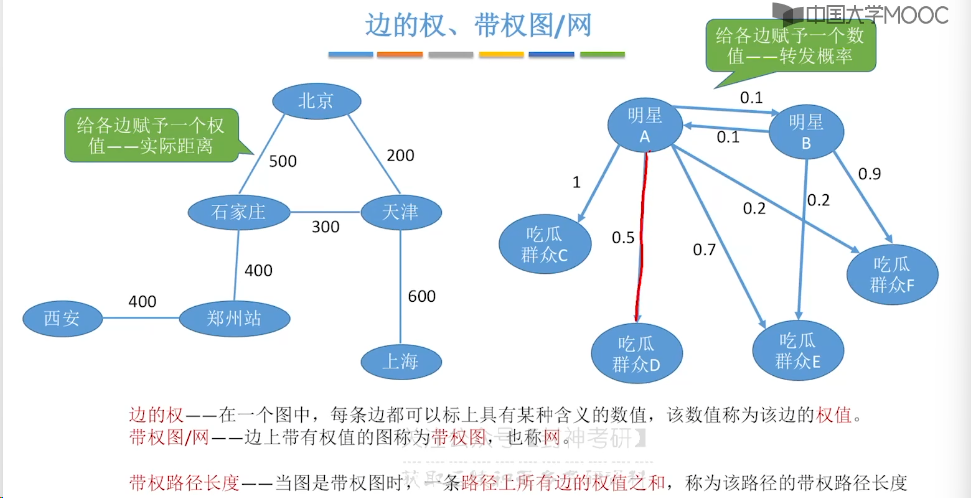
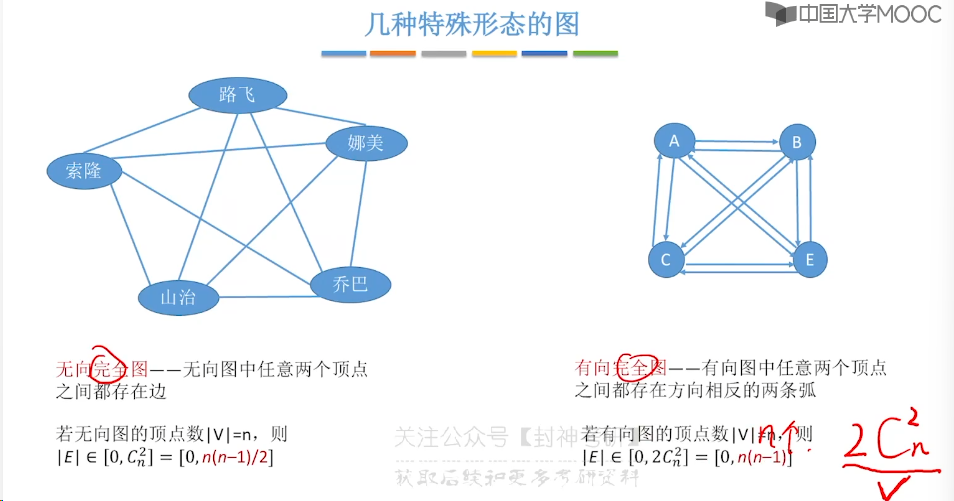
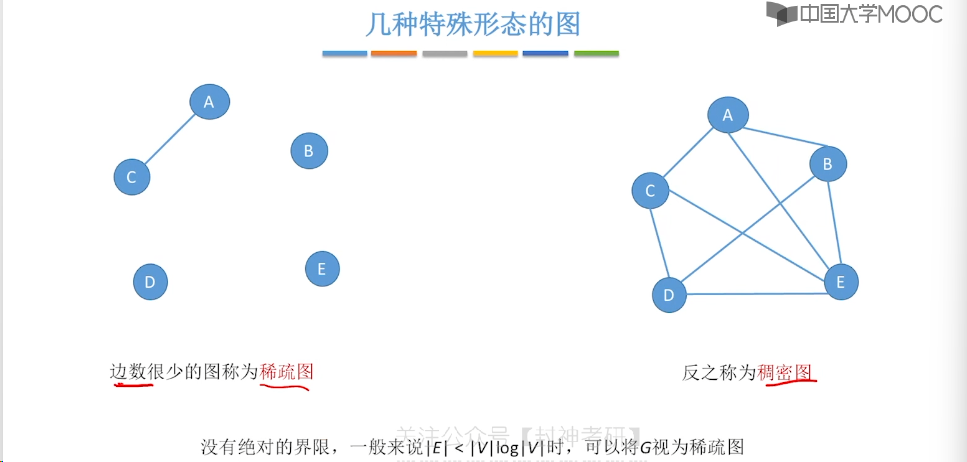
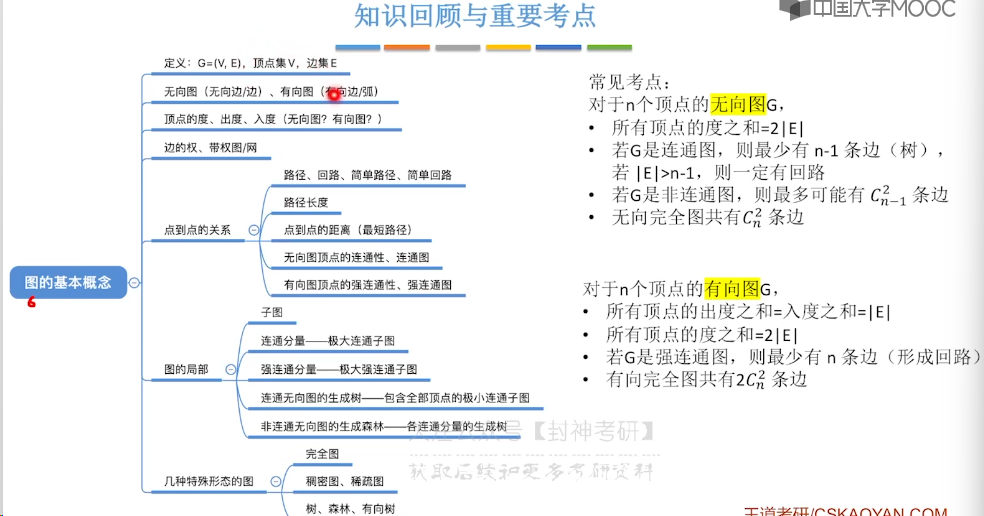
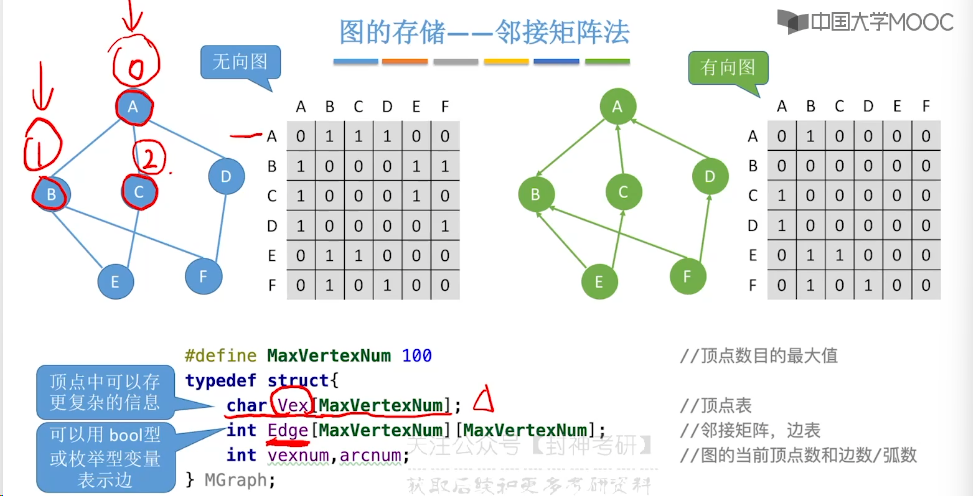
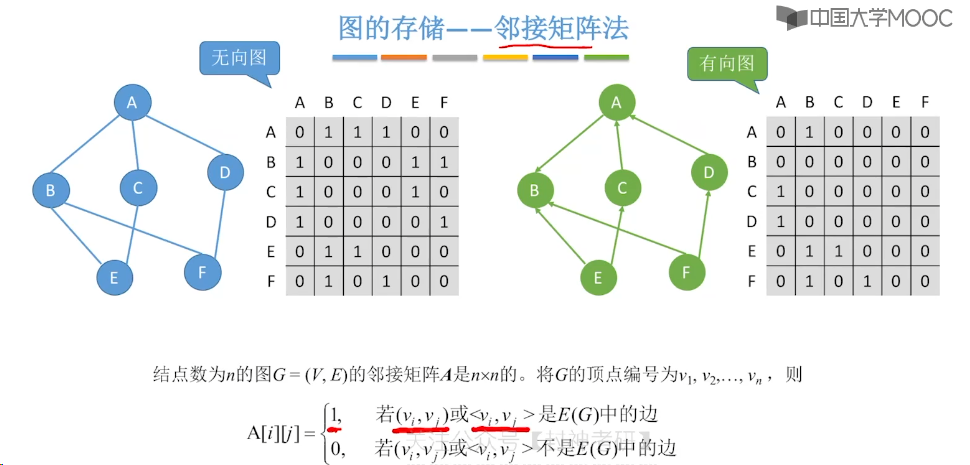
6.2、邻接矩阵法

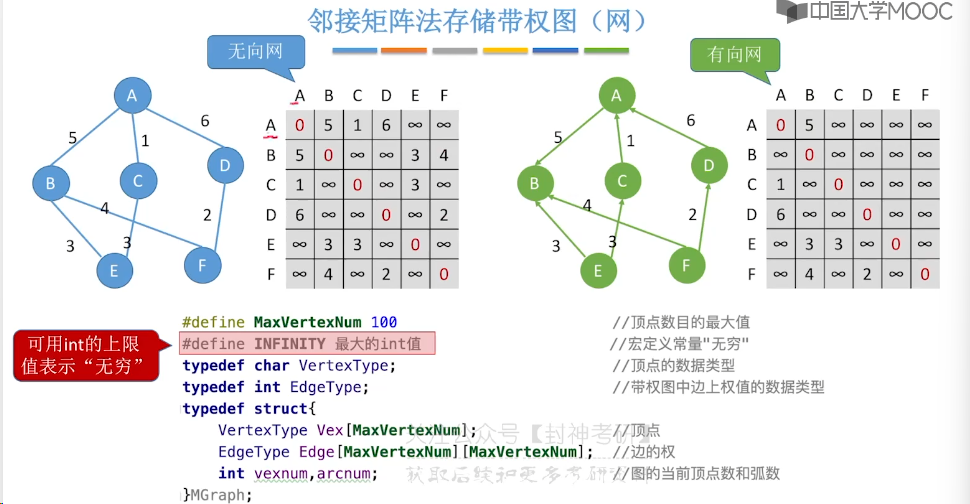
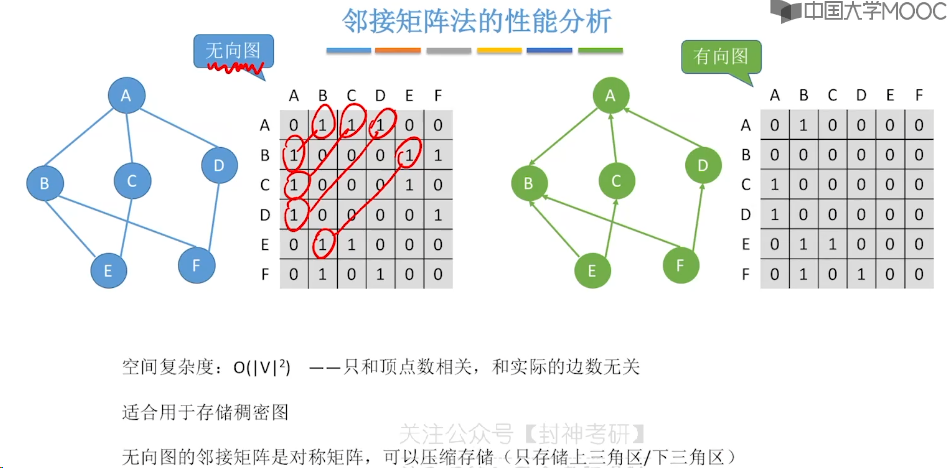
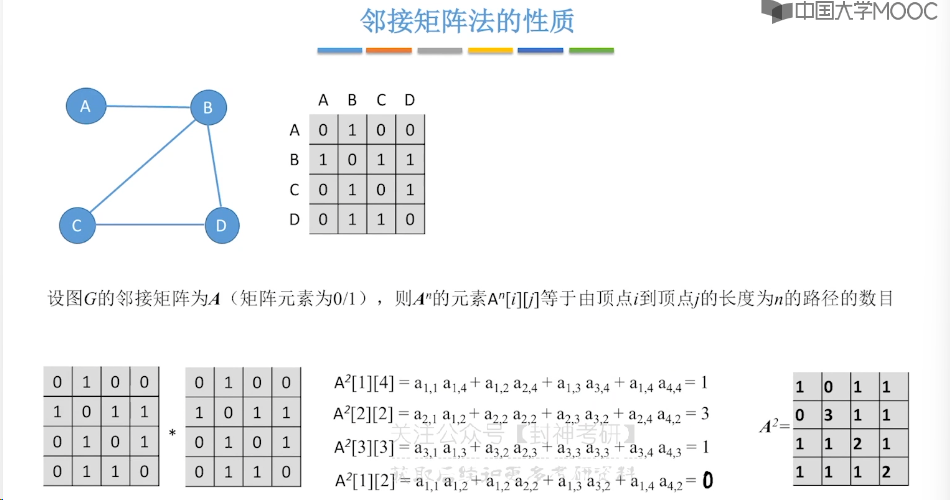
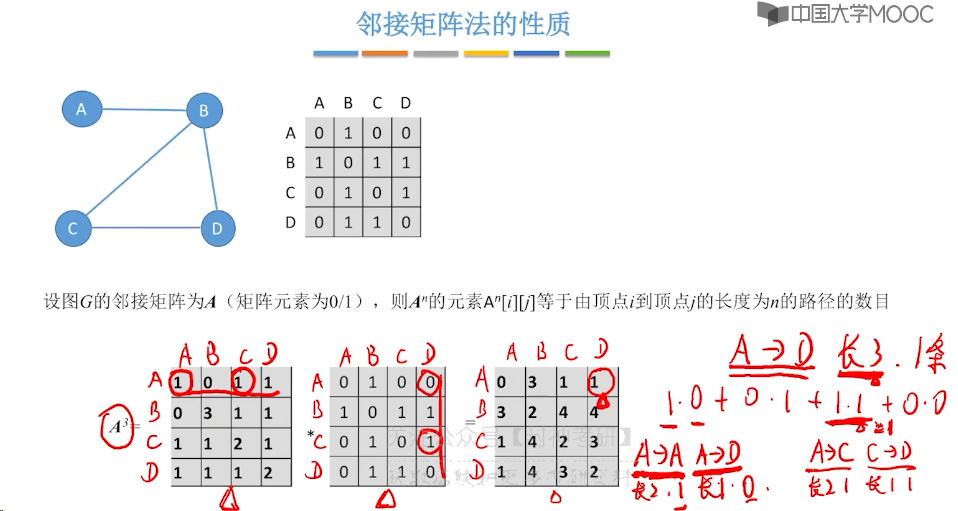

6.3、邻接表法
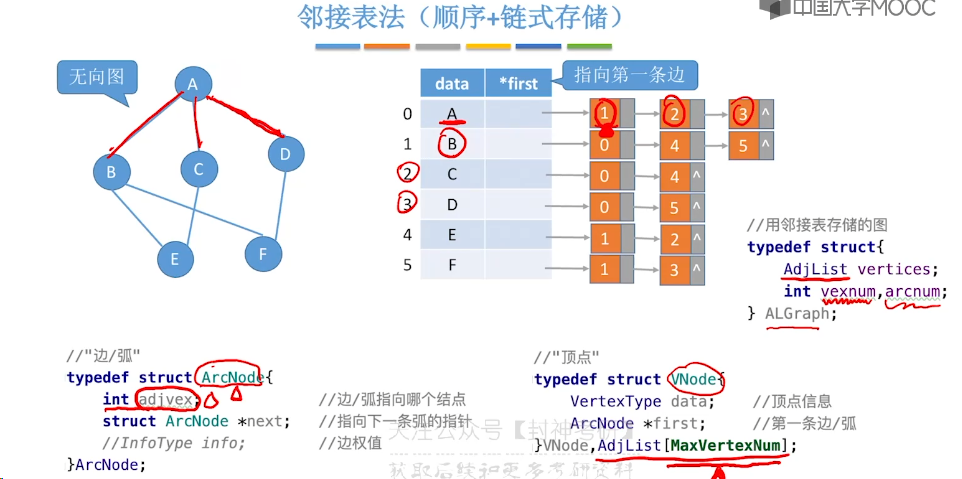
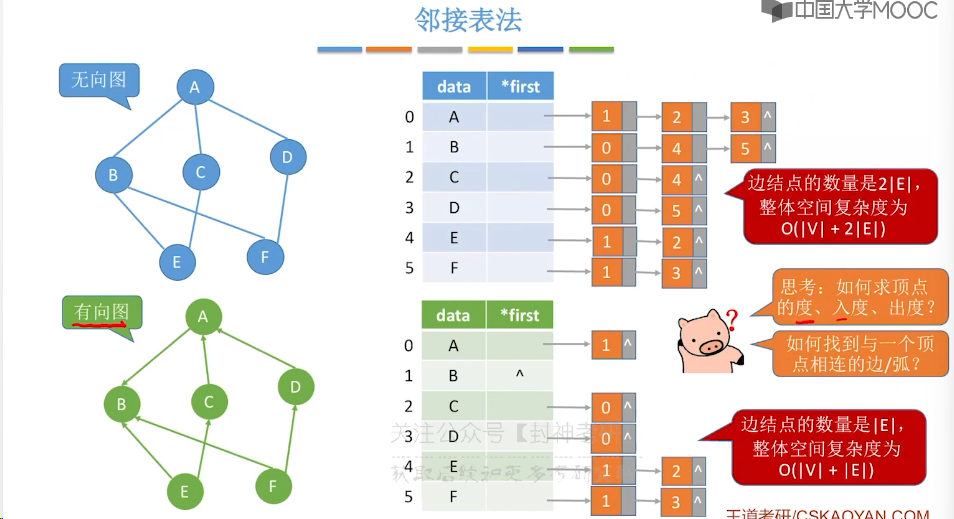
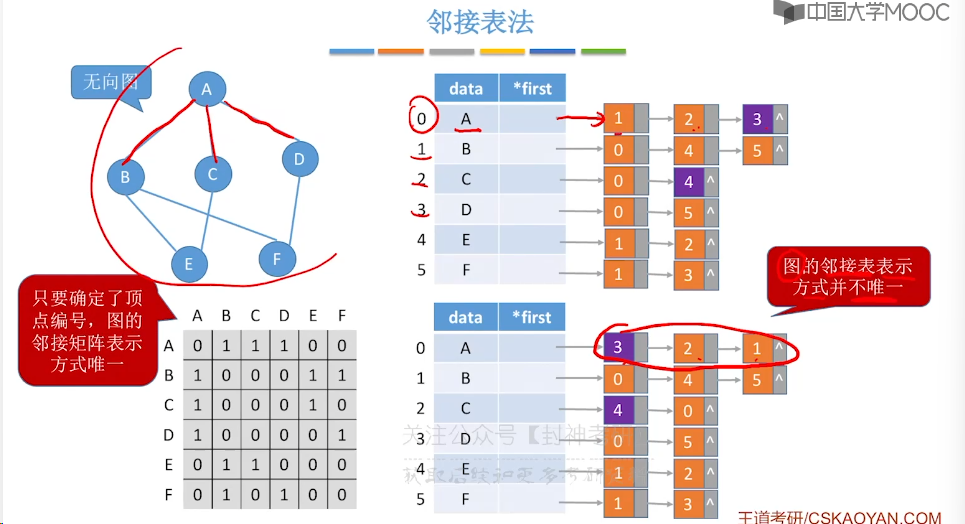
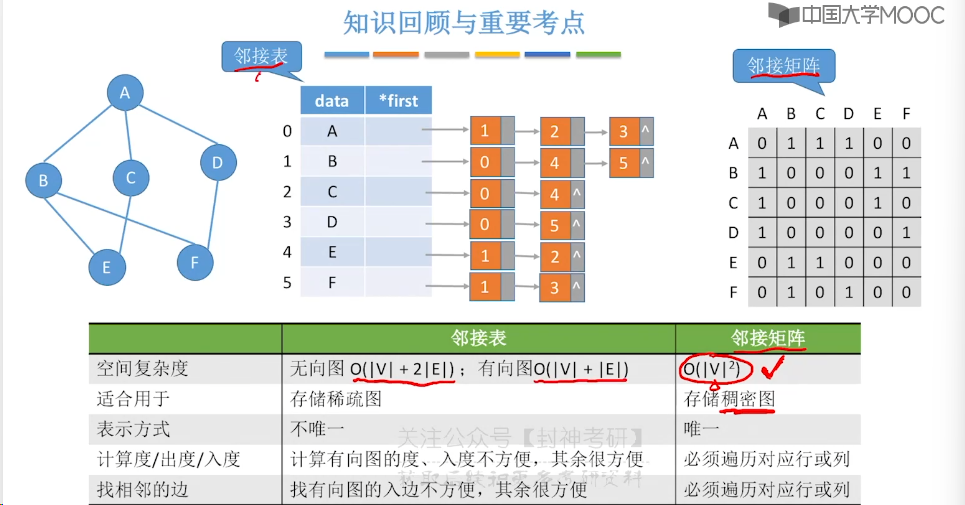
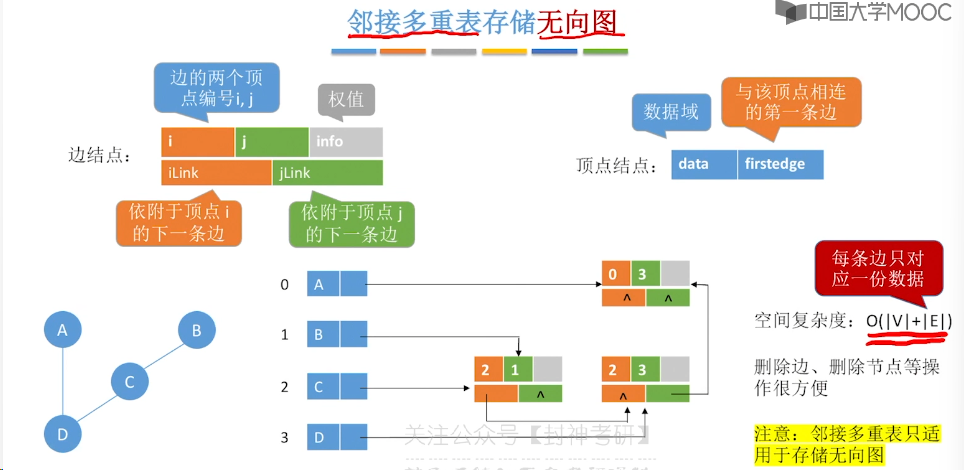
6.4、十字链表、邻接多重表
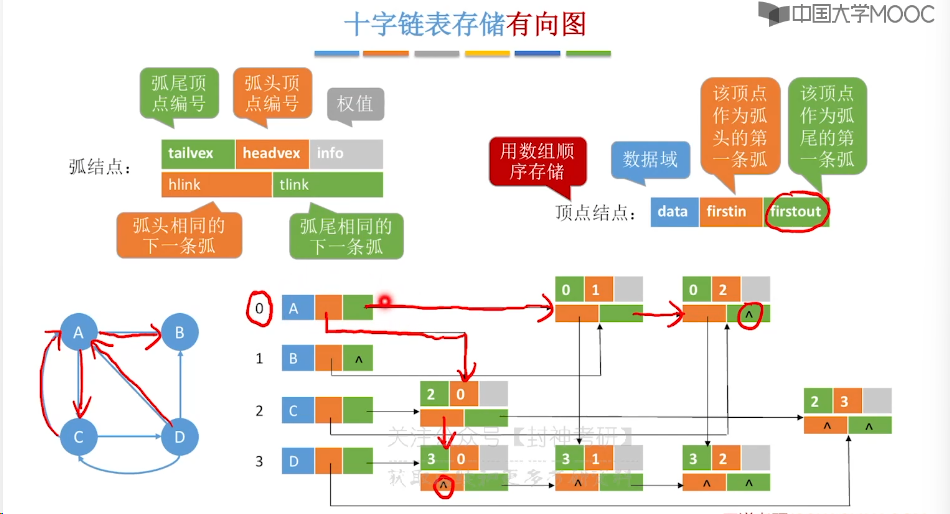
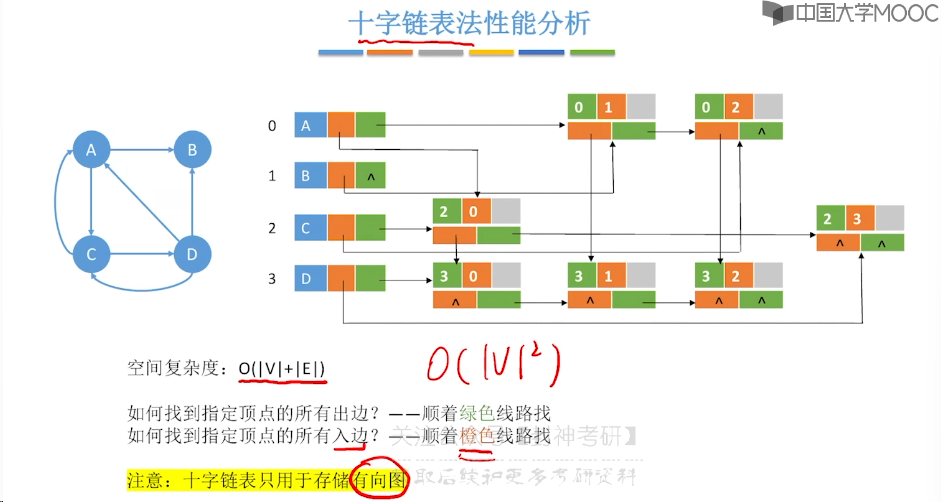
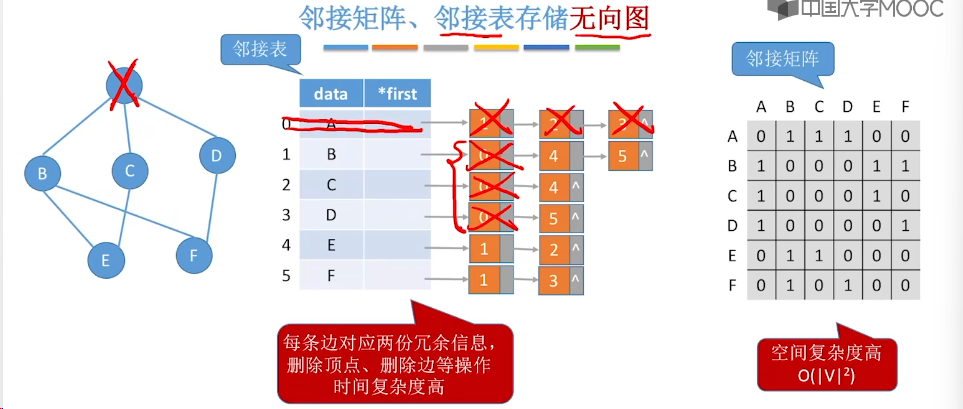
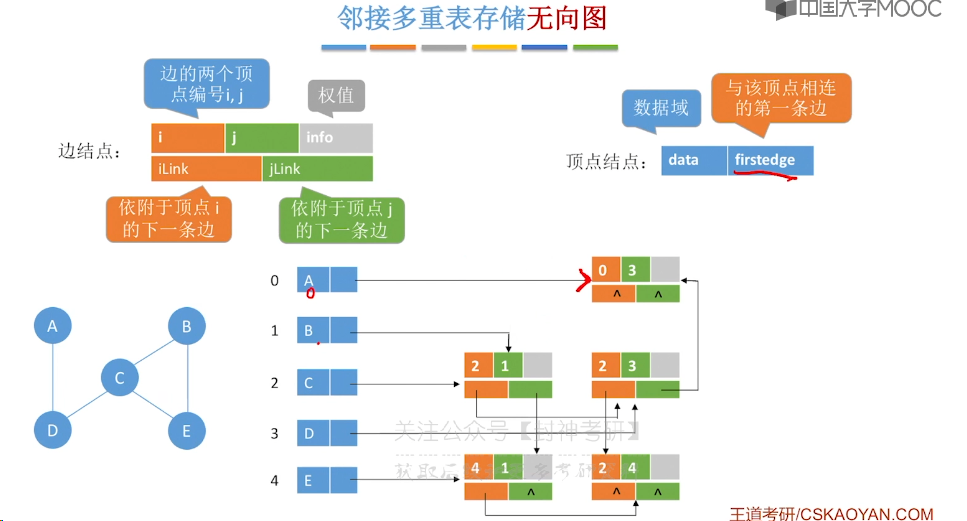

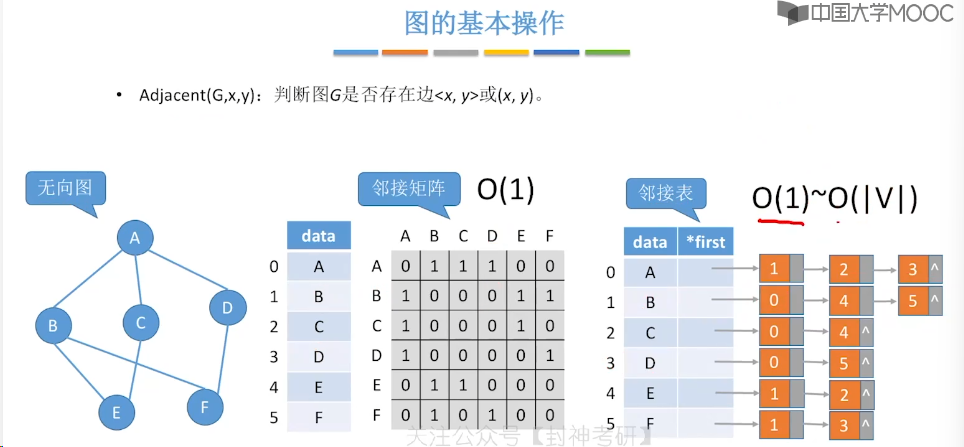
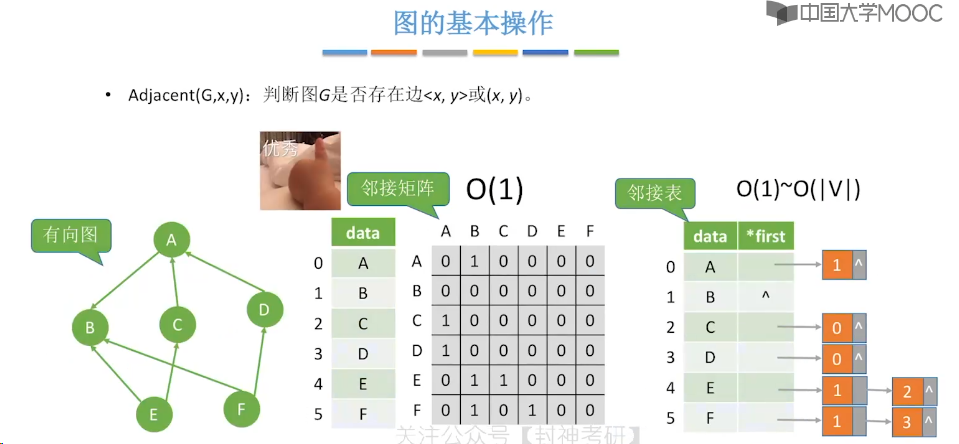
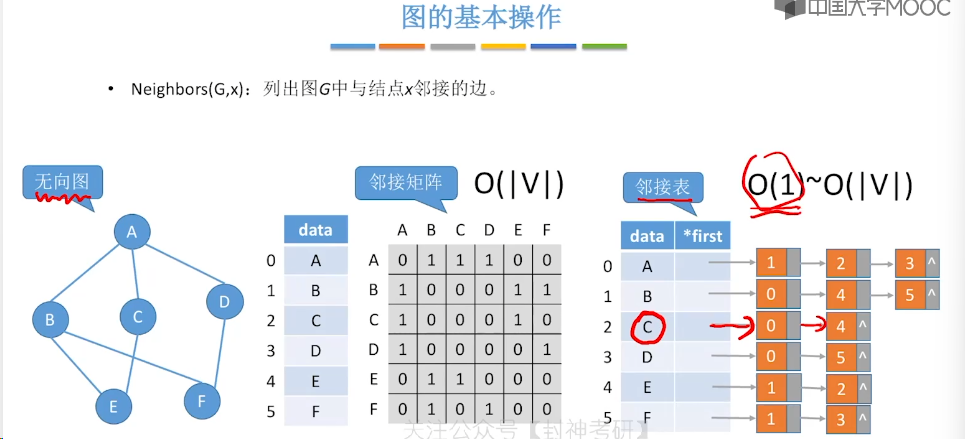
6.5、图的基本操作

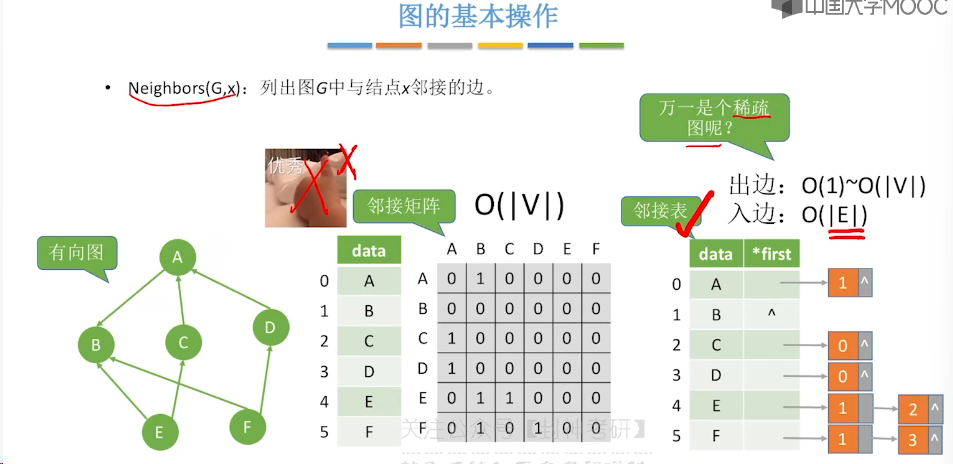
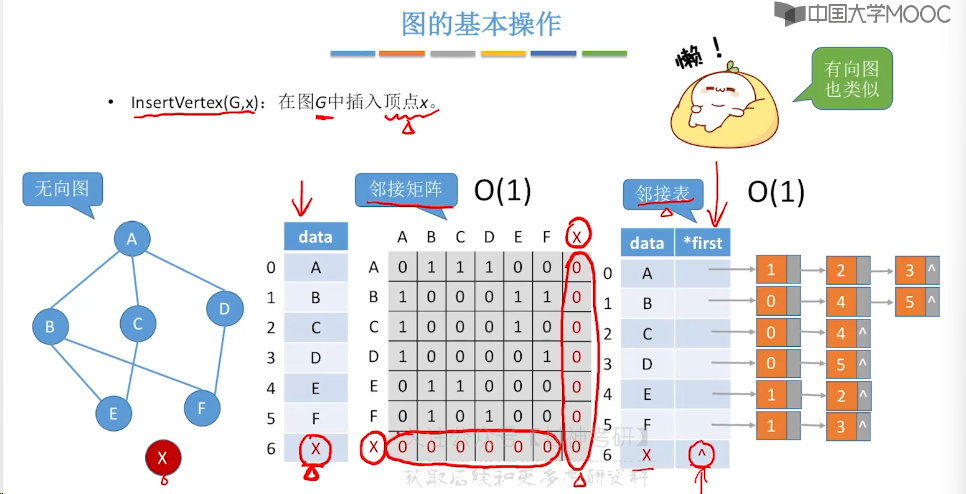
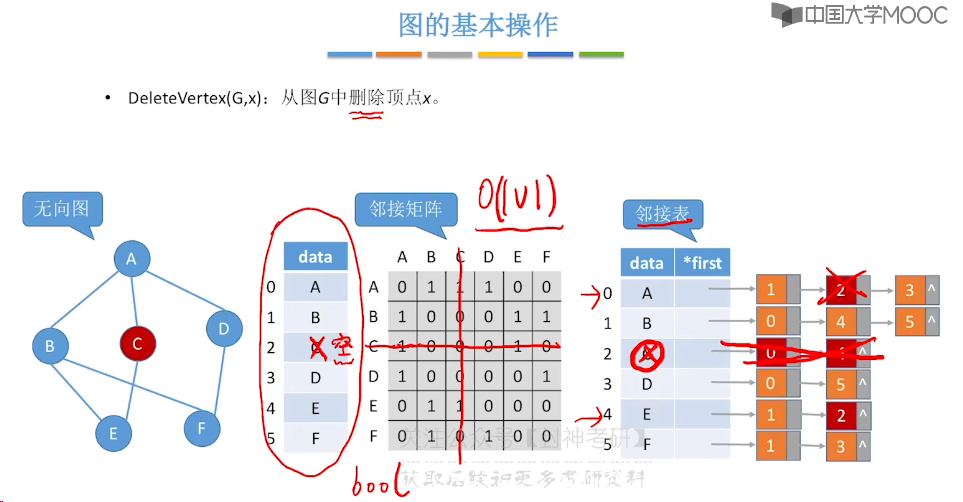
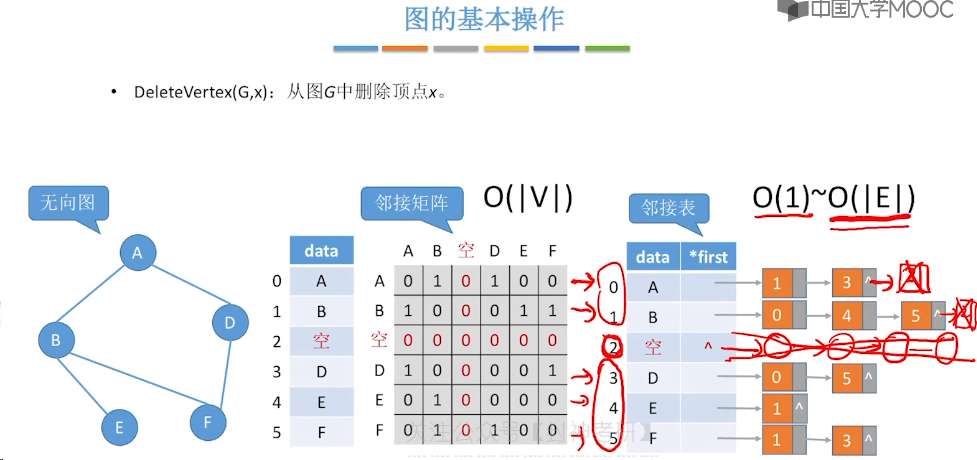

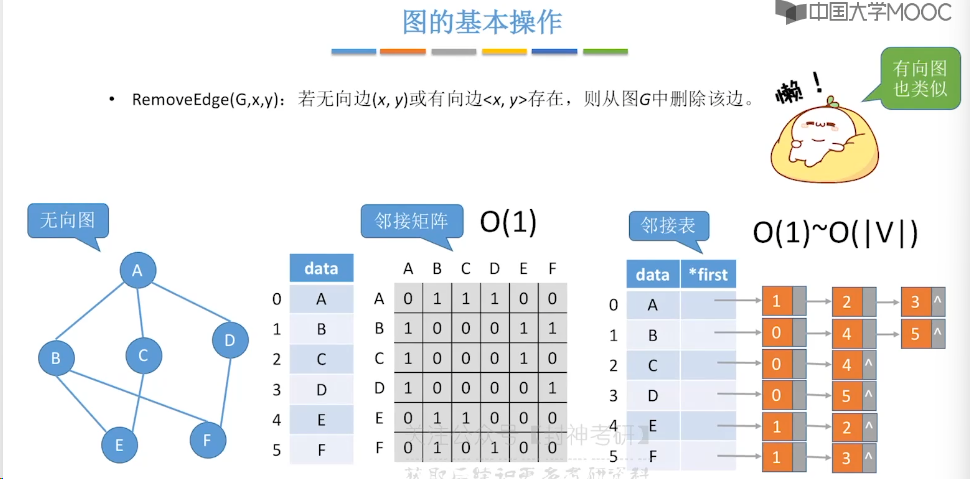
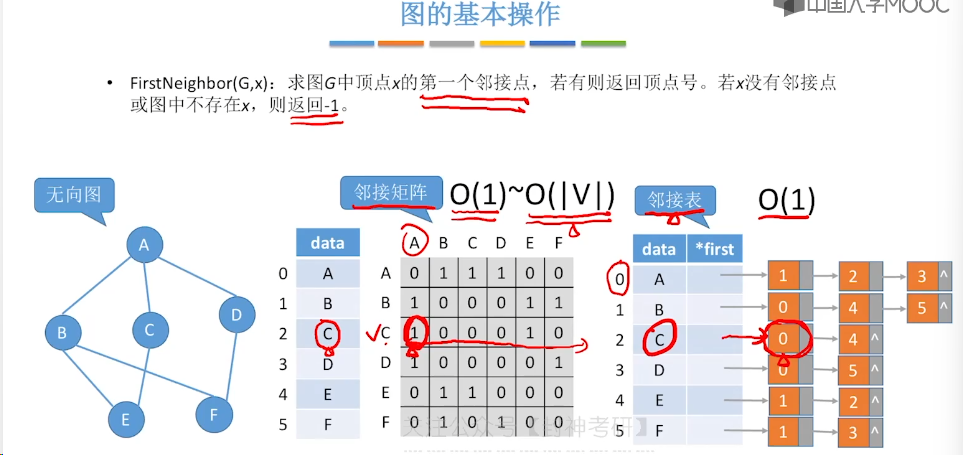
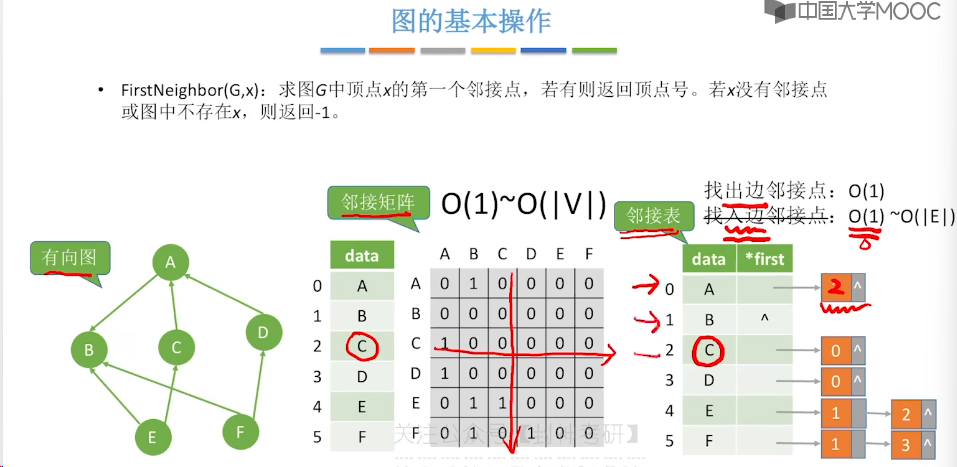
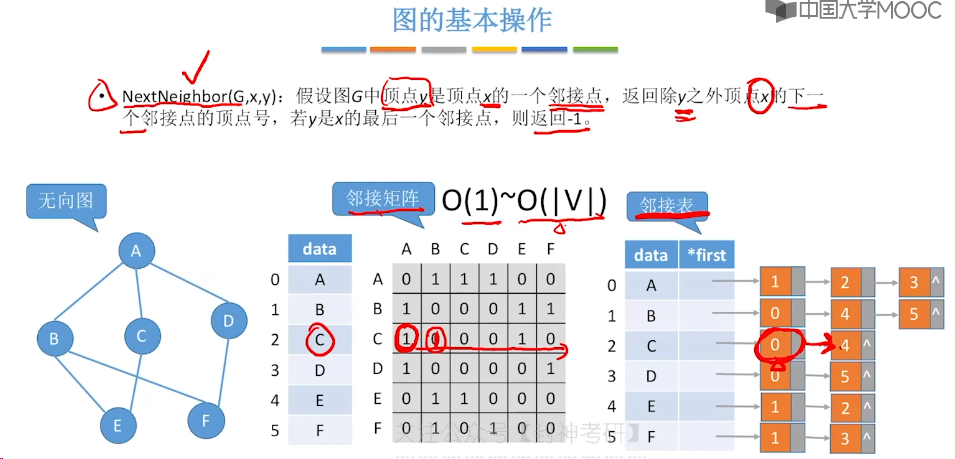
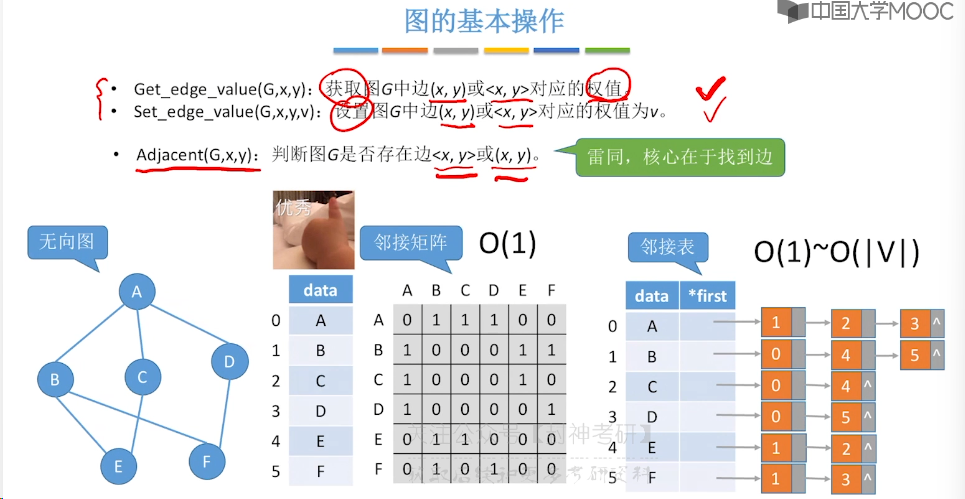
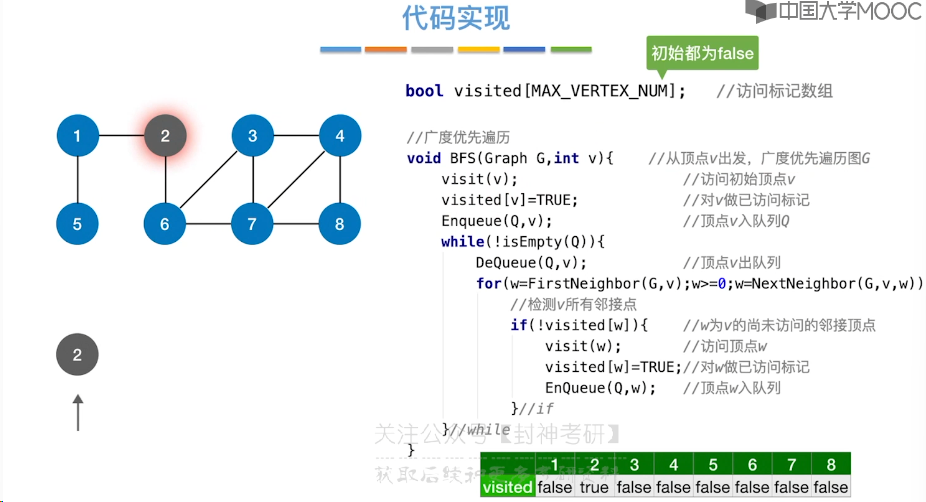
6.6、图的广度优先遍历
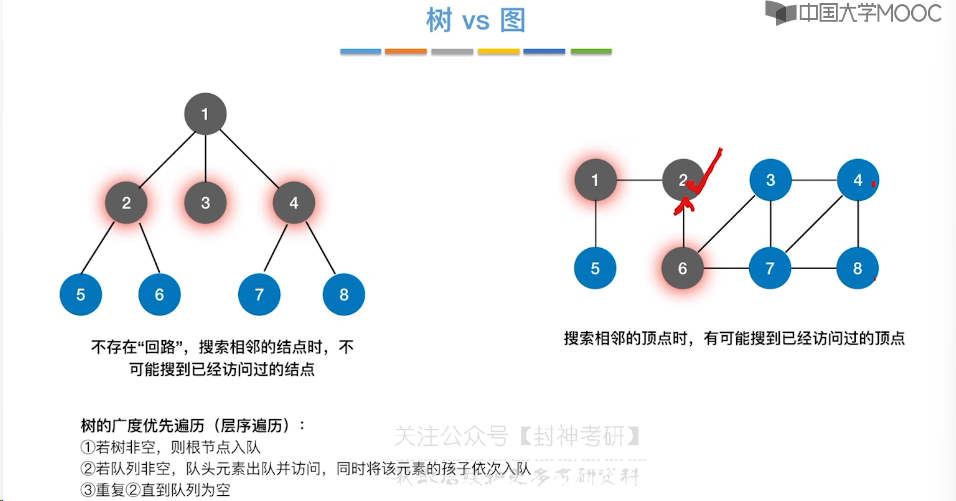
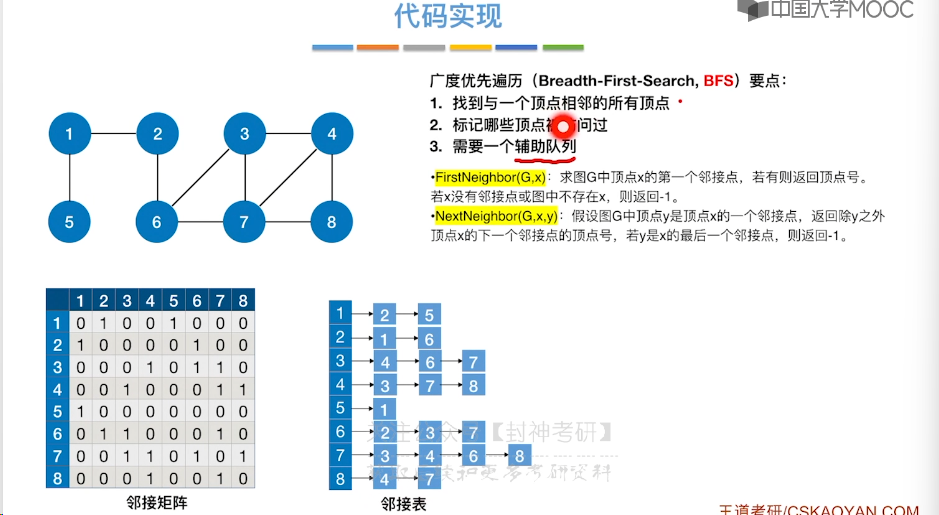
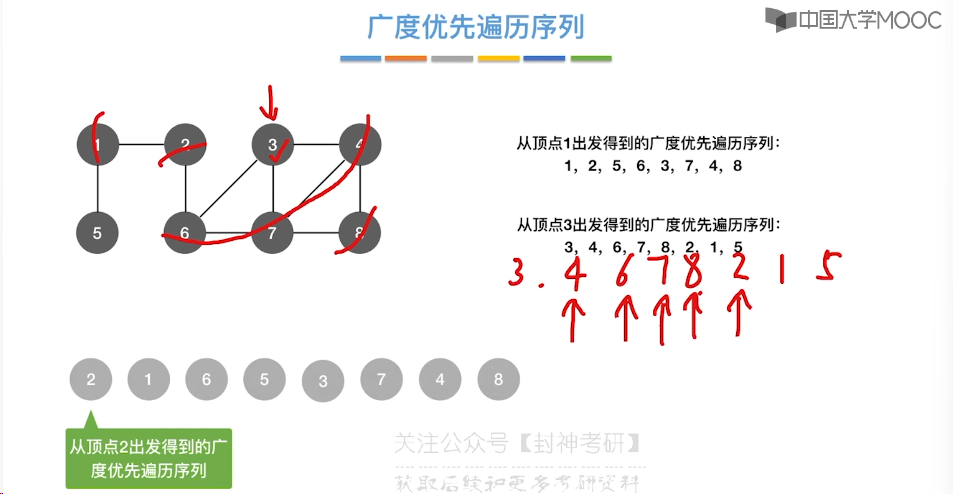
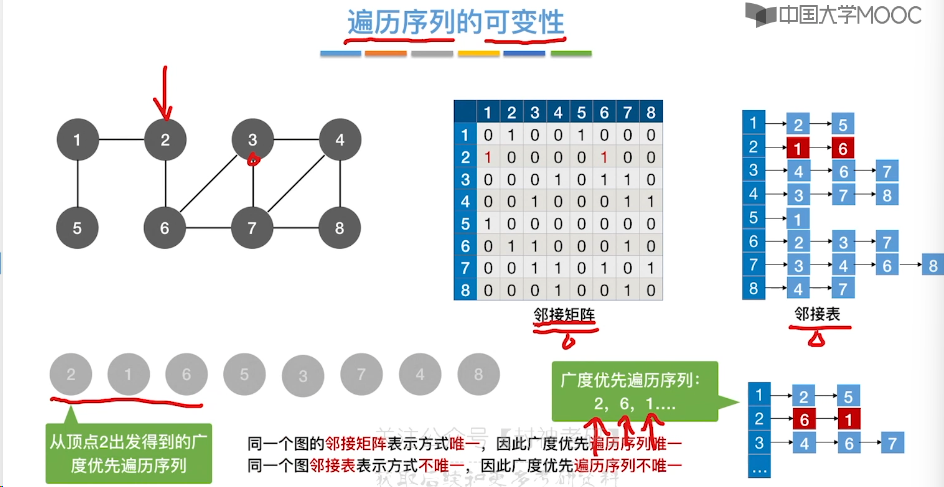

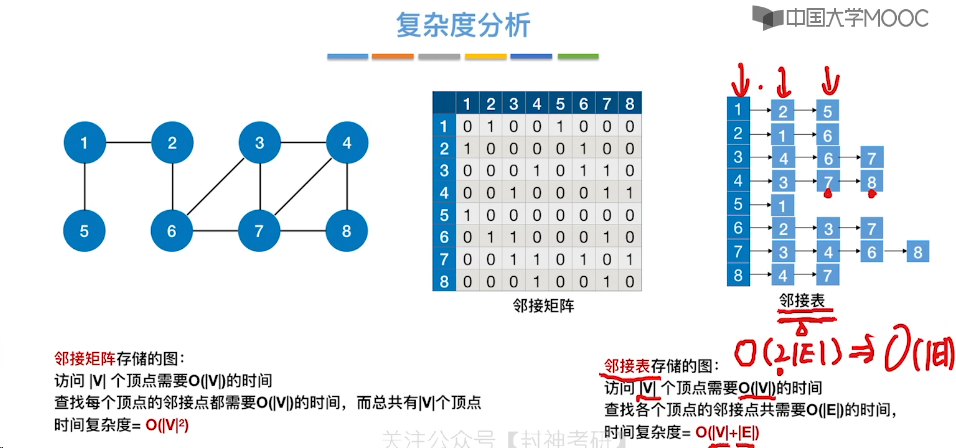
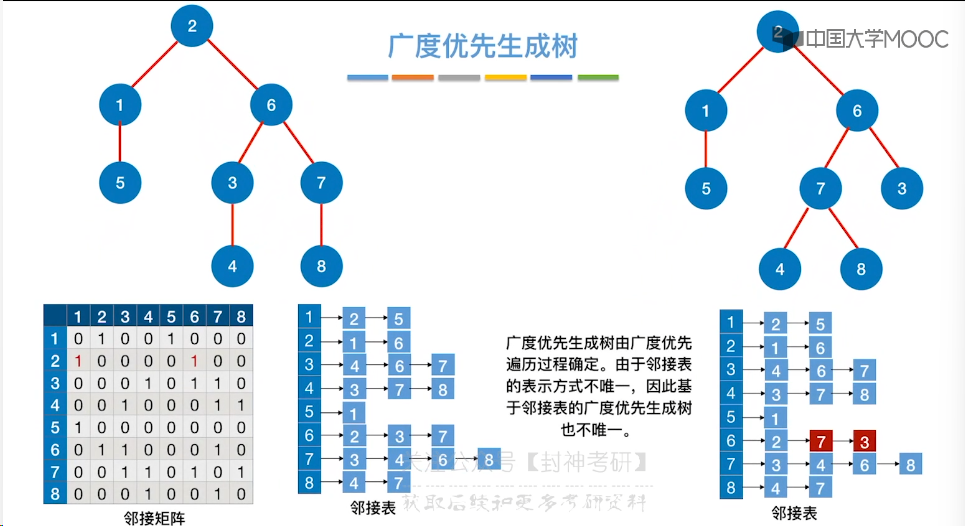
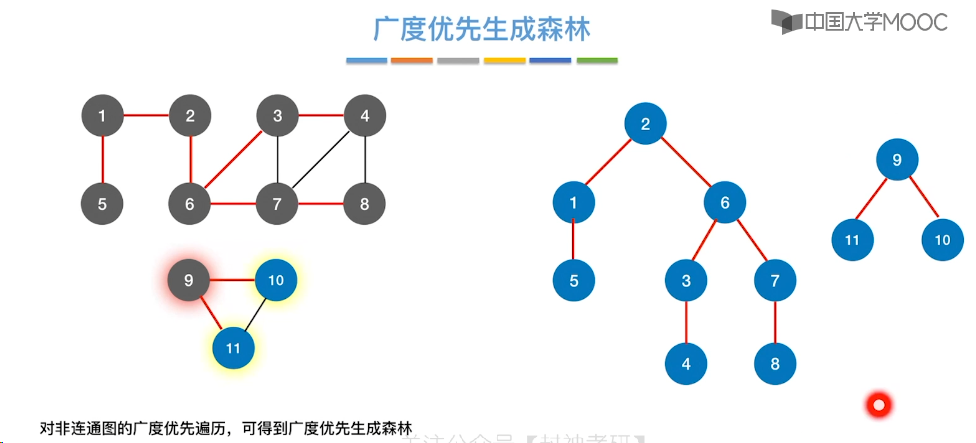
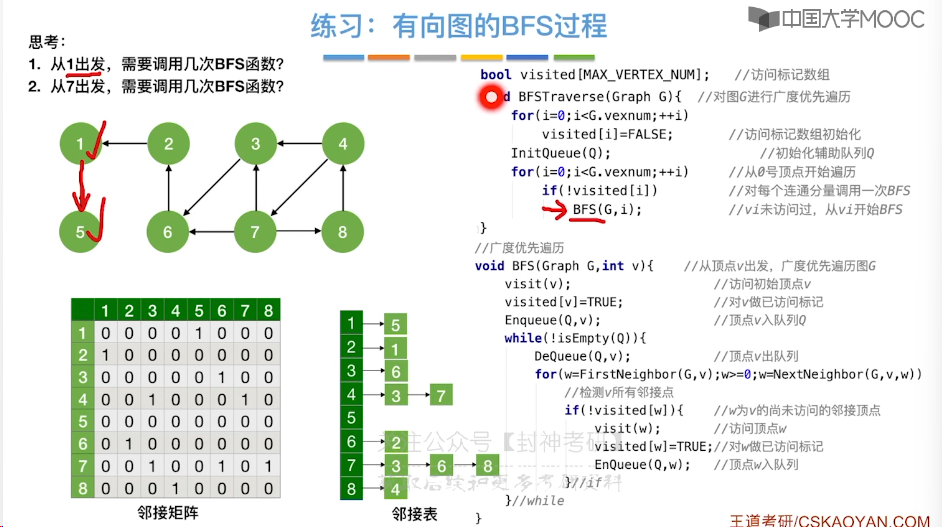
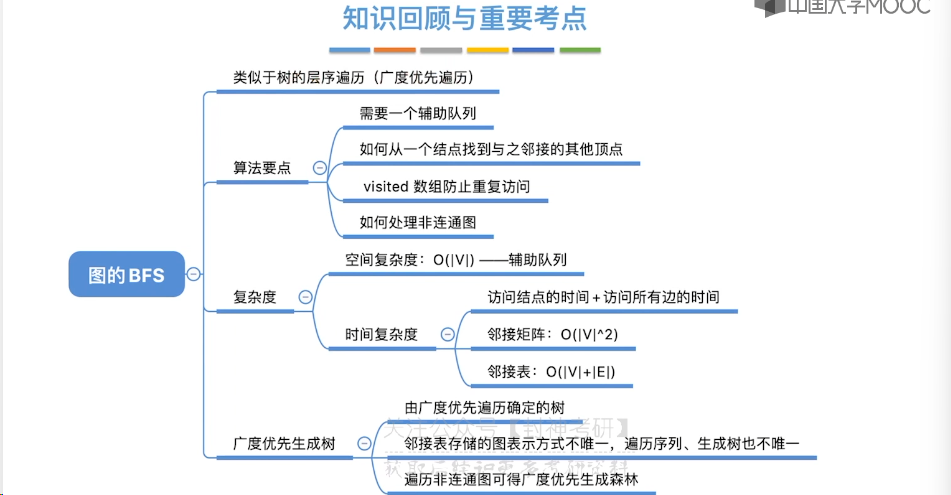
6.6、图的深度优先遍历
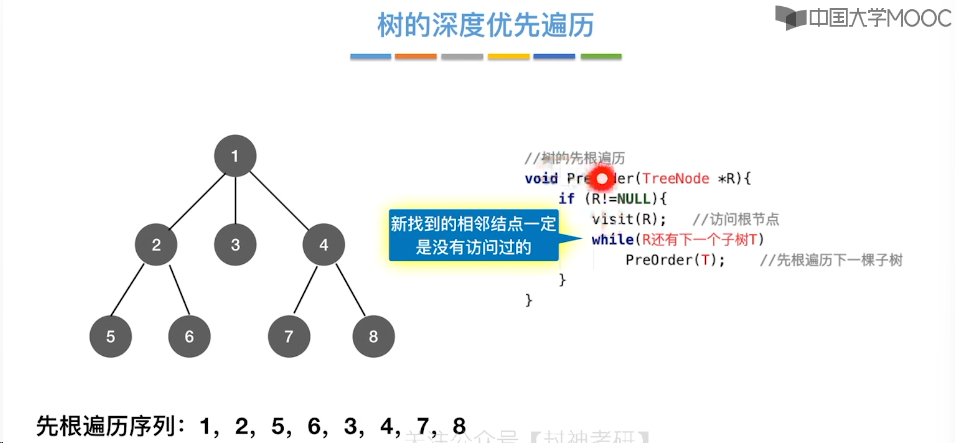
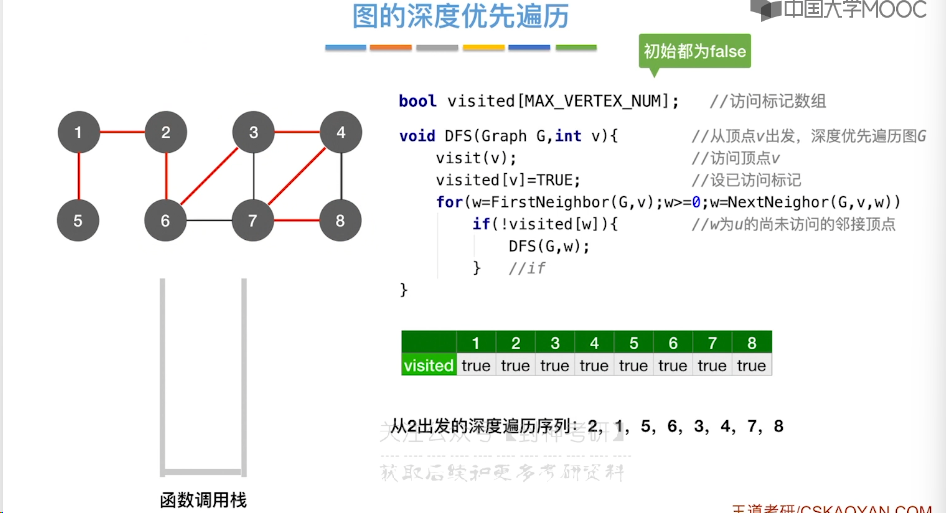

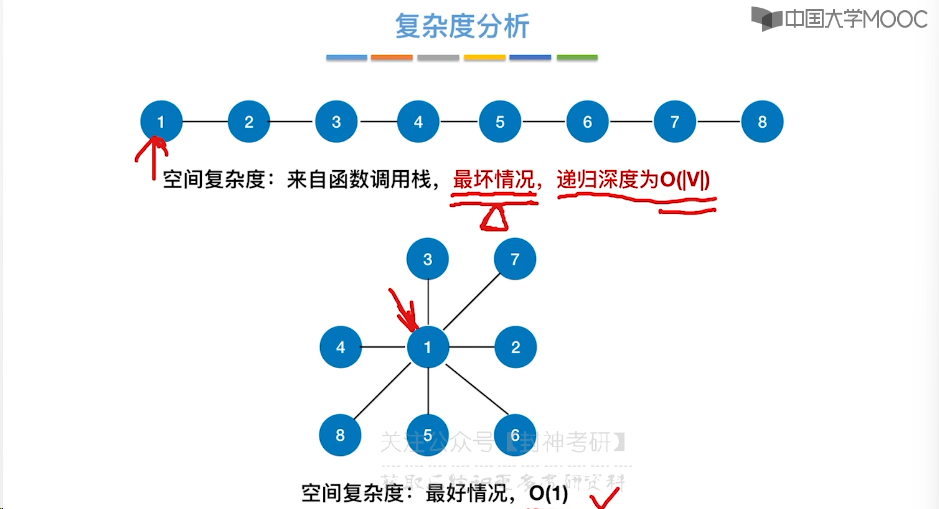
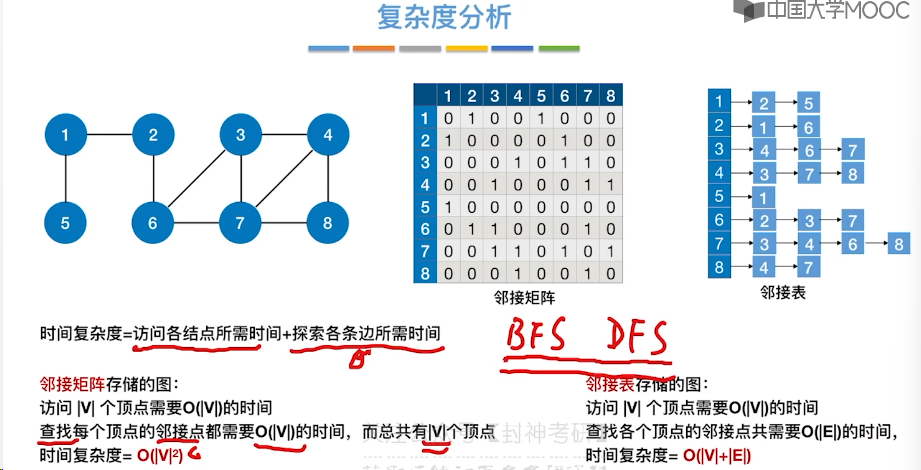
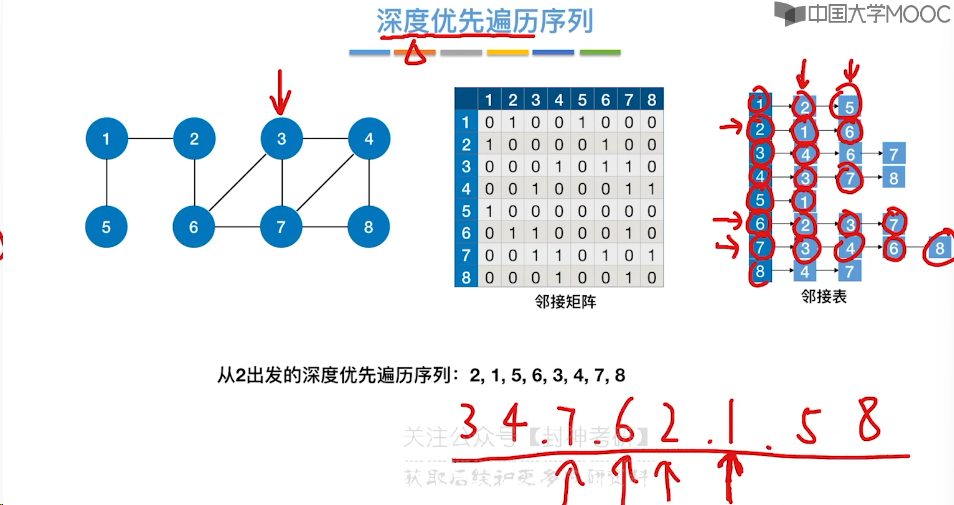
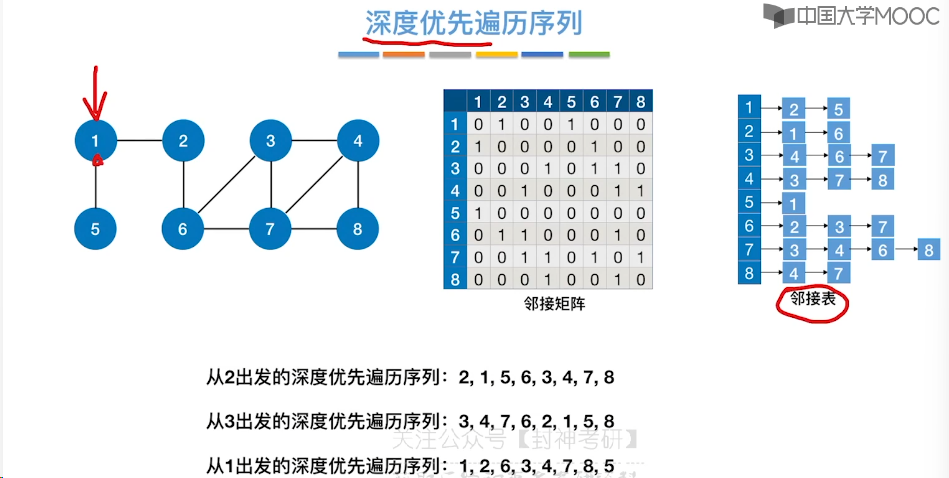
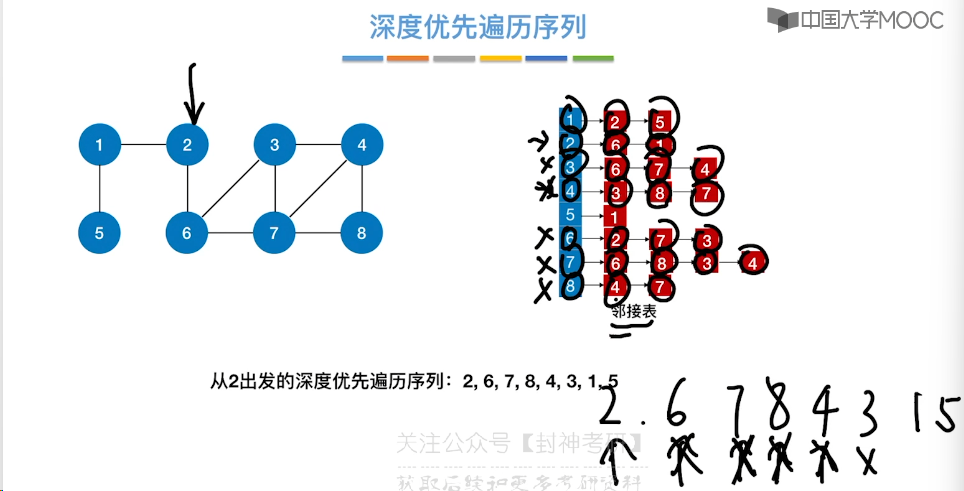
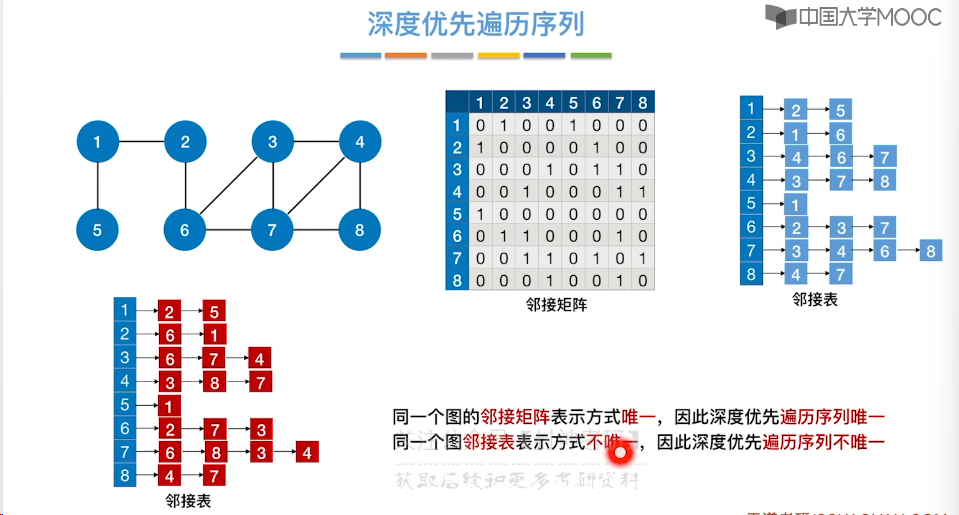
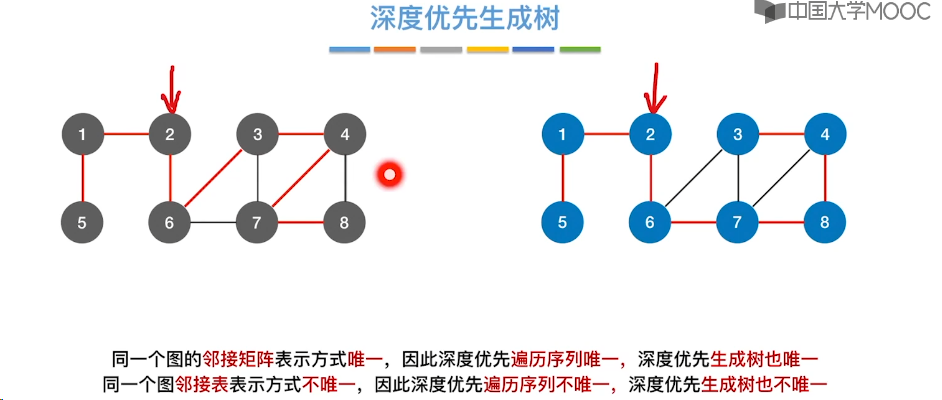
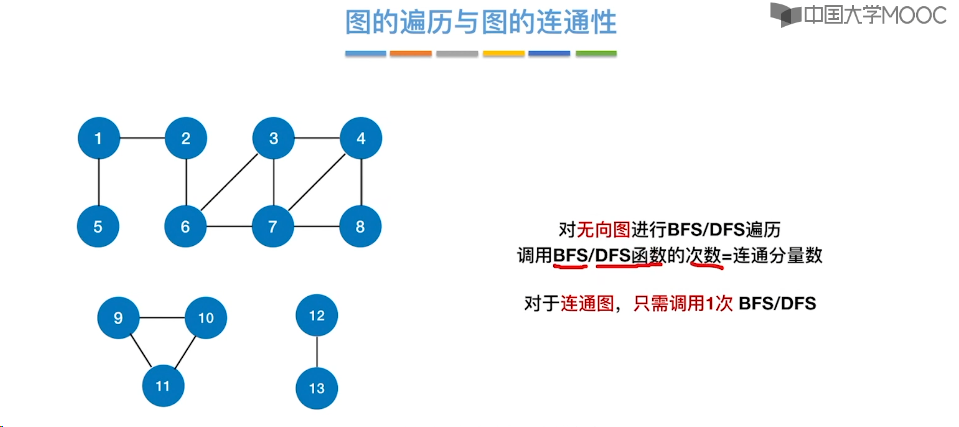
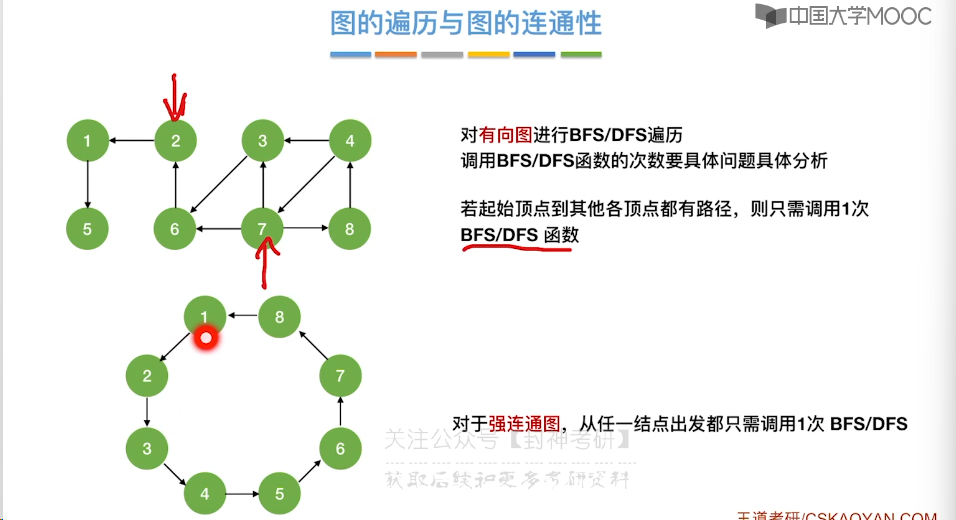
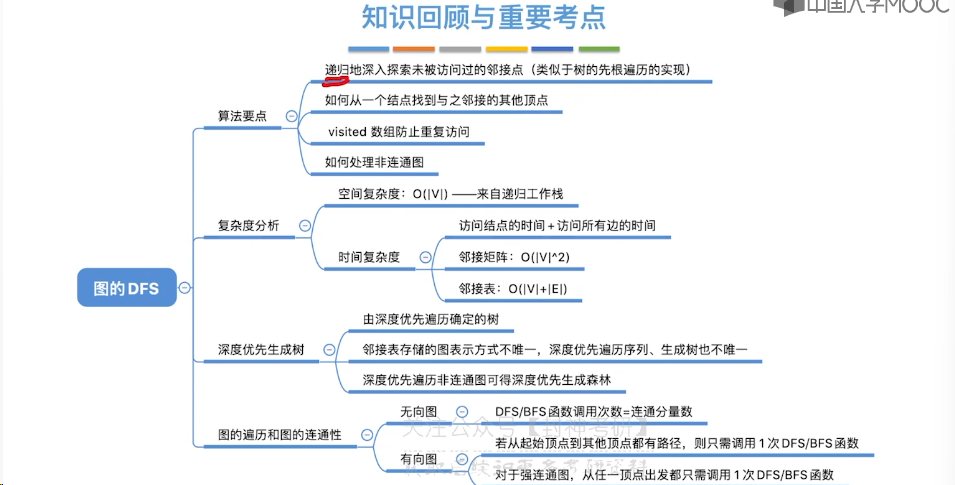
6.7、最小生成树

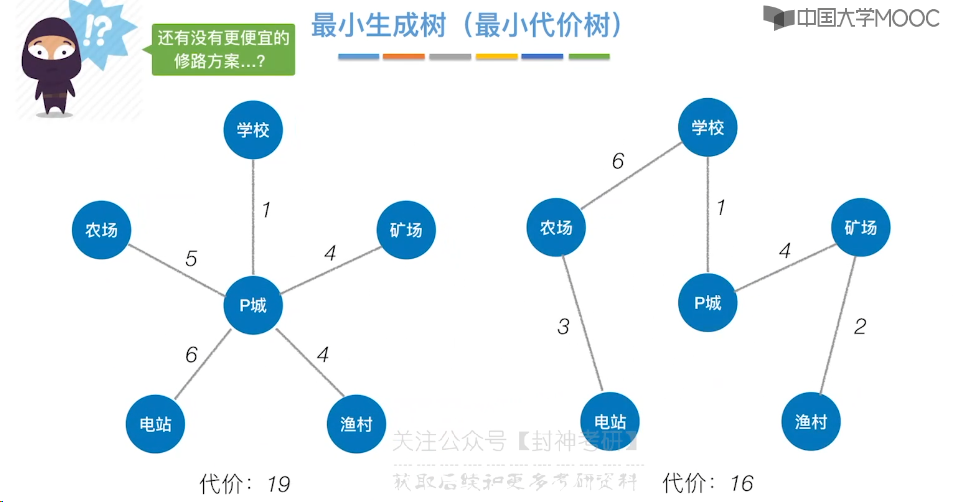
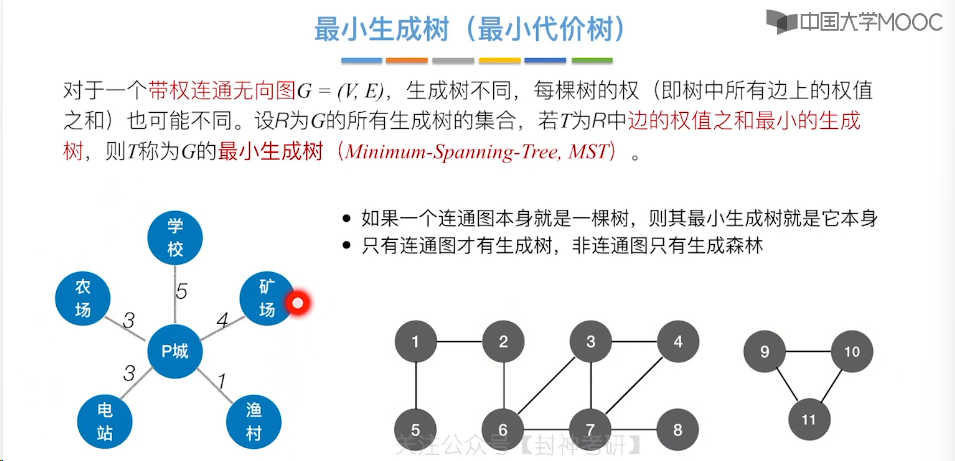

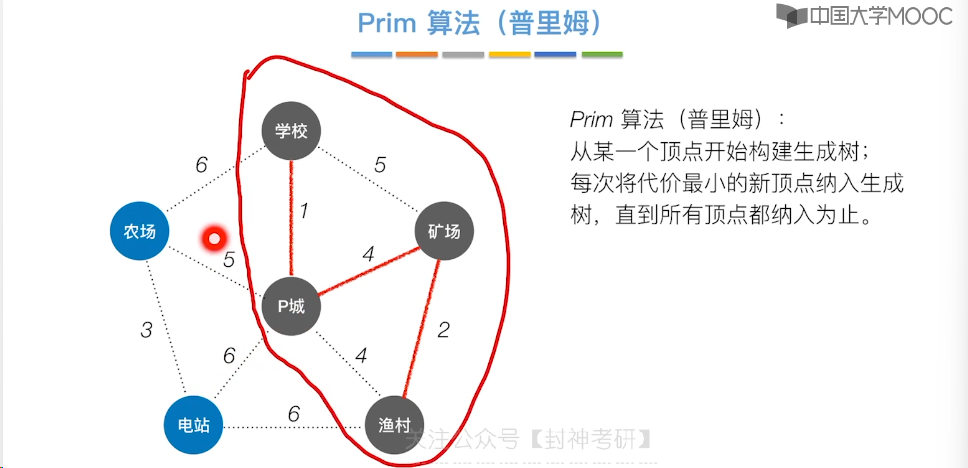
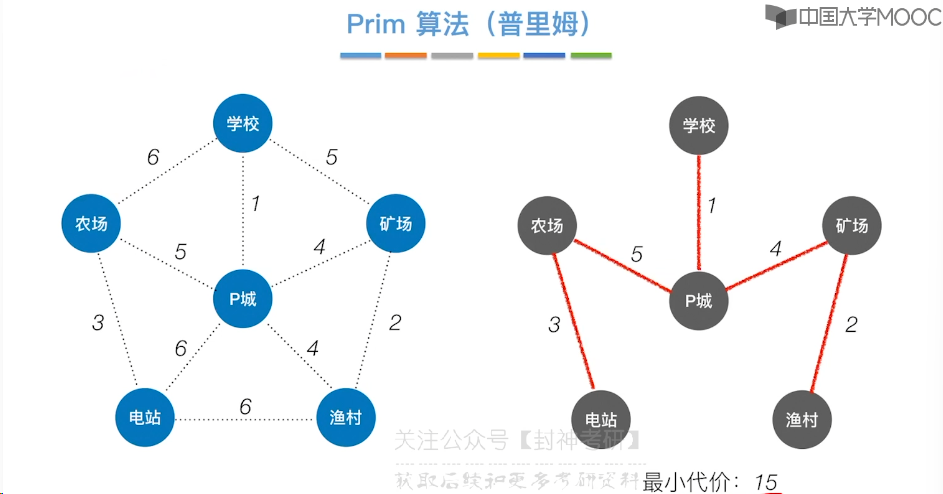
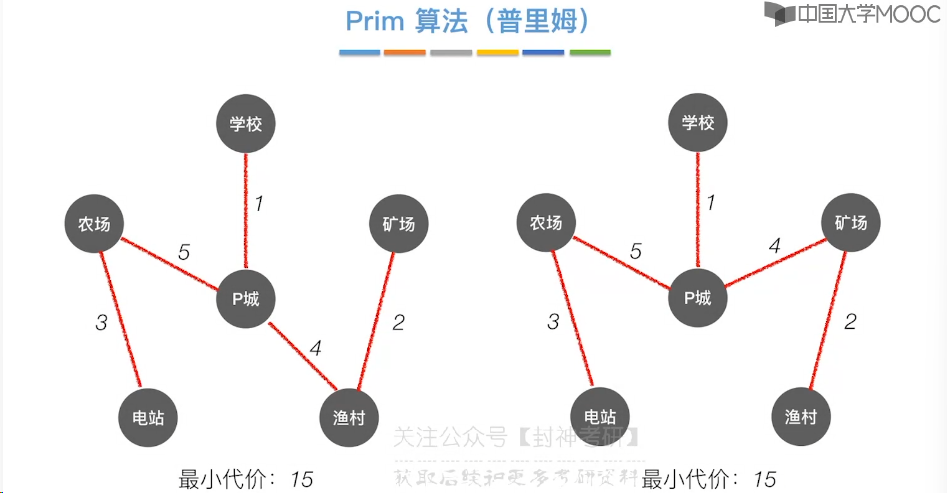
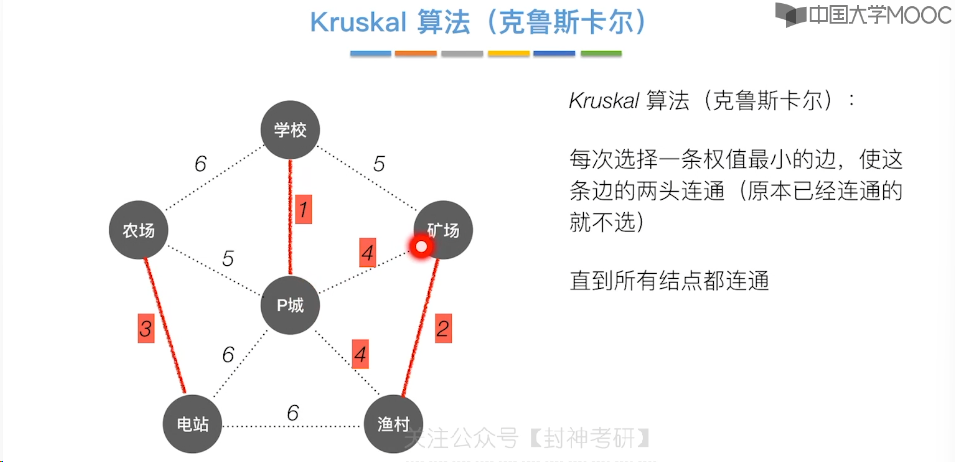

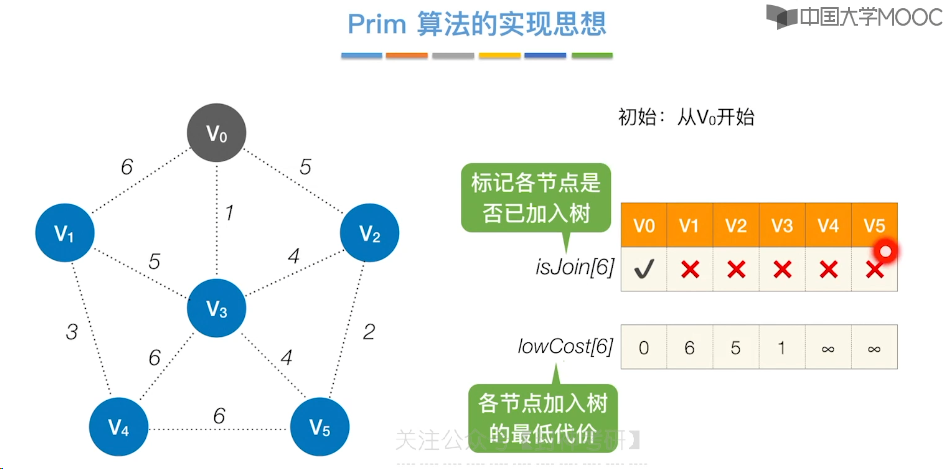
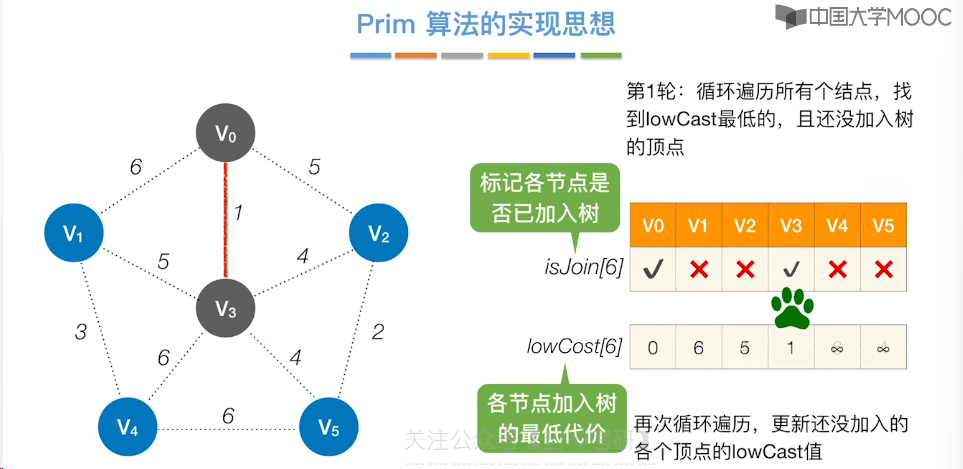
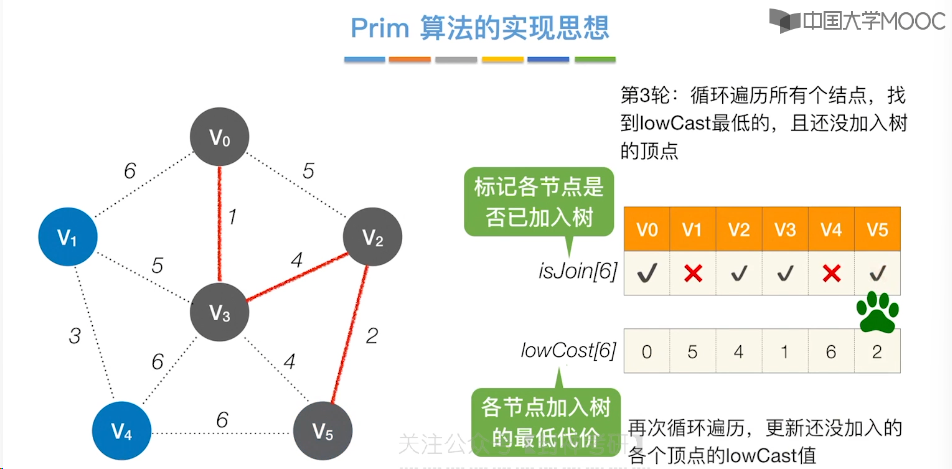
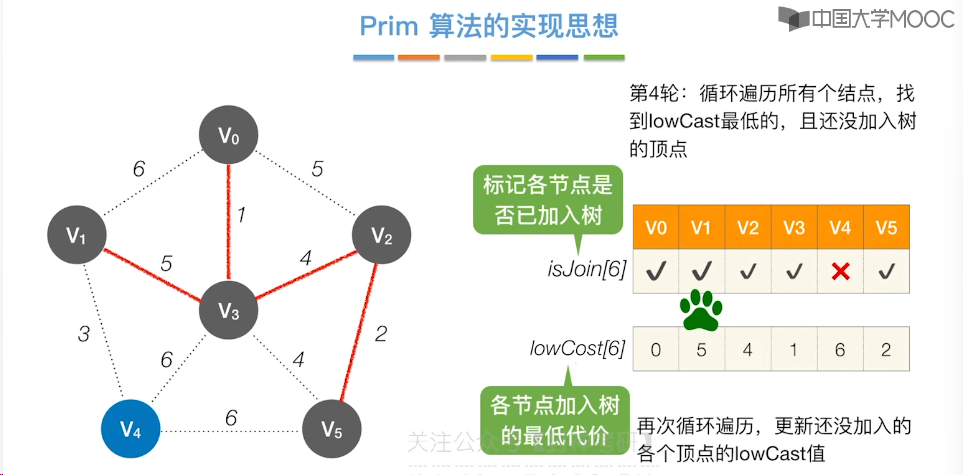
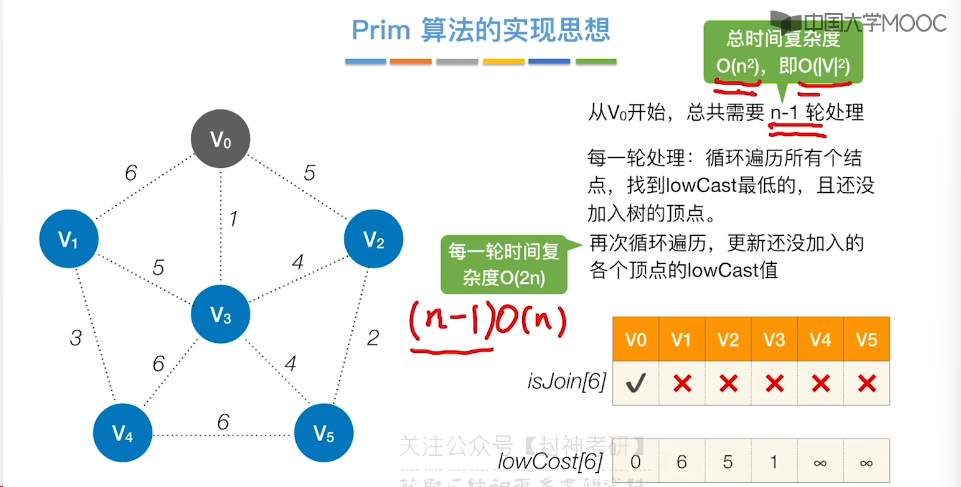
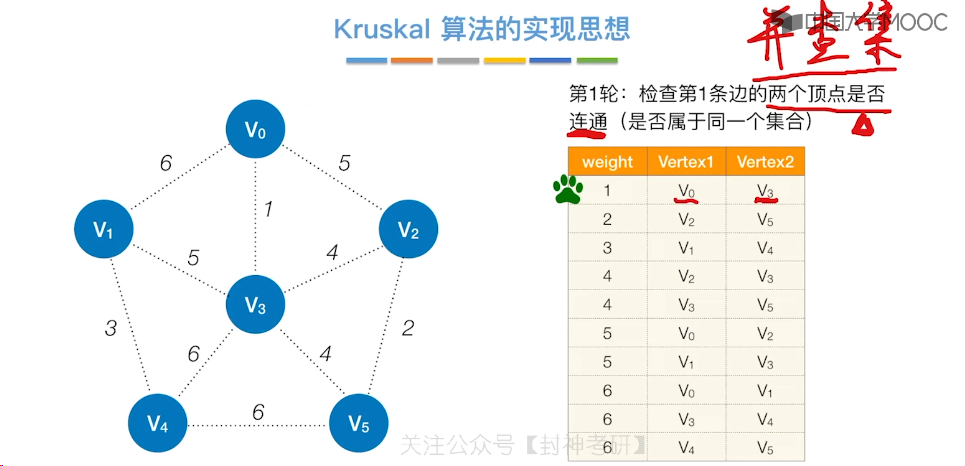
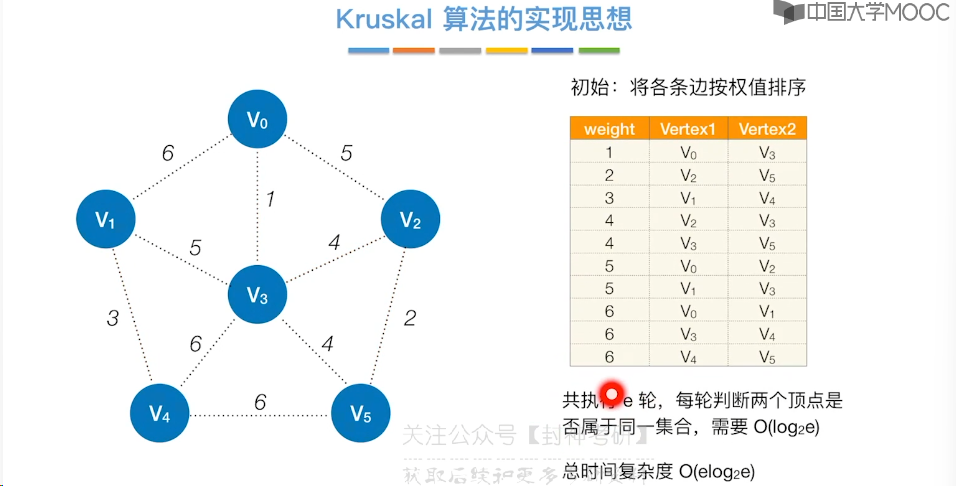
6.8、最短路径问题 - BFS 算法
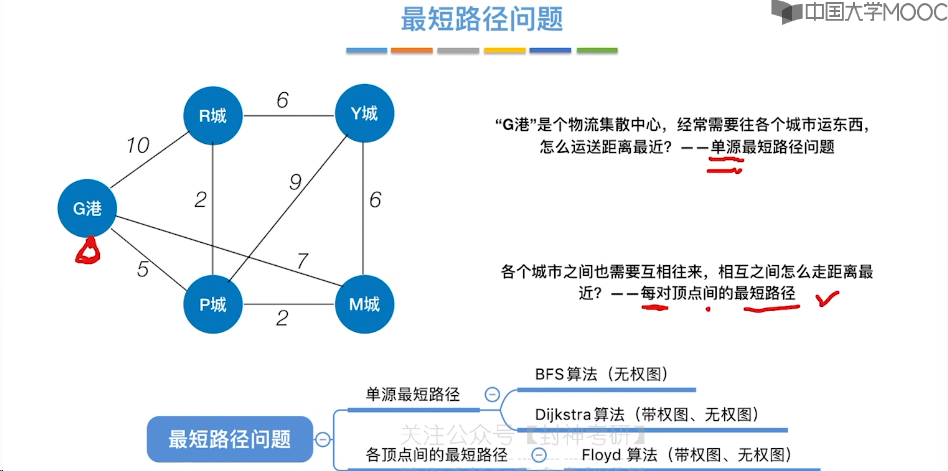
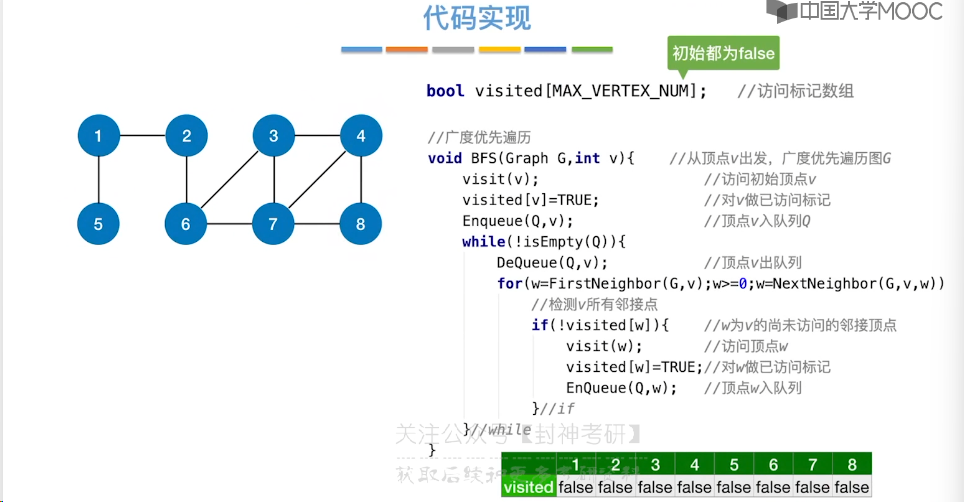
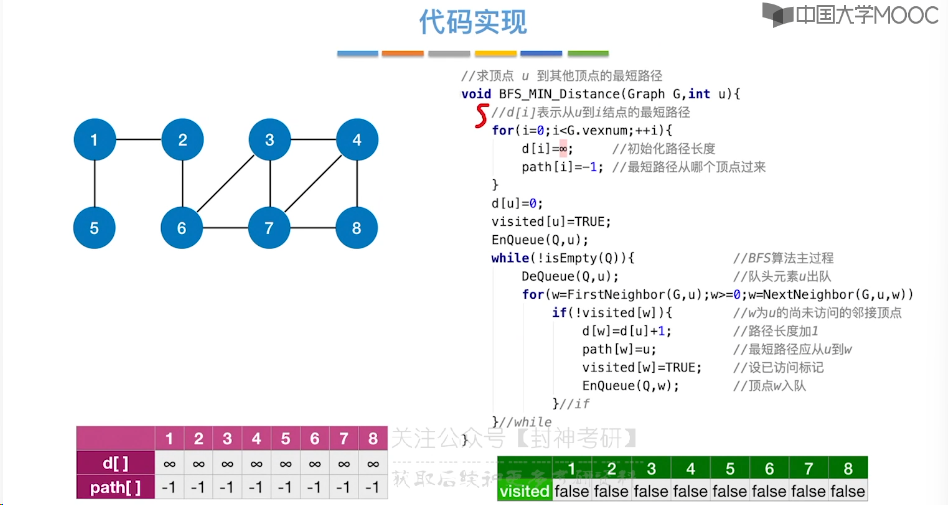
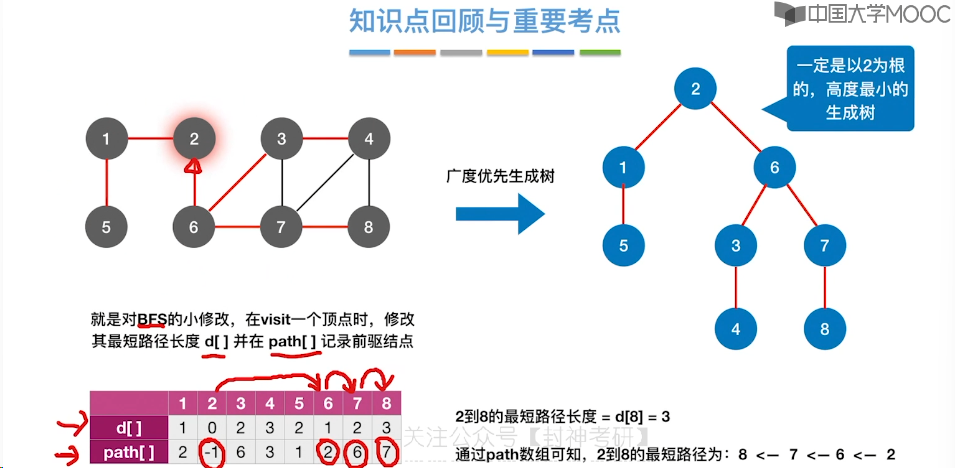
6.9、最短路径问题 - Dijkstra 算法

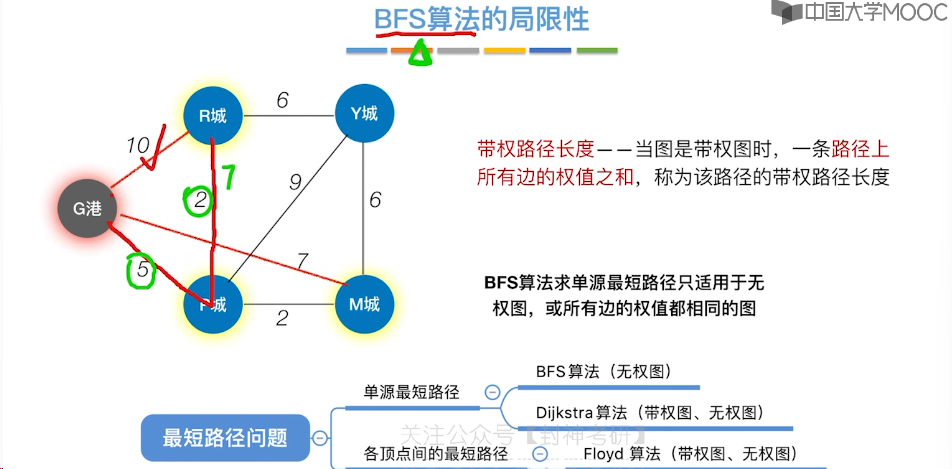
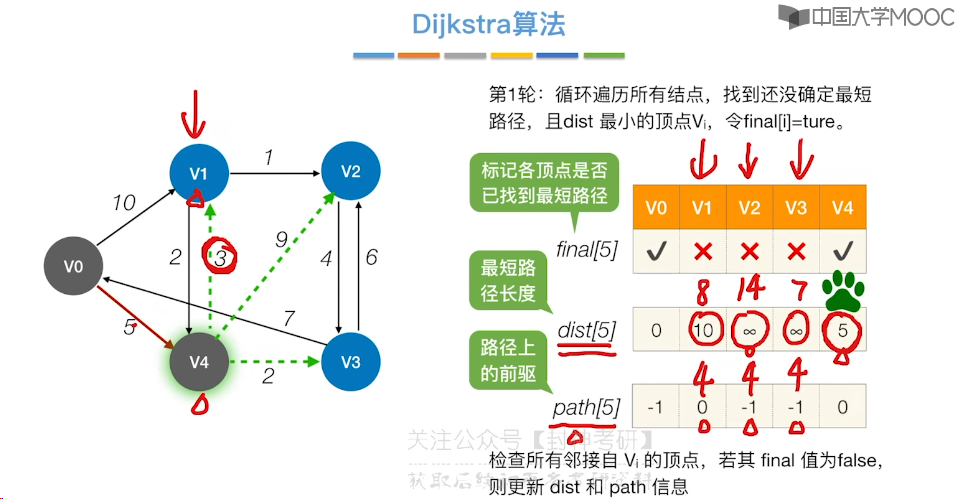
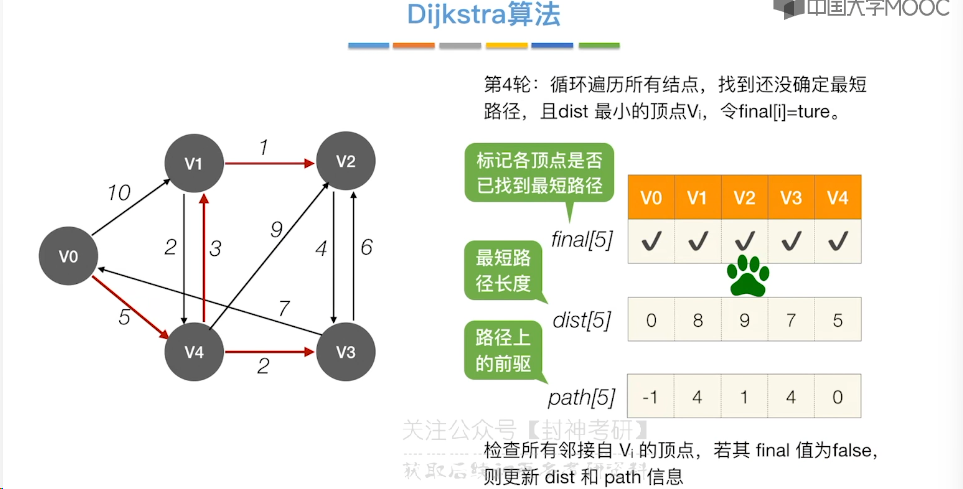
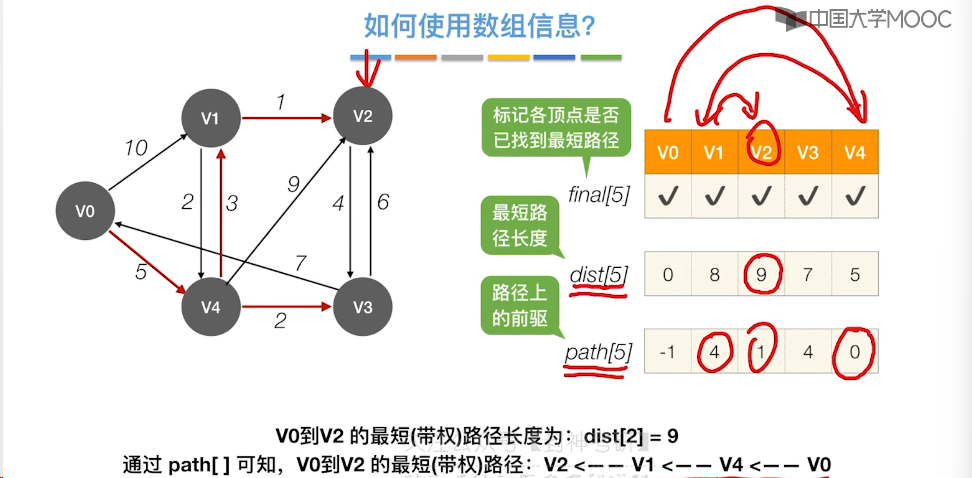
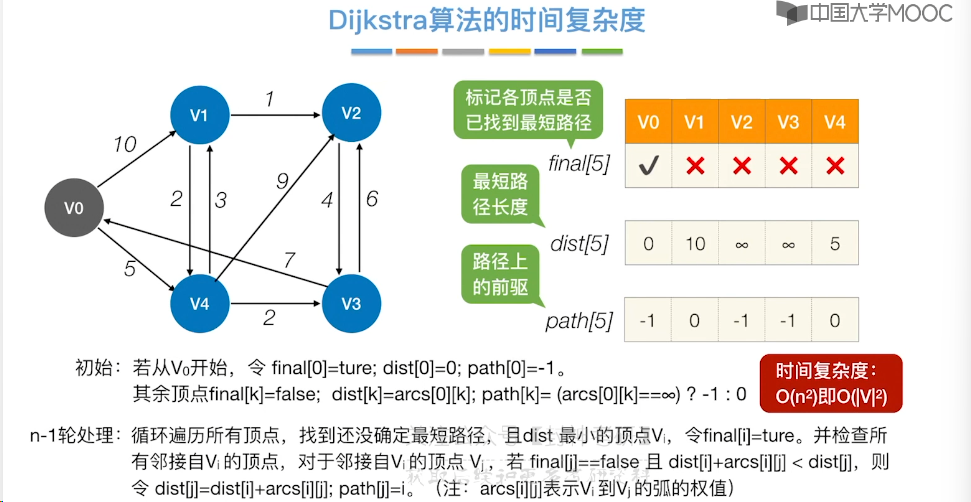
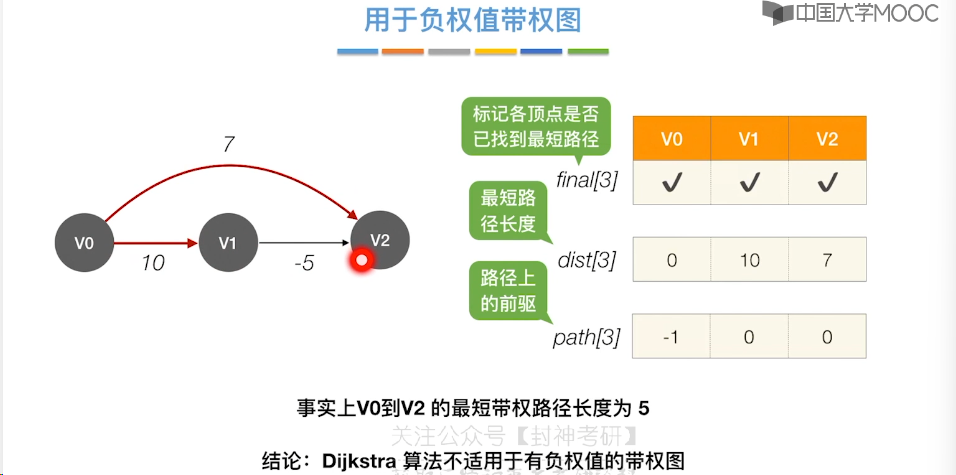
6.10、最短路径问题 - Floyd 算法


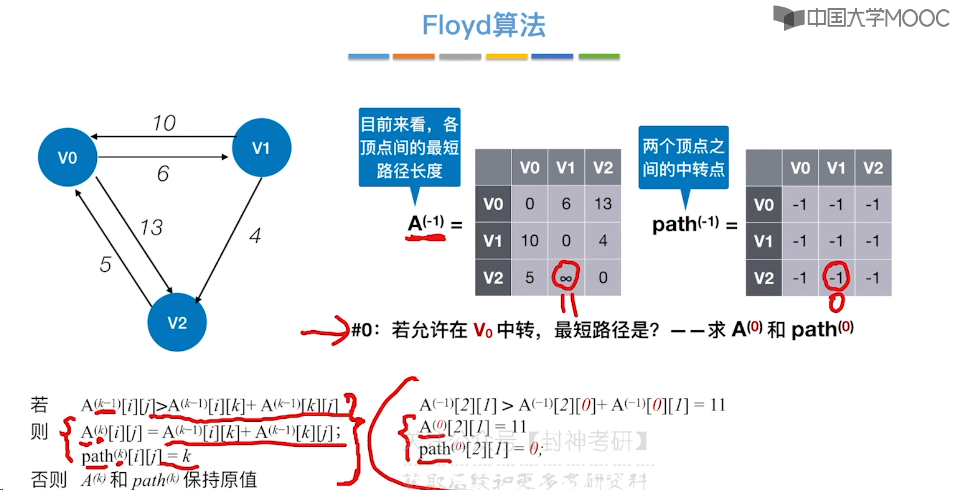
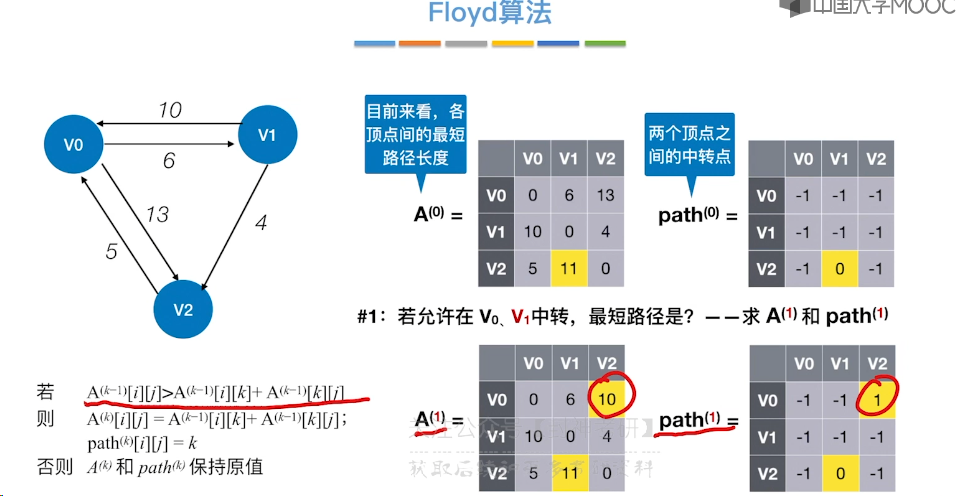
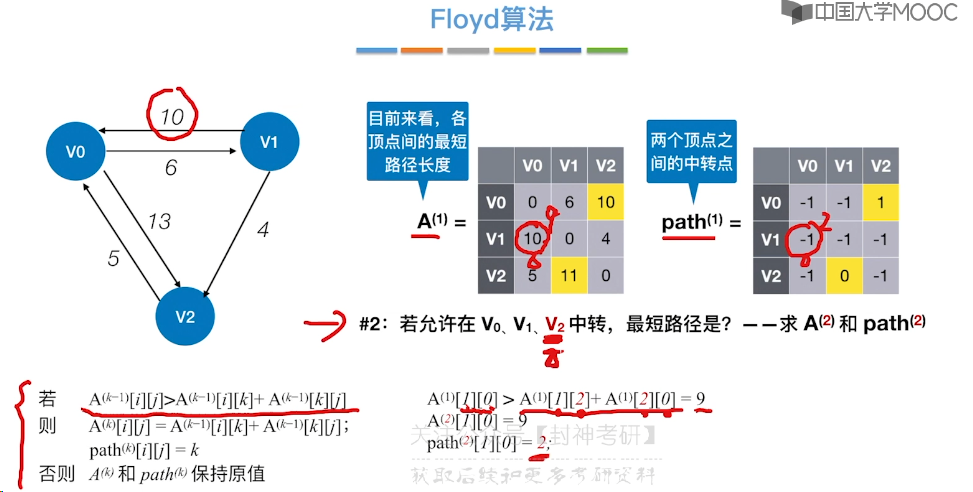
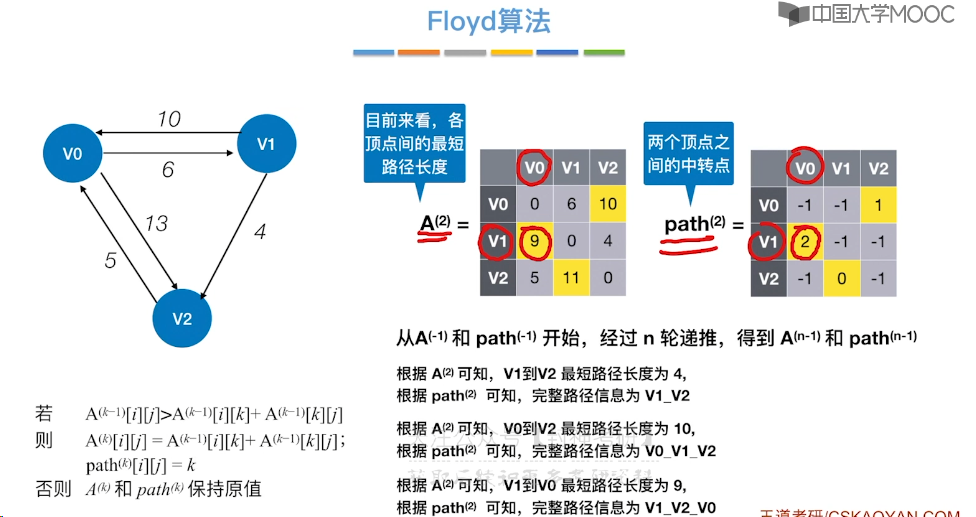
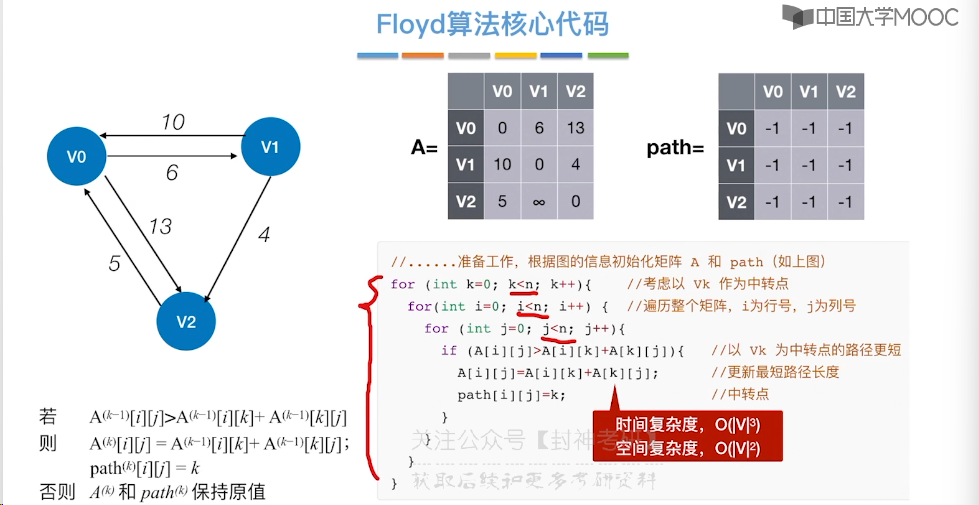
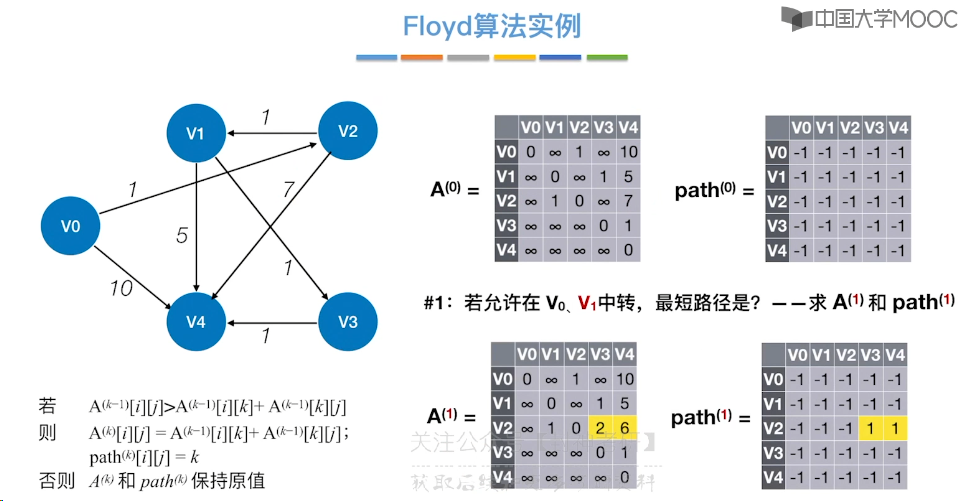
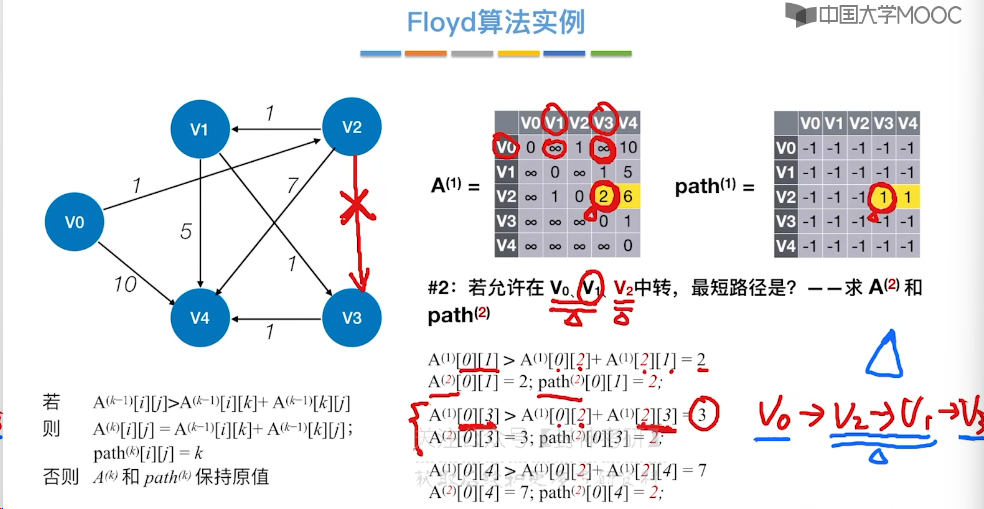
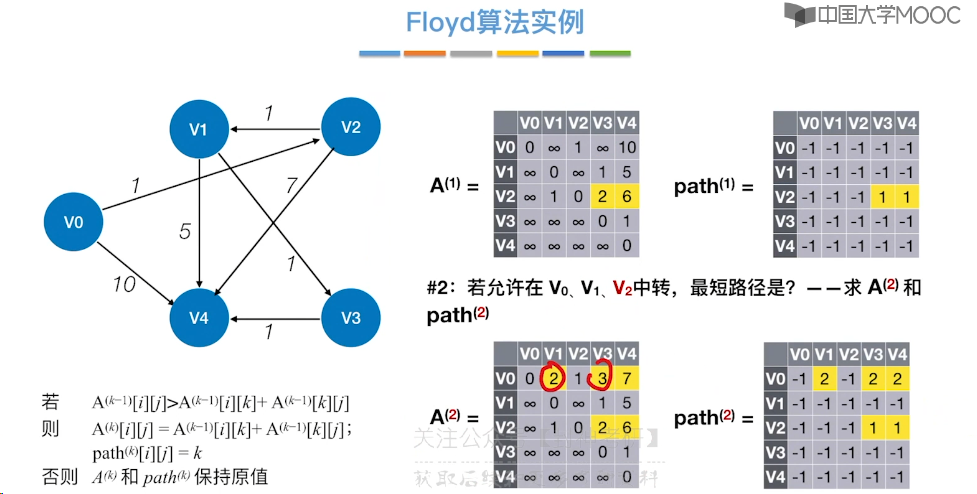
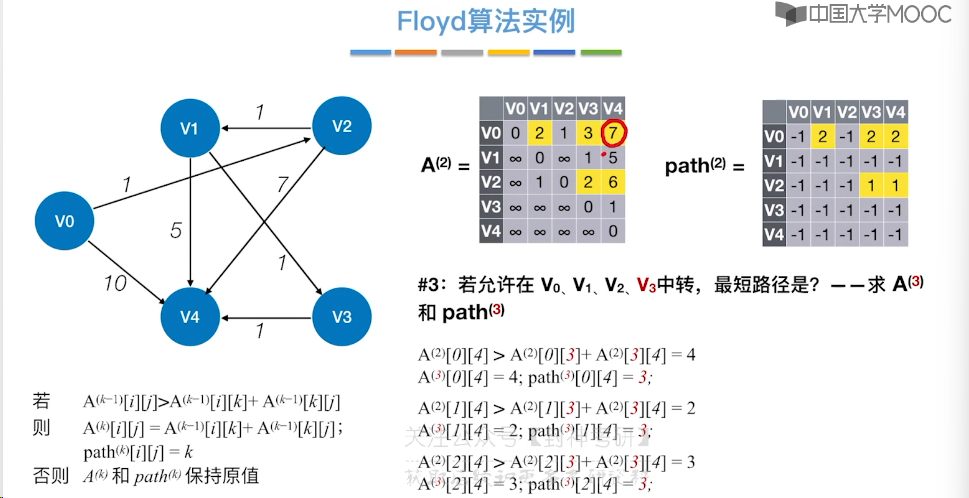
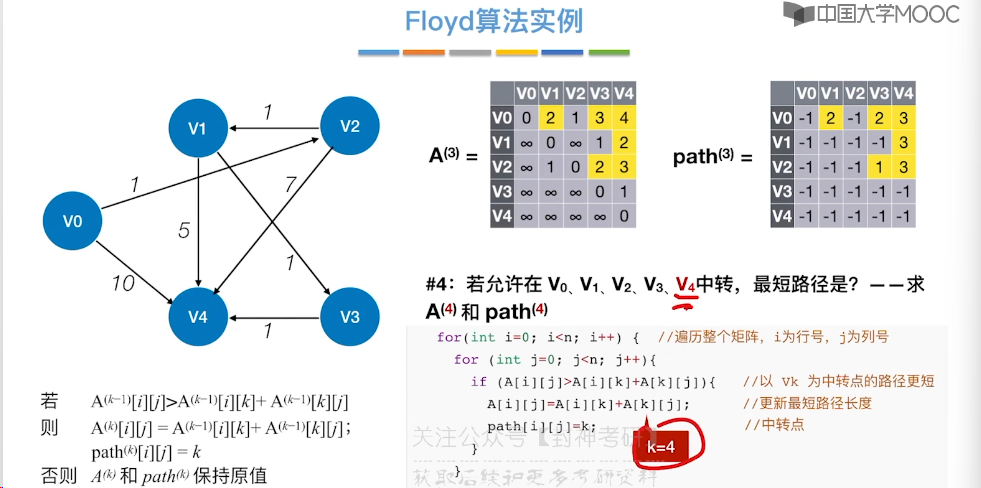
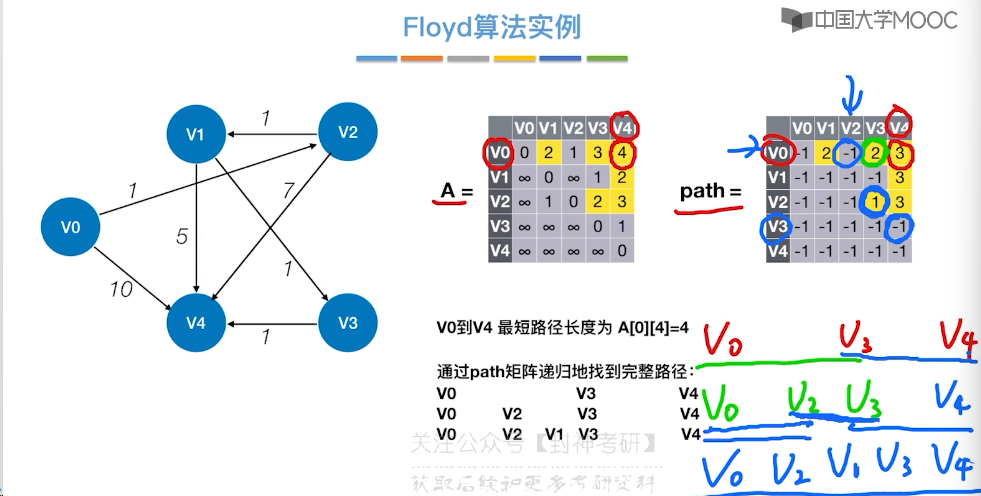
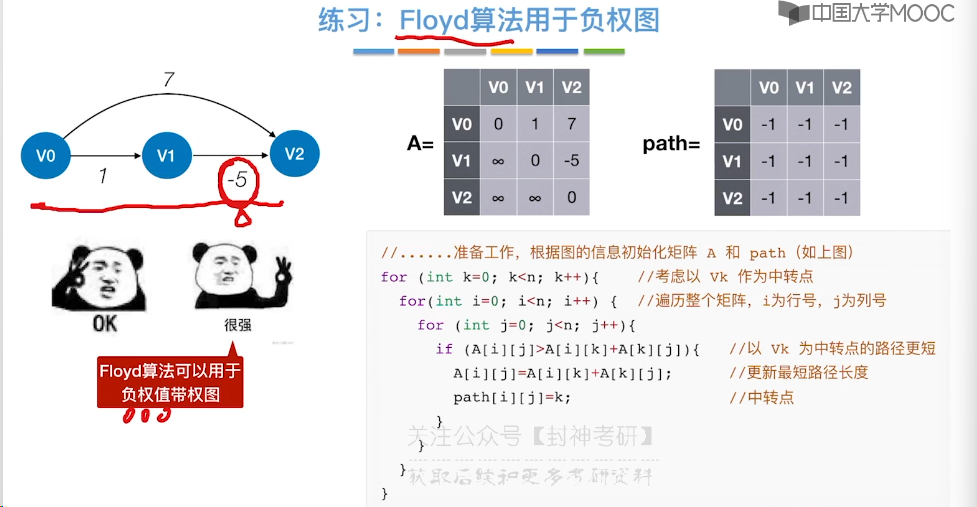
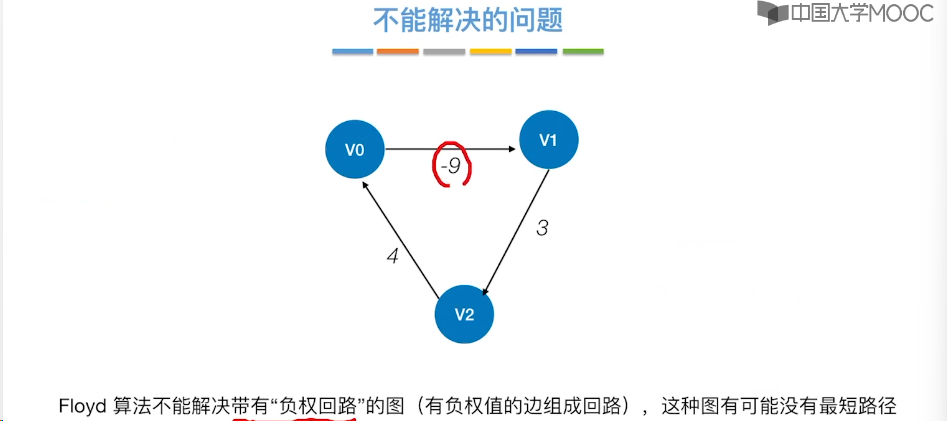
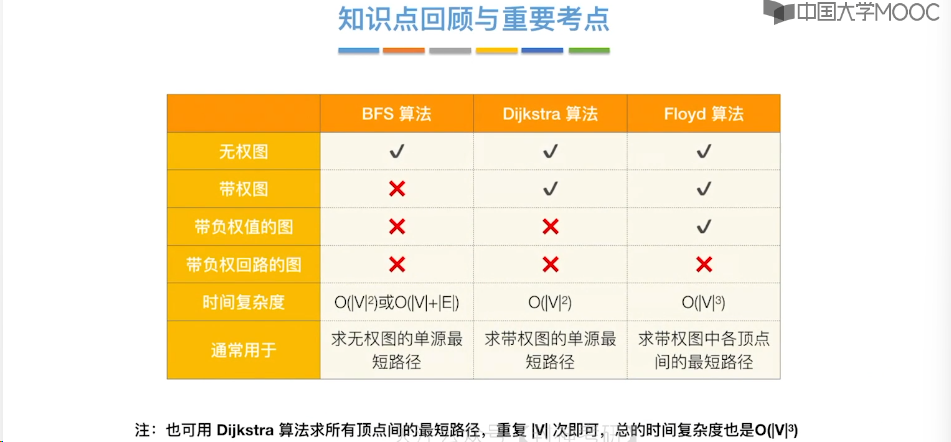
6.11、拓扑排序
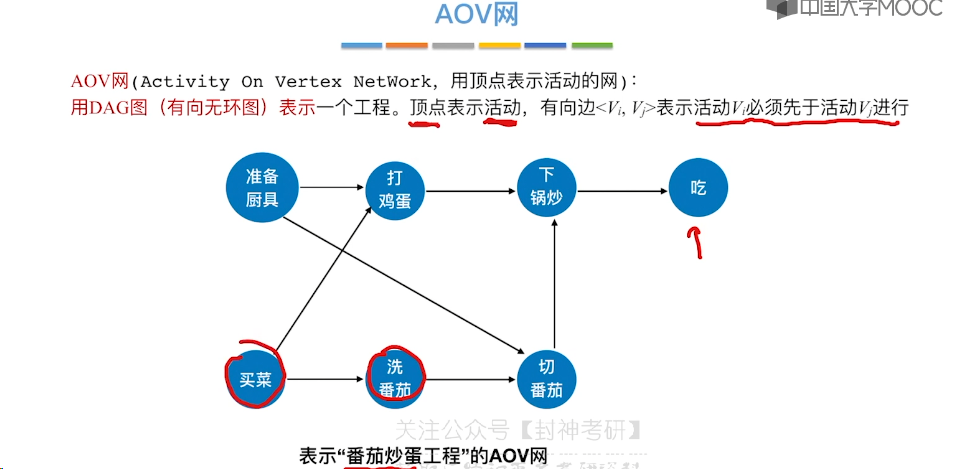
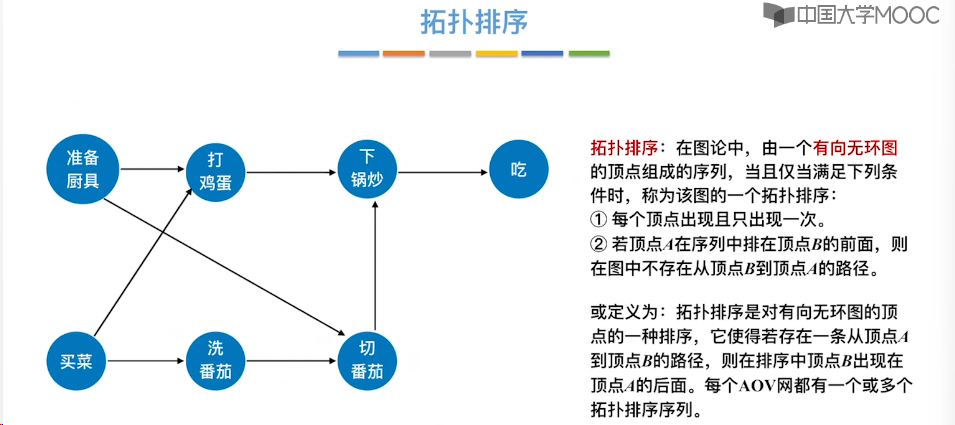

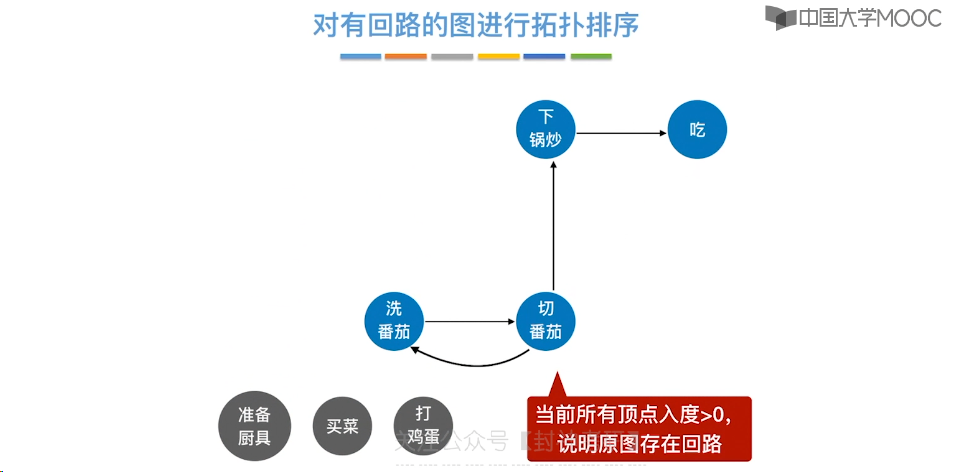
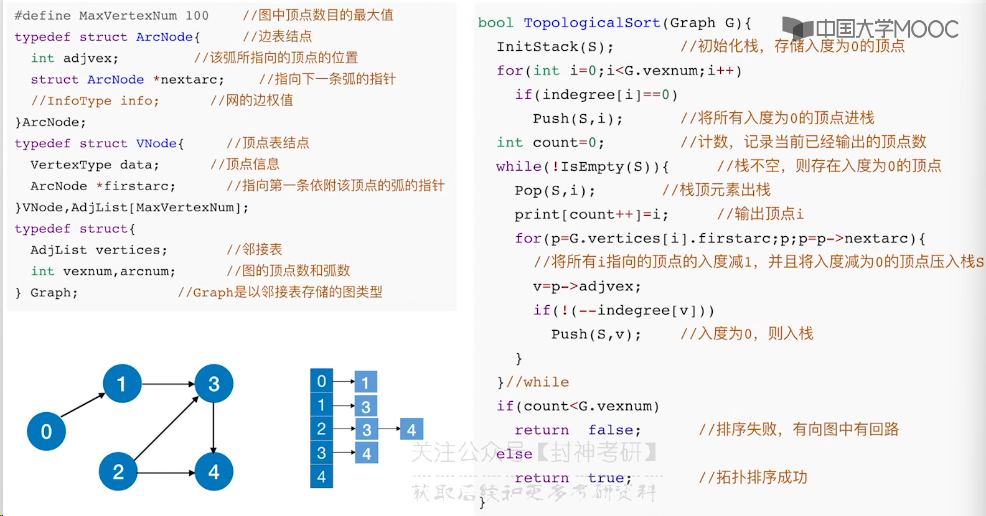
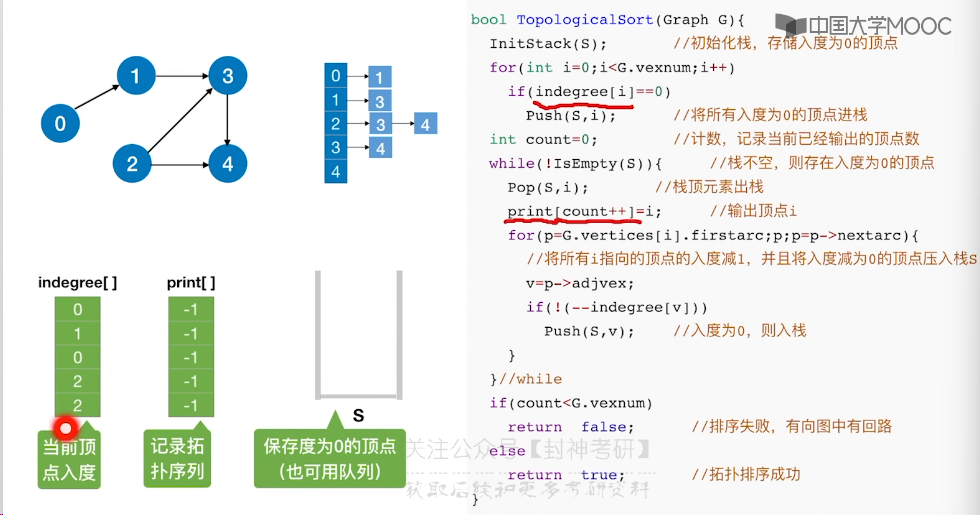
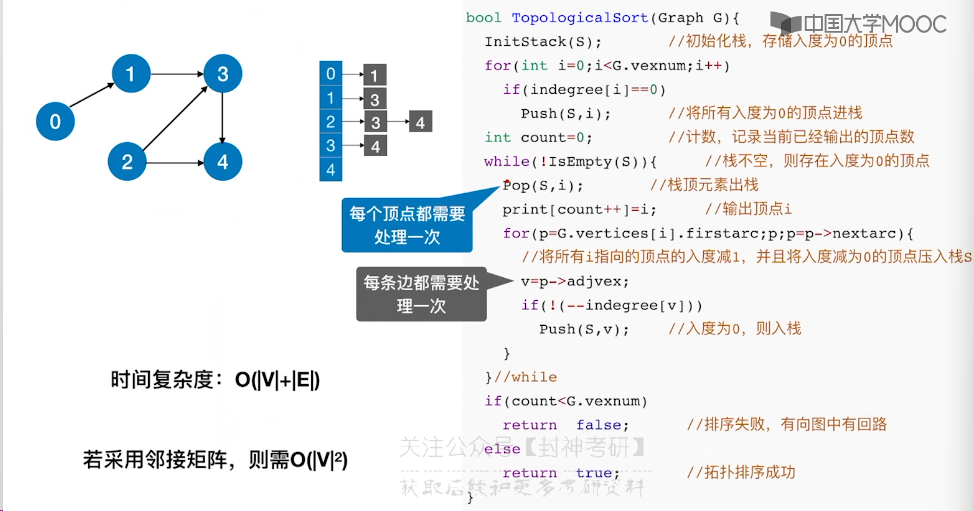
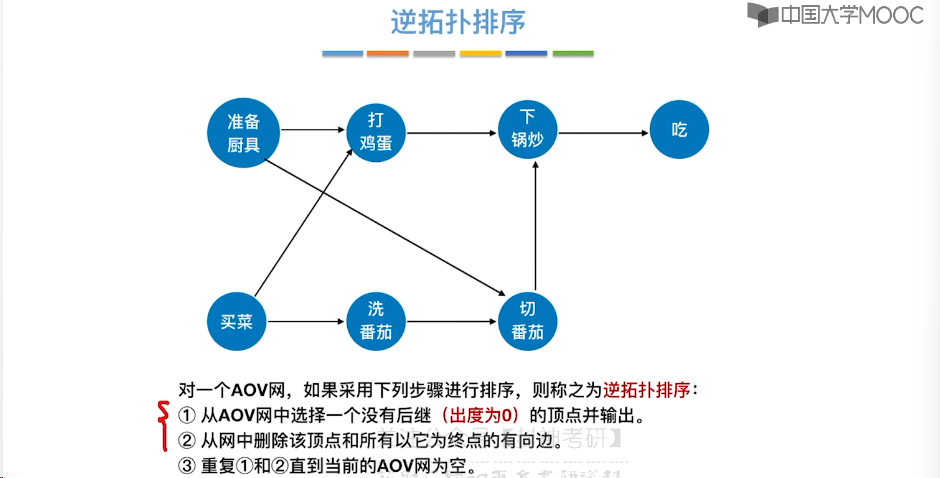

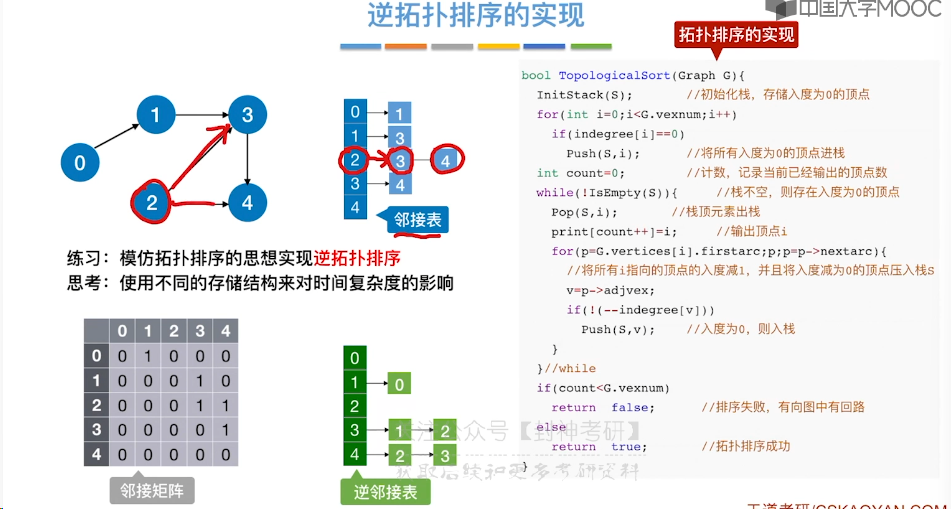

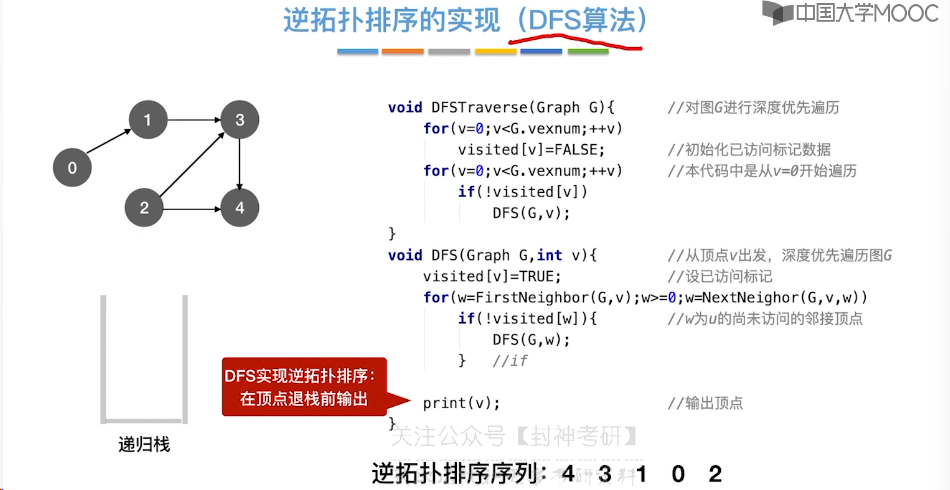
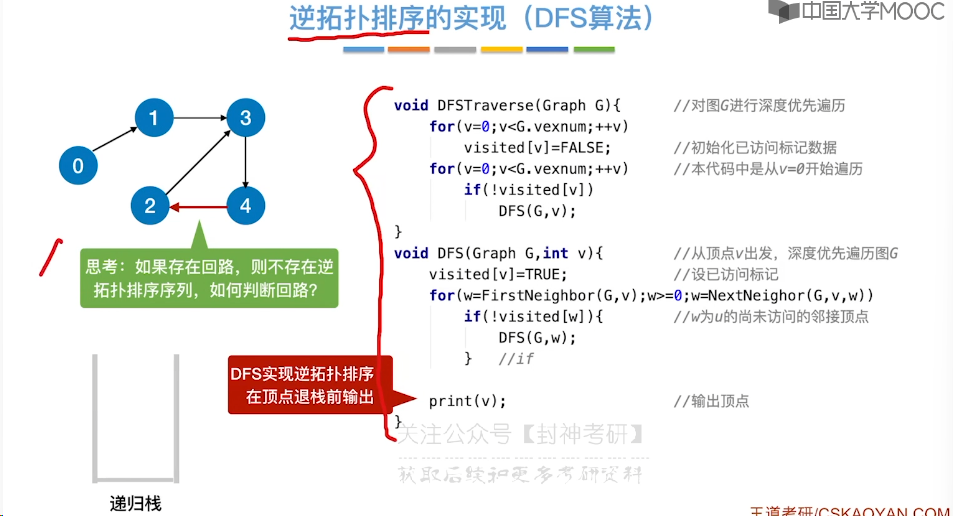
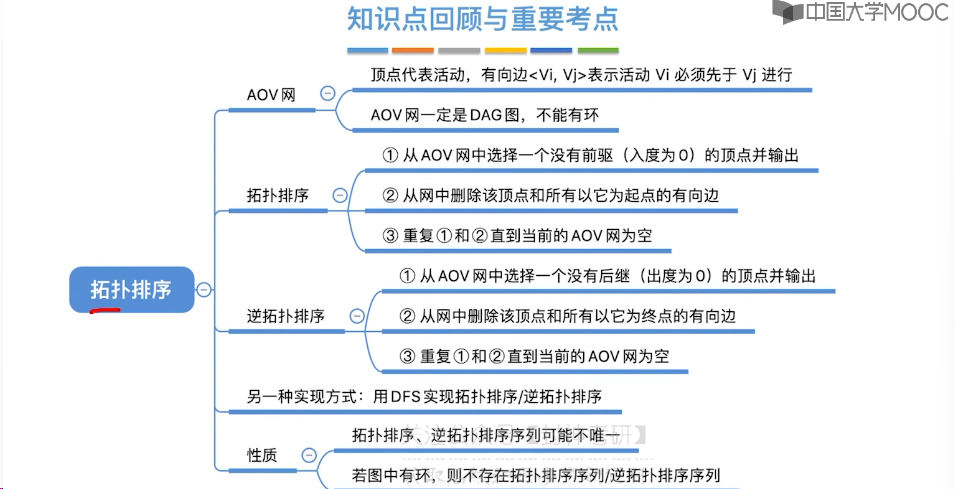
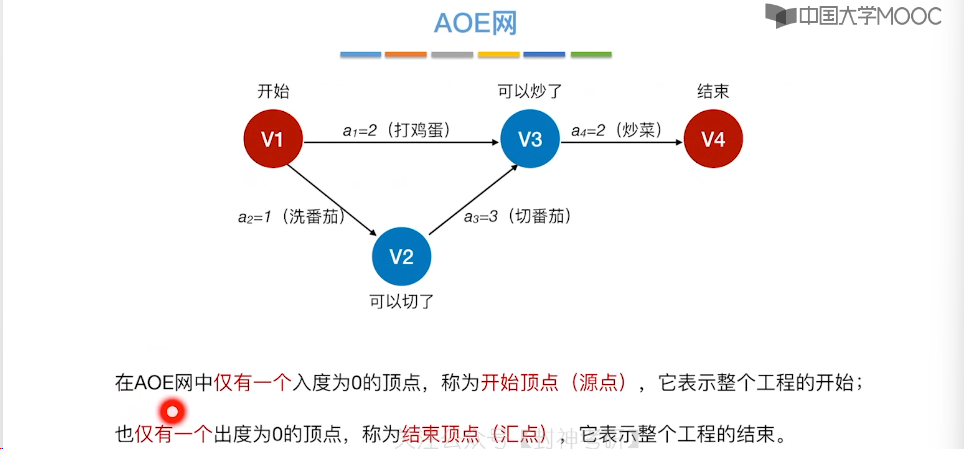
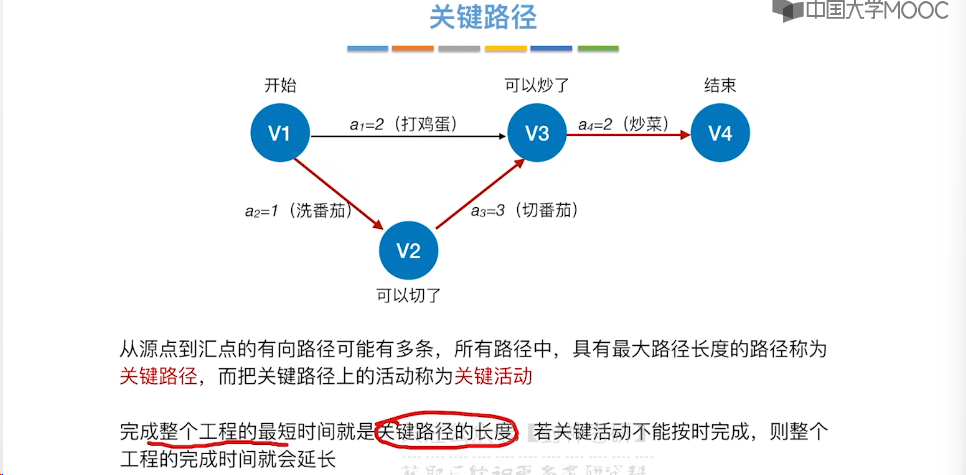
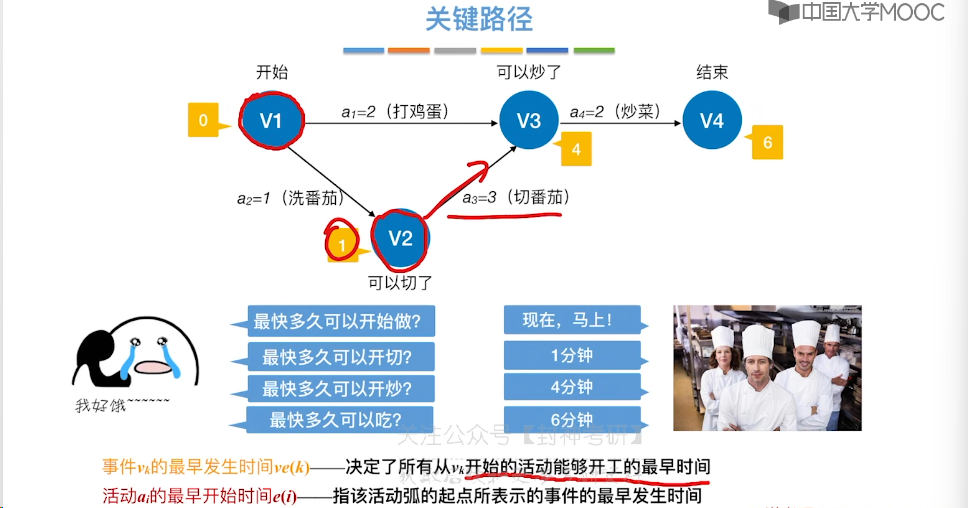
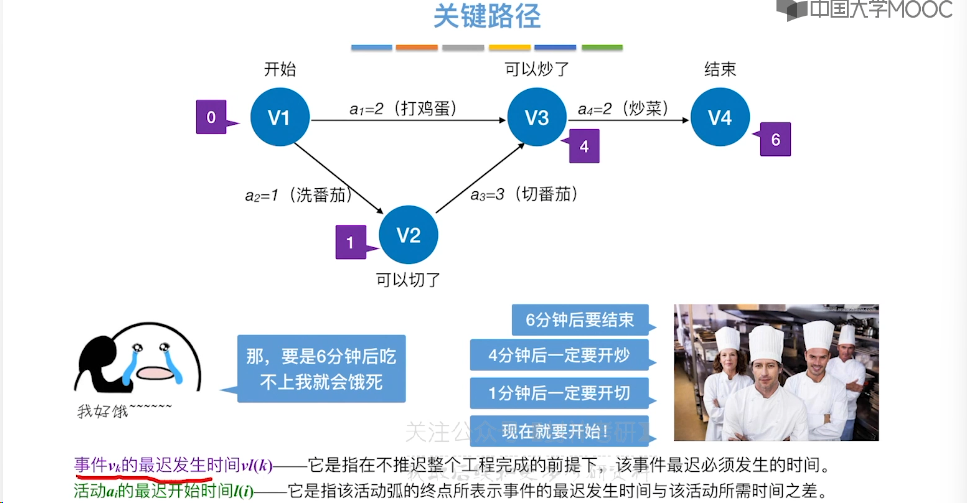
6.12、关键路径
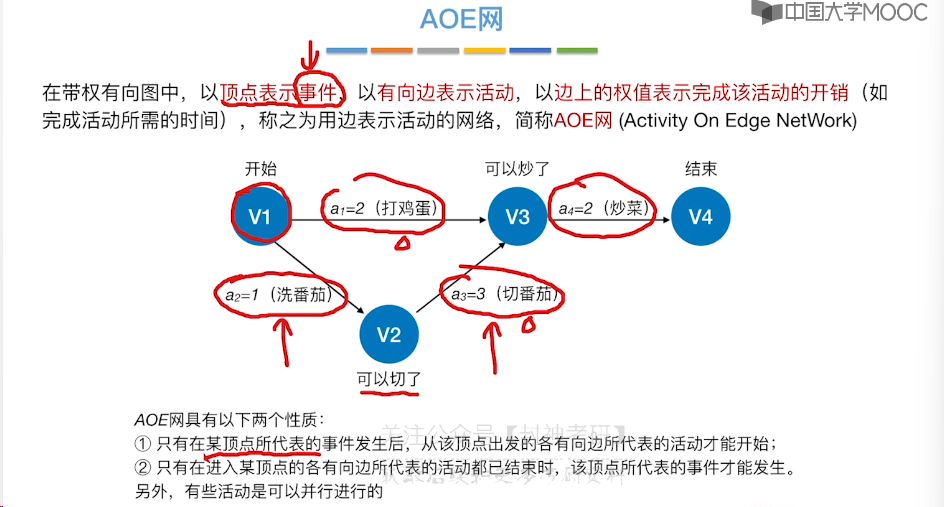
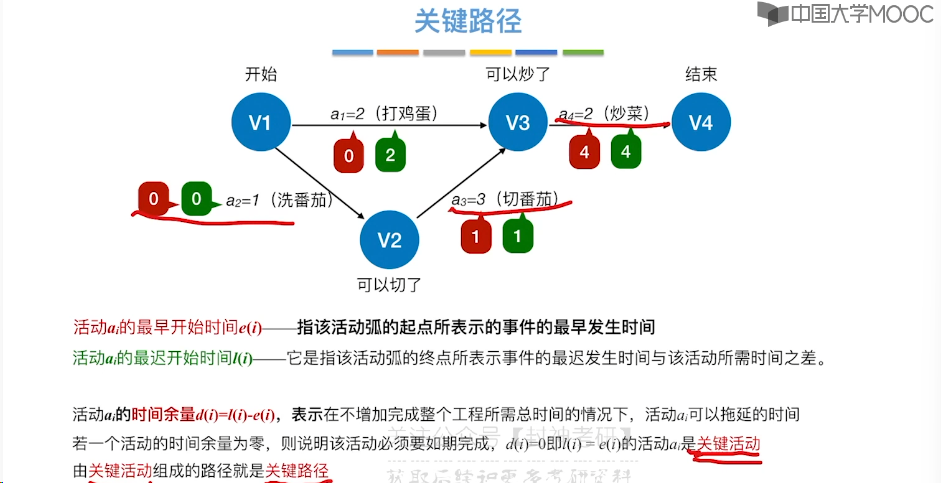
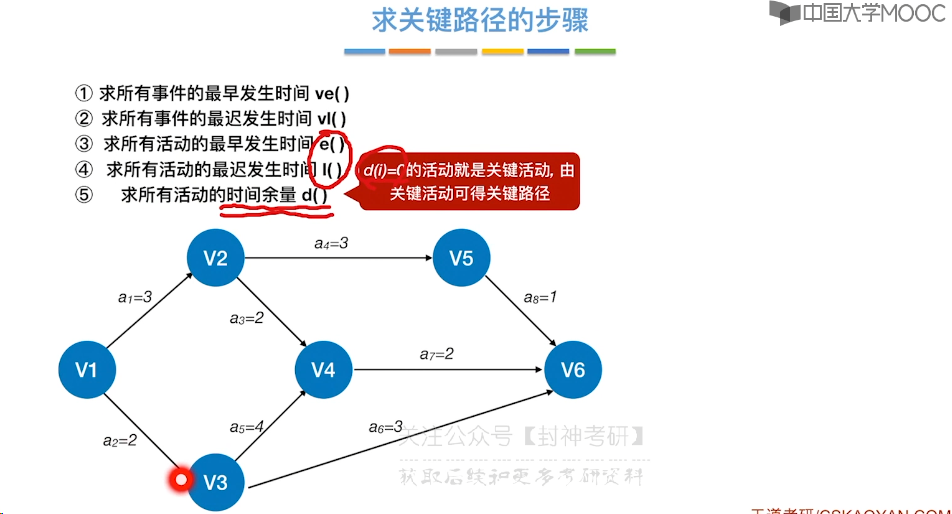
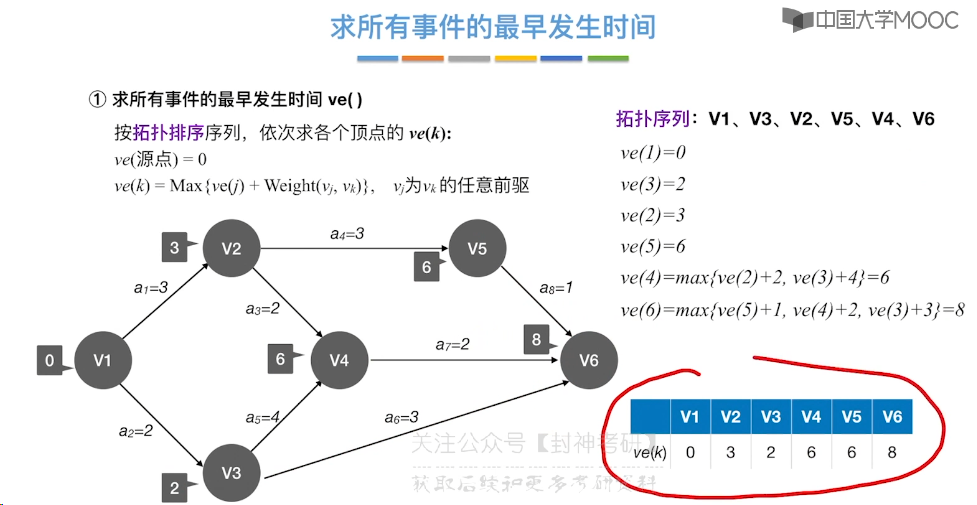
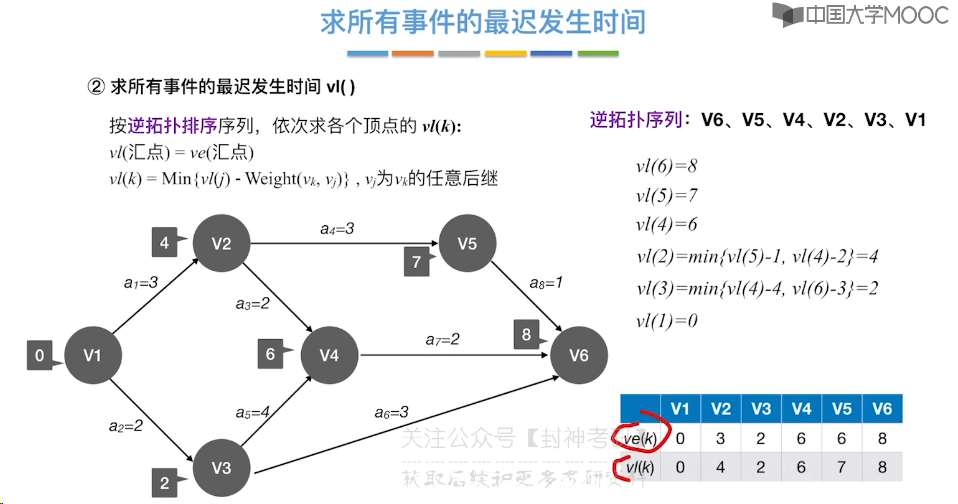
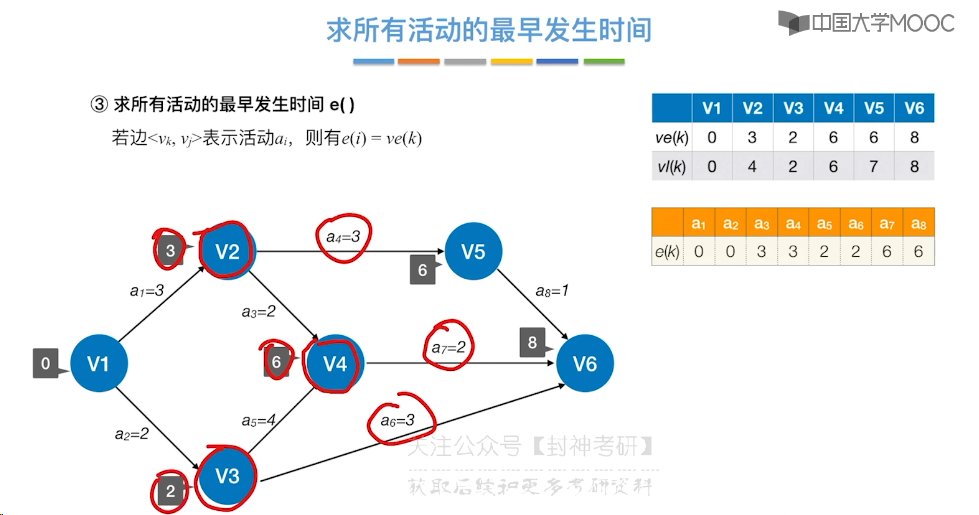
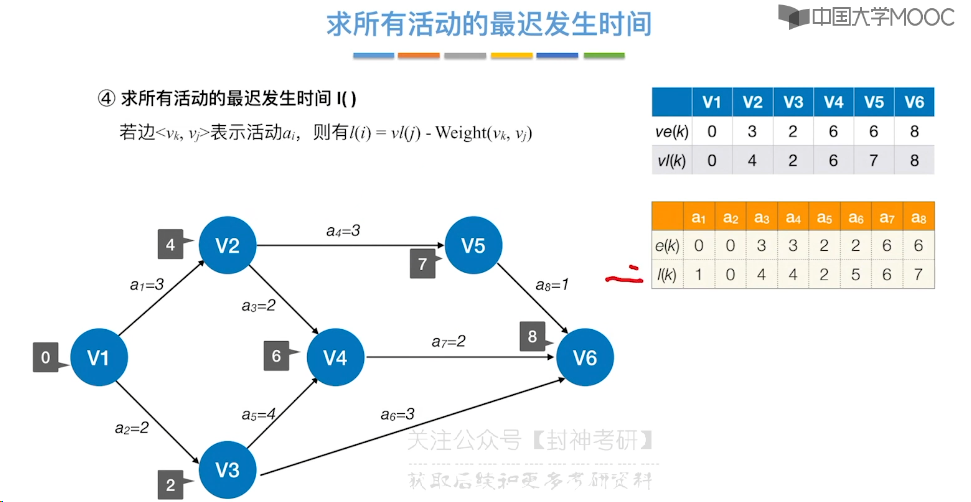
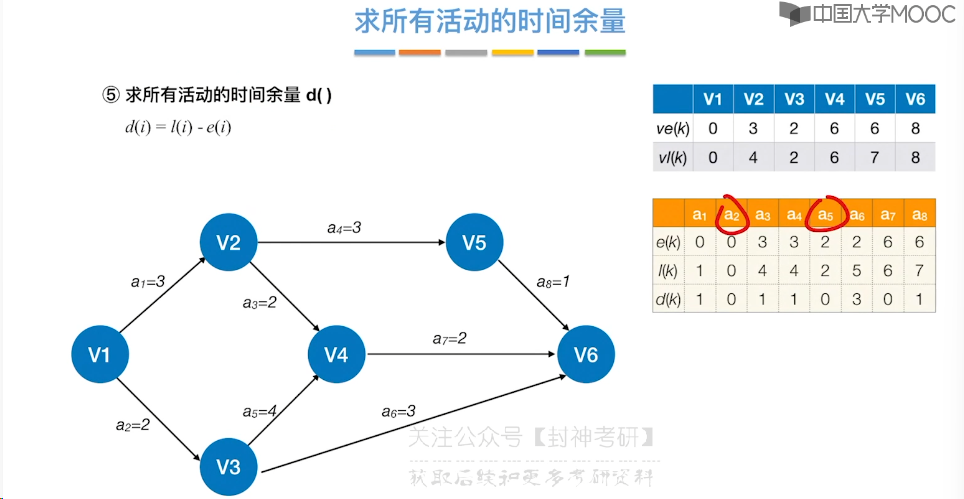
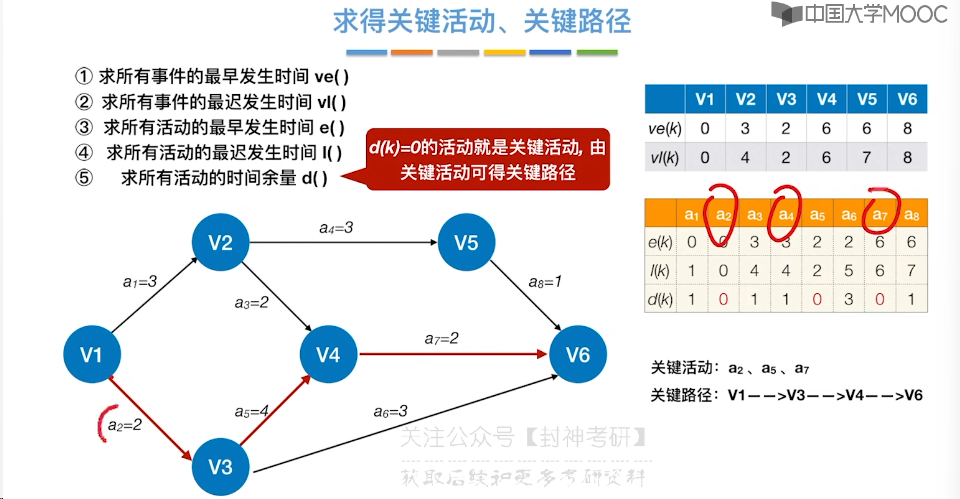
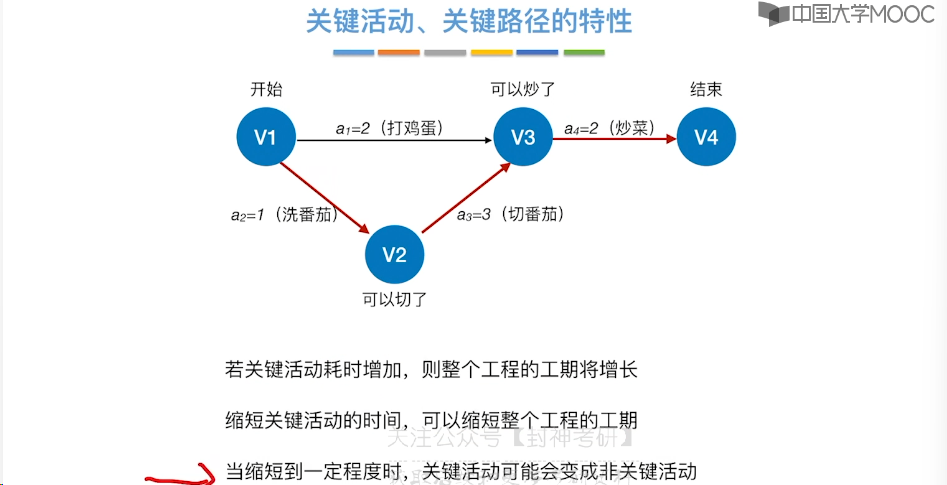
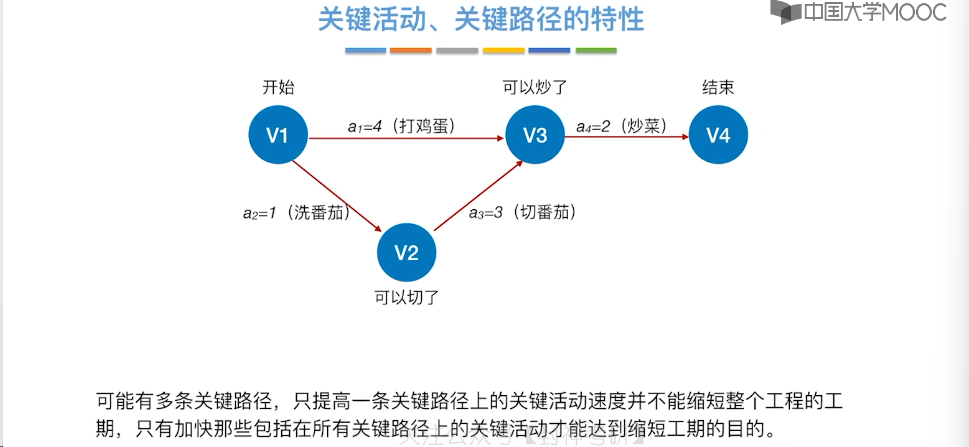


7、查找
7.1、查找的基本概念
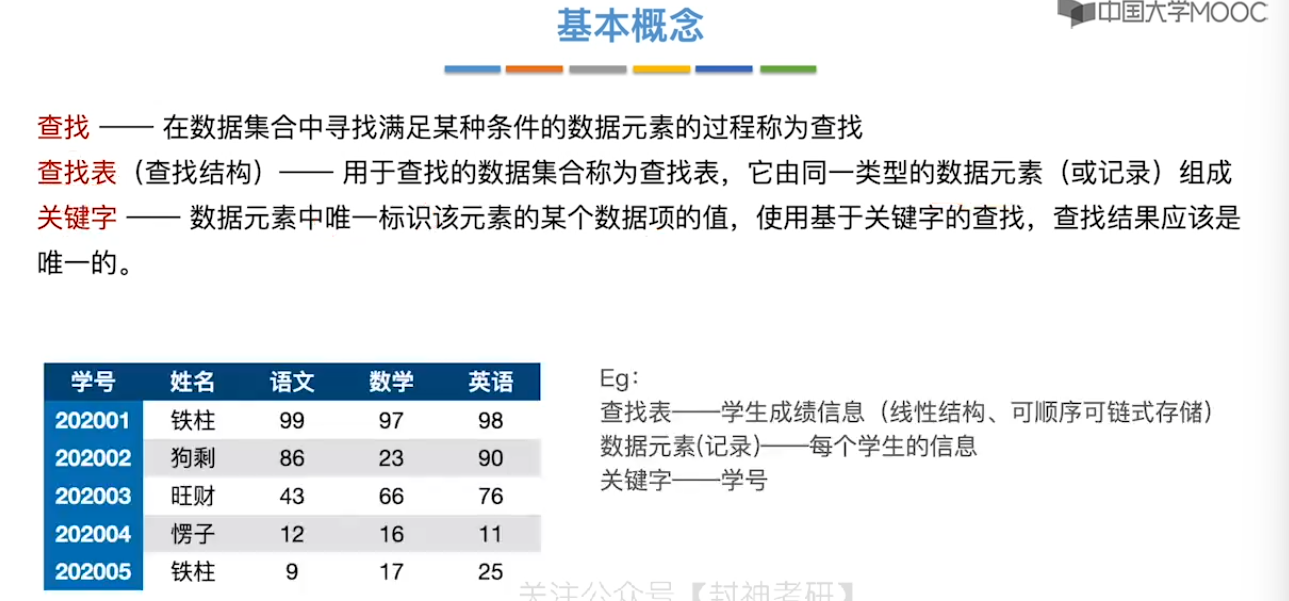
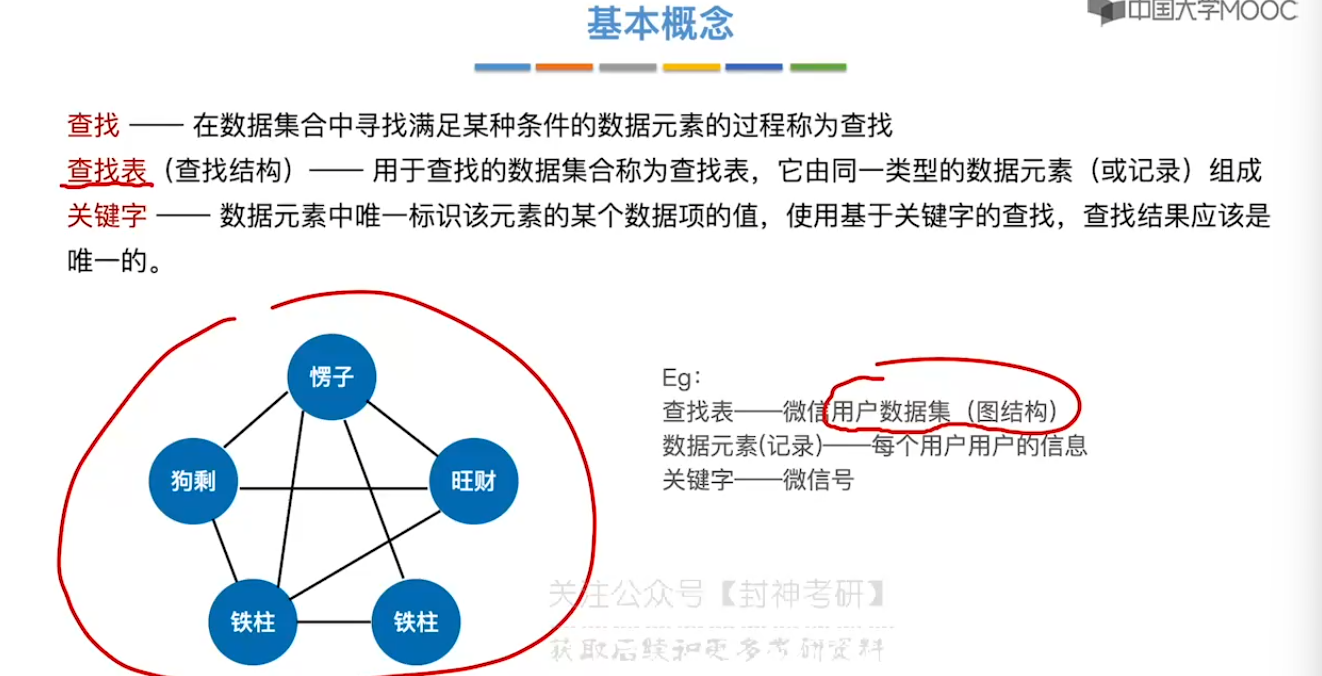
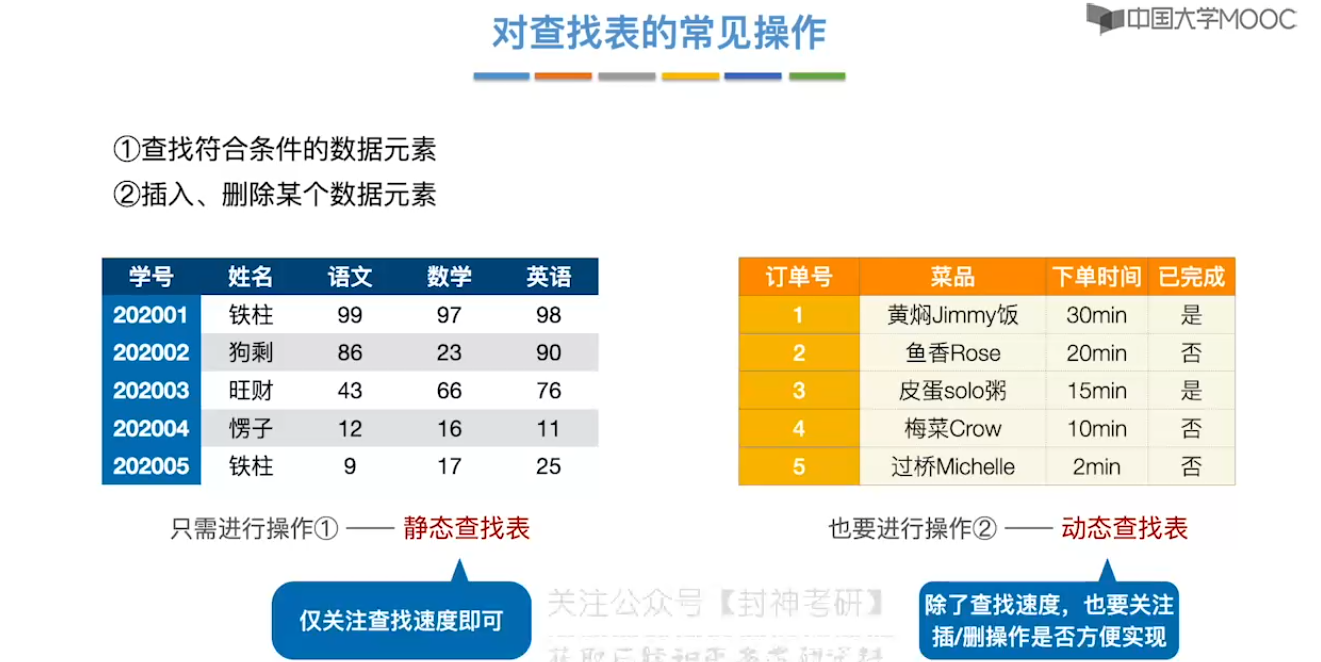
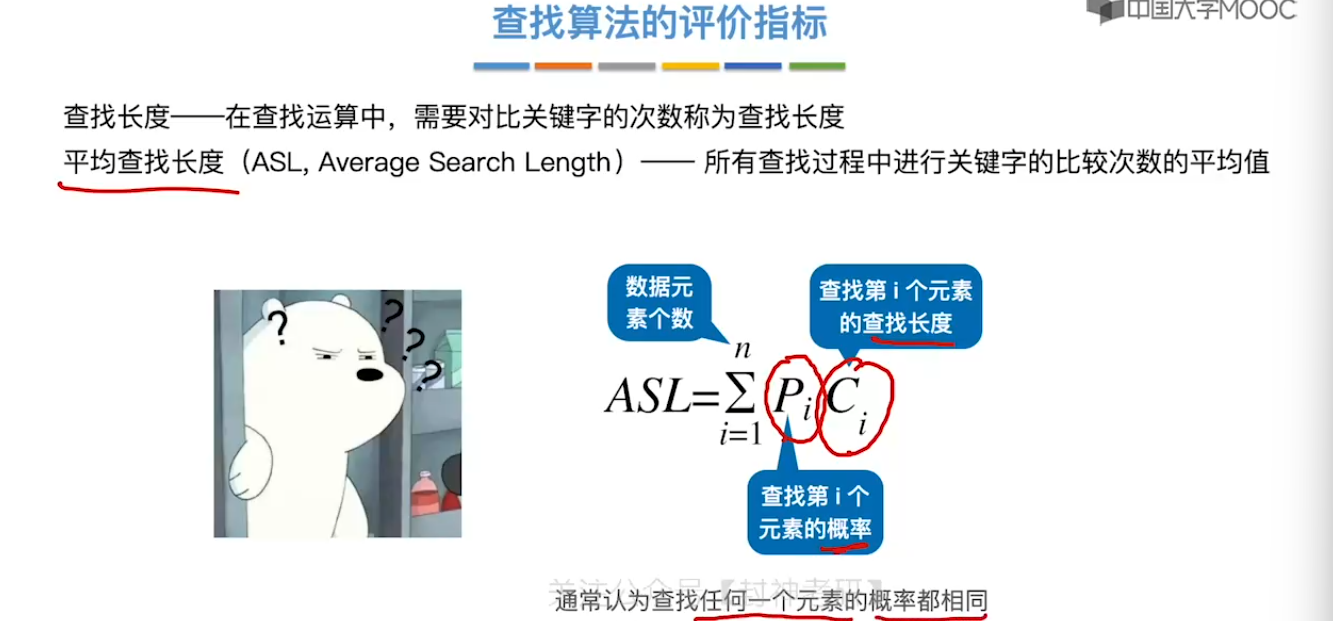
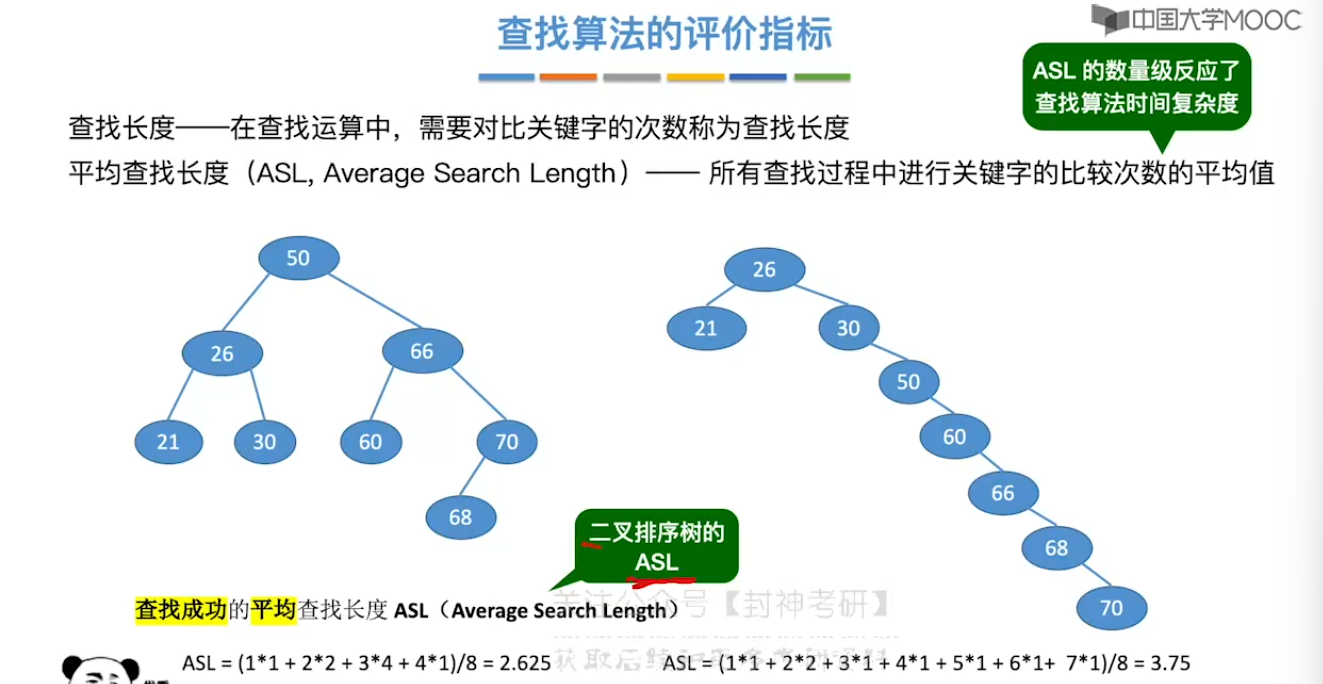
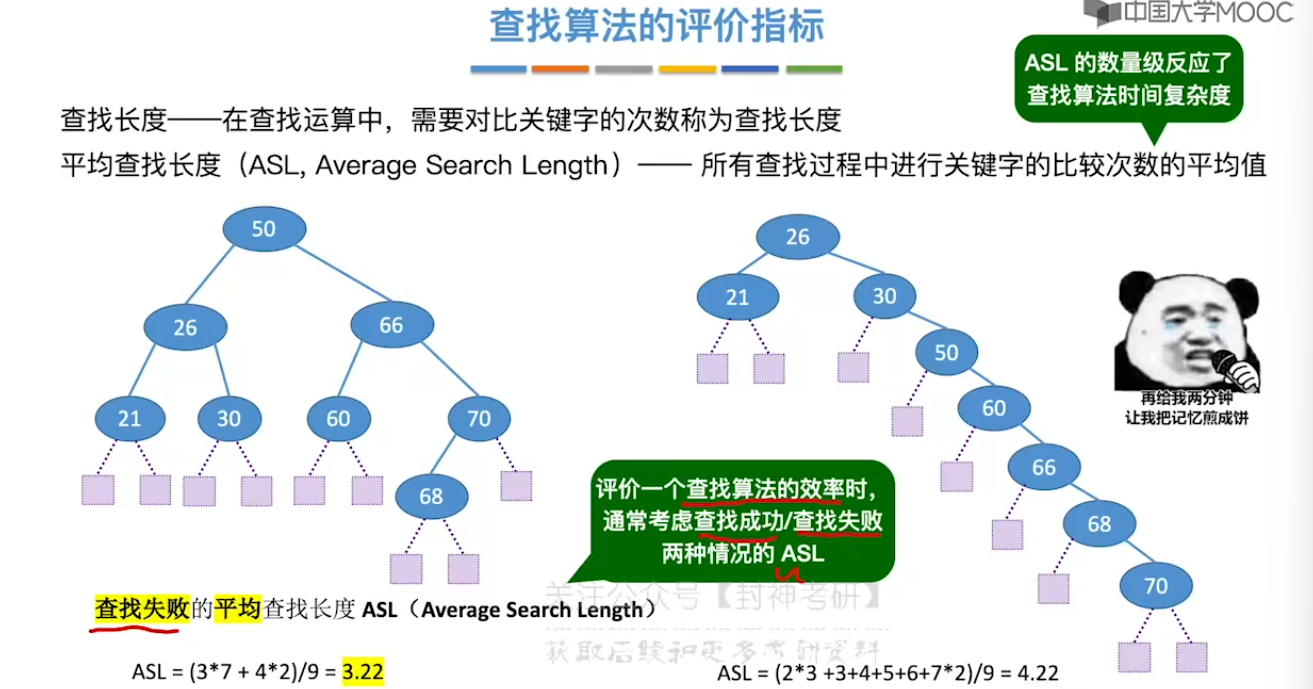
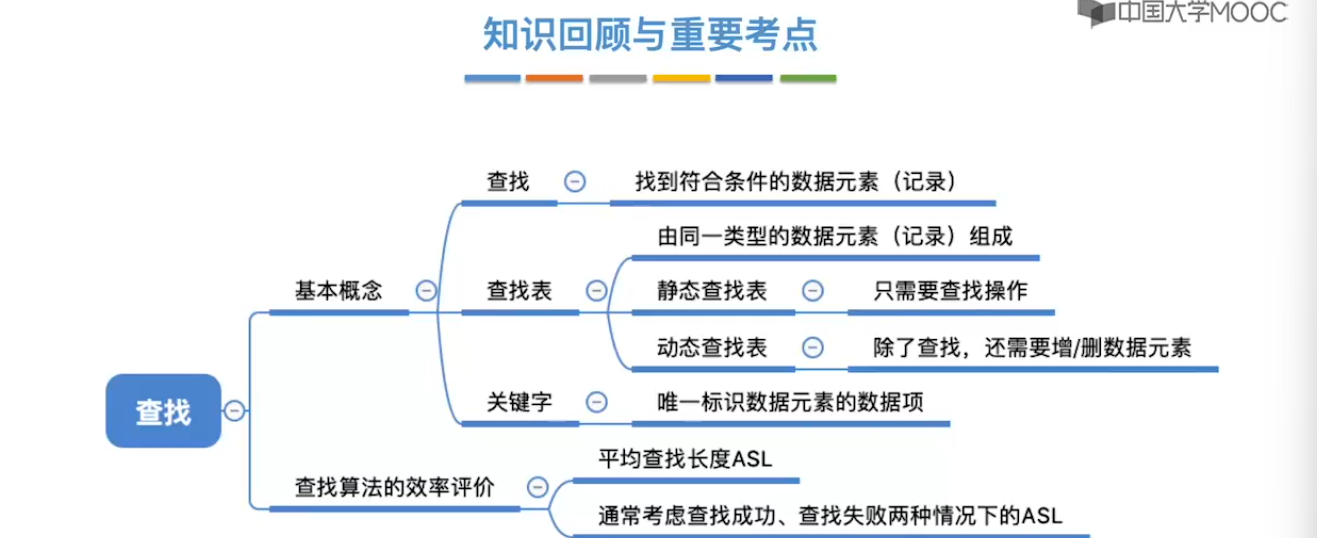
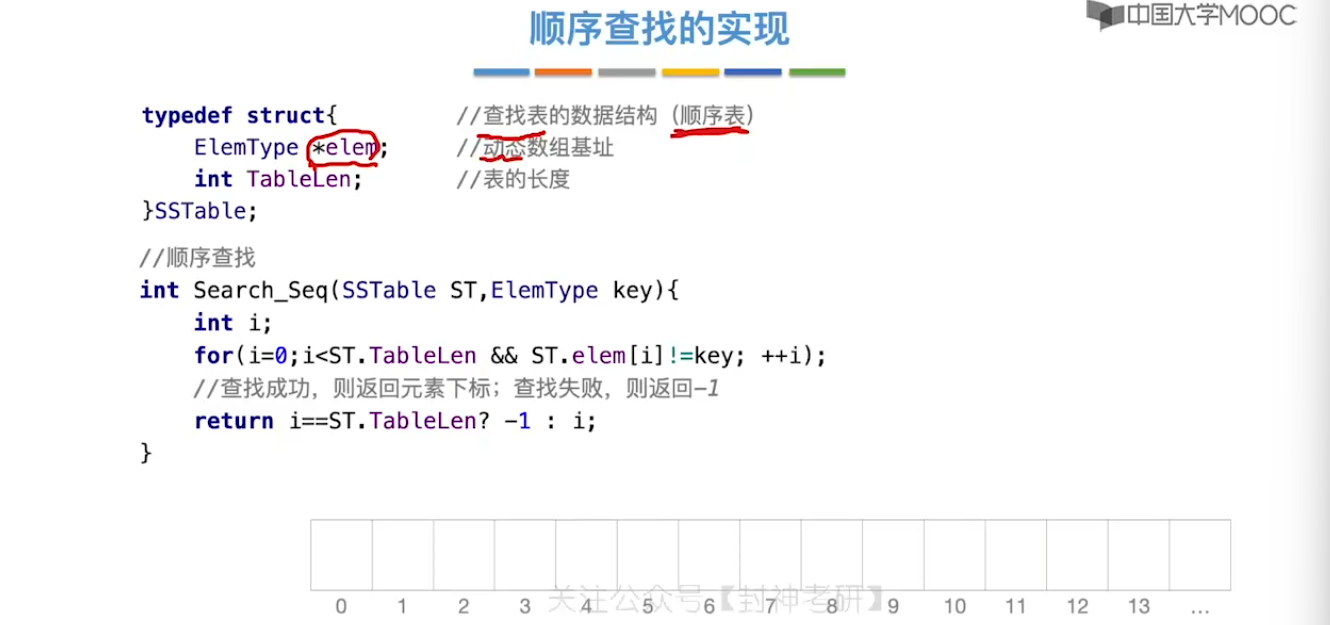
7.2、顺序查找


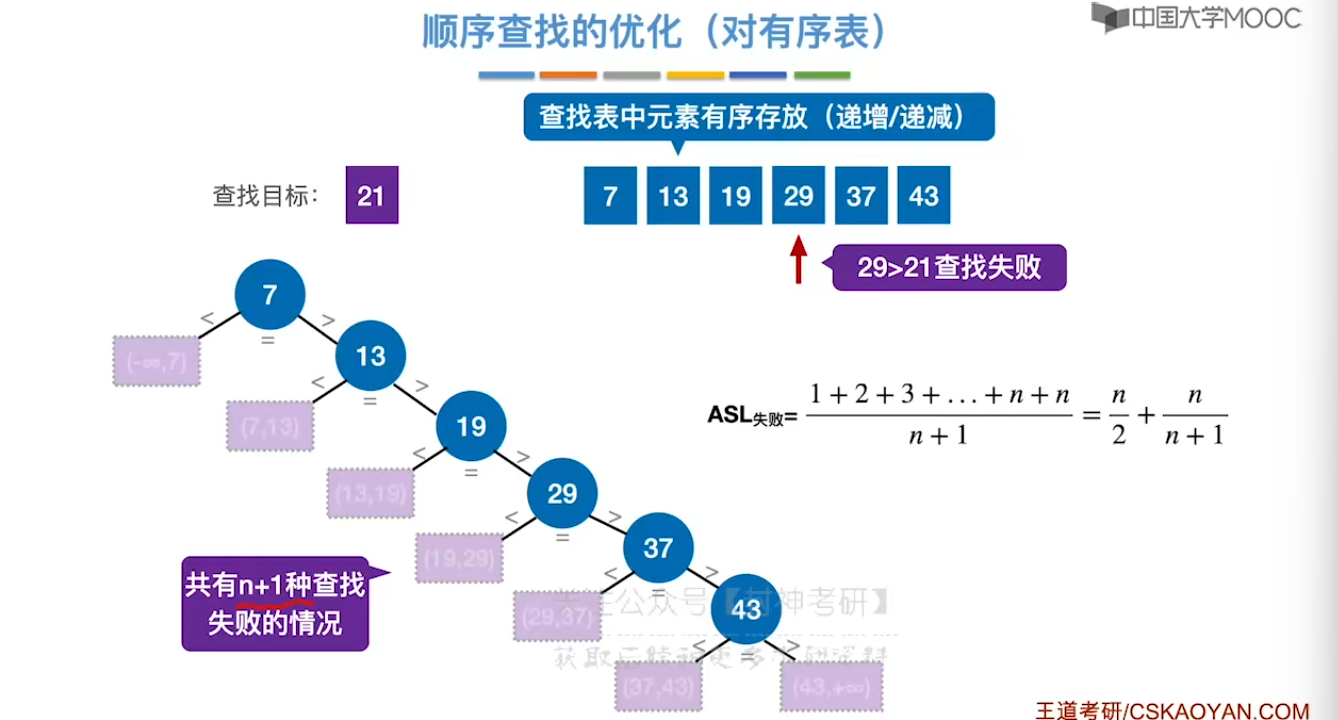
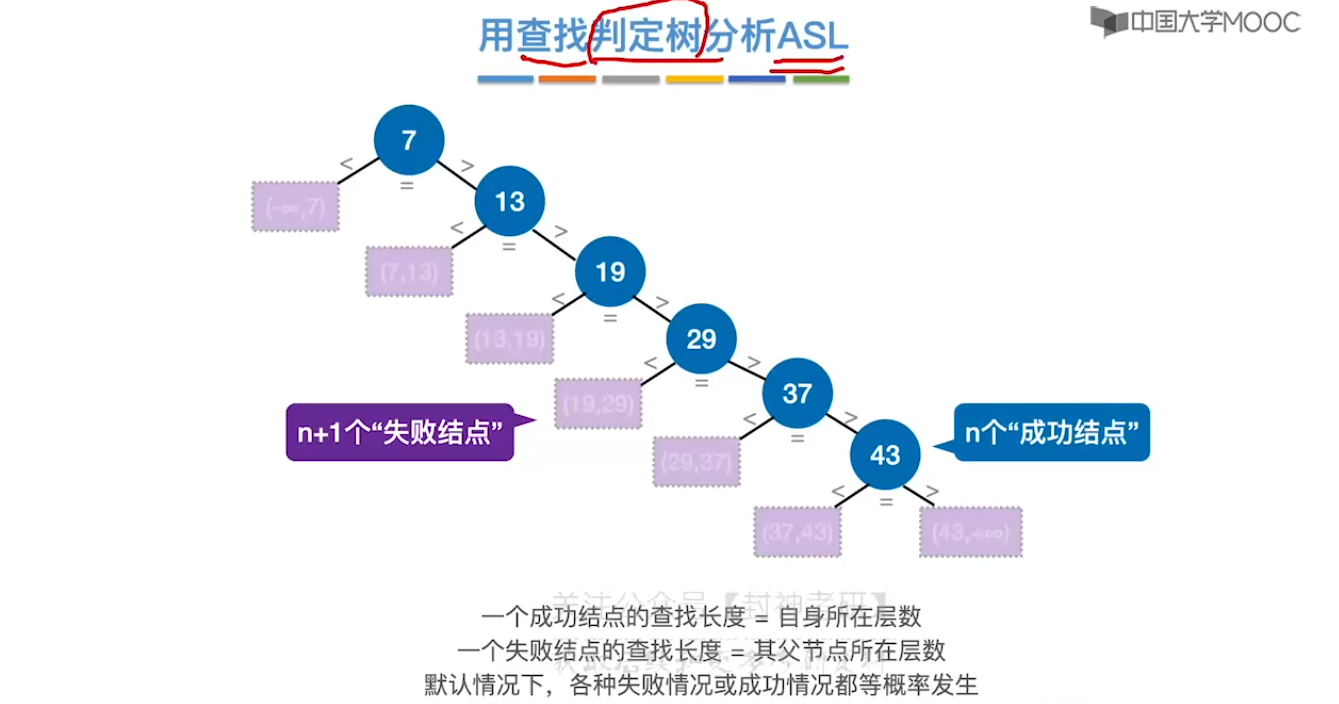
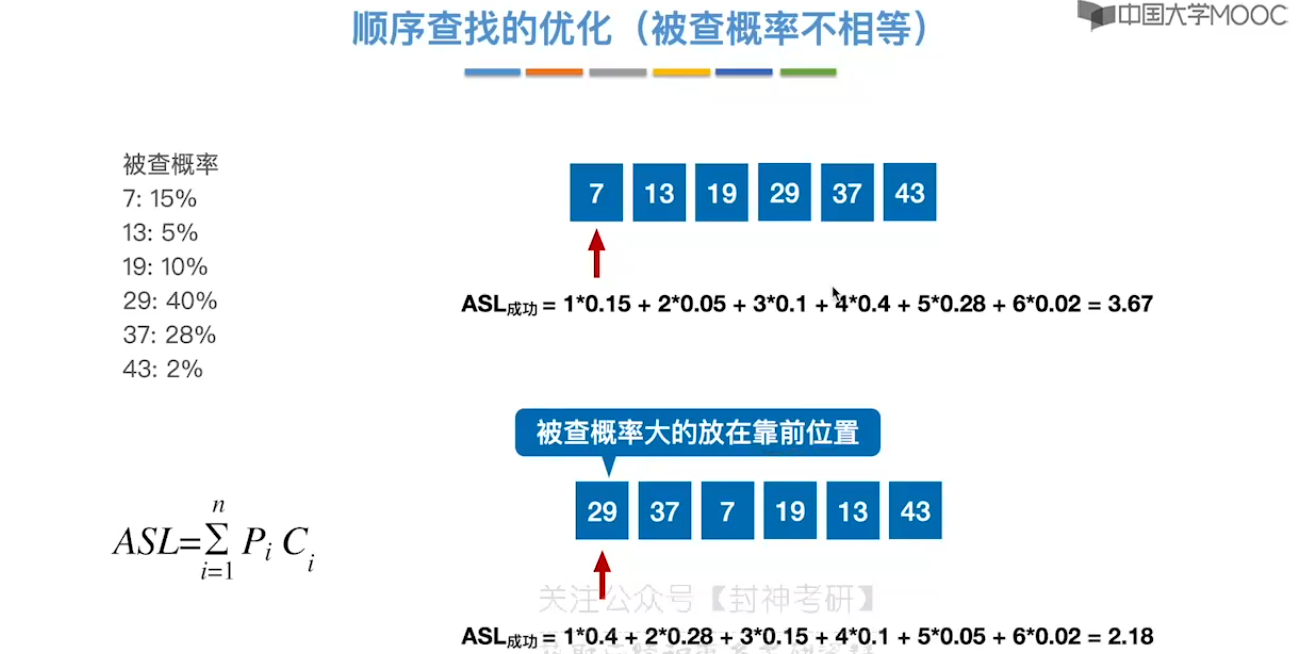

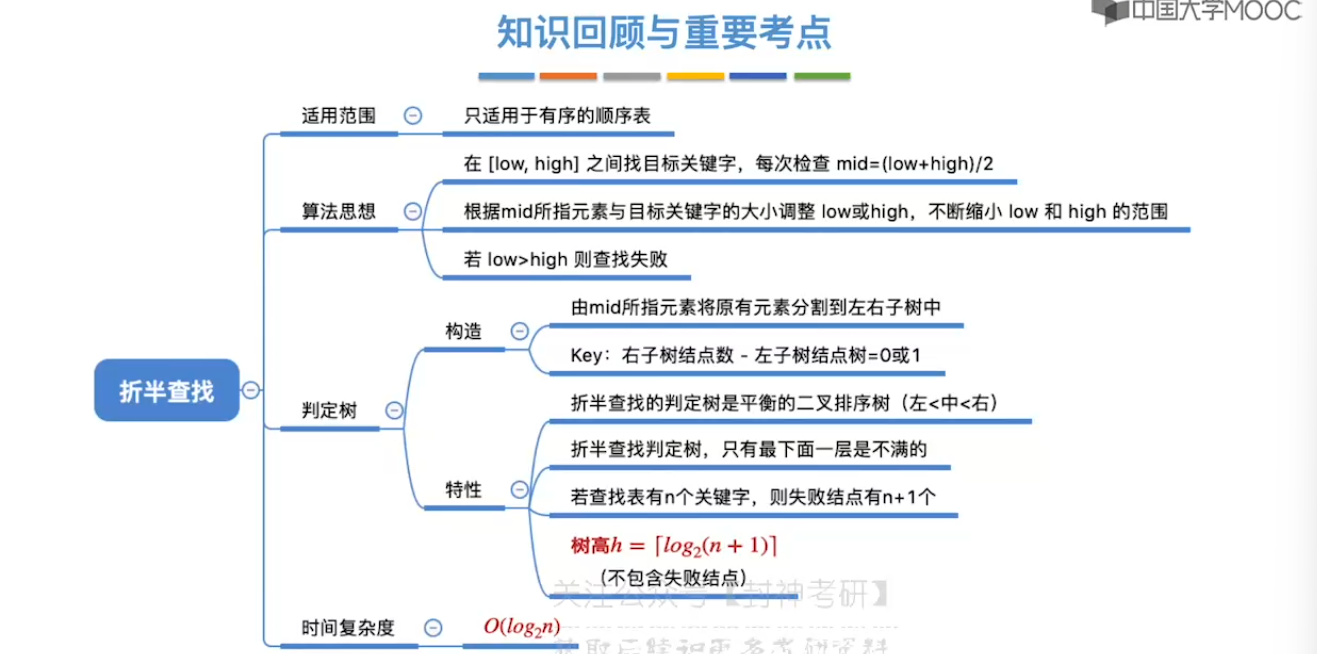
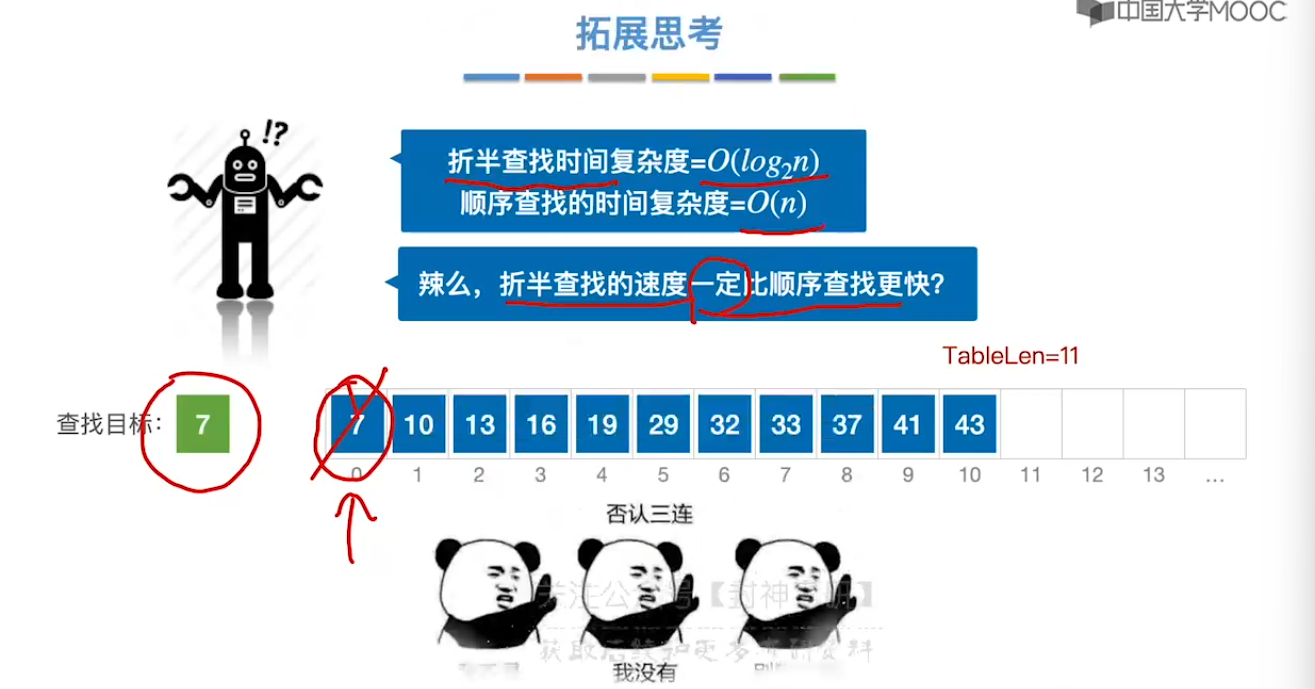
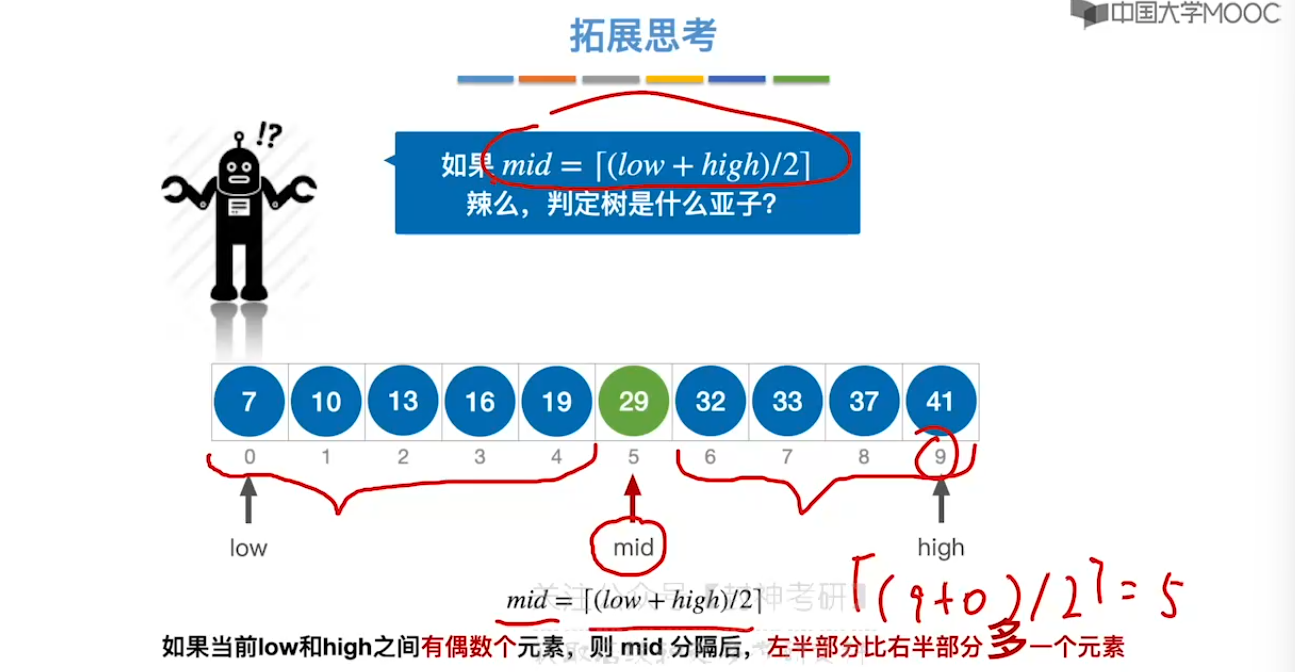
7.3、折半查找
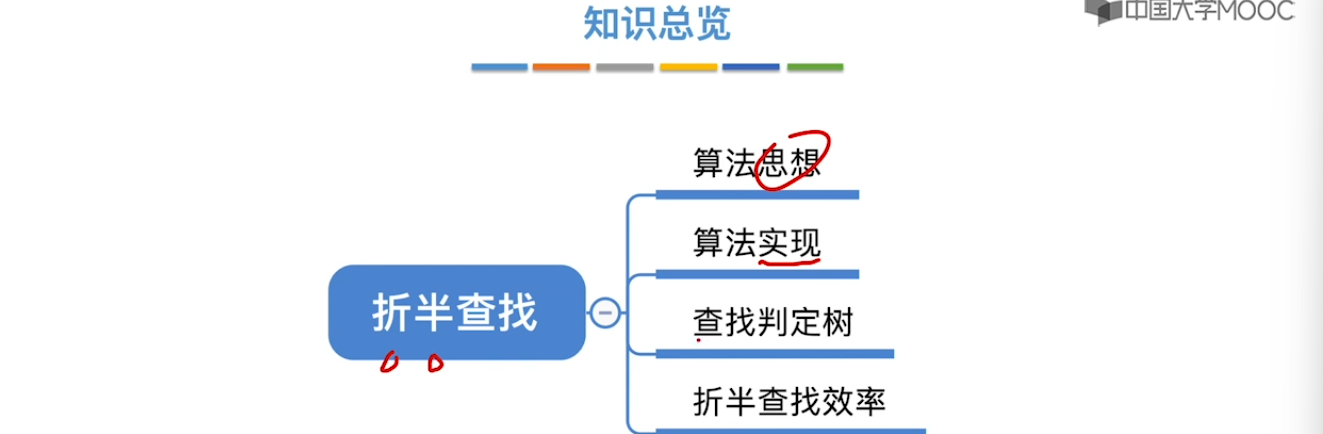
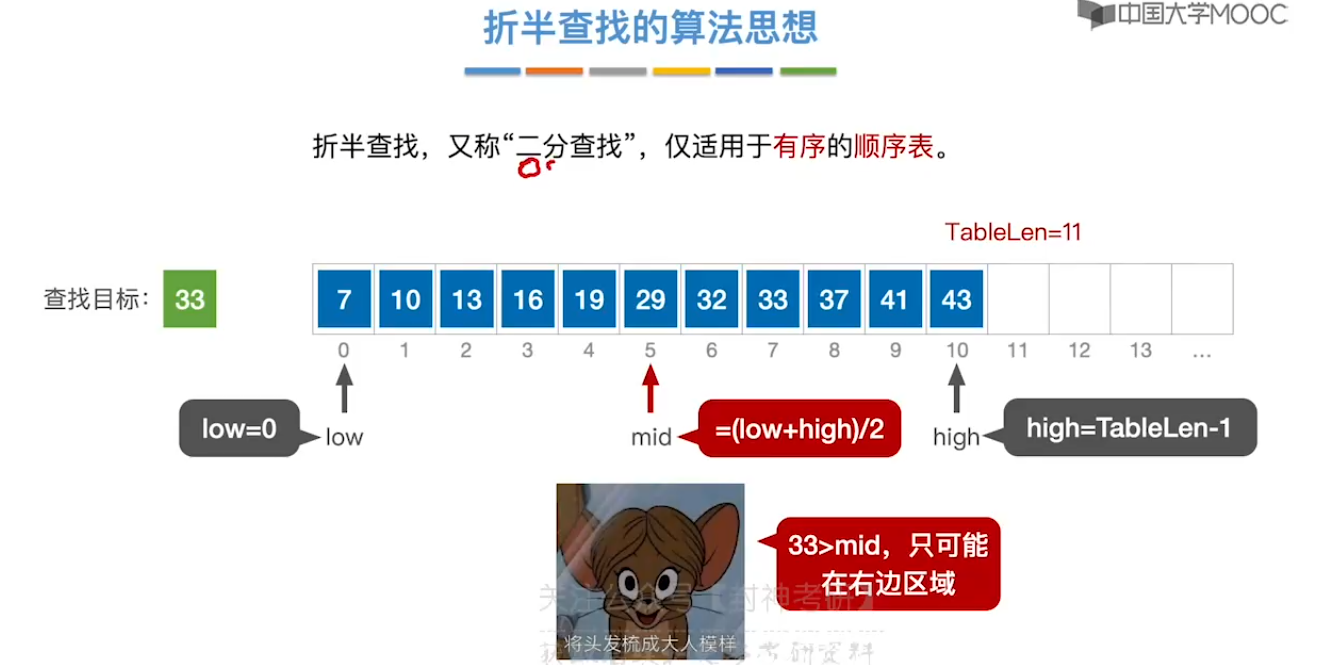
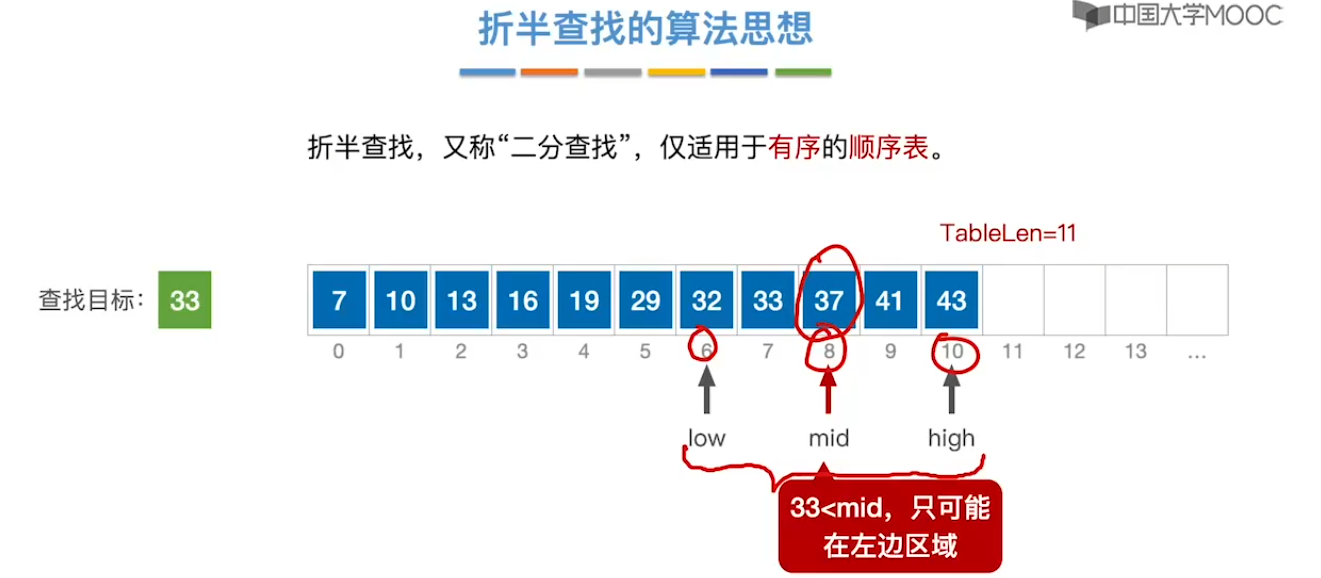
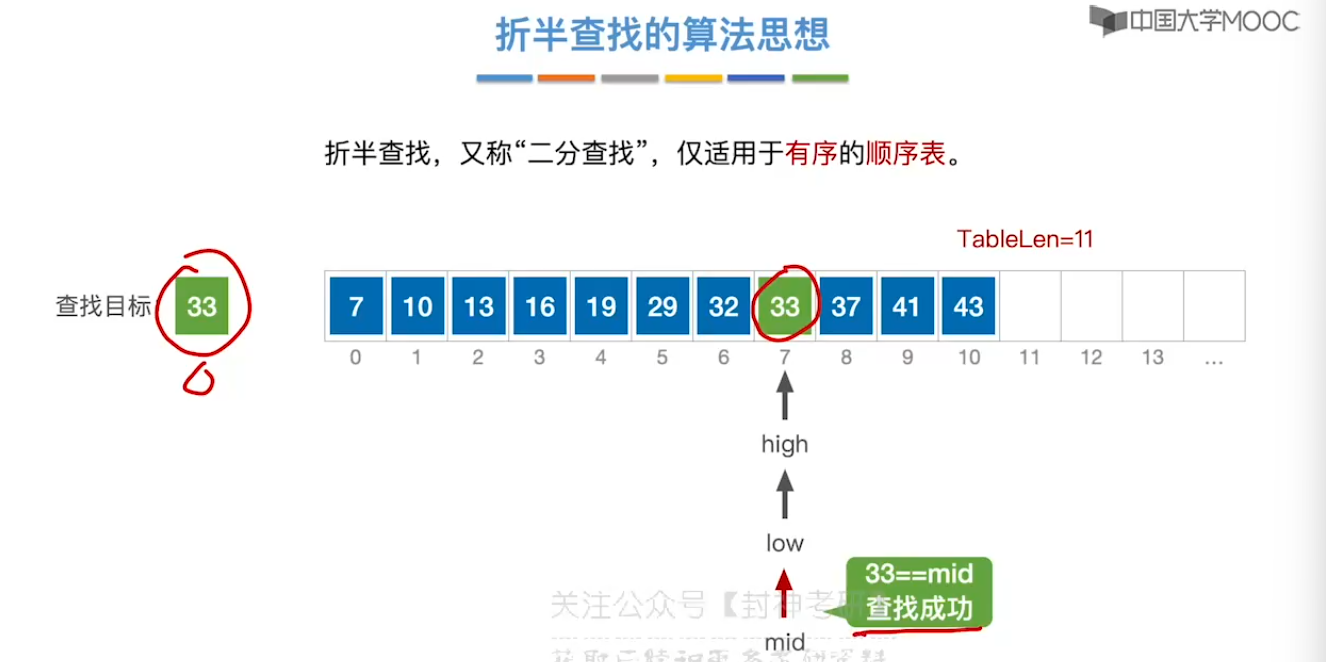
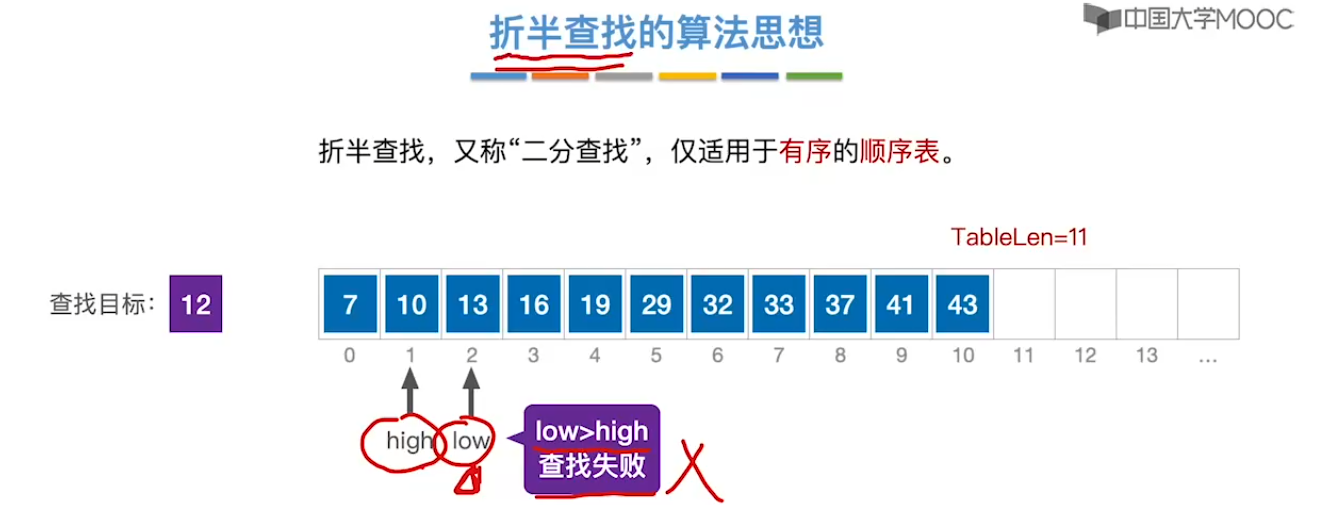


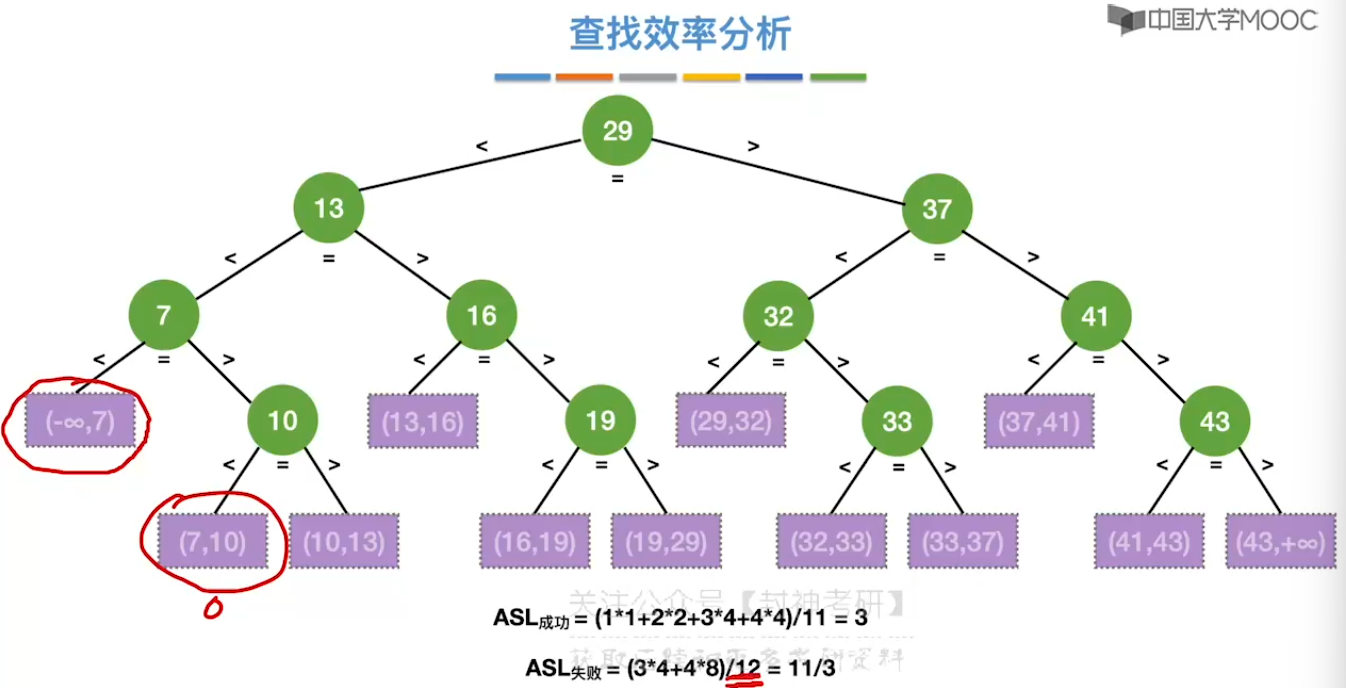
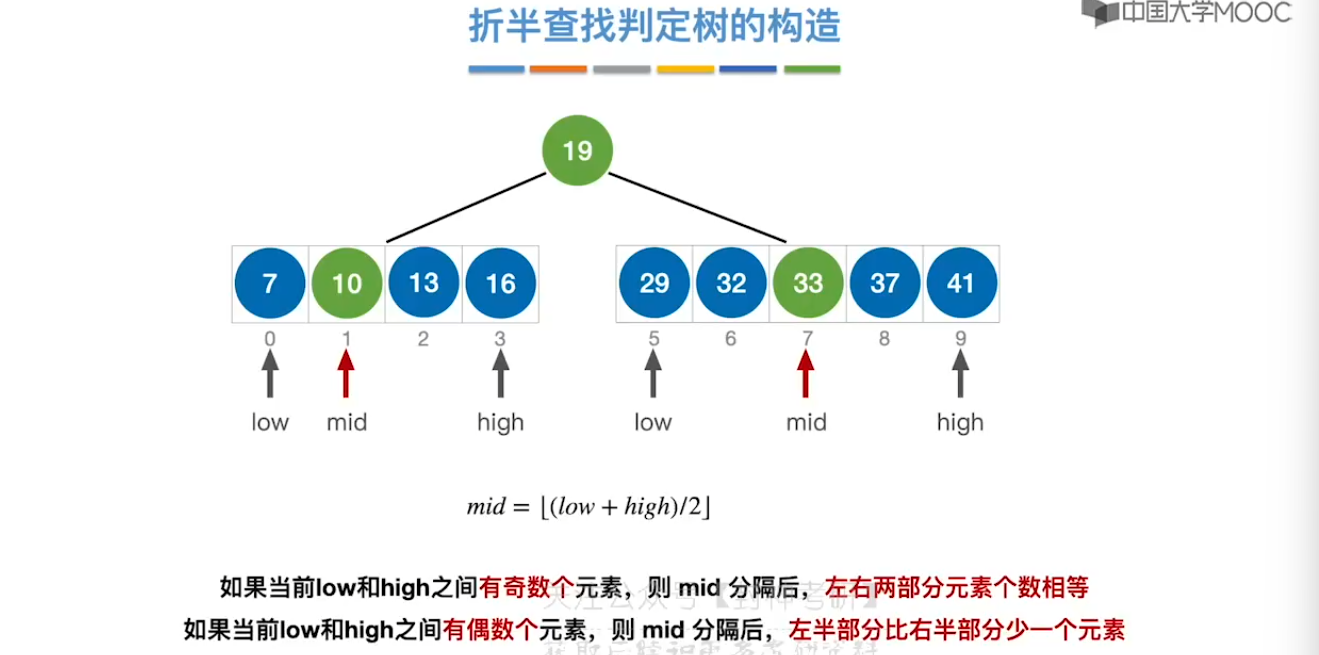

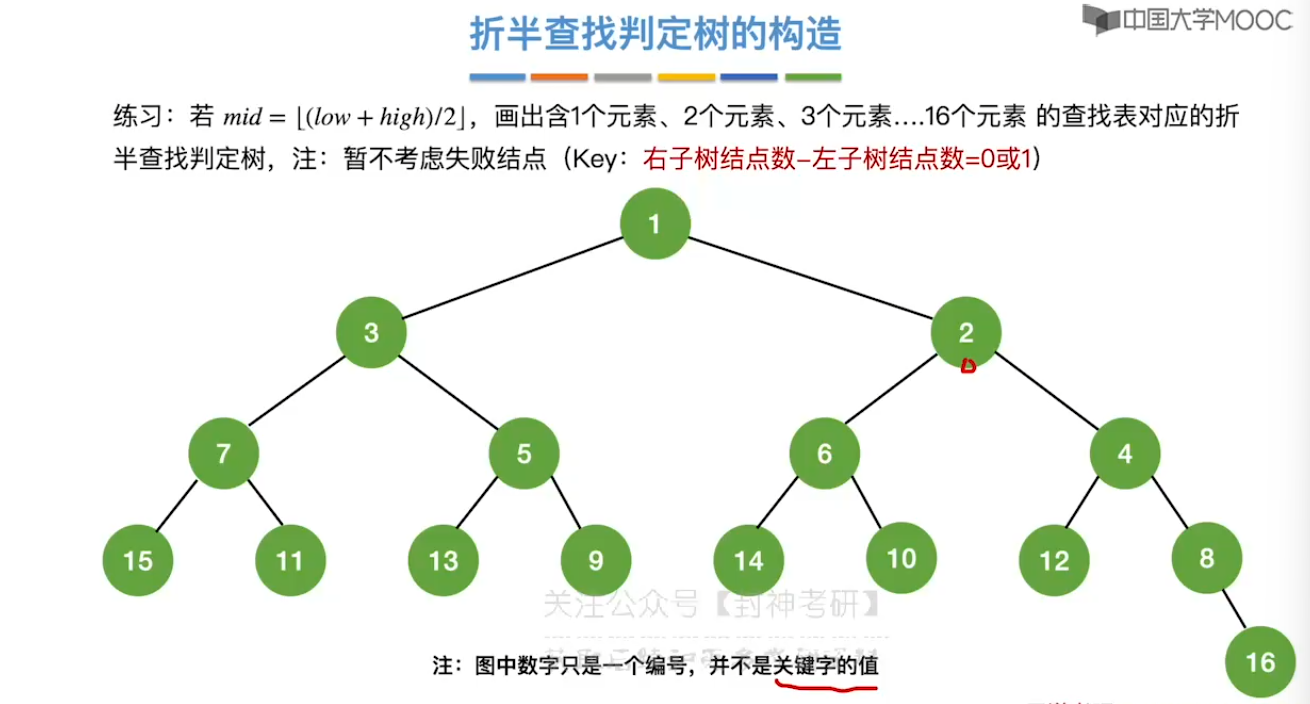
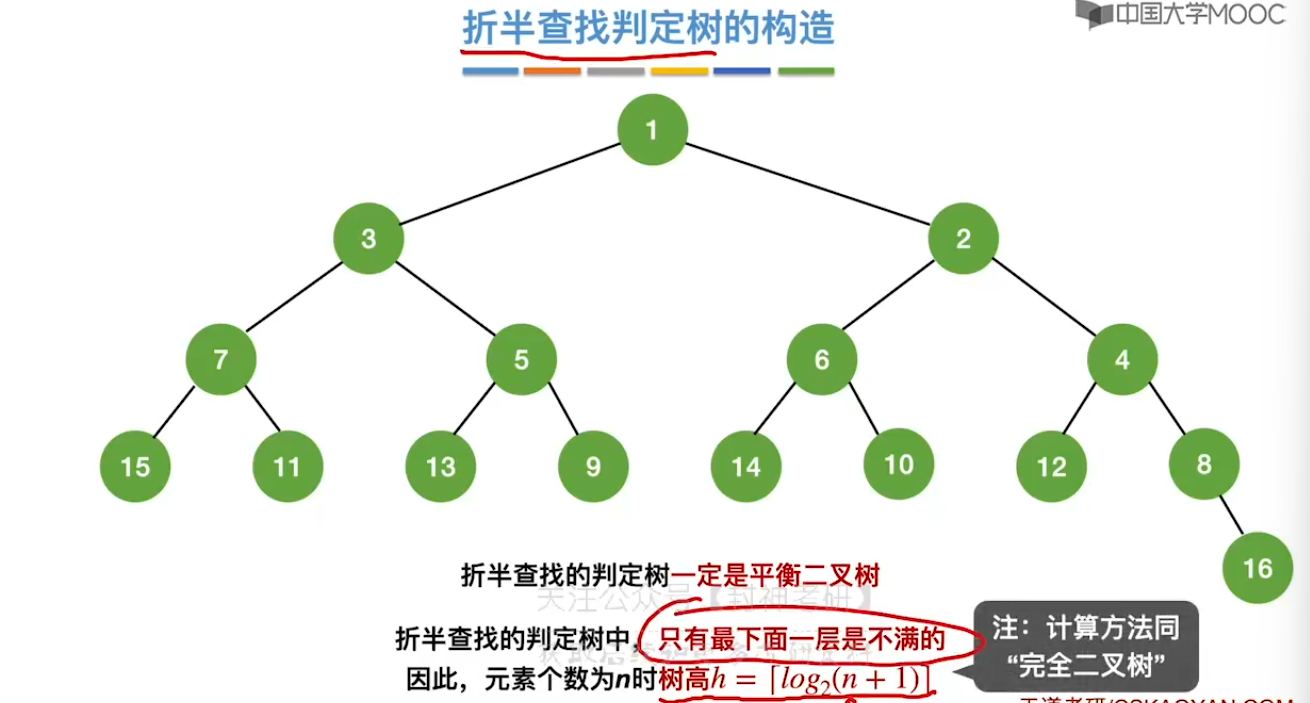
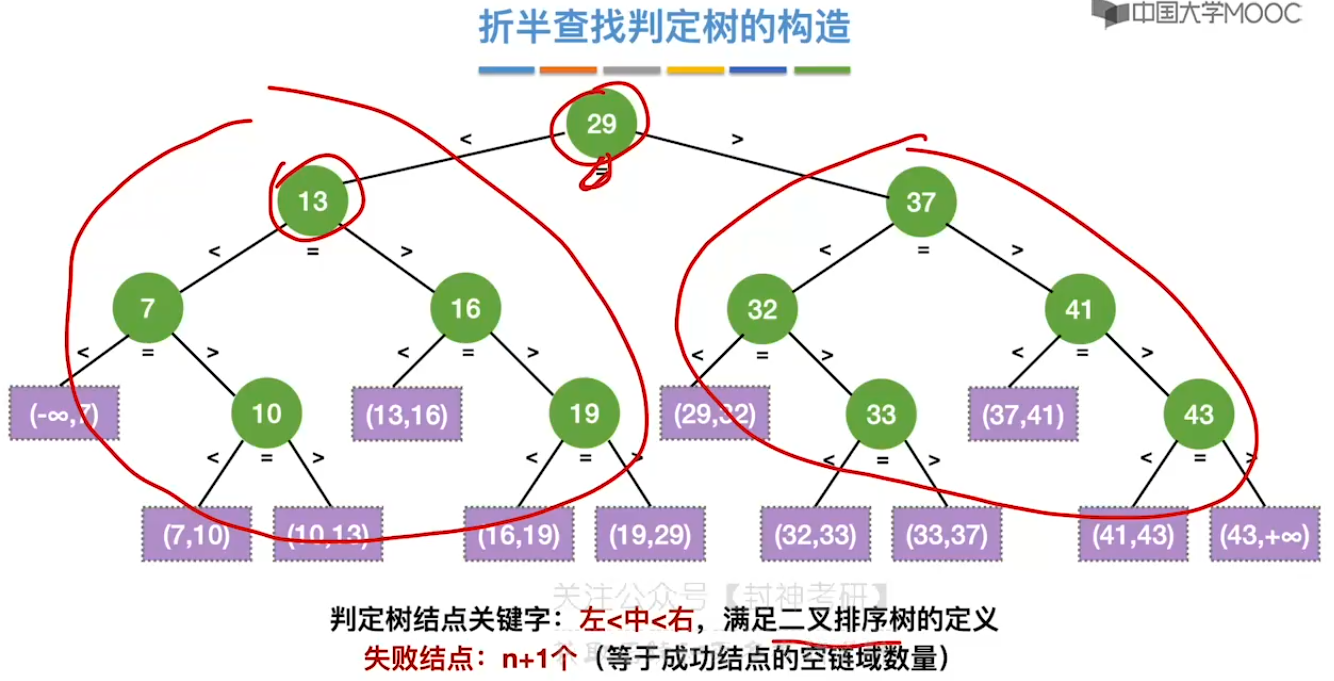
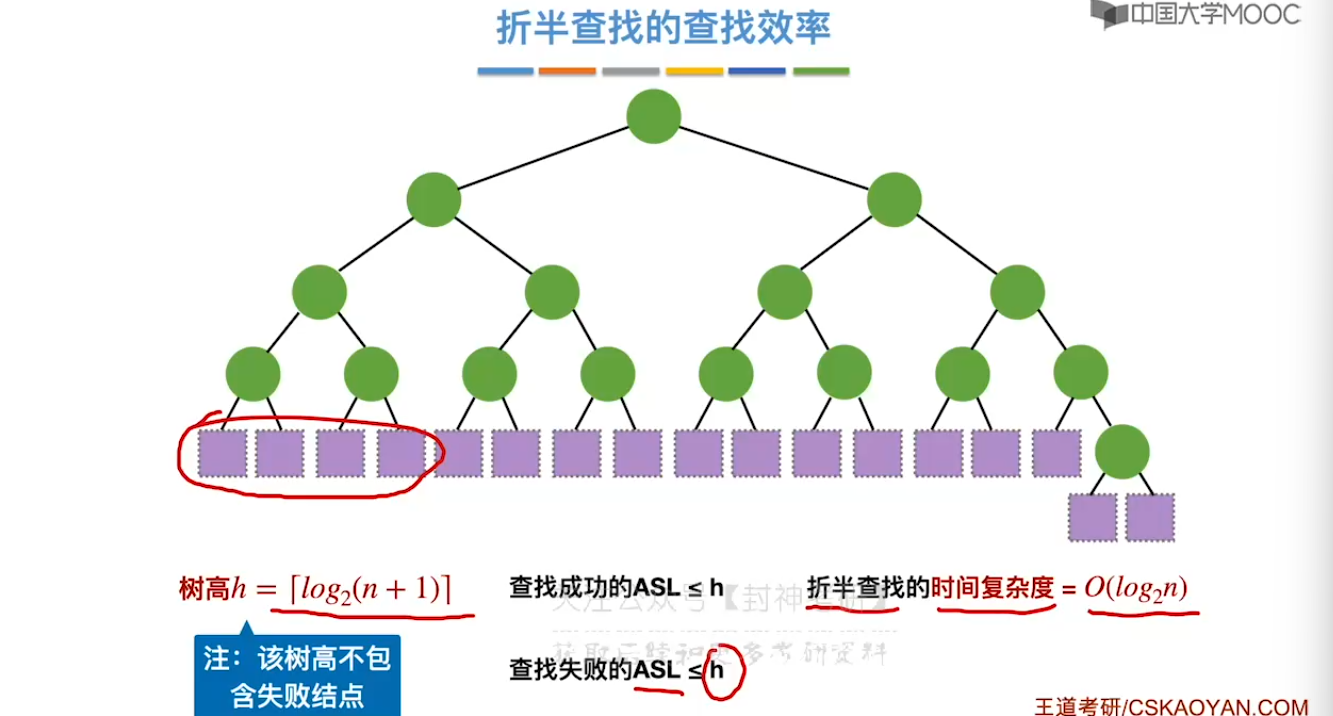
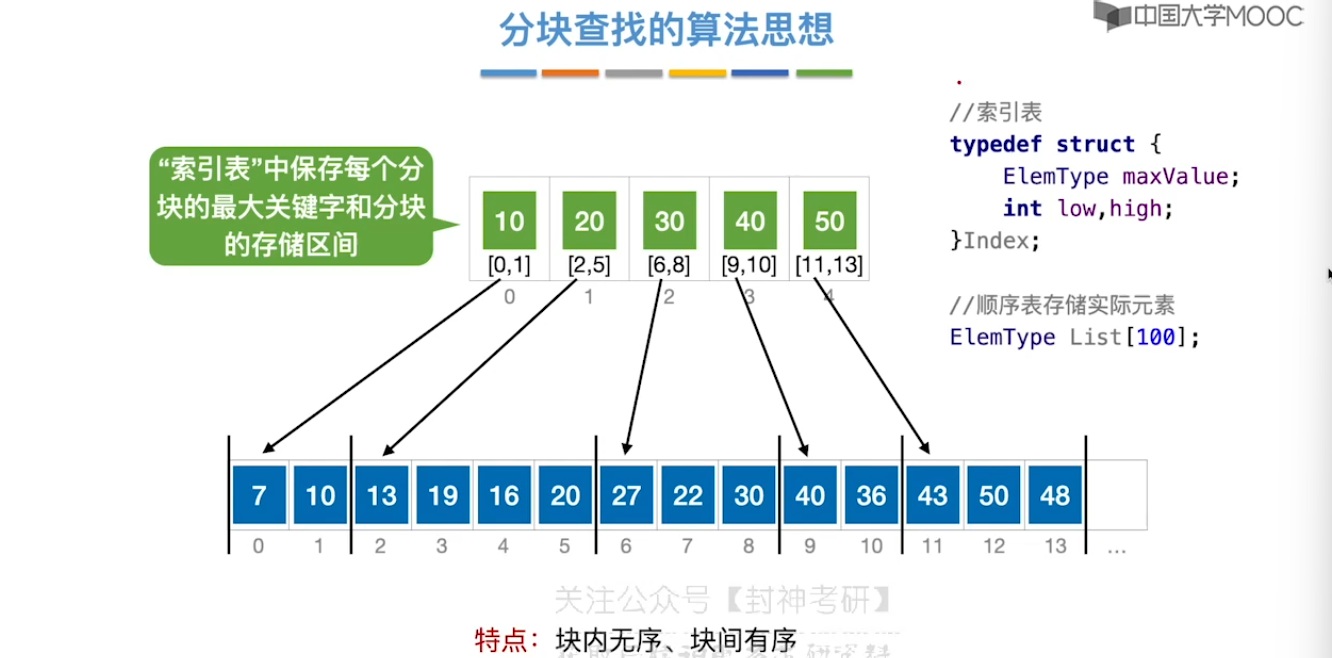
7.4、分块查找
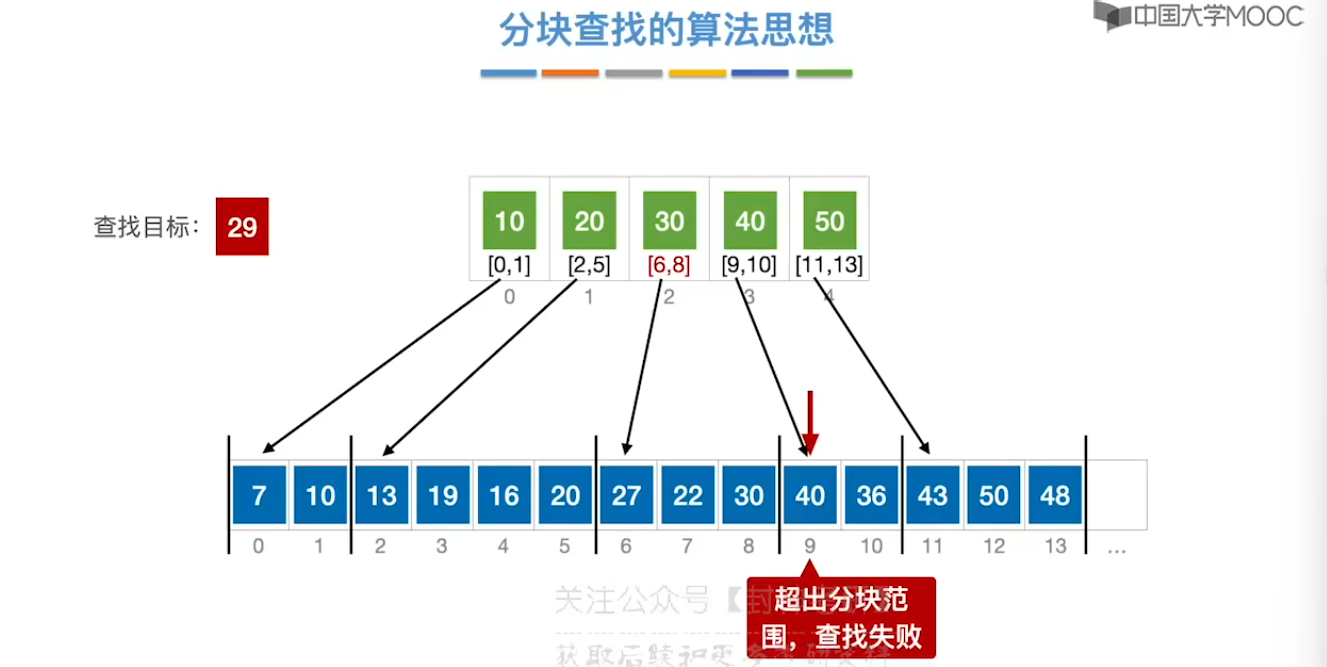
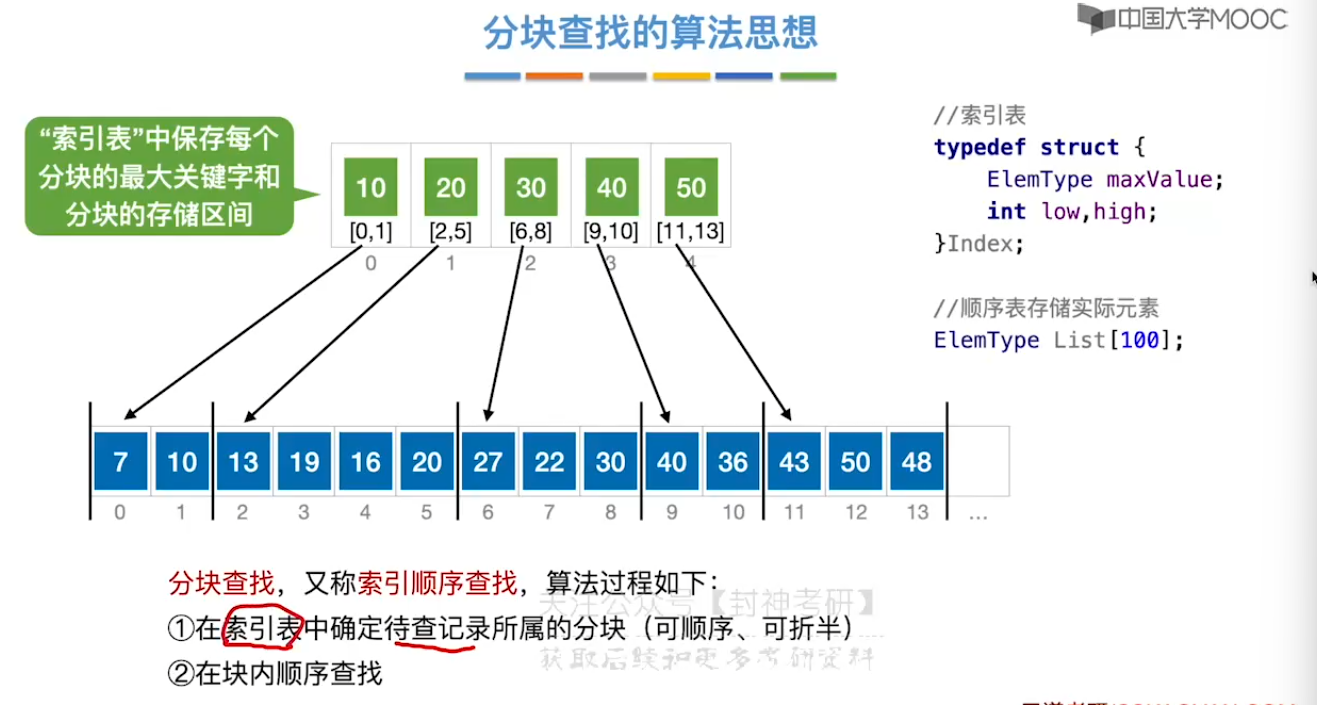
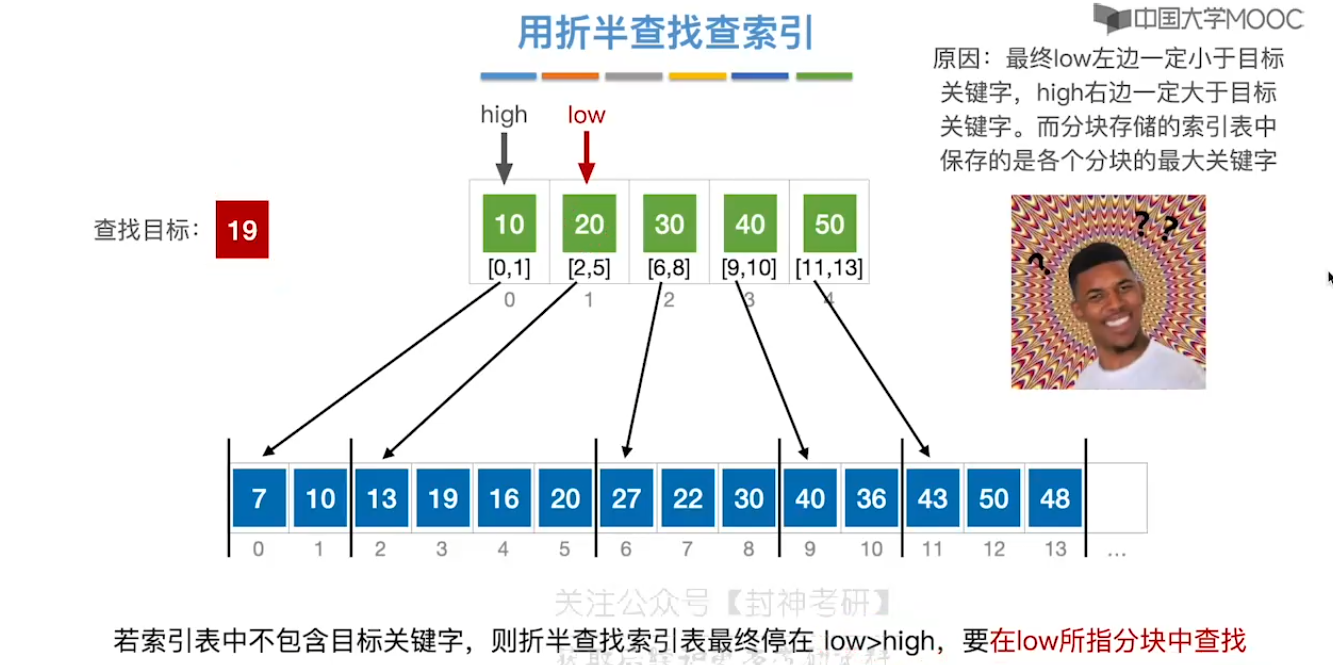
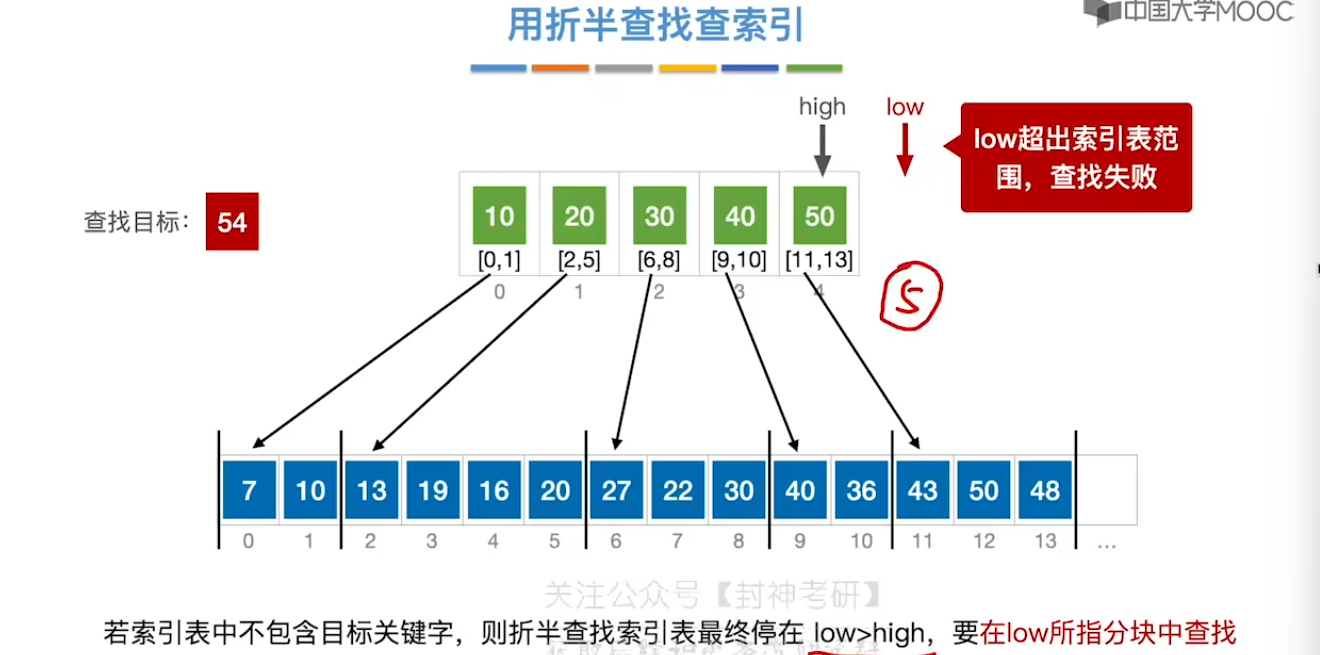
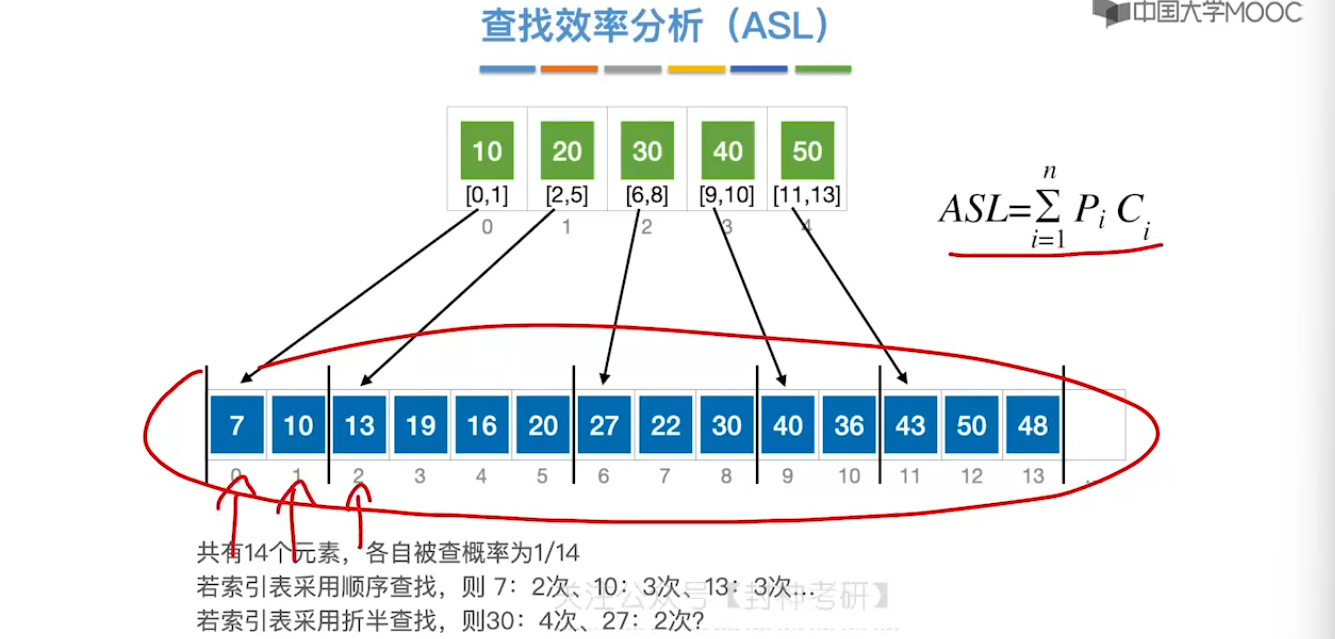
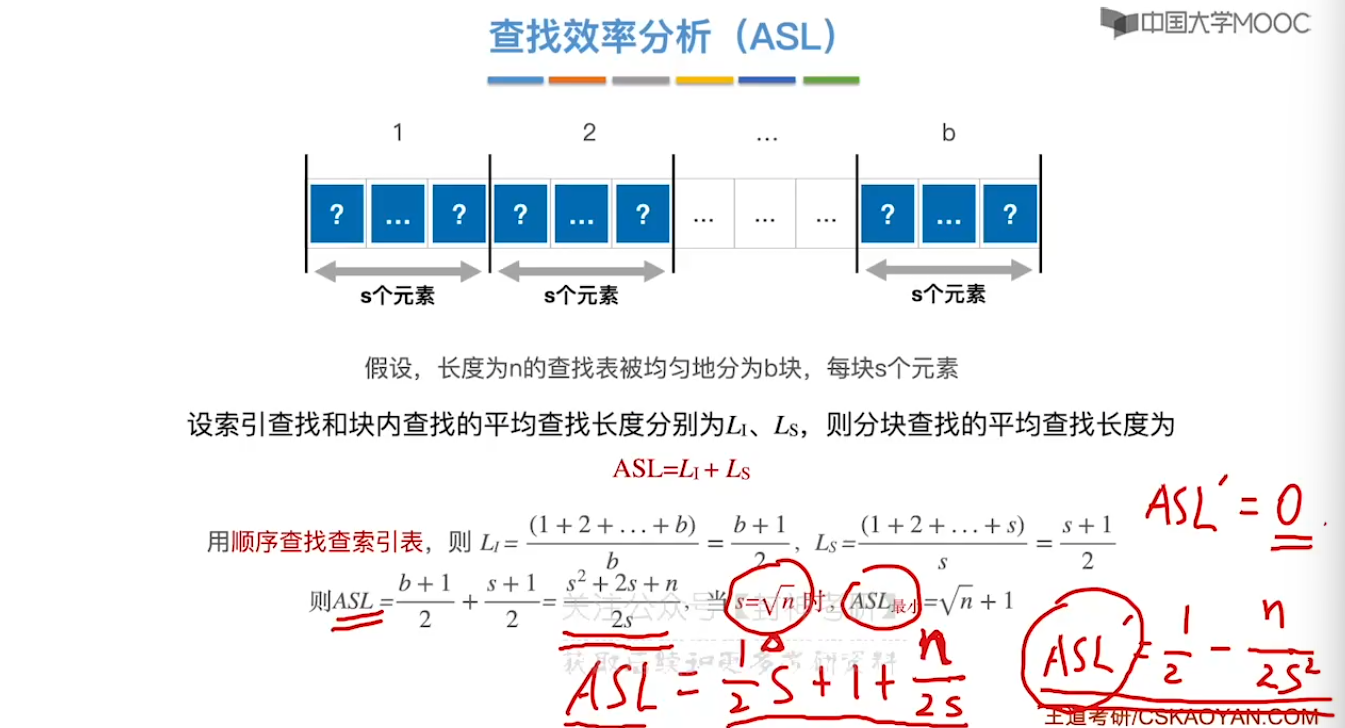
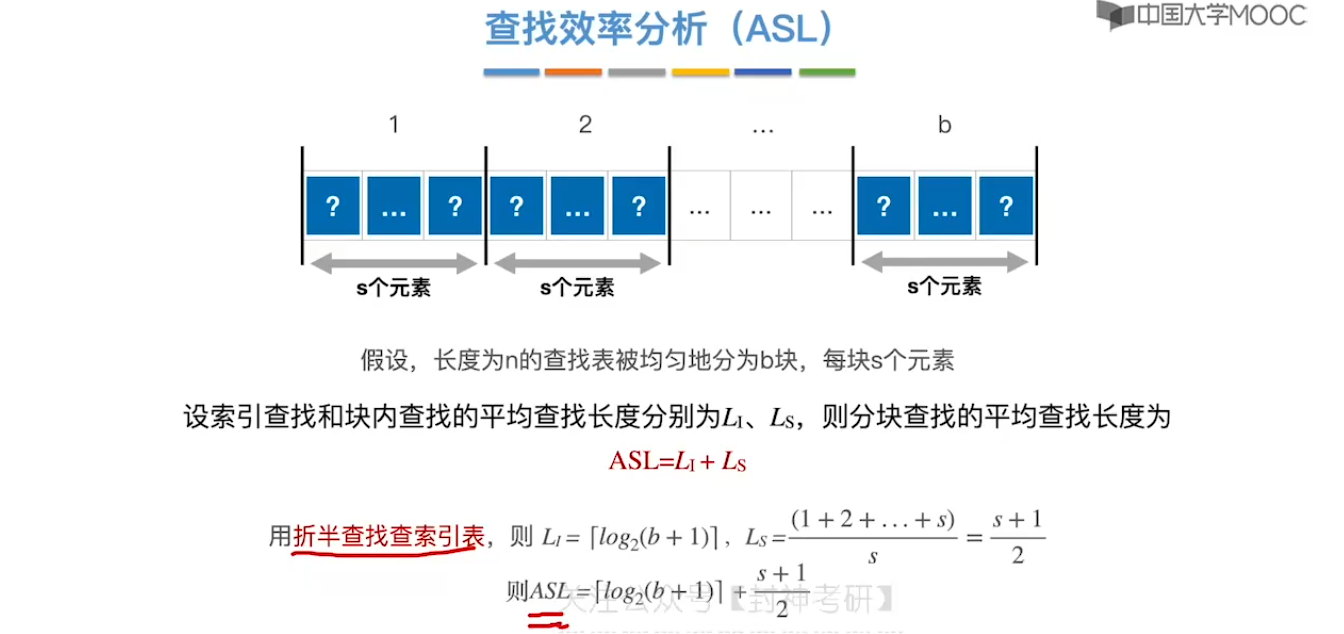
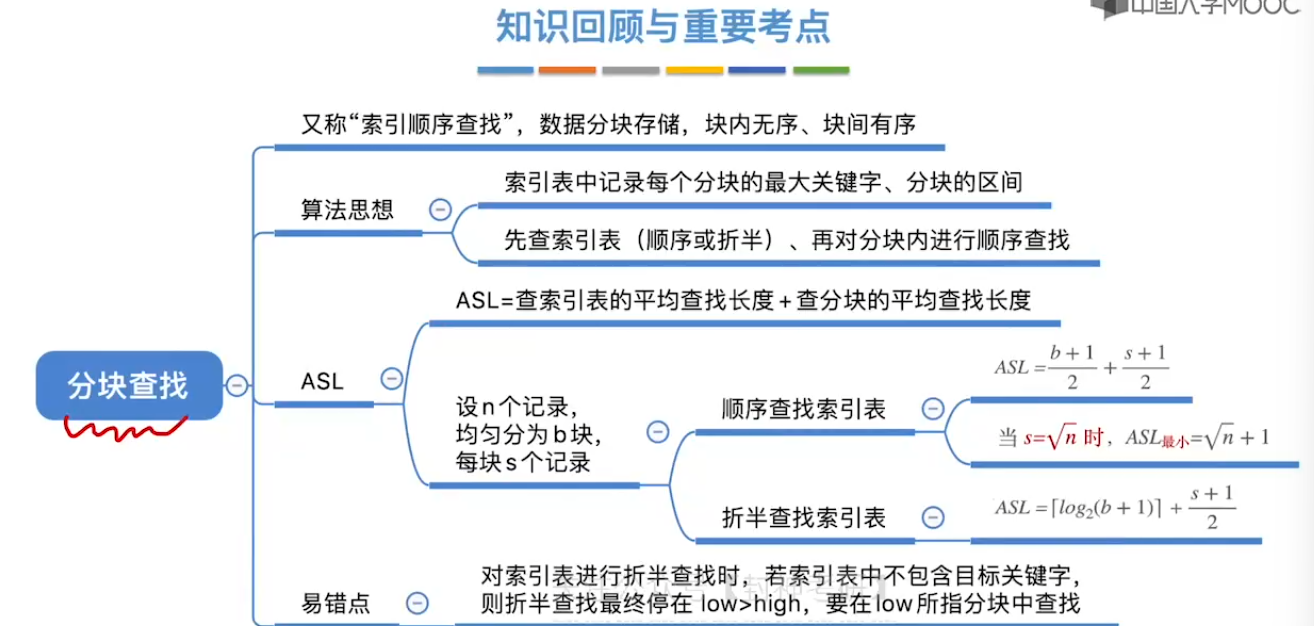
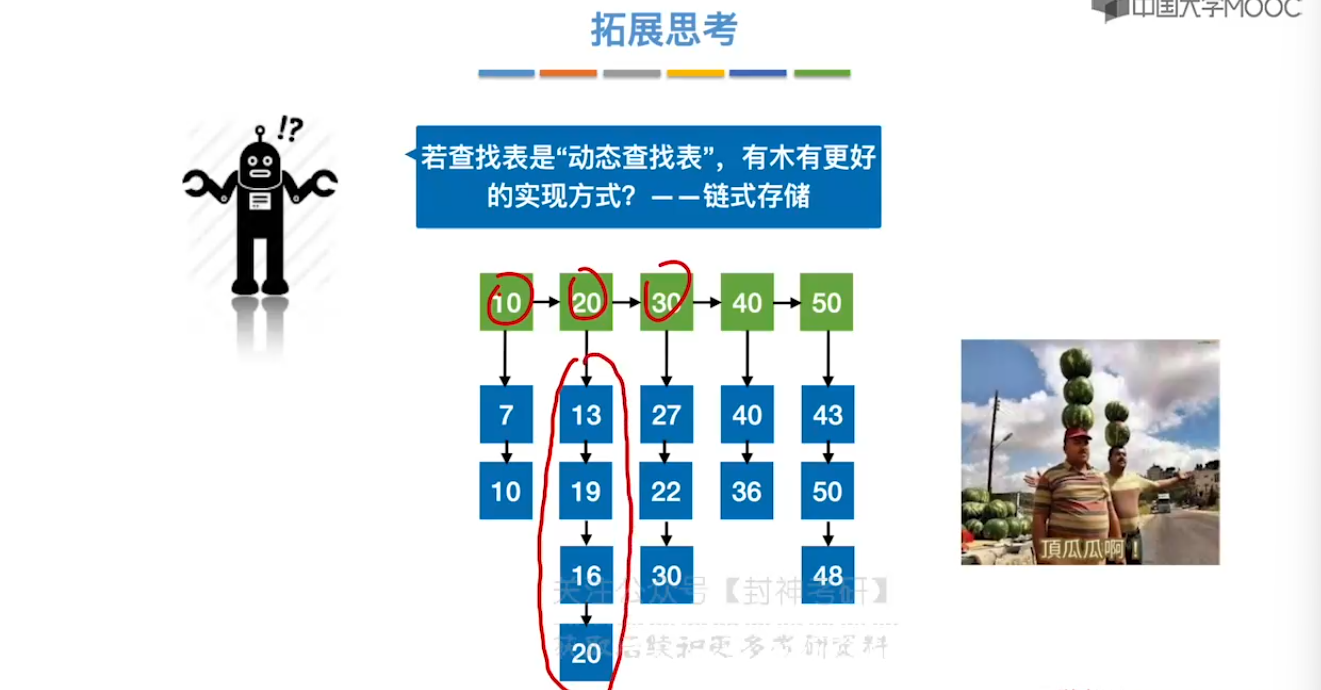
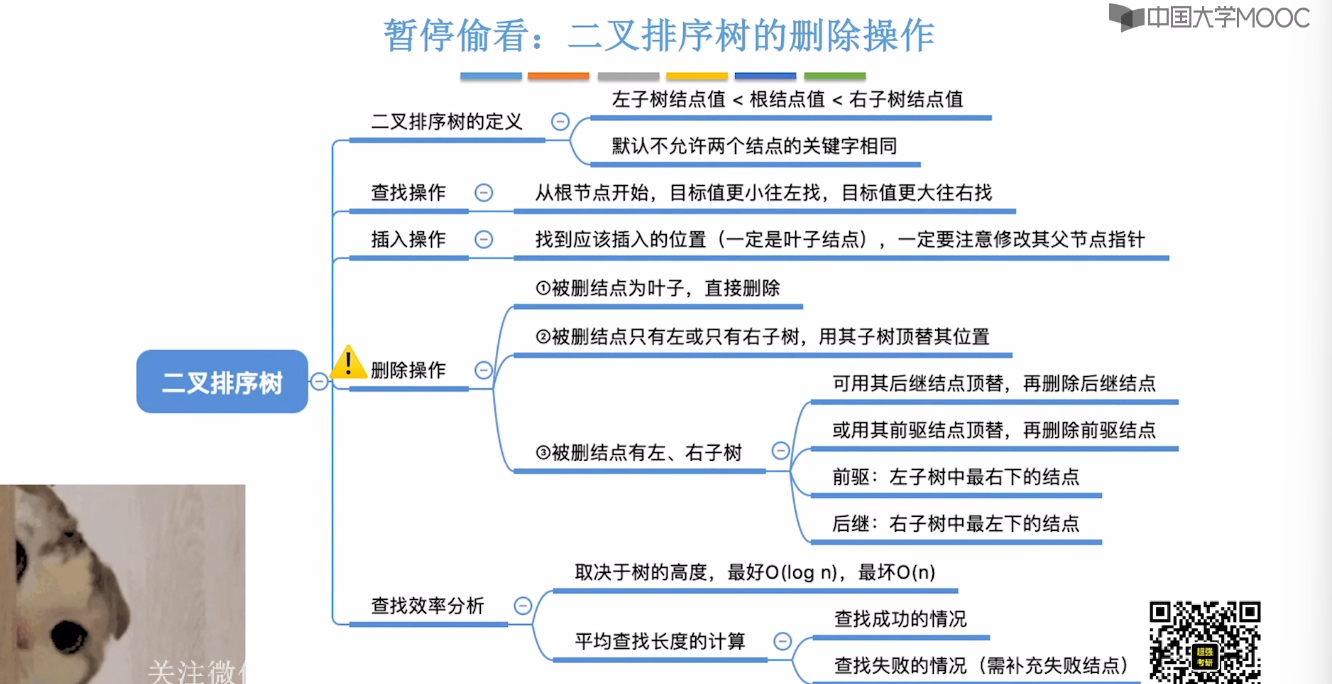
7.5、二叉排序树
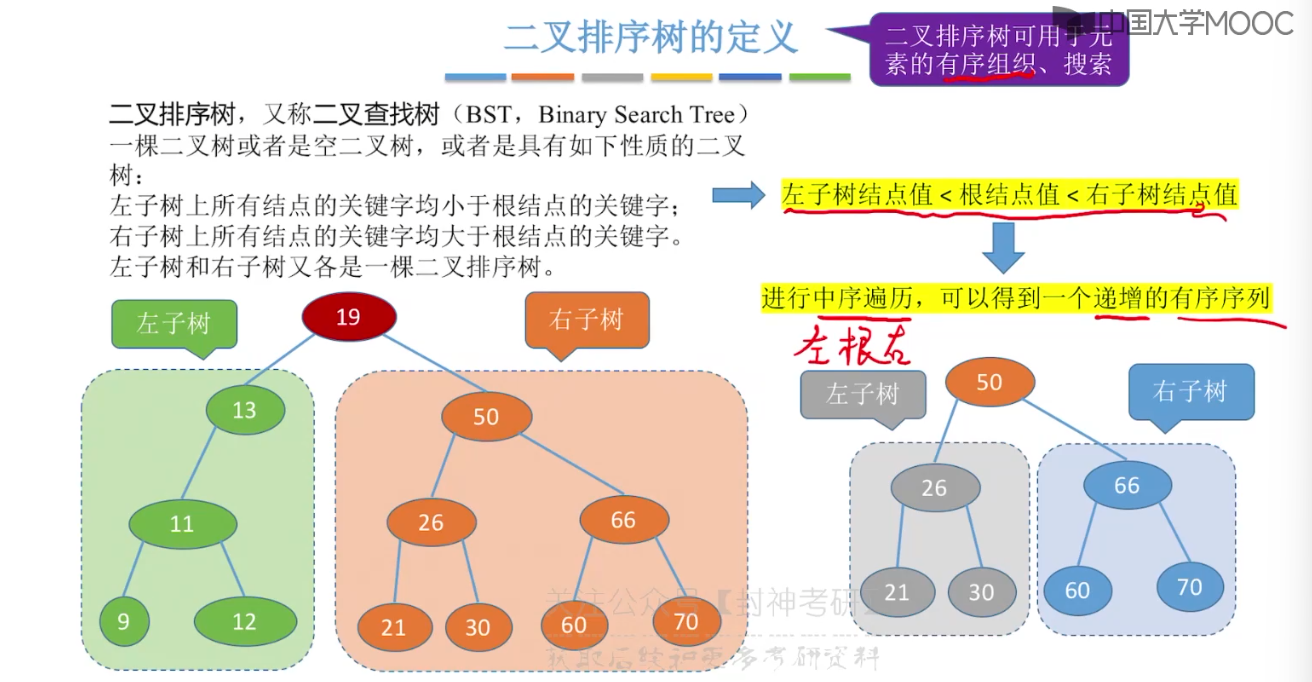
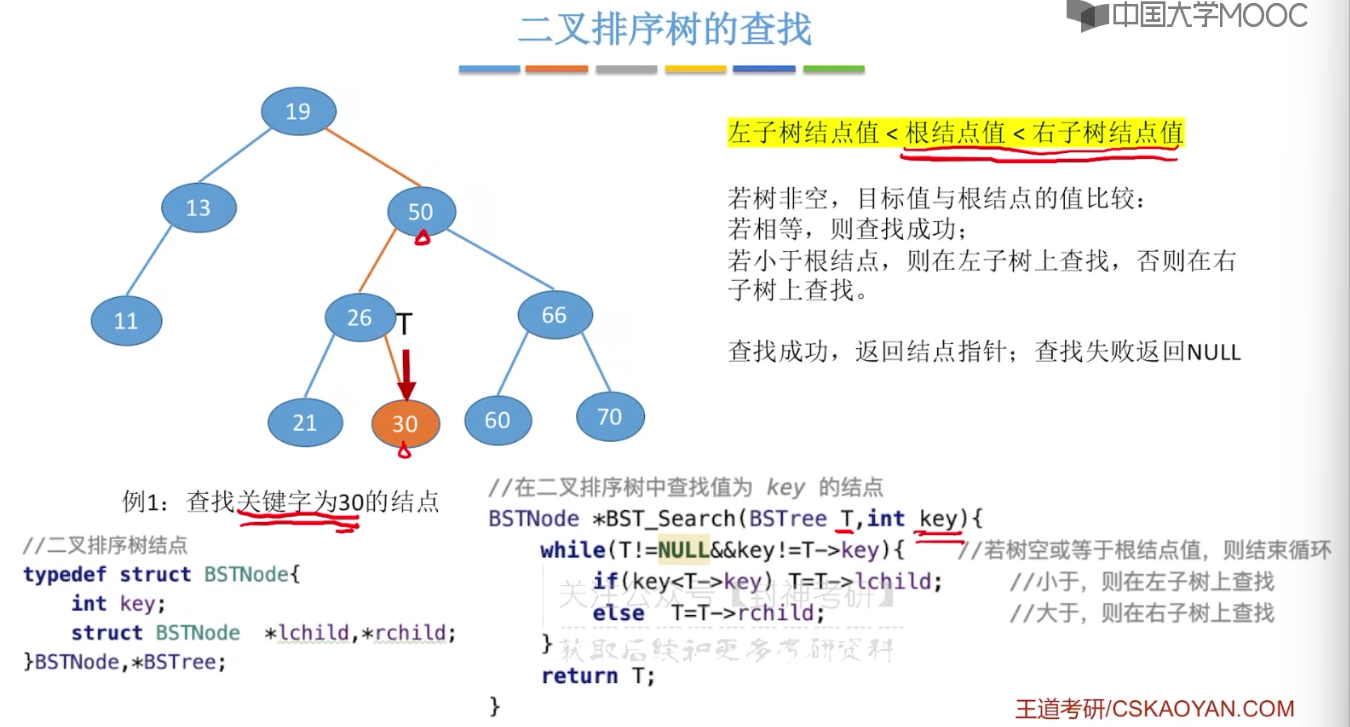

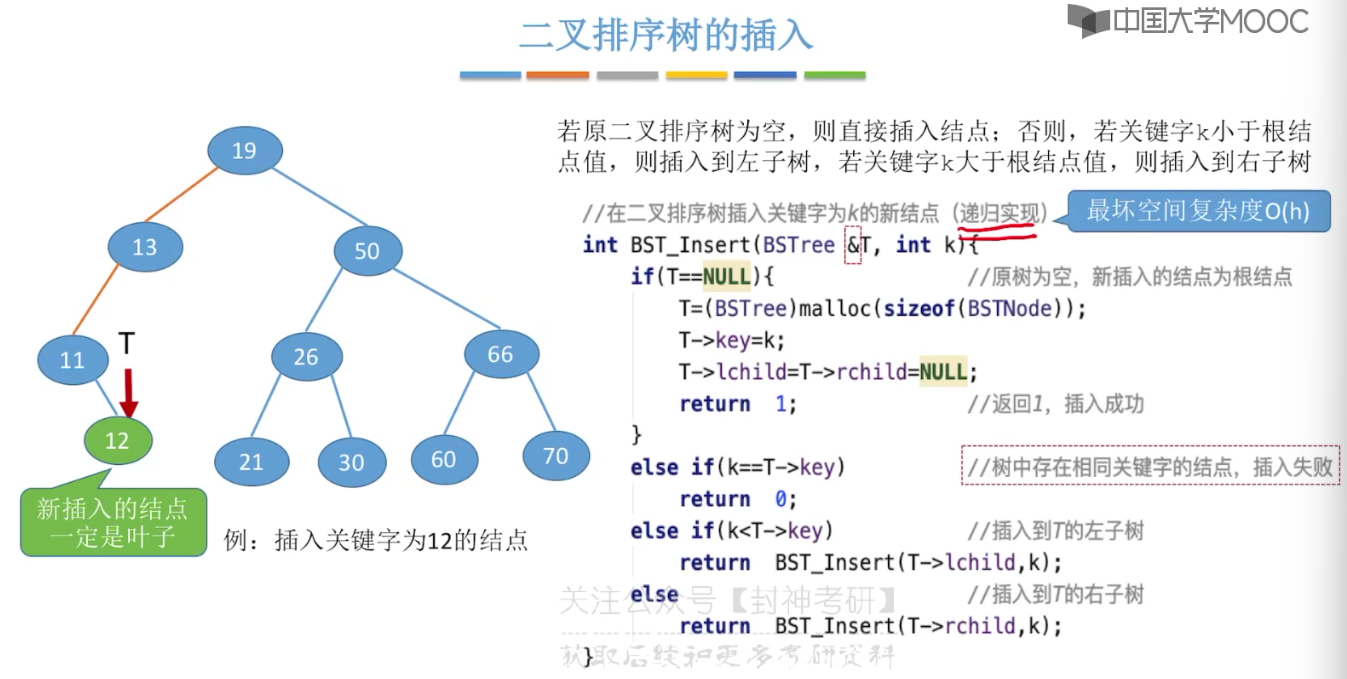
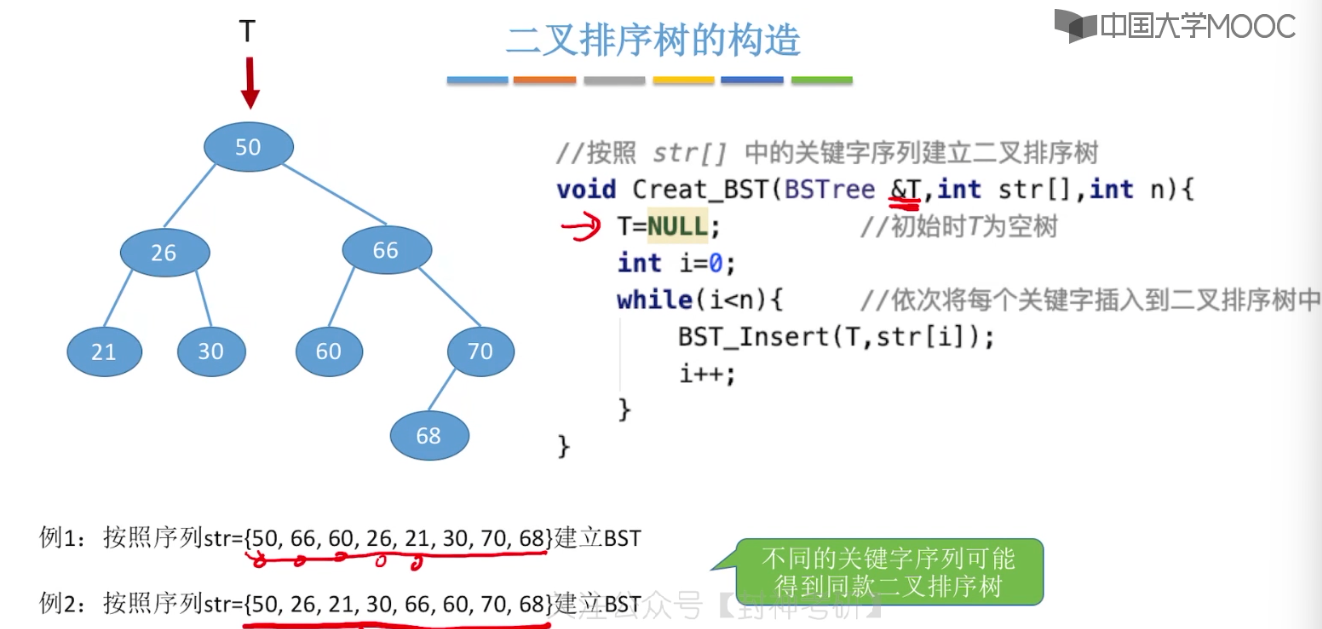
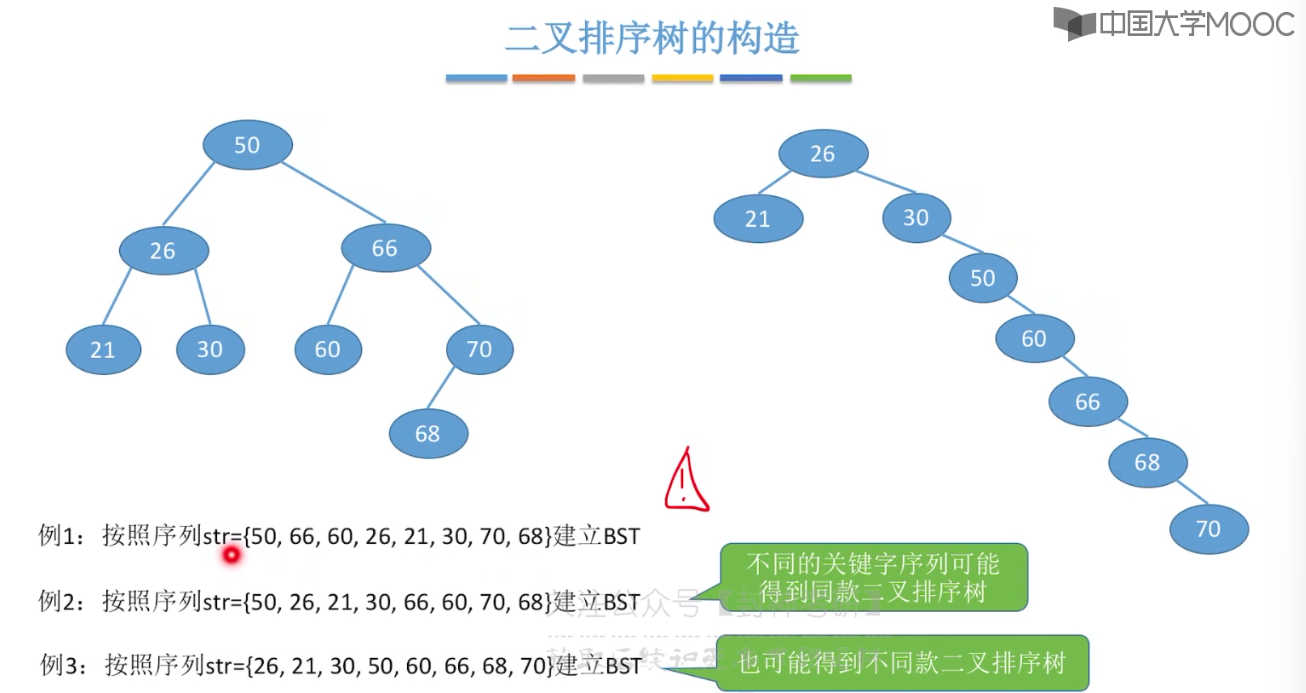
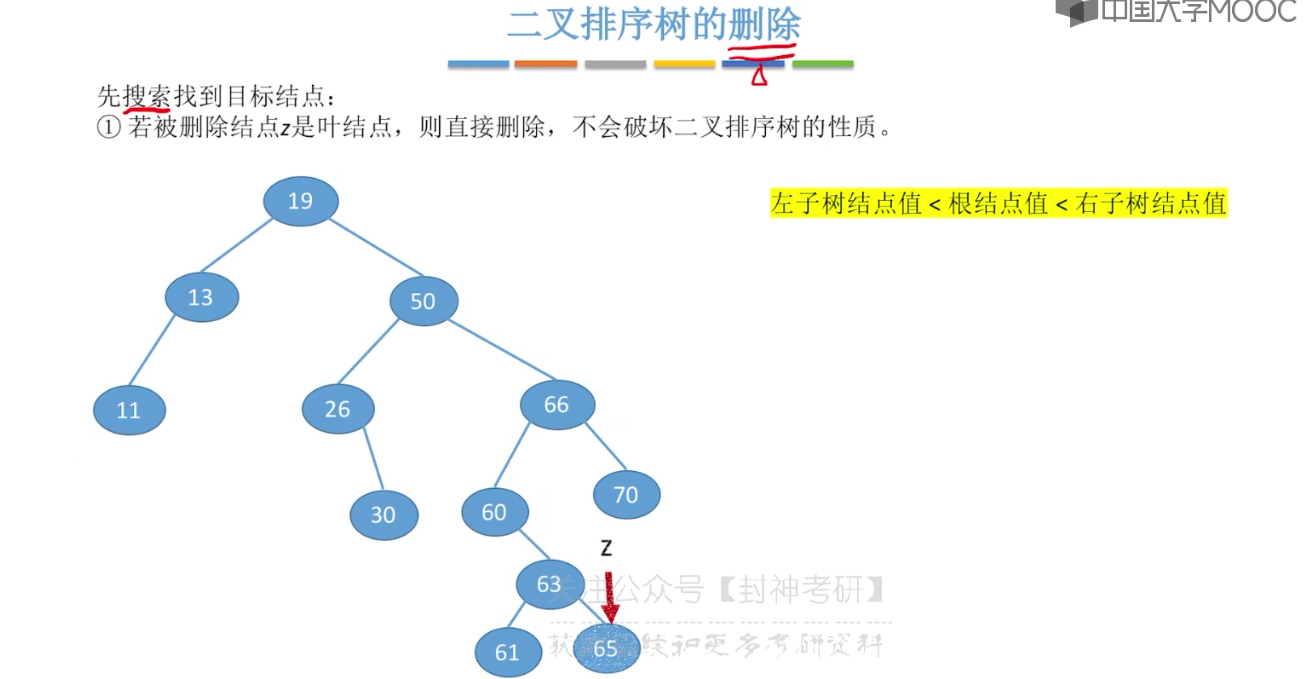
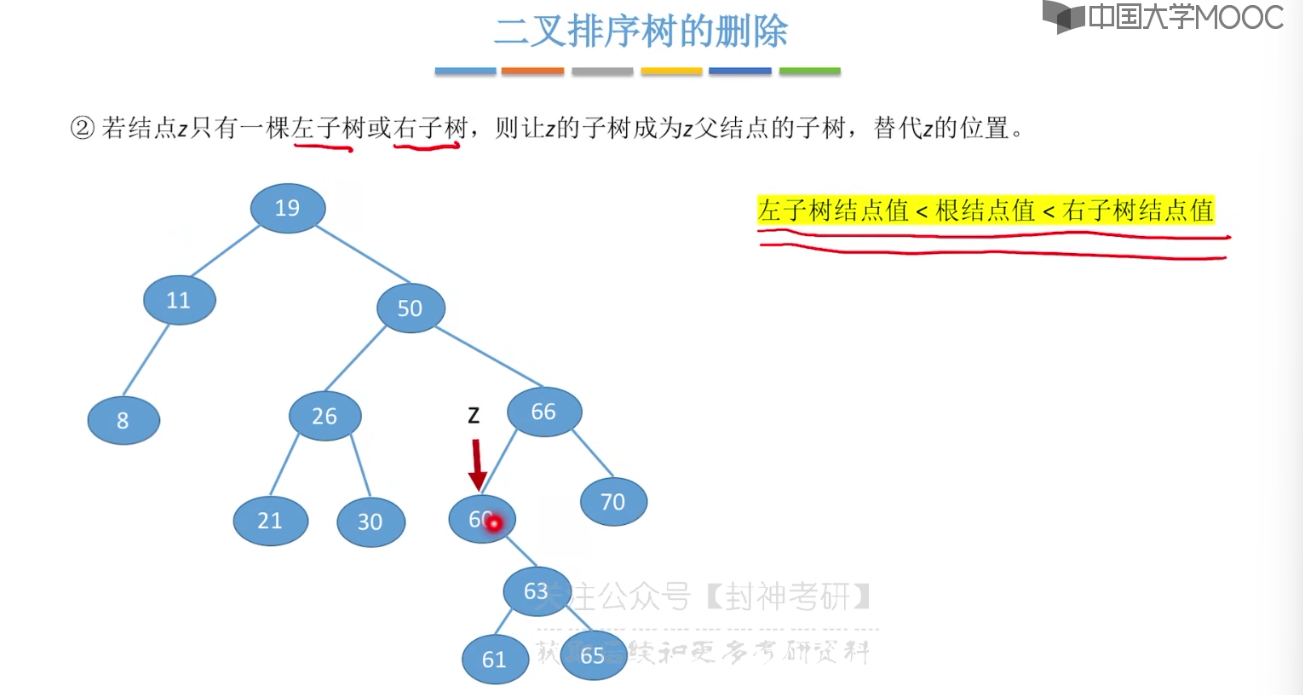
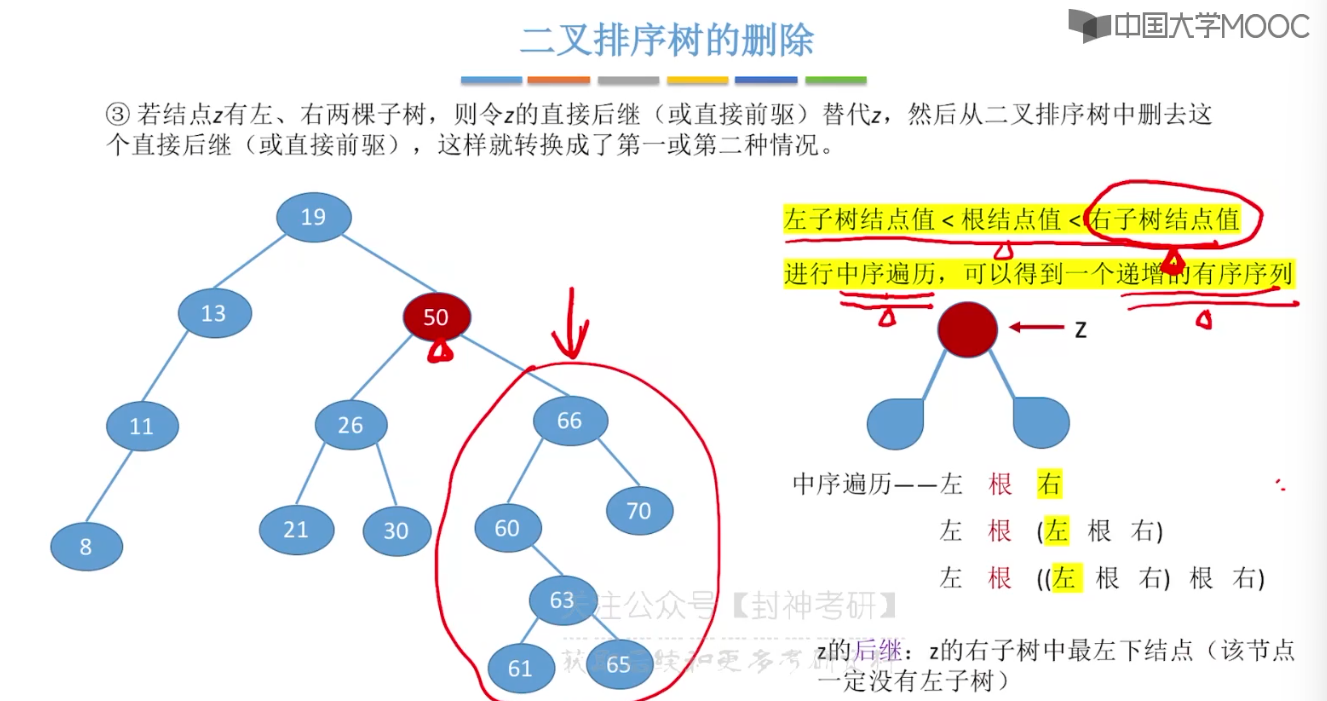
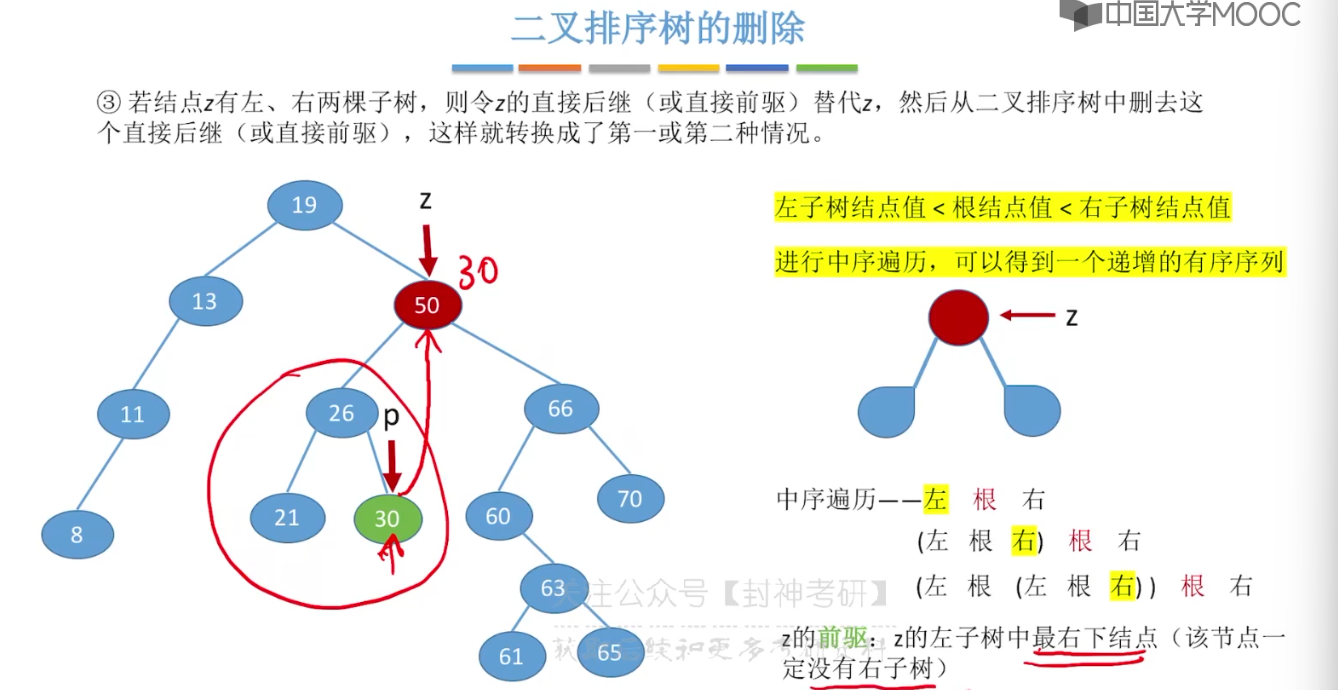
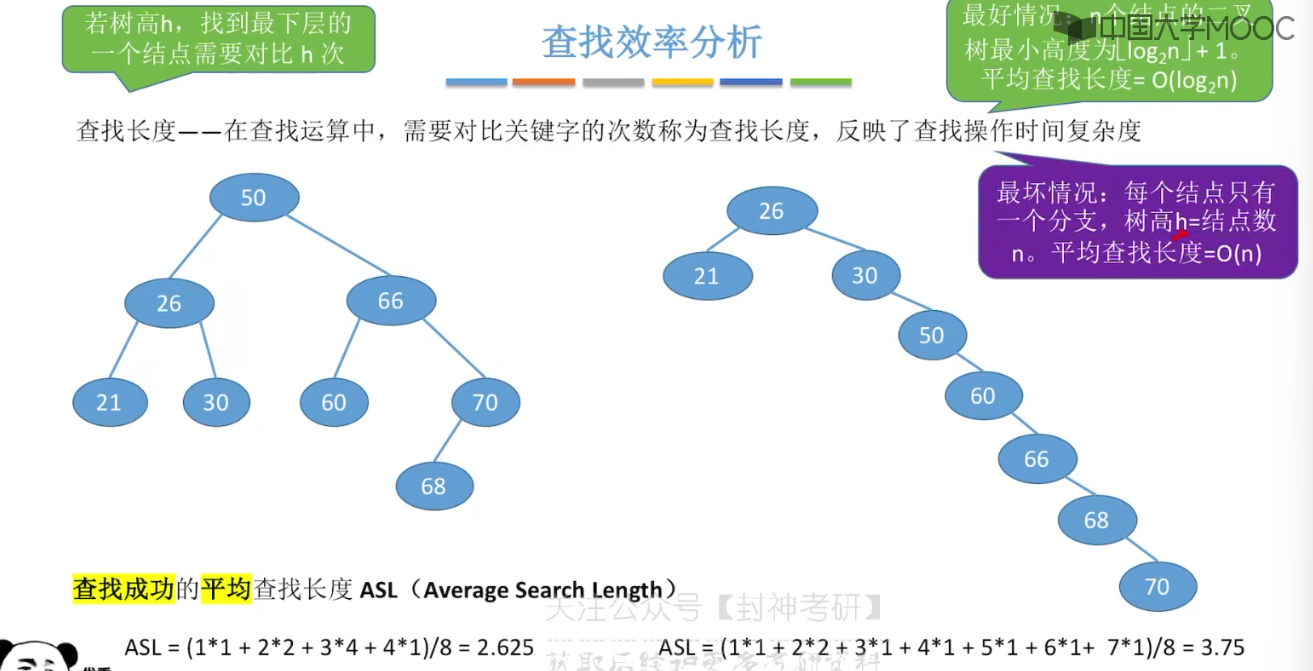
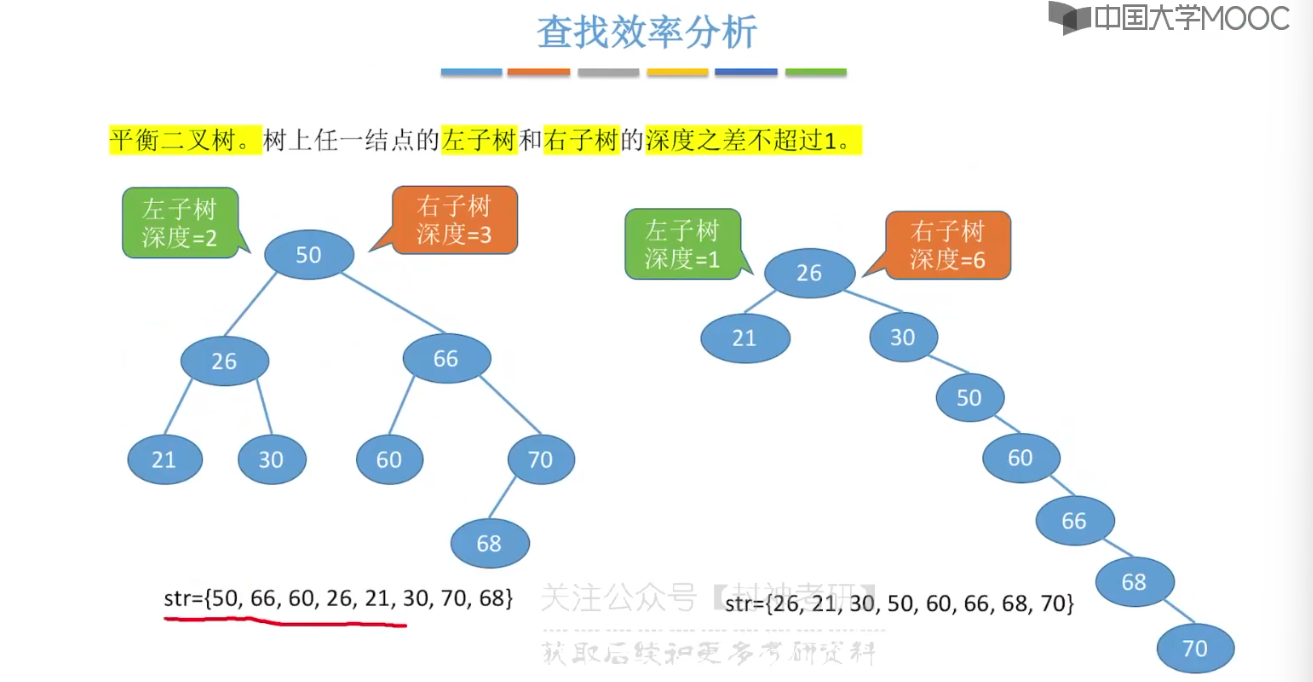
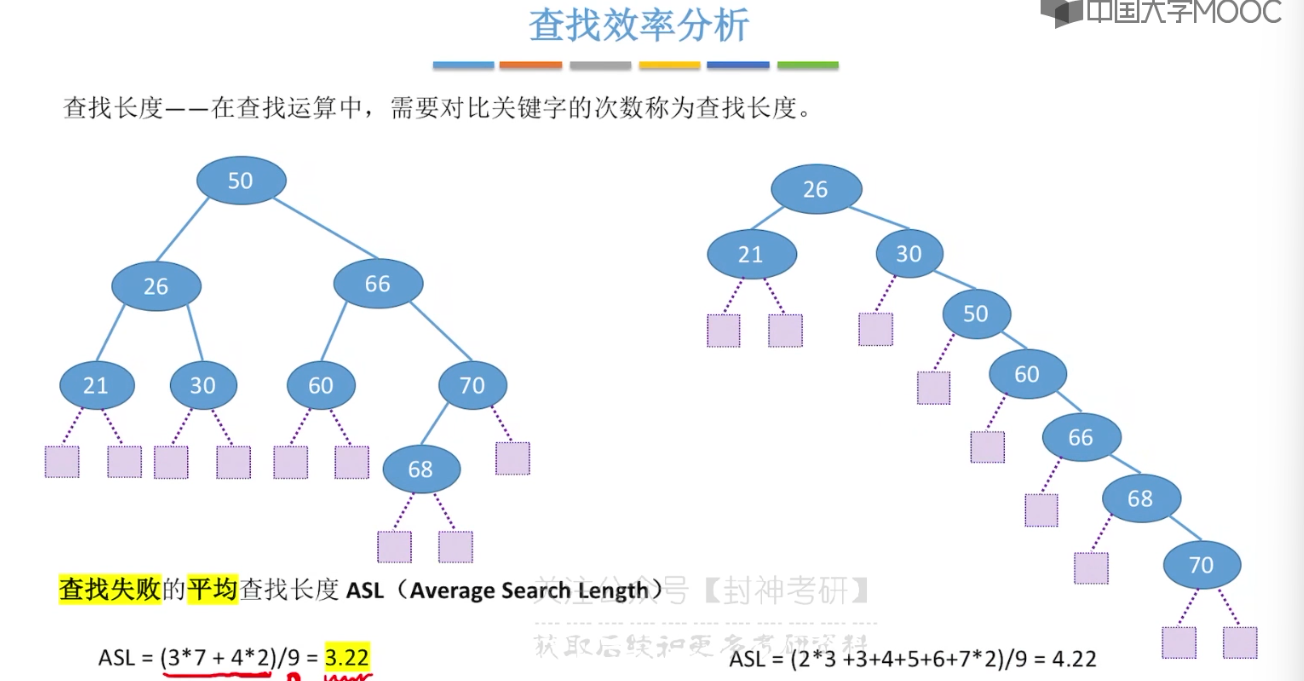
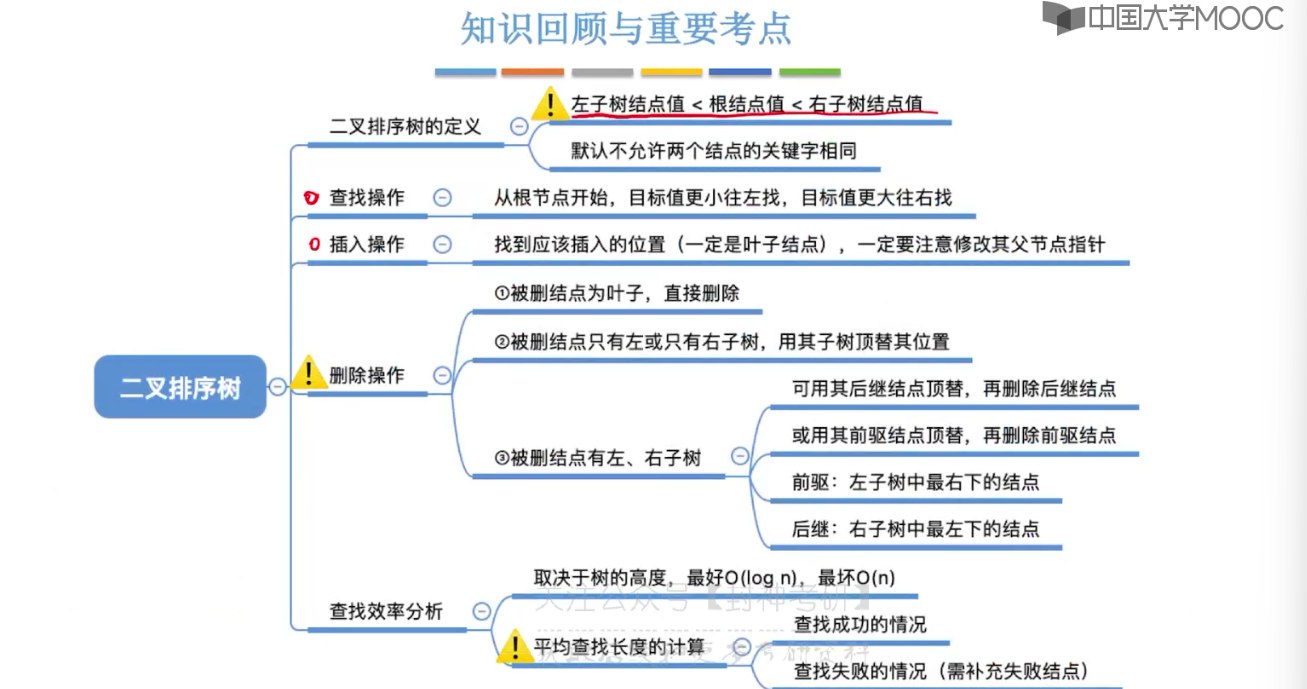
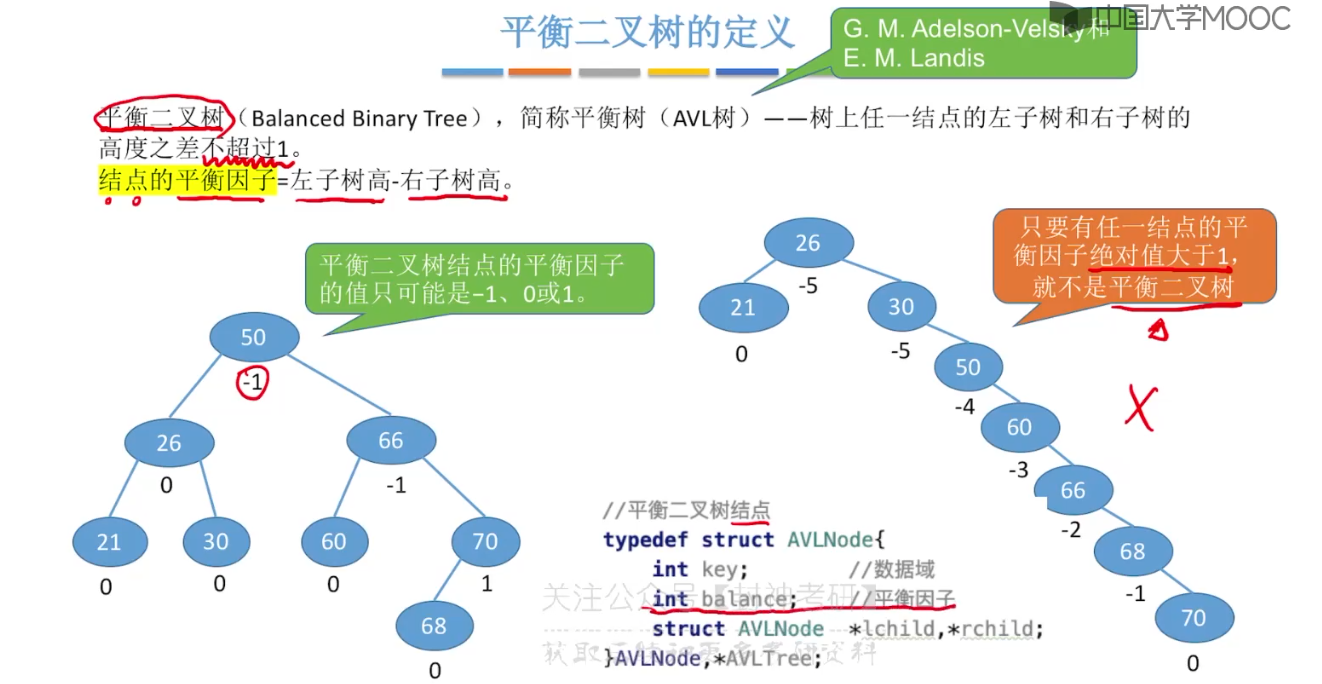
7.6、平衡二叉树
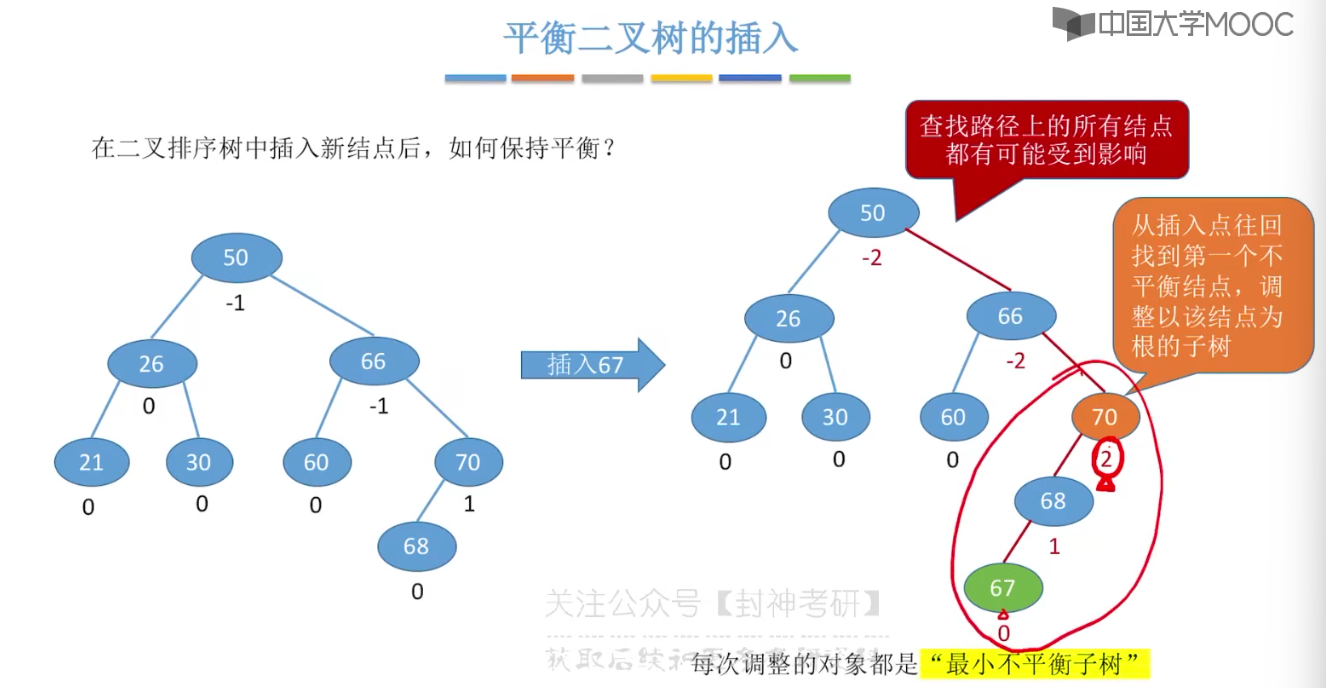
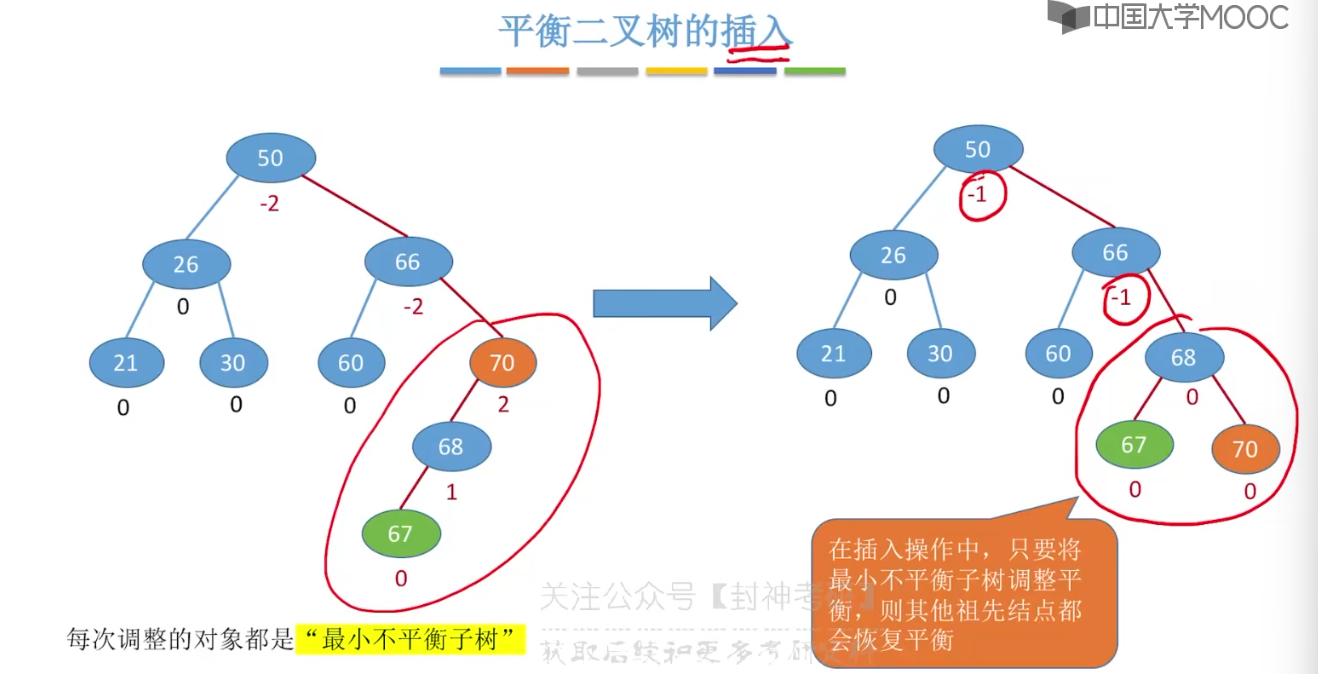
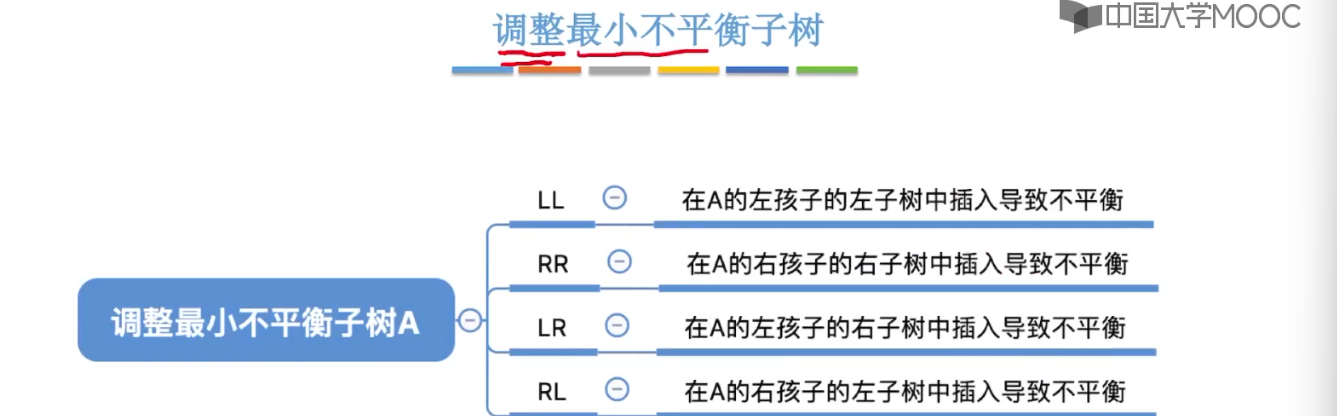
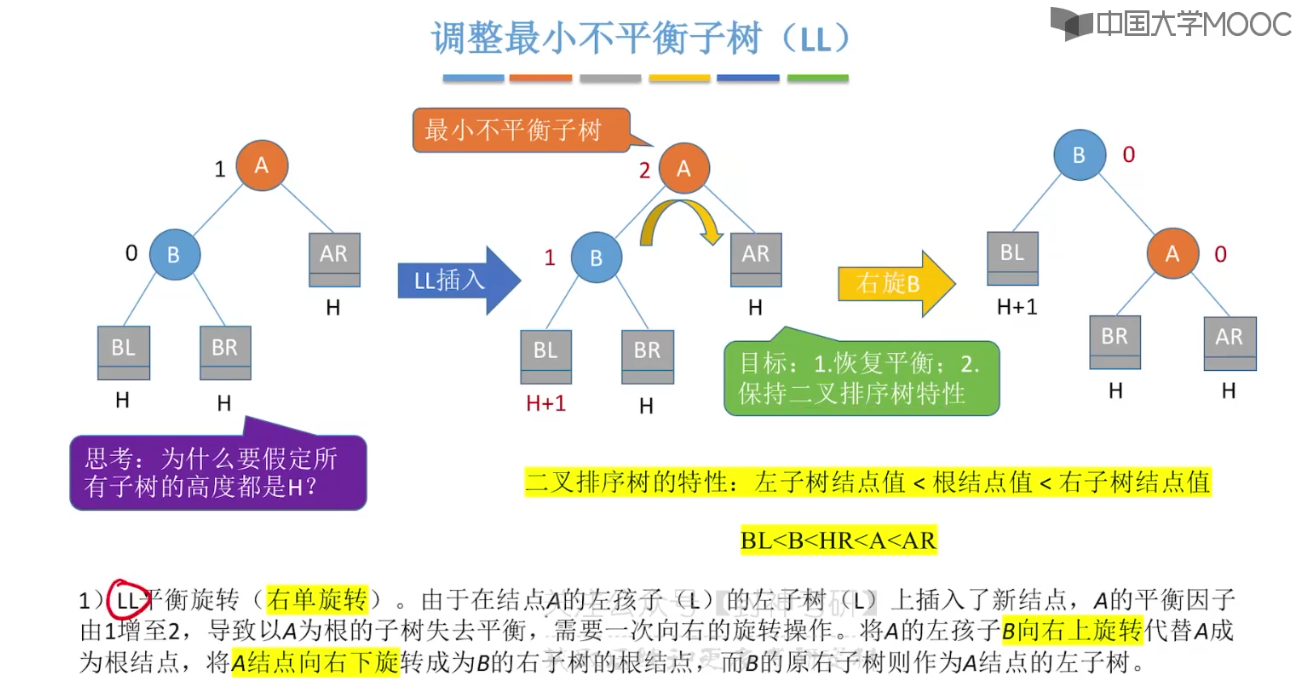
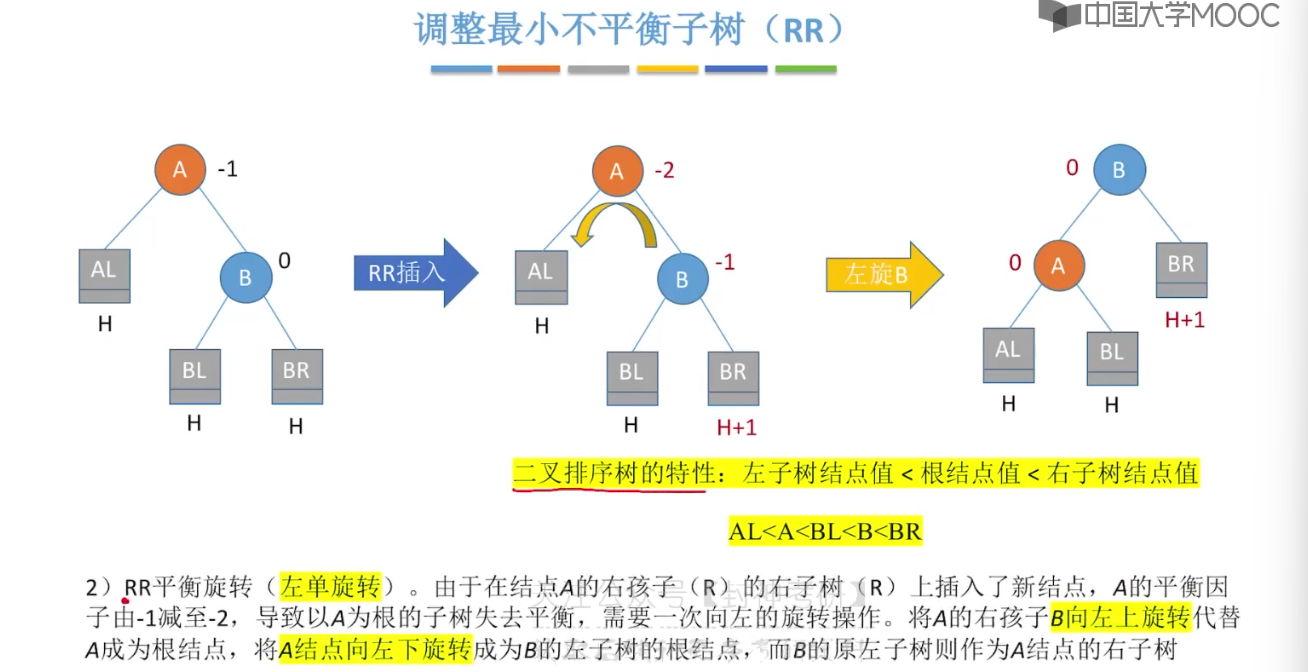
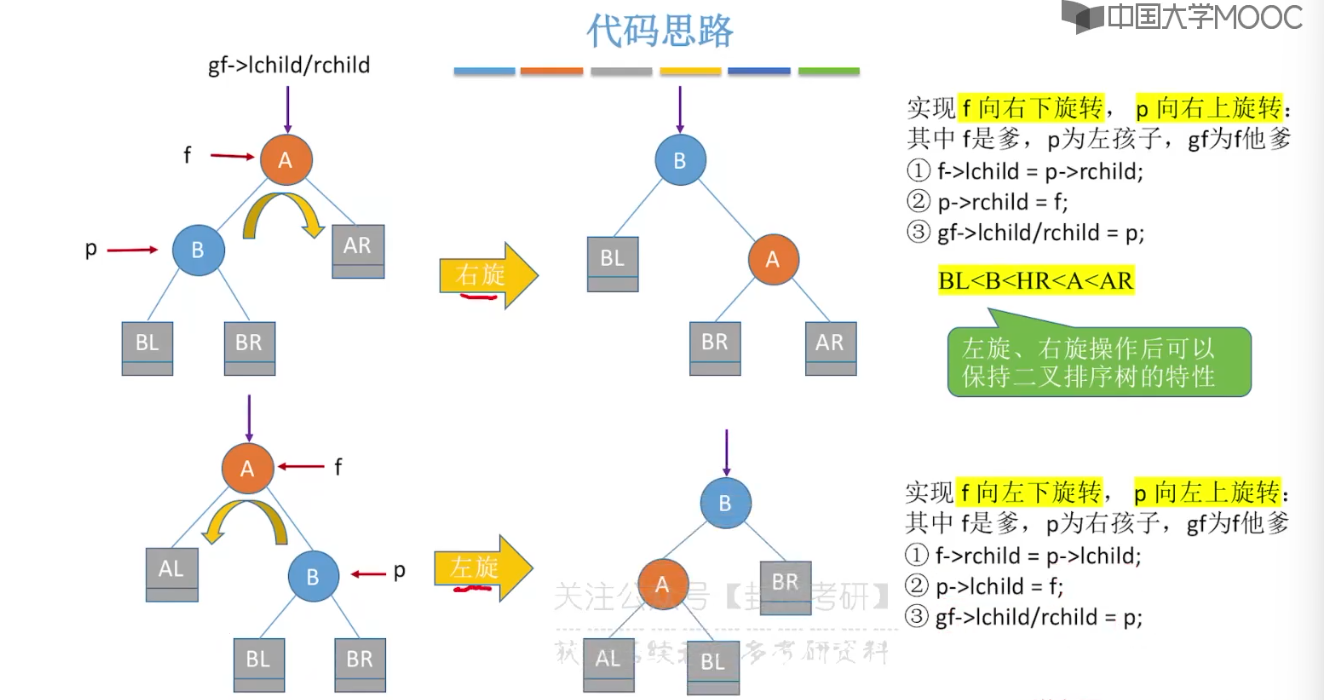
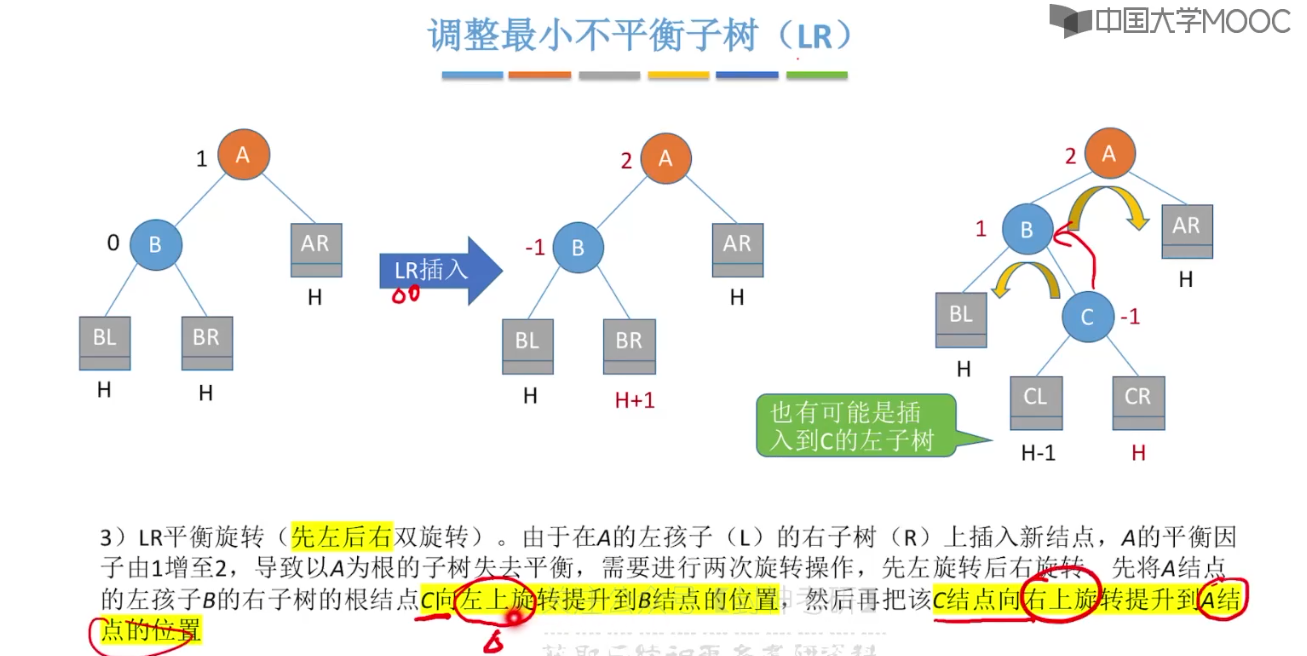
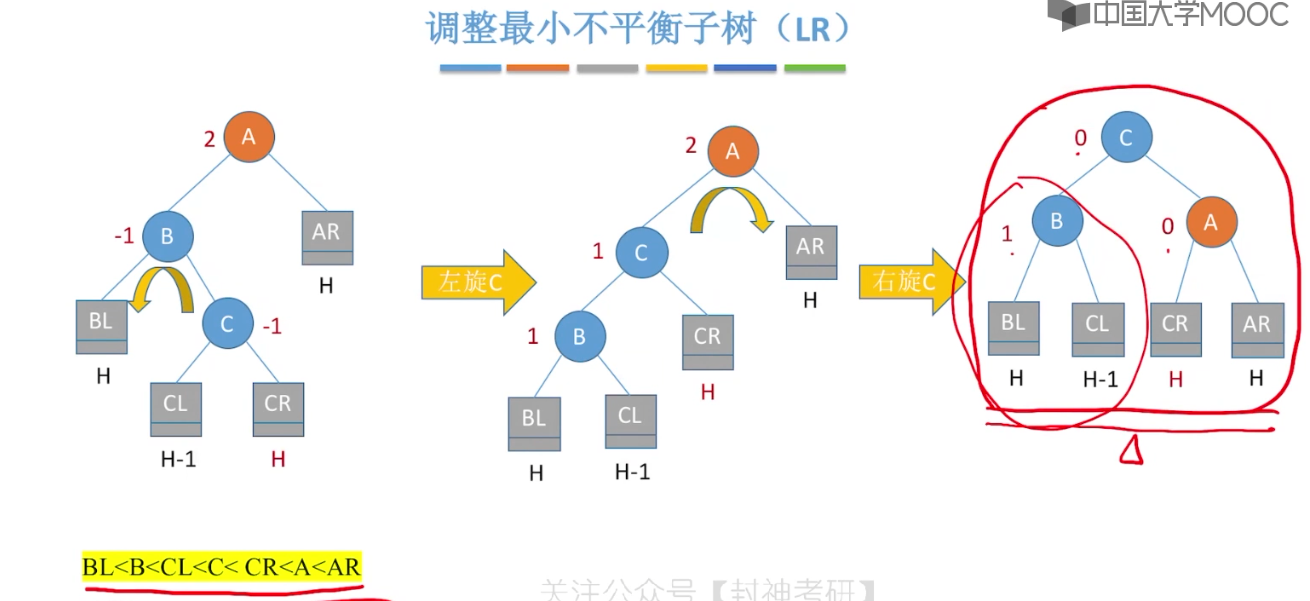
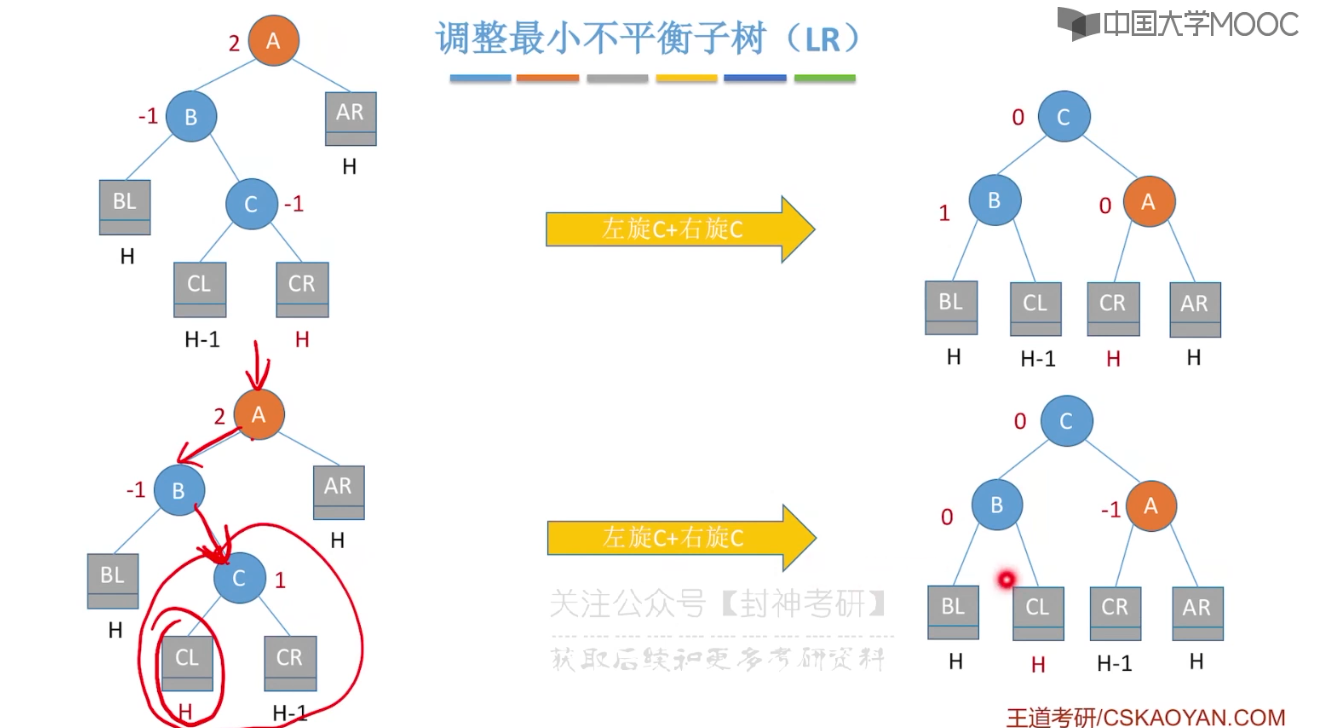
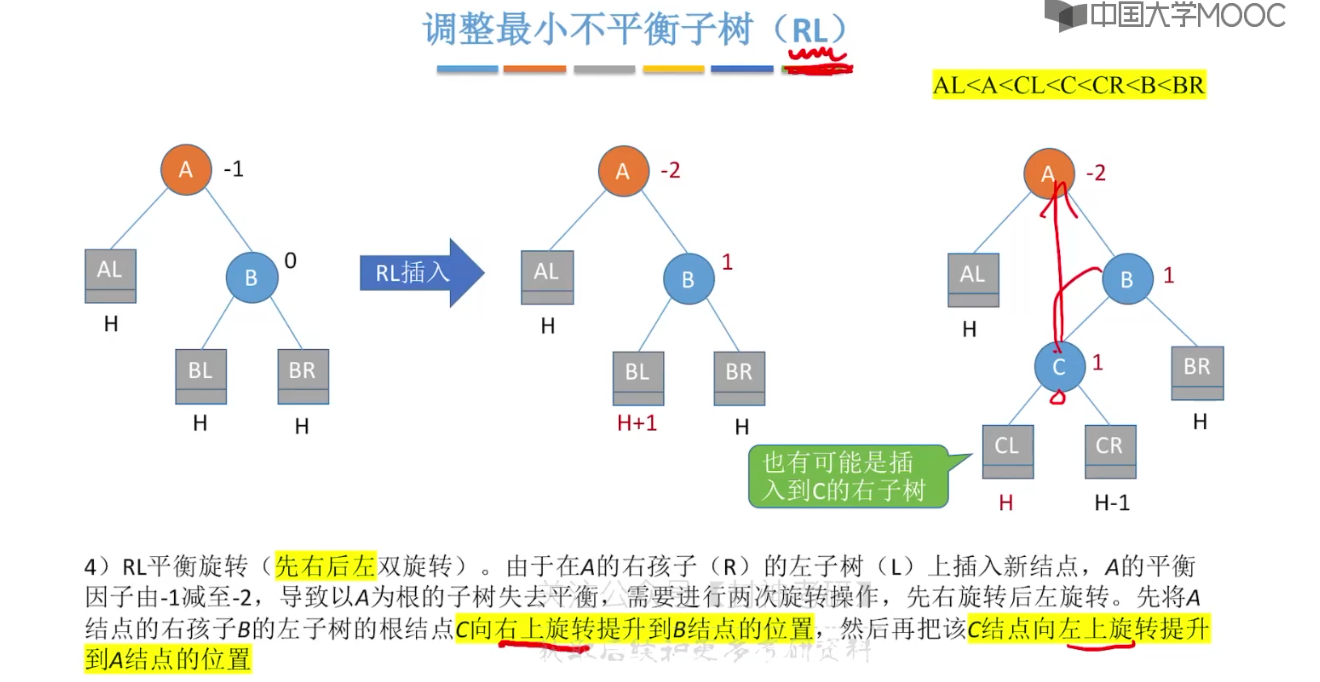
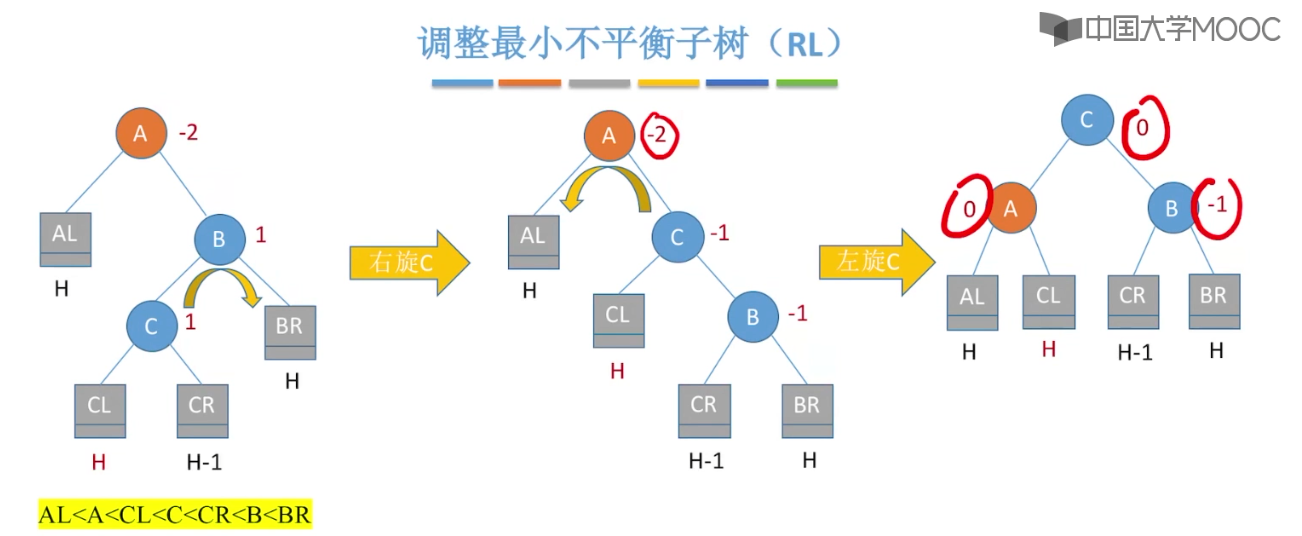
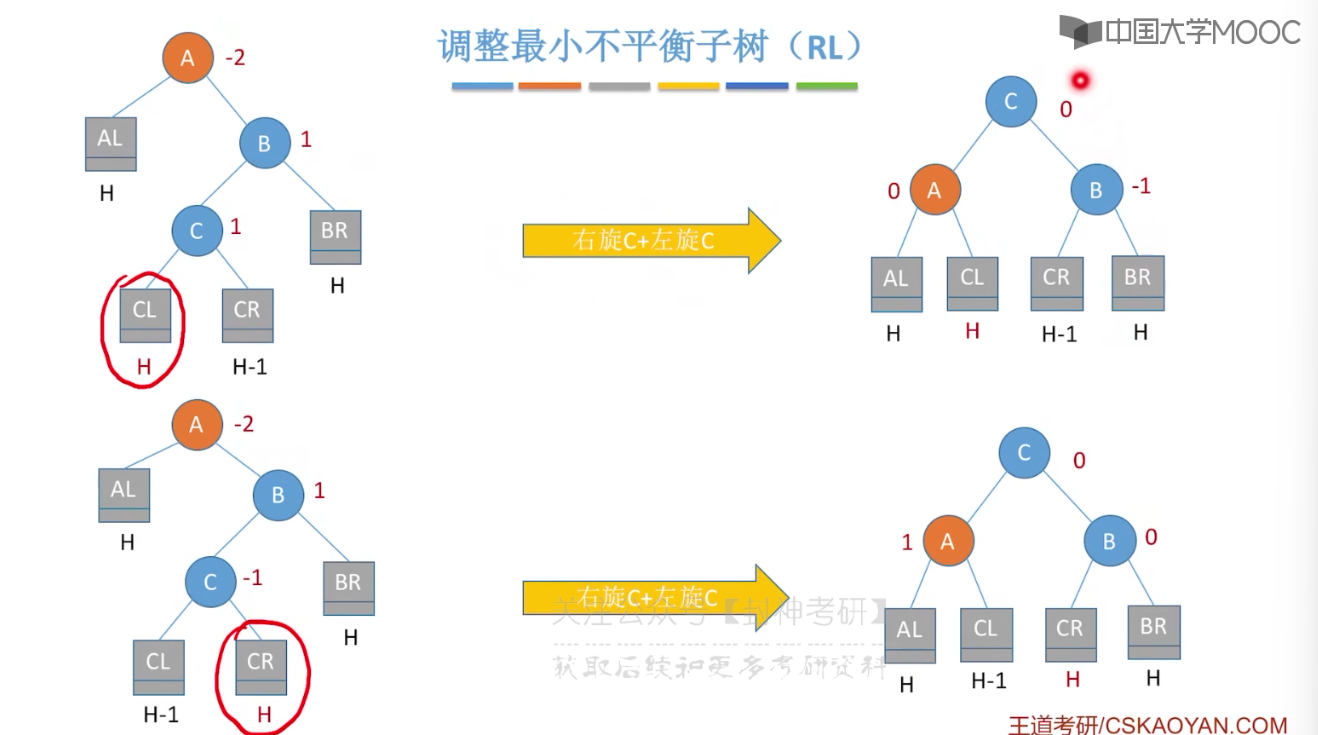
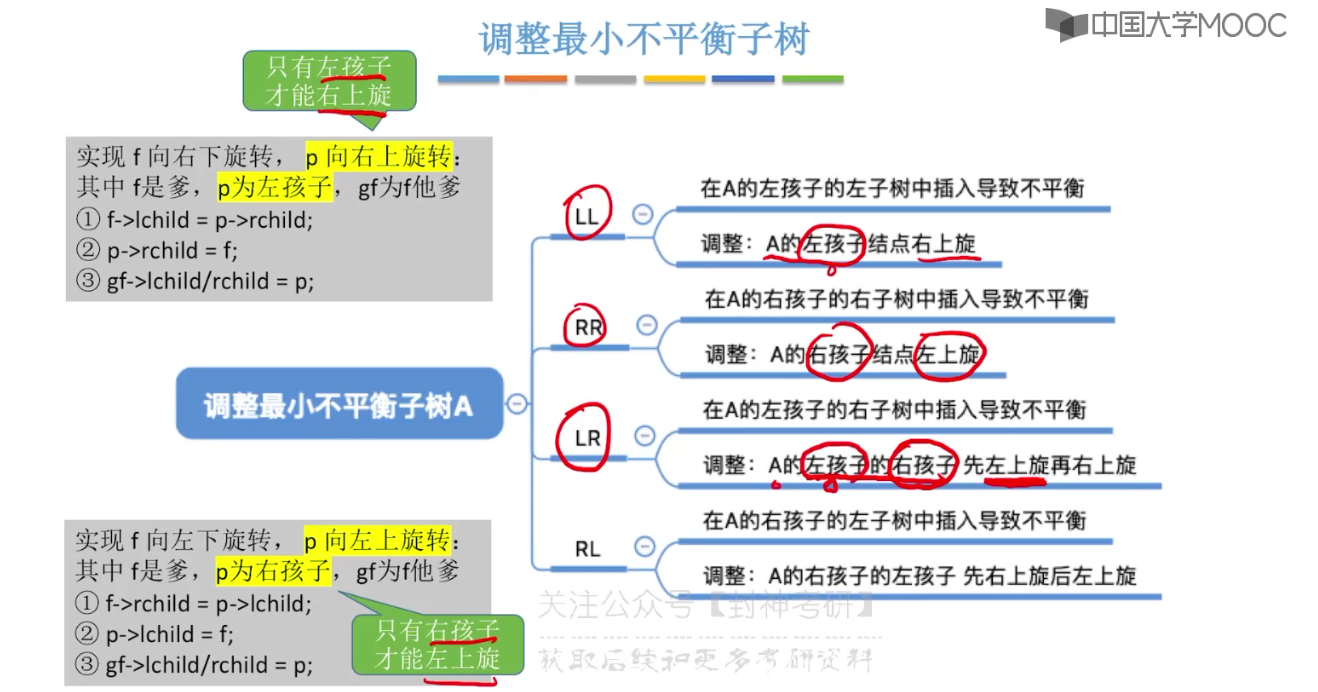
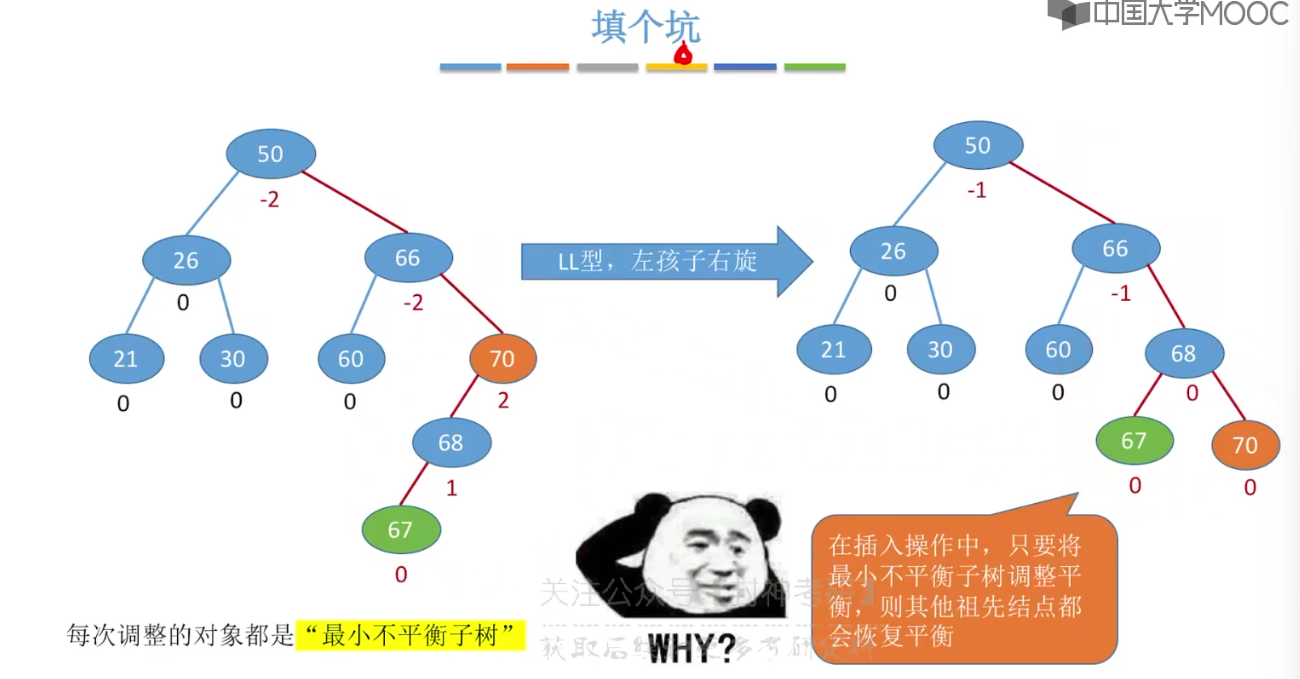
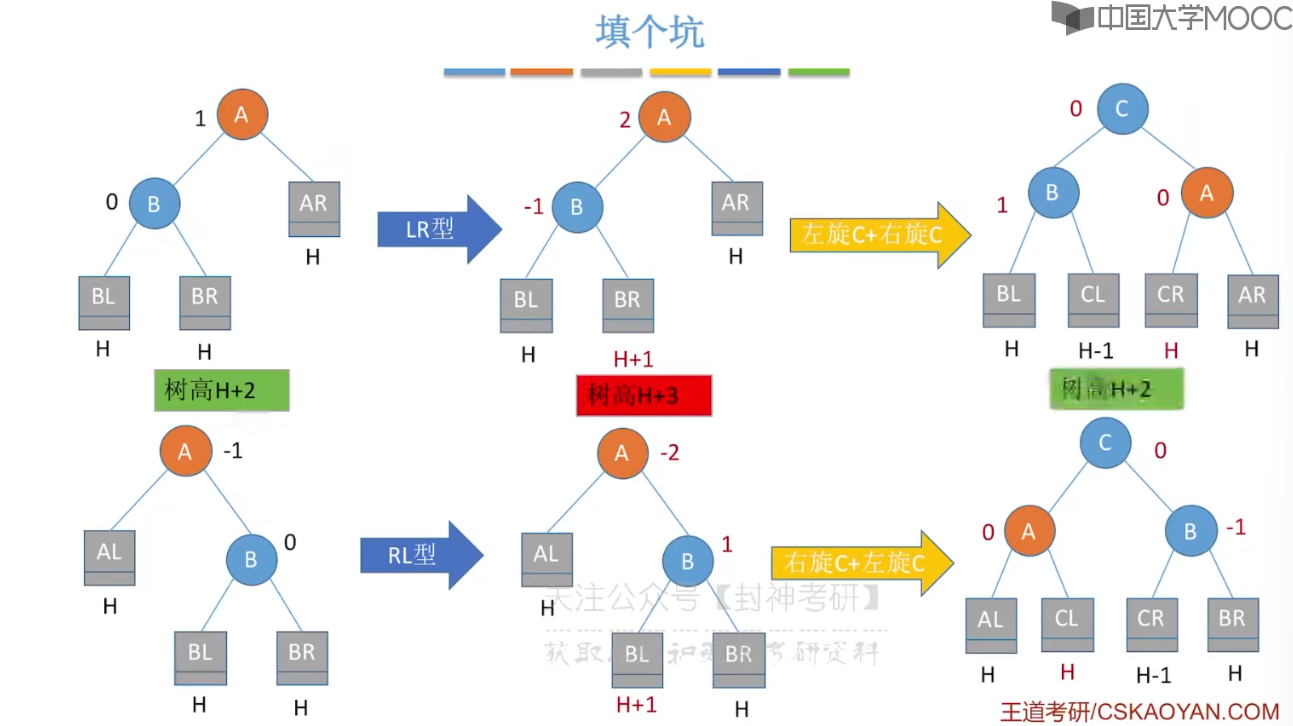
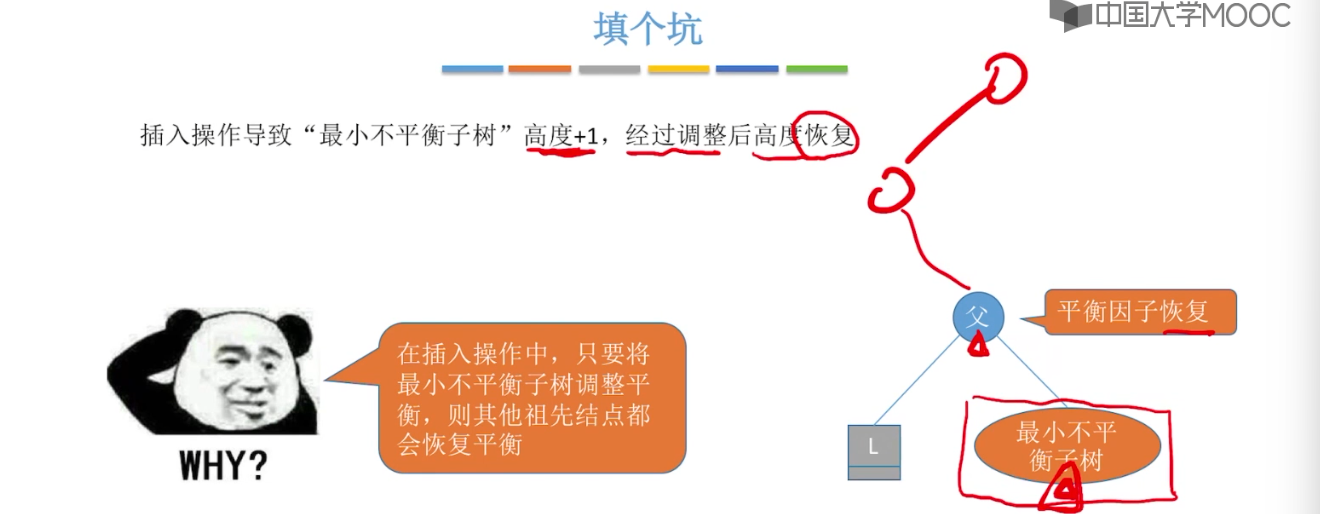
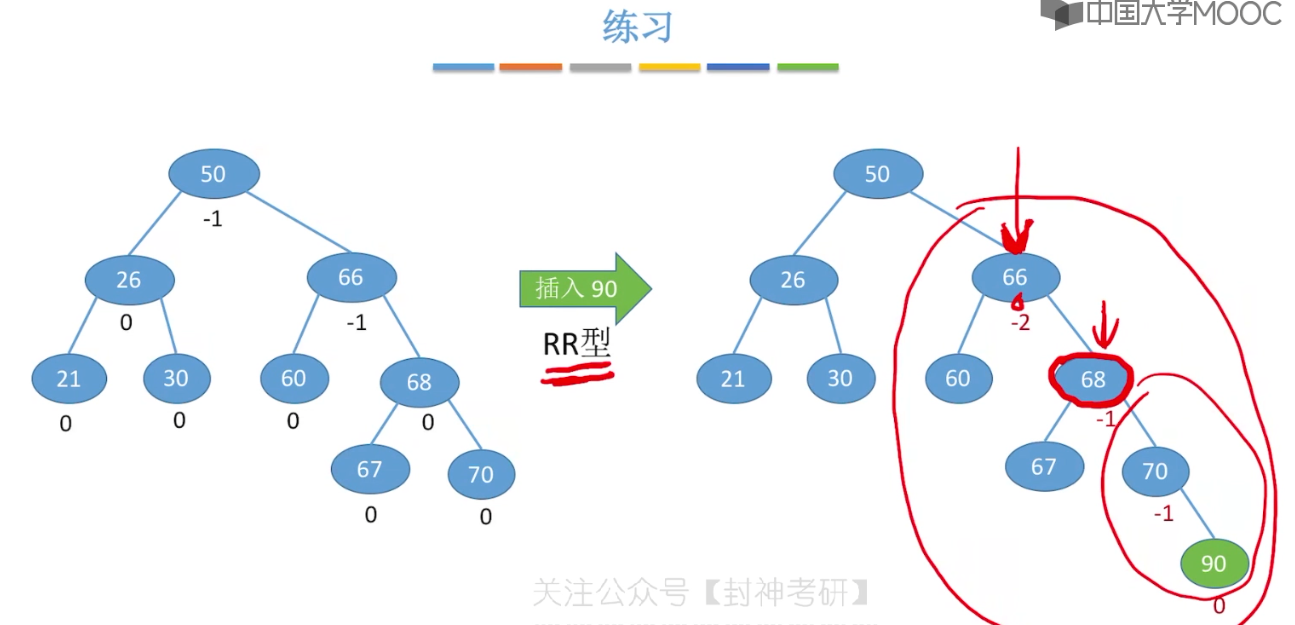
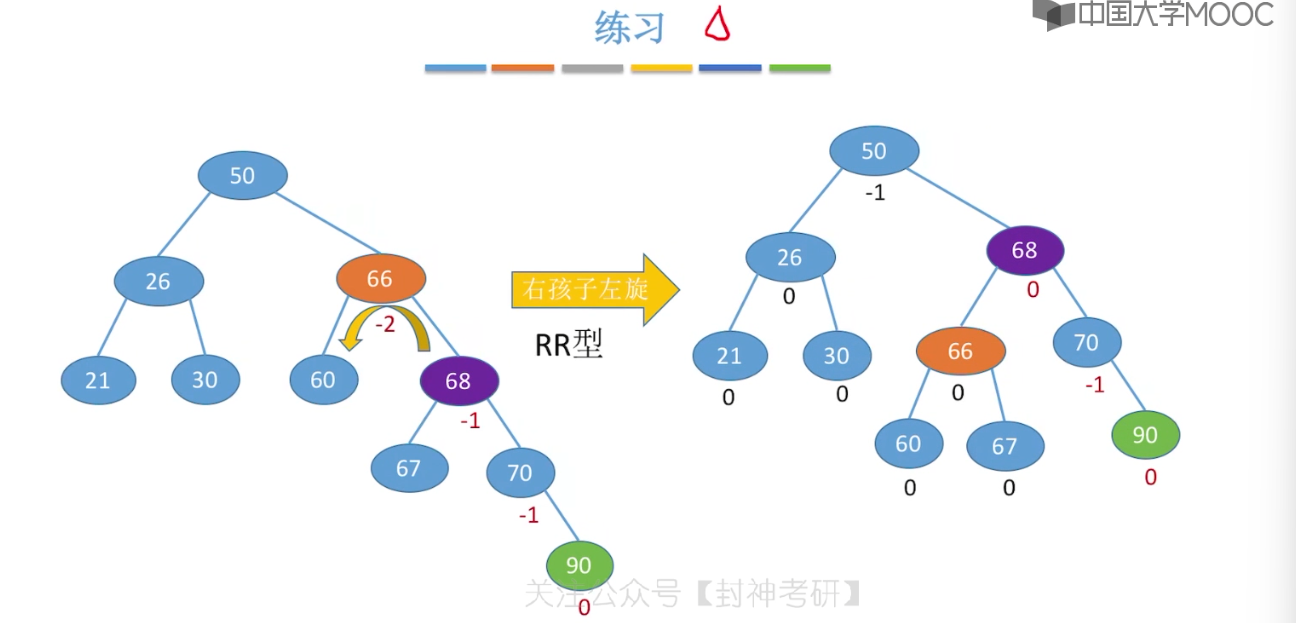
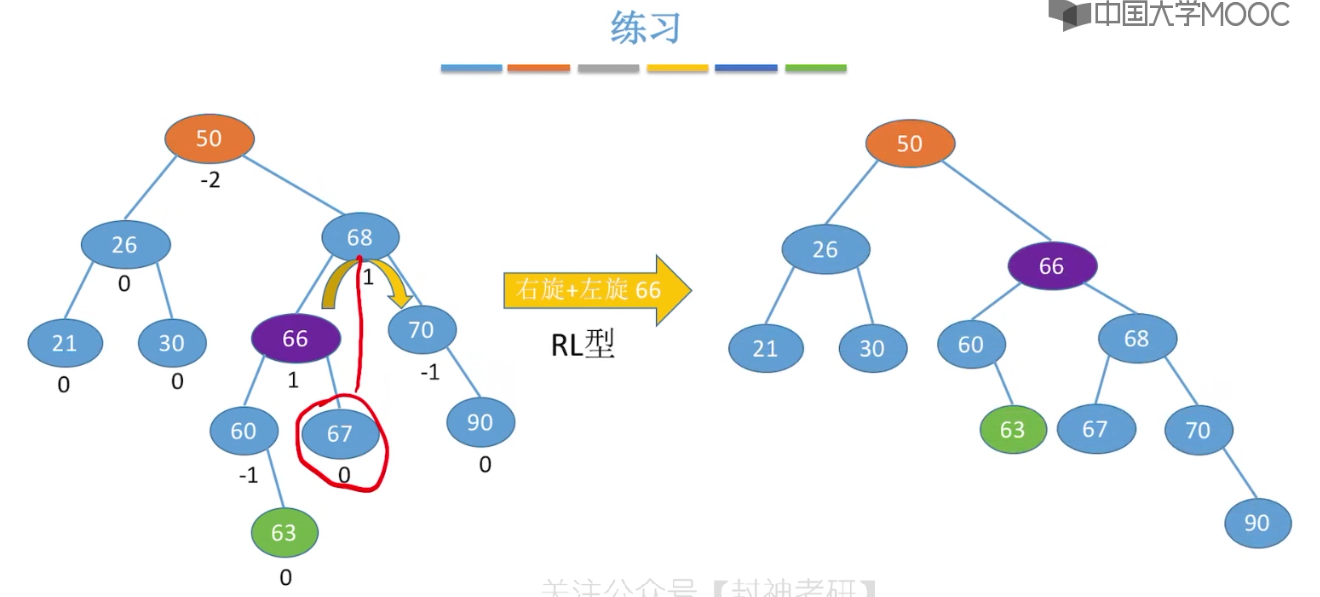
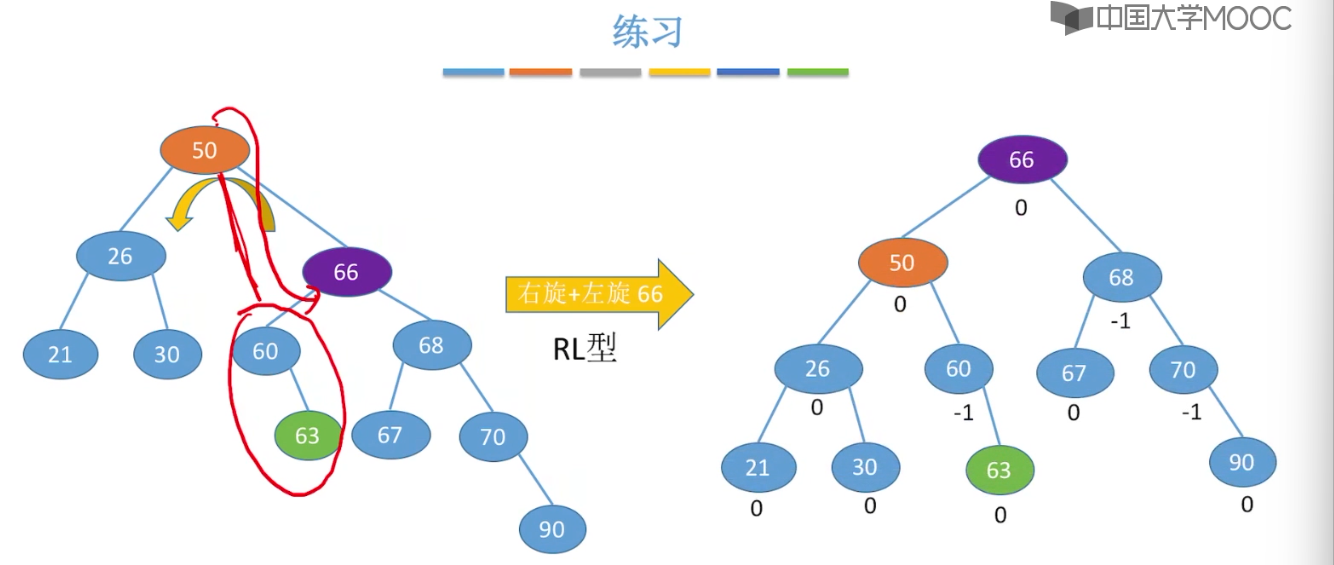



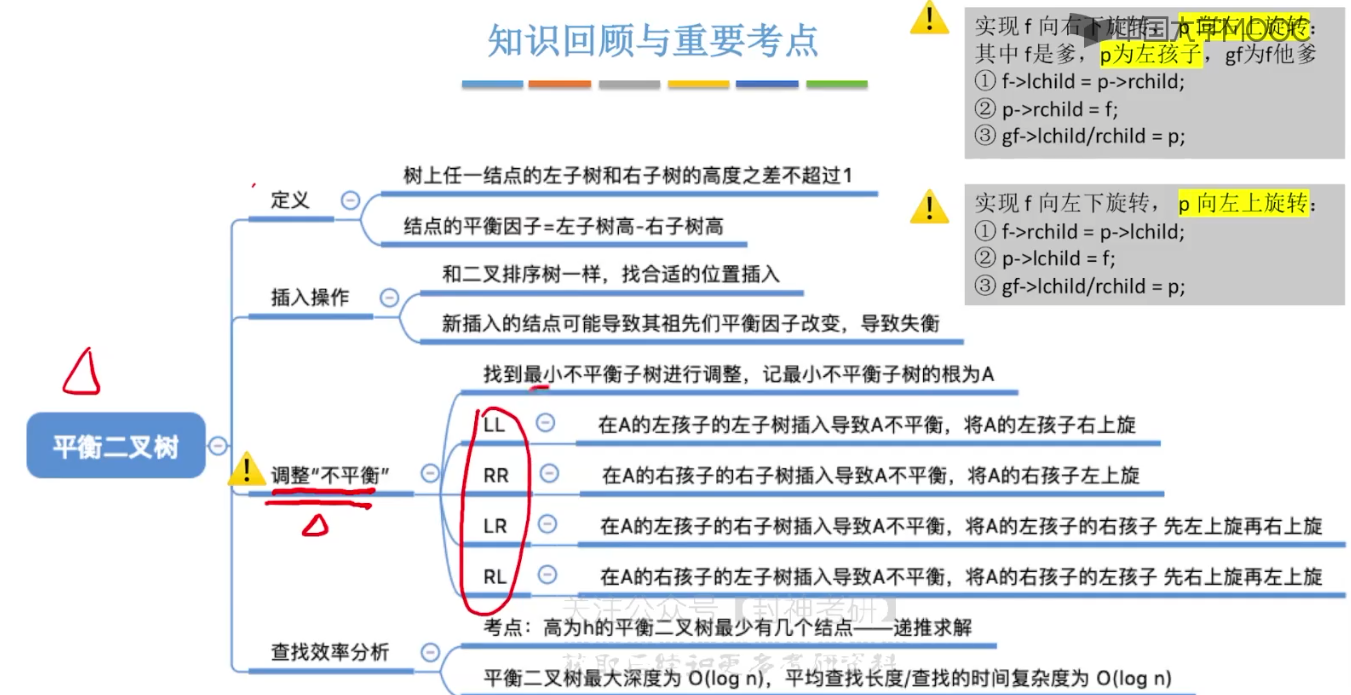
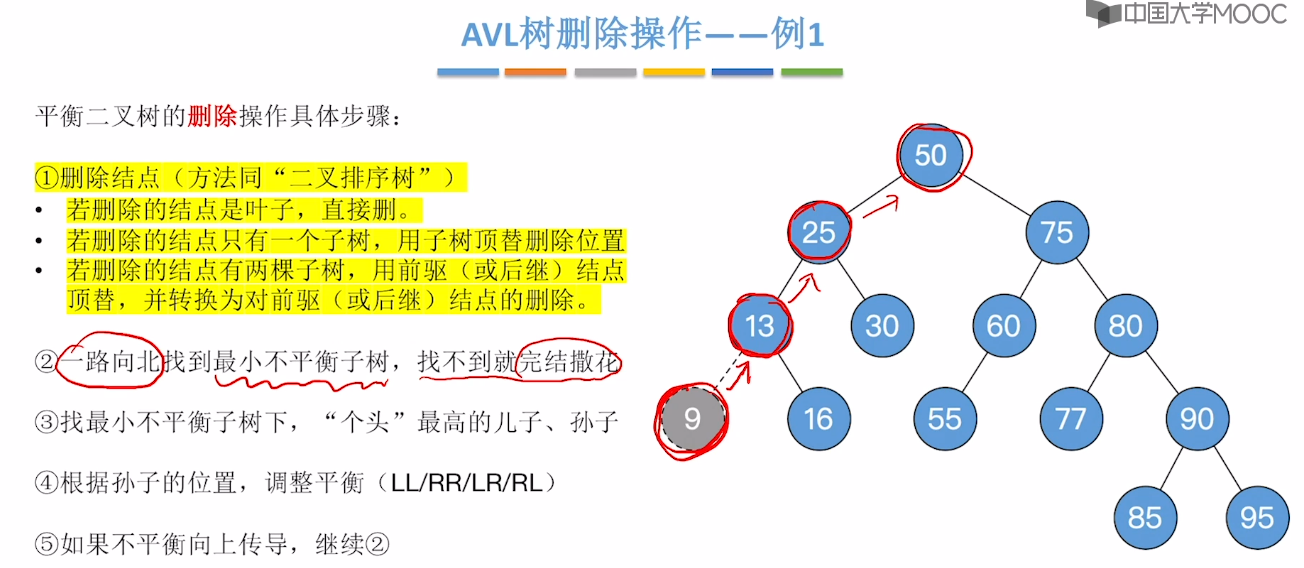
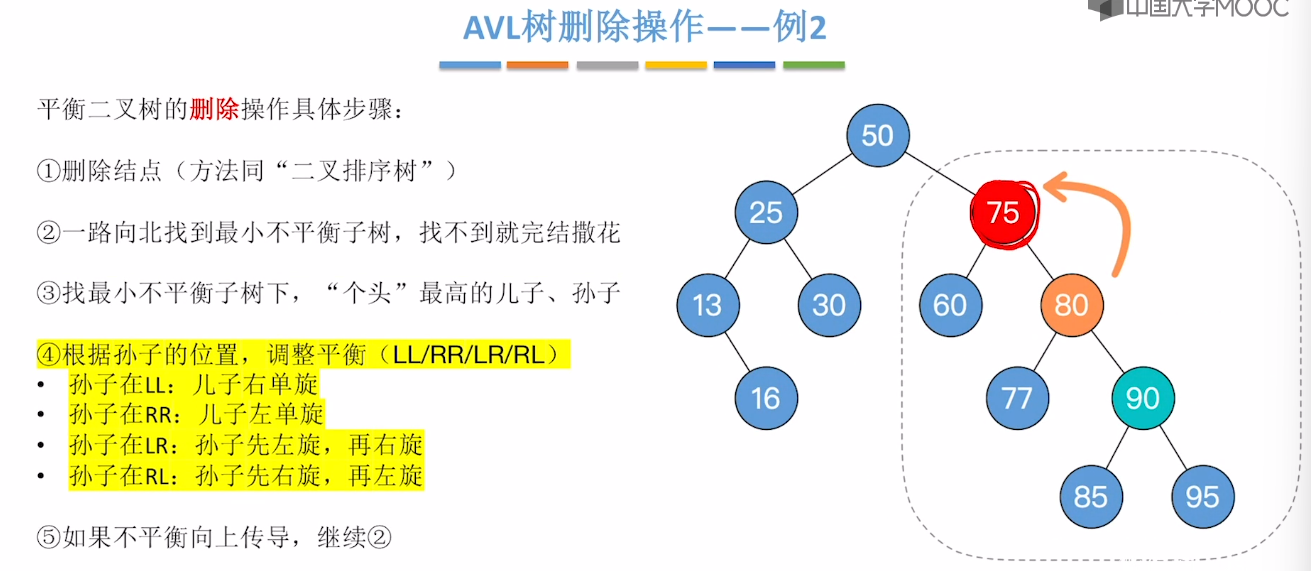
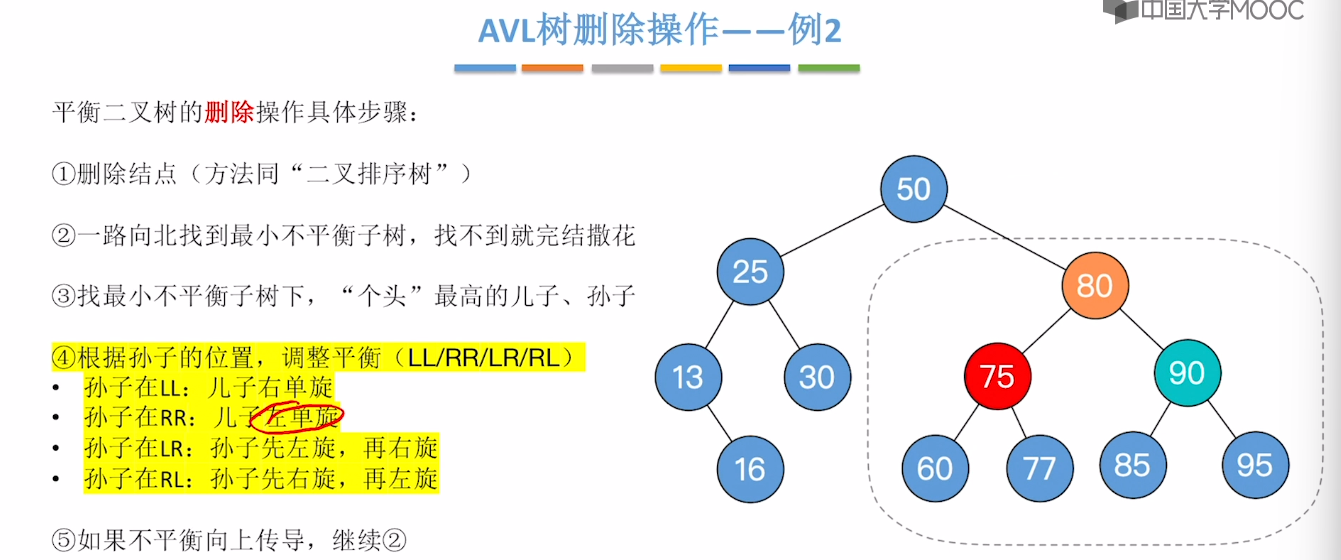
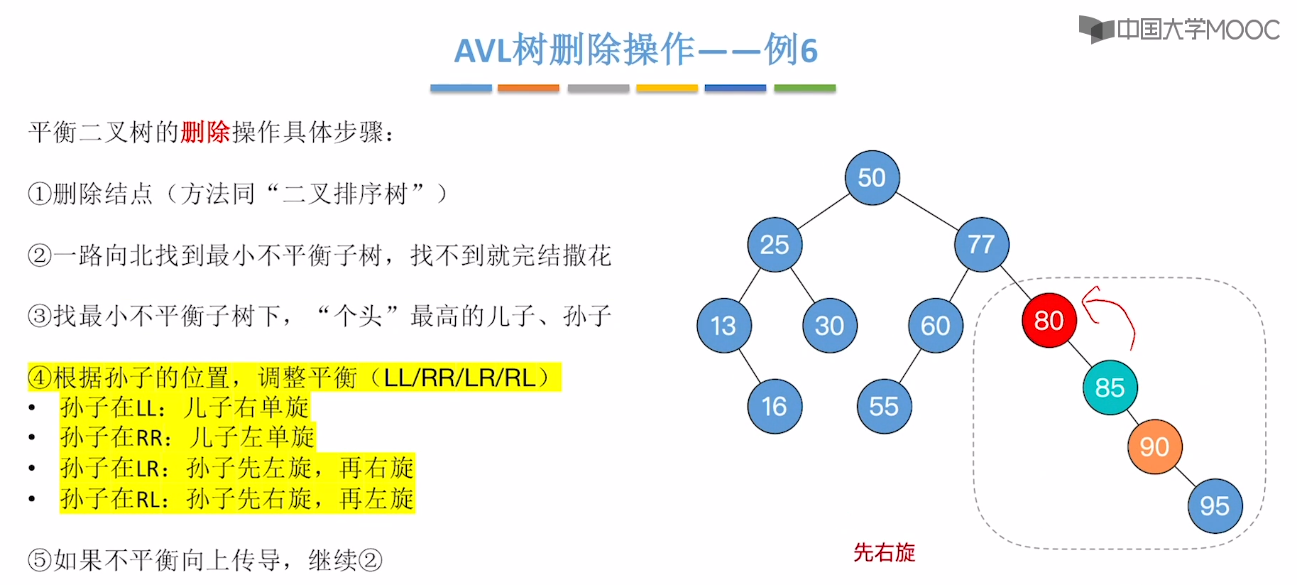
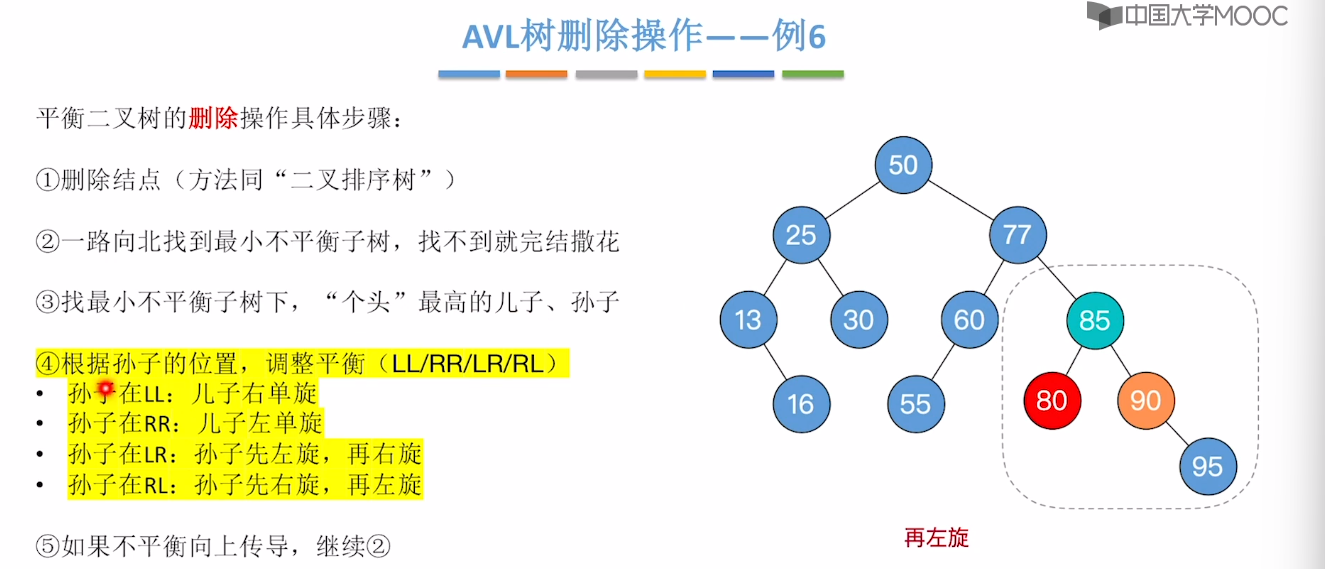
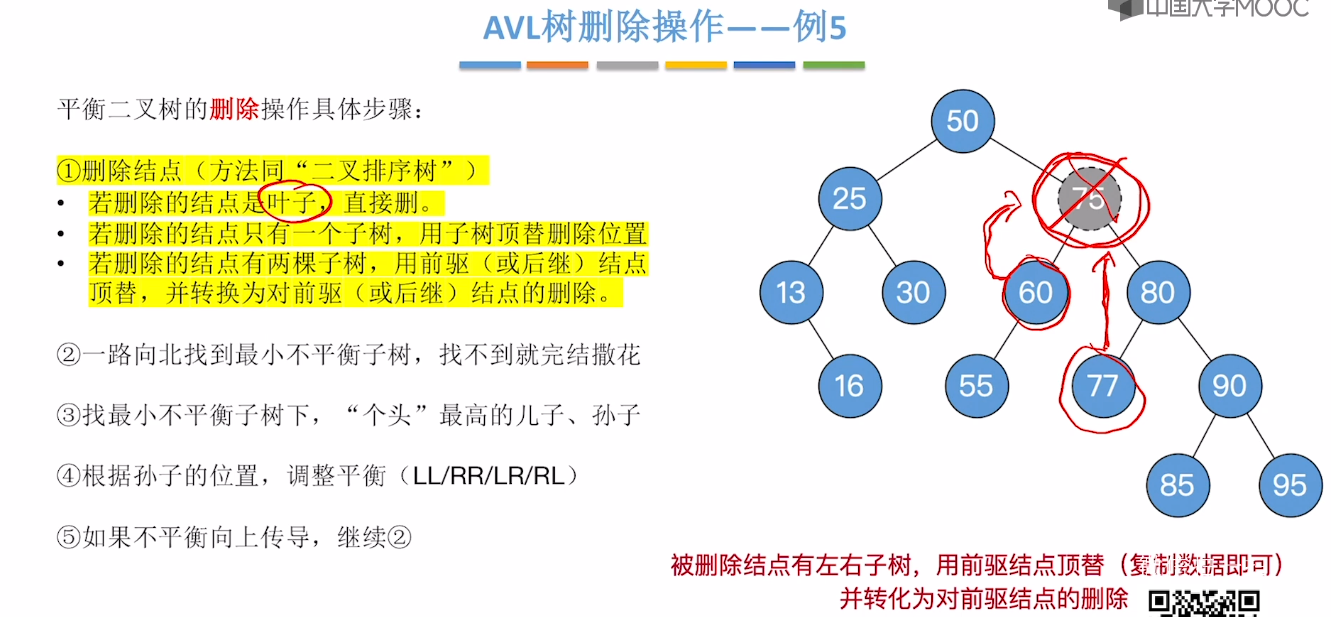
7.7、平衡二叉树的删除


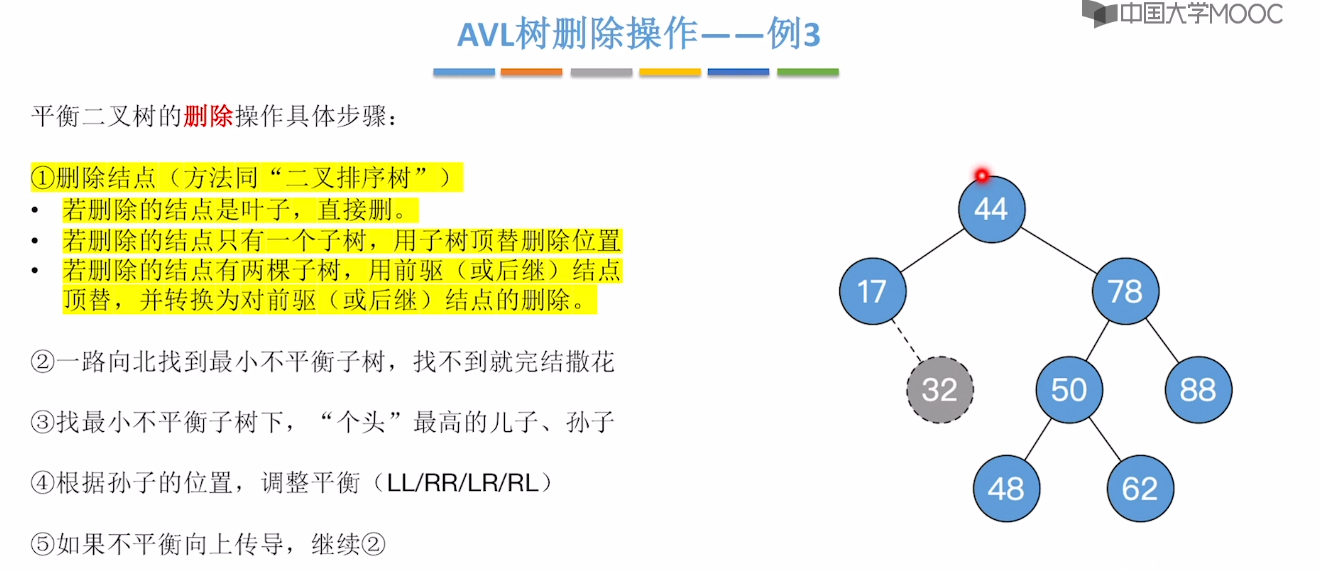
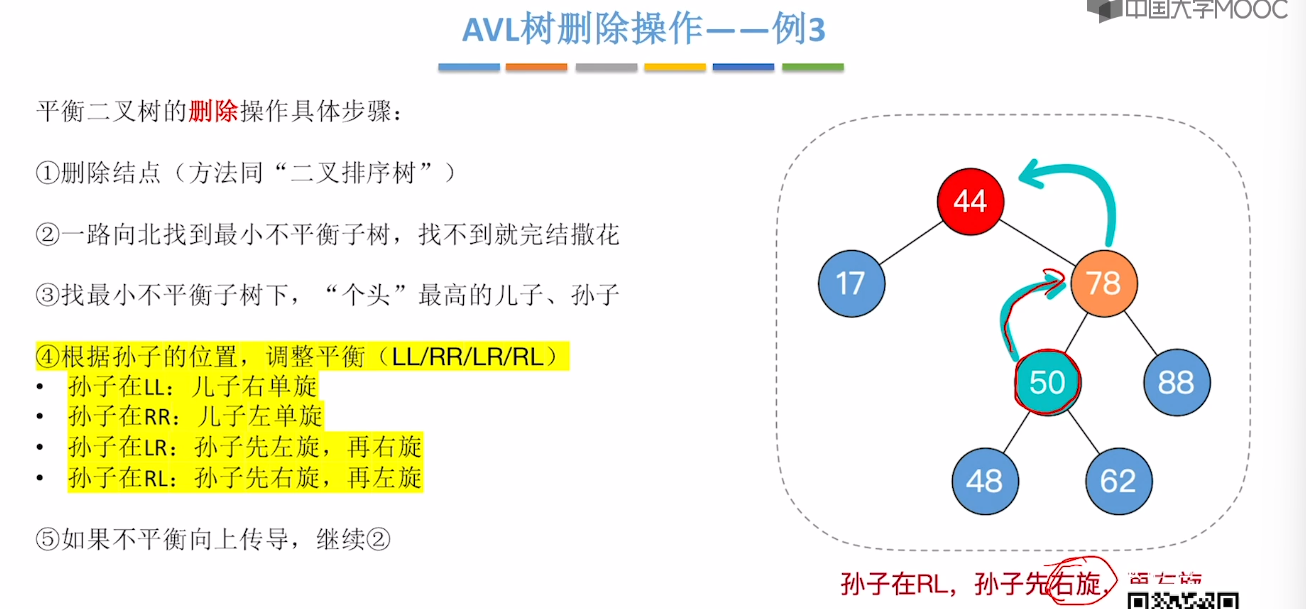
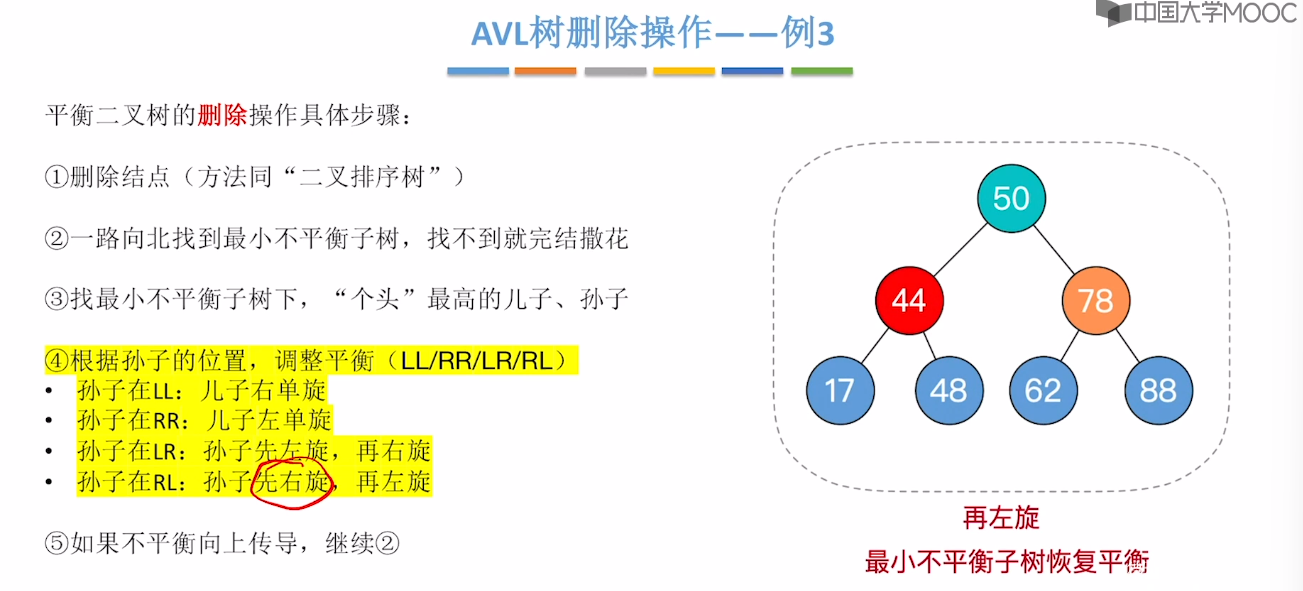
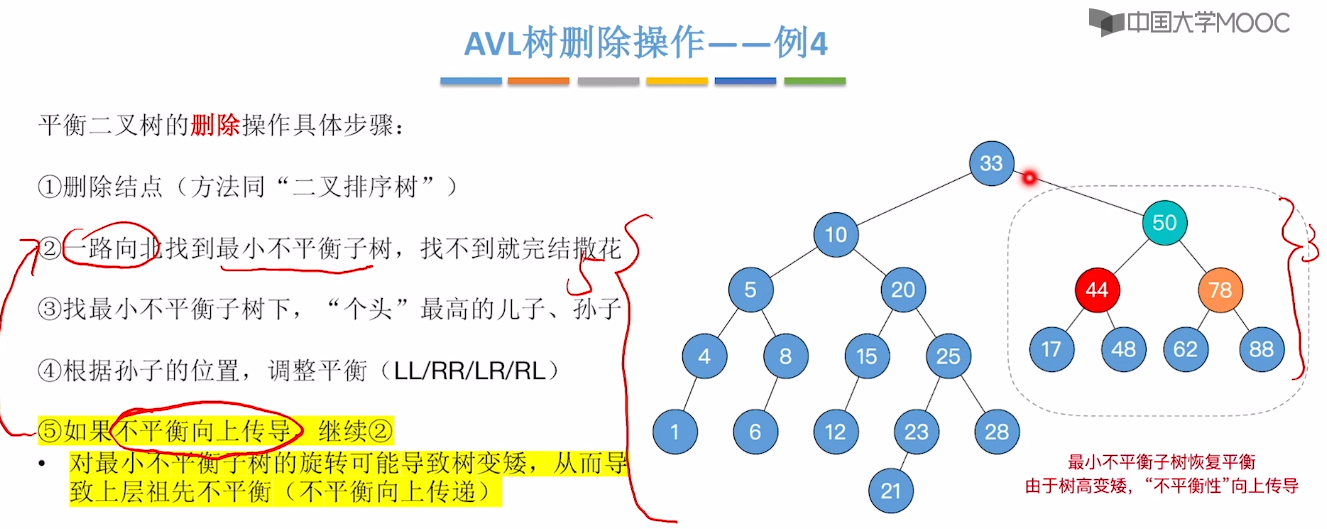
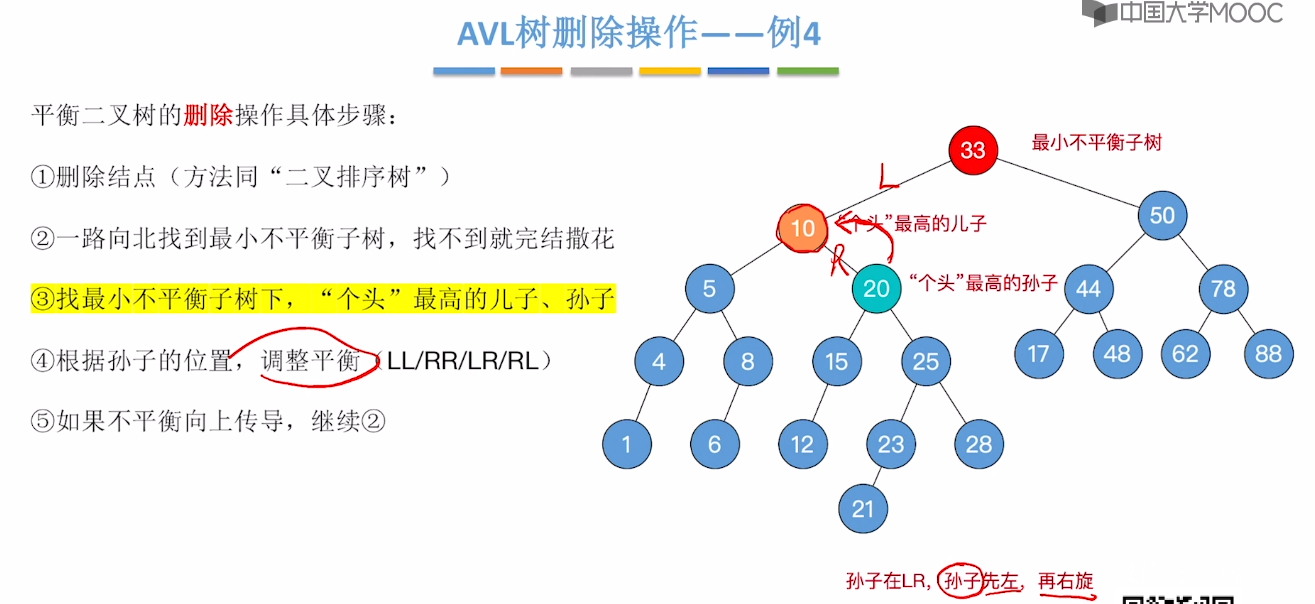
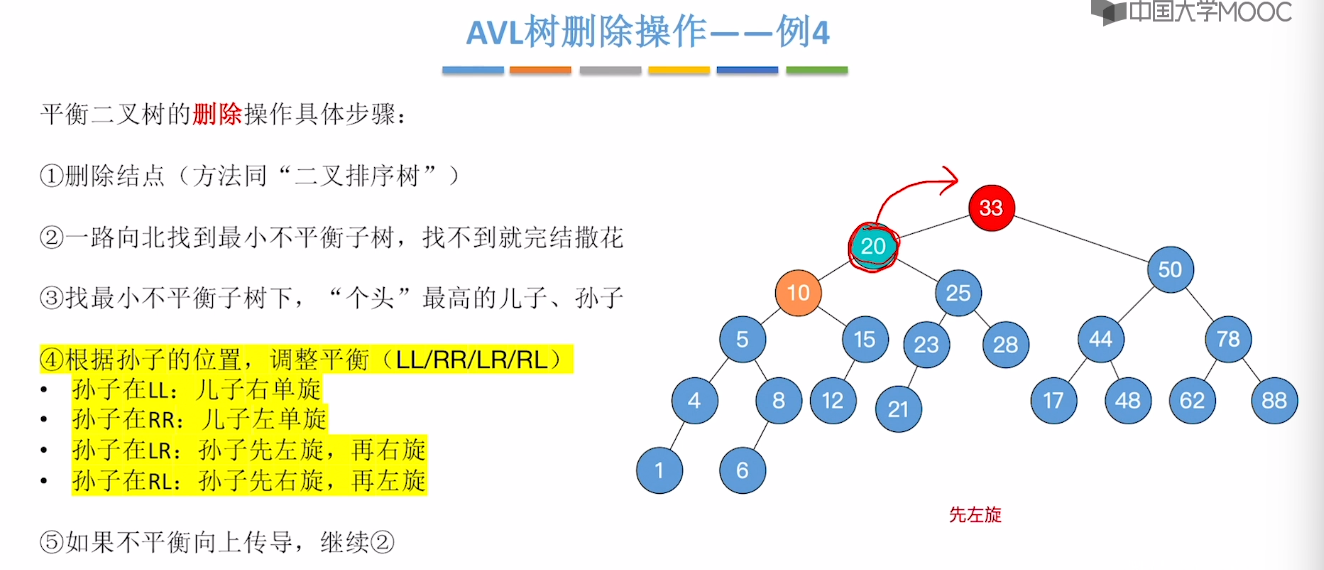
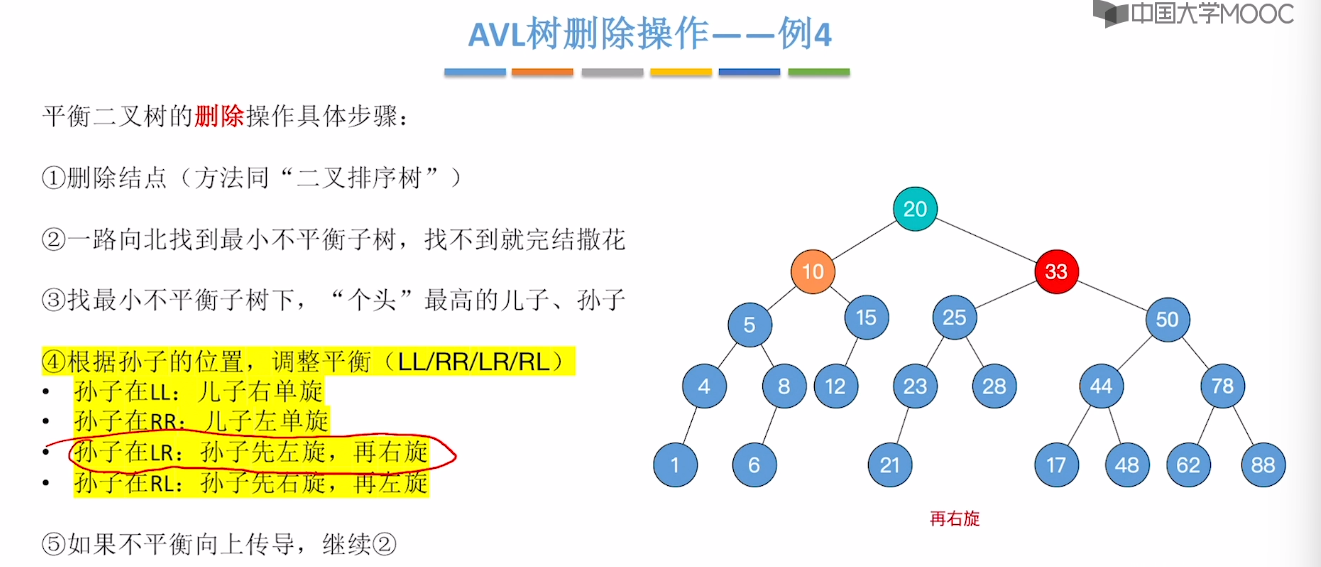
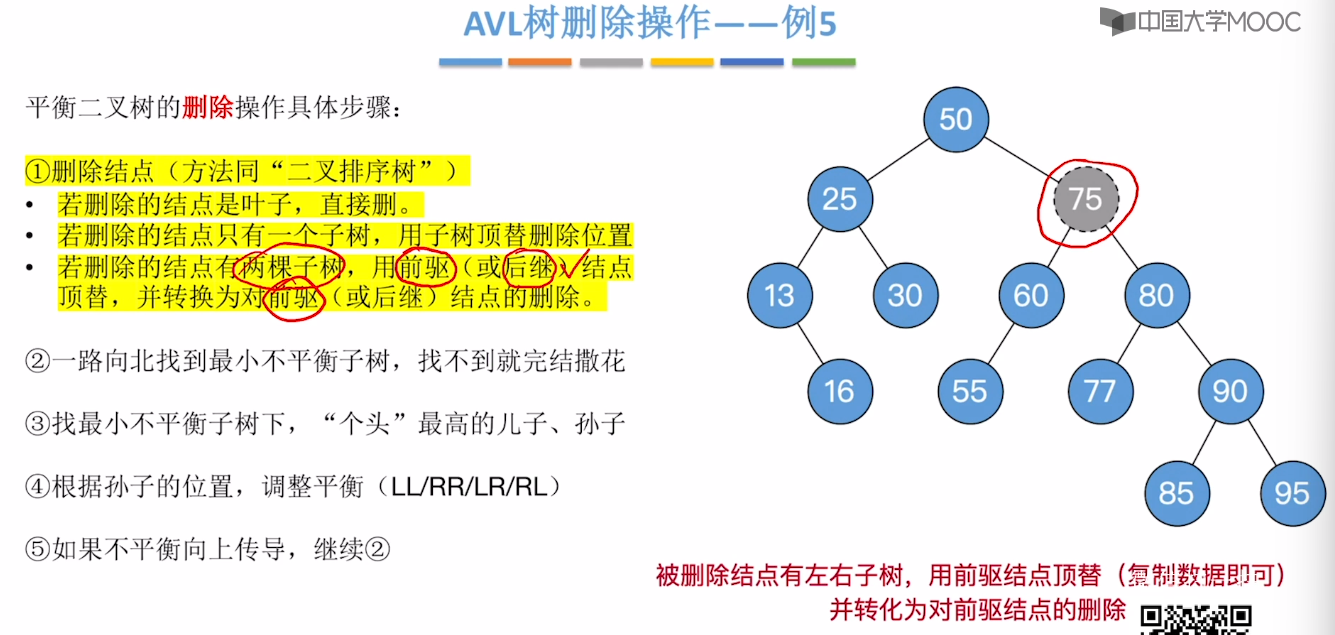
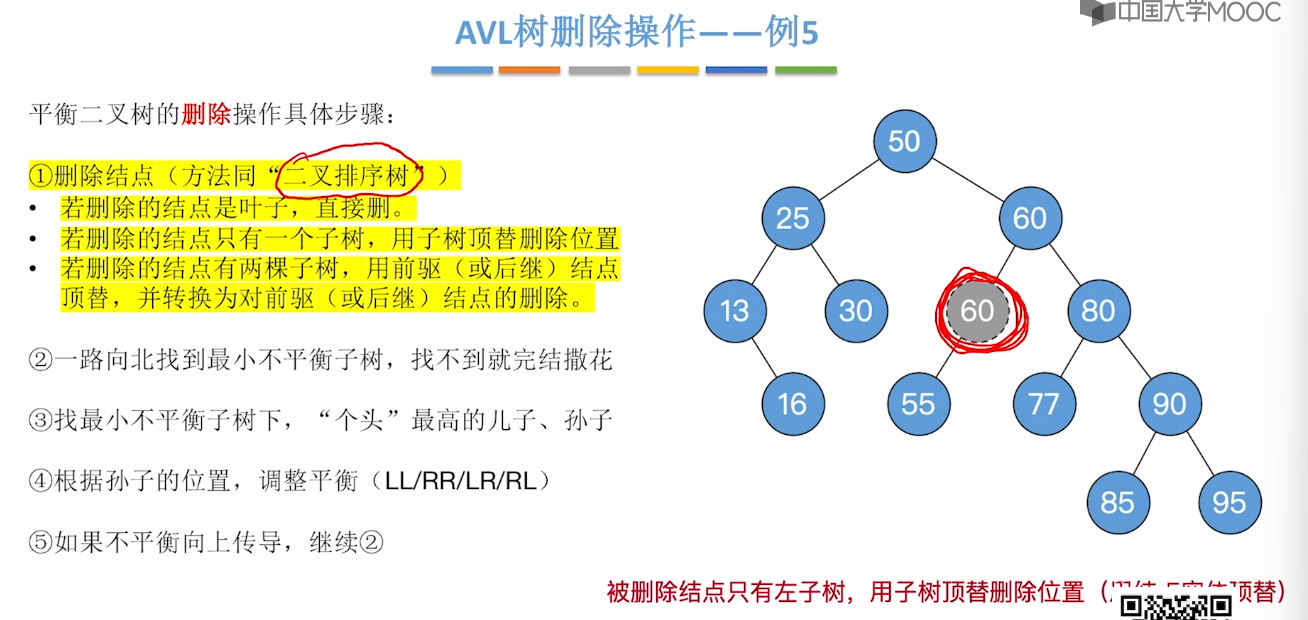
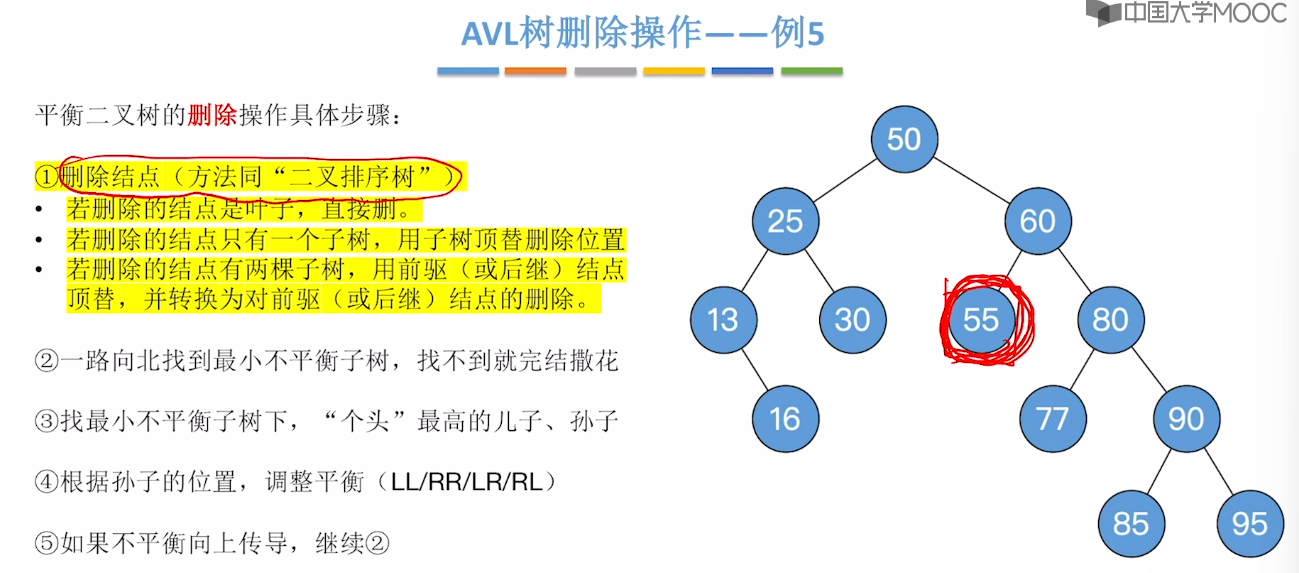
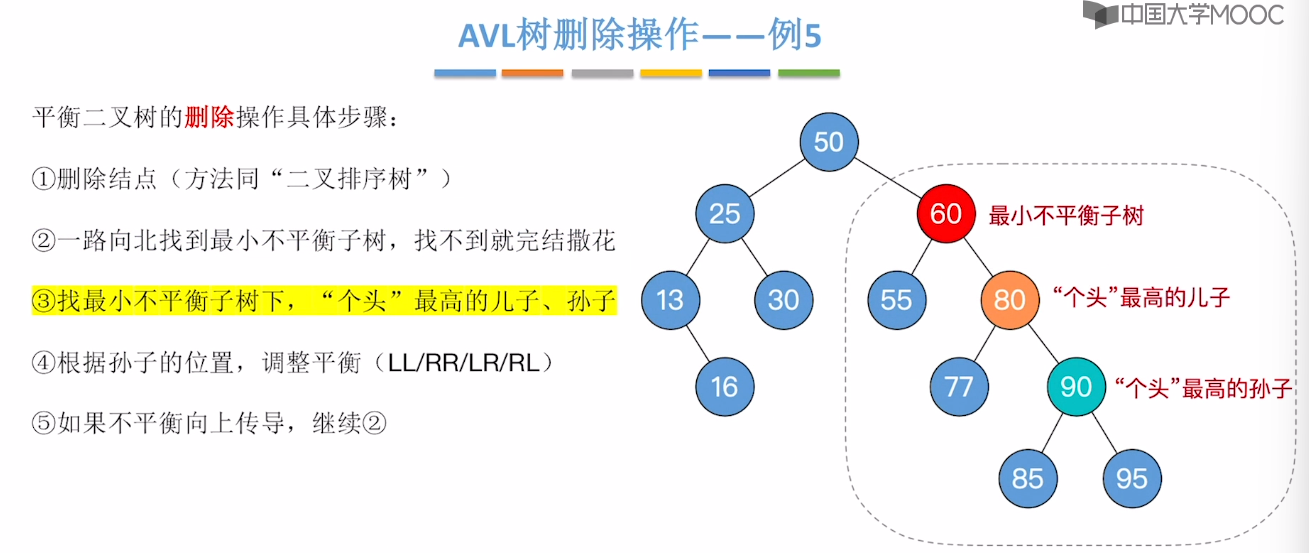
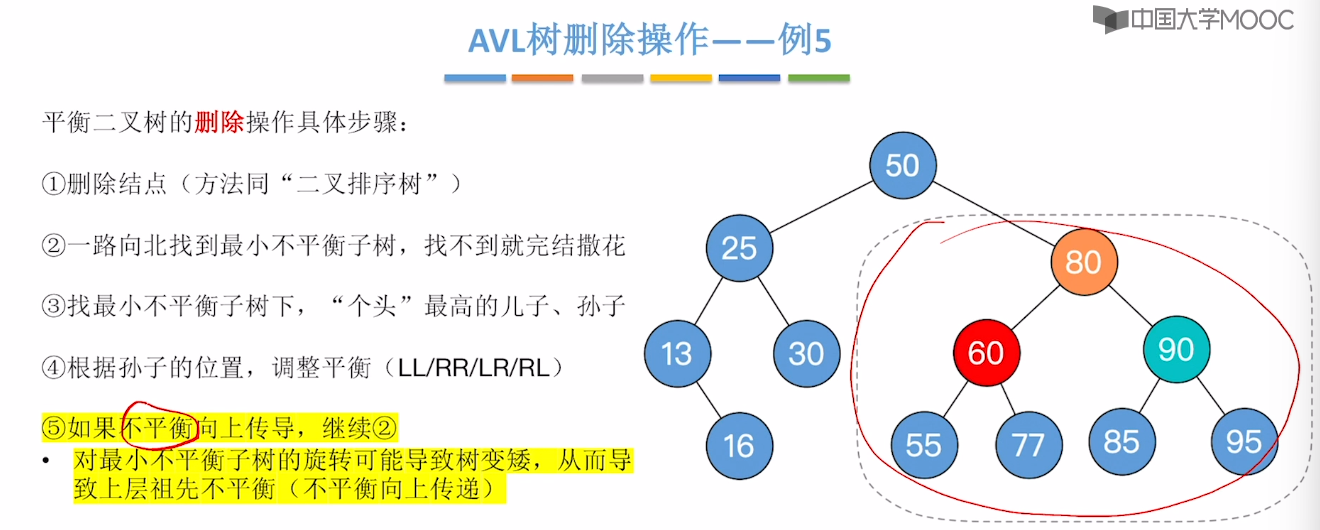
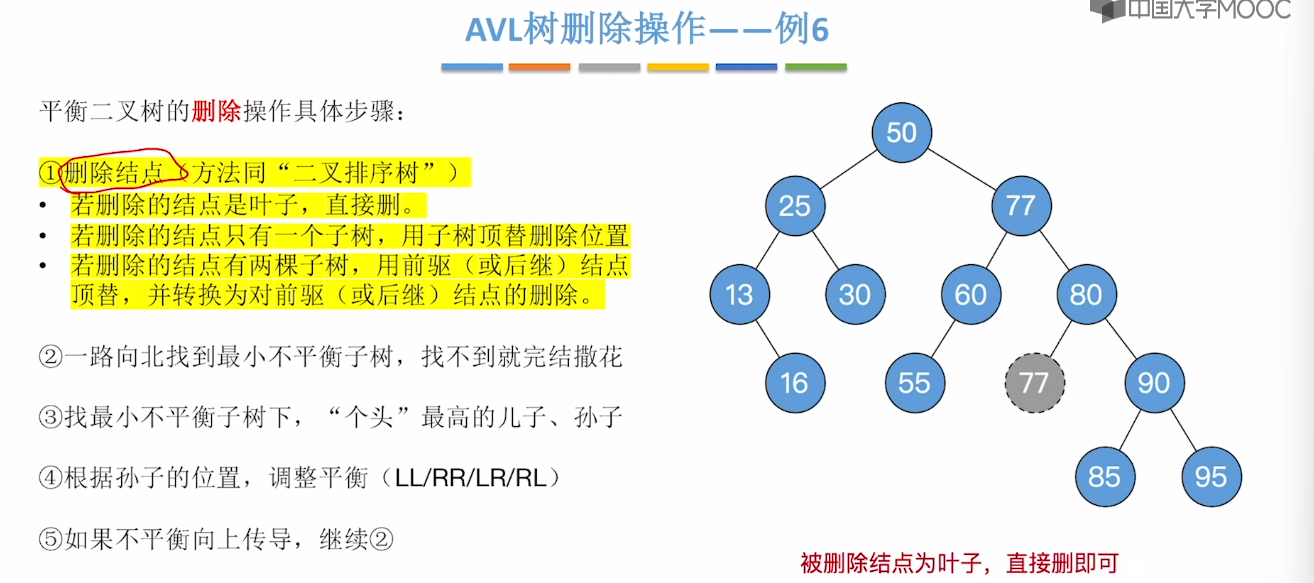
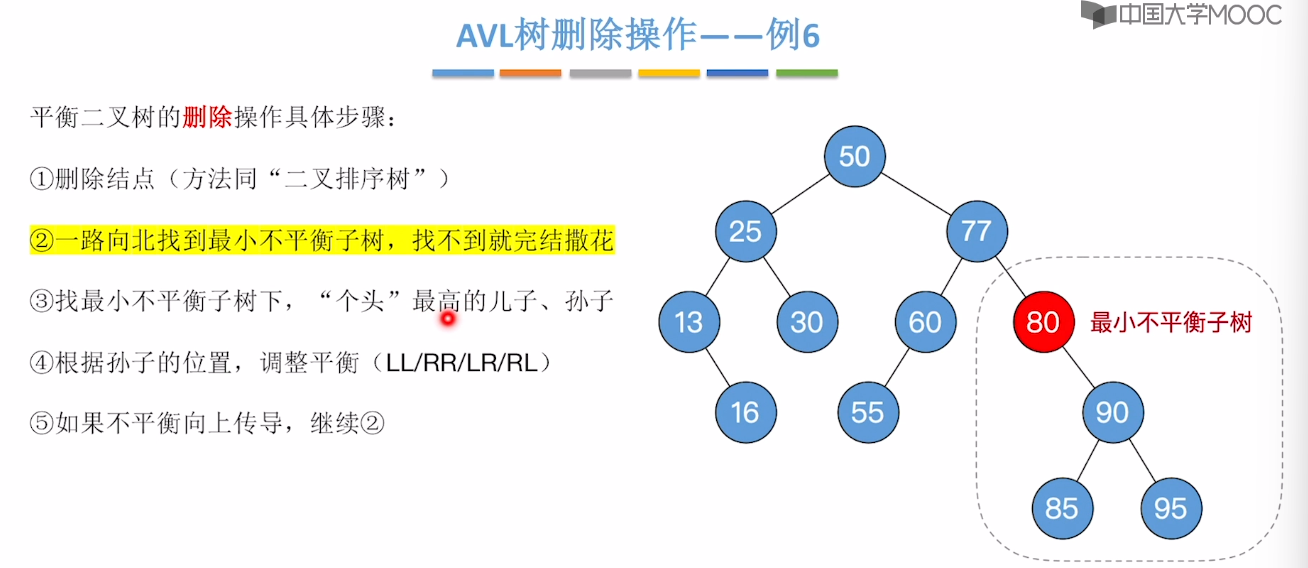
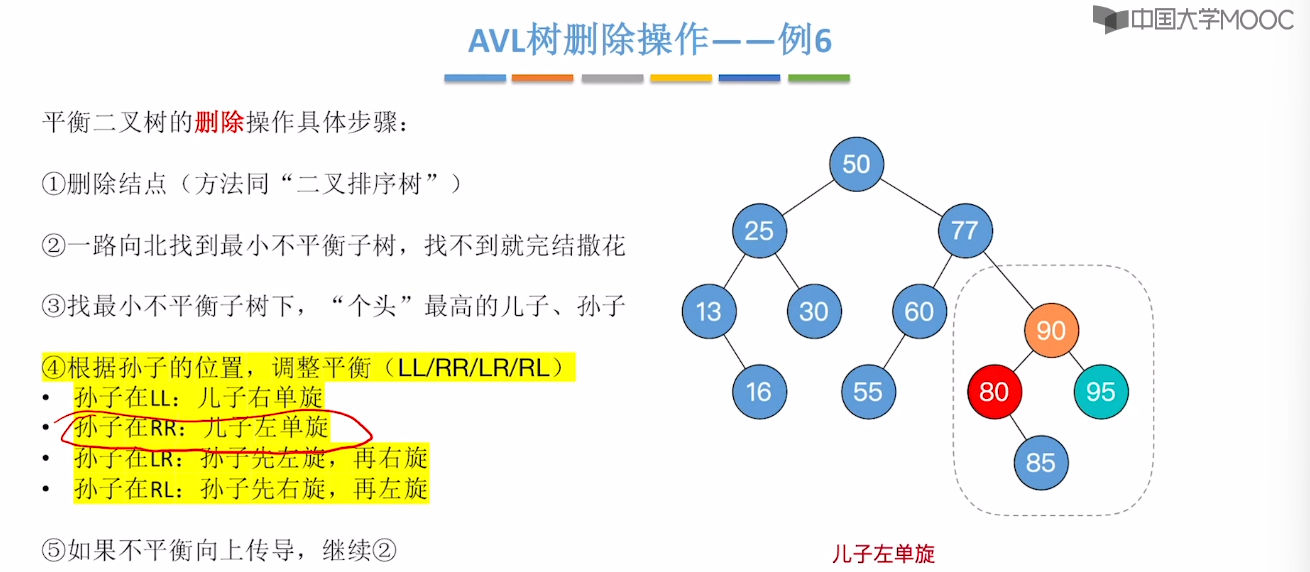
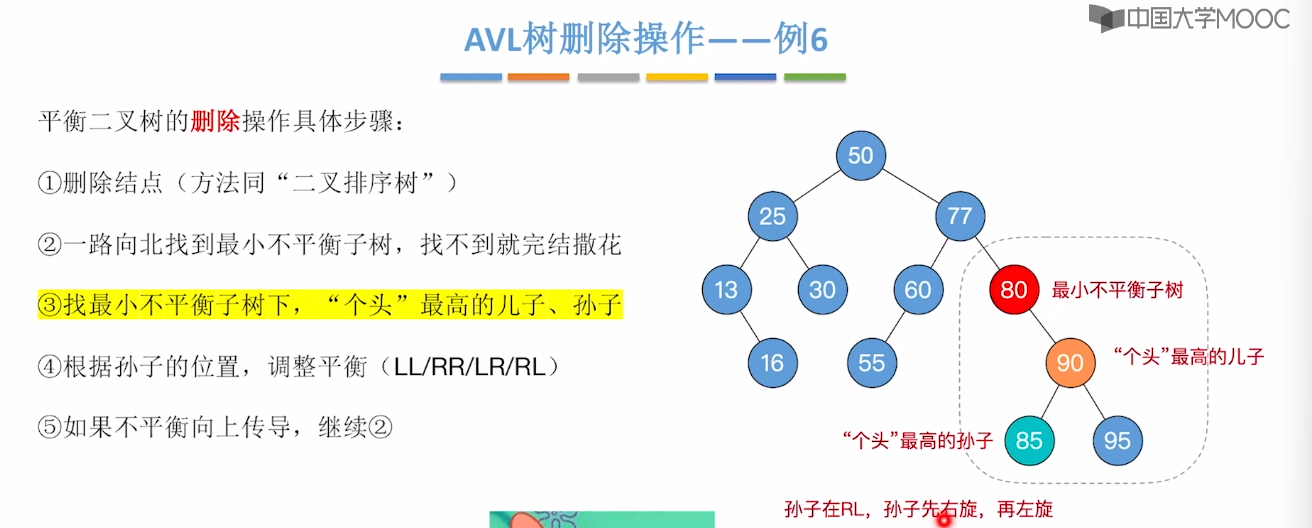

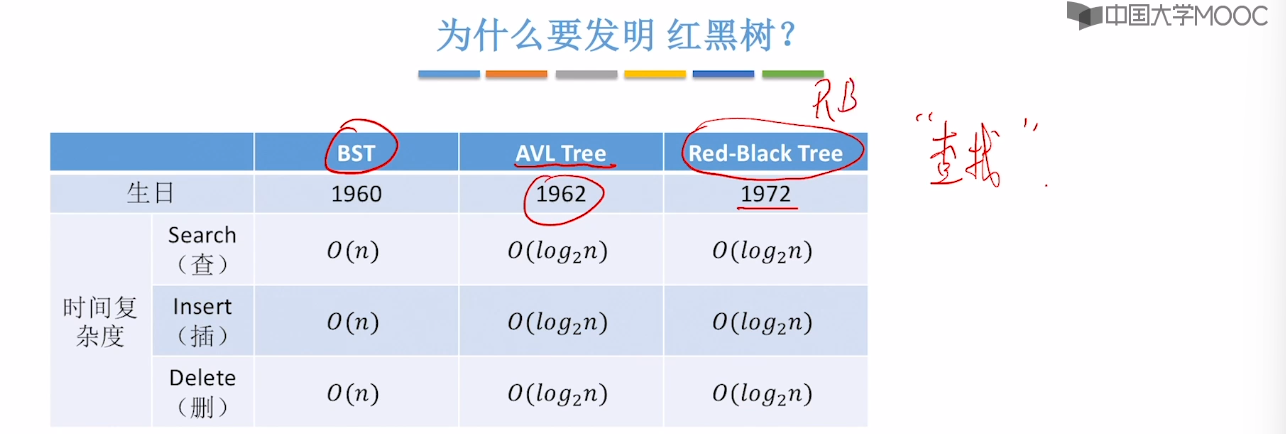
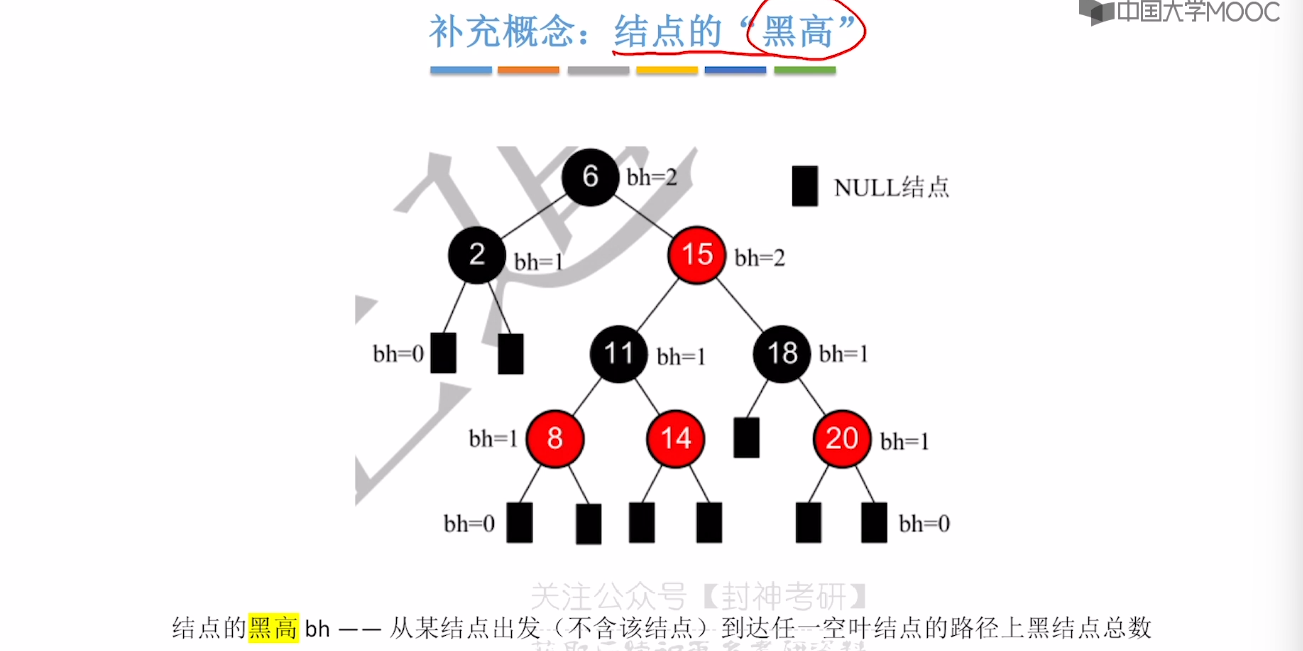
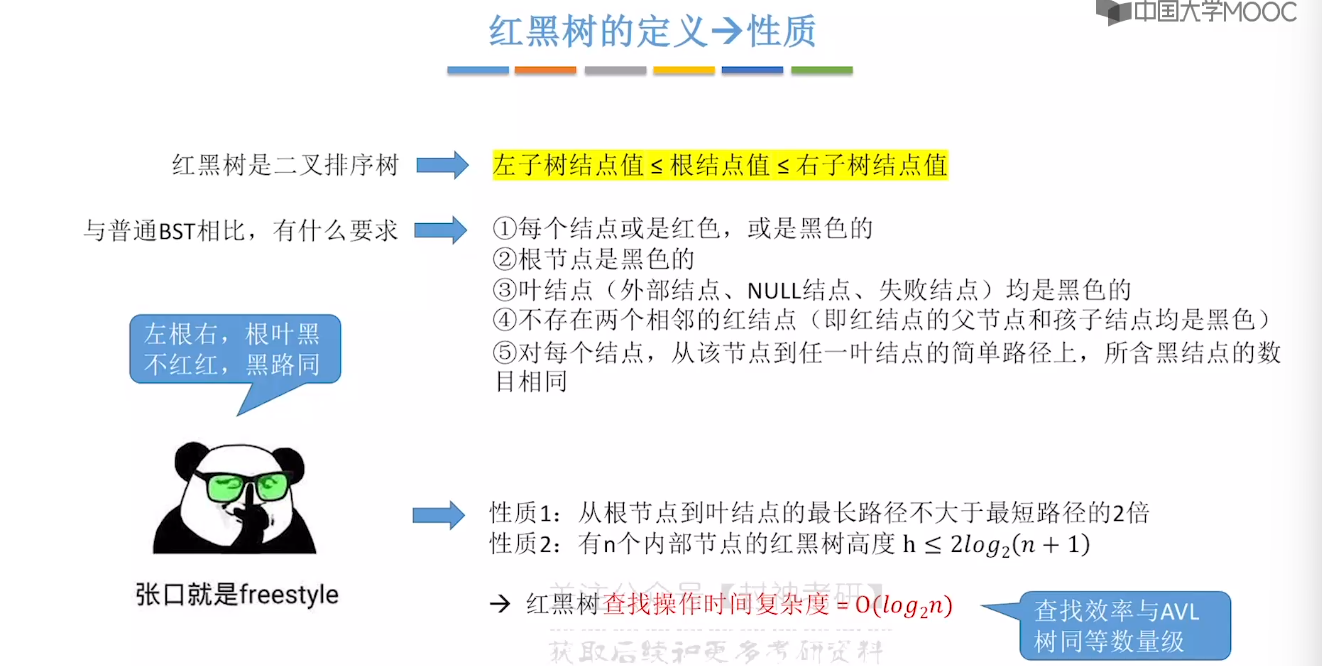
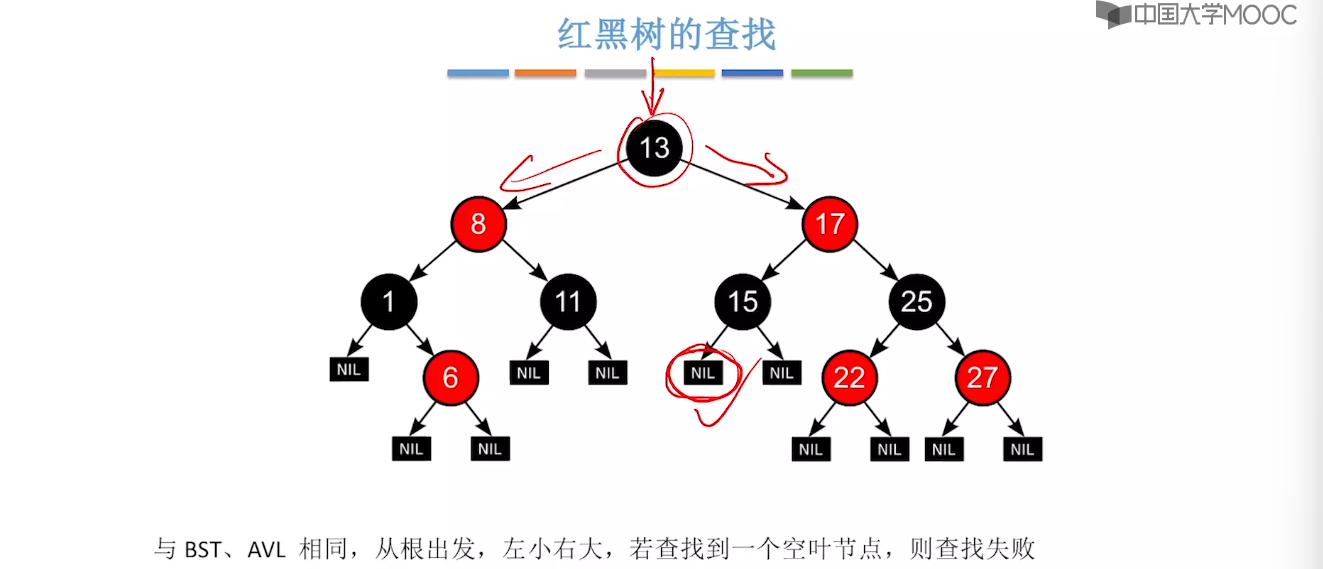
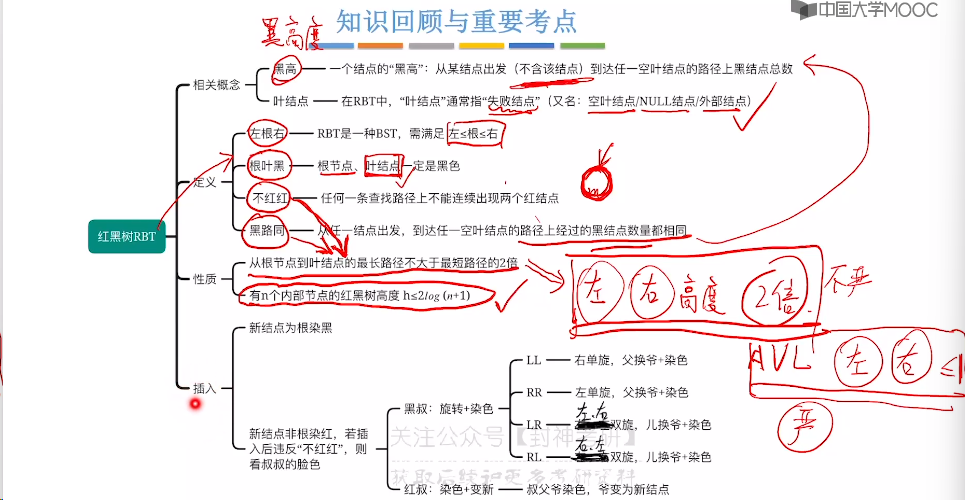
7.8、红黑树的定义和性质
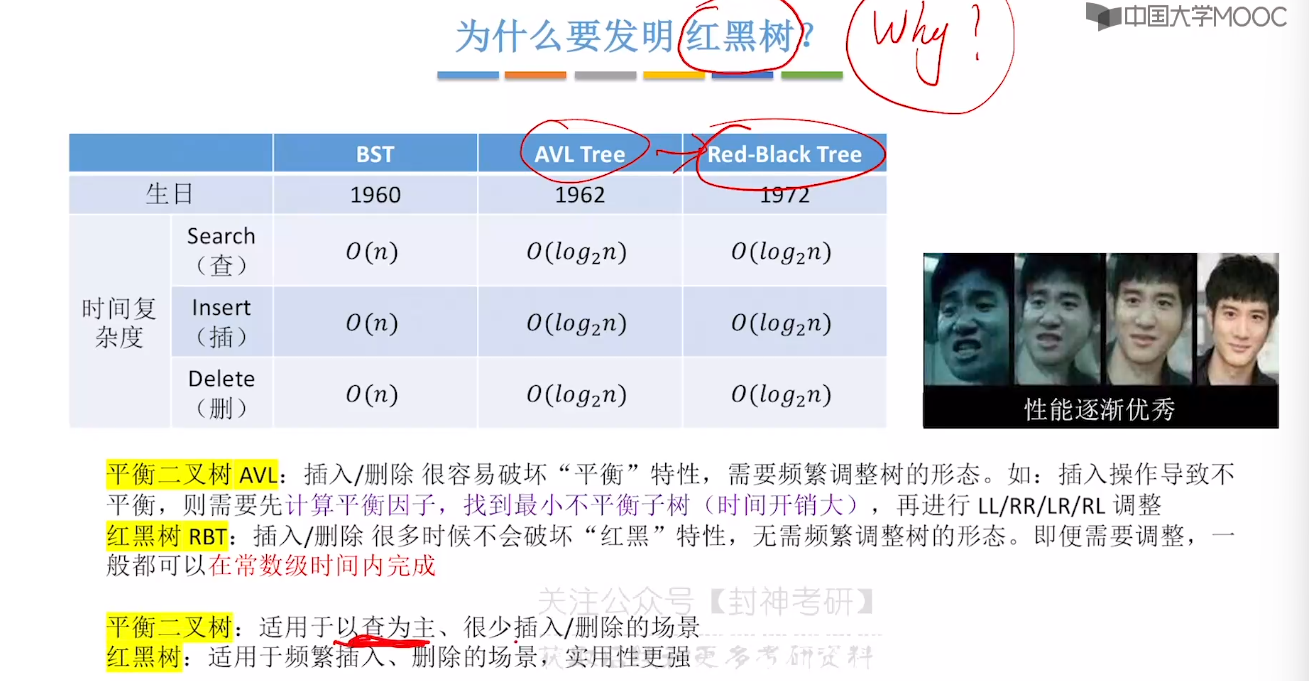

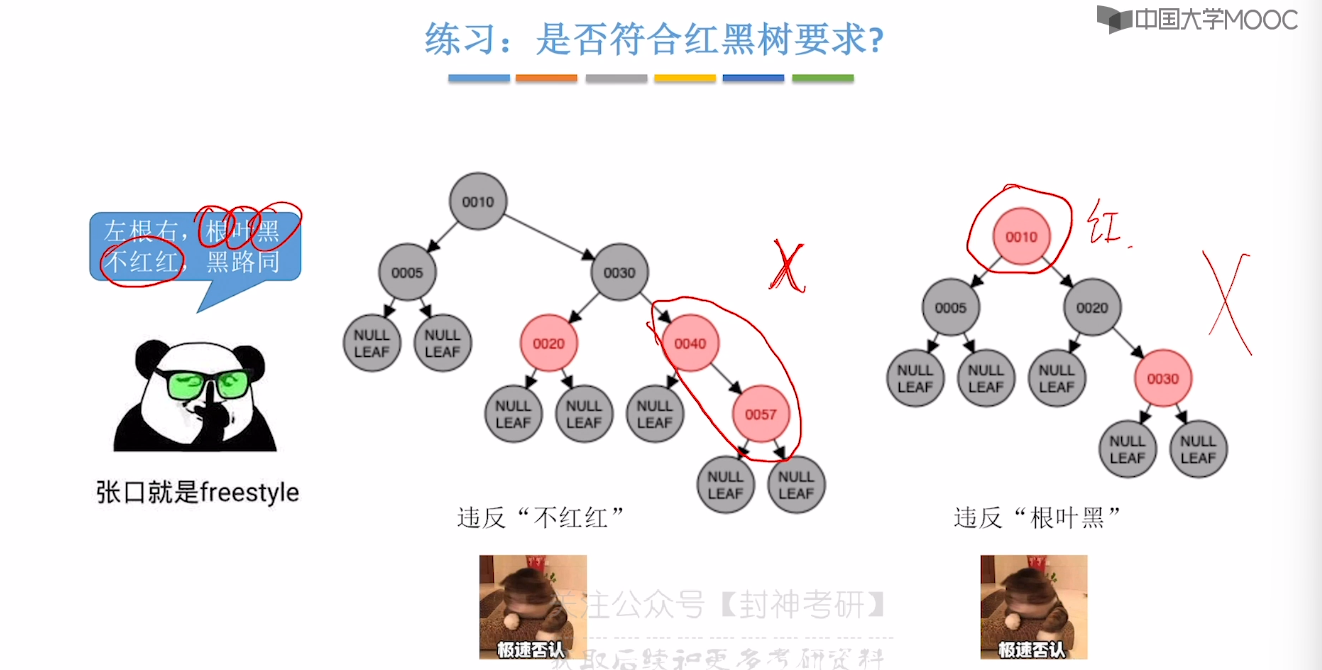
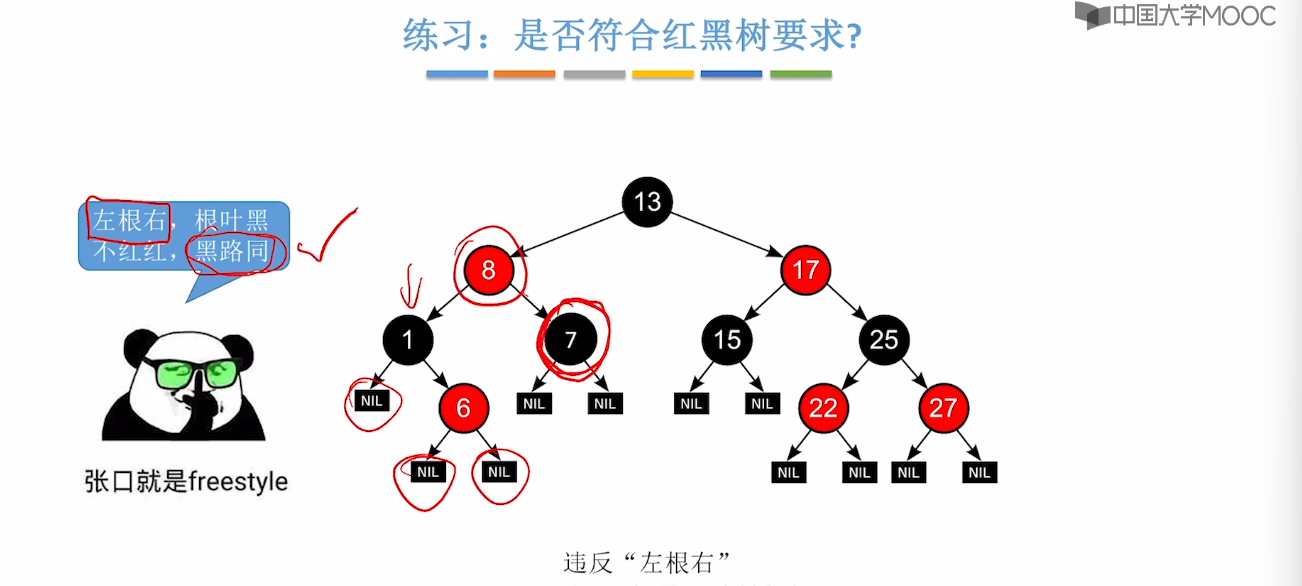
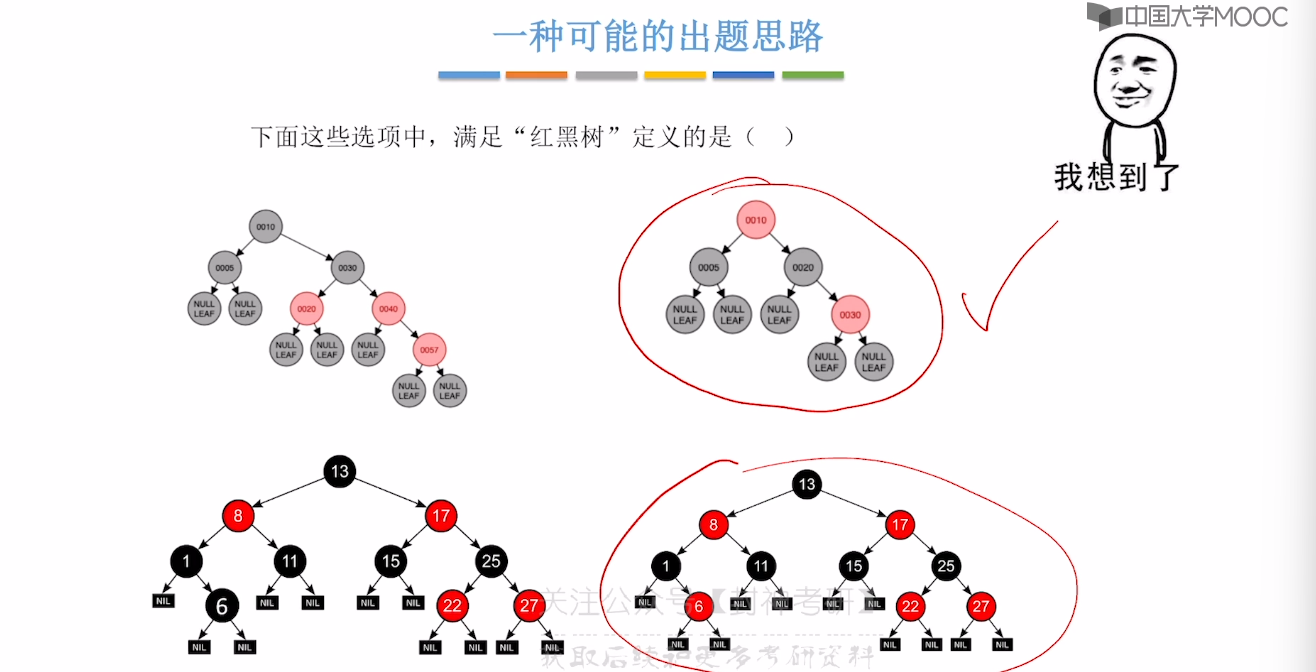
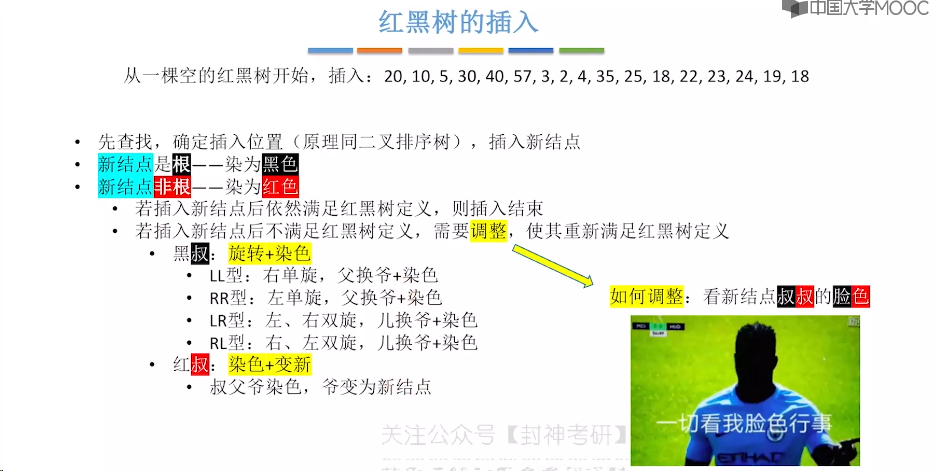
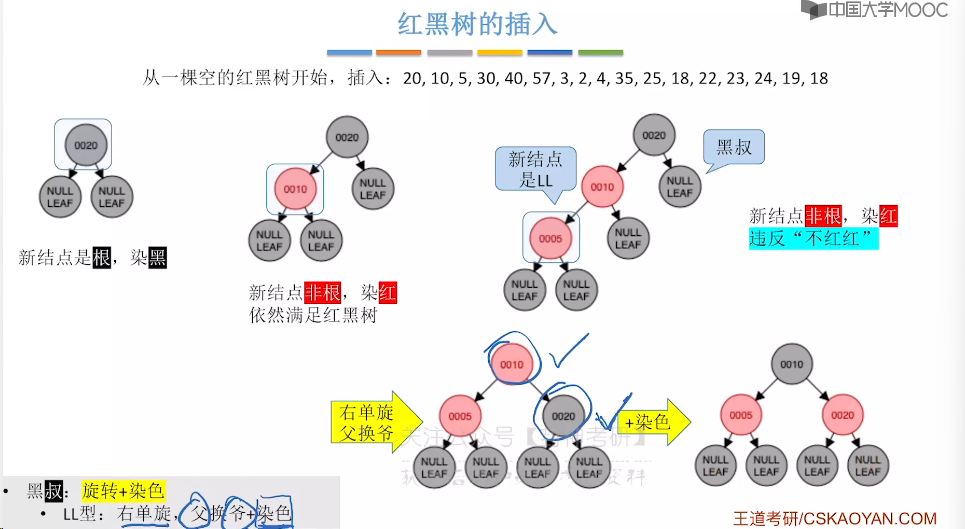
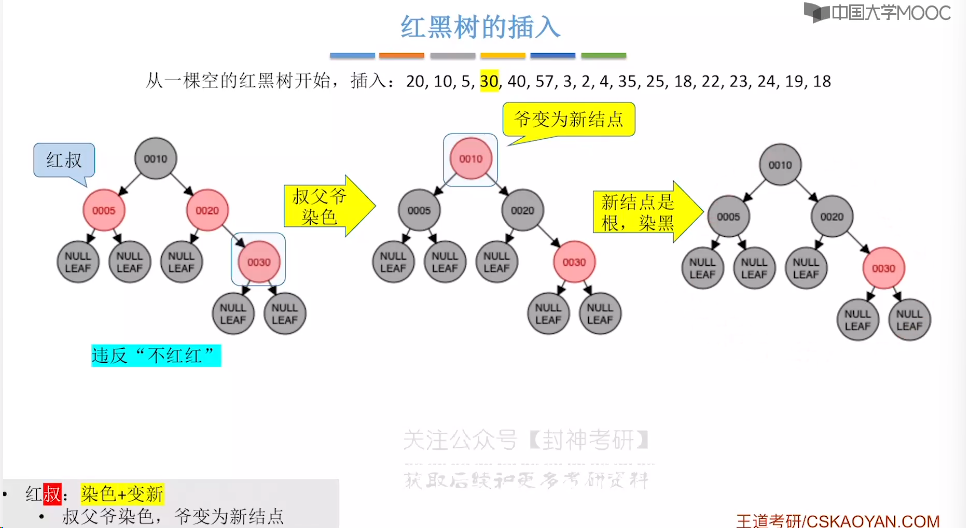
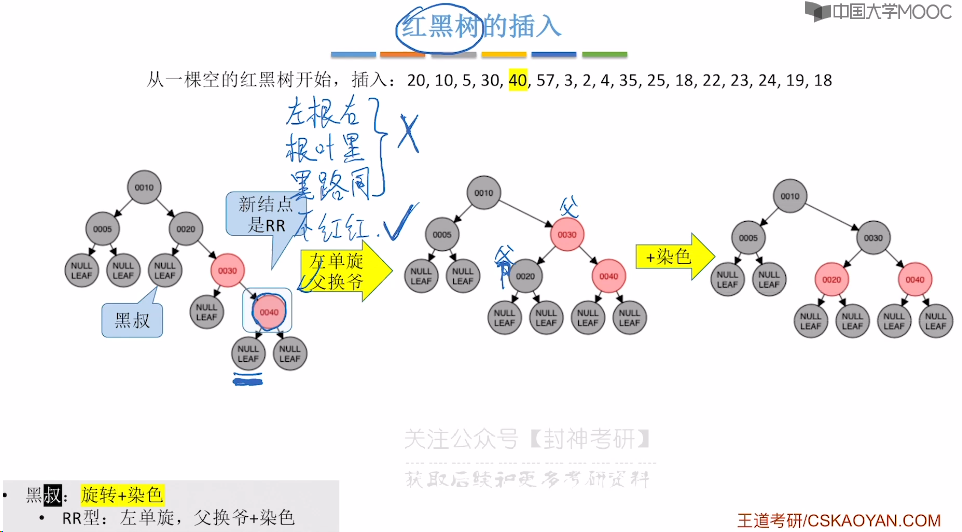
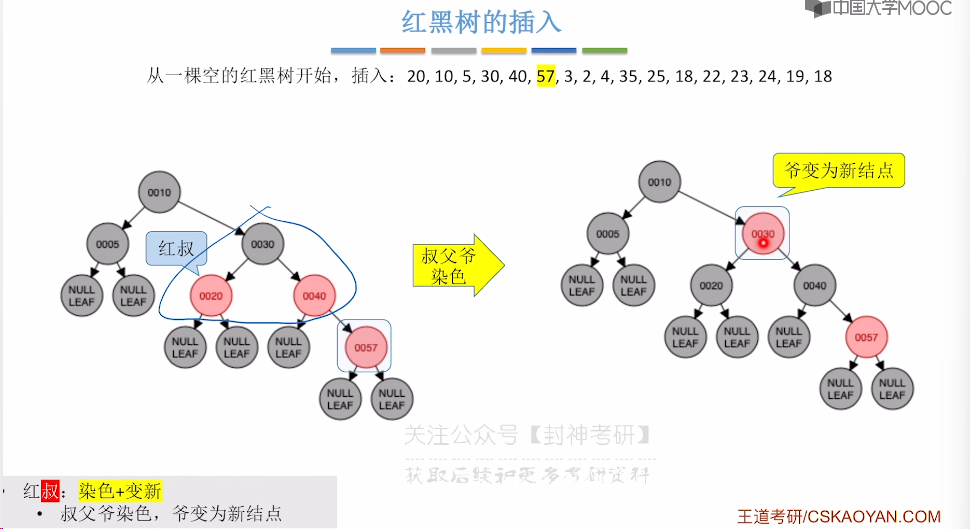
7.9、红黑树的插入
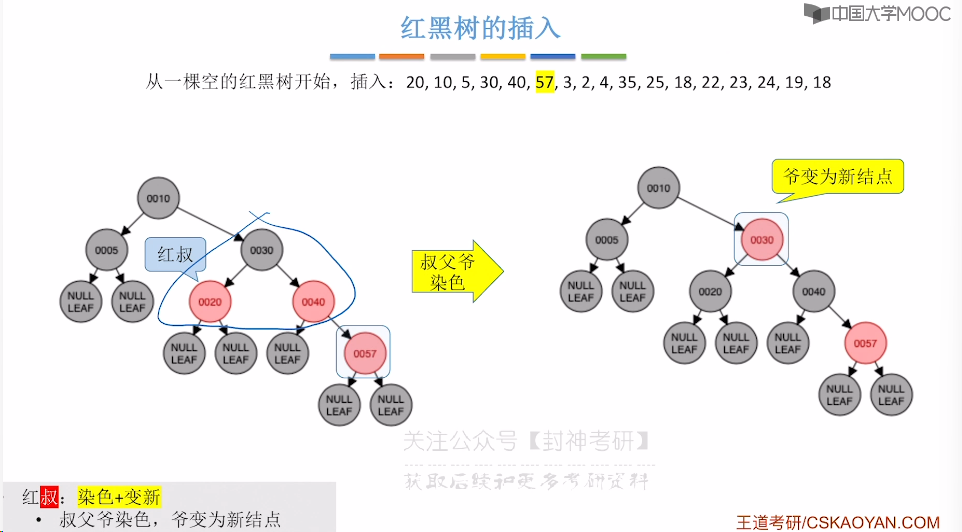
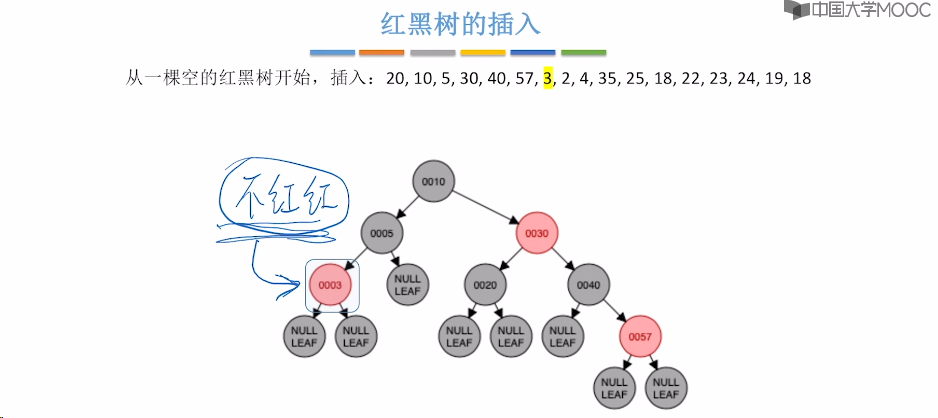
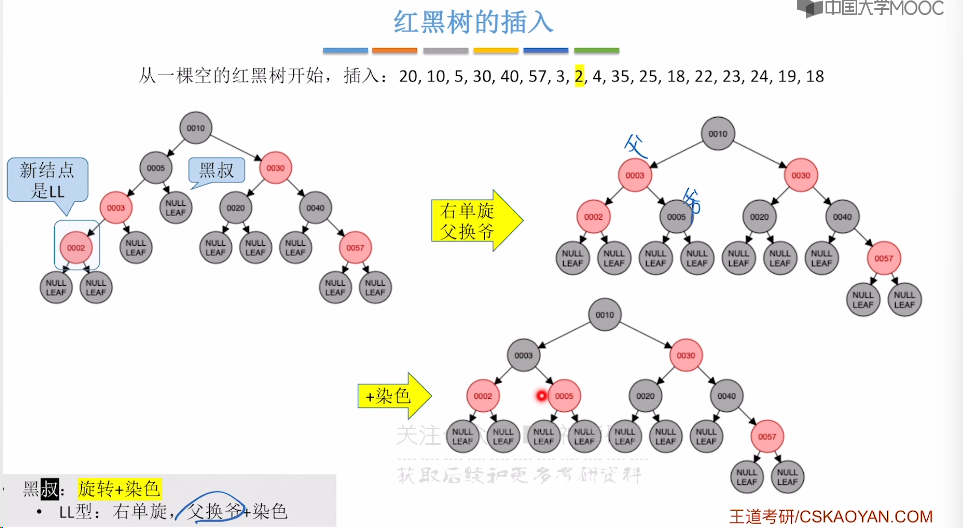
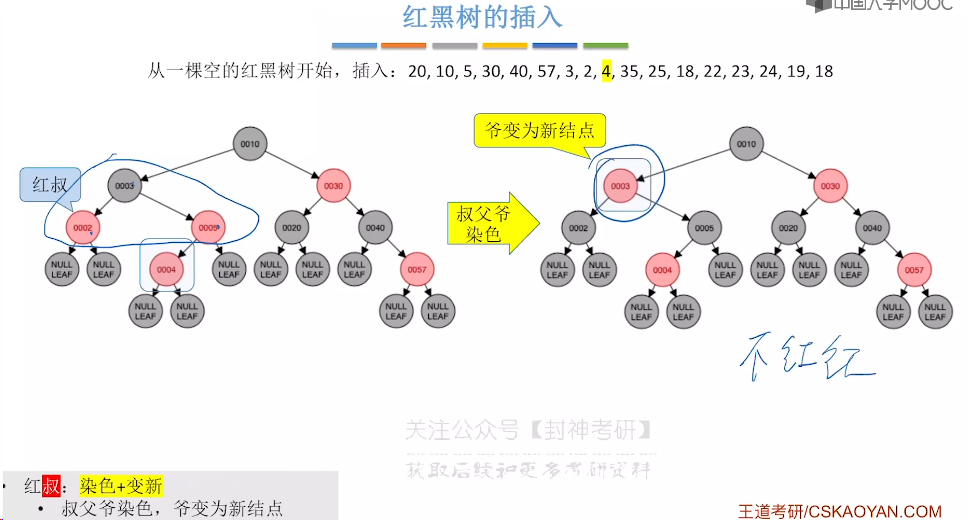

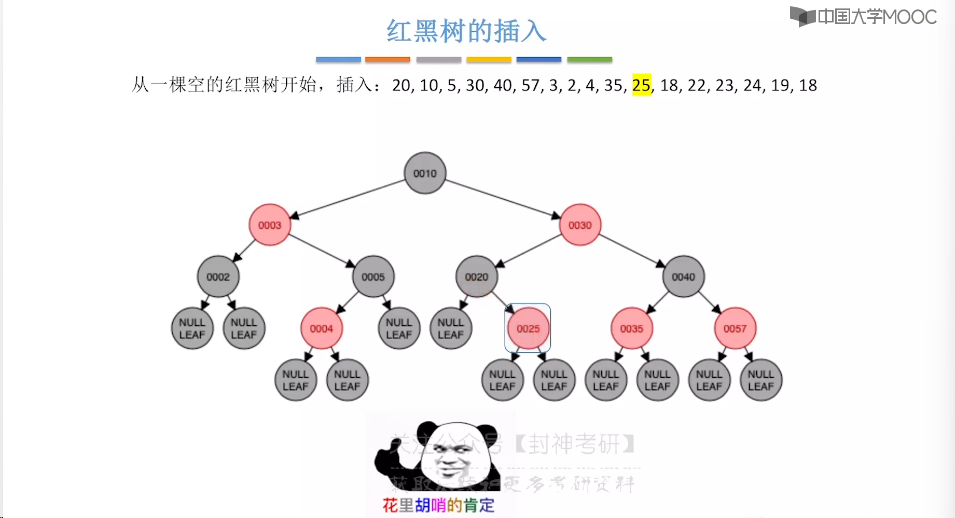
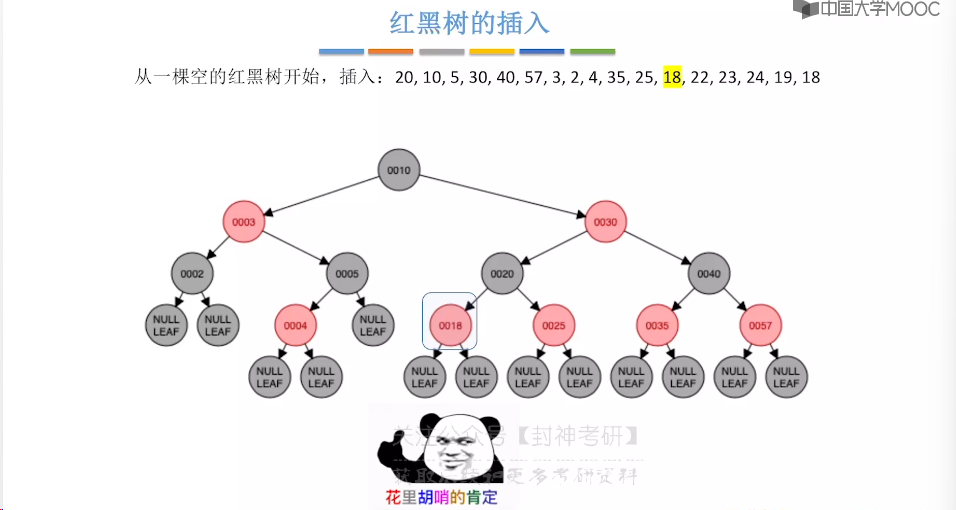
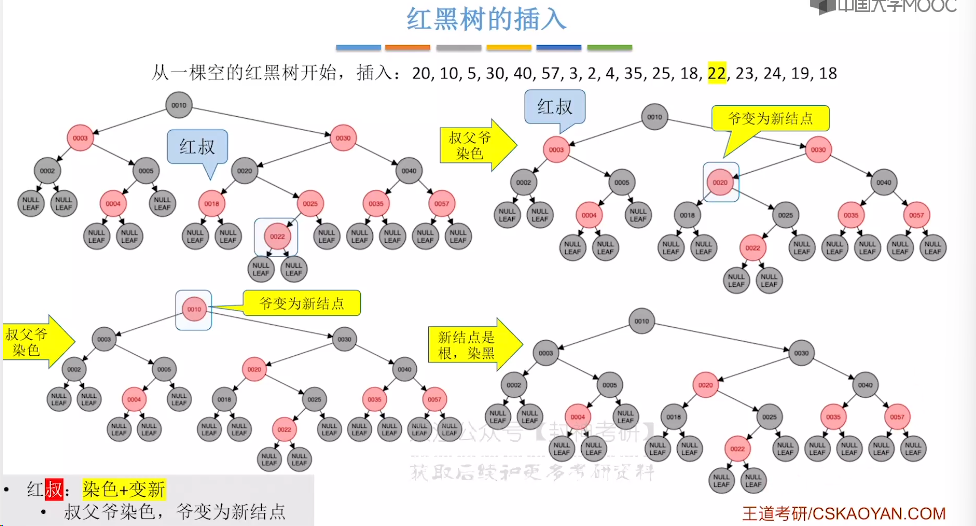
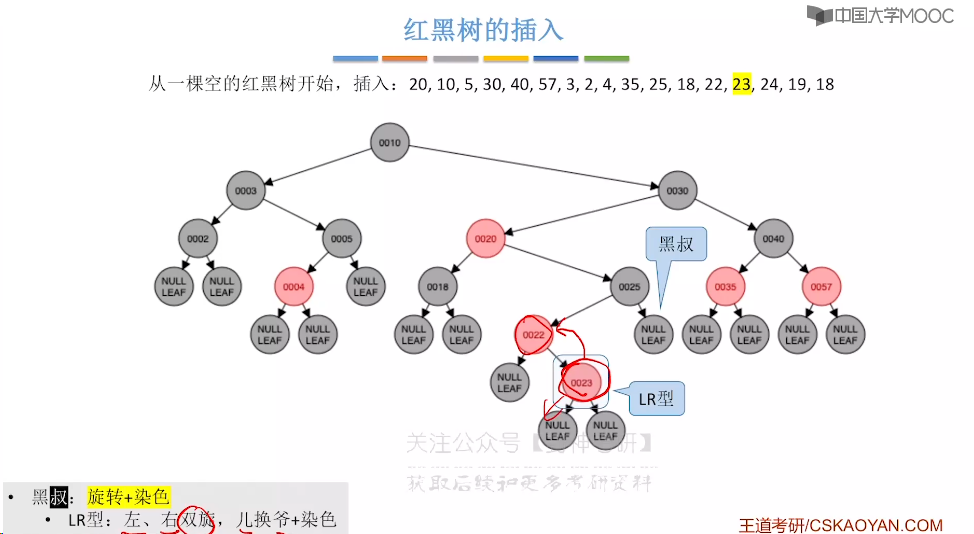
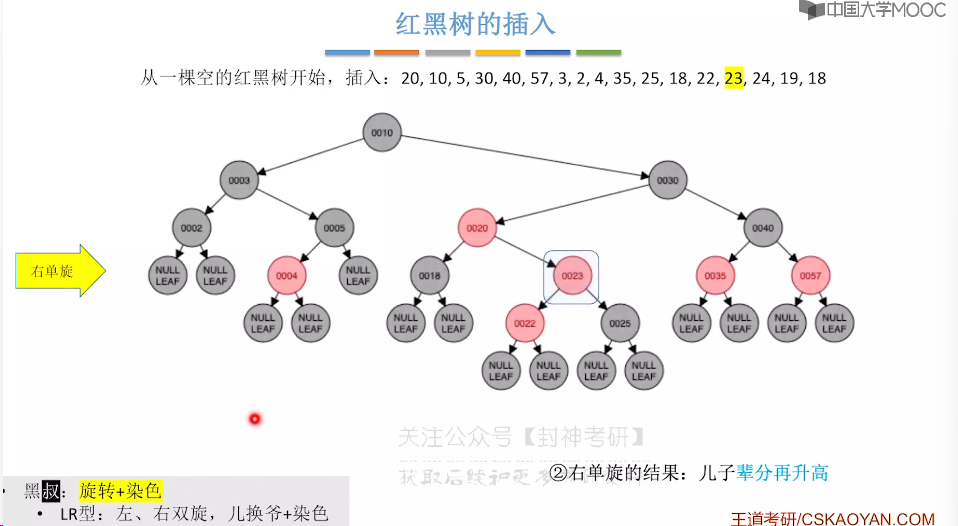
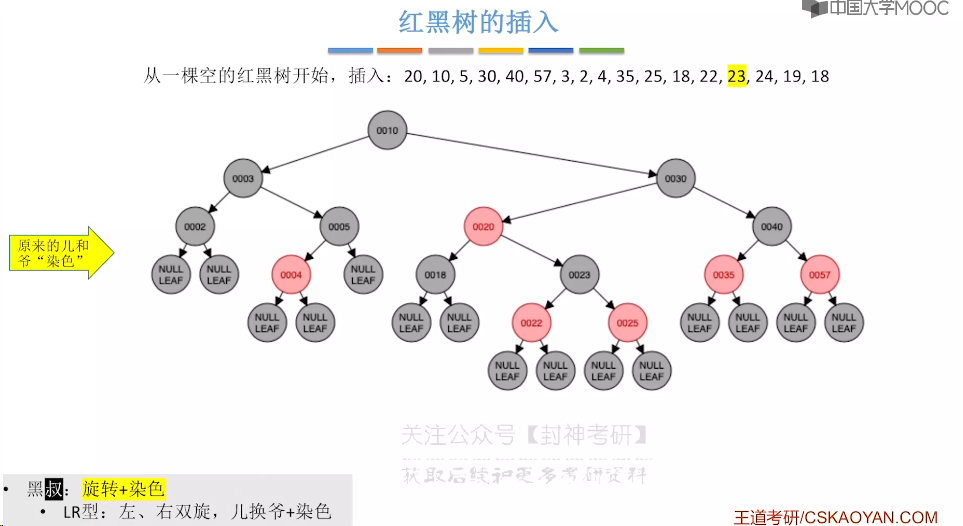
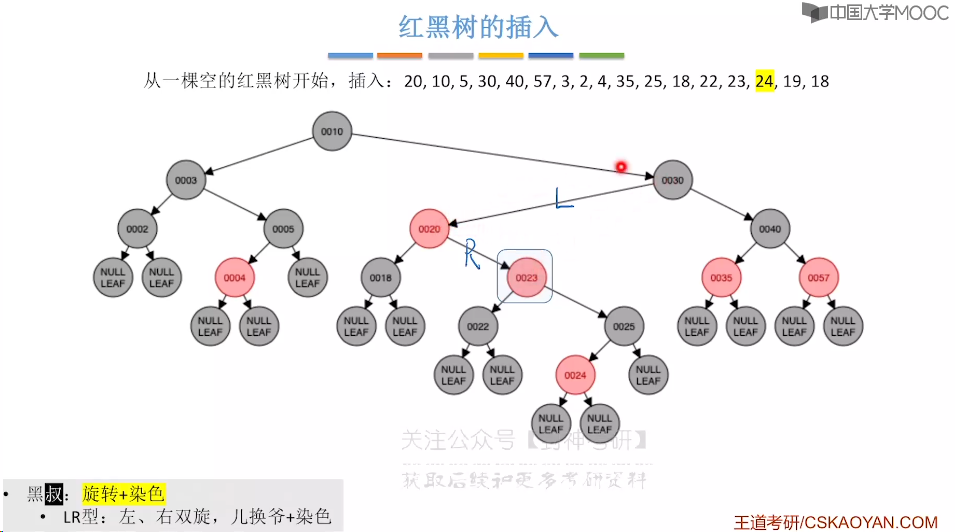
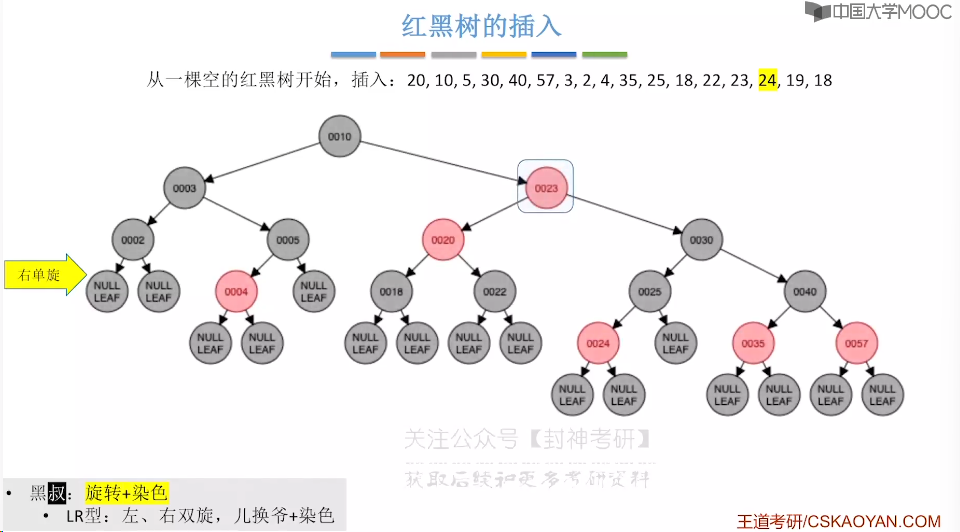
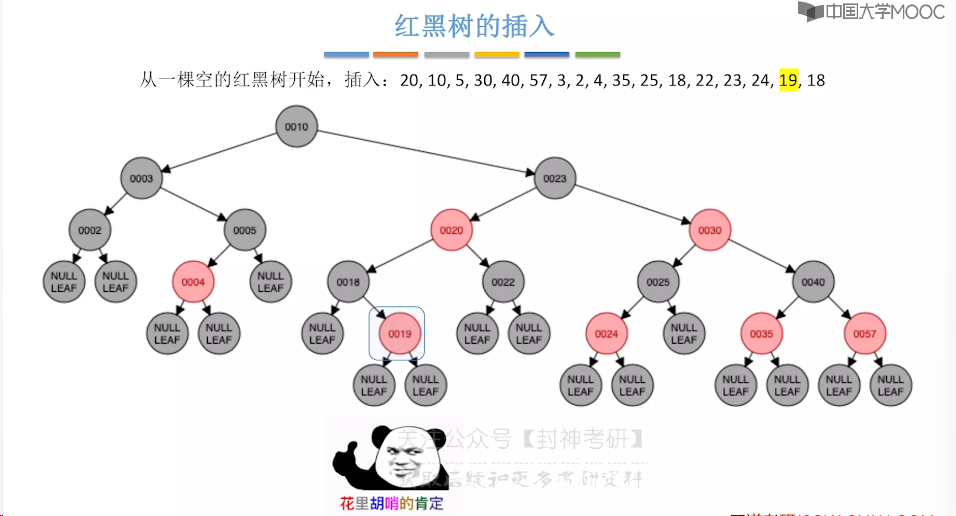
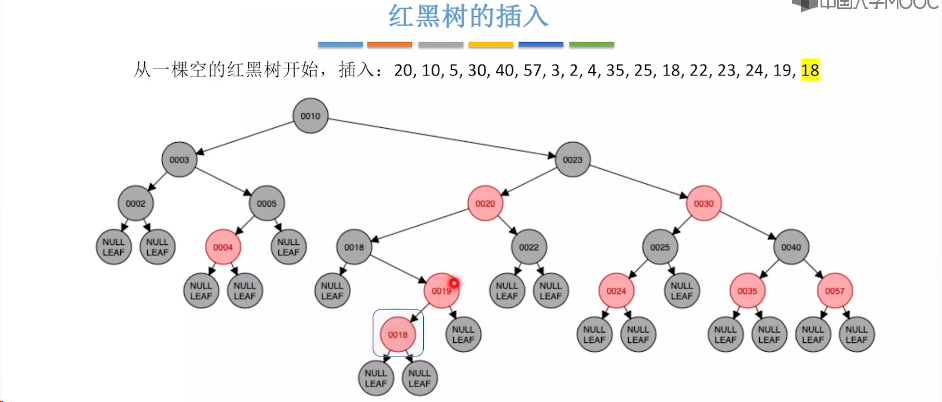
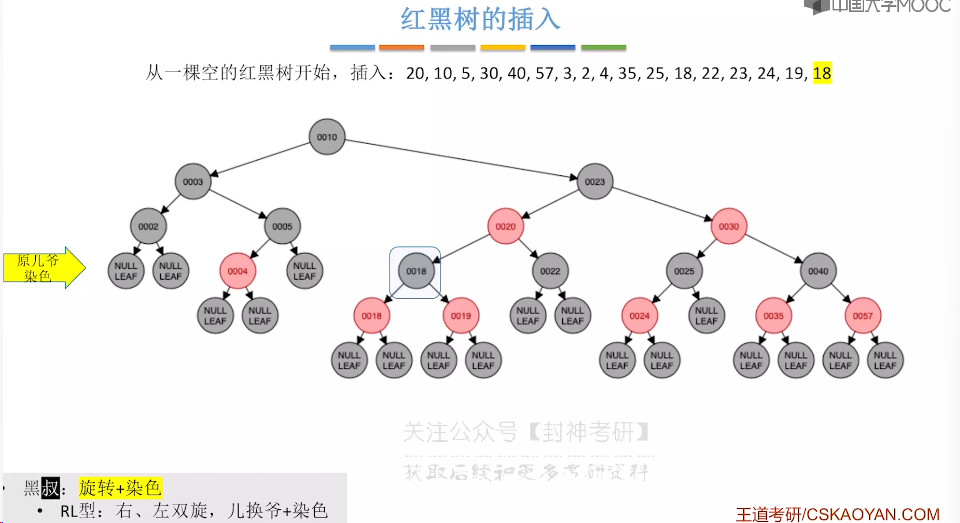
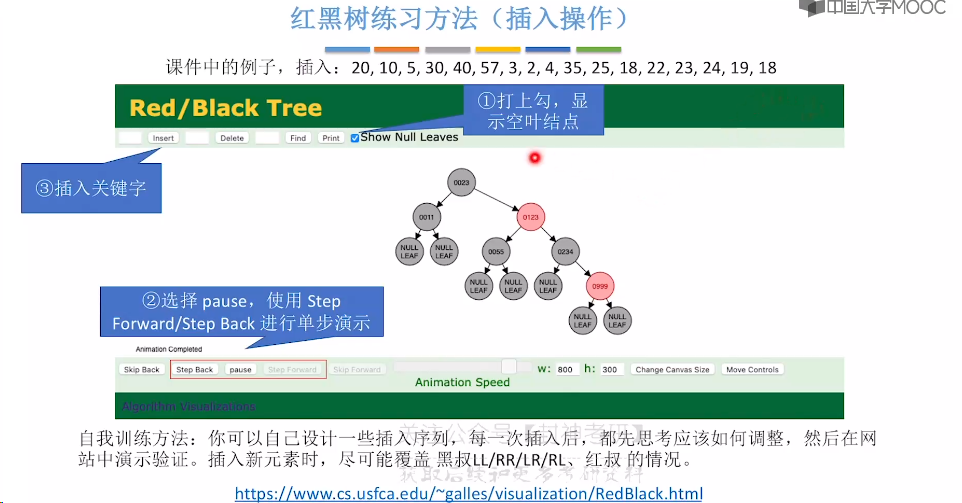
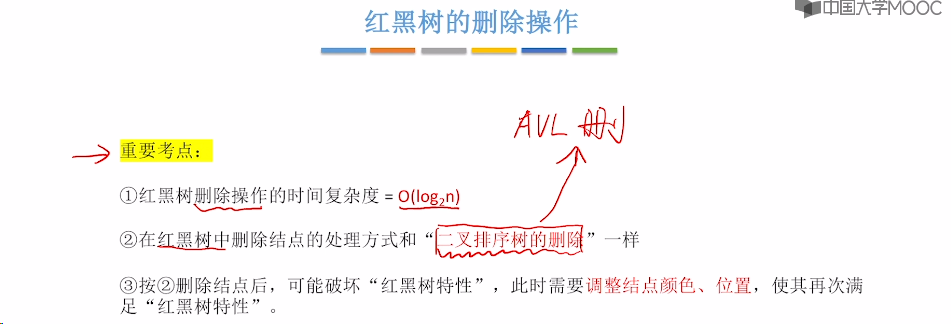
7.10、红黑树的删除
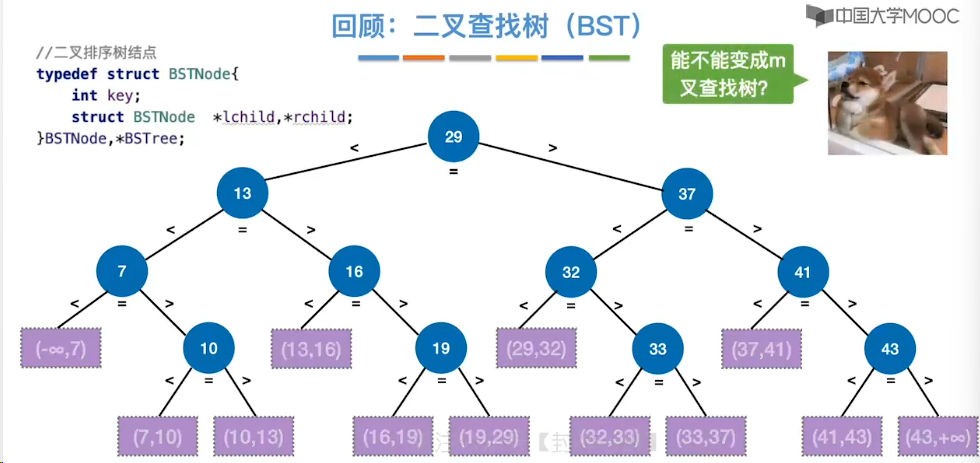
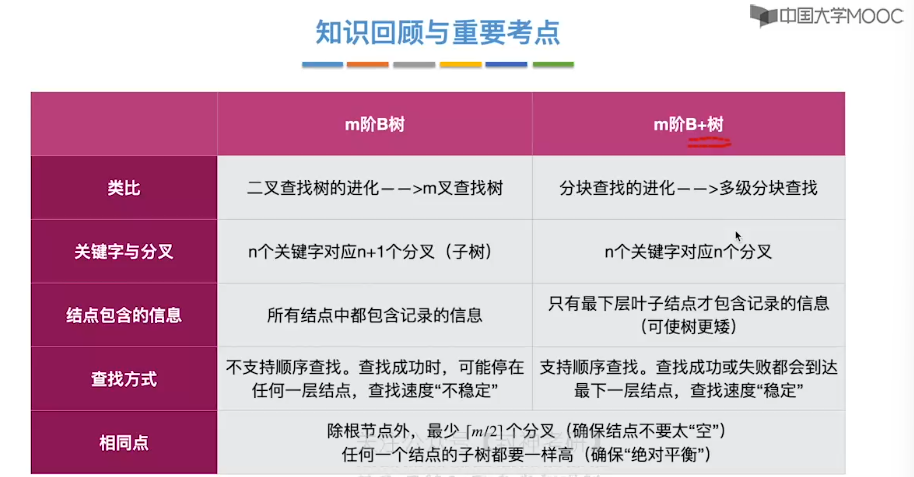
7.11、B 树
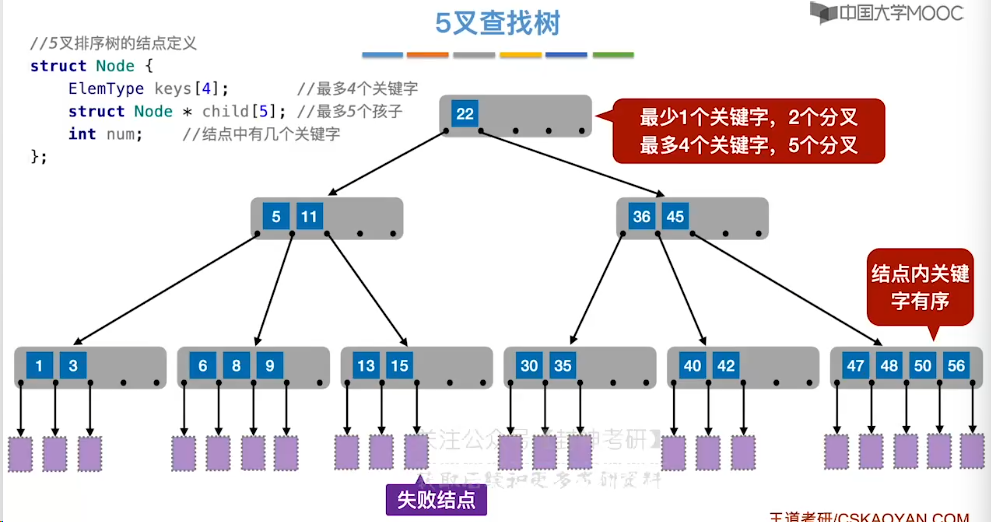
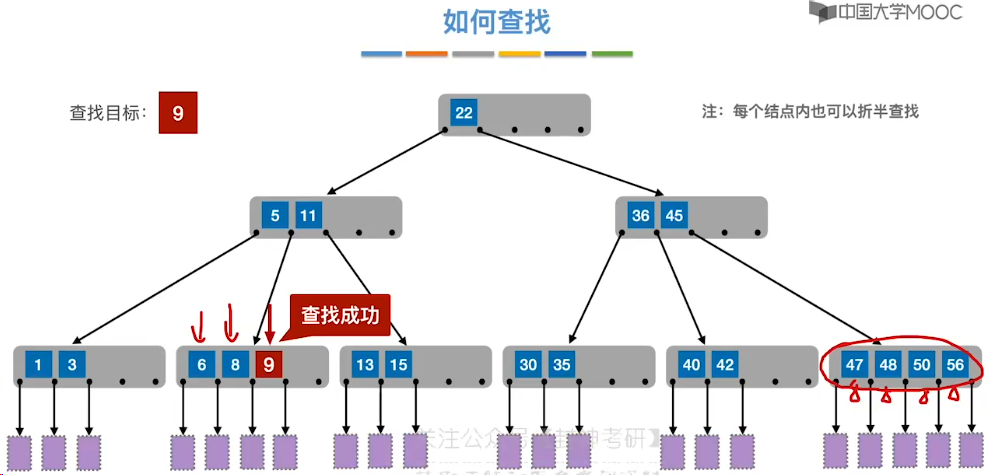
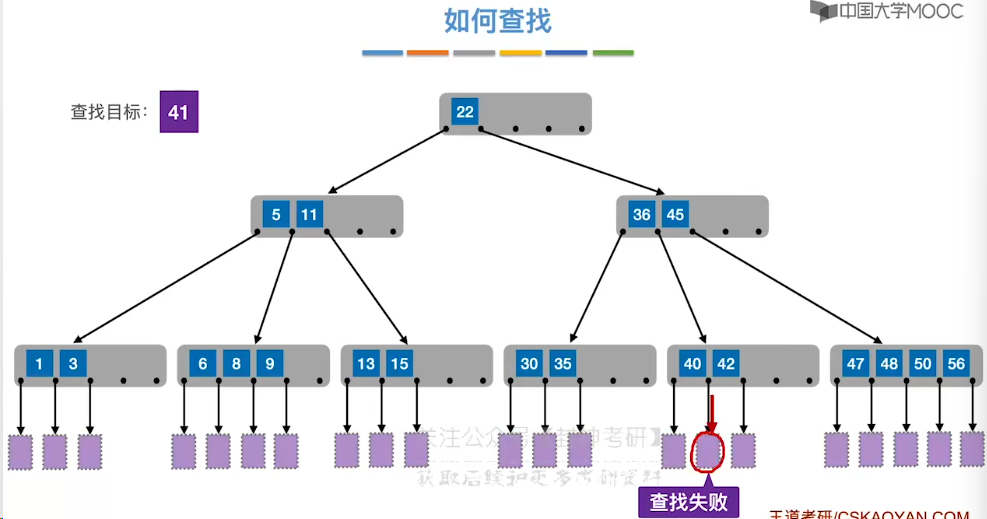
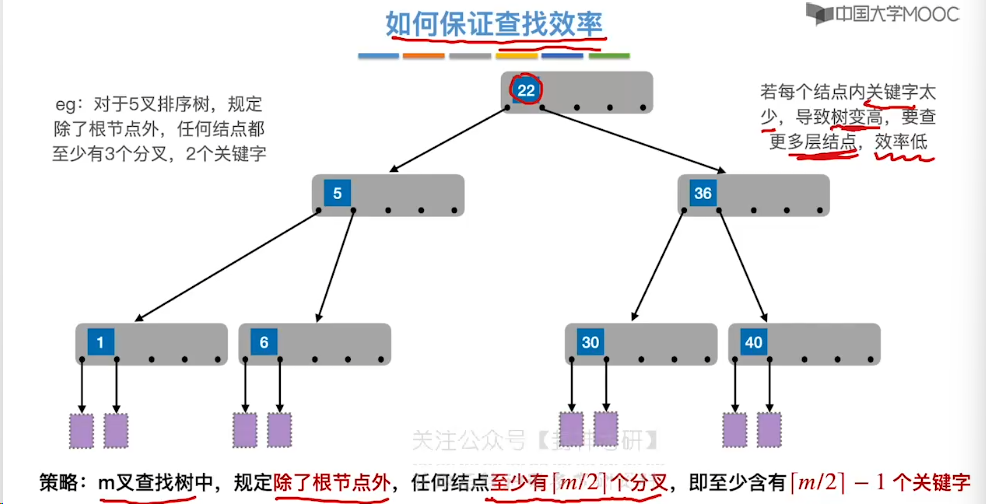
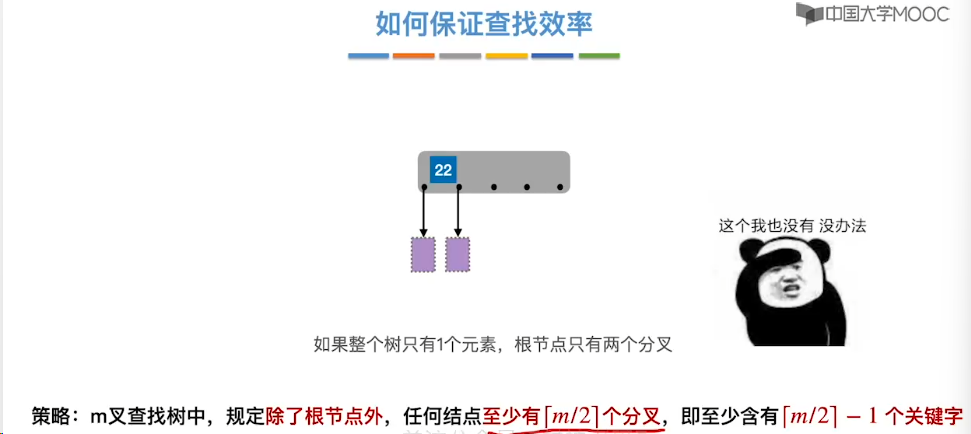
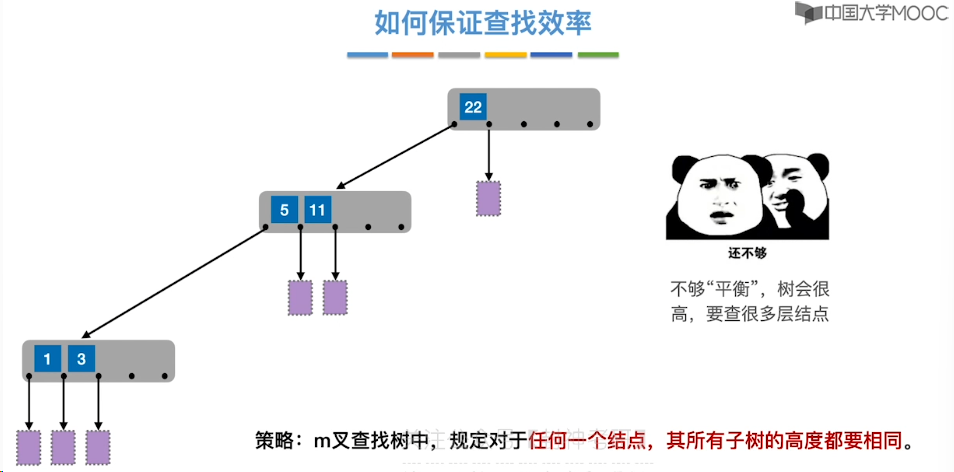
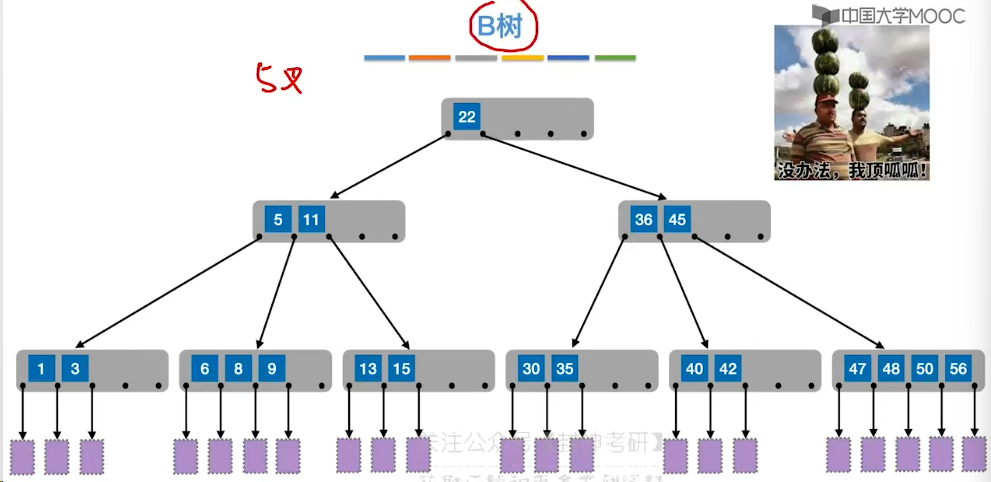
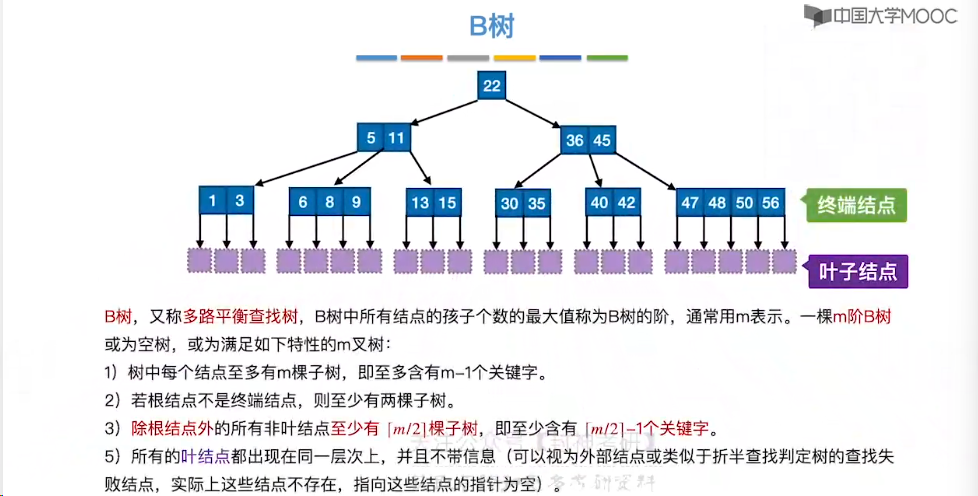
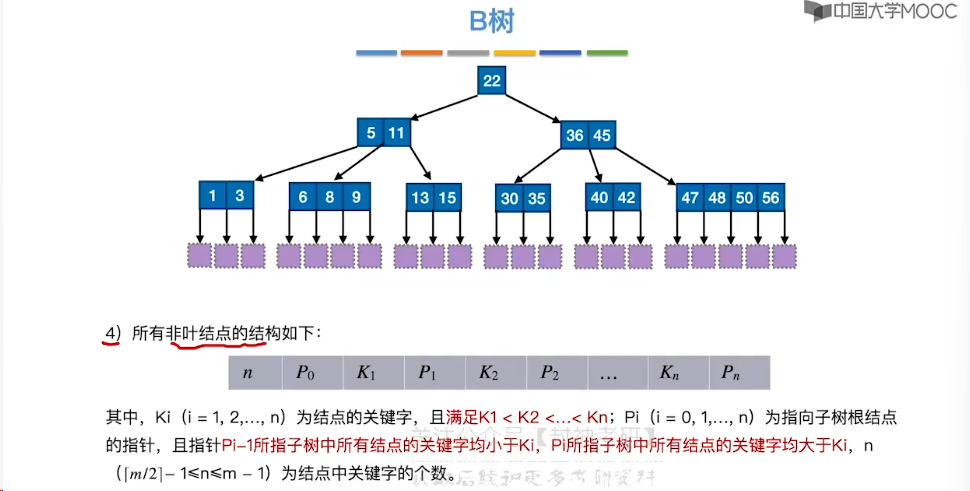

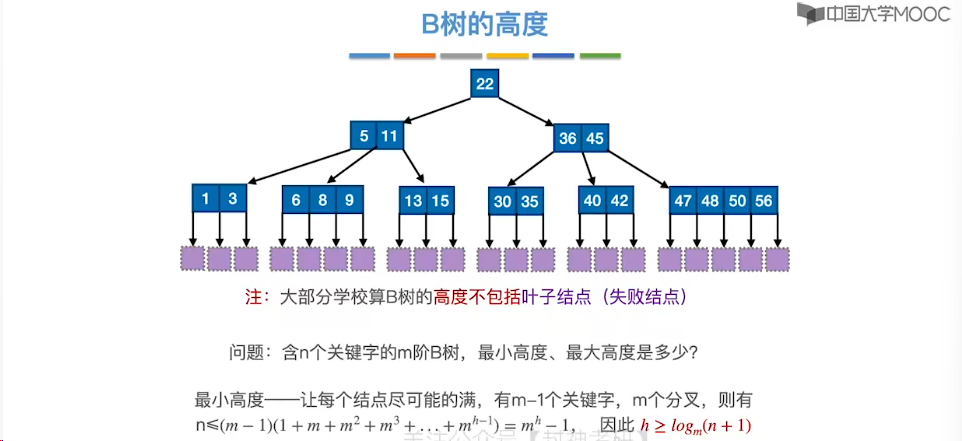

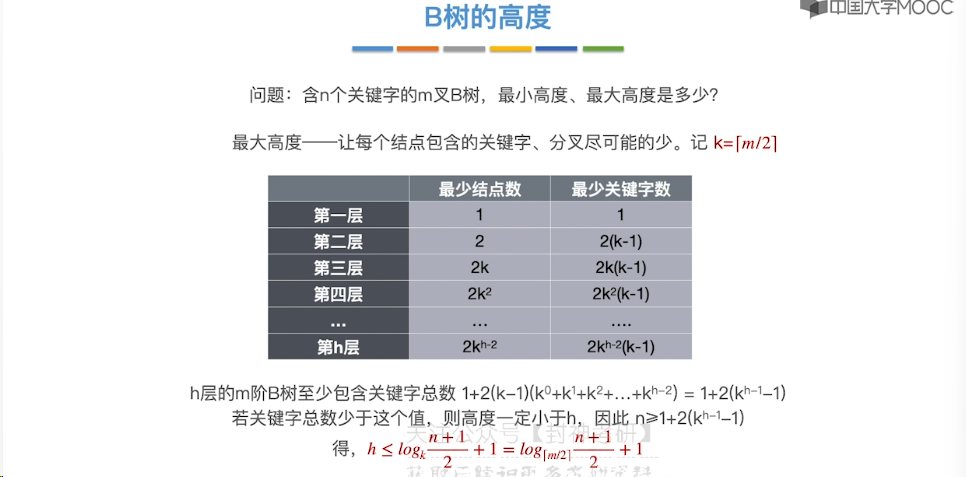
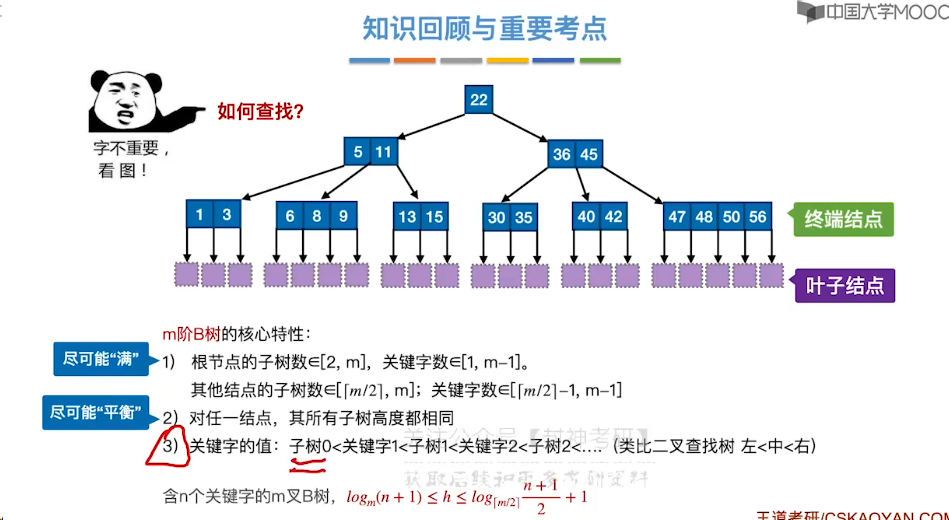
7.12、B 树的插入和删除
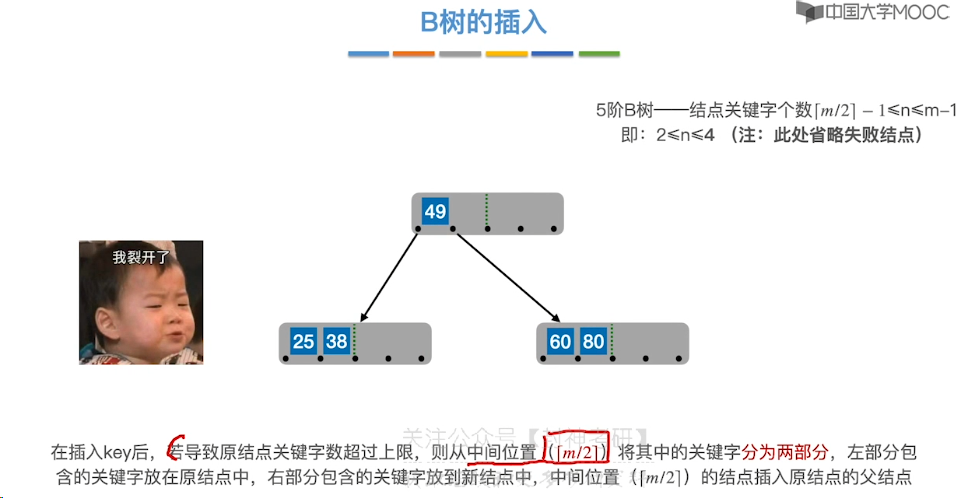
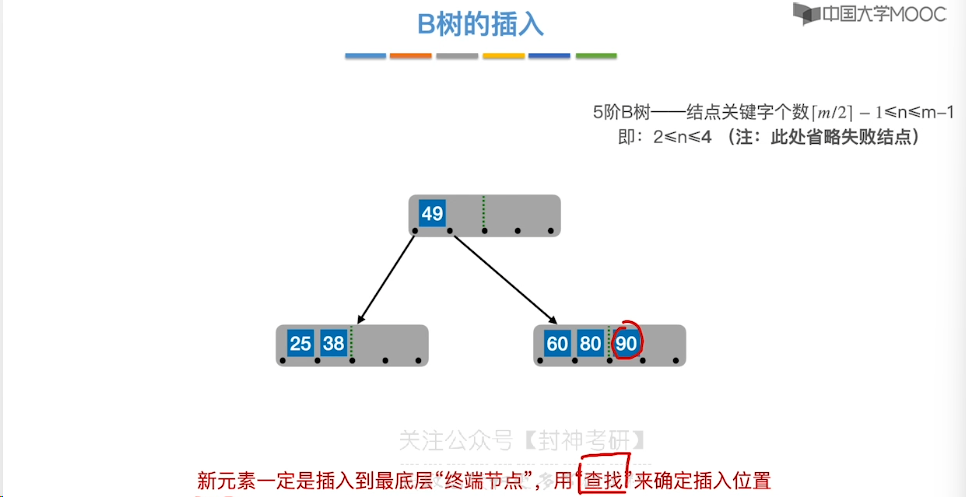
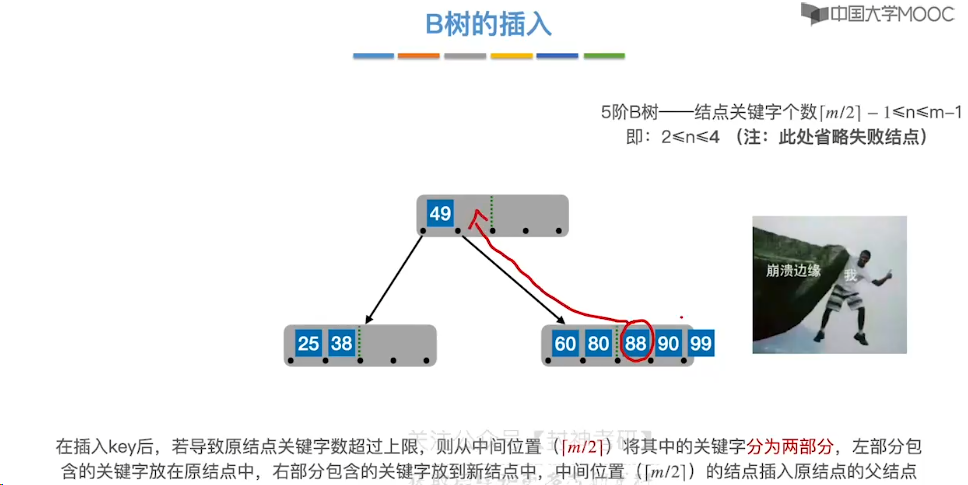
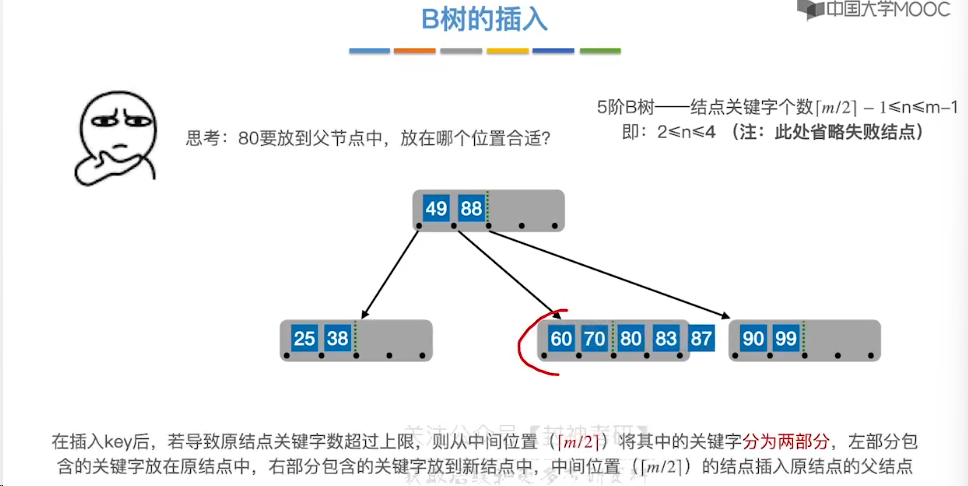
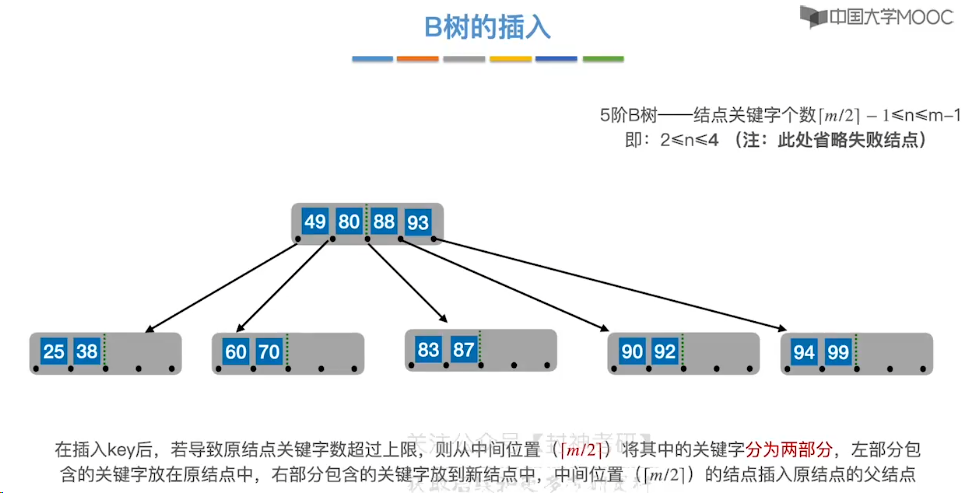
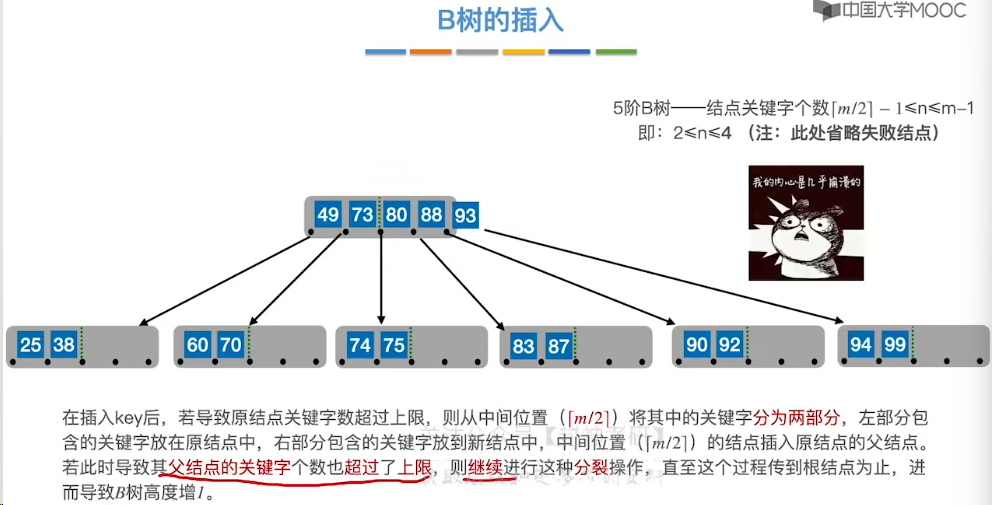
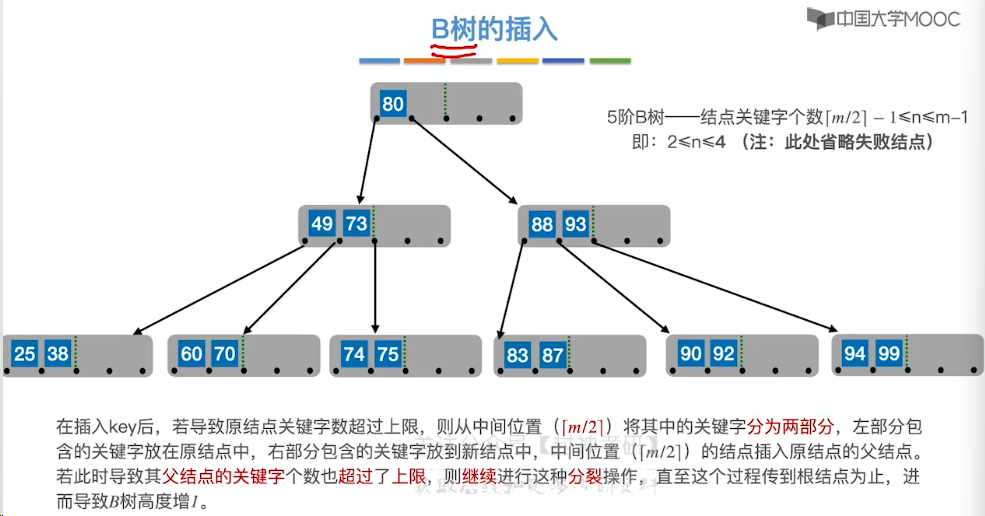

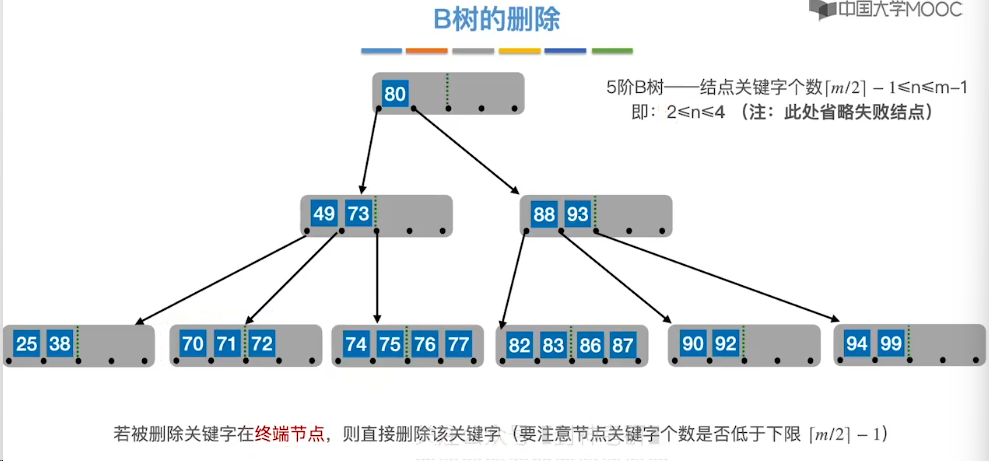
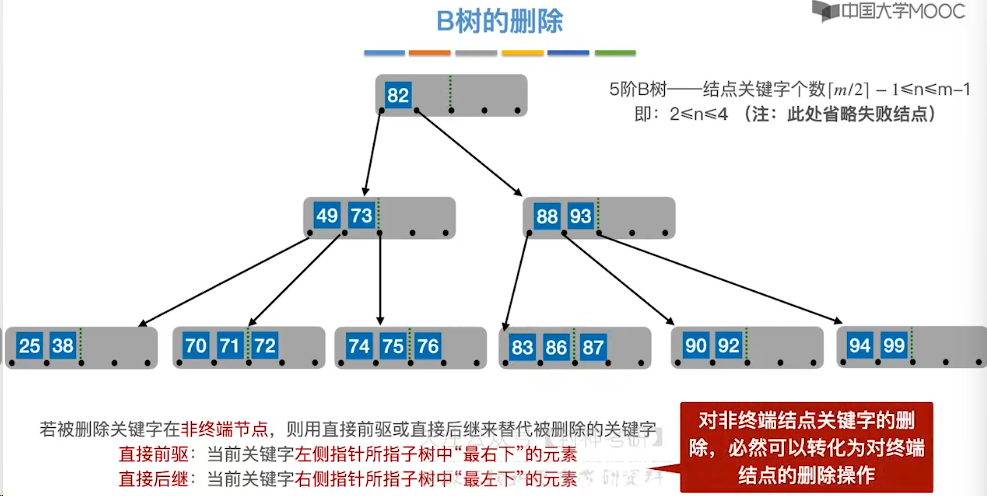
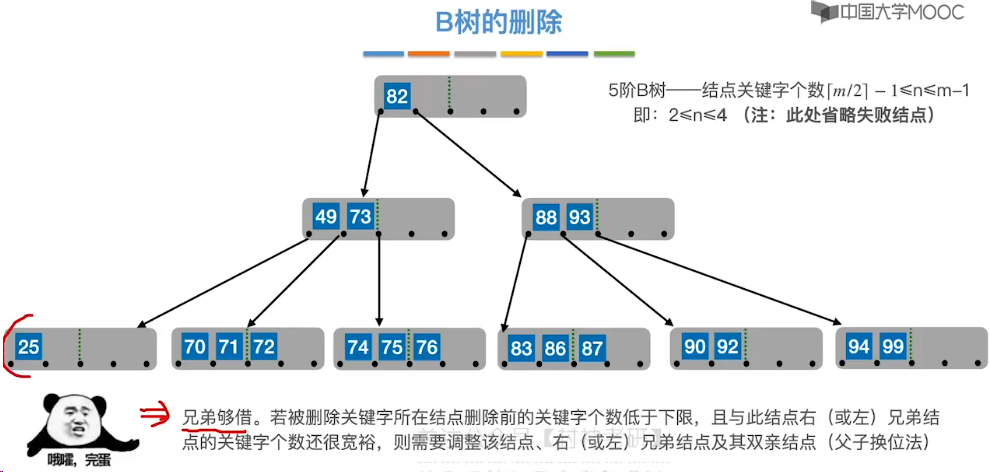
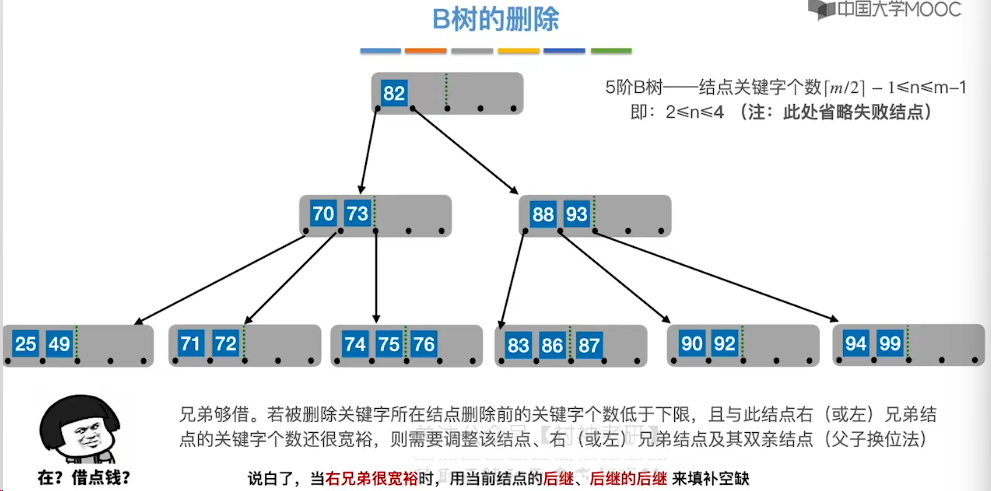
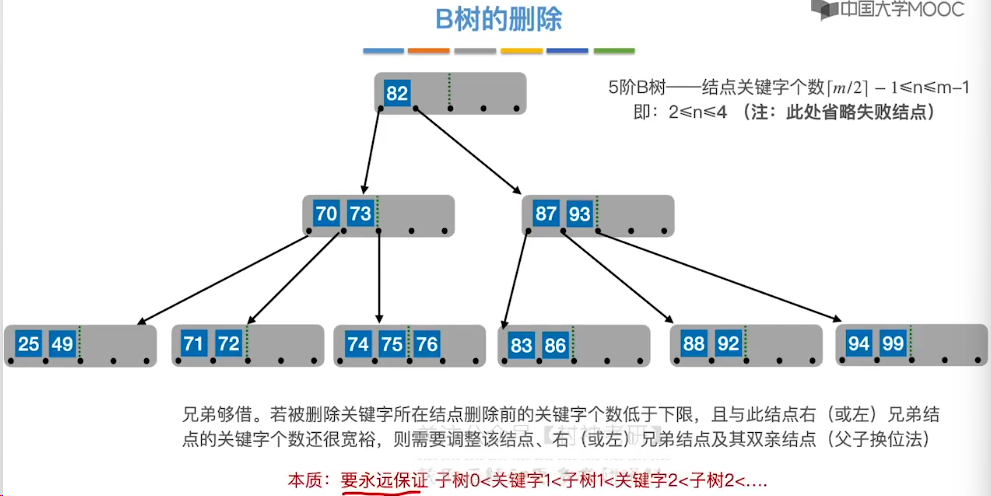
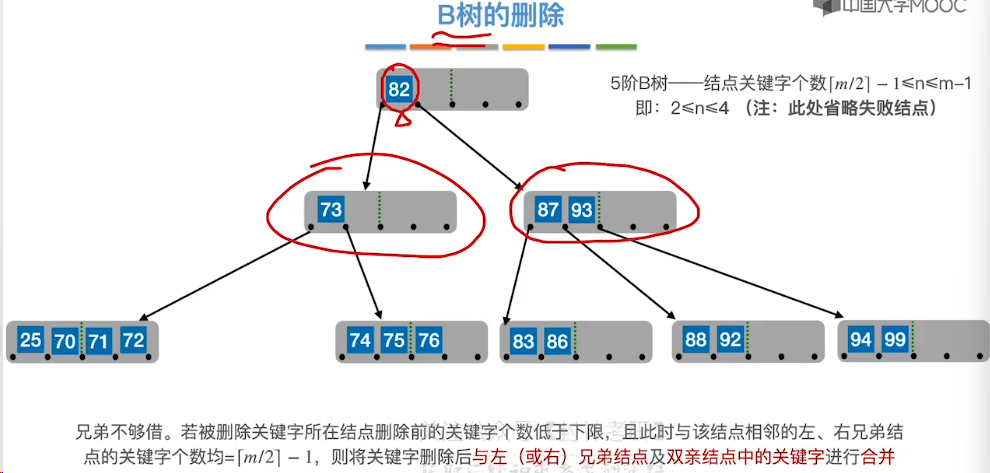
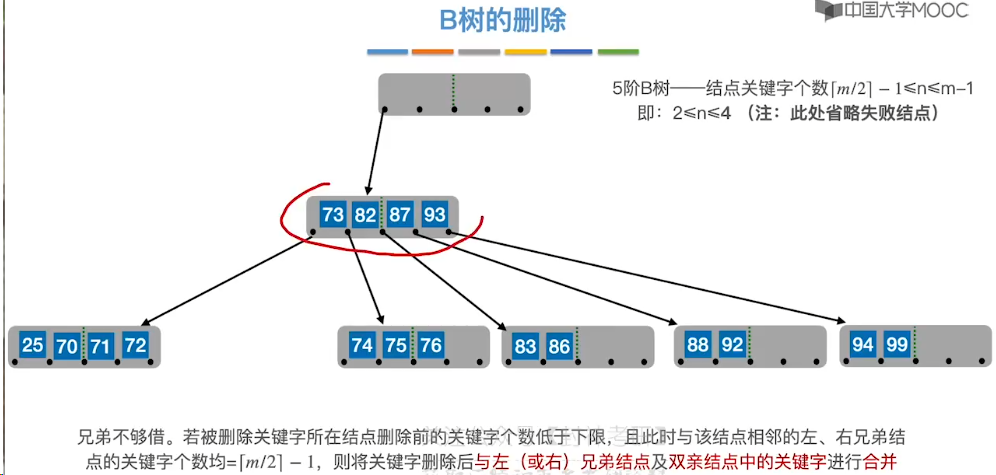
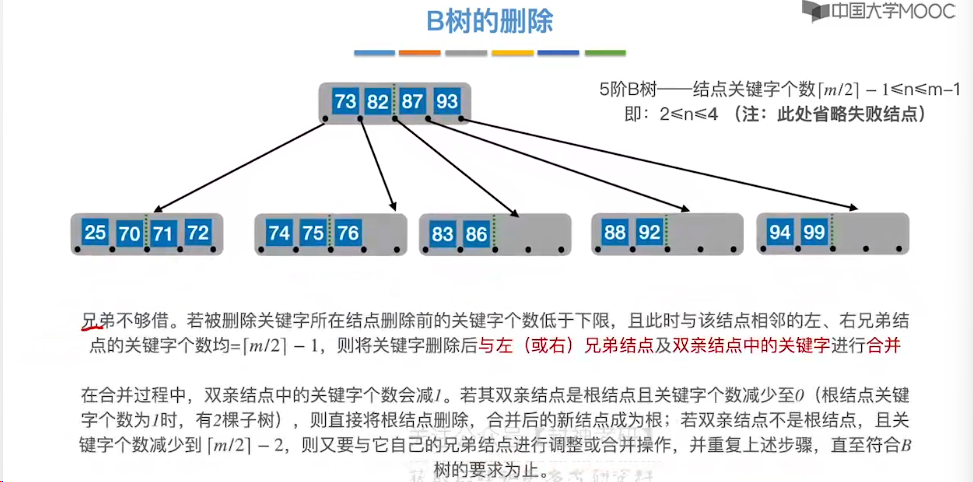
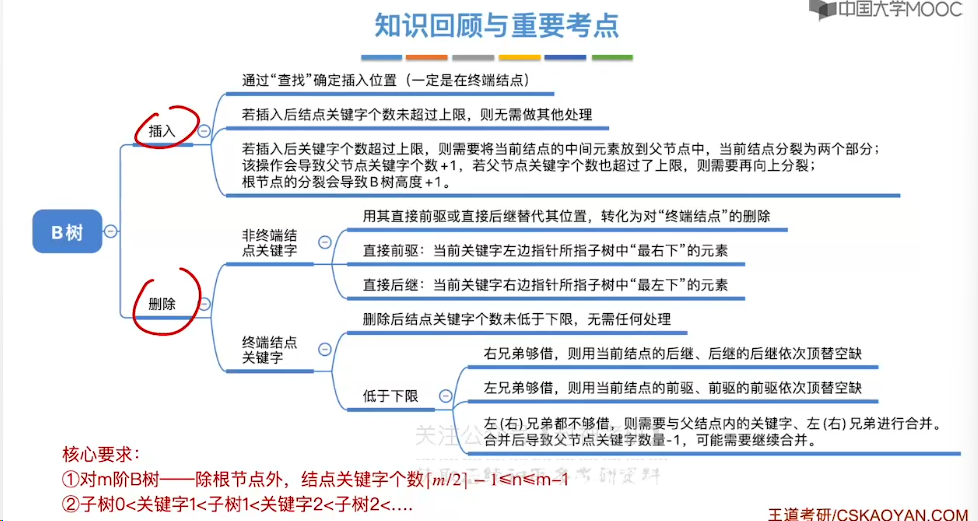
7.14、B+ 树
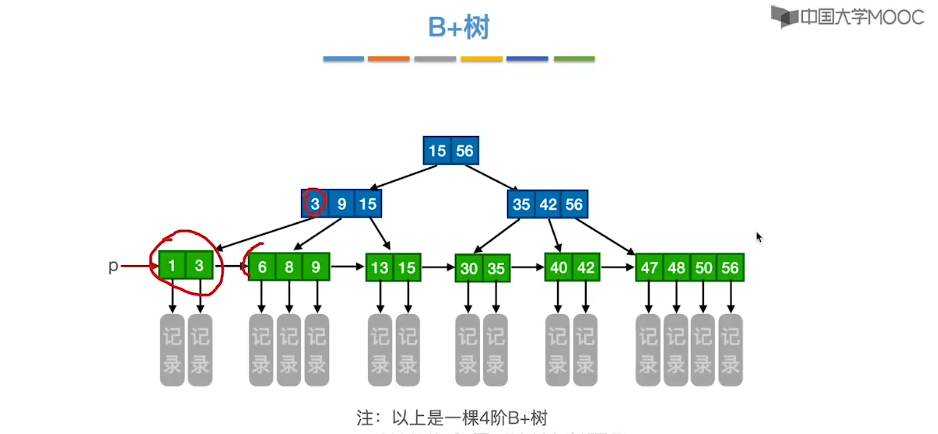
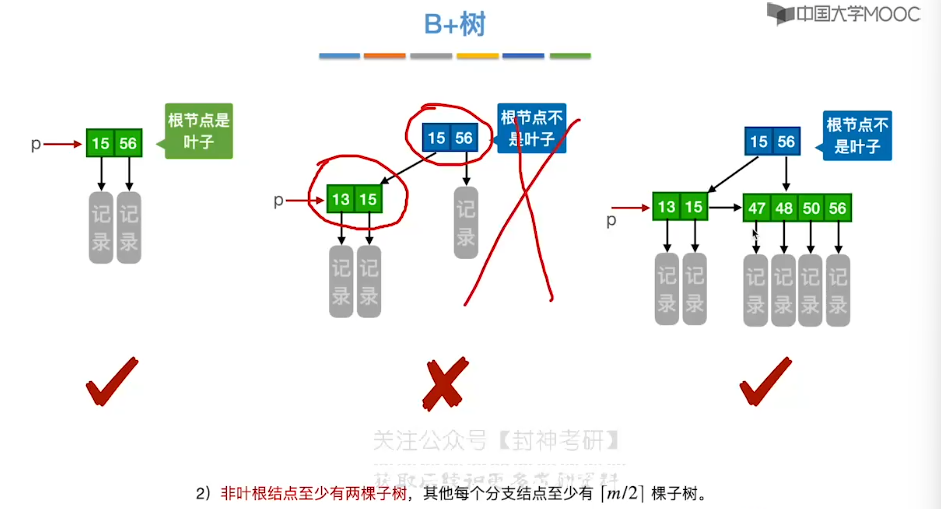
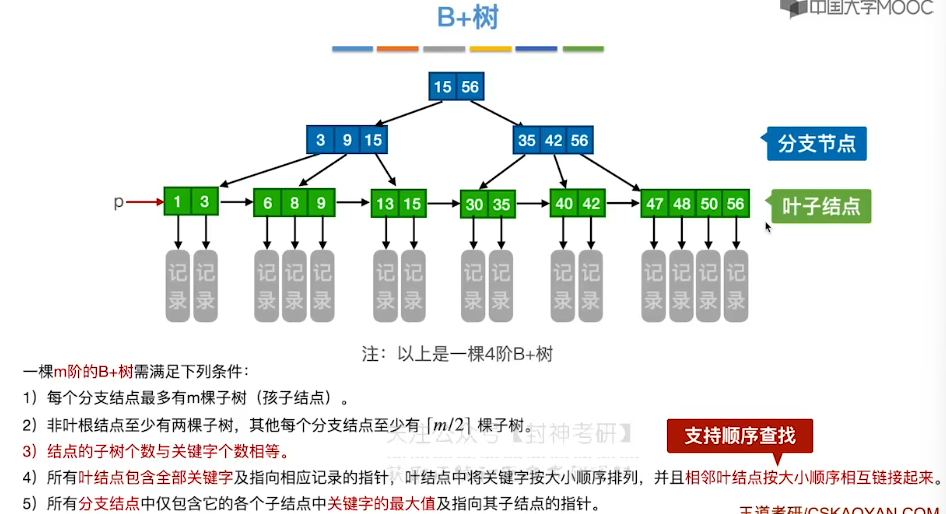
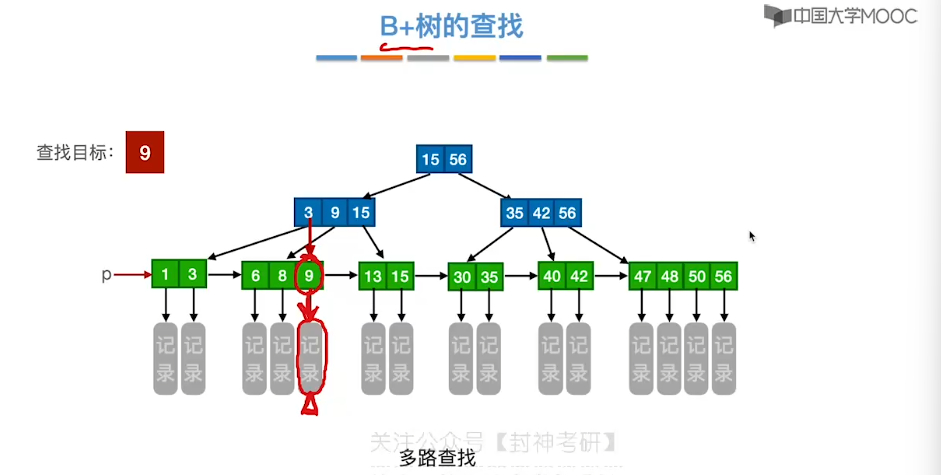
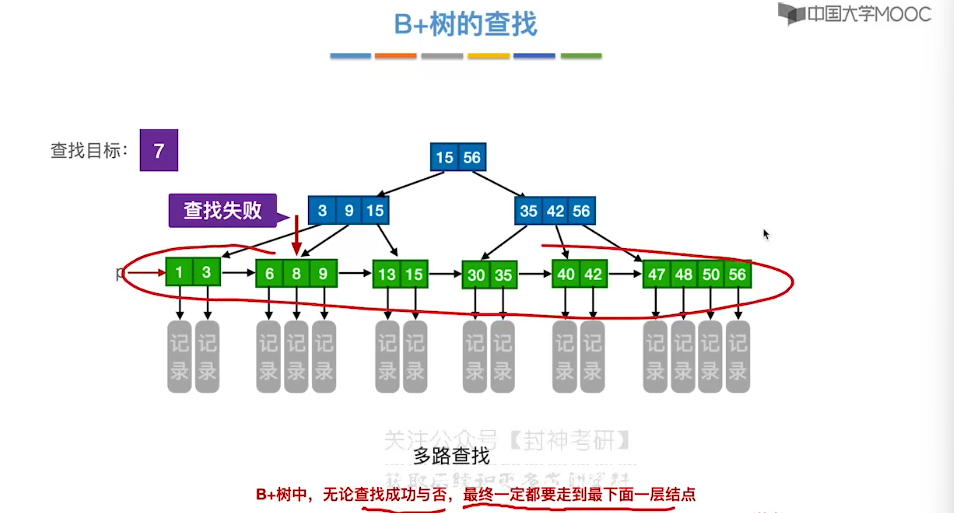
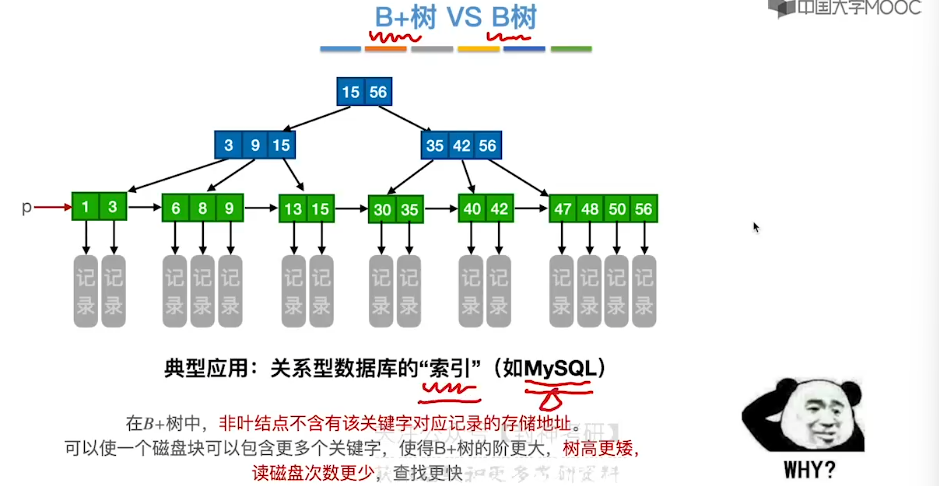
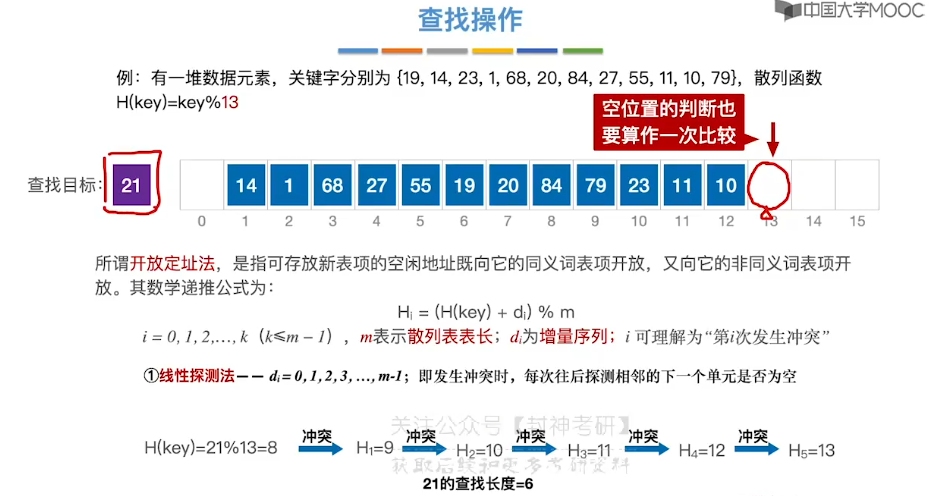
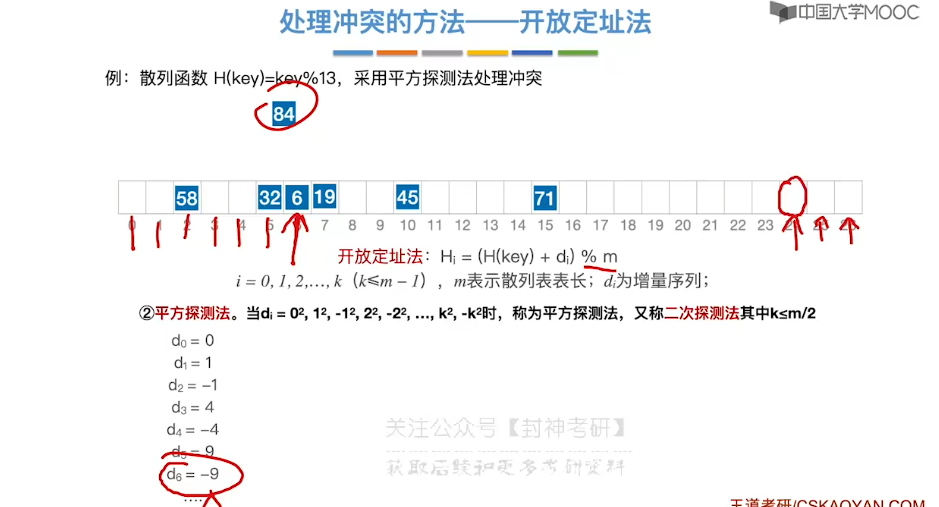
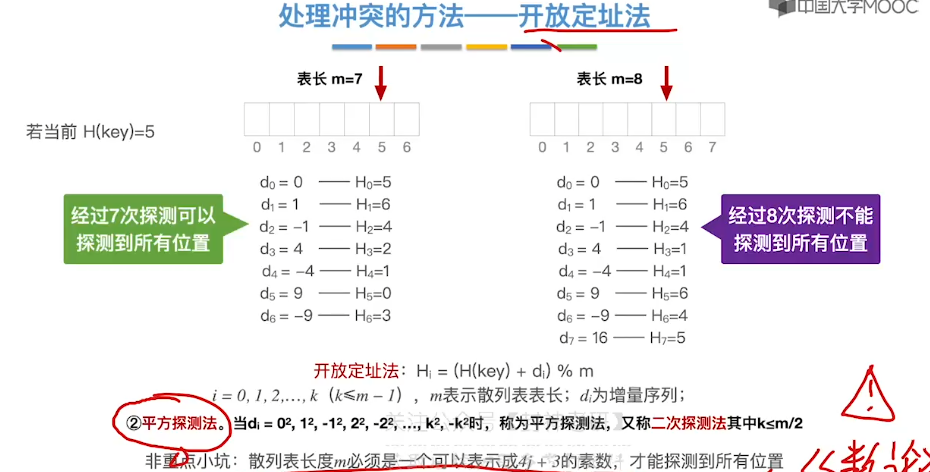
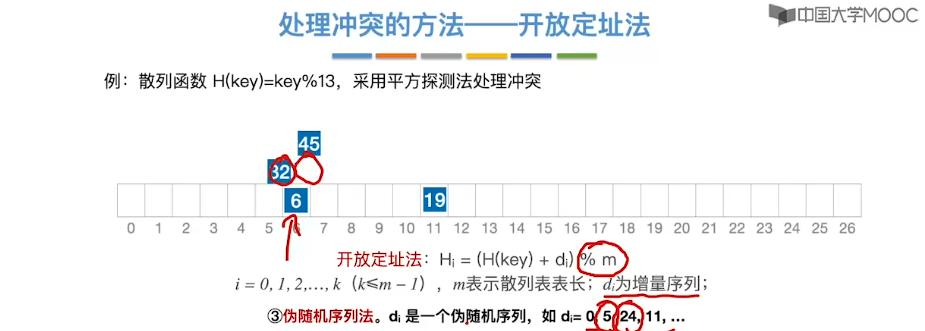
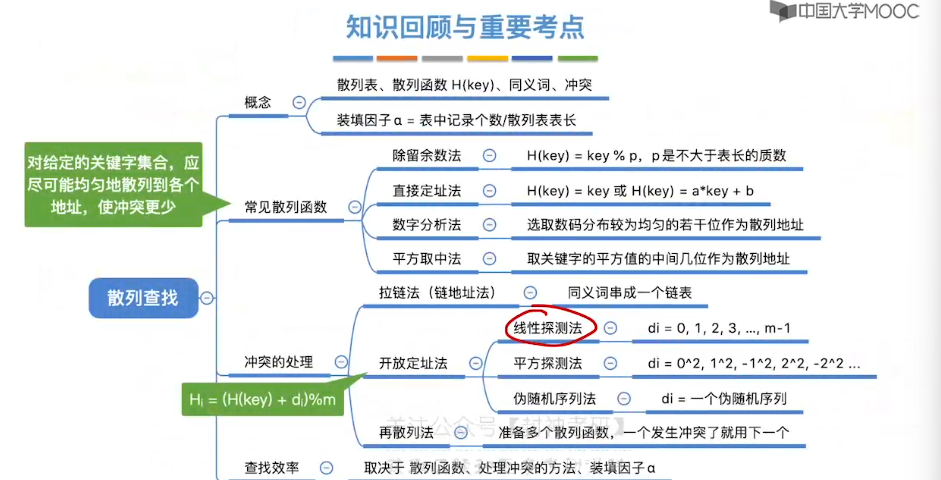
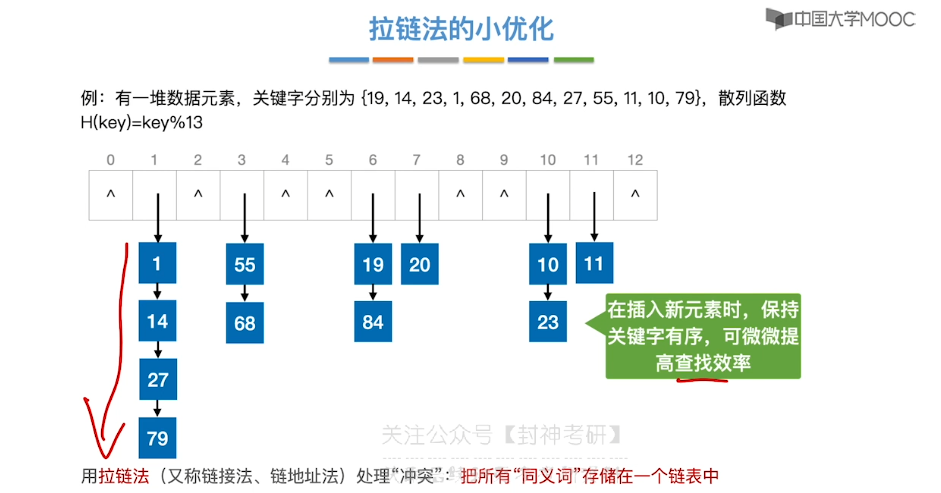
7.15、散列查找

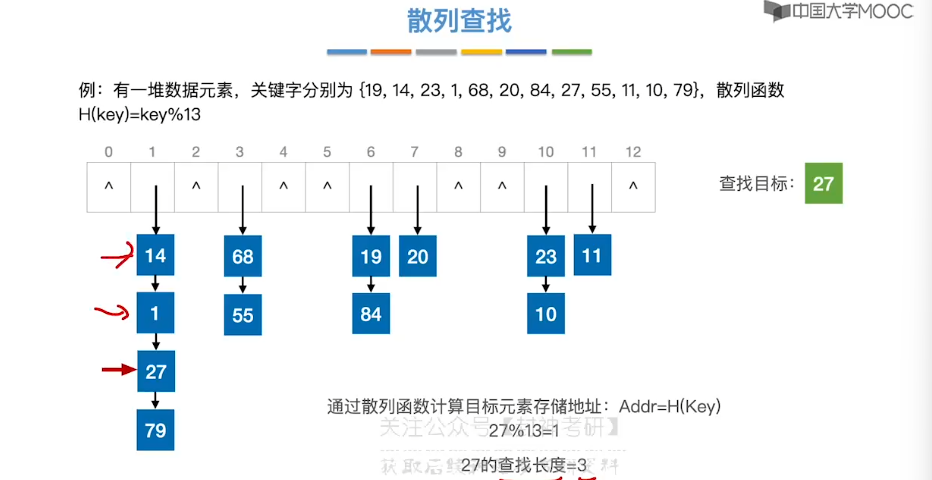
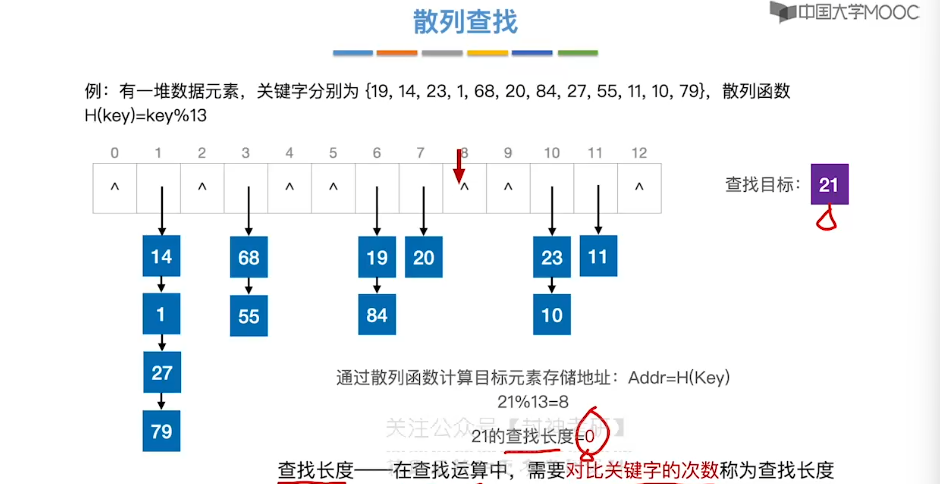
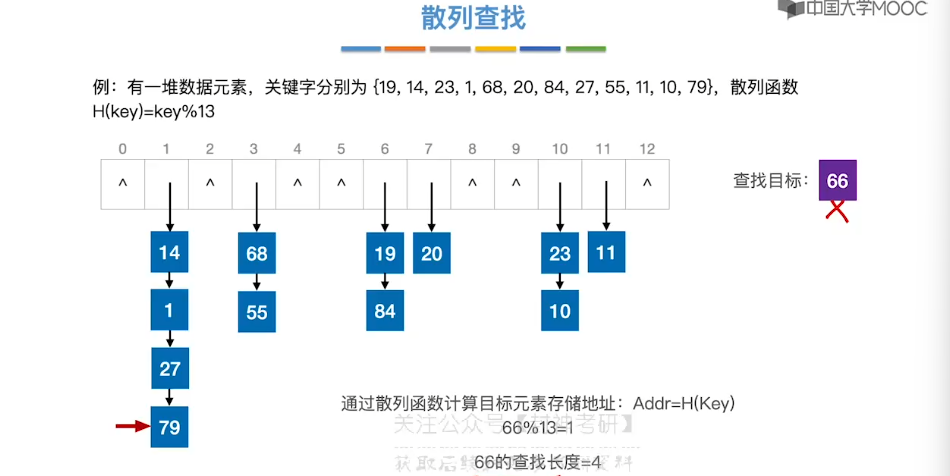
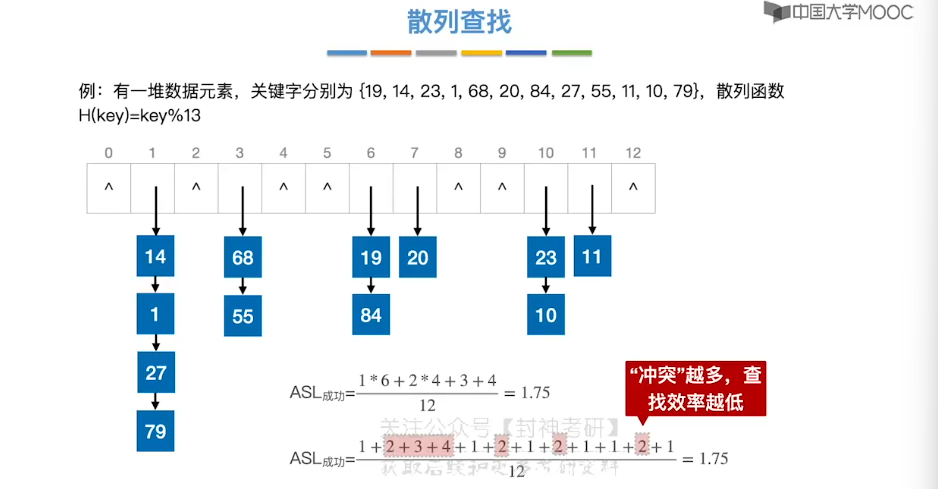
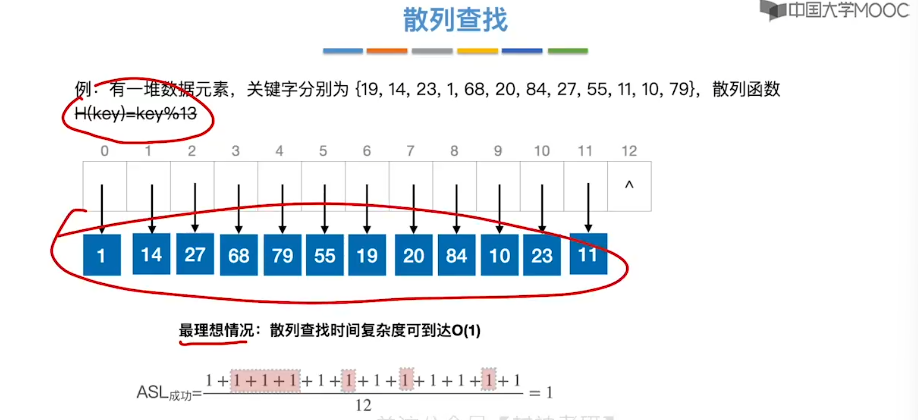
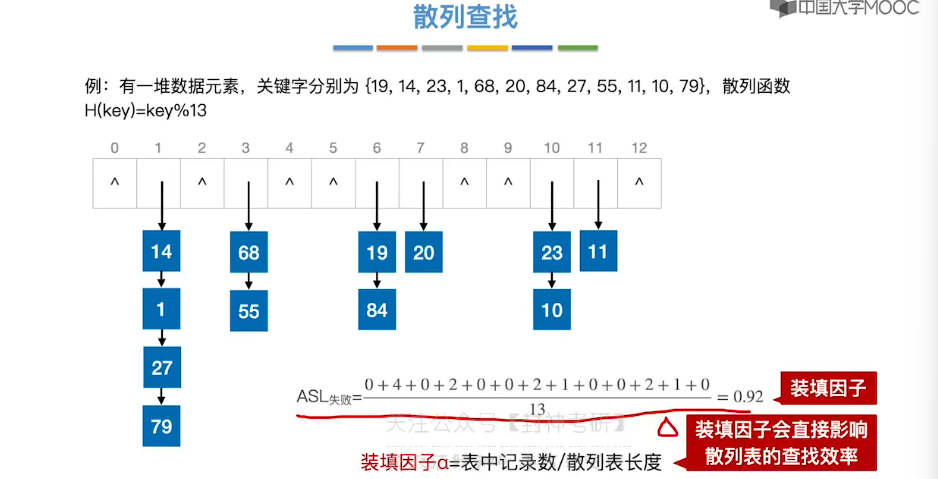

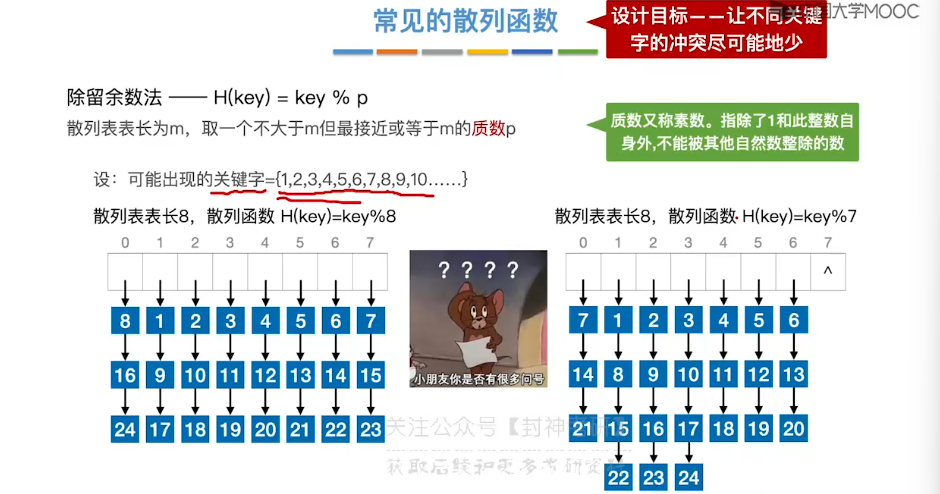
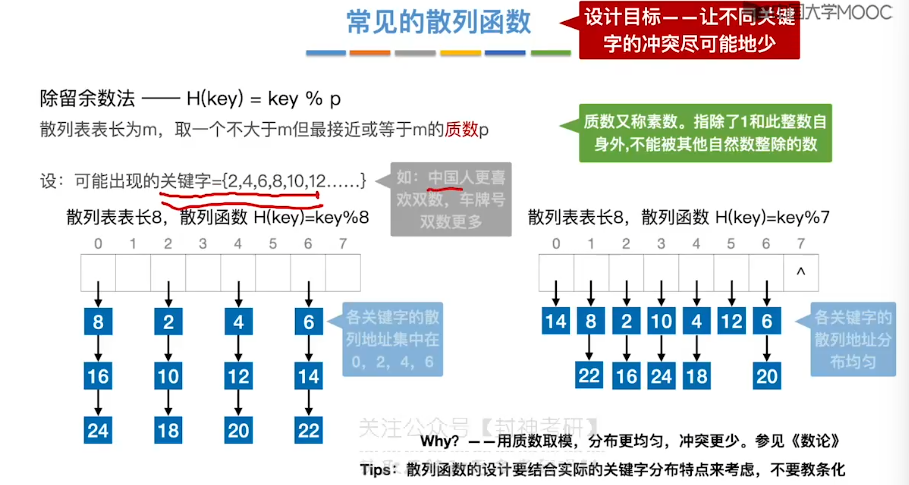

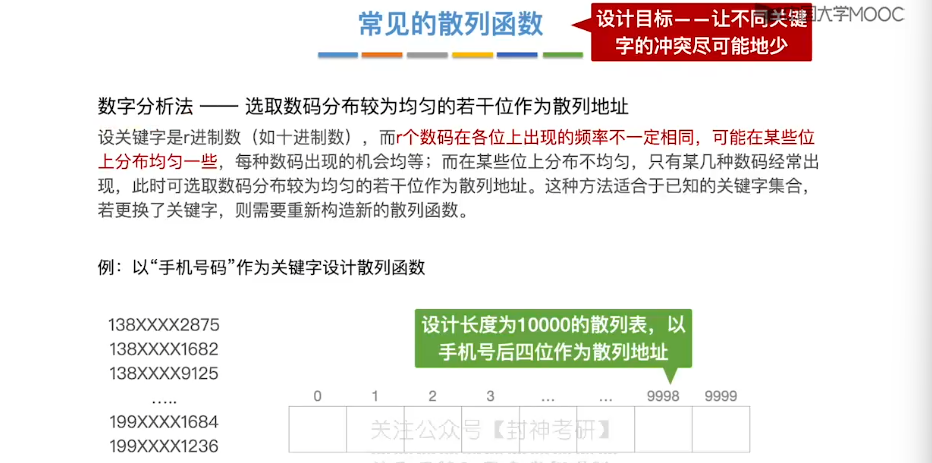
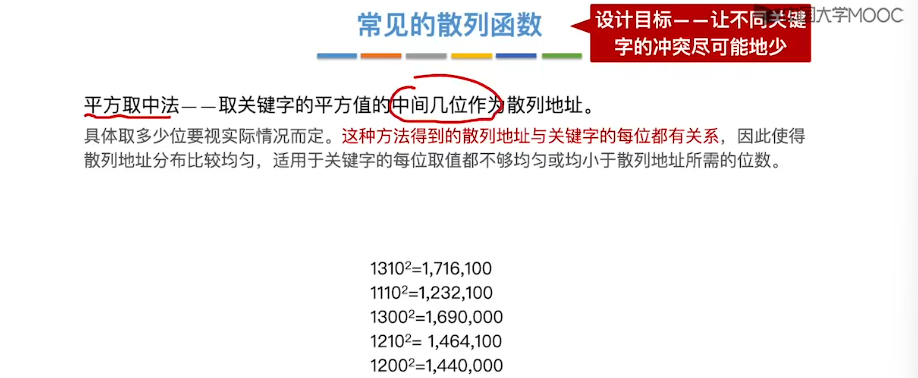
















8、排序
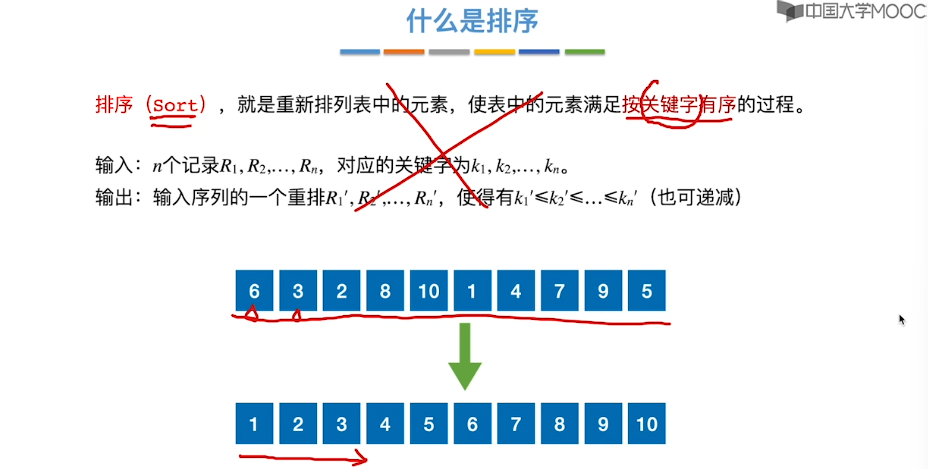
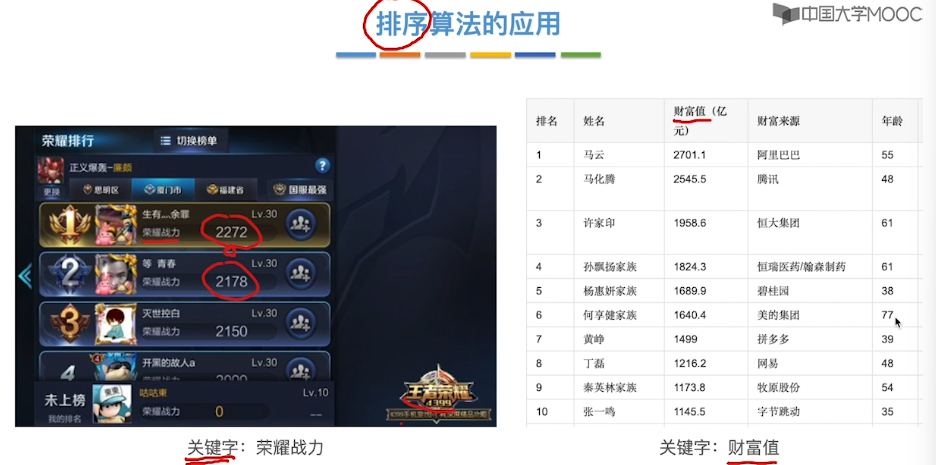
8.1、排序的基本概念
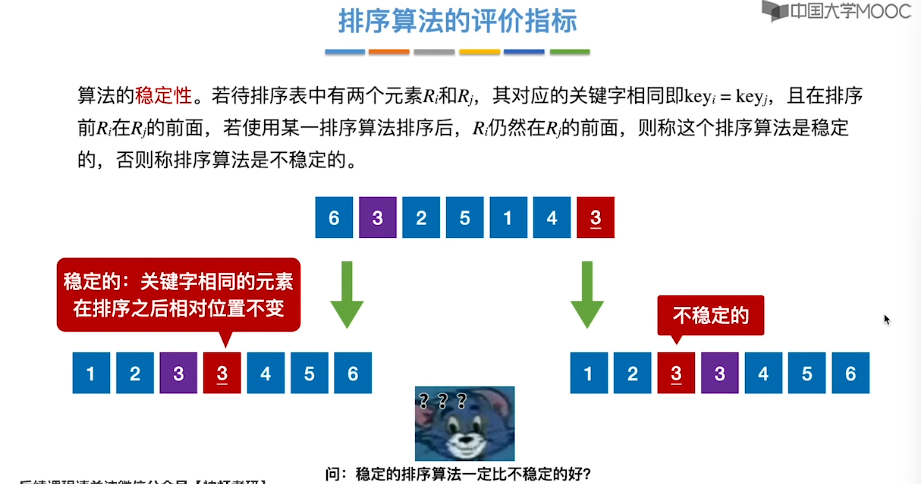
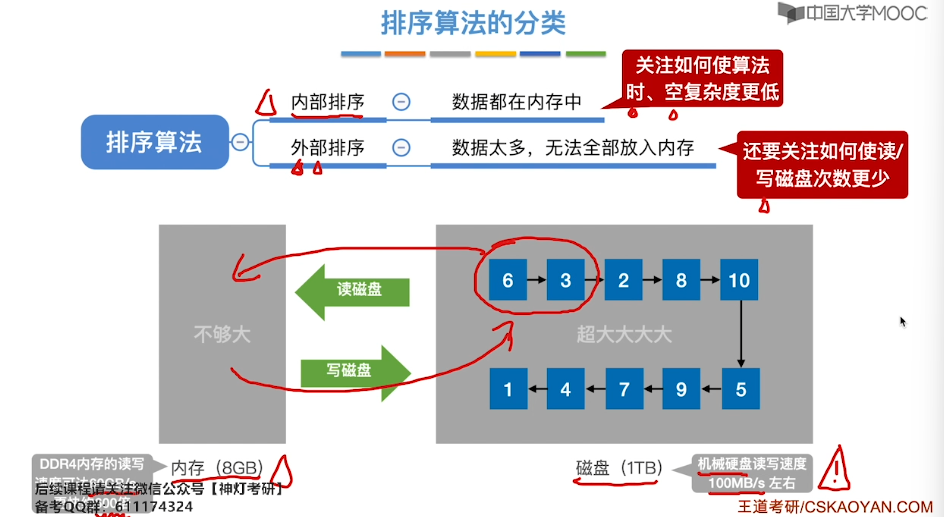
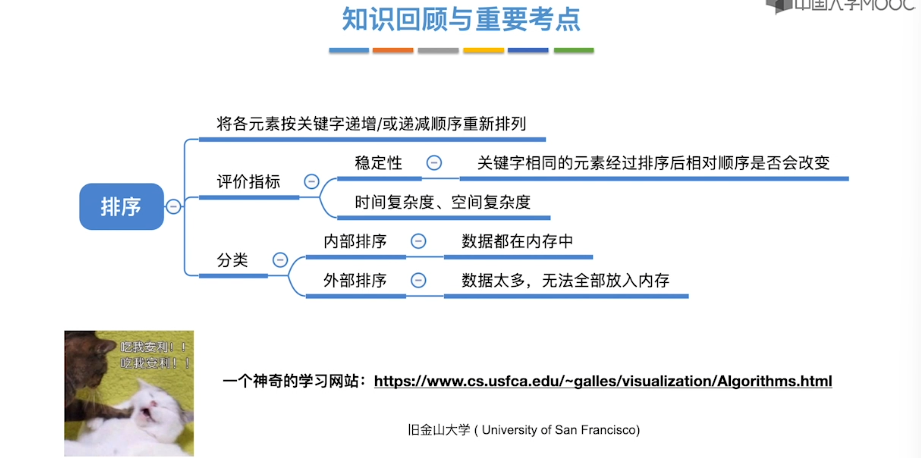
8.2、插入排序






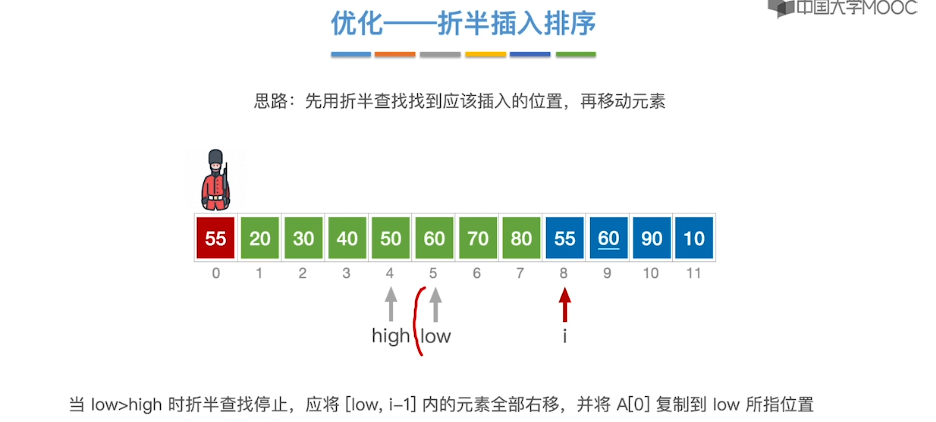
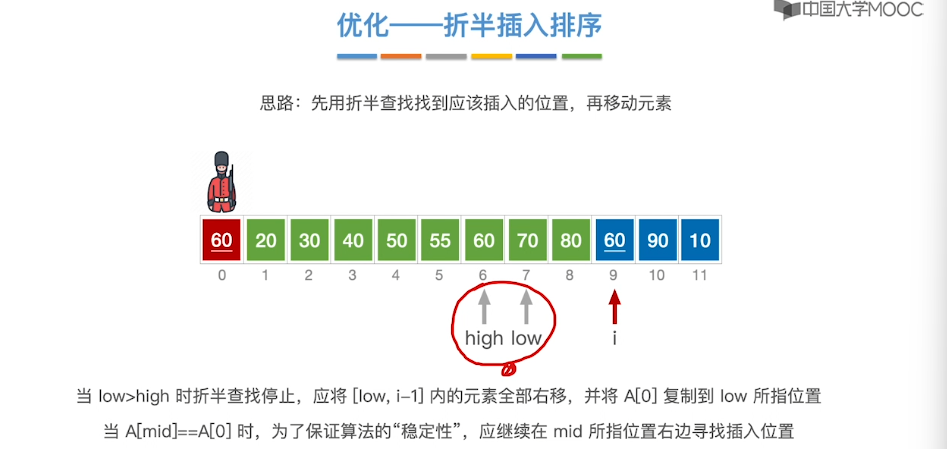

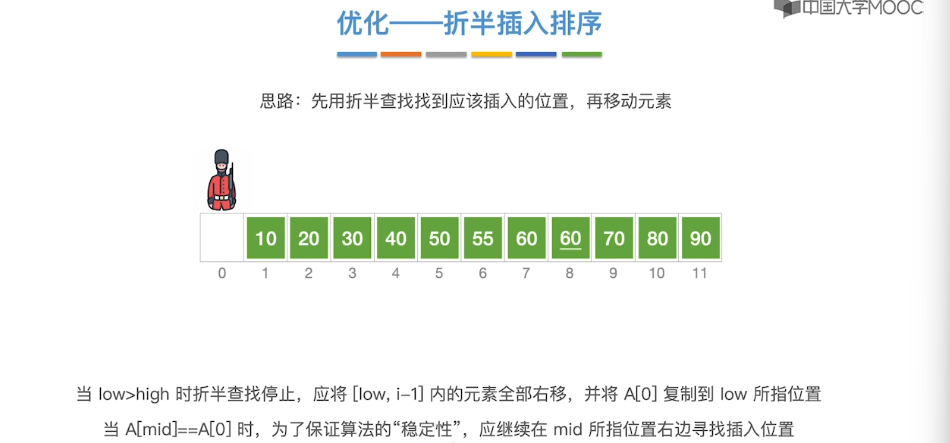

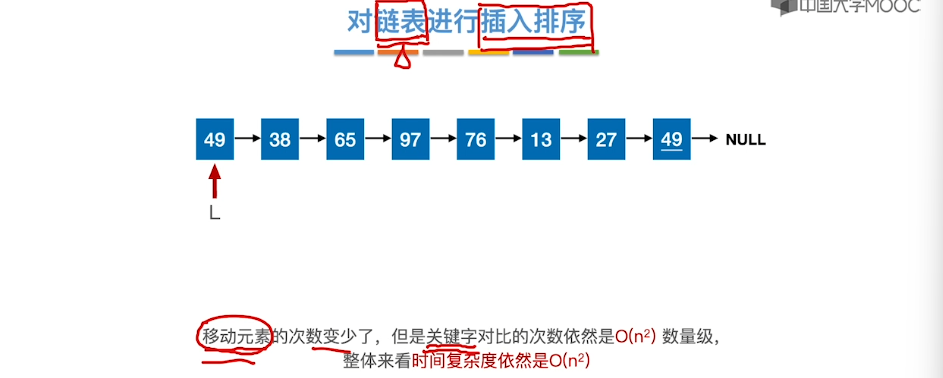
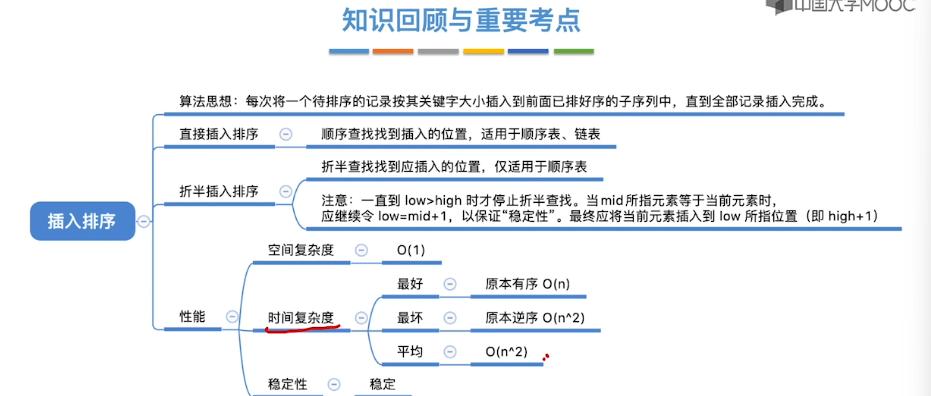
8.3、希尔排序
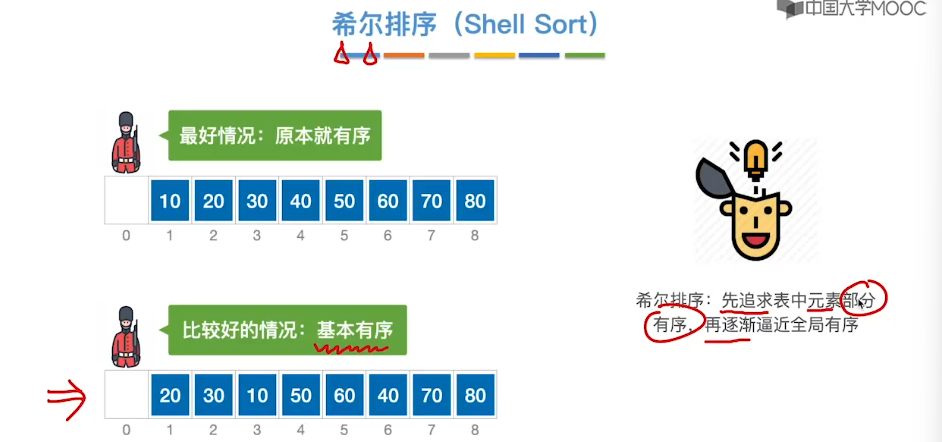
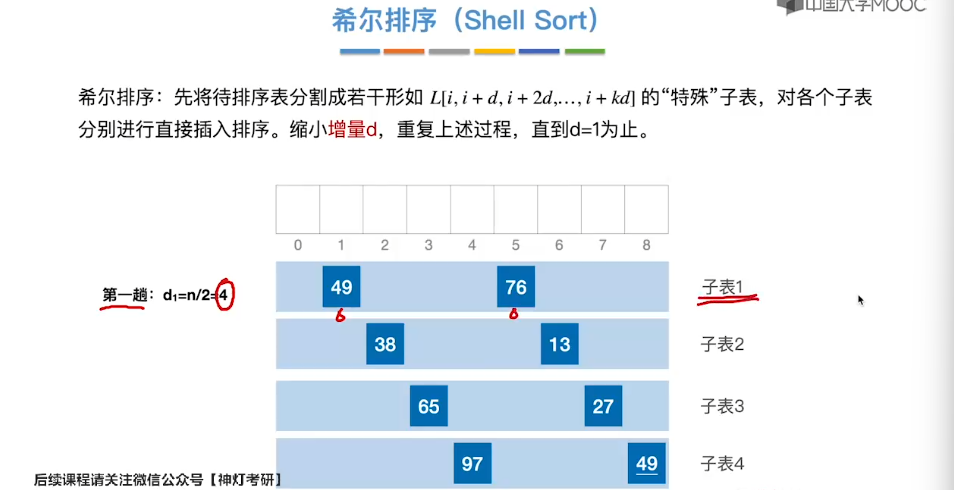
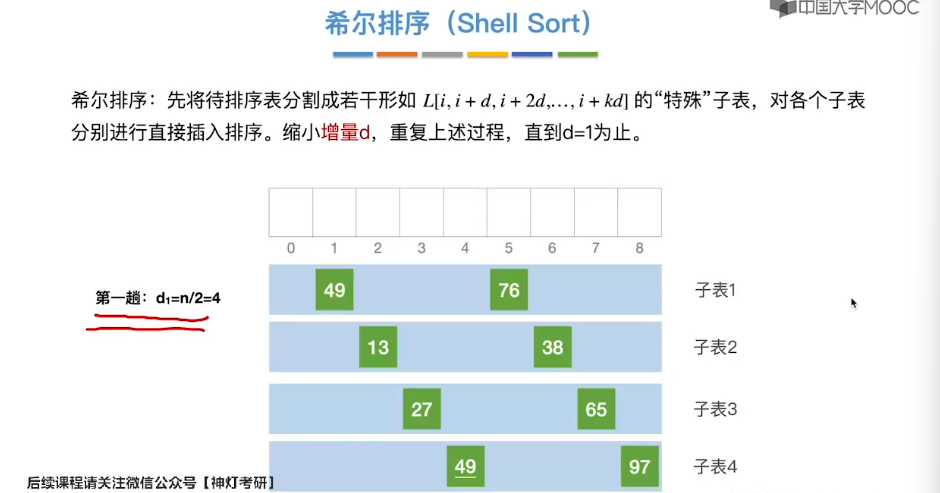



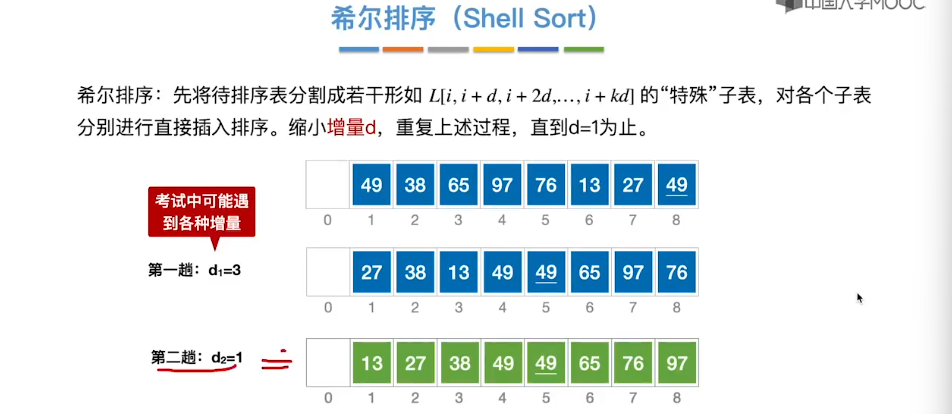

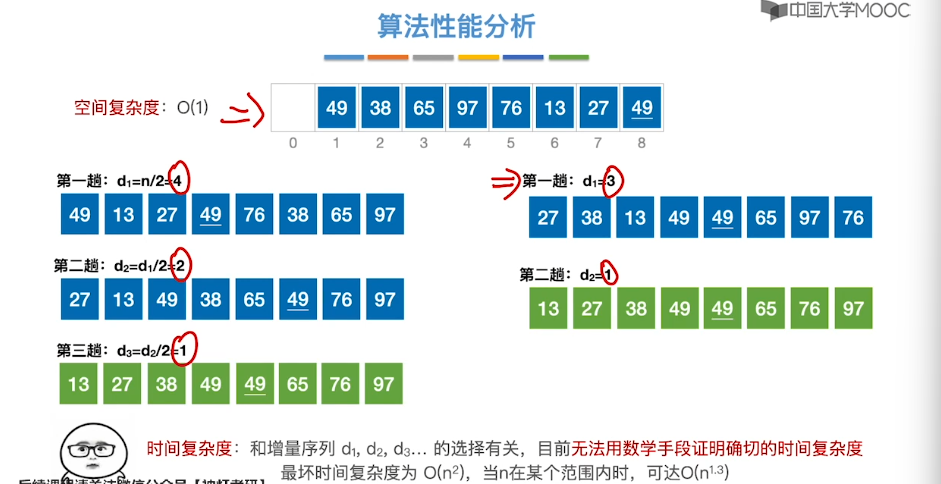
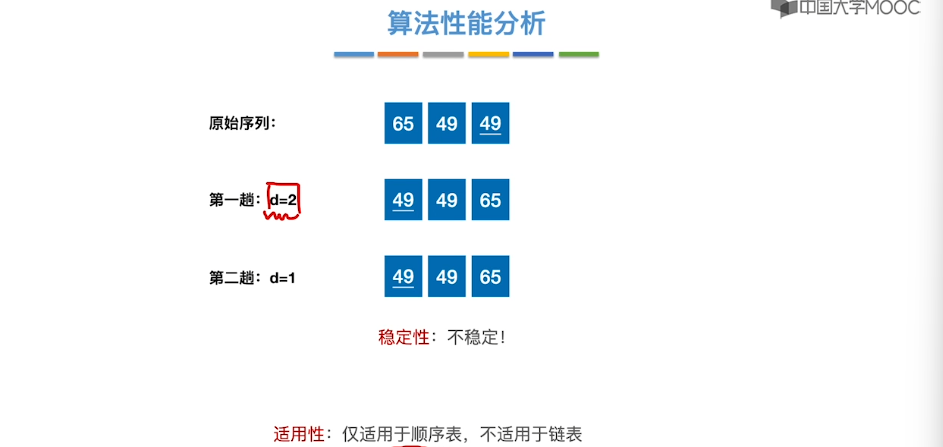
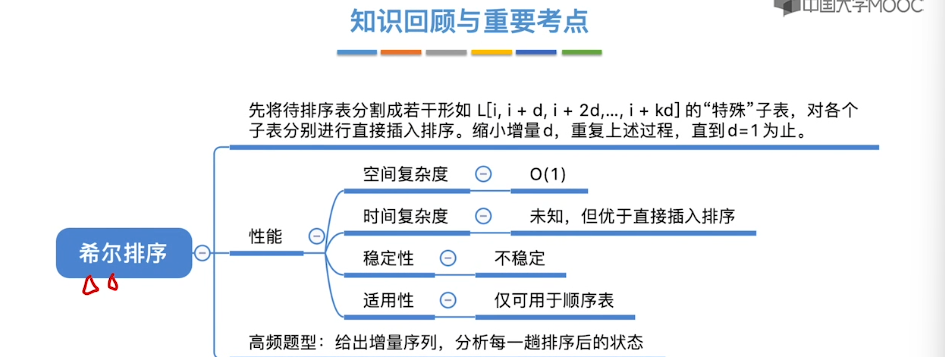
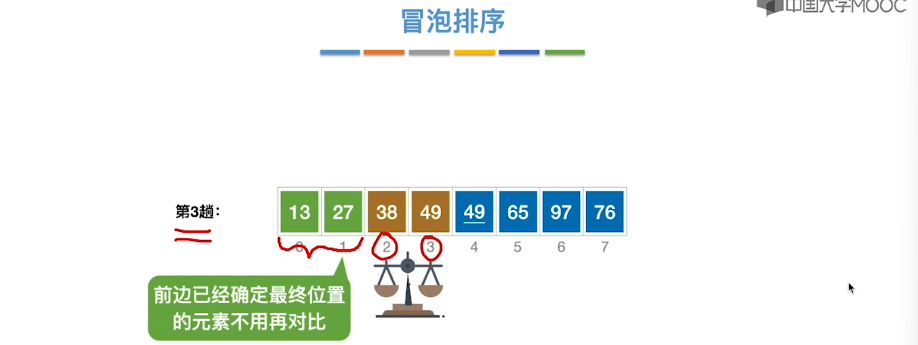
8.4、冒泡排序





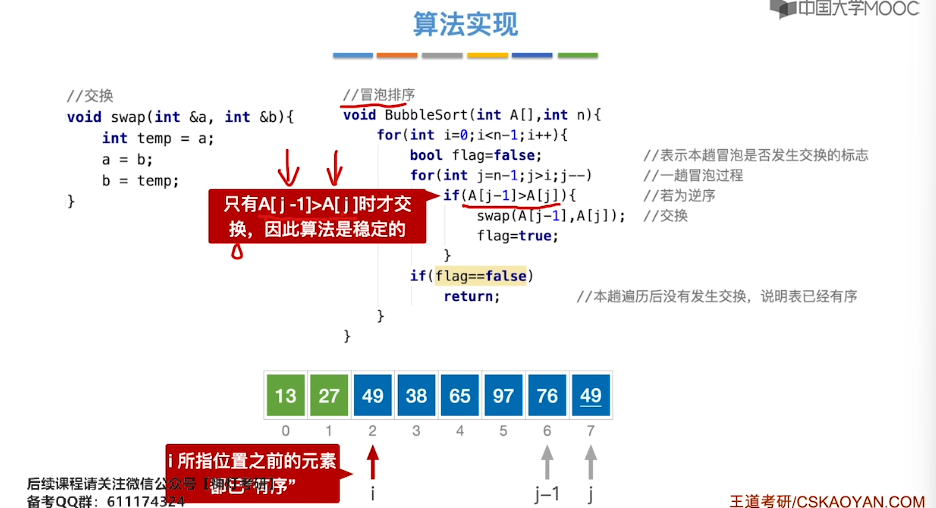
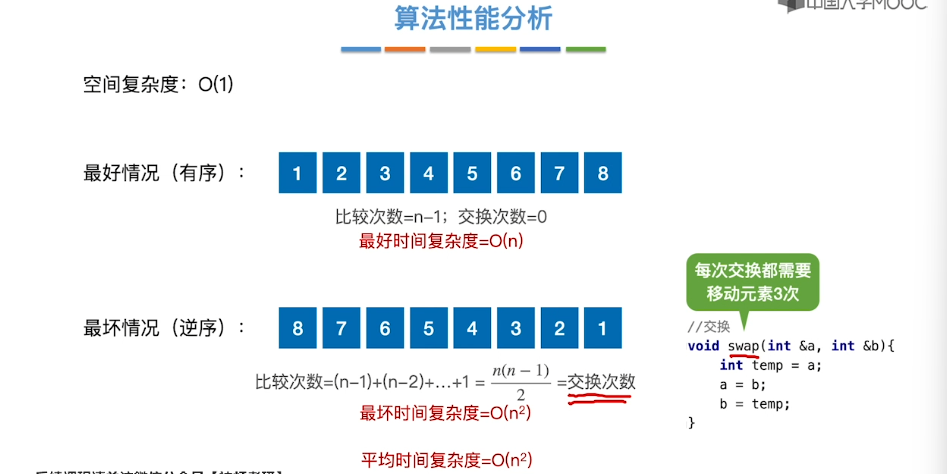
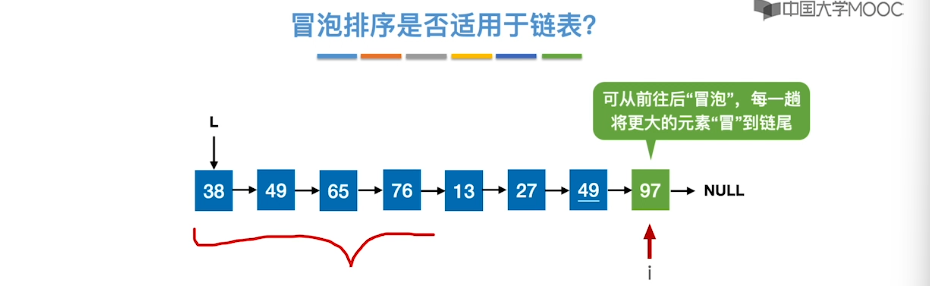
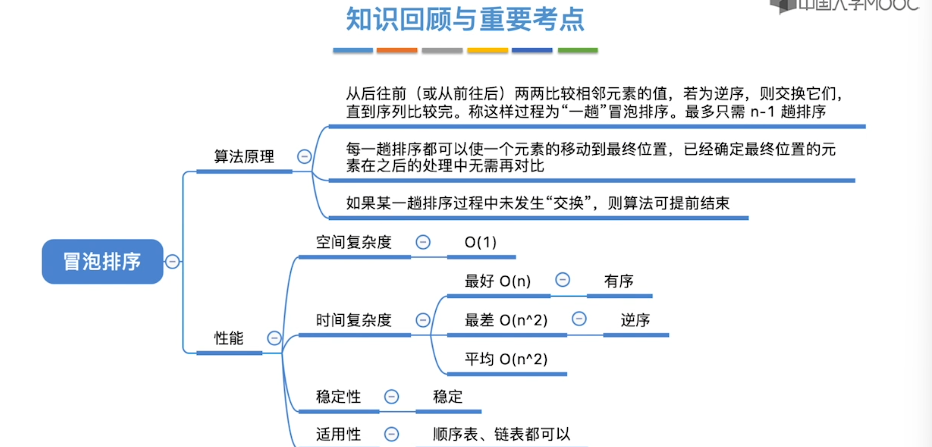
8.5、快速排序
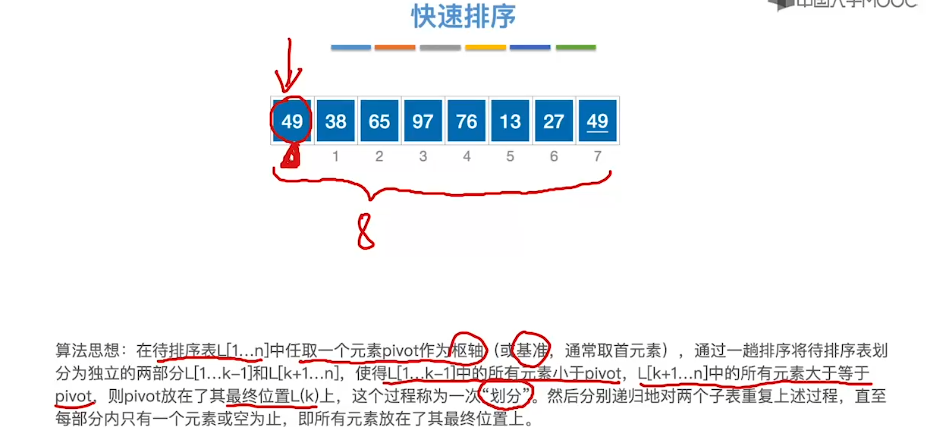
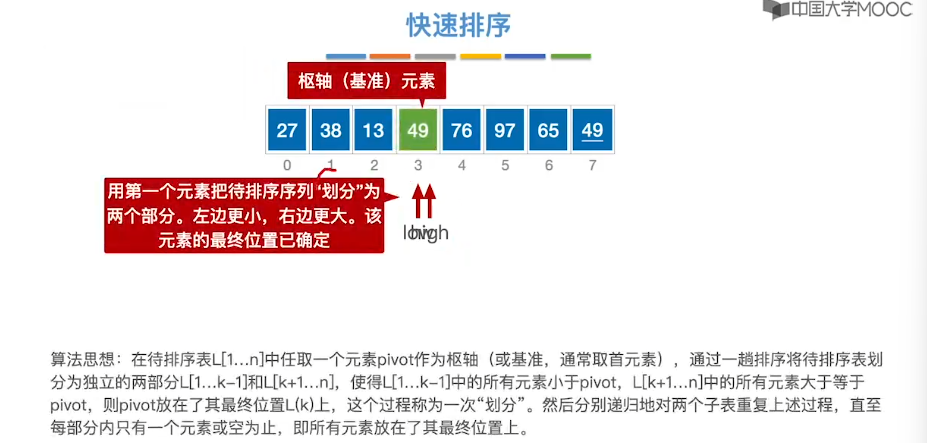

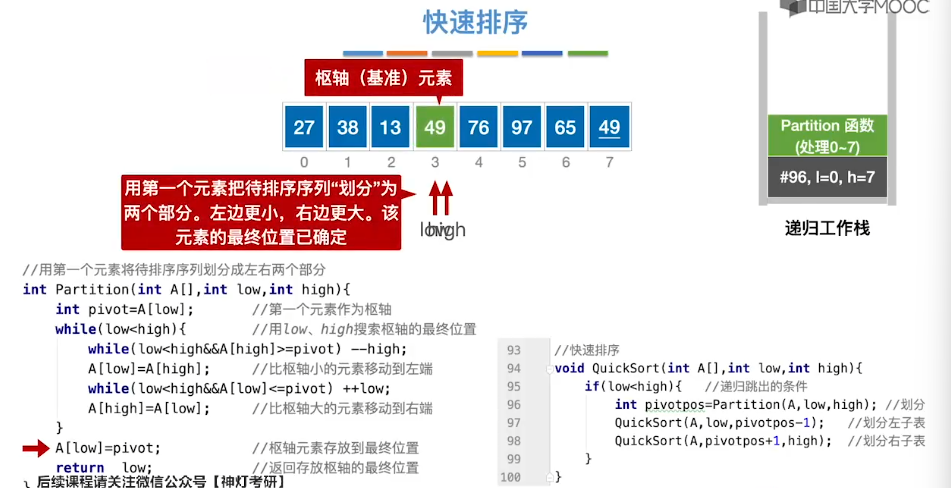

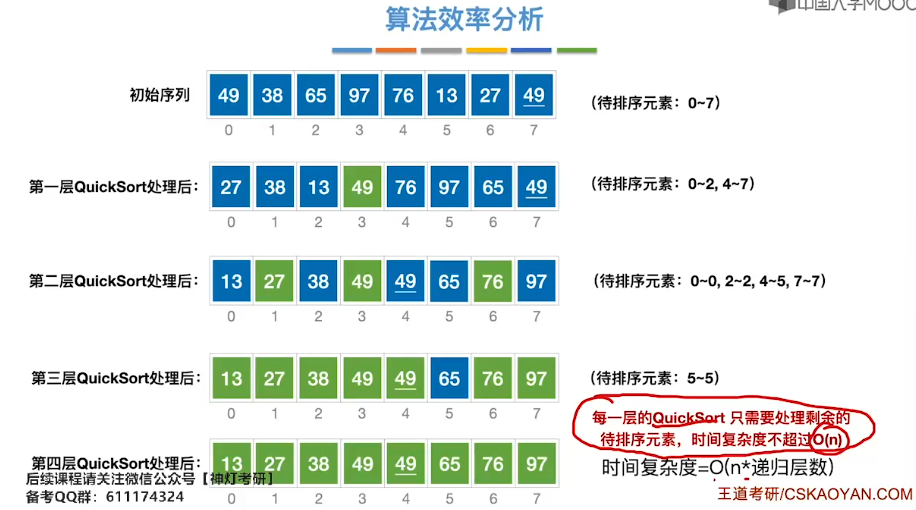
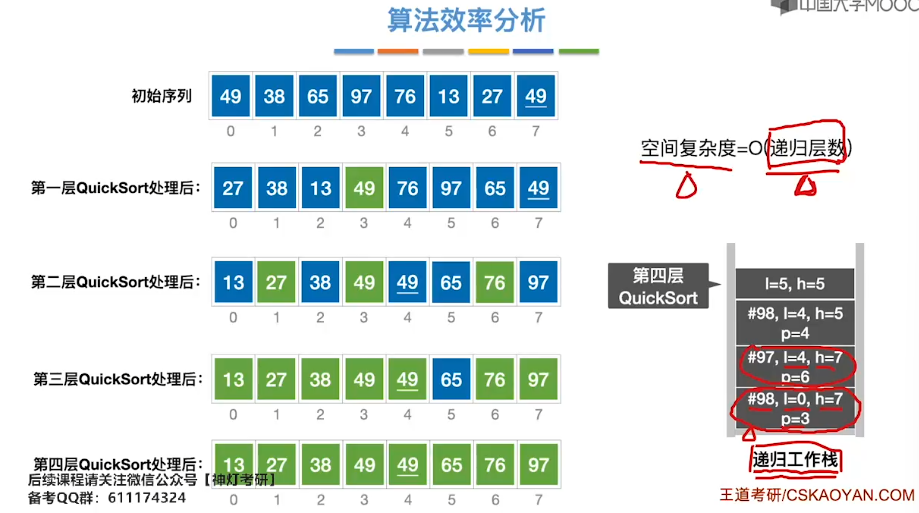


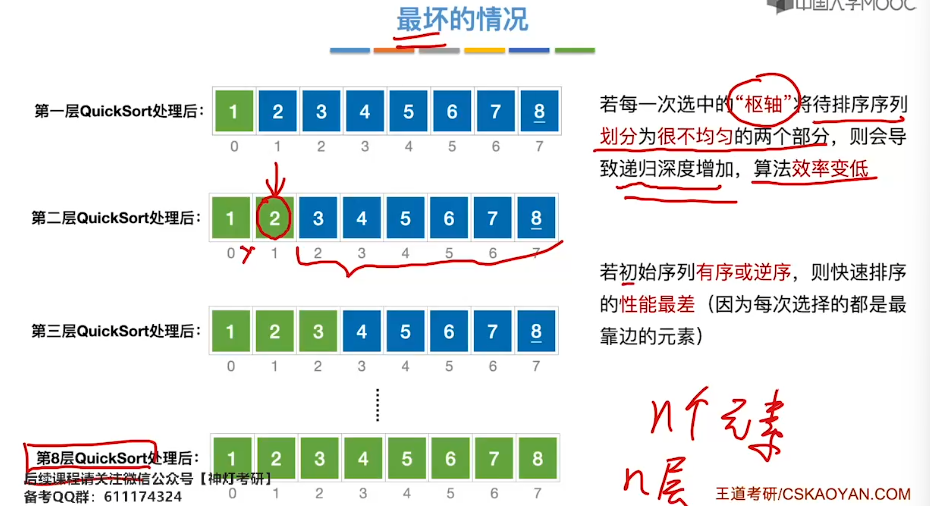

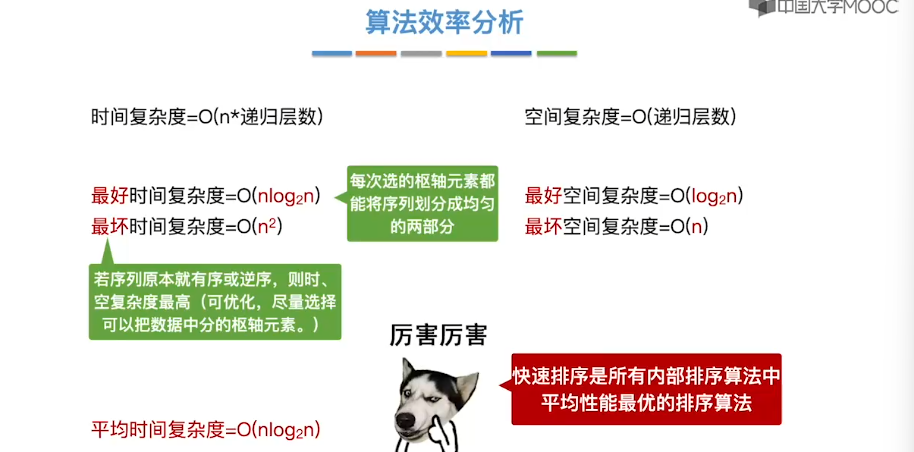
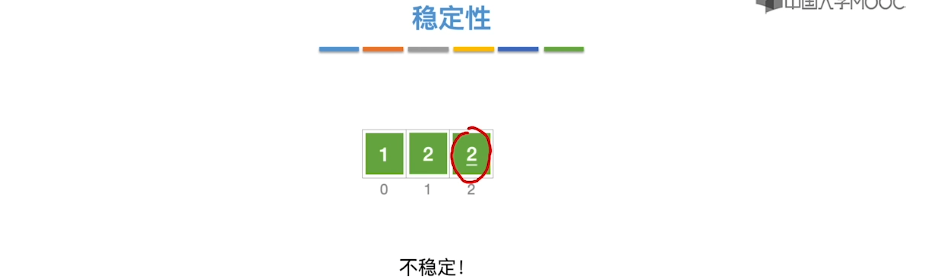
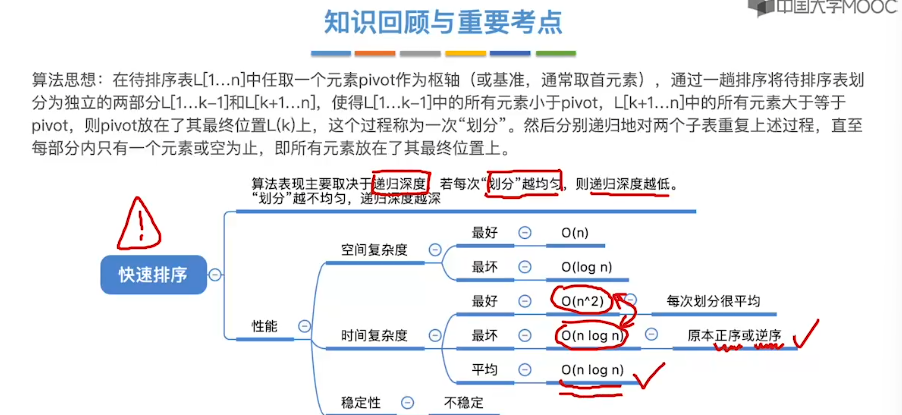
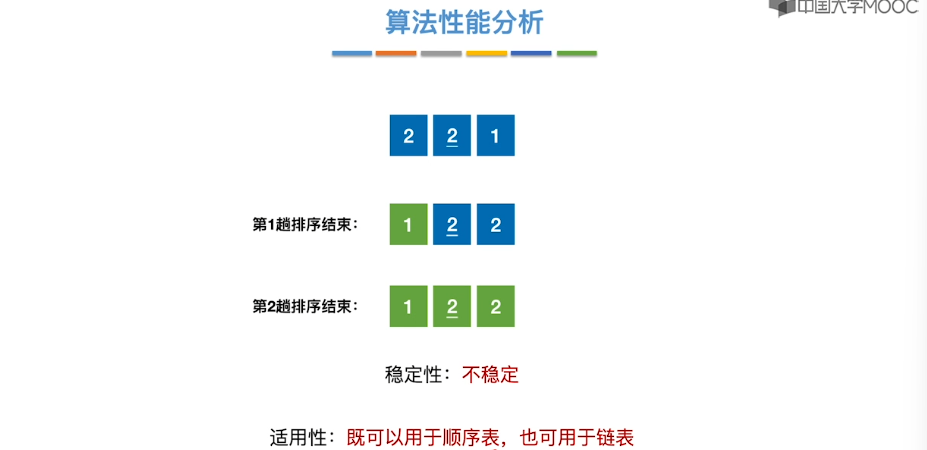
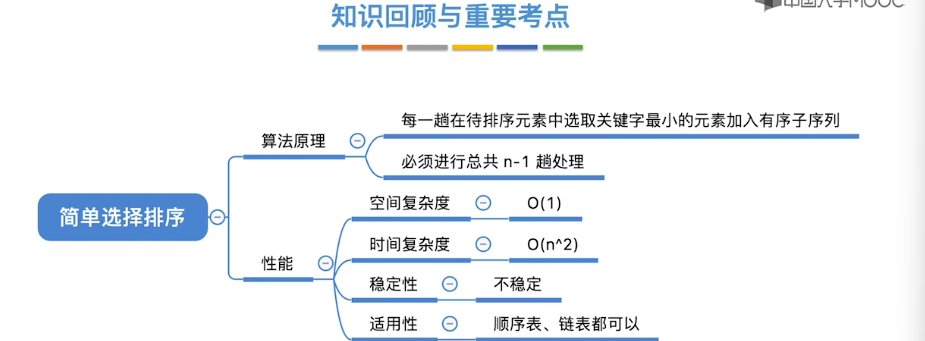
8.6、简单选择排序

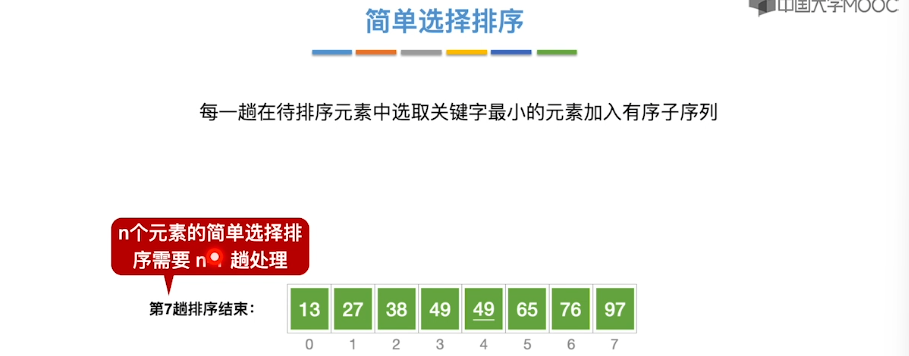
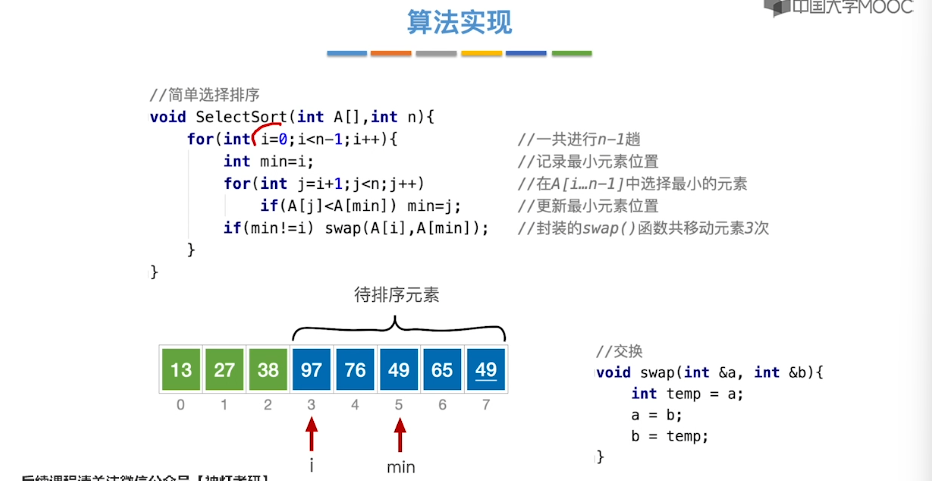

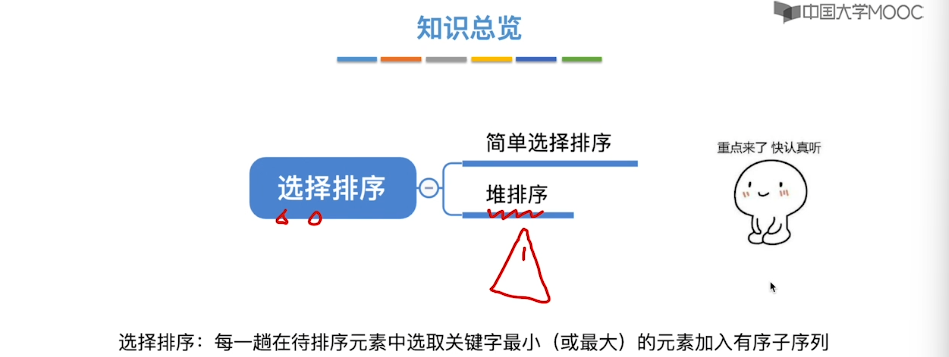
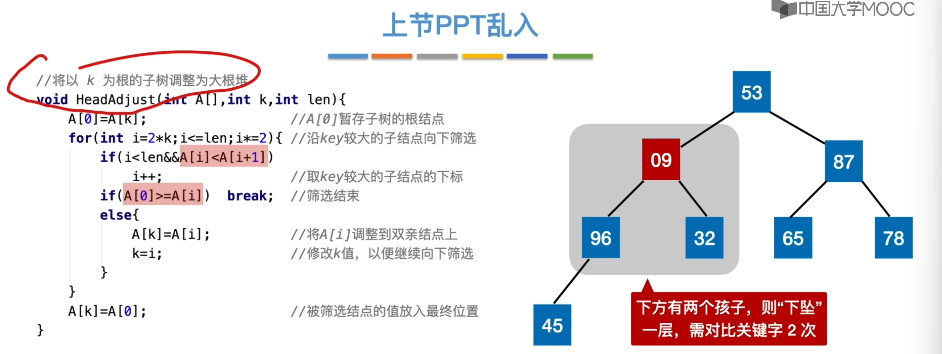
8.7、堆排序

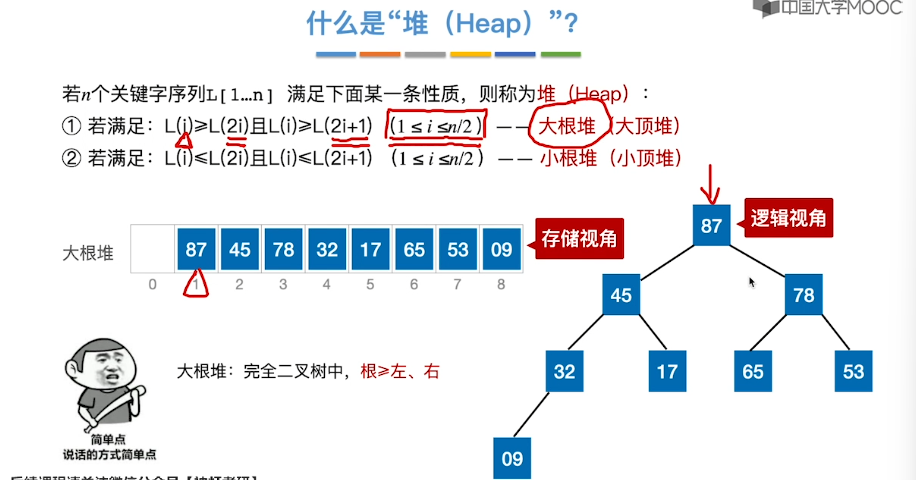
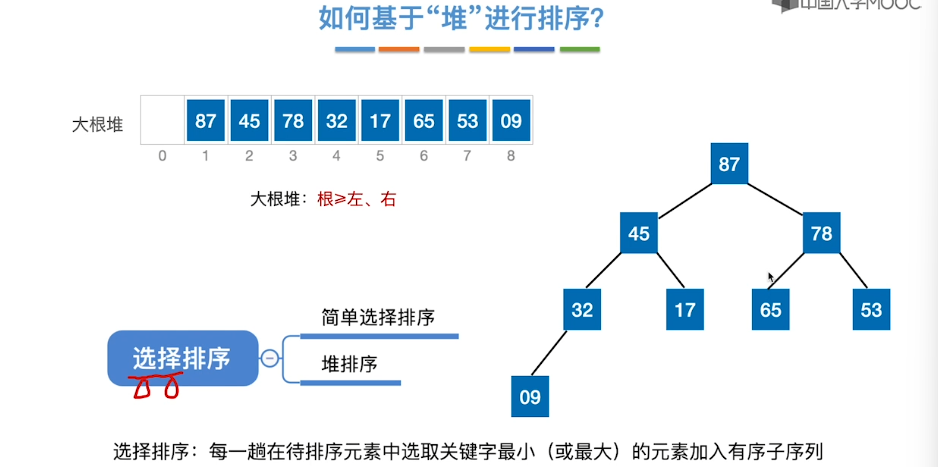
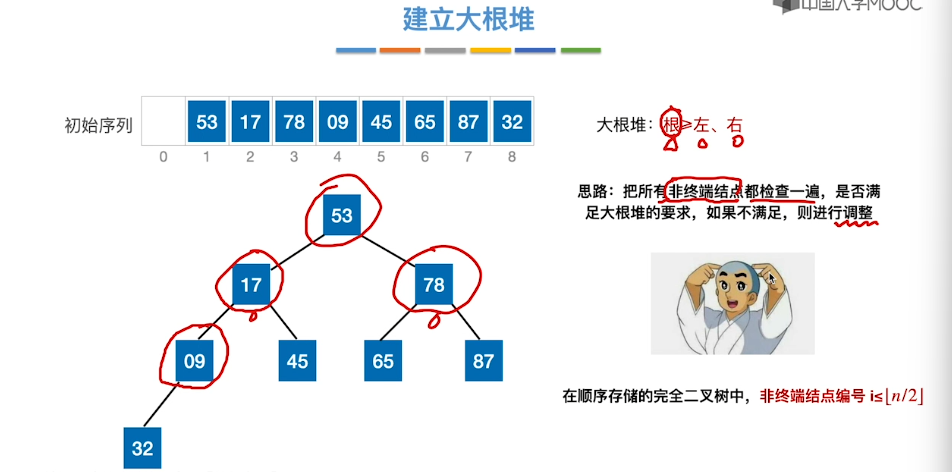
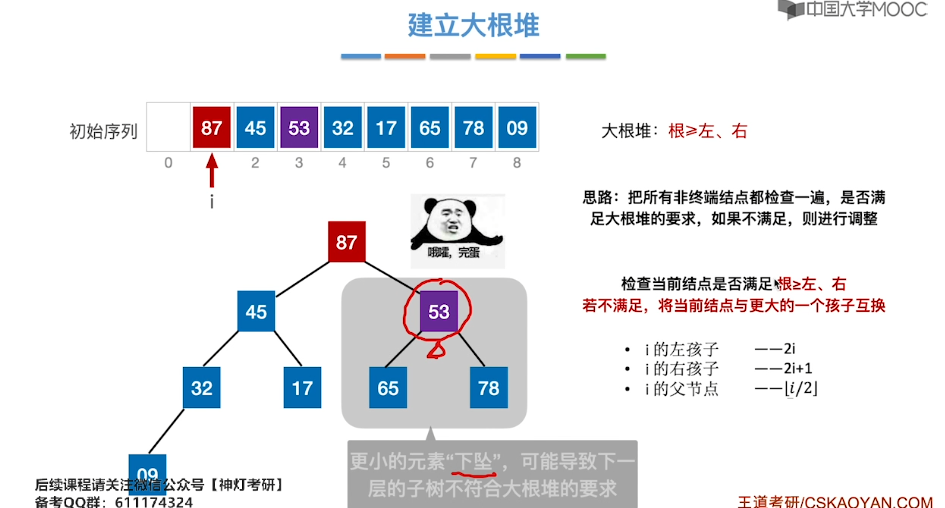
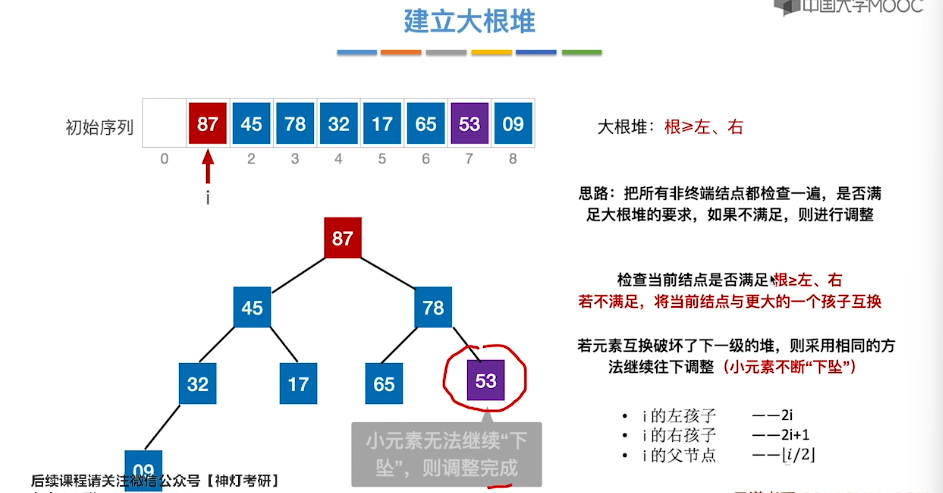
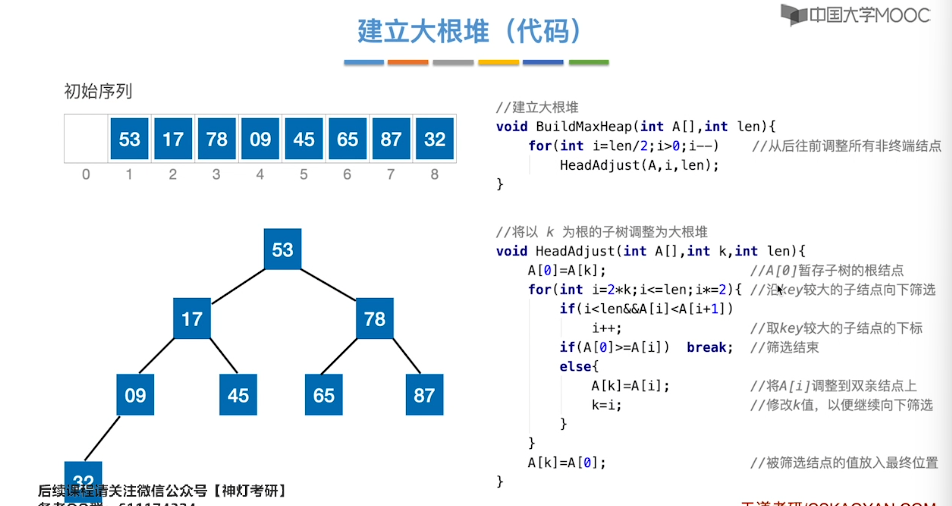
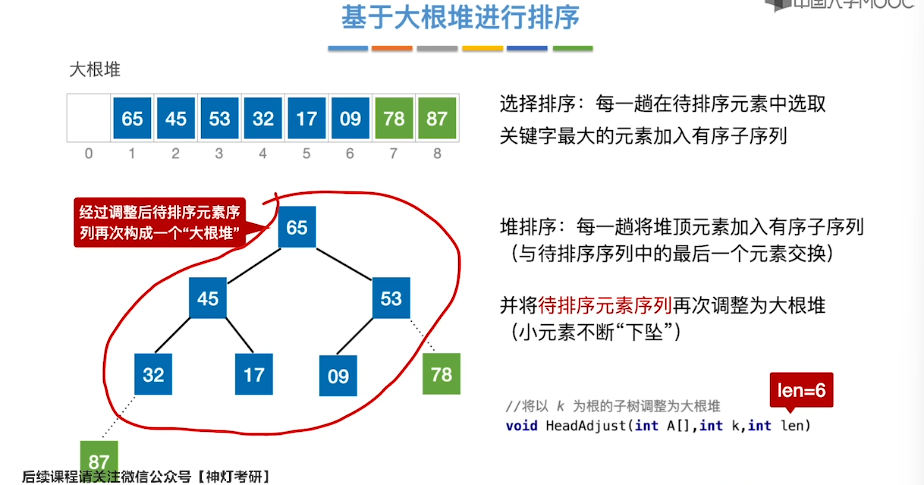
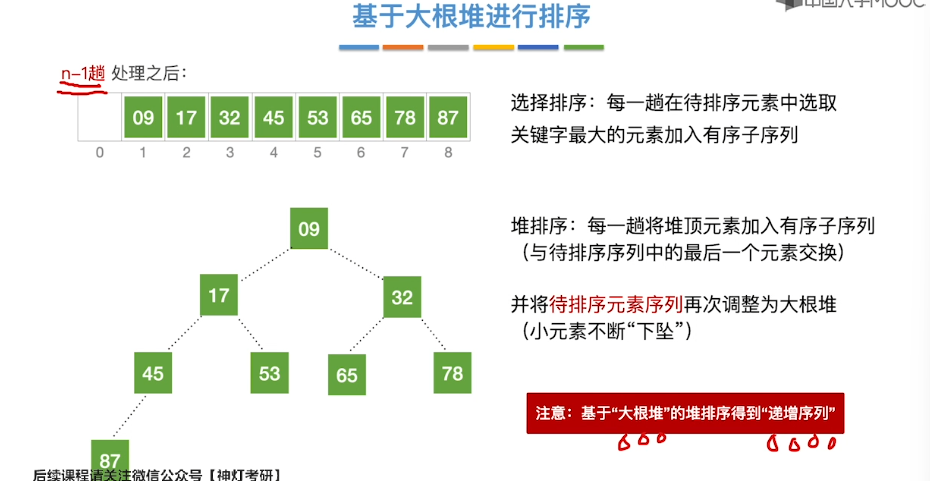
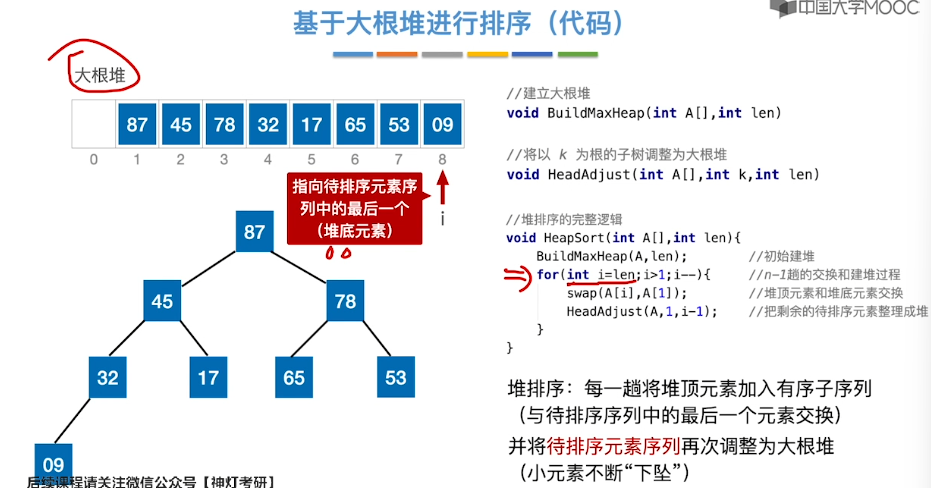

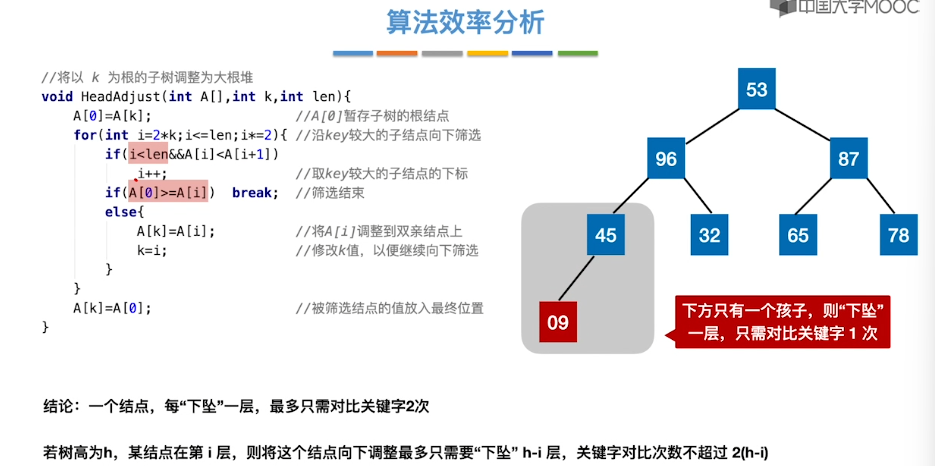




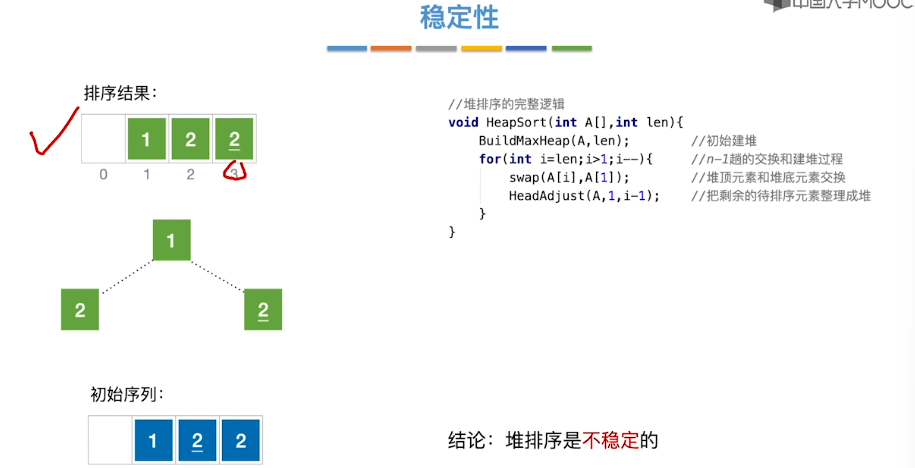
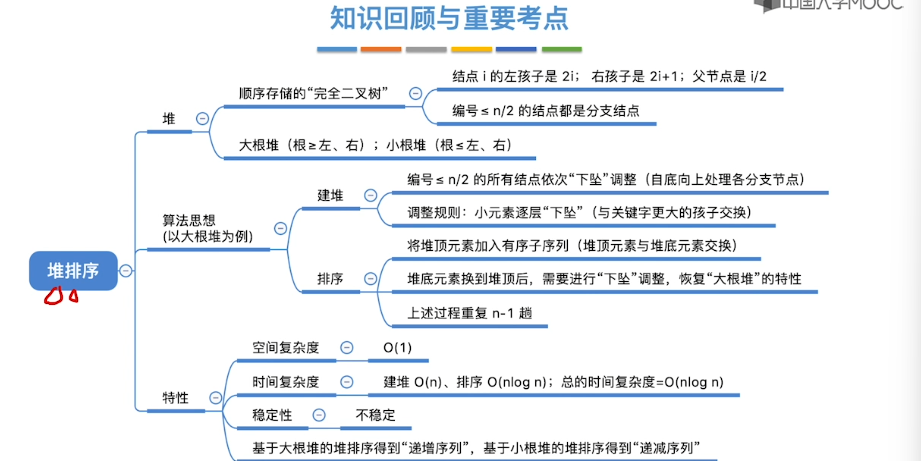
8.8、堆的插入和删除

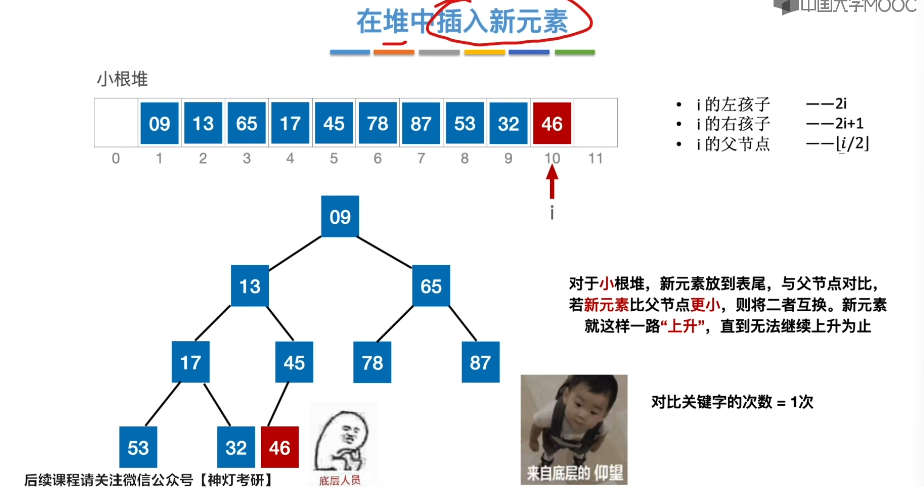

8.9、归并排序

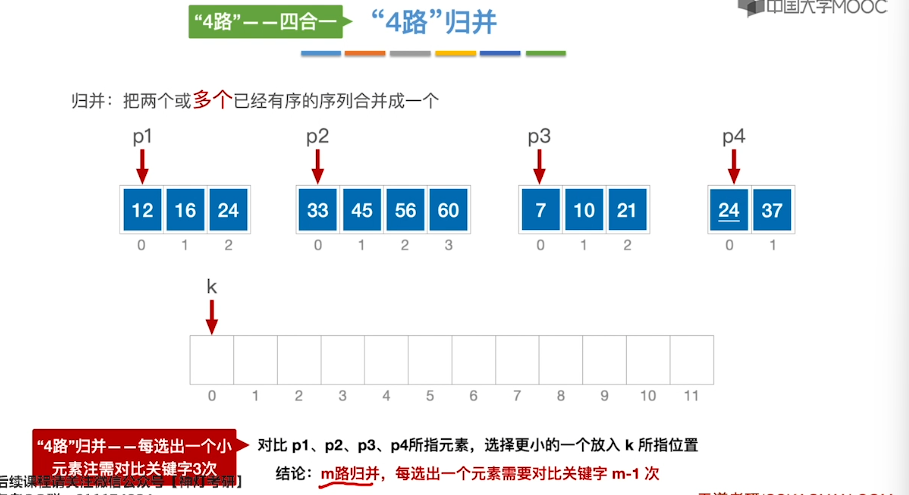
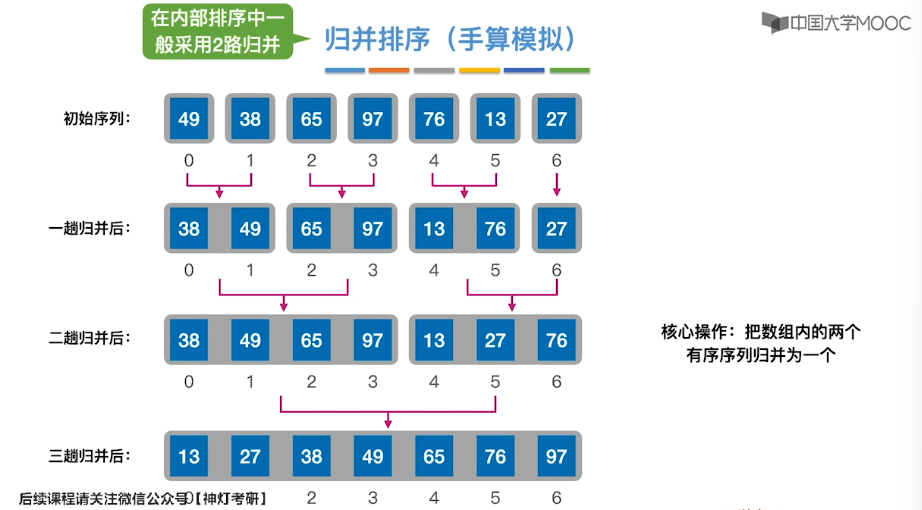
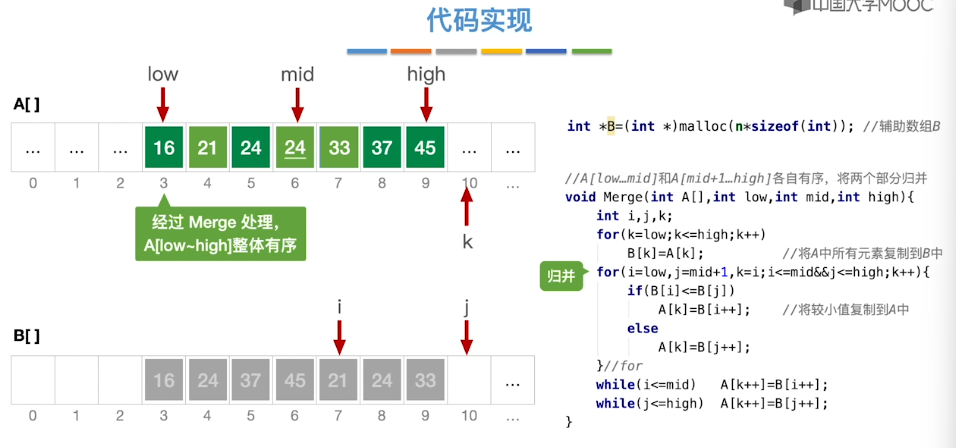
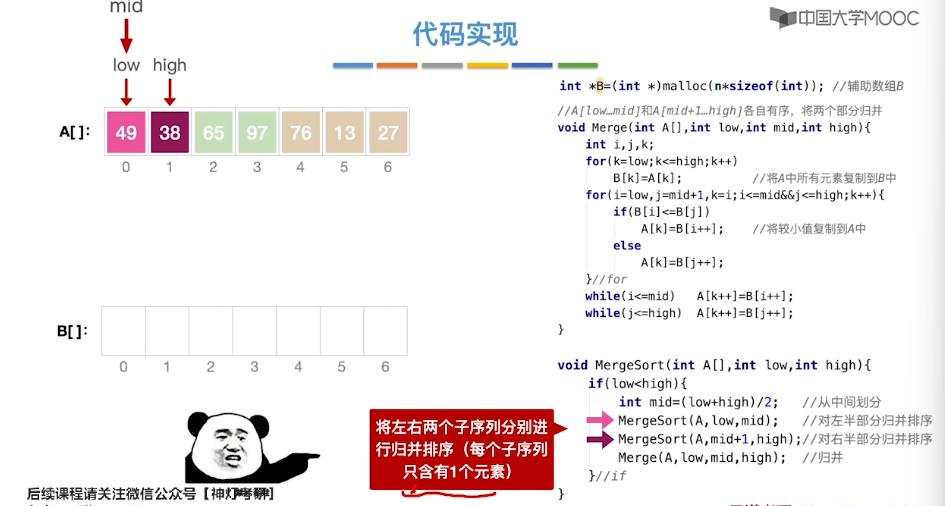
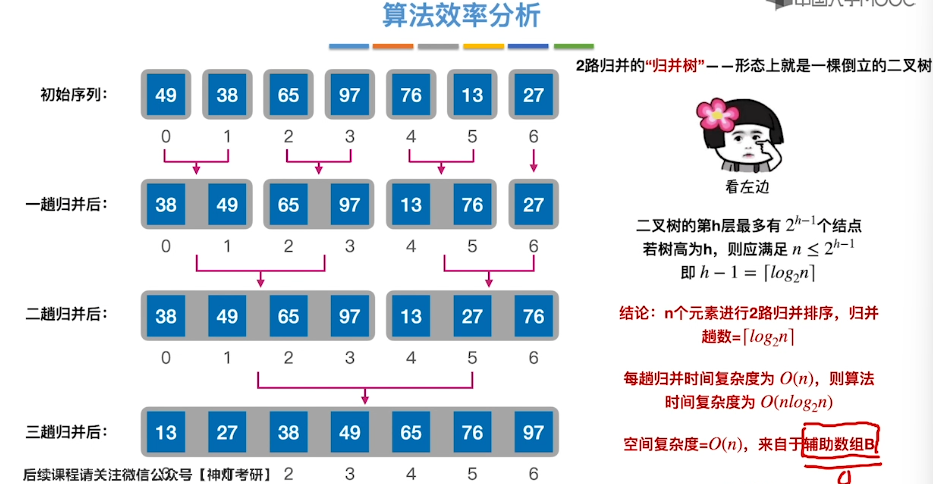
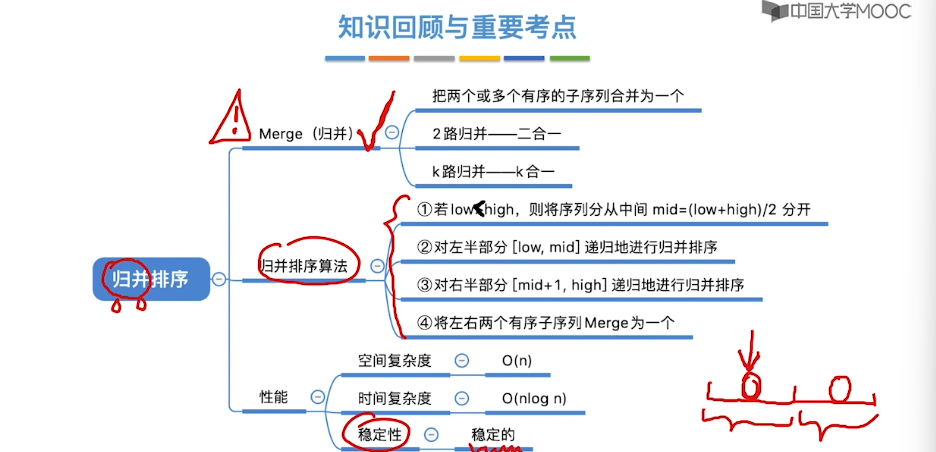
8.10、基数排序
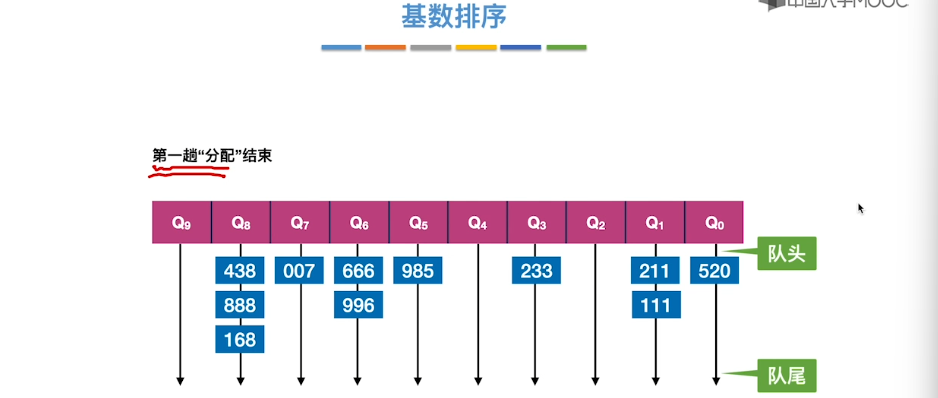
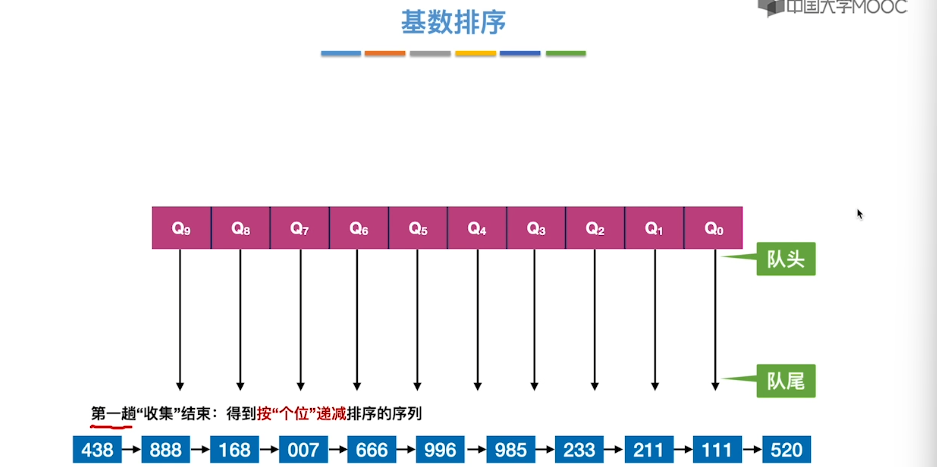
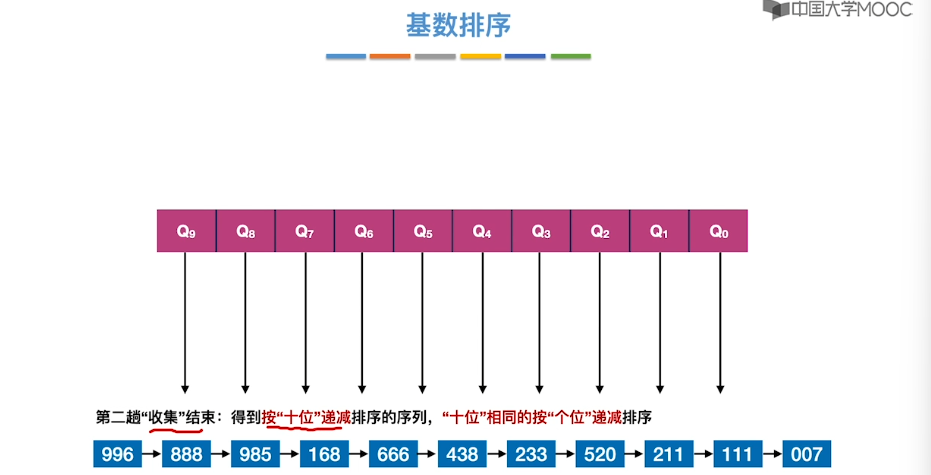
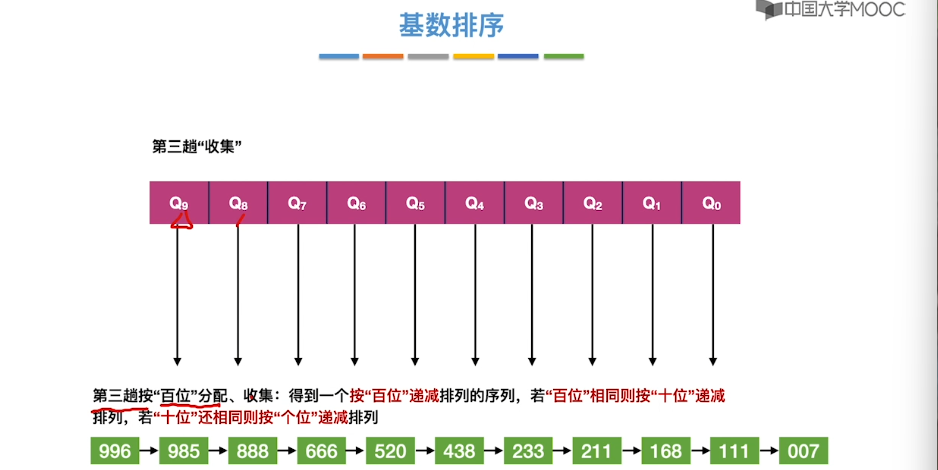
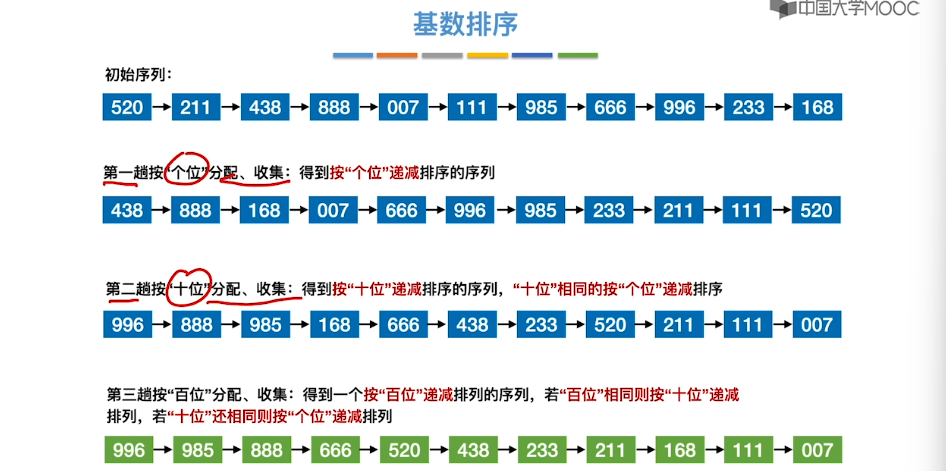
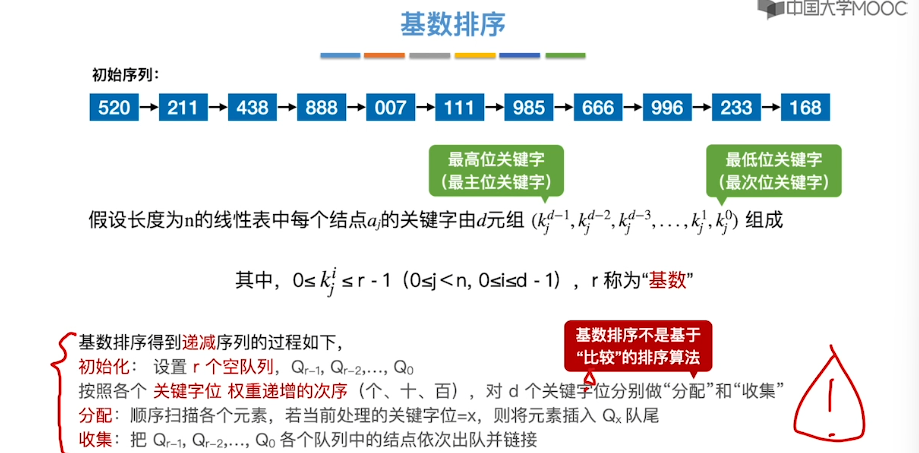
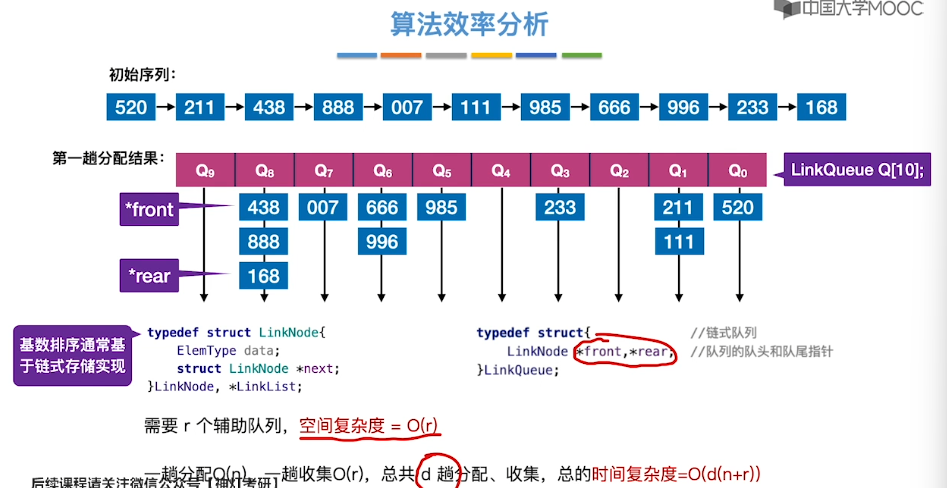

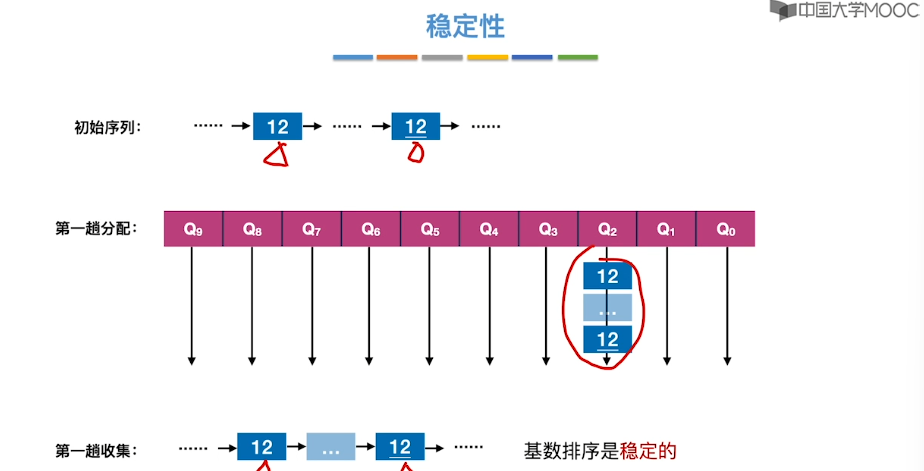
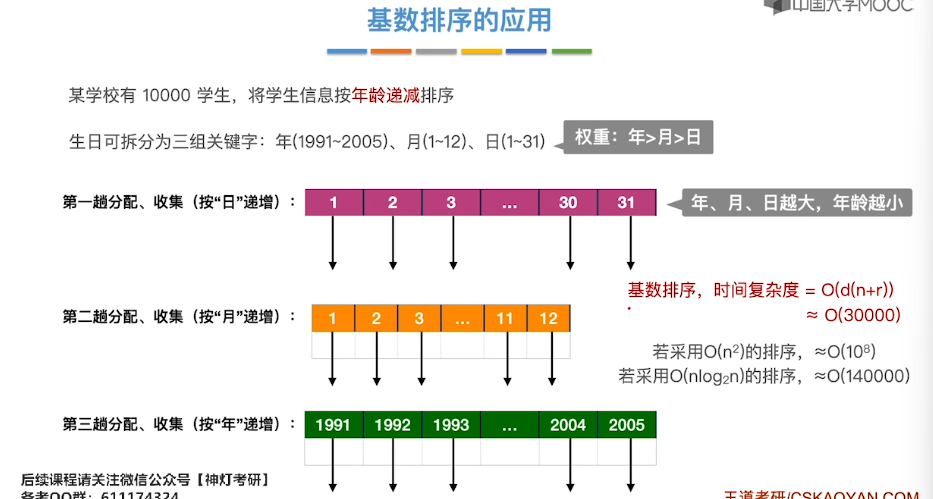

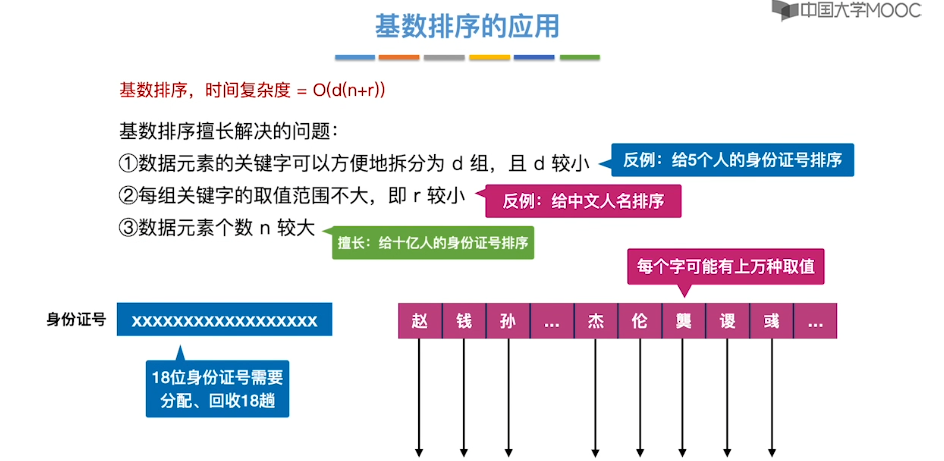

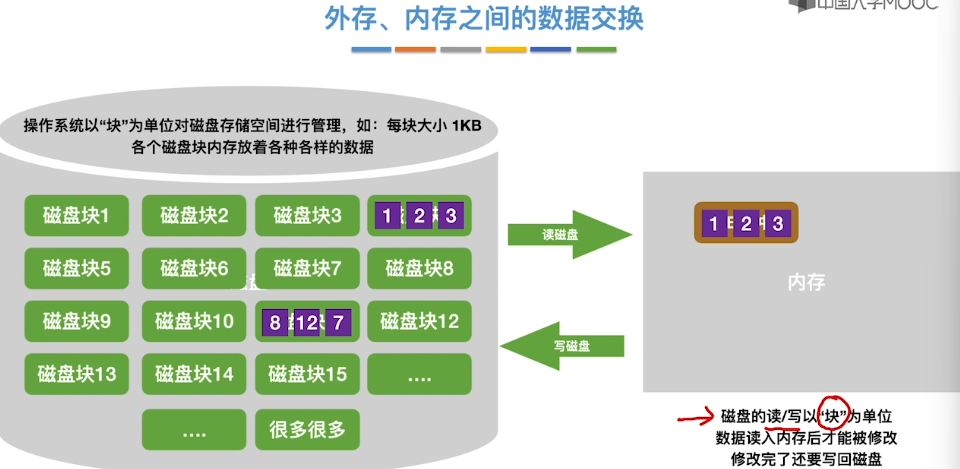
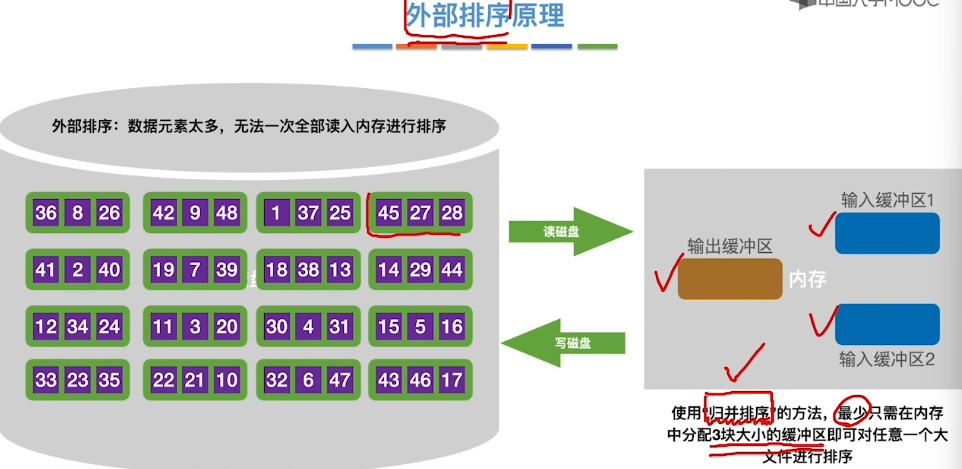
8.11、外部排序

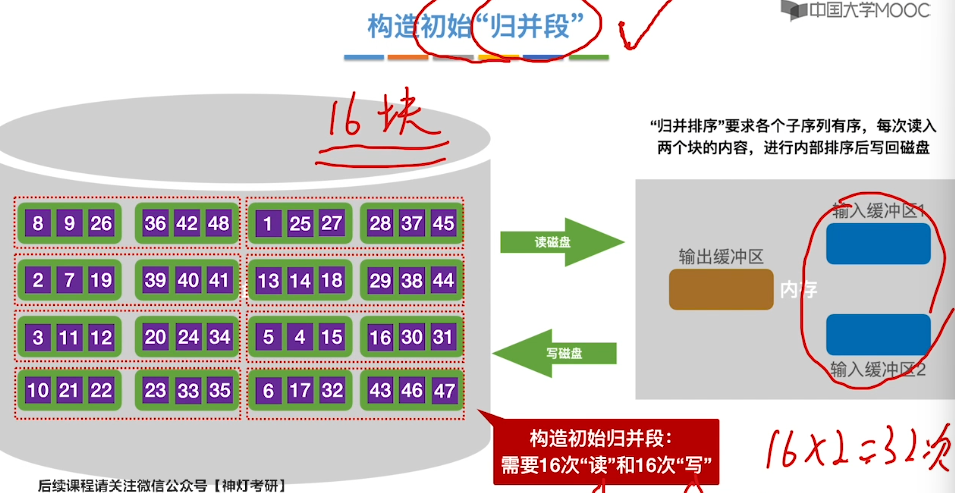
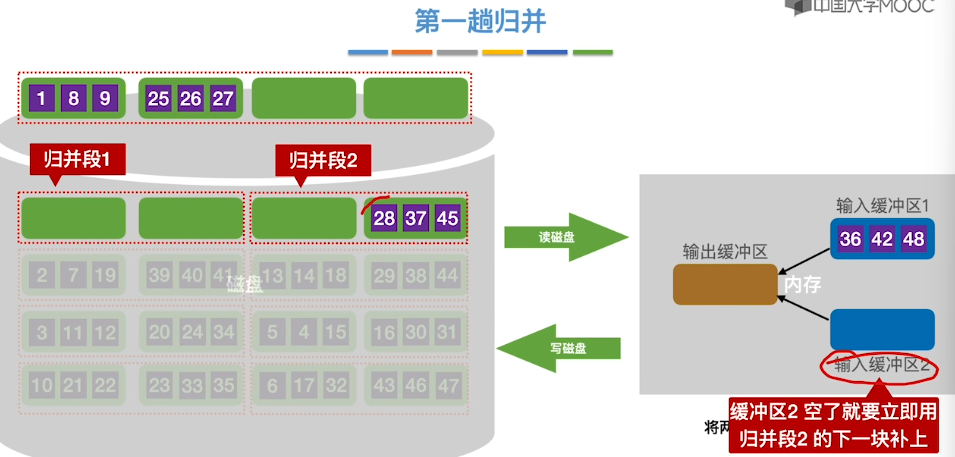
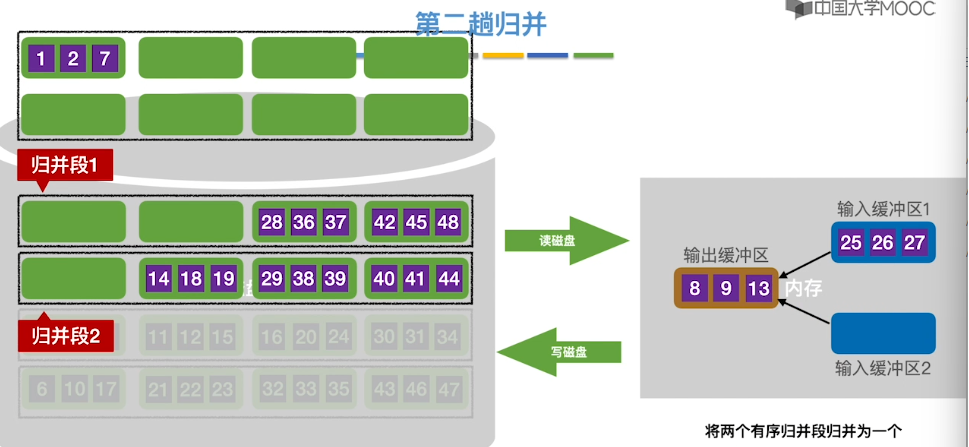
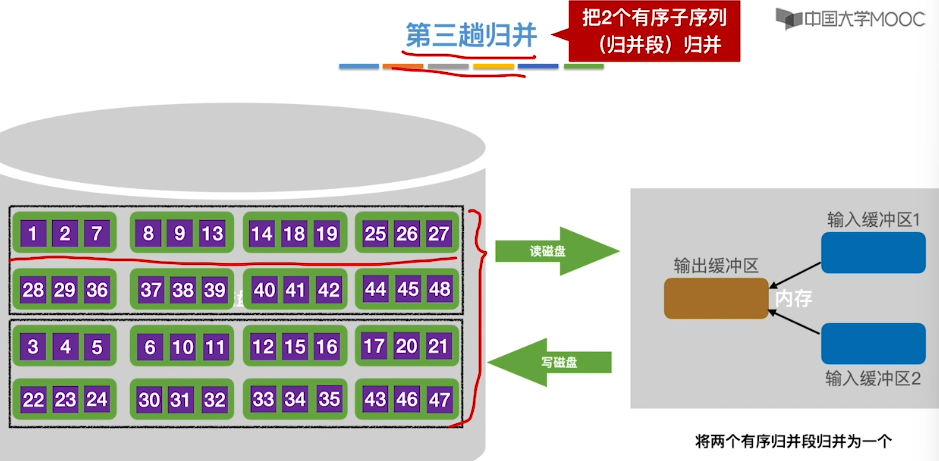
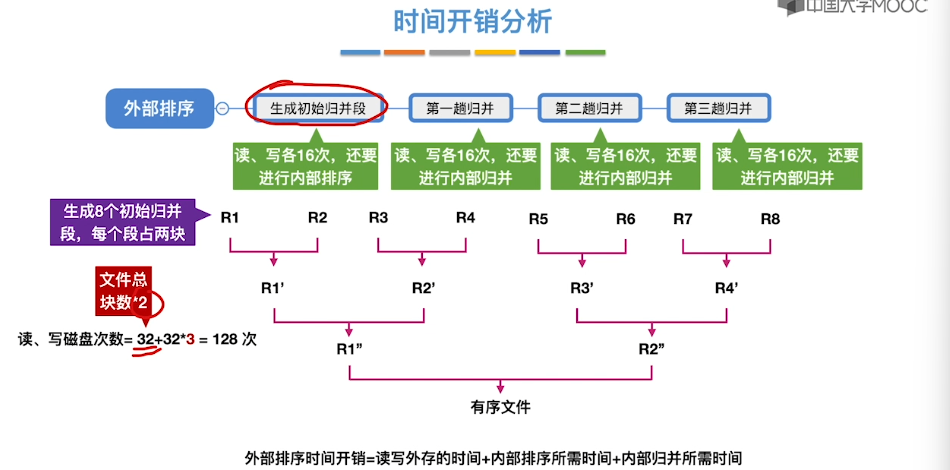
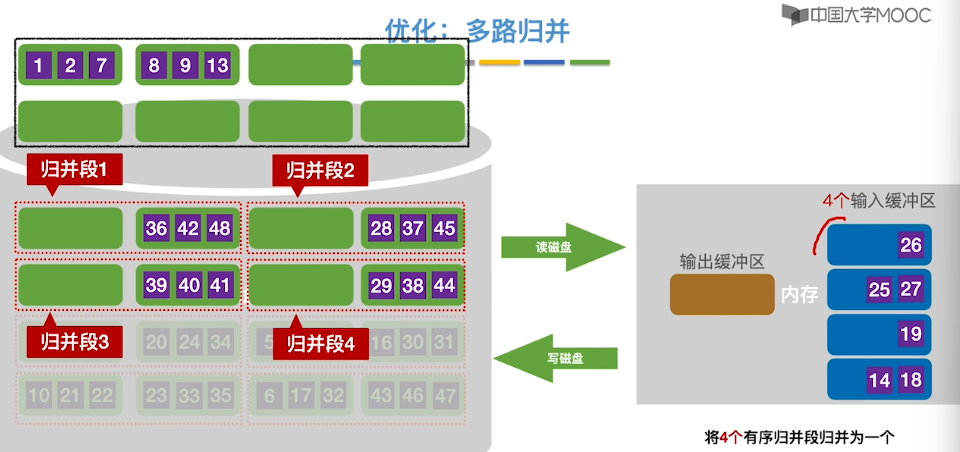
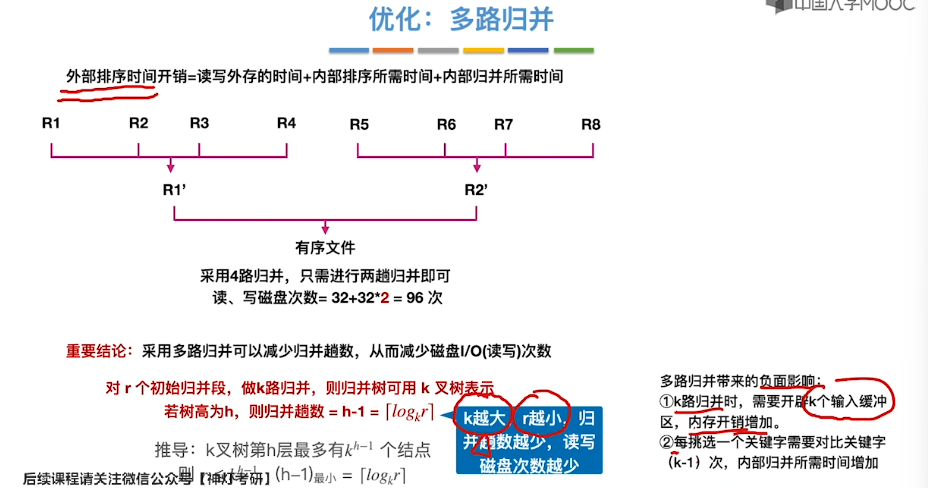
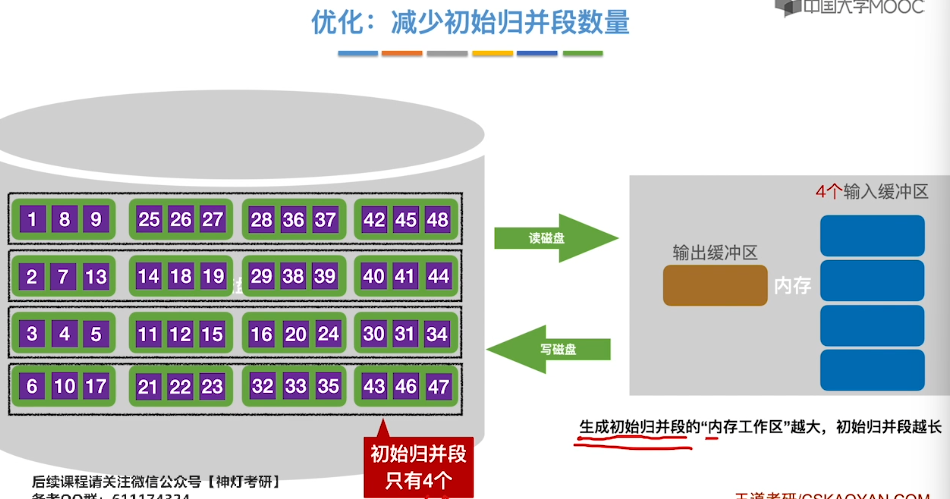
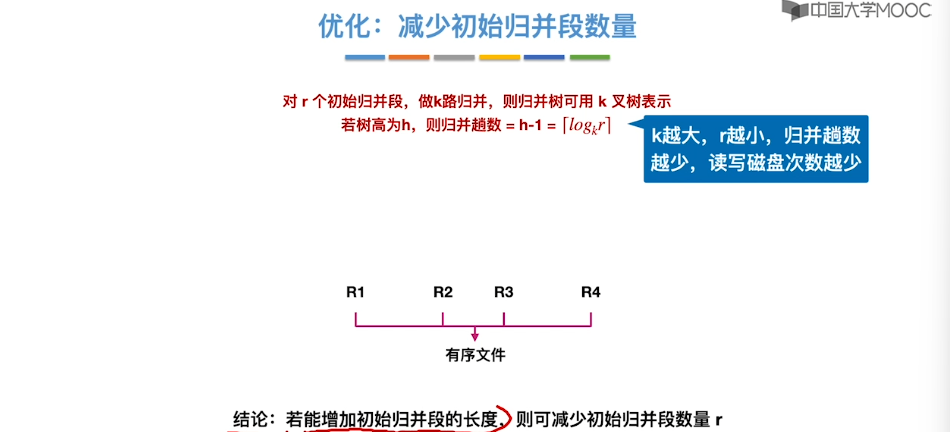
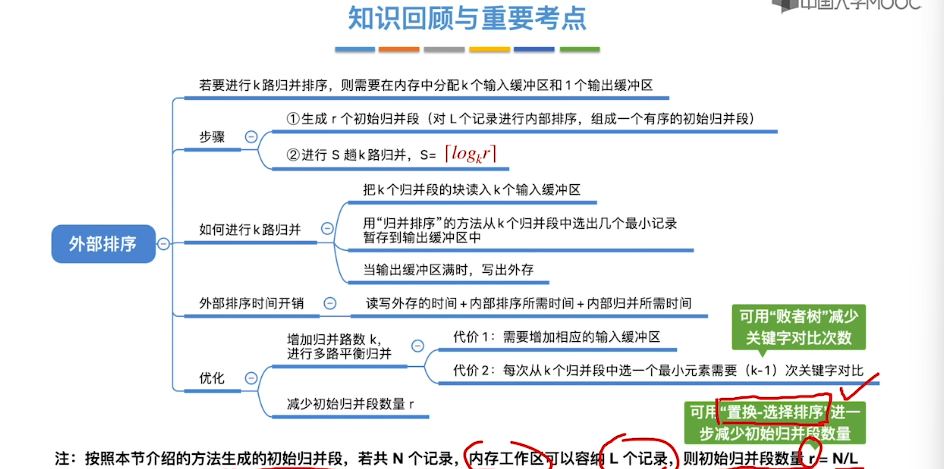
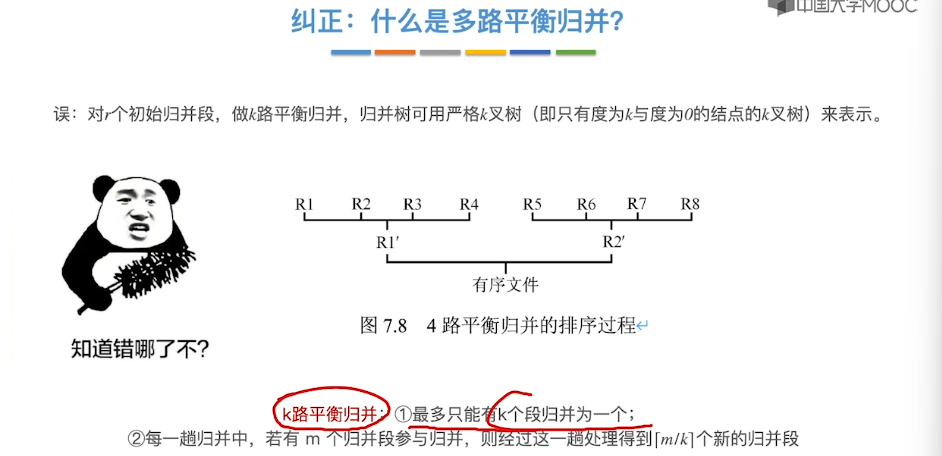
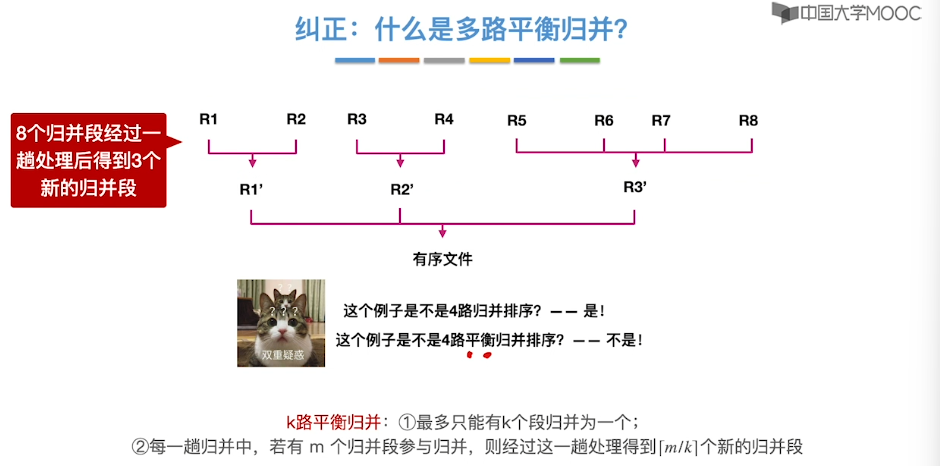
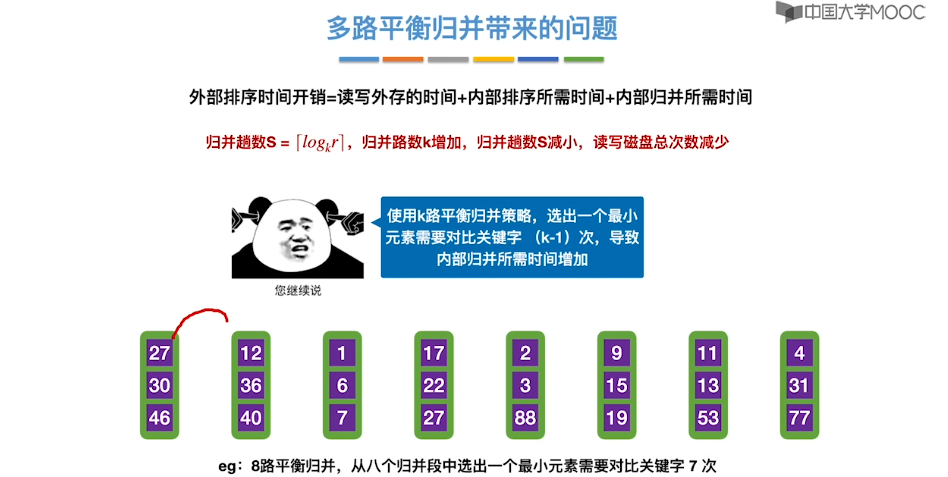
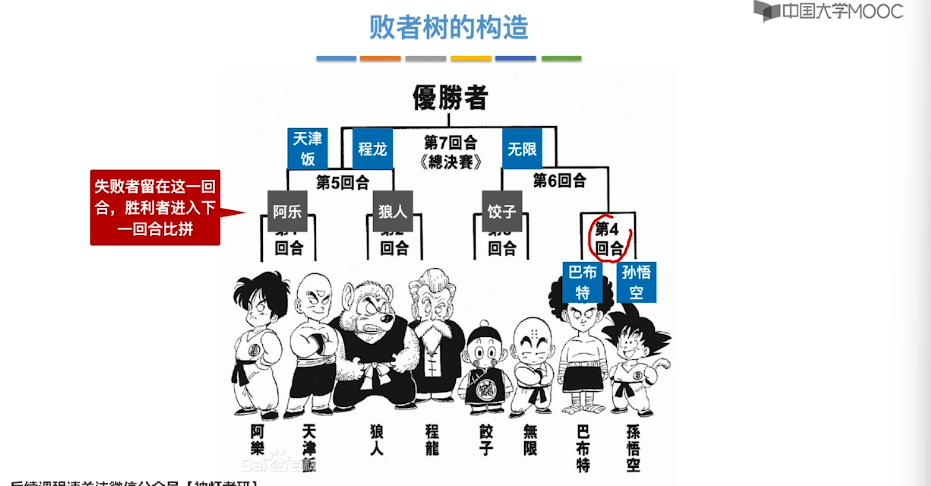
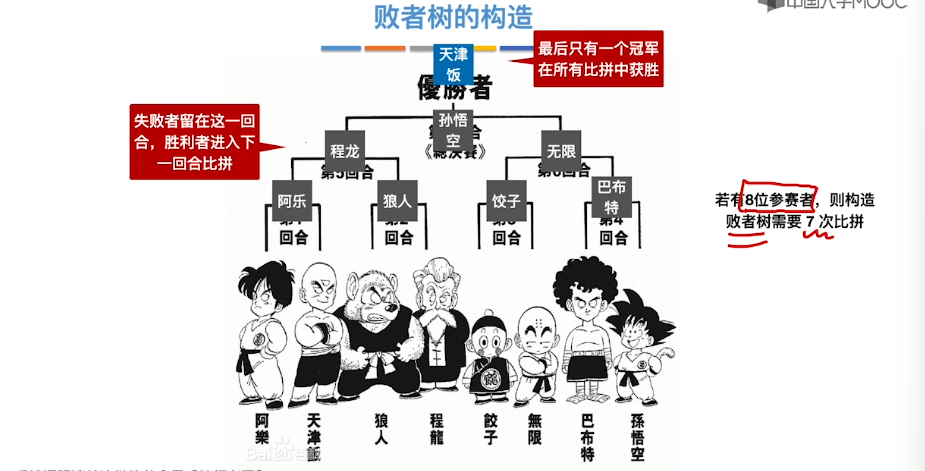
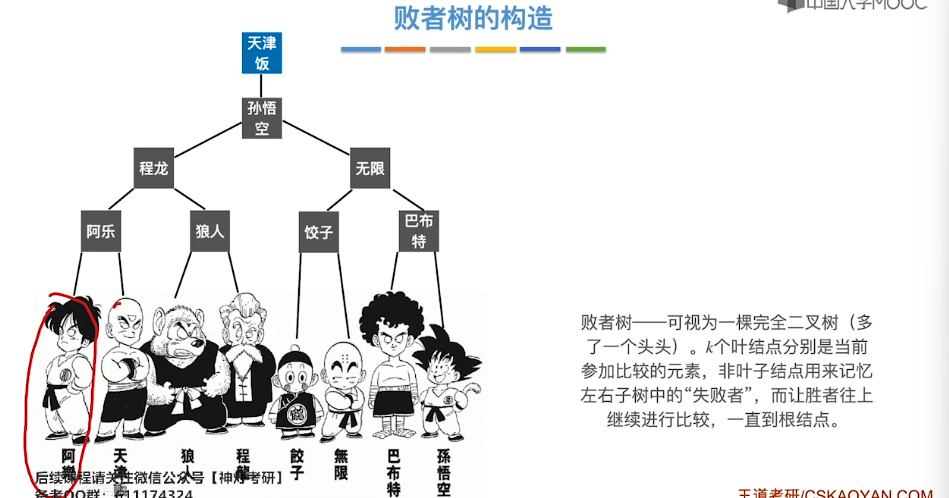
8.12、败者树
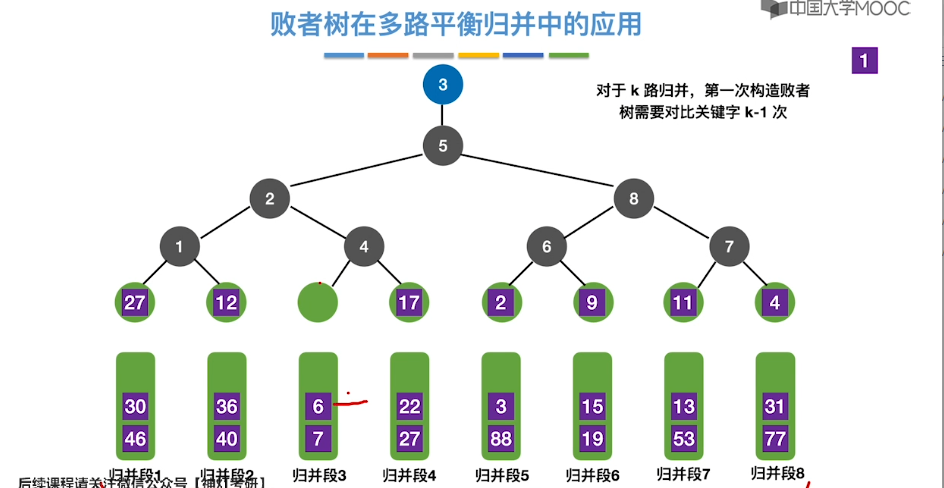
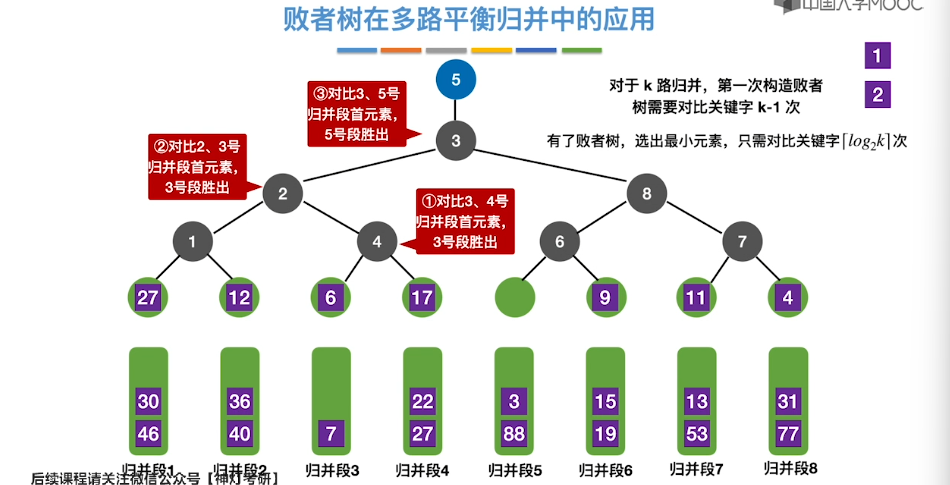
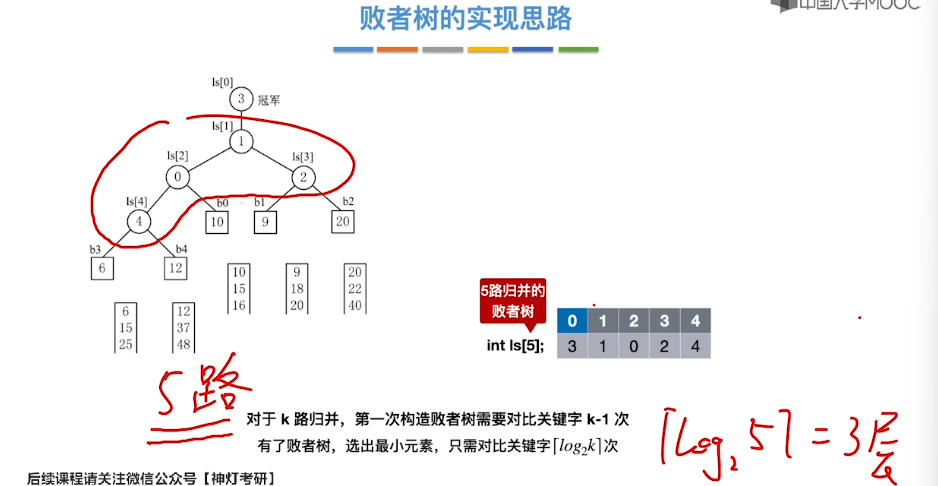
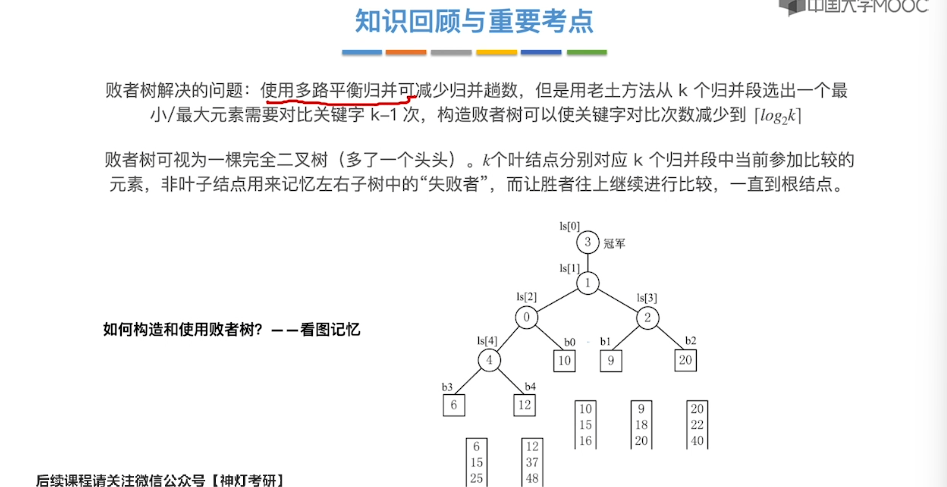
8.13、置换-选择排序
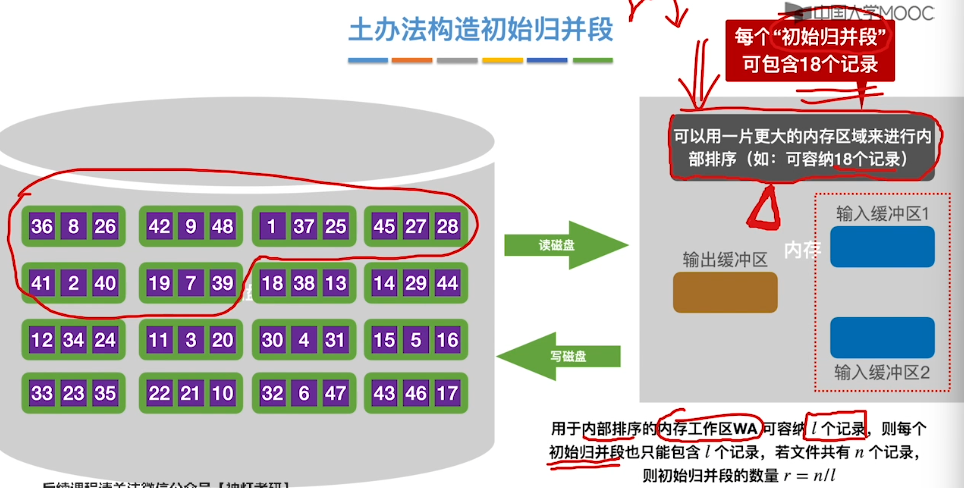
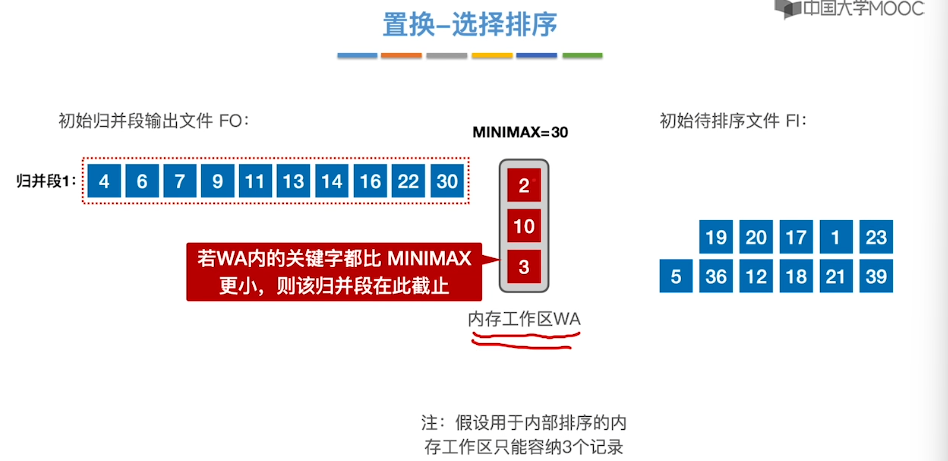
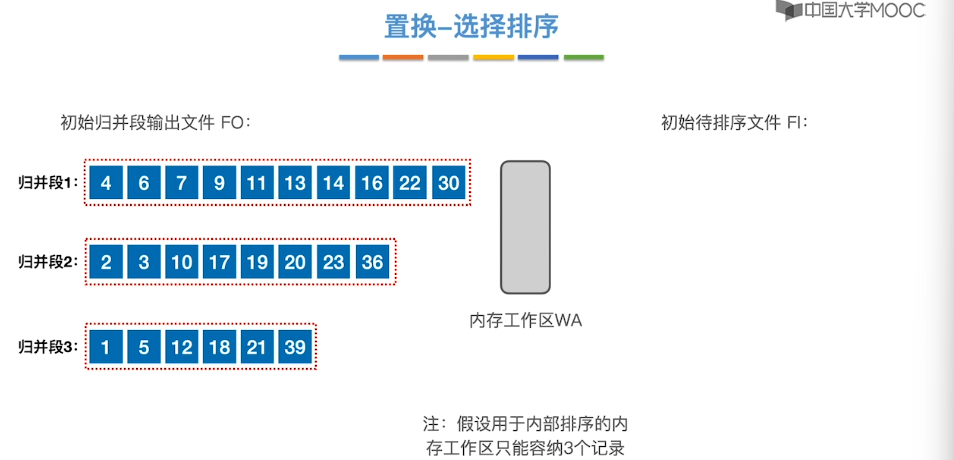

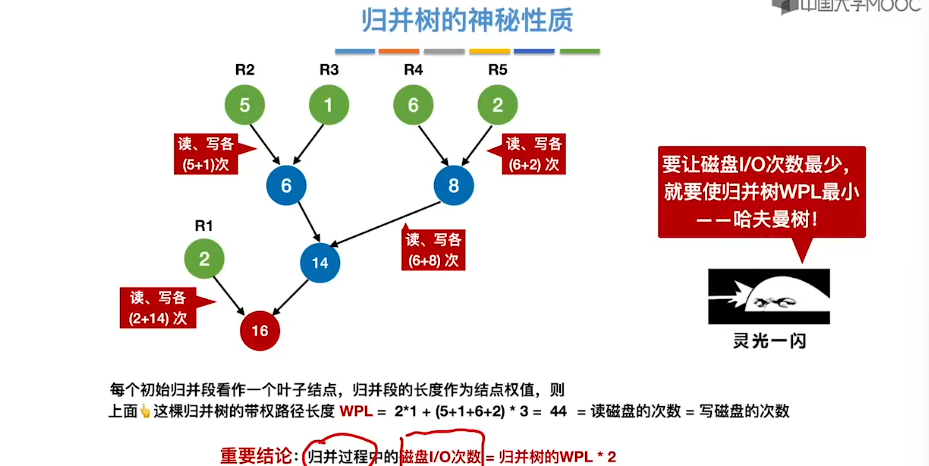
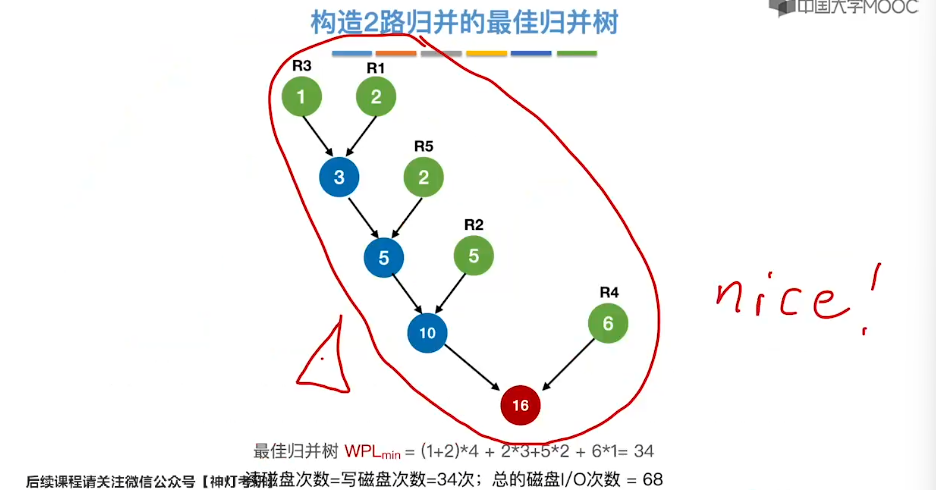
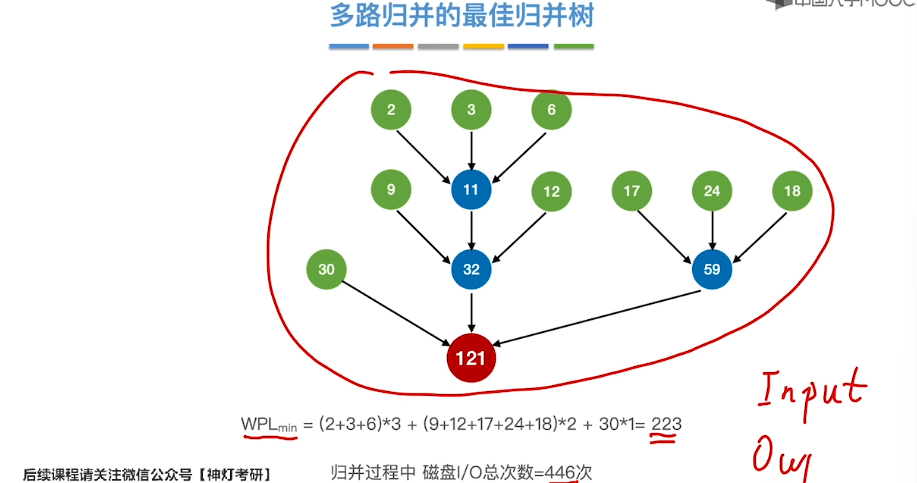
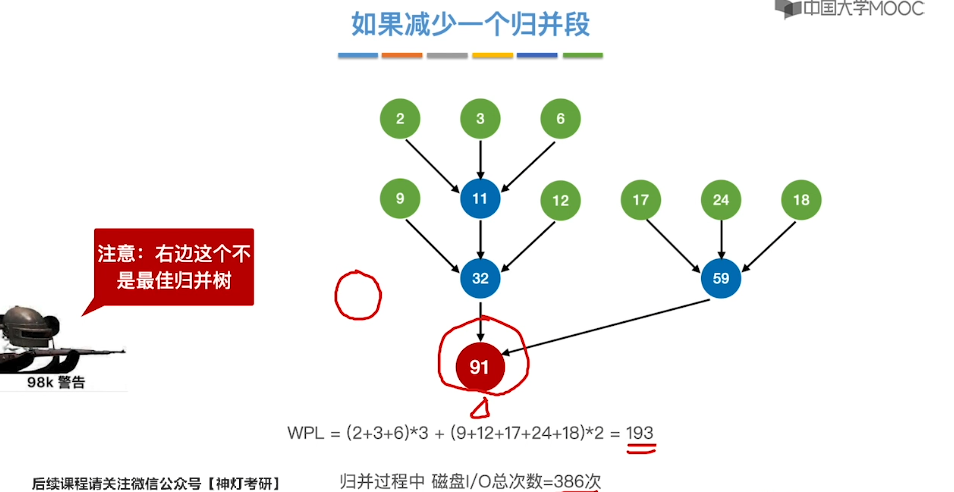
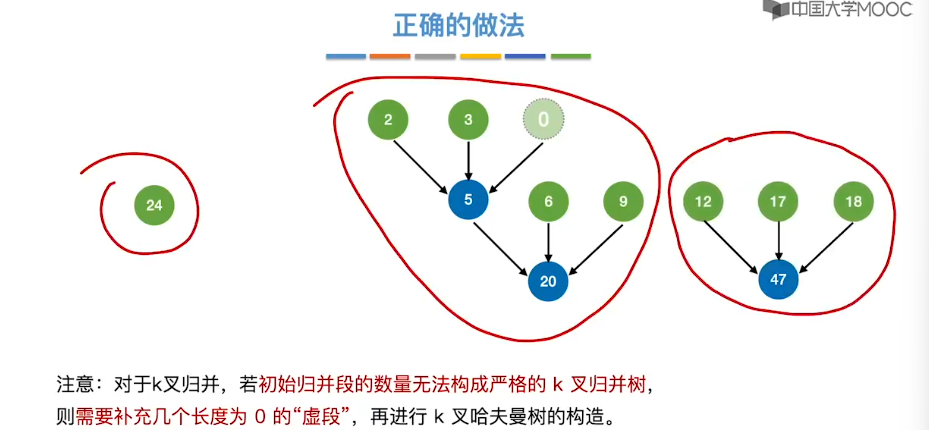
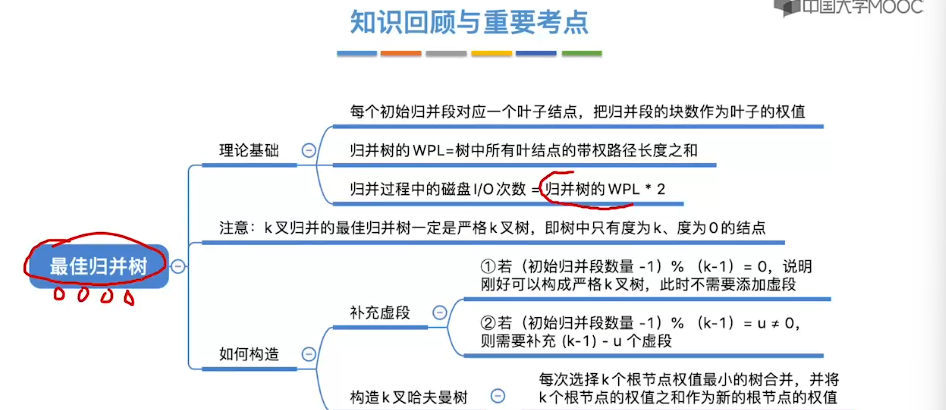
8.14、最佳归并树

end

