一、图的生成树和最小生成树
生成树(SpanningTree):如果一个图的子图是一个包含图所有节点的树,那这个子图就称为生成树。图的生成树不惟一。从不同的顶点出发进行遍历,可以得到不同的生成树。专业的说法:在一个无向连通图中,如果存在一个连通子图包含原图中所有的结点和部分边,且这个子图不存在回路,那么我们称这个子图为原图的一棵生成树。
最小生成树:在带权图中,所有的生成树中边权和最小的那棵(或几棵)被称为最小生成树。
二、应用
1.问题(最小连通网问题)
要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同,因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

2.解决方案
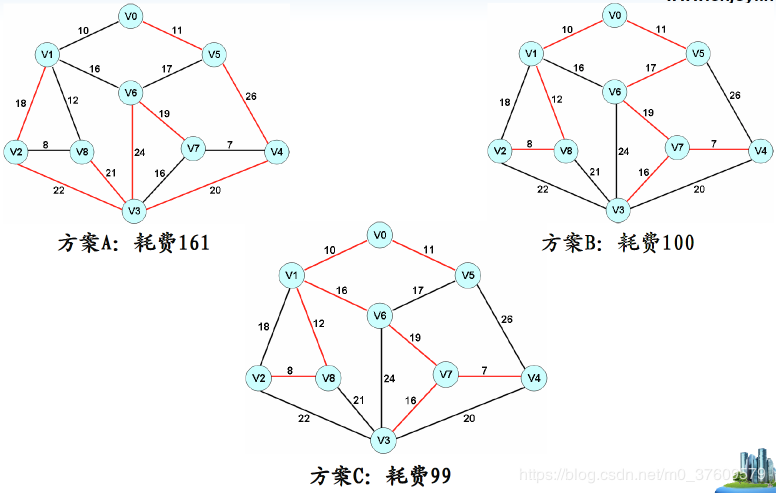
如何在图中选择n-1条边使得n个顶点间两两可达,且这n-1条边的权值之和最小?
- 必须使用且仅使用该网络中的n-1条边来联结网络中的n个顶点;
- 不能使用产生回路的边;
- 各边上的权值的总和达到最小。
三、Prim(普里姆)算法-(适合稠密图)
Prime算法是一种贪心算法,它最初将无向连通图G中所有顶点V分成两个顶点集合VA和VB。在计算过程中VA中的点为已经选好连接入生成树的点,否则属于VB。最开始的时候VA只包含任意选取的图G中的一个点u,其余的点属于VB,每次添加一个VB中的点到VA,该点是集合VB到集合VA中距离最小的一个点。直到V个顶点全部属于VA,算法结束。显然出发点不同,最小生成树的形态就不同,但边权和的最小值是唯一的。
- 从图 N = { V, E }中选择某一顶点 u0 进行标记,之后选择与它关联的具有最小权值的边(u0, v),并将顶点 v 进行标记
- 反复在一个顶点被标记,而另一个顶点未被标记的各条边中选择权值最小的边(u, v),并将未标记的顶点进行标记
- 如此继续下去,直到图中的所有顶点都被标记为止
- 有两个嵌套循环,所以时间复杂度为 O(n2)O(n2)。
- 是以某顶点为起点,逐步找各顶点上最小权值的边来构建最小生成树。
1.手工寻找最小连通网:
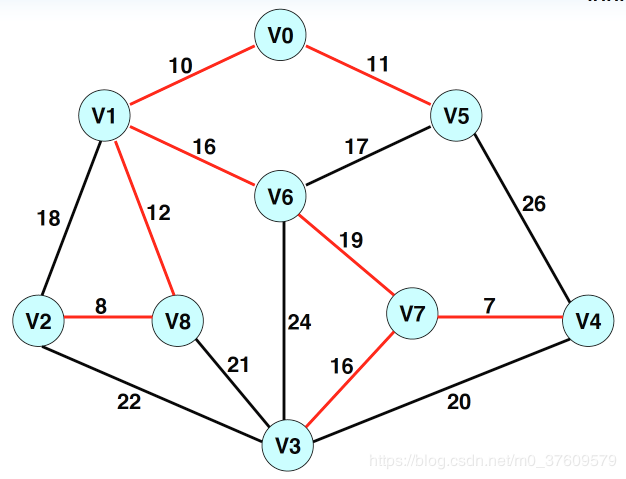
2.算法步骤
选定图中的任意一个顶点v0,从v0开始生成最小生成树。
(1)初始化dist[v0]=0,其他点的距离值dist[i]=∞。其中dist[i]表示集合VB中的点到VA中的点的距离值。
(2)经过N次如下步骤操作,最后得到一棵含N个顶点,N-1条边的最小生成树:
-
选择一个未标记的点k,并且dist[k]的值是最小的
-
标记点k进入集合VA
-
以k为中间点,修改未标记点j,即VB中的点到VA的距离值
(3)得到最小生成树T。
四、克鲁斯卡尔(Kruskal)算法(适合稀疏图)
用并查集优化后时间复杂度:O(mlogm+mα(n)),α(n)是一次并查集的复杂度。
1.算法思想
Kruskal算法也是一种贪心算法,它是将边按权值排序,每次从剩下的边集中选择权值最小且两个端点不在同一集合的边加入生成树中,反复操作,直到加入了n-1条边。
2.算法步骤
- 将G中的边按权值从小到大快排。
- 按照权值从小到大依次选边。若当前选取的边加入后使生成树T形成环,则舍弃当前边,否则标记当前边并计数。
- 重复上一步操作,直到生成树T中包含n-1条边,否则当遍历完所有边后,选取不到n-1条边,表示最小生成树不存在。
算法的关键在于如何判定新加入的边会不会使图G'产生环,在这里用并查集,如果新加入的边的两个端点在并查集的同一集合中,说明存在环,需要舍弃这条边,否则保留当前边,并合涉及的两个集合。
简单说就是首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止。
五、代码实现
public class MatrixUDG { private int mEdgNum;//边的数量 private char[] mVexs;//顶点集合 private int[][] mMatrix;//邻接矩阵 private static final int INF = Integer.MAX_VALUE;//最大值 /** * 创建图 * @param vexs --顶点数组 * @param matrix --矩阵数据 */ public MatrixUDG(char[] vexs, int[][] matrix){ this.mVexs = vexs;//初始化顶点 this.mMatrix = matrix;//初始化矩阵 //统计边:边有3种类型:0(自己到自己),数字(相邻边),INF(不是相邻边) int vlen = vexs.length; for(int i = 0; i < vlen; i++){ for(int j = i + 1; j < vlen; j++){ if(mMatrix[i][j] != INF){ mEdgNum++; } } } } /** * 返回在顶点的位置 * @param ch * @return */ private int getPosition(char ch){ for(int i = 0; i < mVexs.length; i++){ if(ch == mVexs[i]){ return i; } } return -1; } /** * 打印邻接矩阵 */ private void print(){ System.out.println("邻接矩阵:"); for (int[] matrix : mMatrix) { for (int ch : matrix) { System.out.print(ch + " "); } System.out.println(); } } /** * prime最小生成树算法 */ public void prime(int start){ int num = mVexs.length;//顶点个数 int[] weights = new int[num];//顶点间边的权重 char[] prims = new char[num];//prime最小生成树的结果 int index = 0;//prime数组的当前索引 //第一个数是start顶点 prims[index ++] = mVexs[start]; //初始化权重 for(int i = 0; i < num; i++){ weights[i] = mMatrix[start][i]; } weights[start] = 0;//自己到自己的权重为0 for(int i = 0; i < num; i++){ if(i == start){//由于从start开始不需要进行处理 continue; } //从剩余的边中找到最小权重 int min = INF;//最小权重 int minIndex = 0;//最小权重所在的索引 for(int j = 0; j < num; j++){ if(weights[j] != 0 && weights[j] < min){//0表示已经加入最小权重 min = weights[j]; minIndex = j; } } //将最小权重加入到数组中,并设置为0 prims[index++] = mVexs[minIndex]; weights[minIndex] = 0; //更新其他权重的值:取双方权重值最小的 for(int j = 0; j < num; j++){ if(weights[j] != 0 && mMatrix[minIndex][j] < weights[j]){ weights[j] = mMatrix[minIndex][j]; } } } //计算最小生成树的权重 int sum = 0; for(int i = 1; i < index; i++){ int min = INF; int n = getPosition(prims[i]); //求当前节点到上面其他节点的最小值 for(int j = 0; j < i; j++){ int m = getPosition(prims[j]); if(mMatrix[m][n] < min){ min = mMatrix[m][n]; } } sum += min; } //打印最小生成树 System.out.printf("PRIME(%c)=%d:", mVexs[start], sum); for(int i = 0; i < index; i ++){ System.out.printf("%c ", prims[i]); } System.out.printf("\n"); } /** * kruskal生成最小生成树 */ public void kruskal(){ int index = 0;//结果数组的当前索引 EData[] results = new EData[mEdgNum];//结果数组 int[] vends = new int[mEdgNum];//保存的是某个顶点在该最小生成树的终点 //获取图中所有的边 EData[] edges = getEdges(); //将边按权重从小到大排序 sortEdges(edges); for(int i = 0; i < mEdgNum; i++){ int p1 = getPosition(edges[i].start); int p2 = getPosition(edges[i].end); int m = getEnd(vends, p1); int n = getEnd(vends, p2); if(m != n){//表示没有形成闭环 vends[m] = n; results[index++] = edges[i]; } } //统计并打印最小生成树的信息 int length = 0; for(int i = 0; i < index; i++){ length += results[i].weight; } System.out.printf("kruskal=%d", length); for(int i = 0; i < index; i++){ System.out.printf("(%c,%c) ", results[i].start,results[i].end); } System.out.printf("\n"); } /** * 获取图中的边 */ private EData[] getEdges(){ int index = 0; EData[] edges = new EData[mEdgNum]; for(int i = 0; i < mVexs.length; i++){ for(int j = i + 1; j < mVexs.length; j++){ if(mMatrix[i][j] != INF){ edges[index++] = new EData(mVexs[i],mVexs[j],mMatrix[i][j]); } } } return edges; } /** * 根据权重大小排序(从小到大) * @param edges */ private void sortEdges(EData[] edges){ EData tmp; for(int i = 0; i < edges.length; i++){ for(int j = (i + 1); j < edges.length; j++){ if(edges[i].weight > edges[j].weight){//若大于则交换位置 tmp = edges[i]; edges[i] = edges[j]; edges[j] = tmp; } } } } /** * 取终点 */ private int getEnd(int[] vends, int i){ //若C->D,D->F则取F的值 while(vends[i] != 0){ i = vends[i]; } return i; } //边的数据结构 private static class EData{ char start;//边的起点 char end;//边的终点 int weight;//边的权重 public EData(char start, char end, int weight) { this.start = start; this.end = end; this.weight = weight; } } public static void main(String[] args) { char[] vexs = {'A','B','C','D','E','F','G'}; int[][] matrix = { //A //B //C //D //E //F //G {0, 12, INF, INF, INF, 16, 14}, //A {12, 0, 10, INF, INF, 7, INF}, //B {INF, 10, 0, 3, 5, 6, INF}, //C {INF, INF, 3, 0, 4, INF, INF}, //D {INF, INF, 5, 4, 0, 2, 8}, //E {16, 7, 6, INF, 2, 0, 9}, //F {14, INF, INF, INF, 8, 9, 0} //G }; MatrixUDG matrixUDG = new MatrixUDG(vexs, matrix); matrixUDG.prime(0);//PRIME(A)=36:A B F E D C G matrixUDG.kruskal();//kruskal=36(E,F) (C,D) (D,E) (B,F) (E,G) (A,B) } }
六、总结
- Prim算法是针对顶点展开的,适合于边的数量较多的情况
- Kruskal算法是针对边展开的,适合于边的数量较少的情况
我的微信公众号:架构真经(id:gentoo666),分享Java干货,高并发编程,热门技术教程,微服务及分布式技术,架构设计,区块链技术,人工智能,大数据,Java面试题,以及前沿热门资讯等。每日更新哦!

参考资料:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号