程序员的算法课（18）-常用的图算法：广度优先（BFS）

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/m0_37609579/article/details/100110089

一、广度优先搜索介绍

广度优先搜索算法(Breadth First Search)，又称为"宽度优先搜索"或"横向优先搜索"，简称BFS。

它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2...的顶点。

二、广度优先搜索图解

1.无向图的广度优先搜索

下面以"无向图"为例，来对广度优先搜索进行演示。还是以上面的图G1为例进行说明。

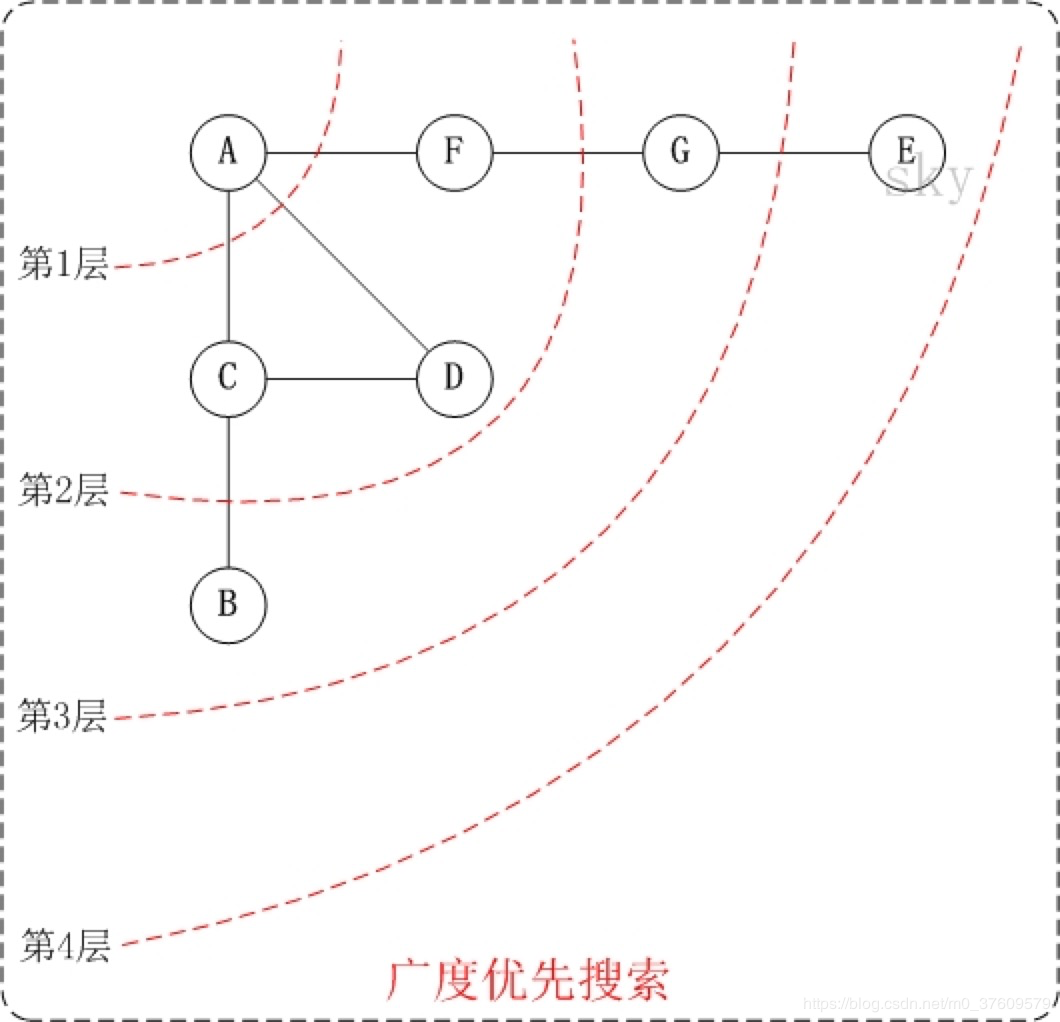
1. 第1步：访问A。 
2. 第2步：依次访问C,D,F。 在访问了A之后，接下来访问A的邻接点。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，C在"D和F"的前面，因此，先访问C。再访问完C之后，再依次访问D,F。 
3. 第3步：依次访问B,G。在第2步访问完C,D,F之后，再依次访问它们的邻接点。首先访问C的邻接点B，再访问F的邻接点G。 
4. 第4步：访问E。 在第3步访问完B,G之后，再依次访问它们的邻接点。只有G有邻接点E，因此访问G的邻接点E。

因此访问顺序是：A -> C -> D -> F -> B -> G -> E

2.有向图的广度优先搜索

下面以"有向图"为例，来对广度优先搜索进行演示。还是以上面的图G2为例进行说明。

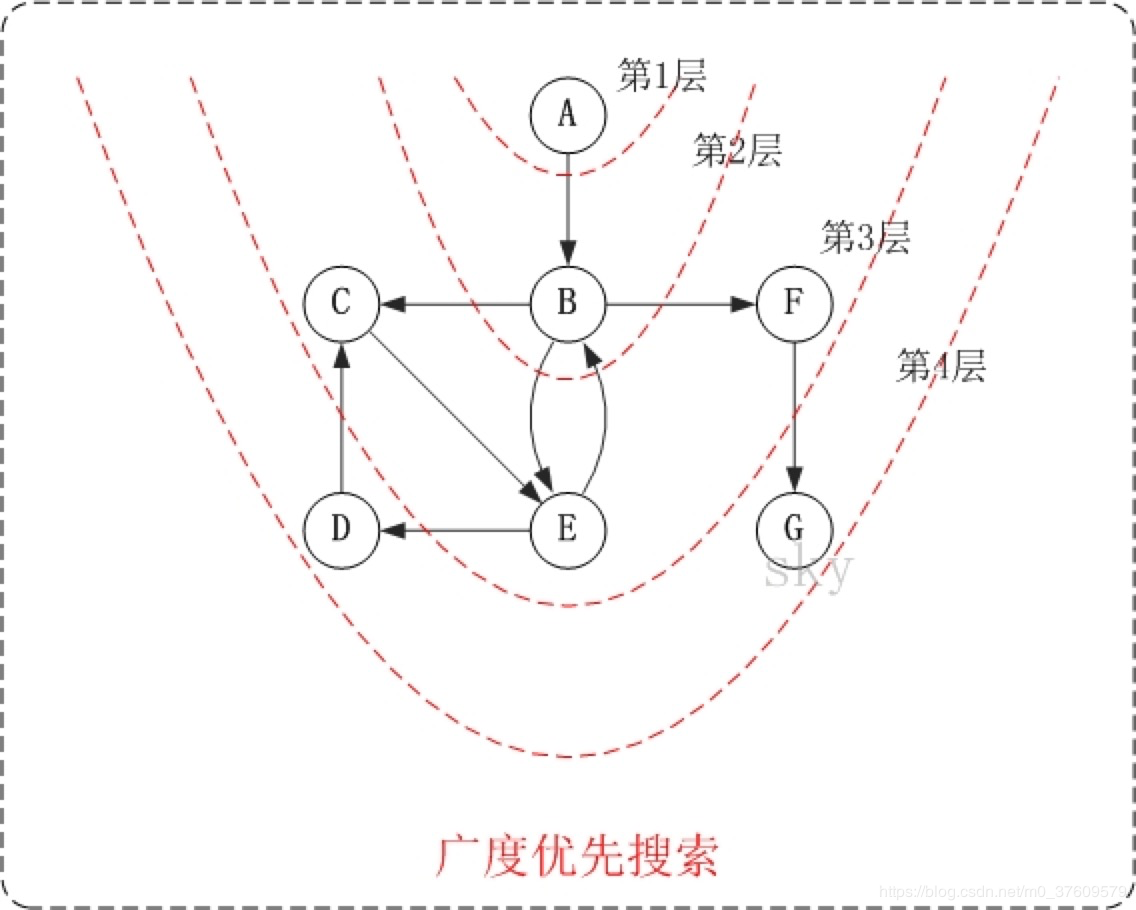
1. 第1步：访问A。 
2. 第2步：访问B。 
3. 第3步：依次访问C,E,F。 在访问了B之后，接下来访问B的出边的另一个顶点，即C,E,F。前面已经说过，在本文实现中，顶点ABCDEFG按照顺序存储的，因此会先访问C，再依次访问E,F。 
4. 第4步：依次访问D,G。在访问完C,E,F之后，再依次访问它们的出边的另一个顶点。还是按照C,E,F的顺序访问，C的已经全部访问过了，那么就只剩下E,F；先访问E的邻接点D，再访问F的邻接点G。

因此访问顺序是：A -> B -> C -> E -> F -> D -> G

三、代码实现

核心代码：

/**
 * 图的广度优先遍历算法
 */
private void boardFirstSearch(int i) {
    LinkedList<Integer> queue = new LinkedList<>(); 
    System.out.println("访问到了：" + i + "顶点");
    isVisited[i] = true;
    queue.add(i);
    
    while (queue.size() > 0) {
        int w = queue.removeFirst().intValue();
        int n = getFirstNeighbor(w);
        while (n != -1) {
            if (!isVisited[n]) {
                System.out.println("访问到了：" + n + "顶点");
                isVisited[n] = true;
                queue.add(n);
            }
            n = getNextNeighbor(w, n);
        }
    }
}

 

 

四、图的DFS和BFS完整代码

import java.util.LinkedList;

public class Graph {
    
    private int vertexSize; // 顶点数量
    private int[] vertexs; // 顶点数组
    private int[][] matrix; // 包含所有顶点的数组
    // 路径权重
    // 0意味着顶点自己到自己，无意义
    // MAX_WEIGHT也意味着到目的顶点不可达
    private static final int MAX_WEIGHT = 1000;
    private boolean[] isVisited; // 某顶点是否被访问过
    
    public Graph(int vertextSize) {
        this.vertexSize = vertextSize;
        matrix = new int[vertextSize][vertextSize];
        vertexs = new int[vertextSize];
        for (int i = 0; i < vertextSize; i++) {
            vertexs[i] = i;
        }
        isVisited = new boolean[vertextSize];
    }
    
    /**
     * 获取指定顶点的第一个邻接点
     * 
     * @param index
     *          指定邻接点
     * @return
     */
    private int getFirstNeighbor(int index) {
        for (int i = 0; i < vertexSize; i++) {
            if (matrix[index][i] < MAX_WEIGHT && matrix[index][i] > 0) {
                return i;
            }
        }
        return -1;
    }
    
    /**
     * 获取指定顶点的下一个邻接点
     * 
     * @param v
     *          指定的顶点
     * @param index
     *          从哪个邻接点开始
     * @return
     */
    private int getNextNeighbor(int v, int index) {
        for (int i = index+1; i < vertexSize; i++) {
            if (matrix[v][i] < MAX_WEIGHT && matrix[v][i] > 0) {
                return i;
            }
        }
        return -1;
    }
    
    /**
     * 图的深度优先遍历算法
     */
    private void depthFirstSearch(int i) {
        isVisited[i] = true;
        int w = getFirstNeighbor(i);
        while (w != -1) {
            if (!isVisited[w]) {
                // 需要遍历该顶点
                System.out.println("访问到了：" + w + "顶点");
                depthFirstSearch(w); // 进行深度遍历
            }
            w = getNextNeighbor(i, w); // 第一个相对于w的邻接点
        }
    }
    
    /**
     * 图的广度优先遍历算法
     */
    private void boardFirstSearch(int i) {
        LinkedList<Integer> queue = new LinkedList<>(); 
        System.out.println("访问到了：" + i + "顶点");
        isVisited[i] = true;
        queue.add(i);
        
        while (queue.size() > 0) {
            int w = queue.removeFirst().intValue();
            int n = getFirstNeighbor(w);
            while (n != -1) {
                if (!isVisited[n]) {
                    System.out.println("访问到了：" + n + "顶点");
                    isVisited[n] = true;
                    queue.add(n);
                }
                n = getNextNeighbor(w, n);
            }
        }
    }

    public static void main(String[] args) {
        Graph graph = new Graph(9);

        // 顶点的矩阵设置
        int[] a1 = new int[] { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
        int[] a2 = new int[] { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
        int[] a3 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
        int[] a4 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, 24, 16, 21 };
        //int[] a4 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
        int[] a5 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
        int[] a6 = new int[] { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
        int[] a7 = new int[] { MAX_WEIGHT, 16, MAX_WEIGHT, 24, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
        //int[] a7 = new int[] { MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
        int[] a8 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
        int[] a9 = new int[] { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };

        graph.matrix[0] = a1;
        graph.matrix[1] = a2;
        graph.matrix[2] = a3;
        graph.matrix[3] = a4;
        graph.matrix[4] = a5;
        graph.matrix[5] = a6; 
        graph.matrix[6] = a7;
        graph.matrix[7] = a8;
        graph.matrix[8] = a9;
        
        graph.depthFirstSearch(0);
        //graph.boardFirstSearch(0);
    }

}

 

五、总结

• 广度优先遍历表示把每一层都遍历完才能遍历下一层。
• 我们来思考：假设v0有3个邻接点，v1 v2 v3。
  • 我们访问v0后，然后访问v1 v2 v3。完毕后我们要从v1开始遍历它的邻接点，接着从v2开始遍历它的邻接点，最后是从v3开始遍历它的邻接点。
  • 也就是说，3个邻接点访问完后。我们要回过头逐个遍历它们的邻接点。这一点我觉得要用个容器把它们顺序存储下来。然后每次从容器首部取出一个顶点开始遍历。这里我想到LinkedList，因为它适合增删。而且这里不需要遍历集合。

• 我们可以把第一个顶点放进集合，然后while(!queue.isEmpty())或while(queue.size() > 0)都行。开始循环。
  • 然后取出并删除集合中第一个顶点元素的第一个邻接点。对这个顶点进行访问，
    • 如果该顶点未访问过，就访问！然后将该顶点放入集合。
    • 如果该顶点已访问过，就找该顶点的下一个邻接点。

---

我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！

参考资料：

1. https://blog.csdn.net/Strive_Y/article/details/81810012
2. https://www.jianshu.com/p/23b55db1adc0