版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
一、图的定义
在计算机科学中,图(Graphics)是由顶点集合(Vertex)及顶点间的关系(边)集合(Edge)组成的一种数据结构,这些顶点通过一系列边结对(连接)。顶点用圆圈表示,边就是这些圆圈之间的连线。顶点之间通过边连接。
记作G=(V, E) G:Graphics 图形 V:Vertex 顶点 E:Edge 边
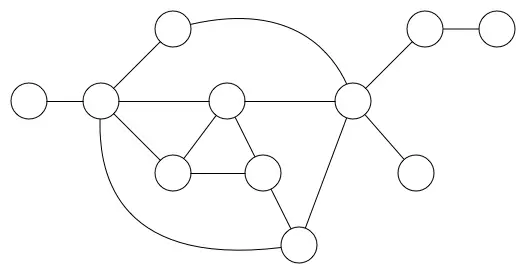
二、图种类
1.有向图和无向图
如果边是有方向的则称为有向图,如果边没有方向则称为无向图
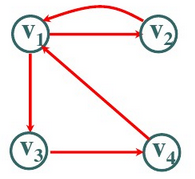
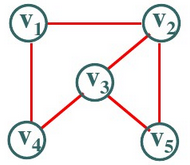
2.无权图和带权图
对图中的边赋予具有一定意义的数值(路程、费用等等)的图称为带权图
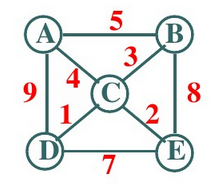
3.完全图:任意两个顶点之间都存在一条边
4.稀疏图:有很少的边
5.稠密图:有很多的边,最稠密的图就是完全图
二、图的术语
顶点(Vertex):表示图中的一个结点
边(Edge):表示顶点和顶点之间的连线
向:图中所有的边都没有方向就是无向图,有方向则是有向图
邻接(adjacency):是两个顶点之间的一种关系,如果两个顶点在同一条边上,则称它们互为邻接点。
关联(incidence):关联是边和顶点之间的关系。
度(Degree):一个顶点 跟它相关联的边的数量称为度
- 对于无向图,顶点v的度就是和v相关联的边的条数
- 对于有向图,顶点v的度根据方向分为入度(in-degree)和出度(out-degree)
权(Weight):与图的边相关的数字叫做权,权常用来表示图中顶点间的距离或者耗费
路径(path):顶点与定点之间的边就称为路径
- 无权图的路径长就是路径包含的边数。
- 有权图的路径长要乘以每条边的权。
连通性:如果图中任意两个顶点都是连通的,则称该图是连通图。
- 对于有向图,如果图中每一对顶点Vi和Vj是双向连通的,则该图是强连通图。
三、现实建模
图可用于对现实中很多系统建模
- 对交通流量建模
- 顶点可以表示街道的十字路口, 边可以表示街道
- 加权的边可以表示限速或者车道的数量或者街道的距离
- 建模人员可以用这个系统来判定最佳路线以及最可能堵车的街道
- 对飞机航线建模
- 航空公司可以用图来为其飞行系统建模
- 将每个机场看成顶点, 将经过两个顶点的每条航线看作一条边
- 加权的边可以表示从一个机场到另一个机场的航班成本, 或两个机场间的距离
- 建模人员可以利用这个系统有效的判断从一个城市到另一个城市的最小航行成本
四、图的表示
我们知道一个图包含很多顶点, 另外包含顶点和顶点之间的连线(边), 这两个都是非常重要的图信息, 因此都需要在程序中体现出来。
1.邻接矩阵法
基本思想:
- 用一维数组存储顶点 – 描述顶点相关的数据
- 用二维数组存储边 – 描述顶点间的边
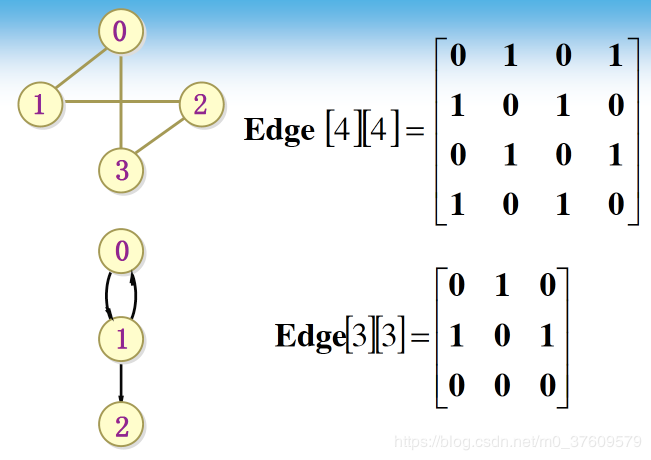
- 无向图的邻接矩阵是对称的
- 有向图的邻接矩阵可能是不对称的
优缺点:
- 优点:直观,容易实现
- 缺点:当顶点数较多,而边数较少时浪费时间和空间
2.邻接链表法
基本思想:
- 从同一个顶点发出的边链接在同一个链表中
- 每一个链表结点代表一条边, 结点中保存边的另一顶点的下标和权值
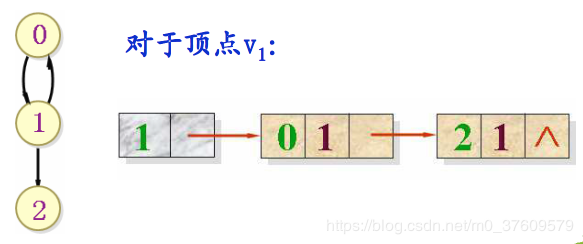
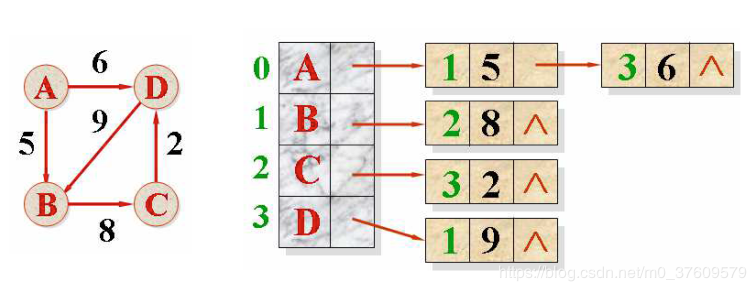
优缺点:
- 优点:有效利用空间,非常适合边数较少的图
- 缺点:实现相对复杂,不容易查找两个顶点间的权值
五、图论算法
- 拓扑排序
- 最短路径
- 最小生成树
- 关键路径
- 网络流问题
六、总结
- 图是一种扩展的树结构,每个结点可以指向任意的其它结点
- 链表是特殊的树结构,树是特殊的图结构
- 图这种数据结构常用于网络规划和路径路径规划等领域
我的微信公众号:架构真经(id:gentoo666),分享Java干货,高并发编程,热门技术教程,微服务及分布式技术,架构设计,区块链技术,人工智能,大数据,Java面试题,以及前沿热门资讯等。每日更新哦!

参考资料:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号