版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
一、霍夫曼（Huffman）的由来
1.历史上的远距通信问题
最初的远距通信用于传递文本信息，主要是电报。
- 小A：如何将一段文字内容为“BADCADFEED”通过网络传递给别人呢？
- 小B：利用二进制对这些字母进行编码，然后传输这个编码就行啊。
- 小D：是的，电报不就“滴”和“答”嘛？！
- 小A：那怎么编码呢？
- 小C：难道你没听说过ASCII码？
- 小A：那时有没有ASCII码哦？
2.最初的解决方案
对于文本”BADCADFEED”的传输而言，因为重复出现的只有”ABCDEF”这6个字符，因此可以用下面的方式编码：
接收方可以根据每3个bit进行一次，字符解码的方式还原文本信息。
3.但是这个方案存在严重的性能问题：
- 这样的编码方式需要30个bit位才能表示10个字符
- 那么当传输一篇500个字符的情报时，需要15000个bit位
在战争年代，这种编码方式对于情报的发送和接受是很低效且容易出错的。
4.如何提高收发效率？
二、霍夫曼编码
1.新的编码方式
要提高效率，必然要从编码方式的改进入手，要避免每个字符都占用相同的bit位。
2.效率提升
- 改进的编码方式只需要25个bit位就能表示10个字符
- 随着传输字符的增加，这种优势会更明显
- 效率上得到17%的提高！！！
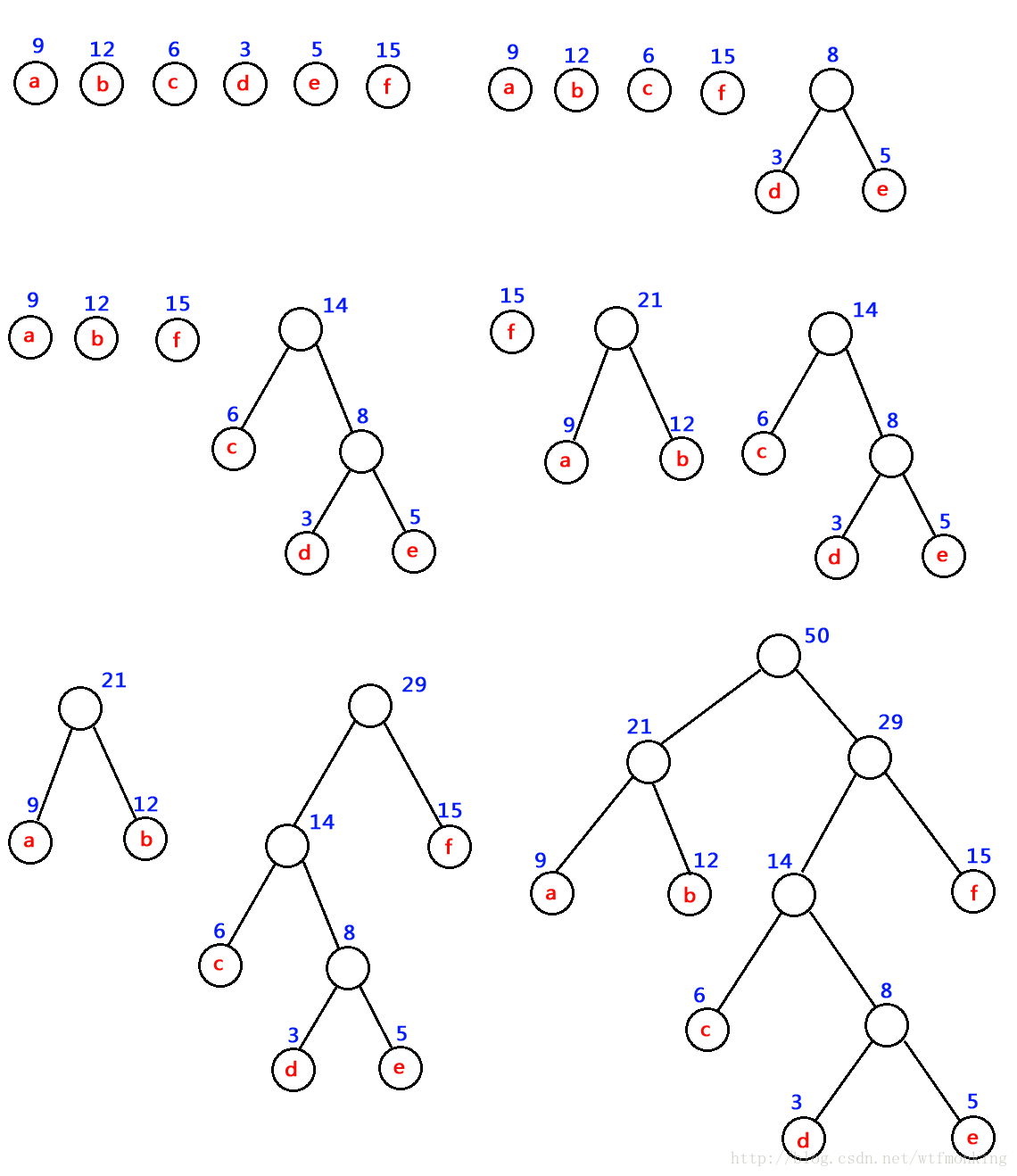
三、霍夫曼树的构建步骤
精妙之处：任一字符的编码都不是另一个字符编码的前缀！
假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：
- 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；
- 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
- 从森林中删除选取的两棵树，并将新树加入森林；
- 重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。
四、总结
- 霍夫曼树是一种特殊的二叉树
- 霍夫曼树应用于信息编码和数据压缩领域
- 霍夫曼树是现代压缩算法的基础
我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！
参考资料：
