一、计算机科学中的树
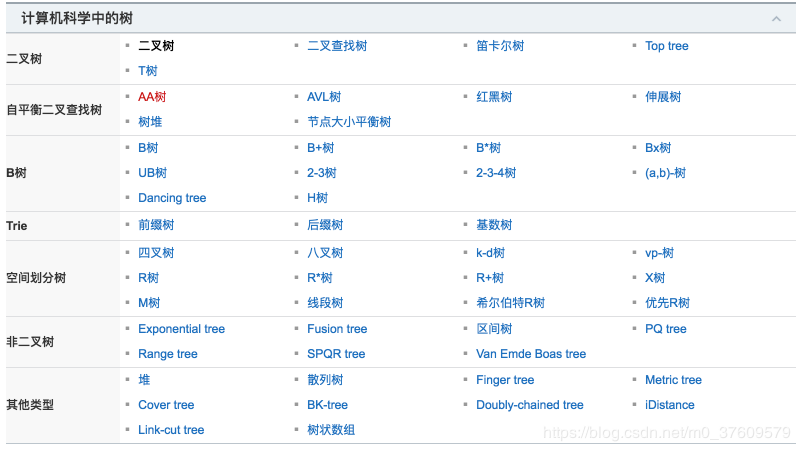
二、二叉树的定义
一棵树，它的每个节点最多只能有两个子节点，此时就叫二叉树。（我们一般在书中试题中见到的树是二叉树，但并不意味着所有的树都是二叉树。如果节点多于两个，我们也称之为多路树）
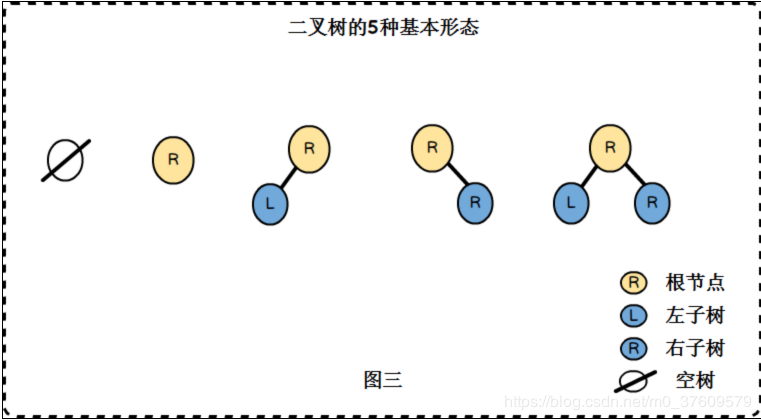
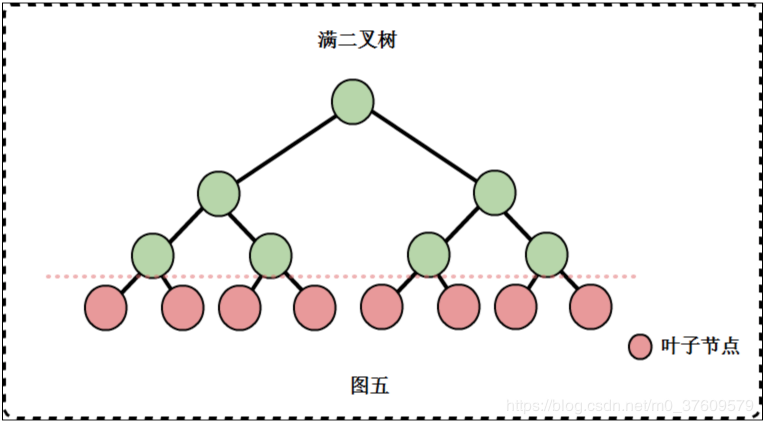
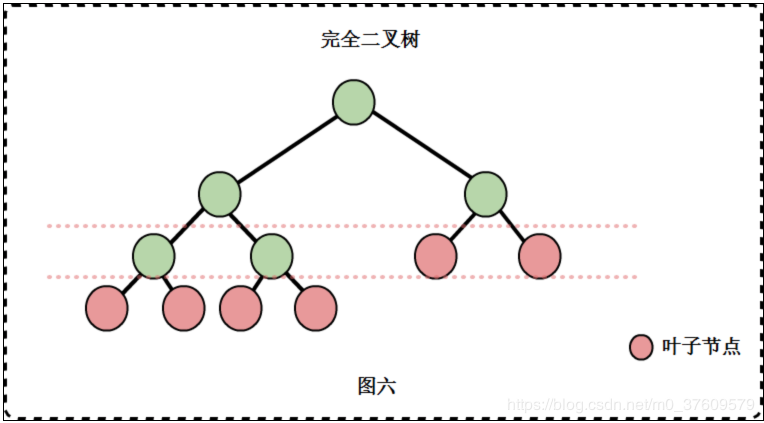
可以看出： 满二叉树一定是完全二叉树；完全二叉树不一定是满二叉树。
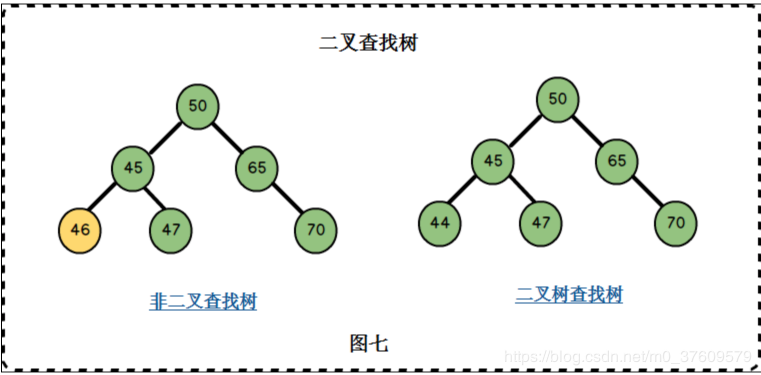
如果我们给二叉树加一个额外的条件，就可以得到一种被称作二叉查找树(binary search tree)的特殊二叉树。
二叉查找树要求：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。【左边下边小，右边上边大】
三、二叉查找树的日常操作
PS:二叉树很多，但对我们来说，在实际的应用中，二叉排序树的应用比较多。
1.插入新节点
假设我们要为数组 a[] = {10 ， 5 ， 15 ， 6 ， 4 ， 16 }构建一个二叉排序树，我们按顺序逐个插入元素。
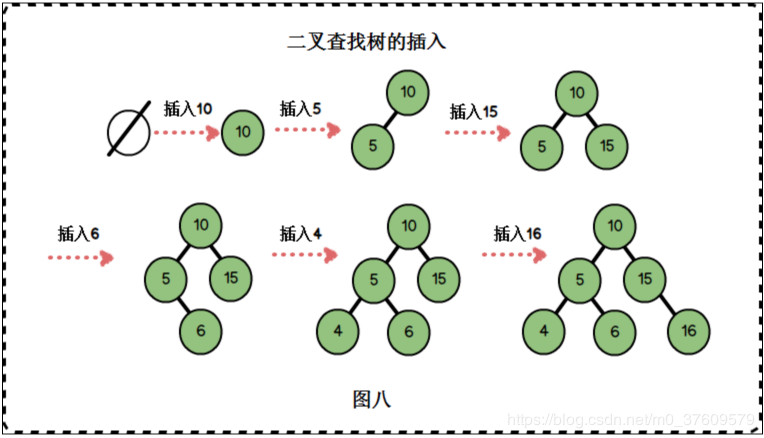
插入过程是这样的：
如果是空树，则创建一个新节点，新节点作为根，因此以元素10构建的节点为该二叉查找树的根。
- 插入5，5比10小，与10的左孩子节点进行比较，10的左孩子节点为空，进行插入。
- 插入15，15比10大，与10的右孩子节点进行比较，10的右孩子节点为空，进行插入。
- 插入6，6比10小，与10的左孩子节点5比较；6比5大，与5的右孩子节点进行比较，5的右孩子为空，进行插入。
- 插入4，4比10小，与10的左孩子节点5比较；4比5小，与5的左孩子节点进行比较，5的左孩子为空，进行插入。
- 插入16，16比10大，与10的右孩子节点15比较；16比15大，与15的右孩子节点进行比较，15的右孩子为空，进行插入。
从这个过程我们可以总结出插入新元素的步骤：
- 寻找元素合适的插入位置：新元素与当前结点进行比较，若值大于当前结点，则从右子树进行寻找；否则从左子树进行寻找.
- 找到插入位置之后，以元素的值构建新节点，插入二叉排序树中。
2.遍历平衡二叉树
【百度百科】平衡二叉搜索树，又被称为AVL树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。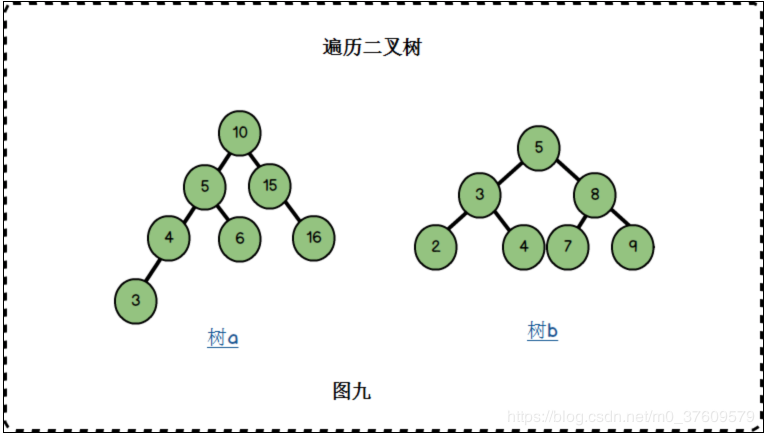 
遍历平衡二叉树，就是以某种方式逐个“访问”二叉树的每一个节点。举例说明：
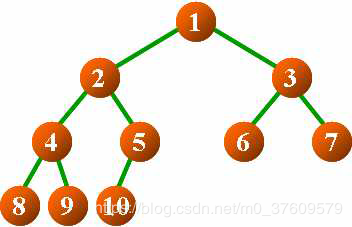
前序遍历
- 访问根结点中的数据
- 前序遍历左子树
- 前序遍历右子树
前序遍历结果：
1, 2, 4, 8, 9, 5, 10, 3, 6, 7
中序遍历
- 中序遍历左子树
- 访问根结点中的数据
- 中序遍历右子树
中序遍历结果：
8, 4, 9, 2, 10, 5, 1, 6, 3, 7
后序遍历
- 后序遍历左子树
- 后序遍历右子树
- 访问根结点中的数据
后序遍历结果：
8, 9, 4, 10, 5, 2, 6, 7, 3, 1
层次遍历
- 访问根结点中的数据
- 访问第二层所有结点的数据
- 访问第三层所有结点的数据
- ……
层次遍历结果：
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
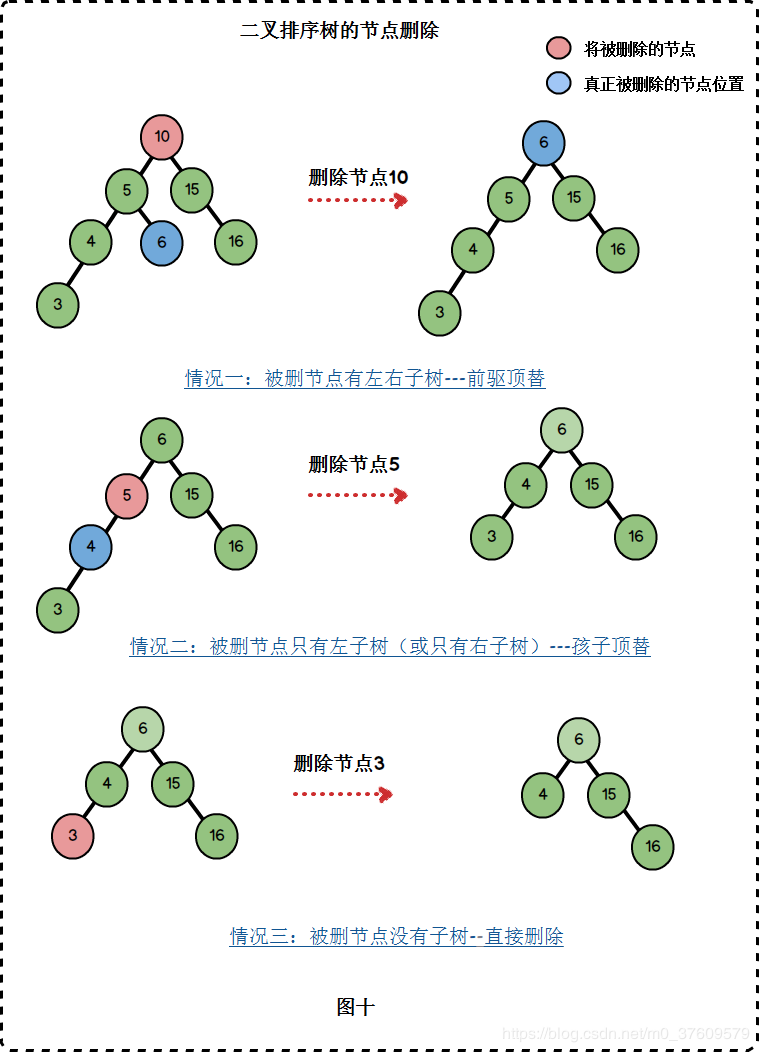
3.删除节点
删除二叉排序树的某个节点有三种情况：
- 被删除节点同时有左子树与右子树。将前驱节点的值保存在当前结点，继而删除前驱节点。
- 被删除节点只有左子树或只有右子树。直接用子树替换被删节点。
- 被删除节点没有子树。可以直接删除节点。
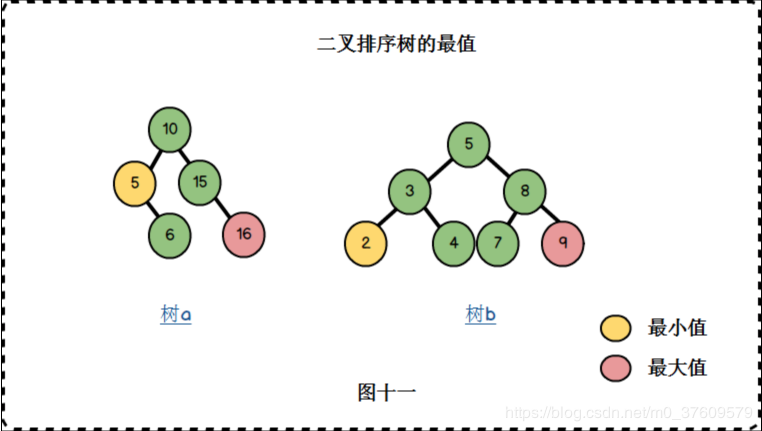
4.查找最值元素
二叉排序树的最小值位于其最左节点上；最大值位于其最右节点上
我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！
四、参考资料
https://blog.csdn.net/wannuoge4766/article/details/83998377
https://www.cnblogs.com/shixiangwan/p/7530015.html
https://www.cnblogs.com/ysocean/p/8032642.html
https://blog.csdn.net/u014634338/article/details/42465089
http://www.it610.com/article/3607922.htm
