接下来我们将会介绍另外一种数据结构——树。二叉树是树这种数据结构的一员，后面我们还会介绍红黑树，2-3-4树等数据结构。那么为什么要使用树？它有什么优点？
前面我们介绍数组的数据结构，我们知道对于有序数组，查找很快，并介绍可以通过二分法查找，但是想要在有序数组中插入一个数据项，就必须先找到插入数据项的位置，然后将所有插入位置后面的数据项全部向后移动一位，来给新数据腾出空间，平均来讲要移动N/2次，这是很费时的。同理，删除数据也是。
然后我们介绍了另外一种数据结构——链表，链表的插入和删除很快，我们只需要改变一些引用值就行了，但是查找数据却很慢了，因为不管我们查找什么数据，都需要从链表的第一个数据项开始，遍历到找到所需数据项为止，这个查找也是平均需要比较N/2次。
那么我们就希望一种数据结构能同时具备数组查找快的优点以及链表插入和删除快的优点，于是 树 诞生了。
一、树的定义
【百度百科】树状图是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树。这就是一棵树-------------------—》》》》》》》》》
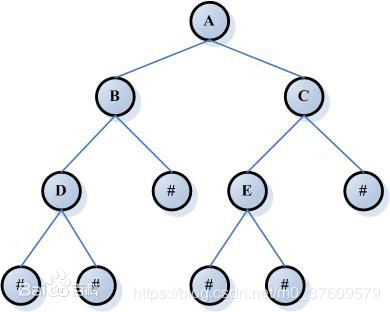
二、树的基本概念及特点
树的基本概念
树（tree）是包含n（n>=0）个结点的有穷集，其中：
每个元素称为结点（node）；
有一个特定的结点被称为根结点或树根（root）；
除根结点之外的其余数据元素被分为m（m≥0）个互不相交的集合T1，T2，……Tm-1，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）。
树的特点：
①每个节点有零个或多个子节点；
②没有父节点的节点称为根节点；
③每一个非根节点有且只有一个父节点；
④除了根节点外，每个子节点可以分为多个不相交的子树；
三、树的常用术语
①路径：顺着节点的边从一个节点走到另一个节点，所经过的节点的顺序排列就称为“路径”。
②根：树顶端的节点称为根。一棵树只有一个根，如果要把一个节点和边的集合称为树，那么从根到其他任何一个节点都必须有且只有一条
③父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；B是D的父节点。
④子节点：一个节点含有的子树的根节点称为该节点的子节点；D是B的子节点。
⑤兄弟节点：具有相同父节点的节点互称为兄弟节点；比如上图的D和E就互称为兄弟节点。
⑥叶节点：没有子节点的节点称为叶节点，也叫叶子节点，比如上图的H、E、F、G都是叶子节点。
⑦子树：每个节点都可以作为子树的根，它和它所有的子节点、子节点的子节点等都包含在子树中。
⑧节点的层次：从根开始定义，根为第一层，根的子节点为第二层，以此类推。
⑨深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0；
⑩高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；
四、树的分类
类型上来讲
- 无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树;
- 有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；
- 二叉树：每个节点最多含有两个子树的树称为二叉树；
- 完全二叉树
- 满二叉树
- 霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
算法上来讲
二叉查找树（二叉排序树）、平衡二叉树（AVL树）、红黑树、B-树、B+树、字典树（trie树）、后缀树、广义后缀树。
五、树的操作
- 创建树
- 销毁树
- 清空树
- 插入结点
- 删除结点
- 获取结点
- 获取根结点
- 获取树的结点数
- 获取树的高度
- 获取树的度
我的微信公众号：架构真经（id：gentoo666），分享Java干货，高并发编程，热门技术教程，微服务及分布式技术，架构设计，区块链技术，人工智能，大数据，Java面试题，以及前沿热门资讯等。每日更新哦！
六、参考资料
https://www.cnblogs.com/ysocean/p/8032642.html
https://www.cnblogs.com/shixiangwan/p/7530015.html
https://blog.csdn.net/wannuoge4766/article/details/83998377
