五边形数
五边形数
五边形数是能排成五边形的多边形数,一般用到的是广义五边形数。
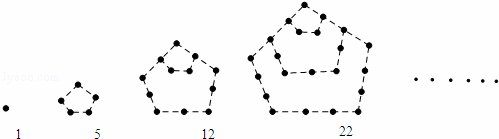
广义五边形数
广义五边形数的公式和五边形数相同,只是 \(n\) 可以为负数和零,\(n\) 依序为 \(0, 1, -1, 2, -2, 3, -3, 4...\)
五边形数和拆分数有着密切的关系。
具体的,拆分数的生成函数是
\[\prod_{i=1}^{+\infty}\frac{1}{(1-x^i)}
\]
而
\[\prod_{i=1}^{+\infty}{(1-x^i)}=\sum_{i=-\infty}^{+\infty}(-1)^ix^{\frac{i(3i-1)}2}
\]
即这个东西在模 \(x^n\) 意义下只有 \(\sqrt{n}\) 项的系数是有值的。
所以可以手动求逆求出拆分数,时间复杂度 \(n\sqrt{n}\) 。
最有用的东西实际上是那个多项式在无穷项时系数不为 \(0\) 的项十分有限。
int - > long long
0 - > 100

 五边形数
五边形数
