HAOI2012 容易题

题意

给定一个长度为\(m\)的数组，每个位置上只能取\(1-n\)的数，并且有些位置不能取一些数，求可能构成的数列的所有数的积的和，也就是先乘起来再加。

分析

一看这数据\(n\)的范围已经到了\(10^9\)，显然枚举这个不可能，所以考虑把他们当一个整体用。

如果没有限制，每个位置上可以取的数如下图，idx表示下标，val表示值。

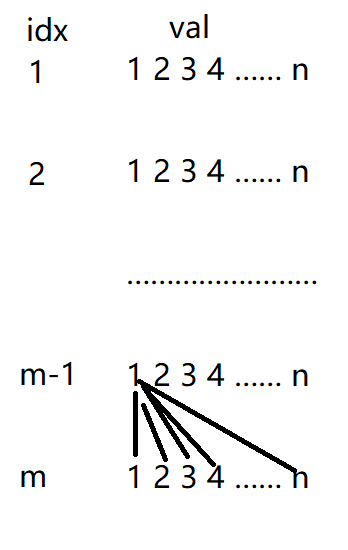
从m开始往前推，对第m-1行，1可以与m行的val都乘一遍，类似分步乘法，2也是，一直到n，最后再把这些数加起来，类似分类加法，就能得到这两行的积的和，是\(\sum_{i=1}^n×\sum_{i=1}^n\)，然后发现这其实是一个等差数列，\(\sum_{i=1}^n=\)\(n(n+1)\over2\)，所以\(\sum_{i=1}^n×\sum_{i=1}^n=\)(\(n(n+1)\over2\)\()^2\) ，然后用数学归纳法一步一步往前推，可以得到这\(m\)个位置的和为(\(n(n+1)\over2\)\()^m\) ，\(n(n+1)\over2\)这个式子最大也不会超过longlong，开始我傻了我乘出来十的八十一次方，可以先把这个求出。

然后考虑有限制的情况，假设是\(m-1\)行不能取\(1\)，可以得到下图。

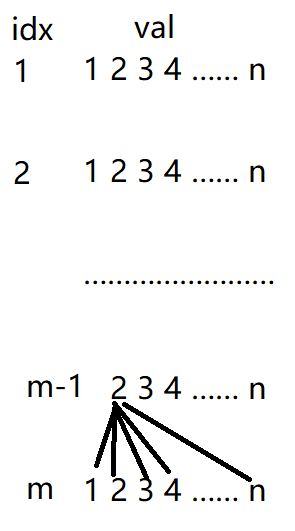
这个不太好看，因为每个位置和每个位置没有绝对的关系，所以可以变换得到下图，就是把有限制条件的放到最后再算。

这样的话没有限制条件的就是(\(n(n+1)\over2\)\()^{m-1}\)，有限制条件的呢？发现还可以跟之前推的方法类似，就是每个可能取到的数乘一遍再加起来，即\(n(n+1)\over2\) \(-1\)，减去别的数也是一样。

于是假设有\(cnt\)个位置有限制，可以先用快速幂求出不受限制的位置的答案，即(\(n(n+1)\over2\)\()^{m-cnt}\)，然后枚举这\(cnt\)个位置，每个位置对答案的贡献是\(n(n+1)\over2\)\(-不能取的数的和\)，然后记得取Mod就行了。
还有因为题目没说保证给出的条件不重复，所以要去重。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int N=1e5+10;
const int Mod=1e9+7;
struct Node{
    int idx,w;
    bool operator <(const Node &A)const {
        if(idx==A.idx)return w<A.w;
        return idx<A.idx;
    }
}p[N];
ll sum[N];
ll fpow(ll a,ll b){
    ll res=1;
    while(b){
        if(b&1)res=(res*a)%Mod;
        a=a*a%Mod;
        b>>=1;
    }
    return res%Mod;
}
int main(){
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=k;i++)
        scanf("%d%d",&p[i].idx,&p[i].w);
    sort(p,p+k+1);
    int cnt=0;
    int tot=((n+1ll)*n%Mod)/2;
    for(int i=1;i<=k;i++){
        if(p[i].idx!=p[i-1].idx)
            sum[++cnt]=tot;
        else if(p[i].w==p[i-1].w)
            continue;
        sum[cnt]-=p[i].w;
        sum[cnt]=(sum[cnt]+Mod)%Mod;
    } 
    ll ans=fpow(tot,m-cnt);
    for(int i=1;i<=cnt;i++)
        ans=(ans*sum[i])%Mod;
    printf("%lld\n",ans);
    return 0;
}