CF1051F The Shortest Statement 倍增+最短路

分析

这个题第一眼看见查询的次数就知道不可能每次都跑一遍Dij，看到\(n\)的范围就知道Floyd不可，然后想，反正跑的是最短路，用一个最小生成树呗，答案显然是错的。

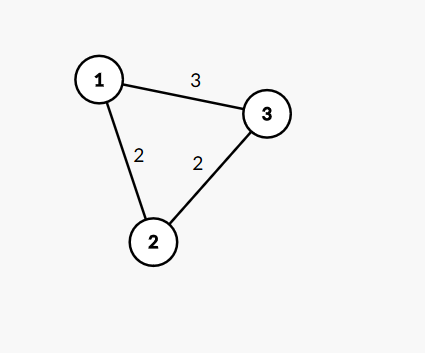
这样的话1到3的最短路会算成4而不是3，接下来注意到它不断在提的东西，边和点的差值不会很大，也就是说如果搭出一棵树，最短路中大部分边甚至所有的边都会在树上，而对于不在树上的情况，可以从每条不在树上的边的起点和终点开始跑一遍Dij，这样最后转移时就考虑一下各种情况就行，主要情况其实就两种：

• 两点树上的距离
• 经过不在树上的边

对于情况一，倍增LCA就能解决，对于情况二，枚举先跑到哪个点然后尝试更新答案即可。
还是那句话，题不难，不好调。。。。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define ll long long
using namespace std;
const int N=2e5+10;
struct Edge{
    int to,nxt,val,fro;
    bool operator <(const Edge&A)const{
        return val<A.val;
    }
    bool idx;
}E[N],e[N];
struct Node{
    int id;ll val;
    Node(){}
    Node(int u,ll v){
        id=u;val=v;
    }
    bool operator <(const Node &A)const {
        return val>A.val;
    }
};
int h[N],idx;
void Ins(int a,int b,int c){
    e[idx].to=b;e[idx].nxt=h[a];
    e[idx].val=c;h[a]=idx++;
}
int n,m,f[N];
int find(int x){
    return f[x]==x?x:(f[x]=find(f[x]));
}
void Mer(int a,int b){
    f[find(a)]=find(b);
}
void kru(){
    sort(E+1,E+m+1);
    for(int i=1;i<=n;i++)f[i]=i;
    for(int i=1;i<=m;i++){
        int u=E[i].fro,v=E[i].to;
        if(find(u)!=find(v)){
            Mer(u,v);
            Ins(u,v,E[i].val);Ins(v,u,E[i].val);
        }else E[i].idx=1;
    }
}
int p[N][20],dep[N];
ll dist[N];
void dfs(int u){
    for(int i=0;p[u][i];i++)
        p[u][i+1]=p[p[u][i]][i];
    for(int i=h[u];~i;i=e[i].nxt){
        int v=e[i].to;
        if(v==p[u][0])continue;
        p[v][0]=u;
        dist[v]=dist[u]+e[i].val;
        dep[v]=dep[u]+1;
        dfs(v);
    }
}
int cnt;
ll dis[50][N];
bool vis[N];
void dij(int num,int s){
    memset(dis[num],0x3f,sizeof(dis[num]));
    memset(vis,0,sizeof(vis));
    priority_queue<Node > q;
    dis[num][s]=0;
    q.push(Node(s,0));
    while(!q.empty()){
        Node u=q.top();q.pop();
        if(vis[u.id])continue;
        vis[u.id]=1;
        for(int i=h[u.id];~i;i=e[i].nxt){
            int v=e[i].to;
            if(dis[num][v]>dis[num][u.id]+e[i].val){
                dis[num][v]=dis[num][u.id]+e[i].val;
                q.push(Node(v,dis[num][v]));
            }
        }
    }
}
int lca(int a,int b){
    if(dep[a]<dep[b])swap(a,b);
    int d=dep[a]-dep[b];
    for(int i=0;d;d>>=1,i++)
        if(d&1)a=p[a][i];
    if(a==b)return a;
    for(int i=19;i>=0;i--)
        if(p[a][i]!=p[b][i]){
            a=p[a][i];b=p[b][i];
        }
    return p[a][0];
}
int main(){
    //freopen("a.txt","r",stdin);
    memset(h,-1,sizeof(h));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int a,b,c;
        scanf("%d%d%d",&E[i].fro,&E[i].to,&E[i].val);
    }
    kru();
    for(int i=1;i<=n;i++)
        if(!dep[i])dfs(i);
    for(int i=1;i<=m;i++)
        if(E[i].idx){
            Ins(E[i].fro,E[i].to,E[i].val);
            Ins(E[i].to,E[i].fro,E[i].val);
        }
    for(int i=1;i<=m;i++)
        if(E[i].idx){
            dij(++cnt,E[i].fro);
            dij(++cnt,E[i].to);
        }
    int q;
    scanf("%d",&q);
    while(q--){
        int a,b;
        scanf("%d%d",&a,&b);
        ll ans=dist[a]+dist[b]-2*dist[lca(a,b)];
        for(int i=1;i<=cnt;i++){
            ans=min(ans,dis[i][a]+dis[i][b]);
        }
        printf("%lld\n",ans);
    }
}