【状压dp】cf906C. Party

需要稍加分析结论；还有一些小细节

Arseny likes to organize parties and invite people to it. However, not only friends come to his parties, but friends of his friends, friends of friends of his friends and so on. That's why some of Arseny's guests can be unknown to him. He decided to fix this issue using the following procedure.

At each step he selects one of his guests A, who pairwise introduces all of his friends to each other. After this action any two friends of Abecome friends. This process is run until all pairs of guests are friends.

Arseny doesn't want to spend much time doing it, so he wants to finish this process using the minimum number of steps. Help Arseny to do it.

Input

The first line contains two integers n and m (1 ≤ n ≤ 22; 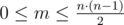) — the number of guests at the party (including Arseny) and the number of pairs of people which are friends.

Each of the next m lines contains two integers u and v (1 ≤ u, v ≤ n; u ≠ v), which means that people with numbers u and v are friends initially. It's guaranteed that each pair of friends is described not more than once and the graph of friendship is connected.

Output

In the first line print the minimum number of steps required to make all pairs of guests friends.

In the second line print the ids of guests, who are selected at each step.

If there are multiple solutions, you can output any of them.

---

 

题目大意

给定一些关系(u,v)代表两个人是朋友。每次可以选择一个人i，使i的朋友都相互变成朋友。问最少需要选择多少人，使得所有的人都能够相互认识。

题目分析

一些初步的想法

一开始比较自然地会考虑完全子图的情况。

那么有一个想法是：能不能把这整个完全子图给看成一个人？既然他们互相认识，那么这样它连出的边可以等效吗？

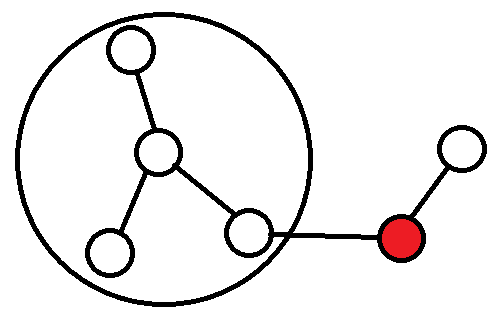
但这个想法的问题在于，这个完全子图的关系“不可拓展”，也就是说在他们的朋友介绍新朋友时，新加进来的人并不能和其他人认识。

那么贪心？

考虑到新加进人的过程是不可逆的。那么能不能够贪心地每次选尽可能多的点呢？

这样似乎还没有找到反例。但是这个做法的潜在危险在于其复杂度基于答案大小，有可能会因为答案数过大而TLE/MLE.

#include<bits/stdc++.h>
const int INF = 0x3f3f3f3f;
const int maxn = 31;

int n,m,ans,id;
struct node
{
    int val,vis[maxn],pr[maxn],deg[maxn];
    std::bitset<maxn> mp[maxn];
    bool legal()
    {
        for (int i=1; i<=n; i++)
            if (mp[i].count() < n) return 0;
        return 1;
    }
    void print()
    {
        for (int i=1; i<=val; i++)
            printf("%d ",pr[i]);
        puts("");
    }
}now,tmp,chg;
std::queue<node> q;

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch=getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch=getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
int main()
{
    freopen("party.in","r",stdin);
    freopen("party.out","w",stdout);
    n = read(), m = read(), now.val = 0, ans = INF;
    for (int i=1; i<=n; i++) now.mp[i][i] = 1;
    for (int i=1; i<=m; i++)
    {
        int u = read(), v = read();
        now.mp[u][v] = 1, now.mp[v][u] = 1;
    }
    q.push(now);
    while (q.size())
    {
        tmp = q.front(), q.pop();
        if (tmp.legal()){
            ans = tmp.val;
            printf("%d\n",ans);
            tmp.print();
            break;
        }
        bool fnd = 0;
        while (!fnd){
        id = 0;
        for (int i=1; i<=n; i++)
            if (!tmp.vis[i]){
                tmp.deg[i] = tmp.mp[i].count();
                if (tmp.deg[i] > tmp.deg[id]) id = i;
            }
        for (int i=1; i<=n; i++)
            if (tmp.deg[i]==tmp.deg[id]){
                bool upd = 0;
                chg = tmp, chg.val++;
                chg.vis[i] = 1, chg.pr[chg.val] = i;
                for (int j=1; j<=n; j++)
                    for (int k=1; k<=n; k++)
                        if (j!=k&&chg.mp[i][j]&&chg.mp[i][k]&&!chg.mp[j][k])
                            chg.mp[k][j] = chg.mp[j][k] = 1, upd = 1;
                if (upd) fnd = 1, q.push(chg);
                else tmp.vis[i] = 1;
            }
        }
    }
    return 0;
}

状压dp

注意到特殊的数据范围，考虑状压。

首先明确两个结论：

1. 答案与合并顺序无关
2. 对图$G=\{V,E\}$中一个完全子图$G'=\{V',E'\}$中的点$x\in V'$进行操作后，其所在的完全子图$G''=\{V'+V_x,E'+E_x\},E_x=\{x,V_x\}\in E$。换句话说就是操作集合内的点能使集合变大。

第一条是因为操作点$x$之后$\forall (x,y_i)$，$y_i$之间都存在边，那么下一步选取$y_i$时会把其他的$y_j$也都连在一起；第二条比较容易理解。

那么用$f[i]$表示$i$的二进制状态下，这些人相互认识的最小代价。

于是转移就是经典的状压转移；顺便再记录一下转移的位置就好了。

需要注意的细节是原图是否已经连通，那么这个就是预处理的时候再判断一下。

 

#include<bits/stdc++.h>
const int maxn = 35;
const int maxs = 5000035;
const int INF = 0x3f3f3f3f;

bool fnd;
int n,m,mx;
int s[maxn],f[maxs],fa[maxs],pr[maxs];

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch=getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch=getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void fndScheme(int st)
{
    if (fa[st]) fndScheme(fa[st]);
    printf("%d ",pr[st]);
}
int main()
{
//    freopen("party.in","r",stdin);
//    freopen("party.out","w",stdout);
    memset(f, 0x3f3f3f3f, sizeof f);
    n = read(), m = read(), mx = (1<<n)-1;
    for (int i=0; i<n; i++) s[i+1] = 1<<i;
    for (int i=1; i<=m; i++)
    {
        int x = read()-1, y = read()-1;
        s[x+1] |= 1<<y, s[y+1] |= 1<<x;
    }
    fnd = 1;
    for (int i=1; i<=n; i++)
    {
        f[s[i]] = 1, pr[s[i]] = i;
        if (s[i]!=mx) fnd = 0;
    }
    if (fnd){
        puts("0");
        return 0;
    }
    for (int st=1; st<=mx; st++)
        if (f[st]!=INF){
            for (int i=1; i<=n; i++)
                if (((st>>(i-1))&1)&&(f[st]+1 < f[st|s[i]])){
                    f[st|s[i]] = f[st]+1;
                    fa[st|s[i]] = st;
                    pr[st|s[i]] = i;
                }
        }
    printf("%d\n",f[mx]);
    fndScheme(mx);
    return 0;
}

 

 

 

 

END