【动态规划】bzoj1584: [Usaco2009 Mar]Cleaning Up 打扫卫生
思路自然的巧妙dp
Description
有N头奶牛，每头那牛都有一个标号Pi，1 <= Pi <= M <= N <= 40000。现在Farmer John要把这些奶牛分成若干段，定义每段的不河蟹度为：若这段里有k个不同的数，那不河蟹度为k*k。那总的不河蟹度就是所有段的不河蟹度的总和。
Input
第一行：两个整数N，M
第2..N+1行：N个整数代表每个奶牛的编号
Output
一个整数，代表最小不河蟹度
Sample Input
13 4
1
2
1
3
2
2
3
4
3
4
3
1
4
1
2
1
3
2
2
3
4
3
4
3
1
4
Sample Output
11
题目分析
$O(n^2)$的dp不难得到，即$f_i=min\{f_j+w(j+1,i)\}$.
旁敲侧击
分析一下数据范围，会想到做法大概是$O(nlogn)$或者$O(n\sqrt n)$的。
一开始还往决策单调性的方向想，然而发现颜色个数的平方这个加权并没有决策单调性……
看了题解才发现，是一种思路自然的神奇$O(n\sqrt n)$dp……
$O(n\sqrt n)$dp
考虑答案的下界，即每一个元素单独成组，答案是$n$.这意味着在最优解中，每组颜色个数必然是小于等于$\sqrt n$的。从这个性质出发，可以记$[pos[j],i]$为以$i$为右端点、颜色个数小于等于$j$的最长序列。
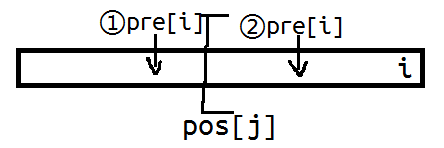
那么就是如何维护$pos[j]$.这个和其他统计颜色的问题类似，记$pre[i],lst[i]$分别为与$a_i$同色的前、后一个位置；$cnt[j]$为当前$pos[j]$的不同颜色数量。那么每当新加进一个元素$i$的时候，就看一下$pre[i]$在$pos[j]$之前还是之后，并根据这个信息维护$pos[j]$的右移。
所以虽然根据答案上界来限定枚举颜色数量的这一步比较难想，后面的过程还是非常巧妙自然的。
1 #include<bits/stdc++.h> 2 const int maxn = 40035; 3 const int maxk = 213; 4 5 int n,m,size; 6 int a[maxn],nxt[maxn],pre[maxn],lst[maxn],f[maxn],pos[maxk],cnt[maxk]; 7 8 int read() 9 { 10 char ch = getchar(); 11 int num = 0; 12 bool fl = 0; 13 for (; !isdigit(ch); ch=getchar()) 14 if (ch=='-') fl = 1; 15 for (; isdigit(ch); ch=getchar()) 16 num = (num<<1)+(num<<3)+ch-48; 17 if (fl) num = -num; 18 return num; 19 } 20 void Min(int &x, int y){x = x<y?x:y;} 21 int main() 22 { 23 memset(f, 0x3f3f3f3f, sizeof f); 24 n = read(), m = read(), size = sqrt(n+0.5), f[0] = 0; 25 for (int i=1; i<=size; i++) pos[i] = 1; 26 for (int i=1; i<=n; i++) 27 { 28 a[i] = read(); 29 pre[i] = lst[a[i]], nxt[lst[a[i]]] = i; 30 lst[a[i]] = i, nxt[i] = n+1; 31 } 32 for (int i=1; i<=n; i++) 33 for (int j=1; j<=size; j++) 34 { 35 if (pre[i] < pos[j]) cnt[j]++; 36 if (cnt[j] > j){ 37 cnt[j]--; 38 while (nxt[pos[j]] < i) pos[j]++; 39 pos[j]++; 40 } 41 Min(f[i], f[pos[j]-1]+1ll*j*j); 42 } 43 printf("%d\n",f[n]); 44 return 0; 45 }
END
