NOIP2018 - 暑期博客整理

暑假写的一些博客复习一遍。顺便再写一遍或者以现在的角度补充一点东西。

盛暑七月

初涉基环外向树dp&&bzoj1040: [ZJOI2008]骑士

比较经典的基环外向树dp。可以借鉴的技巧在于将每一个环拆出一条边，使剩下部分成为树。再然后就是max(f[u][0],f[v][0])思考中可能会出现的纰漏。

44     for (i=1; i<=n; i++)
45     {
46         v[i] = read(), tt = read();
47         if (get(tt)!=get(i)){
48             addedge(i, tt);
49             fa[fa[tt]] = fa[i];
50         }else lDes[++cnt] = tt, rDes[cnt] = i;
51     }

小技巧就是这个。

【线段树】bzoj3585: mex

区间问题。这个算是一类套路吧，和【细节题 离线 树状数组】luoguP4919 Marisa采蘑菇以及HH的项链大同小异。无非是先将询问排序；再利用询问区间不断右移来更新答案；最后数据结构来辅助完成更新区间内答案的这么一个操作。

这类问题，感觉相比而言区间带修莫队没什么优势。

【树形dp】bzoj1304: [CQOI2009]叶子的染色

自底向上这么一个处理过程不难想到。这类问题和贪心“反悔”有那么点相像，大致意思是说，先考虑一个节点$u$在它能力范围内完成要求的代价；之后转移时候再来看能不能省去$u$付出的代价。

但如果节点的要求有一定后效性的话，比如说要求每个节点到根的路径上恰好有$a_i$个白点、$b_i$个黑点；或是至少有$a_i,b_i$个白黑点。可能不能dp？

初涉三元环

这种根号阈值分类的题算是一类分块思想吧。

再者是统计答案时候：1.强制顺序连边；2.根据出度大小更换顺序 。我认为这连个都是将去重做到相当熟练和精妙地步的操作。

    for (int i=3; i<=n; i++)
        for (int j=head[i]; j!=-1; j=nxt[j])
        {
            int x = edges[j];
            if (deg[x] > size)
                for (int t=nxt[j]; t!=-1; t=nxt[t])
                {
                    int y = edges[t];
                    if (y >= x) continue;
                    if (s[x].find(y)!=s[x].end())
                        ans += ...12                 }
            else
                for (int t=head[x]; t!=-1; t=nxt[t])
                {
                    int y = edges[t];
                    if (s[i].find(y)!=s[i].end())
                        ans += ...19                 }
        }

还是记一记，多感受一下吧。

初涉tarjan缩点

这个没什么多说的，大致是结合其他内容应用。比较高端的例如2-sat。

void tarjan(int x)
{
    dfn[x] = low[x] = ++tim, stk[++cnt] = x;
    for (int i=head[x]; i!=-1; i=nxt[i])
    {
        int v = edges[i];
        if (!dfn[v])
            tarjan(v), low[x] = std::min(low[x], low[v]);
        else if (!col[v]) low[x] = std::min(low[x], dfn[v]);
    }
    if (dfn[x]==low[x]){
        col[x] = ++cols, size[cols] = 1;
        for (; stk[cnt]!=x; cnt--)
            col[stk[cnt]] = cols, size[cols]++;
        cnt--;
    }
}
//一分钟敲的，大概没问题

概述「并查集补集转化」模型&&luoguP1330 封锁阳光大学

一种思想（小技巧）。就是说我的敌人1和敌人2可以合并。姑且称作“补集转化”。

【贪心优化dp决策】bzoj1571: [Usaco2009 Open]滑雪课Ski

dp容易想到，转移也不是太难。主要是dp预处理的技巧。

【贪心】bzoj1572: [Usaco2009 Open]工作安排Job

一类经典的有截止时间的区间贪心。建筑抢修是权值相同、完成时间给定；最大收益是权值不同，而且限定开始时间。

其实仔细考虑之后，不难弄明白这类抽象的替换在不同情景下的意义。 讲到底还是贪心中一块重要的“反悔”操作。

【tarjan 拓扑排序 dp】bzoj1093: [ZJOI2007]最大半连通子图

把题读懂之后就是板子题了，直接码就是。

有个技巧，连通块之间防止重边：

 92         for (int i=head[u]; i!=-1; i=nxt[i])
 93         {
 94             int v = edges[i];
 95             if ((--deg[v])==0) q[++qTail] = v;
 96             if (vis[v]==u) continue;
 97             if (f[v] < f[u]+size[v])
 98                 f[v] = f[u]+size[v], g[v] = g[u];
 99             else if (f[v]==f[u]+size[v])
100                 g[v] = (g[v]+g[u])%p;
101             vis[v] = u;
102         }

然后一个小总结。求最长链若$f[i]$表示以$i$为起点的最长链，则dfs；表示以$i$为终点的最长链。则拓扑。

upd：再打了一遍，然而还是有些小错误。主要是：

1. 根据缩点后重建图后的边忘记分开存了
2. 统计方案时候没有判连通块之间的重边
3. 我也不知道为什么tarjan打成了if (dfn[x]!=low[x])……
4. maxm开小了……

这样的对于模板的熟悉程度不行啊……

初涉2-SAT

巧用tarjan的一类问题。熟悉tarjan善于建模即可。

【期望 数学】7.6神经衰弱

期望依旧很差……现在看到还是基本没想法。哎，这个离散数学还是不太行。

有一点头绪了。

大致流程还是把期望爆开，拆成概率和权值。

答案下界是$m$没错。那么把牌都翻了一遍之后，最坏情况下是要再翻$m$次把相同牌拿光的。也就是说，在下界的基础上，之后每一次操作的权值是1；而概率是$1-前m次中没抽到相同牌的概率$。

这样理解要稍微方便一些，但实际上我还是不太熟练……

初涉最小表示法&&bzoj1398: Vijos1382寻找主人 Necklace

再码了一遍。zz地把calc()里的变量名字打错了。

#include<bits/stdc++.h>
const int maxn = 1000035;

bool fl;
int n,sst,tst;
char s[maxn],t[maxn];

int calc(char *s)
{
    int i = 0, j = 1, k = 0;
    while (i < n&&j < n&&k < n)
    {
        if (s[(i+k)%n]==s[(j+k)%n]) k++;
        else{
            if (s[(i+k)%n] > s[(j+k)%n]) i += k+1;
            else j += k+1;
            if (i==j) i++;
            k = 0;
        }
    }
    return std::min(i, j);
}
int main()
{
    scanf("%s%s",s,t);
    fl = 1, n = strlen(s);
    sst = calc(s), tst = calc(t);
    for (int i=0; i<n; i++)
        if (s[(sst+i)%n]!=t[(tst+i)%n]){
            fl = 0;
            break;
        }
    if (!fl){
        puts("No");
        return 0;
    }else puts("Yes");
    for (int i=0; i<n; i++)
        putchar(s[(sst+i)%n]);
    return 0;
}

【树状数组 离散化】bzoj1573: [Usaco2009 Open]牛绣花cowemb

技巧有两点：

1. 圆上直线问题的映射，也就是快速判断圆内直线是否相交。
2. 处理相交但不包含的线段数量。按左端点排序，依次处理，并在处理后加上自己贡献。用一个树状数组维护这个操作就好了。

【meet in middle】poj1840Eqs

meet in middle的板子题，再打了一遍（话说我都忘了poj不能用万能头……）

#include<cstdio>
const int BASE = 25000000;

short f[BASE+35];
int a,b,c,d,e,ans,g[103];

int main()
{
    scanf("%d%d%d%d%d",&a,&b,&c,&d,&e);
    for (int i=-50; i<=50; i++) g[i+50] = i*i*i;
    for (int i=-50; i<=50; i++)
        if (i) for (int j=-50; j<=50; j++)
            if (j){
                int num = -a*g[i+50]-b*g[j+50];
                if (num < 0) num += BASE;
                f[num]++;
            }
    for (int i=-50; i<=50; i++)
        if (i) for (int j=-50; j<=50; j++)
            if (j) for (int k=-50; k<=50; k++)
                if (k){
                    int num = c*g[i+50]+d*g[j+50]+e*g[k+50];
                    if (num < 0) num += BASE;
                    ans += f[num];
                }
    printf("%d\n",ans);
    return 0;
}

遇到这种题如果map太慢，并且存在负数，要记得算好数组空间和偏移量。

【状态压缩 meet in middle】poj3139Balancing the Scale

这里还是一个逐级向上的思想，然后用位运算和状压来辅助这个过程。

要注意的是：

• a[]要sort，因为next_permutation要从最小的开始才行
• next_permutation的过程里，需要do-while。虽然很显然但是容易忘。

还不错的meet in middle。

概述「DAG加边至强连通」模型&&luoguP2746校园网Network of Schools

算是一种思考的方式和技巧吧。

【动态规划】poj2353Ministry

看到博客里写的拓扑序……呃，我也不清楚当时怎么想的。这个当然是要考虑一个个推过来的顺序的啊。

不过这个也是要注意一下，有些时候可能打着顺手就直接不管顺序了。

for (int j=m-1; j>=1; j--)
    if (f[i][j] > f[i][j+1]+a[i][j])

其他都还好，算是比较基础的题。再写了一遍也没有写挂。

【动态规划】bzoj2298: [HAOI2011]problem a

经过建模之后就成了带权线段覆盖问题。这个和bzoj1577: [Usaco2009 Feb]庙会捷运Fair Shuttle有些类似。那题是线段可拆开，这题则是线段不能拆。

这题主要是建模的过程比较好，尤其是一步步转化的严谨推论。

【动态规划】luoguP1941 飞扬的小鸟

10.25：晚上试着在基本忘掉题解的情况下1A，打算稳一点过题。所以节奏比较慢，打了一个多点小时，拍了一个半小时。嗯，感觉这种策略还是挺好的。不过这种策略也是要靠足够的思维速度和代码能力支撑起来吧。

不过第一发MLE90pts……算是一个要记得检查变量（特别是调试用的）教训吧。

#include<bits/stdc++.h>
const int maxn = 10035;
const int maxh = 1003;
const int INF = 0x3f3f3f3f;

int n,m,k,mx,ans;
int up[maxn],dw[maxn],l[maxn],r[maxn];
int f[maxn][maxh],g[maxn][maxh];
bool kick;

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch=getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch=getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void Min(int &x, int y){x = x < y?x:y;}
int main()
{
    freopen("uoj17.in","r",stdin);
    freopen("uoj17.out","w",stdout);
    memset(f, 0x3f3f3f3f, sizeof f);
    memset(g, 0x3f3f3f3f, sizeof g);
    n = read(), m = read(), k = read(), ans = INF;
    for (int i=0; i<=n; i++) l[i] = 1, r[i] = m;
    for (int i=0; i<n; i++) up[i] = read(), dw[i] = read();
    for (int i=1; i<=k; i++)
    {
        int p = read();
        l[p] = read()+1, r[p] = read()-1;
    }
    for (int i=1; i<=m; i++) f[0][i] = 0;
    for (int i=0; i<n; i++)
    {
        kick = 0;
        for (int j=1; j<=m; j++)
        {
            if (i&&(g[i][j]!=INF)&&(std::min(j+up[i-1], m) <= r[i]))
            {
                int tov = std::min(j+up[i-1], m);
                if (f[i][tov] >= g[i][j]+1){
                    f[i][tov] = g[i][j]+1;
                }
                Min(g[i][tov], g[i][j]+1);
            }            
        }
        for (int j=l[i]; j<=r[i]; j++)
            if (f[i][j]!=INF){
                mx = i, kick = 1;
                int tov = std::min(j+up[i], m);
                if (f[i+1][tov] >= f[i][j]+1){
                    f[i+1][tov] = f[i][j]+1;
                }
                Min(g[i+1][tov], f[i][j]+1);
                tov = std::max(j-dw[i], 0);
                if (f[i+1][tov] > f[i][j]&&tov>=l[i+1]&&tov<=r[i+1]){
                    f[i+1][tov] = f[i][j];
                }
            }
        if (!kick) break;
    }
    if (!kick){
        puts("0"), ans = 0;
        for (int i=1; i<=mx; i++)
            if (l[i]!=1||r[i]!=m) ans++;
        printf("%d\n",ans);
    }else{
        puts("1");
        for (int i=1; i<=m; i++) Min(ans, f[n][i]);
        printf("%d\n",ans);
    }
    return 0;
}

看了一下博客，应该说做法大同小异，没什么要补充的。这块还是以加强代码能力为主吧。

【模拟】bzoj1686: [Usaco2005 Open]Waves 波纹

嗯……联赛之前做模拟题这件事是该提上日程了。

概述「贪心“反悔”策略」模型

这里讲了两个相对基础的“反悔”问题。

其实“反悔”的大致思想不难理解，难就难在对于问题的转化和如何合理“反悔”。因为有些转化实际上是不充要的，所以这一步要严谨。

有些时候可能还是要靠感性理解吧……不过这个“感性”也要建立在起码的合理上，比如多对拍一下；打表看看规律之类的。

这里有道最近做的反悔贪心，感觉有些抽象，存在这里先吧……

【计数】7.11跳棋

这题思路很妙啊。

突破点在于考虑到相邻两个棋子最多只需要1个空位，之后的考虑棋子同质这个角度也非常好。

【二分 贪心】bzoj3477: [Usaco2014 Mar]Sabotage

平均值最值的问题算是一种套路吧。然后二分check的过程大同小异，图上是找正/负环；序列就是找个最值正/负序列。

【倍增】7.11fusion

现在看这题大致有点思路。但估计还没有考场上码出的代码能力……

整个思路流程大致是这样的：因为消去的顺序从左至右，那么一个区间若能消去，可以看做是一个一个互不影响的子区间被逐个消去，并且如果左端点固定，接下去消去的过程也是唯一的。由此想到预处理出$[i,nxt[i])$表示以$i$为左端点所能消去的最近右端点。那么查询时候就是一直跳$nxt[i]$，当且仅当存在$nxt[i]==r+1$时区间能够被消除。

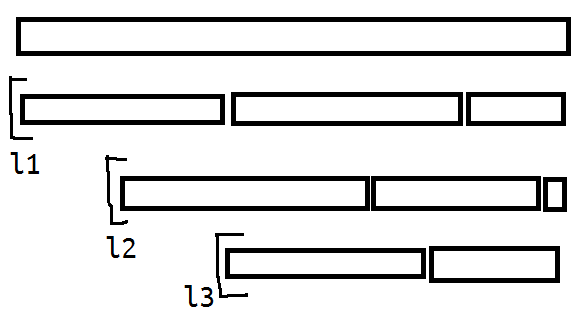
但是这个只能算是一个优化，对于算法复杂度并没有实质性的改变，zzzzz.....的数据就能轻松卡掉。

由此便想到对$nxt[i]$倍增。

既然已经有了大致思路，剩下的就是细节处理了。所以还要加强各种代码能力。

【图论 搜索】bzoj1064: [Noi2008]假面舞会

存在环的情况是比较好判断的，最大值就是所有环长的gcd；最小值应该是最大值的大于三的最小质因数。

不存在环的情况好像没什么想法。

 

什么鬼好像zz了，不存在环的情况就是每个连通块的DAG的最长链总和。

然后这里对于找环有个小技巧，就是原边保留权值为1；建反向边权值为-1.第二次经过说明环长度为两次标记权值之差。

干脆再码了一遍

#include<bits/stdc++.h>
const int maxn = 100035;
const int maxm = 1000035;

int n,m,dis[maxn],mn,mx,chain,ans;
bool vis[maxn];
std::vector<int> f[maxn],g[maxn];
std::pair<int, int> ev[maxm];

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch=getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch=getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
inline int abs(int x){return x>0?x:-x;}
int gcd(int a, int b){return b==0?a:gcd(b, a%b);}
void dfs(int x, int c)
{
    if (vis[x]){
        ans = gcd(abs(c-dis[x]), ans);
        return;
    }
    vis[x] = 1, dis[x] = c;
    mn = std::min(mn, c), mx = std::max(mx, c);
    for (int i=0; i<f[x].size(); i++)
        dfs(f[x][i], c+1);
    for (int i=0; i<g[x].size(); i++)
        dfs(g[x][i], c-1);
}
int main()
{
    n = read(), m = read(), ev[0].first = -1, ev[1].second = -1;
    for (int i=1; i<=m; i++) ev[i].first = read(), ev[i].second = read();
    std::sort(ev+1, ev+m+1);
    for (int i=1; i<=m; i++)
        if (ev[i]!=ev[i-1]){
            int u = ev[i].first, v = ev[i].second;
            f[u].push_back(v), g[v].push_back(u);
        }
    for (int i=1; i<=n; i++)
        if (!vis[i]){
            mn = mx = 0;
            dfs(i, 0);
            chain += mx-mn+1;
        }
    if (ans >= 3){
        for (int i=3; ; i++)
            if (ans%i==0){
                printf("%d %d\n",ans,i);
                return 0;
            }
    }
    if (chain>=3&&!ans) printf("%d %d\n",chain,3);
    else puts("-1 -1");
    return 0;
}

【最短路径树】51nod1443 路径和树

最短路径树这种模型的一个模板。正确性由每一步的贪心得到。

【树链剖分 差分】bzoj3626: [LNOI2014]LCA

将LCA的深度转为LCA到根的距离，这个转化挺不错的；至于差分应该说是套路了。

其他就是大力数据结构了。

#include<bits/stdc++.h>
const int maxn = 50035;
const int maxm = 50035;
const int MO = 201314;

struct QRs
{
    int x,z,id,opt;
    QRs(int a=0, int b=0, int c=0, int d=0):x(a),z(b),id(c),opt(d) {}
    bool operator < (QRs a) const
    {
        return x < a.x;
    }
}q[maxn<<1];
struct node
{
    int tot,son,top,fa;
}a[maxn];
int n,m,tot,ans[maxn];
int f[maxn<<2],ads[maxn<<2];
int chain[maxn],chTot;
int edgeTot,head[maxn],edges[maxm],nxt[maxm];

void addedge(int u, int v)
{
    edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
}
int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch=getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch=getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void dfs1(int x, int fa)
{
    a[x].tot = 1, a[x].son = a[x].top = -1, a[x].fa = fa;
    for (int i=head[x]; i!=-1; i=nxt[i])
    {
        int v = edges[i];
        dfs1(v, x), a[x].tot += a[v].tot;
        if (a[x].son==-1||a[a[x].son].tot < a[v].tot) a[x].son = v;
    }
}
void dfs2(int x, int top)
{
    a[x].top = top, chain[x] = ++chTot;
    if (a[x].son==-1) return;
    dfs2(a[x].son, top);
    for (int i=head[x]; i!=-1; i=nxt[i])
        if (edges[i]!=a[x].son) dfs2(edges[i], edges[i]);
}
void pushup(int rt)
{
    f[rt] = (f[rt<<1]+f[rt<<1|1])%MO;
}
void pushdown(int rt, int lc, int rc)
{
    if (ads[rt]){
        int t = ads[rt];
        ads[rt<<1] = (ads[rt<<1]+t)%MO, ads[rt<<1|1] = (ads[rt<<1|1]+t)%MO;
        f[rt<<1] = (f[rt<<1]+lc*t)%MO, f[rt<<1|1] = (f[rt<<1|1]+rc*t)%MO;
        ads[rt] = 0;
    }
}
int query(int rt, int L, int R, int l, int r)
{
    if (L <= l&&r <= R) return f[rt];
    int mid = (l+r)>>1, ret = 0;
    pushdown(rt, mid-l+1, r-mid);
    if (L <= mid) ret += query(rt<<1, L, R, l, mid);
    if (R > mid) ret += query(rt<<1|1, L, R, mid+1, r);
    return ret;
}
void modify(int rt, int L, int R, int l, int r)
{
    if (L <= l&&r <= R){
        f[rt] = (f[rt]+r-l+1)%MO, ads[rt]++;
        return;
    }
    int mid = (l+r)>>1;
    pushdown(rt, mid-l+1, r-mid);
    if (L <= mid) modify(rt<<1, L, R, l, mid);
    if (R > mid) modify(rt<<1|1, L, R, mid+1, r);
    pushup(rt);
}
void updateNode(int x, int y=1)
{
    while (a[x].top!=a[y].top)
    {
        modify(1, chain[a[x].top], chain[x], 1, n);
        x = a[a[x].top].fa;
    }
    modify(1, chain[y], chain[x], 1, n);
}
int queryNode(int x, int y=1)
{
    int ret = 0;
    while (a[x].top!=a[y].top)
    {
        ret = (ret+query(1, chain[a[x].top], chain[x], 1, n))%MO;
        x = a[a[x].top].fa;
    }
    ret = (ret+query(1, chain[y], chain[x], 1, n))%MO;
    return ret;
}
int main()
{
    memset(head, -1, sizeof head);
    n = read(), m = read();
    for (int i=2; i<=n; i++) addedge(read()+1, i);
    dfs1(1, 0);
    dfs2(1, 1);
    for (int i=1; i<=m; i++)
    {
        int l = read()+1, r = read()+1, c = read()+1;
        q[++tot] = QRs(l-1, c, i, -1);
        q[++tot] = QRs(r, c, i, 1);
    }
    std::sort(q+1, q+tot+1);
    for (int i=1, now=0; i<=tot; i++)
    {
        int pos = q[i].x, fnd = q[i].z, id = q[i].id, opt = q[i].opt;
        while (now < pos) updateNode(++now);
        ans[id] += opt*queryNode(fnd);
    }
    for (int i=1; i<=m; i++) printf("%d\n",(ans[i]+MO)%MO);
    return 0;
}

【计数】51nod1677 treecnt

这个是将答案按边考虑贡献的思想。有些时候还要试着从问题的反面去看待。

【树形背包】bzoj4033: [HAOI2015]树上染色

按边拆贡献的思路同上，然后根据这个思路来做背包。

【树形dp】7.14城市

一样的拆贡献。为什么考试时候我没做出来啊

初涉「带权并查集」&&bzoj3376: [Usaco2004 Open]Cube Stacking 方块游戏

并查集大致可以分为普通、带权两种。带权并查集的特点在于记录了同个集合不同元素之间的关系。更新是等到查询时候延迟自根向下更新。

【单调栈 动态规划】bzoj1057: [ZJOI2007]棋盘制作

求解矩阵最大面积0/1矩形应该算是单调栈最基础的应用了。

与0/1矩阵相关的问题还有例如：

UVA12265 Selling Land：最大周长0/1矩形。　　这个由于周长同样单调，和最大面积一样处理。

COCI 2018/2019 Strah：所有0/1矩形面积和。　　好像是维护x,y,xy的系数，大力拆开维护  待填坑

初涉trie

比较基础的字符串问题

【图论 动态规划拆点】luoguP3953 逛公园

不知道想法对不对：先预处理一趟最短路，然后如果有必要的话可以重建图一下（把已经$dis[u]+w>dis[v]+k$的边$(u,v)$删掉）。$f[i][j]$表示到达点$i$时候距离为$dis[i]+j$的方案数。那么这样状态数量是$O(nk)$的，每个状态只会被经过一次，转移是$O(1)$的。

好吧果然比较NAIVE，没注意到一些转移上的拓扑顺序。这说明了先想清楚做法再开始码题的重要性……

这里一个反向设状态的思路很好啊

计数类动态规划的转移大概就是这个样子。状态$f[i]$可以表示为1 -> i的方案数；也可以表示为i -> n的方案数。

第一种表示通常是提前转移贡献，也就是说在处理$f[i]$的时候，它的贡献已经由$\sum{f[j]}$得到了，处理$f[i]$是为了用它去更新$f[k]$。

第二种表示通常是自己收集贡献。意思是处理$f[i]$的时候，考虑它连出去的所有$f[j]$状态，再使$f[i]=\sum{f[j]}$。

这个举个形象一些的例子就是bzoj1093: [ZJOI2007]最大半连通子图这个地方，$f[i]$两种不同的状态表示决定了刷答案时候是该dfs还是topo。

那么这样看来，在某些特殊情况下topo是比较麻烦的，而记忆化dfs几乎没有任何影响，所以i -> n的状态表示更优秀。

这个有些时候可能还是需要多从其他方面推敲才能想到的。

比较考察dp功底的好题。

【数位dp】bzoj3209: 花神的数论题

注意一些细节问题。

【单调栈 前缀和 异或】7.21序列求和

初步的想法：固定右端点来计数，也就是说在做单调栈的过程中来统计答案。那么如果是随机数据应该能起到不错的效果。但我好像不会计算$\sum_{i=l_1}^{l_2}\oplus_{j=i}^{r}j$……？

啧这个东西怎么拆位啊.xor不同于and/or的特性就在于它运算的过程中每一位都有可能再改变，而不是就此固定下来（所以如果and/or的话应该会好做很多）。难道靠这个特性做文章？

诶好吧，$a_i \le 10^9$的话分位做$log_2n$次每次$n$也可以接受……

 

看来的确应用到这个xor的特性，就转化成了左右端点异或前缀和在这一位不相同这个问题，于是在统计上配合前缀和，思路并不复杂。先前那个想法不是很完善，应该做两遍单调栈处理出$a[i]$为最大值的左右边界。这样在固定下$max\{a[i]\}$的情况下就只需要再枚举二进制位来算贡献。那么看来就是一个普通的拆位算贡献题了。

边界开闭区间的±1需要注意。

【数位dp】bzoj1833: [ZJOI2010]count 数字计数

一眼看去按位拆贡献算。和Fenwick很像，考虑左边的数字是否改变。

于是写了一下，代码长度比数位dp略短一些，时间效率差不多。

思路大同小异，不过我觉得按贡献算的代码会更直观一些。

#include<bits/stdc++.h>
typedef long long ll;

ll a,b,pw[15],pre[15],nxt[15],ans[15];
int f[15],n;

void solve(ll x, int c)
{
    ll num = x;
    for (n=0; num; num/=10) f[++n] = num%10;
    for (int i=n; i>=1; i--) pre[i] = pre[i+1]*10+f[i];
    for (int i=1; i<=n; i++) nxt[i] = nxt[i-1]+pw[i-1]*f[i];
    for (int i=1; i<=n; i++)
    {
        if (i!=n&&f[i]) ans[0] += c*pw[i-1];
        for (int t=1; t<f[i]; t++)
            ans[t] += c*pw[i-1];
        ans[f[i]] += c*nxt[i-1]+c;
    }
    for (int i=1; i<=n; i++)
    {
        if (i!=n) ans[0] += c*(pre[i+1]-1)*pw[i-1];
        for (int t=1; t<=9; t++)
            ans[t] += c*pre[i+1]*pw[i-1];
    }
}
int main()
{
    scanf("%lld%lld",&a,&b);
    pw[0] = 1;
    for (int i=1; i<=15; i++) pw[i] = pw[i-1]*10ll;
    solve(a-1, -1), solve(b, 1);
    for (int i=0; i<=9; i++)
        printf("%lld ",ans[i]);
    return 0;
} 

【状态压缩dp】bzoj1087: [SCOI2005]互不侵犯King

此题的技巧在于预处理出下一行的合法状态。

这里也存在一个拓扑序的问题，那么不妨用$f[i][j][k]$表示第$i$行状态为$k$，还剩$j$个可放的方案数。像这样设状态就能记忆化搜索了。

时间效率也相差不大，代码少个700b左右。

#include<bits/stdc++.h>
typedef long long ll;

ll f[13][103][1203];
bool vis[13][103][1203];
int n,k,mx,cnt[1203],st[1203];
std::vector<int> a[1203];

ll dp(int i, int j, int k)
{
    if (vis[i][j][k]) return f[i][j][k];
    vis[i][j][k] = 1;
    if (i==n){
        if (j) return 0;
        else return f[i][j][k] = 1;
    }
    for (int p=0; p<a[k].size(); p++)
        if (j >= cnt[a[k][p]])
            f[i][j][k] += dp(i+1, j-cnt[a[k][p]], a[k][p]);
    return f[i][j][k];
}
inline int legal(int x)
{
    int ret = 0;
    for (int i=0; i<n; i++)
        if (((x>>i)&1)&&((x>>(i+1))&1)) return -1;
        else if ((x>>i)&1) ret++;
    return ret;
}
inline bool match(int x, int y)
{
    if ((x&y)||(x&(y<<1))||(x&(y>>1))) return 0;
    return 1;
}
void init()
{
    for (int i=0; i<=mx; i++)
        if ((cnt[i] = legal(i))!=-1) st[++st[0]] = i;
    a[0].push_back(0);
    for (int i=1; i<=st[0]; i++)
        for (int j=1; j<i; j++)
        {
            if (match(st[i], st[j])){
                a[st[i]].push_back(st[j]), 
                a[st[j]].push_back(st[i]);
            }
        }
}
int main()
{
    scanf("%d%d",&n,&k);
    mx = (1<<n)-1, init();
    printf("%lld\n",dp(0, k, 0));
    return 0;
}

可能需要注意的小细节：这种倒着来记忆化搜索的做法，一般来说就不需要给每一个值一个“初始值”了。答案由后继状态倒推贡献而来。

【动态规划】bzoj1575: [Usaco2009 Jan]气象牛Baric

等等为什么当时我写了三维dp，好像有点没看懂。

反正遇到一些难处理的转移考虑预处理。

【数位dp】bzoj1799: [Ahoi2009]self 同类分布

数位dp不要虚。发现事情不对就多增状态；发现事情还是不对就再多枚举点东西。重点是心态不要乱。

【线段树 细节题】bzoj1067: [SCOI2007]降雨量

整个思路还是比较清晰的……不过细节需要好好注意吧。

初涉KMP算法

kmp基础.

板子里面注意是 while (t[i+1]!=t[j+1]&&j) j = fail[j]; 而不是 while (t[i+1]!=t[j+1]&&fail[j]) j = fail[j]; 因为无法匹配的时候$j=0$。

然后是一个完全/不完全最短循环节的性质。

再是一个 bzoj3670: [Noi2014]动物园 和 bzoj1511: [POI2006]OKR-Periods of Words 的巧妙思维题。

感觉字符串理论这一块并没有花太多时间……也不是很熟练。

联赛的字符串要求算是比较浅的吧，好好复习kmp、Aho、manacher应该问题不大。

【线段树 集合hash】bzoj4373: 算术天才⑨与等差数列

三次方是一种集合hash方法没错。此外如果集合没有特殊性质要求，还有一种方法是给每个元素rand一个long long出来，集合hash值是元素异或和。这个详情见bzoj3578: GTY的人类基因组计划2。

【数学 exgcd】bzoj1407: [Noi2002]Savage

exgcd的模板

【数学 裴蜀定理】bzoj2257: [Jsoi2009]瓶子和燃料

同样是一种拆分贡献的思想。每个数会对它的不同因子产生贡献，然而这个贡献又是不可共存的。

但这里因为因子之间相互独立，所以并不妨碍我们同时记上贡献。因此只需要在最后再来检查一遍就行了。

【树论 倍增】51nod1709 复杂度分析

依然是拆分贡献的想法。

因为这里二进制位和倍增有很大相性，所以考虑倍增求解。注意到高低位是同质的，那么总体流程就是先枚举每一个二进制位，再从根往下统计贡献。

用$f[i][j]$表示距点$i$距离为$2^j-1$的祖先，那么对于$i$来说，只有root...f[i][j]这些祖先会对第$j$个二进制位产生贡献。

首先考虑此时必定有贡献的祖先$f[i][j]...fa[f[i][j-1]]$，当这些祖先作为$i$和另一个点$k$的LCA时会产生贡献。那么显而易见的是这部分的贡献是$tot[f[i][j]]-tot[f[i][j-1]]$。

再考虑$root...fa[f[i][j]]$这部分可能产生的贡献。注意到$dis[i][f[i][j]]$在二进制下恰好是$j$位1，也就是说对于$f[i][j]$再向上的其他节点，$1...j$二进制位又重新从0计数。那么在只考虑第$j$位的情况下，对于$i$的这部分贡献和对于$f[i][j]$的总贡献是相等的。

一些细节：为了防止上跳时候“溢出”，root的父亲应设为root自身。

时间复杂度：$O(n\log n)$

#include<bits/stdc++.h>
typedef long long ll;
const int maxn = 100035;
const int maxm = 200035;

ll w[maxn],ans;
int n,fa[maxn],tot[maxn];
int f[maxn][23],dep[maxn],chain[maxn],chTot;
int edgeTot,head[maxn],nxt[maxm],edges[maxm];

void addedge(int u, int v)
{
    edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 
    edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 
}
int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch = getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void dfs(int x, int fat)
{
    tot[x] = 1, chain[++chTot] = x;
    dep[x] = dep[fat]+1, f[x][0] = x, f[x][1] = fa[x] = fat;
    for (int i=head[x]; i!=-1; i=nxt[i])
    {
        int v = edges[i];
        if (v!=fat) dfs(v, x), tot[x] += tot[v];
    }
}
int main()
{
    memset(head, -1, sizeof head);
    n = read();
    for (int i=1; i<n; i++) addedge(read(), read());
    dfs(1, 1);
    for (int j=2; j<=20; j++)
        for (int i=1; i<=n; i++)
            f[i][j] = fa[f[f[i][j-1]][j-1]];
    for (int j=1; j<=20; j++)
    {
        memset(w, 0, sizeof w);
        for (int ix=1, i=chain[ix]; ix<=n; i=chain[++ix])
        {
            w[i] = tot[f[i][j]]-tot[f[i][j-1]];
            if (dep[i] > (1<<j)) w[i] += w[fa[f[i][j]]];
            ans += w[i];
        }
    }
    printf("%lld\n",ans);
    return 0;
}

【dp 状态压缩 单调栈】bzoj3591: 最长上升子序列

很有意思的状压dp

记得好像鏼爷在51nod上还出了一题加强版，n=31……不过那题做法就不是状压dp了

主要是用单调栈来构建状压dp的这第一步超级好，令人拍案叫绝。之后的检查合法、转移状态等过程就是比较常规的操作了。

夏末八月

 

鏼