【贪心 哈夫曼树】bzoj2923: [Poi1998]The lightest language
失去了以前用STL乱搞的能力……
题目描述
语言也是数学上经常研究的一种数据。
给出数学上关于语言的如下定义:
- 字母表:大小为 K 的字母表是一个由 K 不同的字符组成的集合。
- 单词:长度为 m 的单词是以 m 个字母表中的字符组成的字符串。
- 语言:语言是由若干个单词组成的集合。
- 非前缀的:一种语言是非前缀的,当且仅当其中任意两个单词不存在前缀关系。
现在每个字母表中的字母有一个权值,单词的权值是单词中每个字母的权值和,语言的权值是单词的权值之和。
例如:
K=2,字母a权值为 2,字母b权值为 5,字符串aba权值为 9。
语言 {ab,aba,b} 不是非前缀的,而非前缀的语言 {aa,ab,b} 权值是 16。
给出n,K,每个字母的权值 Wi,求包含 n 个单词的非前缀语言中最小的权值是多少。
数据范围
对于 20% 的数据,n,K≤5
对于另 30% 的数据,wi=1
对于另 30% 的数据,K=2
对于所有数据,2≤n≤10000,2≤K≤26,1≤wi≤10000
时间限制 1s
空间限制 256 MB
题目分析
整个单词树可以看做trie的样子,
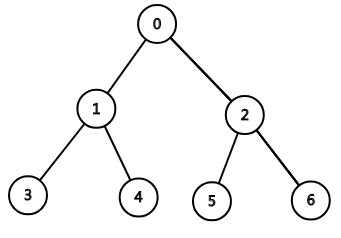
那么我的第一思路就是在这个tire上面树形dp……
既然要dp那么肯定要涉及到开数组空间的问题。
注意到若一层能够“铺满”所有n个节点,那么往下编码是一定不更优的。所以最大情况是补成一个满二叉树。
但是这个数据范围对于树上背包来说不对啊……
于是就活生生卡住一个小时。
回过头来看这个问题:非前缀;最小编码和……
这是个类哈夫曼树的问题啊。
与常规的哈夫曼问题不同,此题既然确定个数而加权不同,就可以从树根往下处理。
于是乎,这么一个贪心扩展的过程,就可以用multiset来维护……
最后STL的细节问题需要注意一下。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 10035; 4 5 ll sum,ans; 6 int n,k,w[maxn]; 7 std::multiset<ll> s; 8 9 int read() 10 { 11 char ch = getchar(); 12 int num = 0; 13 bool fl = 0; 14 for (; !isdigit(ch); ch = getchar()) 15 if (ch=='-') fl = 1; 16 for (; isdigit(ch); ch = getchar()) 17 num = (num<<1)+(num<<3)+ch-48; 18 if (fl) num = -num; 19 return num; 20 } 21 int main() 22 { 23 n = read(), k = read(), ans = 1ll<<40; 24 for (int i=1; i<=k; i++) 25 w[i] = read(), sum += w[i], s.insert(w[i]); 26 for (ll cnt=sum; cnt<ans;) 27 { 28 if (s.size()==n){ 29 if (cnt < ans) ans = cnt; 30 else break; 31 } 32 std::multiset<ll>::iterator p = s.begin(); 33 cnt += sum+(*p)*k; 34 for (int i=1; i<=k; i++) 35 s.insert(w[i]+*p); 36 cnt -= *p, s.erase(p); 37 while (s.size() > n) 38 cnt -= *s.rbegin(), s.erase(--s.end()); 39 } 40 printf("%lld\n",ans); 41 return 0; 42 }
END


