【数学】8.29木板

解锁成就：死于看成平面几何题

题目描述

将一个边长为 N 的正方形裁剪成四个直角三角形。注意面积不能为 0。

EF82BDCE_88DE_4B21_8194_C516DA8CF86E.png

三个必要的切割中的两个始终从一个角落G进行（图中G位于A，实际上也可以是B、C、D），第三次切割必须垂直于前面两个之一（在图中，AE部分垂直于EF部分）。

切割机仅接受整个坐标值，这意味着N必须是整数的，并且点E和F的坐标必须是整数的。 有时候这可能是不可能的。

编写一个程序，根据给出的 N ，确定是否可以将四边形的正方形三角形切割成四个矩形三角形，如果可能的话，可以采用多少种方法来完成。

输入格式

每行一个整数 N，以 0 结尾

输出格式

每行一个整数表示方案数，方案不同当且仅当 E、F、G 的坐标不同

样例数据

input

10
20
100
32
0

output

0
8
72
24

数据范围

对于 40% 的数据，n≤10^7

对于另 10% 的数据，n 是质数

对于 100% 的数据，n≤10^14，不超过5组数据

时间限制 1 s

空间限制 512 MB

题目分析

毕竟信息用的数学和数学竞赛还是不大一样啊……

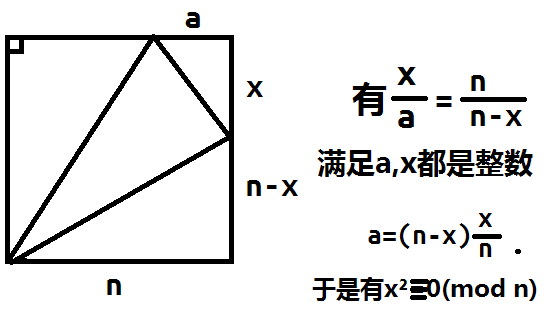
这里非常重要的一步是从a=(n-x)*x/n想到划分剩余类。

于是最朴素的解法就是枚举x.

注意到x有一个充要的命题：

注意是向上取整。

由于x的取值是$[1,n)$，所以x的个数就是：

 

化简一下可以得到：

就可以了。

 

 1 #include<bits/stdc++.h>
 2 typedef long long ll;
 3 const int maxn = 10000000;
 4 
 5 int pr[800035];
 6 bool vis[10000035];
 7 ll n,cnt;
 8 
 9 void makePrime()
10 {
11     for (int i=2; i<=maxn; i++)
12     {
13         if (!vis[i]) pr[++pr[0]] = i;
14         for (int j=1; j<=pr[0]&&pr[j]*i<=maxn; j++)
15         {
16             vis[pr[j]*i] = 1;
17             if (i%pr[j]==0) break;
18         }
19     }
20 }
21 ll qmi(ll a, ll b)
22 {
23     ll ret = 1;
24     while (b)
25     {
26         if (b&1) ret = ret*a;
27         b >>= 1, a = a*a;
28     }
29     return ret;
30 }
31 int main()
32 {
33     register int i;
34     register ll tmp;
35     makePrime();
36     while (scanf("%lld",&n)!=EOF&&n)
37     {
38         cnt = 1;
39         for (i=1; pr[i]<n&&i<=pr[0]; i++)
40         {
41             tmp = 0;
42             while (n%pr[i]==0) tmp++, n /= pr[i];
43             cnt *= qmi(pr[i], tmp/2);
44         }
45         printf("%lld\n",cnt*8ll-8ll);
46     }
47     return 0;
48 }

 

 

 

 

END

posted @ 2018-08-29 15:54  AntiQuality  阅读(135)  评论(0)  编辑  收藏  举报