【动态规划】loj#2485. 「CEOI2017」Chase
有意思的可做dp题;细节有点多,值得多想想
题目描述
在逃亡者的面前有一个迷宫,这个迷宫由 nnn 个房间和 n−1n-1n−1 条双向走廊构成,每条走廊会链接不同的两个房间,所有的房间都可以通过走廊互相到达。换句话说,这是一棵树。
逃亡者会选择一个房间进入迷宫,走过若干条走廊并走出迷宫,但他永远不会走重复的走廊。
在第 iii 个房间里,有 FiF_iFi 个铁球,每当一个人经过这个房间时,他就会受到铁球的阻挡。逃亡者手里有VVV个磁铁,当他到达一个房间时,他可以选择丢下一个磁铁(也可以不丢),将与这个房间相邻的所有房间里的铁球吸引到这个房间。这个过程如下:
- 逃亡者进入房间。
- 逃亡者丢下磁铁。
- 逃亡者走出房间。
- 铁球被吸引到这个房间。
注意逃亡者只会受到这个房间原有的铁球的阻拦,而不会受到被吸引的铁球的阻挡。
在逃亡者走出迷宫后,追逐者将会沿着逃亡者走过的路径穿过迷宫,他会碰到这条路径上所有的铁球。
请帮助逃亡者选择一条路径,使得追逐者遇到的铁球数量减去逃亡者遇到的铁球数量最大化。
输入格式
第一行两个空格隔开的整数整数 nnn 和 VVV。
第二行 nnn 个空格隔开的整数表示 FiF_iFi。
之后的 n−1n-1n−1 行,每行两个空格隔开的整数 xxx 和 yyy,表示有一条走廊连接编号为 xxx 和编号为 yyy 的房间。
输出格式
输出一个整数表示最优情况下追逐者遇到的铁球数量减去逃亡者遇到的铁球数量。
样例
样例输入
12 2
2 3 3 8 1 5 6 7 8 3 5 4
2 1
2 7
3 4
4 7
7 6
5 6
6 8
6 9
7 10
10 11
10 12样例输出
36样例解释
有一个最优方案如下:
- 从 6 号房间进入迷宫并丢下第一个磁铁,他遇到了 5 个铁球,这个时候 6 号房间会有 27 个铁球,而 5 号,7 号,8 号,9 号房间都没有铁球。
- 走到 7 号房间丢下第二个磁铁并走出迷宫,他遇到了 0 个铁球,这个时候 7 号房间会有 41 个铁球,而 2 号,4 号,6 号,10 号房间会没有铁球。
在这个过程中,逃亡者会遇到 5 个铁球而追逐者会遇到 41 个铁球。
数据范围与提示
对于 100% 的数据,有 1≤n≤105;0≤V≤100;0≤Fi≤109
- 子任务 1(20%): 有 1≤n≤10
- 子任务 2(20%): 有 1≤n≤1000
- 子任务 3(30%): 保证存在一条从 1 号房间开始的最优路径;
- 子任务 4(30%): 无特殊限制。
题目分析
搜索
做法分析:
时间复杂度$O(n^22^n)$;期望得分20pts。
贪心
考虑若固定一条路径,应该怎样选取路径上的点使得答案最优。
首先追逐者遇到的铁球可以分成两部分:所有原先路径上的铁球;被吸引到路径上的铁球。而逃亡者遇到的铁球则是所有原先路径上的铁球,减去被吸引的铁球。
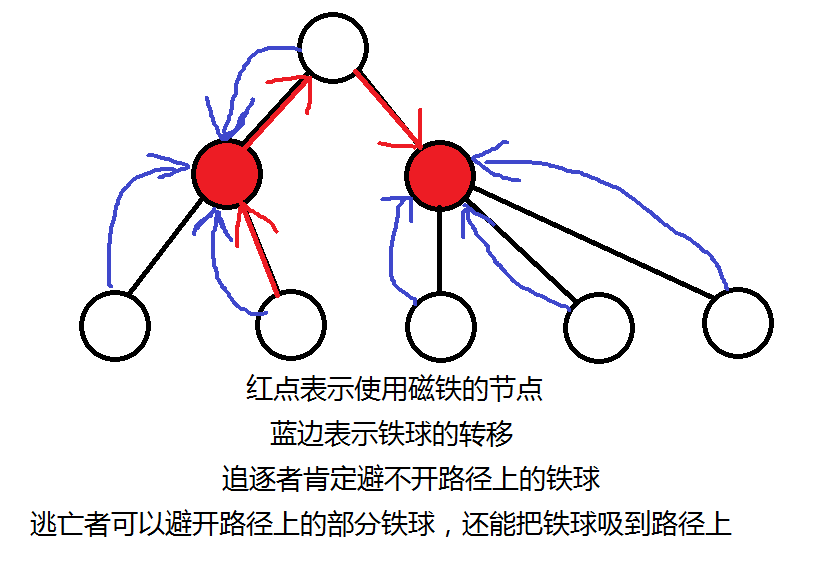
也就是说,两者遇到的铁球的差可以分成两部分:逃亡者避开的铁球+逃亡者从其他路径吸引来的铁球。
那么问题转化为:对于一颗树,定义一条路径的价值为路径上前$v$大的点权之和,要求一条以根为起点的最大价值路径。
这个东西相当于要求支持操作:查询前k大元素和;加入一个元素;删除任意一个元素。
用平衡树当然也是可以的,不过有一种堆的做法。
(最早做的时候,想到了贪心这步但是卡在查询路径前$k$大元素和这步了……一直在想可持久化堆?之类的奇怪东西)
众所周知删除堆有两种非常普遍的方法:1.强制弹出直到堆顶元素为删除元素,之后再依次弹回;2.在堆外标记元素被删除。第二种方法在权值小的时候很通用,不过权值一大且没法离散化时候就不行了。第三种是设置一个“删除堆”,存要删除的元素,当删除堆的堆顶和现在堆顶相同就舍弃现在堆顶。
于是就可以愉快地贪心了。
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 4 int n,v; 5 int p[maxn]; 6 long long ans,sv[133],sum; 7 bool vis[maxn]; 8 std::priority_queue<long long> q,del; 9 int edgeTot,edges[maxn<<1],nxt[maxn<<1],head[maxn]; 10 11 int read() 12 { 13 char ch = getchar(); 14 int num = 0; 15 bool fl = 0; 16 for (; !isdigit(ch); ch = getchar()) 17 if (ch=='-') fl = 1; 18 for (; isdigit(ch); ch = getchar()) 19 num = (num<<1)+(num<<3)+ch-48; 20 if (fl) num = -num; 21 return num; 22 } 23 void addedge(int u, int v) 24 { 25 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 26 edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 27 } 28 void clears(std::priority_queue<long long> &q) 29 { 30 std::priority_queue<long long> emt; 31 std::swap(q, emt); 32 } 33 void dfs(int x, int fa) 34 { 35 long long res = 0, cnt = 0; 36 int tot = 0; 37 for (int i=head[x]; i!=-1; i=nxt[i]) 38 if (!vis[edges[i]]) cnt += p[edges[i]]; 39 q.push(cnt), vis[x] = 1, sum += cnt; 40 for (int i=head[x]; i!=-1; i=nxt[i]) 41 { 42 int to = edges[i]; 43 if (!vis[to]){ 44 dfs(to, x); 45 } 46 } 47 if (sum > ans){ 48 while (tot<v&&q.size()) 49 { 50 while (del.size()&&del.top()==q.top()) 51 q.pop(), del.pop(); 52 if (q.empty()) break; 53 sv[++tot] = q.top(), res += q.top(); 54 q.pop(); 55 } 56 ans = ans > res?ans:res; 57 for (int i=1; i<=tot; i++) q.push(sv[i]); 58 } 59 sum -= cnt, vis[x] = 0, del.push(cnt); 60 } 61 int main() 62 { 63 memset(head, -1, sizeof head); 64 n = read(), v = read(); 65 for (int i=1; i<=n; i++) p[i] = read(); 66 for (int i=1; i<n; i++) addedge(read(), read()); 67 if (n <= 1000) 68 for (int i=1; i<=n; i++) 69 clears(q), clears(del), dfs(i, i); 70 else dfs(1, 1); 71 printf("%lld\n",ans); 72 return 0; 73 }
做法分析:
$n$次枚举起点,每次枚举起点后$n$次枚举终点。对于每一条路径$vlogv$更新答案。
由于用了优先队列,常数略大,需要卡常或者如上剪枝。
时间复杂度$O(n^2vlogv)$;期望得分70pts。
浅层的动态规划
枚举树根,令$f[i][j]$表示以$i$为根的子树内,以$i$为起点,选取$j$个点的一条链获得的最大价值。
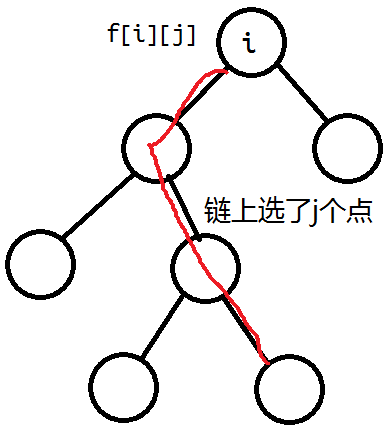
由于枚举树根,因此所有情况都会被包括在内。
做法分析:
$n$次枚举树根,每次dp状态$O(nv)$,转移$O(1)$.
时间复杂度$O(n^2v)$;期望得分70pts。
深入的动态规划
上一个做法的瓶颈在于考虑的是整条路径,因此多次dp中重叠的信息较难合并,只能枚举树根。
事实上可以强制以$1$为根,规定“上”和“下”的顺序。于是就和求树的直径很类似地,合法的路径要么一条上;一条下;两条上下的组合起来。
用$up[x][i]$表示从$x$的子树中某个节点向上走到$x$,总共使用了$i$个节点的最大价值;相同的,$dx[x][i]$表示一条向下路径使用$i$个节点的最大价值。
现在的关键就在于转移时候的去重,不能使两条链有重复部分。
因此update部分是这个样子:
1 void update(int x, int y, int fa) 2 { 3 for (int i=1; i<v; i++) getMax(ans, up[x][i]+dw[y][v-i]); 4 for (int i=1; i<=v; i++) 5 getMax(up[x][i], max(up[y][i], up[y][i-1]+sum[x]-p[y])), 6 getMax(dw[x][i], max(dw[y][i], dw[y][i-1]+sum[x]-p[fa])); 7 }
还有需要注意的一点是,从$s$到$t$的路径价值和从$t$到$s$的价值是不一样的,所以每一次dfs还需要把子节点的顺序反过来再做一遍。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 100001; 4 5 int n,v; 6 int p[maxn]; 7 ll ans,up[maxn][101],dw[maxn][101],sum[maxn]; 8 std::vector<int> g[maxn]; 9 10 #define BUF_SIZE 100000 11 #define OUT_SIZE 100000 12 inline char nc(){ 13 static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE; 14 if (p1==pend){ 15 p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin); 16 if (pend==p1)return -1; 17 } 18 return *p1++; 19 } 20 int read() 21 { 22 char ch = nc(); 23 int num = 0; 24 bool fl = 0; 25 for (; !isdigit(ch); ch = nc()) 26 if (ch=='-') fl = 1; 27 for (; isdigit(ch); ch = nc()) 28 num = (num<<1)+(num<<3)+ch-48; 29 if (fl) num = -num; 30 return num; 31 } 32 void getMax(ll &x, ll y){x=(x>y)?x:y;} 33 ll max(ll x, ll y){return x>y?x:y;} 34 void update(int x, int y, int fa) 35 { 36 for (int i=1; i<v; i++) getMax(ans, up[x][i]+dw[y][v-i]); 37 for (int i=1; i<=v; i++) 38 getMax(up[x][i], max(up[y][i], up[y][i-1]+sum[x]-p[y])), 39 getMax(dw[x][i], max(dw[y][i], dw[y][i-1]+sum[x]-p[fa])); 40 } 41 void dfs(int x, int fa) 42 { 43 for (int i=1; i<=v; i++) up[x][i] = sum[x], dw[x][i] = sum[x]-p[fa]; 44 for (auto &to:g[x]) 45 if (to!=fa) 46 dfs(to, x), update(x, to, fa); 47 std::reverse(g[x].begin(), g[x].end()); 48 for (int i=1; i<=v; i++) up[x][i] = sum[x], dw[x][i] = sum[x]-p[fa]; 49 for (auto &to:g[x]) 50 if (to!=fa) update(x, to, fa); 51 getMax(ans, max(up[x][v], dw[x][v])); 52 } 53 int main() 54 { 55 n = read(), v = read(); 56 for (int i=1; i<=n; i++) p[i] = read(); 57 for (int i=1; i<n; i++) 58 { 59 int x = read(), y = read(); 60 g[x].push_back(y), g[y].push_back(x); 61 sum[x] += p[y], sum[y] += p[x]; 62 } 63 dfs(1, 0); 64 printf("%lld\n",ans); 65 return 0; 66 }
做法分析:
这里总的状态数是$O(nv)$的。对于$O(n)$个点来说,其每一个子节点的转移是$O(v)$的。每个点只会作为子节点被转移一次,因此复杂度是$O(nv)$的。
时间复杂度$O(nv)$;期望得分100。
END


 浙公网安备 33010602011771号
浙公网安备 33010602011771号