初涉点分治

不能说是一个算法，应该算是一类思想

点分治

概念

点分治就是把树上问题中的节点拿来分治。

这所谓的“分治”是一个很抽象的概念，那么就先来介绍它的常见应用和其他性质。

大致框架

 1 void getRoot(int x, int fa)        //找重心 
 2 {
 3     size[x] = 1, son[x] = 0;
 4     for (int i=head[x]; i!=-1; i=nxt[i])
 5     {
 6         int v = edges[i].y;
 7         if (v==fa||vis[v]) continue;    //在点分树内寻找重心 
 8         getRoot(v, x), size[x] += size[v];
 9         son[x] = std::max(son[x], size[v]);
10     }
11     son[x] = std::max(son[x], tot-size[x]);
12     if (son[x] < son[root]) root = x;    //root即重心
13 }
14 void dfs(int x, int fa, int c)
15 {
16     record distance_c        //将长度为c的路径记录下来
17     for (int i=head[x]; i!=-1; i=nxt[i])
18     {
19         int v = edges[i].y;
20         if (v==fa||vis[v]) continue;
21         dfs(v, x, c+edges[i].val);    //dfs下去的长度加上边长
22     }
23 }
24 int calc(int x, int c)        //为了容斥而存在的calculate
25 {
26     int ret = 0;
27     dfs(x, 0, c);
28     ...
29     return ret;
30 }
31 void deal(int rt)
32 {
33     ans += calc(rt, 0), vis[rt] = 1;    //vis[rt]表示点rt被作为重心分治过 
34     for (int i=head[rt]; i!=-1; i=nxt[i])
35     {
36         int v = edges[i].y;
37         if (vis[v]) continue;
38         ans -= calc(v, edges[i].val);    //容斥 
39         root = 0, tot = size[v];
40         getRoot(v, 0), deal(v);
41     }
42 }
43 int main()
44 {
45     ...
46     getRoot(1, 0);
47     deal(root);
48     ...
49     return 0;
50 }

常见应用

统计树上点对路径长度为$d=k$的条数

显然路径规模是$O(n^2)$的。

注意到这$n^2$路径间有很多共用的部分。

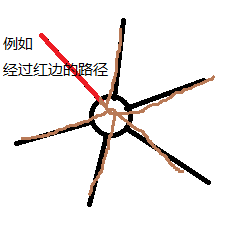
对于有重叠的路径，可以看做这样的至少有一个重叠点的形式。

自然想到类似的“按边统计贡献”的方式，对于点来统计路径的长度。显然这样可以重复利用大量的共同信息。

 1 void deal(int rt)
 2 {
 3     vis[rt] = num[0] = 1, sv[0] = 0;
 4     for (int i=head[rt]; i!=-1; i=nxt[i])
 5     {
 6         int v = edges[i].y;
 7         if (vis[v]) continue;
 8         top = 0, dis[v] = edges[i].val, dfs(v, rt);
 9         for (int i=1; i<=top; i++) query(stk[i]);　　//当前有一条长度为stk[i]的链，并在之前储存过的链长中匹配
10         for (int i=1; i<=top; i++) num[stk[i]] = 1, sv[++sv[0]] = stk[i];　　　　//标记链长为stk[i]的链
11     }
12 }

大概是这样的代码。

注意到若选取了一个点来计算经过路径数，为了计算不重复，相当于操作后在树上就要将这个点和与之相连的边都删去。

于是选取子树的重心使得复杂度在树退化为链的最坏情况下降低为$O(nlogn)$。

统计树上点对路径长度为$d≡k(mod p)$的条数

由于一般询问的都是简单路径，那么需要稍稍容斥一下。将过重心的路径划分剩余类，那么记长度为$x$的路径的个数为$cnt[x]$。例如当$p=3$时，答案就是每一次deal时$ans+=cnt[1]*cnt[2]*2+cnt[0]*cnt[0]$，再在重心子树时$ans-=cnt[1]*cnt[2]*2+cnt[0]*cnt[0]$。

其他性质

纯粹点分治的时间复杂度是$O(nlogn)$的。

考虑树退化为链的最坏情况：每一次分治，在长度为$d$的链上，当前的重心将链分为了两条长度不超过$d/2$的链。考虑递归过程的终止情况即链长为1。那么总复杂度就为$1*(n/1)+2*(n/2)+4*(n/4)+...+n*(n/n)=nlogn$。

点分治题目

【$q=k$路径】P3806 【模板】点分治1

题目背景

感谢hzwer的点分治互测。

题目描述

给定一棵有n个点的树

询问树上距离为k的点对是否存在。

输入输出格式

输入格式：

n,m 接下来n-1条边a,b,c描述a到b有一条长度为c的路径

接下来m行每行询问一个K

输出格式：

对于每个K每行输出一个答案，存在输出“AYE”,否则输出”NAY”(不包含引号)

说明

对于30%的数据n<=100

对于60%的数据n<=1000,m<=50

对于100%的数据n<=10000,m<=100,c<=1000,K<=10000000

题目分析

题目只要求判断路径是否存在。

那么先读进询问，再点分治一下，询问路径长度就可以了。

 1 #include<bits/stdc++.h>
 2 const int maxn = 10035;
 3 const int maxk = 10000035;
 4 
 5 struct Edge
 6 {
 7     int y,val;
 8     Edge(int a=0, int b=0):y(a),val(b) {} 
 9 }edges[maxn<<1];
10 int stk[maxn],top;
11 int n,m,tot,root,q[maxn],sv[maxn];
12 int edgeTot,nxt[maxn<<1],head[maxn];
13 int size[maxn],dis[maxn],son[maxn];
14 bool vis[maxn],ans[maxn],num[maxk];
15 
16 int read()
17 {
18     char ch = getchar();
19     int num = 0;
20     bool fl = 0;
21     for (; !isdigit(ch); ch = getchar())
22         if (ch=='-') fl = 1;
23     for (; isdigit(ch); ch = getchar())
24         num = (num<<1)+(num<<3)+ch-48;
25     if (fl) num = -num;
26     return num;
27 }
28 void getRoot(int x, int fa)
29 {
30     size[x] = 1, son[x] = 0;
31     for (int i=head[x]; i!=-1; i=nxt[i])
32     {
33         int v = edges[i].y;
34         if (v==fa||vis[v]) continue;
35         getRoot(v, x), size[x] += size[v];
36         son[x] = std::max(son[x], size[v]);
37     }
38     son[x] = std::max(son[x], n-size[x]);
39     if (son[x] < son[root]) root = x;
40 }
41 void addedge(int u, int v, int c)
42 {
43     edges[++edgeTot] = Edge(v, c), nxt[edgeTot] = head[u], head[u] = edgeTot;
44     edges[++edgeTot] = Edge(u, c), nxt[edgeTot] = head[v], head[v] = edgeTot;
45 }
46 void query(int x)
47 {
48     for (int i=1; i<=m; i++)
49         if (q[i] >= x) ans[i] |= num[q[i]-x];
50 }
51 void dfs(int x, int fa)
52 {
53     stk[++top] = dis[x];
54     for (int i=head[x]; i!=-1; i=nxt[i])
55     {
56         int v = edges[i].y;
57         if (v==fa||vis[v]) continue;
58         dis[v] = dis[x]+edges[i].val, dfs(v, x);
59     } 
60 }
61 void deal(int rt)
62 {
63     vis[rt] = num[0] = 1, sv[0] = 0;
64     for (int i=head[rt]; i!=-1; i=nxt[i])
65     {
66         int v = edges[i].y;
67         if (vis[v]) continue;
68         top = 0, dis[v] = edges[i].val, dfs(v, rt);
69         for (int i=1; i<=top; i++) query(stk[i]);
70         for (int i=1; i<=top; i++) num[stk[i]] = 1, sv[++sv[0]] = stk[i];
71     }
72     for (int i=1; i<=sv[0]; i++) num[sv[i]] = 0;
73     for (int i=head[rt]; i!=-1; i=nxt[i])
74     {
75         int v = edges[i].y;
76         if (vis[v]) continue;
77         root = 0, tot = size[v];
78         getRoot(v, 0), deal(root);
79     }
80 }
81 int main()
82 {
83     memset(head, -1, sizeof head);
84     son[0] = tot = n = read(), m = read(), root = 0;
85     for (int i=1; i<n; i++)
86     {
87         int u = read(), v = read();
88         addedge(u, v, read());
89     }
90     for (int i=1; i<=m; i++) q[i] = read(); 
91     getRoot(1, 0);
92     deal(root);
93     for (int i=1; i<=m; i++)
94         if (ans[i])
95             puts("AYE");
96         else puts("NAY");
97     return 0;
98 }

 

【$q≡k$路径】bzoj2152: 聪聪可可

Description

聪聪和可可是兄弟俩，他们俩经常为了一些琐事打起来，例如家中只剩下最后一根冰棍而两人都想吃、两个人都想玩儿电脑（可是他们家只有一台电脑）……遇到这种问题，一般情况下石头剪刀布就好了，可是他们已经玩儿腻了这种低智商的游戏。他们的爸爸快被他们的争吵烦死了，所以他发明了一个新游戏：由爸爸在纸上画n个“点”，并用n-1条“边”把这n个“点”恰好连通（其实这就是一棵树）。并且每条“边”上都有一个数。接下来由聪聪和可可分别随即选一个点（当然他们选点时是看不到这棵树的），如果两个点之间所有边上数的和加起来恰好是3的倍数，则判聪聪赢，否则可可赢。聪聪非常爱思考问题，在每次游戏后都会仔细研究这棵树，希望知道对于这张图自己的获胜概率是多少。现请你帮忙求出这个值以验证聪聪的答案是否正确。

Input

输入的第1行包含1个正整数n。后面n-1行，每行3个整数x、y、w，表示x号点和y号点之间有一条边，上面的数是w。

Output

以即约分数形式输出这个概率（即“a/b”的形式，其中a和b必须互质。如果概率为1，输出“1/1”）。

Sample Input

5
1 2 1
1 3 2
1 4 1
2 5 3

Sample Output

13/25
【样例说明】
13组点对分别是(1,1) (2,2) (2,3) (2,5) (3,2) (3,3) (3,4) (3,5) (4,3) (4,4) (5,2) (5,3) (5,5)。
【数据规模】
对于100%的数据，n<=20000。

题目分析

乍一看好像要像上一种方法一样，按照p,2p,3p枚举下去。

然则可以灵活地控制点分治中deal操作的内容。

将以重心为起点的链长度划分剩余类，即可得到$cnt[0],cnt[1],cnt[2]$。由于题目要求的是有序点对，自然答案应该是包括了$cnt[0]*cnt[0]+2*cnt[1]*cnt[2]$。

之所以用了“包括”一次，是因为若两条链相重叠，统计时就会重复。那么只需要容斥地去将重心每一个子树内的贡献减去就行了，恰好这个过程可以放在deal操作内。

 

 1 #include<bits/stdc++.h>
 2 const int maxn = 20035;
 3 
 4 struct Edge
 5 {
 6     int y,val;
 7     Edge(int a=0, int b=0):y(a),val(b) {}
 8 }edges[maxn<<1];
 9 int n,ans;
10 int edgeTot,nxt[maxn<<1],head[maxn];
11 int tot,root,son[maxn],size[maxn];
12 int cnt[4],dis[maxn];
13 bool vis[maxn];
14 
15 int read()
16 {
17     char ch = getchar();
18     int num = 0;
19     bool fl = 0;
20     for (; !isdigit(ch); ch = getchar())
21         if (ch=='-') fl = 1;
22     for (; isdigit(ch); ch = getchar())
23         num = (num<<1)+(num<<3)+ch-48;
24     if (fl) num = -num;
25     return num;
26 }
27 int gcd(int a, int b){return b==0?a:gcd(b, a%b);}
28 void addedge(int u, int v, int c)
29 {
30     edges[++edgeTot] = Edge(v, c), nxt[edgeTot] = head[u], head[u] = edgeTot;
31     edges[++edgeTot] = Edge(u, c), nxt[edgeTot] = head[v], head[v] = edgeTot;
32 }
33 void getRoot(int x, int fa)
34 {
35     size[x] = 1, son[x] = 0;
36     for (int i=head[x]; i!=-1; i=nxt[i])
37     {
38         int v = edges[i].y;
39         if (v==fa||vis[v]) continue;
40         getRoot(v, x), size[x] += size[v];
41         son[x] = std::max(son[x], size[v]);
42     }
43     son[x] = std::max(son[x], tot-size[x]);
44     if (son[x] < son[root]) root = x;
45 }
46 void dfs(int x, int fa)
47 {
48     cnt[dis[x]]++;
49     for (int i=head[x]; i!=-1; i=nxt[i])
50     {
51         int v = edges[i].y;
52         if (v==fa||vis[v]) continue;
53         dis[v] = (dis[x]+edges[i].val)%3;
54         dfs(v, x);
55     }
56 }
57 int calc(int x, int c)
58 {
59     dis[x] = c, cnt[0] = cnt[1] = cnt[2] = 0;
60     dfs(x, 0);
61     return 2*cnt[1]*cnt[2]+cnt[0]*cnt[0];
62 }
63 void deal(int rt)
64 {
65     ans += calc(rt, 0), vis[rt] = 1;
66     for (int i=head[rt]; i!=-1; i=nxt[i])
67     {
68         int v = edges[i].y;
69         if (vis[v]) continue;
70         ans -= calc(v, edges[i].val);
71     }
72     for (int i=head[rt]; i!=-1; i=nxt[i])
73     {
74         int v = edges[i].y;
75         if (vis[v]) continue;
76         root = 0, tot = size[v];
77         getRoot(v, 0), deal(root);
78     }
79 }
80 int main()
81 {
82     memset(head, -1, sizeof head);
83     tot = son[0] = n = read(), ans = root = 0;
84     for (int i=1; i<n; i++)
85     {
86         int u = read(), v = read();
87         addedge(u, v, read()%3);
88     }
89     getRoot(1, 0);
90     deal(root);
91     int gc = gcd(ans, n*n);
92     printf("%d/%d\n",ans/gc,n*n/gc);
93     return 0;
94 }

 

【$q≥k$路径】bzoj1468: Tree

Description

给你一棵TREE,以及这棵树上边的距离.问有多少对点它们两者间的距离小于等于K

Input

N（n<=40000） 接下来n-1行边描述管道，按照题目中写的输入 接下来是k

Output

一行，有多少对点之间的距离小于等于k

Sample Input

7
1 6 13
6 3 9
3 5 7
4 1 3
2 4 20
4 7 2
10

Sample Output

5

题目分析

其实和$q=k$的做法相差不大，只需要将过重心的路径存下来后线性扫一遍就好了。

 

 1 #include<bits/stdc++.h>
 2 const int maxn = 40035;
 3 
 4 struct Edge
 5 {
 6     int y,val;
 7     Edge(int a=0, int b=0):y(a),val(b) {} 
 8 }edges[maxn<<1];
 9 int edgeTot,nxt[maxn<<1],head[maxn];
10 int dis[maxn],son[maxn],size[maxn],root,tot;
11 int n,k,ans,sv[maxn];
12 bool vis[maxn];
13 
14 int read()
15 {
16     char ch = getchar();
17     int num = 0;
18     bool fl = 0;
19     for (; !isdigit(ch); ch = getchar())
20         if (ch=='-') fl = 1;
21     for (; isdigit(ch); ch = getchar())
22         num = (num<<1)+(num<<3)+ch-48;
23     if (fl) num = -num;
24     return num;
25 }
26 void addedge(int u, int v, int c)
27 {
28     edges[++edgeTot] = Edge(v, c), nxt[edgeTot] = head[u], head[u] = edgeTot;
29     edges[++edgeTot] = Edge(u, c), nxt[edgeTot] = head[v], head[v] = edgeTot;
30 }
31 void getRoot(int x, int fa)
32 {
33     size[x] = 1, son[x] = 0;
34     for (int i=head[x]; i!=-1; i=nxt[i])
35     {
36         int v = edges[i].y;
37         if (v==fa||vis[v]) continue;
38         getRoot(v, x), size[x] += size[v];
39         son[x] = std::max(son[x], size[v]);
40     }
41     son[x] = std::max(son[x], tot-size[x]);
42     if (son[x] < son[root]) root = x;
43 }
44 void dfs(int x, int fa, int c)
45 {
46     sv[++sv[0]] = c;
47     for (int i=head[x]; i!=-1; i=nxt[i])
48     {
49         int v = edges[i].y;
50         if (v==fa||vis[v]) continue;
51         dfs(v, x, c+edges[i].val);
52     }
53 }
54 int calc(int x, int c)
55 {
56     int ret = 0,l,r;
57     sv[0] = 0, dfs(x, 0, c);
58     std::sort(sv+1, sv+sv[0]+1);
59     l = 1, r = sv[0];
60     while (l <= r)
61         if (sv[l]+sv[r] <= k) ret += r-l, l++;
62         else r--;
63     return ret;
64 }
65 void deal(int rt)
66 {
67     ans += calc(rt, 0), vis[rt] = 1;
68     for (int i=head[rt]; i!=-1; i=nxt[i])
69     {
70         int v = edges[i].y;
71         if (vis[v]) continue;
72         ans -= calc(v, edges[i].val);
73         root = 0, tot = size[v];
74         getRoot(v, 0), deal(v);
75     }
76 }
77 int main()
78 {
79     memset(head, -1, sizeof head);
80     tot = son[0] = n = read(), root = 0;
81     for (int i=1; i<n; i++)
82     {
83         int u = read(), v = read();
84         addedge(u, v, read());
85     }
86     k = read();
87     getRoot(1, 0);
88     deal(root);
89     printf("%d\n",ans);
90     return 0;
91 }

 

 

 

 

END

posted @ 2018-08-06 12:00  AntiQuality  阅读(193)  评论(0)  编辑  收藏  举报