【树论 倍增】51nod1709 复杂度分析
倍增与位运算有很多共性;这题做法有一点像「线段树上二分」和「线段树套二分」的关系。
给出一棵n个点的树(以1号点为根),定义dep[i]为点i到根路径上点的个数。众所周知,树上最近公共祖先问题可以用倍增算法解决。现在我们需要算出这个算法精确的复杂度。我们定义计算点i和点j最近公共组先的精确复杂度为bit[dep[i]-dep[lca(i,j)]]+bit[dep[j]-dep[lca(i,j)]](bit[i]表示i在二进制表示下有多少个1,lca(i,j)表示点i和点j的最近公共祖先)。为了计算平均所需的复杂度为多少,请你帮忙计算任意两点计算最近公共组先所需复杂度的总和。
即计算 ∑n−1i=1∑nj=i+1 bit[dep[i]-dep[lca(i,j)]]+bit[dep[j]-dep[lca(i,j)]]
Input
第一行一个数n表示点数(1<=n<=100,000)
接下来n-1行每行两个数x,y表示一条边(1<=x,y<=n)
Output
一个数表示答案
Input示例
4 1 2 1 3 2 4
Output示例
8
题目分析
题目已经良心地把要求的式子给出来了。
自上向下的方法一
位运算计数题自然而然考虑按位计算贡献,注意到要求的是bit即个数,也就是说高位和低位是同性的。而这题略有特殊的是在于可以与倍增相结合做一些有趣的事情。
由于边权为1,倍增预处理的到祖先节点的二的幂次,就是到祖先节点的距离的二进制拆分。
那么就可以先枚举logn数量的每一种2^i深度d,再枚举所有n个点。对于每一个枚举的点,统计与它相距2^{d-1}<dis≤2^d的祖先节点的贡献。
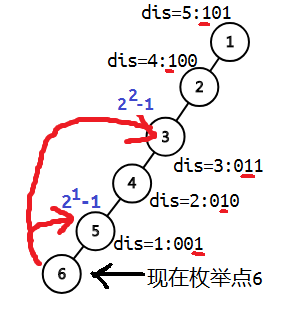
直观来说就是这张图。主要代码是这样的:
1 for (int d=0; d<19; d++) 2 { 3 memset(w, 0, sizeof w); 4 for (int ix=1; ix<=n; ix++) 5 { 6 int i = chain[ix]; //树的dfs序,因为要自上向下做 7 w[i] = tot[f[i][d+1]]-tot[f[i][d]]; 8 if (dep[i] > 1<<(d+1)) w[i] += w[fa[f[i][d+1]]]; 9 ans += w[i]; 10 } 11 }
如果想要更加程式化的描述,见51Nod1709 复杂度分析这篇博客。
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 4 int n,w[maxn]; 5 long long ans; 6 int chain[maxn],tot[maxn],chTot; 7 int f[maxn][23],dep[maxn],fa[maxn]; 8 int edgeTot,edges[maxn<<1],nxt[maxn<<1],head[maxn]; 9 10 int read() 11 { 12 char ch = getchar(); 13 int num = 0; 14 bool fl = 0; 15 for (; !isdigit(ch); ch = getchar()) 16 if (ch=='-') fl = 1; 17 for (; isdigit(ch); ch = getchar()) 18 num = (num<<1)+(num<<3)+ch-48; 19 if (fl) num = -num; 20 return num; 21 } 22 void addedge(int u, int v) 23 { 24 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 25 edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 26 } 27 void dfs(int x, int fat) 28 { 29 f[x][0] = x, f[x][1] = fa[x] = fat, dep[x] = dep[fat]+1; 30 tot[x] = 1, chain[++chTot] = x; 31 for (int i=head[x]; i!=-1; i=nxt[i]) 32 { 33 int v = edges[i]; 34 if (v!=fat){ 35 dfs(v, x); 36 tot[x] += tot[v]; 37 } 38 } 39 } 40 int main() 41 { 42 memset(head, -1, sizeof head); 43 n = read(); 44 for (int i=1; i<n; i++) addedge(read(), read()); 45 dfs(1, 1); 46 for (int j=2; j<=19; j++) 47 for (int i=1; i<=n; i++) 48 f[i][j] = fa[f[f[i][j-1]][j-1]]; 49 for (int d=0; d<19; d++) 50 { 51 memset(w, 0, sizeof w); 52 for (int ix=1; ix<=n; ix++) 53 { 54 int i = chain[ix]; 55 w[i] = tot[f[i][d+1]]-tot[f[i][d]]; 56 if (dep[i] > 1<<(d+1)) w[i] += w[fa[f[i][d+1]]]; 57 ans += w[i]; 58 } 59 } 60 printf("%lld\n",ans); 61 return 0; 62 }
自上向下的方法二
在这里给出一种O(nlog)的做法。记录每个节点的fa和子树size。
枚举一个k,用s[i]表示节点i子树内和i距离小于 2^k 大于等于2^k−1的节点数,v[i]表示节点i子树内和i距离小于 2^k 大于等于 2^k−1 的节点和i距离的bit总数,now[i]表示i向上的第 2^k−1 个祖先。
每次倍增计算每个点子树内和它距离小于 2^k 大于等于 2^k−1 的点的距离对答案的贡献即可。@hzq84621 自http://www.51nod.com/question/index.html#!questionId=1546
【博客园抽风没法正常显示数学公式我也很难受啊】
END


