初涉trie

trie：字符串算法中的重要“数据结构”

什么是trie

trie就是利用字符串的公共前缀所建成的树。

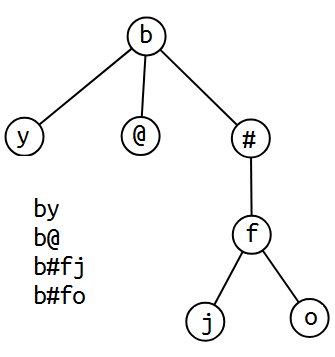
众所周知树是有很多很好的性质的，于是trie可以结合其他知识点做一些有趣的事情。

trie的例题

注意

trie的题一般数组开成$f[lensSum][size]$，其中$lensSum$是所有字符串的长度之和，$size$是字符集大小。

【判断前缀】poj3630Phone List

Description

Given a list of phone numbers, determine if it is consistent in the sense that no number is the prefix of another. Let's say the phone catalogue listed these numbers:

• Emergency 911
• Alice 97 625 999
• Bob 91 12 54 26

In this case, it's not possible to call Bob, because the central would direct your call to the emergency line as soon as you had dialled the first three digits of Bob's phone number. So this list would not be consistent.

Input

The first line of input gives a single integer, 1 ≤ t ≤ 40, the number of test cases. Each test case starts with n, the number of phone numbers, on a separate line, 1 ≤ n ≤ 10000. Then follows n lines with one unique phone number on each line. A phone number is a sequence of at most ten digits.

Output

For each test case, output "YES" if the list is consistent, or "NO" otherwise.

Sample Input

2
3
911
97625999
91125426
5
113
12340
123440
12345
98346

Sample Output

NO
YES

---

 

题目分析

这个是trie最基础的应用——判断前缀。

#include<cstdio>
#include<cctype>
#include<cstring>
const int maxn = 100035;
const int maxe = 13;

int tt,n,tot;
int f[maxn][maxe];
char ch[maxe];
bool vis[maxn],fl;

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch = getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void insert(char *s)
{
    int n = strlen(s), rt = 1;
    for (int i=0; i<n; i++)
    {
        int w = s[i]-'0';
        if (!f[rt][w]) f[rt][w] = ++tot;
        else if (i==n-1) fl = 1;
        rt = f[rt][w];
        if (vis[rt]) fl = 1;
    }
    vis[rt] = 1;
}
int main()
{
    tt = read();
    while (tt--)
    {
        memset(vis, 0, sizeof vis);
        memset(f, 0, sizeof f);
        fl = 0, tot = 1, n = read();
        for (int i=1; i<=n; i++)
        {
            scanf("%s",ch);
            insert(ch);
        }
        printf("%s\n",!fl?"YES":"NO");
    }
    return 0;
}

 

【前缀统计】bzoj1590: [Usaco2008 Dec]Secret Message 秘密信息

Description

    贝茜正在领导奶牛们逃跑．为了联络，奶牛们互相发送秘密信息．

    信息是二进制的，共有M(1≤M≤50000)条．反间谍能力很强的约翰已经部分拦截了这些信息，知道了第i条二进制信息的前bi(l《bi≤10000)位．他同时知道，奶牛使用N(1≤N≤50000)条密码．但是，他仅仅了解第J条密码的前cj(1≤cj≤10000)位．

    对于每条密码J，他想知道有多少截得的信息能够和它匹配．也就是说，有多少信息和这条密码有着相同的前缀．当然，这个前缀长度必须等于密码和那条信息长度的较小者．

    在输入文件中，位的总数（即∑Bi+∑Ci）不会超过500000.

Input

    第1行输入N和M，之后N行描述秘密信息，之后M行描述密码．每行先输入一个整数表示信息或密码的长度，之后输入这个信息或密码．所有数字之间都用空格隔开．

Output

    共M行，输出每条密码的匹配信息数．

---

题目分析

那么显然就是一个前缀计数。分成两类：其他是它前缀；它是其他前缀。

#include<bits/stdc++.h>
const int maxn = 10035;
const int maxe = 2;
const int maxNode = 500035;

struct node
{
    int end,pass;
}a[maxNode];
int f[maxNode][maxe];
int n,m,lens,tot,r[maxn];

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch = getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void insert()
{
    int u = 1;
    for (int i=1; i<=lens; i++)
    {
        if (!f[u][r[i]]) f[u][r[i]] = ++tot;
        u = f[u][r[i]];
        a[u].pass++;
    }
    a[u].pass--, a[u].end++;
}
void query()
{
    int cnt = 0, u = 1;
    for (int i=1; i<=lens; i++)
    {
        u = f[u][r[i]];
        if (!u) break;
        cnt += a[u].end;
    }
    cnt += a[u].pass;
    printf("%d\n",cnt);
}
int main()
{
    tot = 1, n = read(), m = read();
    for (int i=1; i<=n; i++)
    {
        lens = read();
        for (int j=1; j<=lens; j++) r[j] = read();
        insert();
    }
    for (int i=1; i<=m; i++)
    {
        lens = read();
        for (int j=1; j<=lens; j++) r[j] = read();
        query();
    }
    return 0;
}

 

 

 

【xor最值】bzoj4260: Codechef REBXOR

Description

Input

输入数据的第一行包含一个整数N，表示数组中的元素个数。

第二行包含N个整数A1,A2,…,AN。

Output

输出一行包含给定表达式可能的最大值。

Sample Input

5
1 2 3 1 2

Sample Output

6

HINT

满足条件的(l1,r1,l2,r2)有：(1,2,3,3)，(1,2,4,5)，(3,3,4,5)。

对于100%的数据，2 ≤ N ≤ 4*105，0 ≤ Ai ≤ 109。

---

 

题目分析

这题就是要稍加建模的题了。

若用dp的思想：$l[i]$表示$1≤l≤r≤i$的最大异或和，$r[i]$表示$i≤l≤r≤n$的最大异或和，那么有$ans=max\{l[i]+r[i+1]\}$。

问题就在于求$l[i],r[i]$，这里讨论$l[i]$的求法，$r[i]$同理。若$r!=i$，那么$l[i]=l[i-1]$；否则就是固定了右端点，再找一个左端点使得$a[x]~a[i]$异或和最大。

粗看xor是没有前缀和加法性质的。但是这不就等于在一个集合里找一个数求其与给定数最大的异或和吗？这就转化成为trie的另一个经典应用了。

#include<bits/stdc++.h>
const int maxn = 400035;
const int maxe = 3;

int n,tot,cnt,ans;
int f[maxn<<5][maxe],a[maxn];
int l[maxn],r[maxn];

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch = getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void insert(int x)
{
    int u = 1;
    for (int i=1<<30; i; i>>=1)
    {
        int c = (x&i)?1:0;
        if (!f[u][c]) f[u][c] = ++tot;
        u = f[u][c];
    }
}
int find(int x)
{
    int u = 1, ret = 0;
    for (int i=1<<30; i; i>>=1)
    {
        int c = (x&i)?0:1;
        if (f[u][c])
            ret += i, u = f[u][c];
        else u = f[u][1-c];　　//这里u打成c调了半小时……
    }
    return ret;
}
int main()
{
    n = read();
    for (int i=1; i<=n; i++) a[i] = read();
    memset(f, 0, sizeof f);
    tot = 1, cnt = 0, insert(0);
    for (int i=1; i<=n; i++)
    {
        cnt ^= a[i];
        insert(cnt);
        l[i] = std::max(l[i-1], find(cnt));
    }
    memset(f, 0, sizeof f);
    tot = 1, cnt = 0, insert(0);
    for (int i=n; i>=1; i--)
    {
        cnt ^= a[i];
        insert(cnt);
        r[i] = std::max(r[i+1], find(cnt));
    }
    for (int i=1; i<n; i++)
        ans = std::max(ans, l[i]+r[i+1]);
    printf("%d\n",ans);
    return 0;
}

 

 

END