【树形背包】bzoj4033: [HAOI2015]树上染色
仔细思考后会发现和51nod1677 treecnt有异曲同工之妙
Description
有一棵点数为N的树，树边有边权。给你一个在0~N之内的正整数K，你要在这棵树中选择K个点，将其染成黑色，并
将其他的N-K个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。
问收益最大值是多少。
Input
第一行两个整数N,K。
接下来N-1行每行三个正整数fr,to,dis，表示该树中存在一条长度为dis的边(fr,to)。
输入保证所有点之间是联通的。
N<=2000,0<=K<=N
Output
输出一个正整数，表示收益的最大值。
Sample Input
5 2
1 2 3
1 5 1
2 3 1
2 4 2
1 2 3
1 5 1
2 3 1
2 4 2
Sample Output
17
【样例解释】
将点1,2染黑就能获得最大收益。
【样例解释】
将点1,2染黑就能获得最大收益。
题目分析
这题目第一眼看上去根本不像是背包题吧……倒像是个贪心或者奇妙结论题。
但是可以像treecut一样，将答案按照树上每一条边来统计贡献。
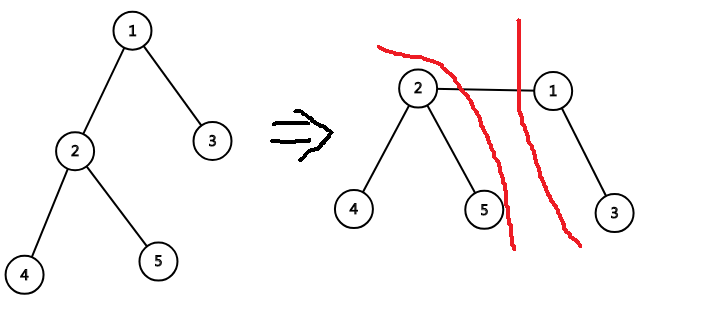
我们把一颗树沿某条边分开，看成这个样子。
那么显然若知道这条边左右两边黑白点各有多少个，就可以计算这个情况下的答案了。
也就是说，如果我们确定一条边来把树分开，那就可以依靠枚举来确定最优答案。
观察一下这个问题是具有最优子结构的，也就是说变成了一个树上背包的形式：左右两边黑白点个数的不同情况各有体积和价值，求最大价值。
我们定义$f[x][i]$表示以$x$为根的子树中，有$i$个黑点，这种情况的最大价值。
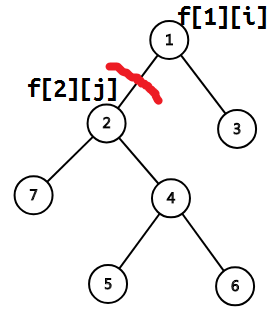
考虑如何转移。自然是要枚举上图中的$i$和$j$。然后就是背包式地转移：
1 for (int j=mn; j>=0; j--) 2 for (int l=0; l<=upp&&l<=j; l++) 3 { 4 ll left = 1ll*l*(k-l)*w; 5 ll right = 1ll*(size[v]-l)*(n-size[v]-k+l)*w; 6 f[x][j] = std::max(f[x][j], f[v][l]+f[x][j-l]+left+right); 7 }
其中mn和upp表示枚举的上界。
这个把统计转化为各个边的贡献，然后转为背包做还是很妙的。
总结
一类难以通过树形结构直接转移的动态规划问题，可以考虑对于边将树划分为两个部分的子问题，再分别维护答案。
后记
隔了几天回来看又作为一个不会做这题的人表示讲的有一点不详细。
首先有一个很大的疑问是：讲是把答案拆开统计，但是到底怎么计算这个“贡献”？这个“贡献”又是什么东西？
没写过题的人看了代码肯定又有疑问：为什么统计一下点数再乘个边权就行了？
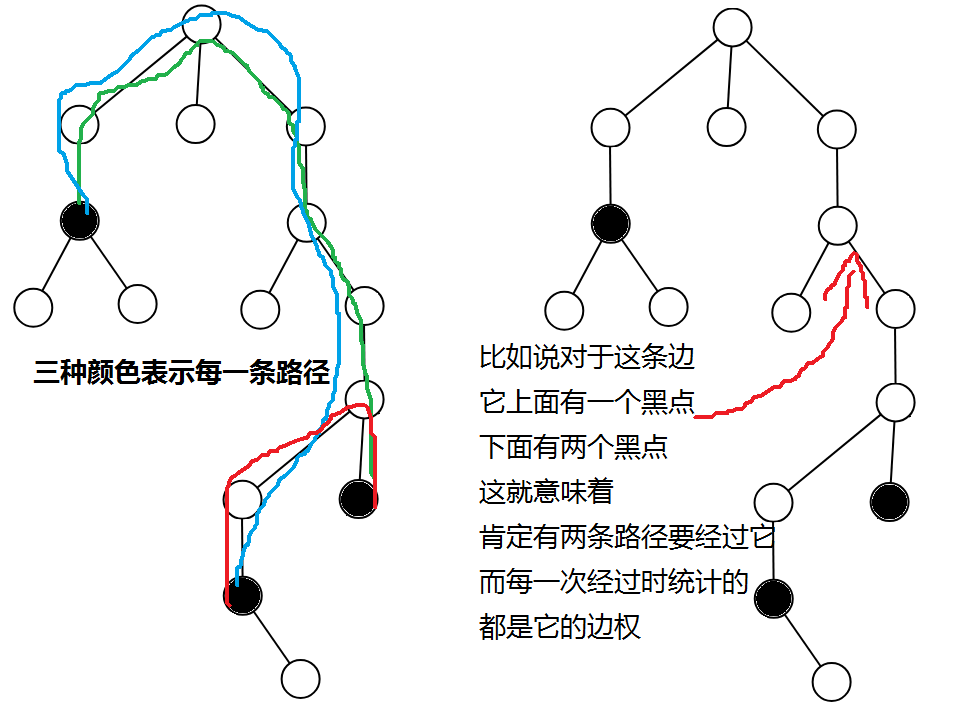
这里放张图，备忘一下
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 2003; 4 const int maxm = 5003; 5 const ll INF = 112921504606846976ll; 6 7 struct Edge 8 { 9 int y,val; 10 Edge(int a=0, int b=0):y(a),val(b) {} 11 }edges[maxm]; 12 int n,k; 13 int size[maxn]; 14 int edgeTot,nxt[maxm],head[maxn]; 15 ll f[maxn][maxn]; 16 17 int read() 18 { 19 char ch = getchar(); 20 int num = 0; 21 bool fl = 0; 22 for (; !isdigit(ch); ch = getchar()) 23 if (ch=='-') fl = 1; 24 for (; isdigit(ch); ch = getchar()) 25 num = (num<<1)+(num<<3)+ch-48; 26 if (fl) num = -num; 27 return num; 28 } 29 void dfs(int x, int fa) 30 { 31 size[x] = 1; 32 for (int i=head[x]; i!=-1; i=nxt[i]) 33 if (edges[i].y!=fa) dfs(edges[i].y, x), size[x] += size[edges[i].y]; 34 } 35 void addedge(int u, int v, int w) 36 { 37 edges[++edgeTot] = Edge(v, w), nxt[edgeTot] = head[u], head[u] = edgeTot; 38 } 39 void dp(int x, int fa) 40 { 41 f[x][0] = f[x][1] = 0; 42 if (size[x]==1) return; 43 int mn = std::min(k, size[x]); 44 for (int i=head[x]; i!=-1; i=nxt[i]) 45 { 46 int v = edges[i].y, w=edges[i].val, upp = std::min(k, size[v]); 47 if (v!=fa){ 48 dp(v, x); 49 for (int j=mn; j>=0; j--) 50 for (int l=0; l<=upp&&l<=j; l++) 51 { 52 ll left = 1ll*l*(k-l)*w; 53 ll right = 1ll*(size[v]-l)*(n-size[v]-k+l)*w; 54 f[x][j] = std::max(f[x][j], f[v][l]+f[x][j-l]+left+right); 55 } 56 } 57 } 58 } 59 int main() 60 { 61 memset(head, -1, sizeof head); 62 n = read(), k = read(); 63 if (k<<1 > n) k = n-k; 64 for (int i=1; i<n; i++) 65 { 66 int u = read(), v = read(), w = read(); 67 addedge(u, v, w); 68 addedge(v, u, w); 69 } 70 dfs(1, 1); 71 for (int i=1; i<=n; i++) 72 for (int j=0; j<=size[i]; j++) 73 f[i][j] = -INF; 74 dp(1, 1); 75 printf("%lld\n",f[1][k]); 76 return 0; 77 }
END
