初涉基环外向树dp&&bzoj1040: [ZJOI2008]骑士
基环外向树dp竟然如此简单……
Description
Z国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各
界的赞扬。最近发生了一件可怕的事情，邪恶的Y国发动了一场针对Z国的侵略战争。战火绵延五百里，在和平环境
中安逸了数百年的Z国又怎能抵挡的住Y国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就像期待有一
个真龙天子的降生，带领正义打败邪恶。骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一
些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出
征的。战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你一个艰巨的任务，从所有
的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的
情况），并且，使得这支骑士军团最具有战斗力。为了描述战斗力，我们将骑士按照1至N编号，给每名骑士一个战
斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。
Input
第一行包含一个正整数N，描述骑士团的人数。接下来N行，每行两个正整数，按顺序描述每一名骑士的战斗力
和他最痛恨的骑士。
Output
应包含一行，包含一个整数，表示你所选出的骑士军团的战斗力。
Sample Input
10 2
20 3
30 1
Sample Output
HINT
N ≤ 1 000 000，每名骑士的战斗力都是不大于 1 000 000的正整数。
题目分析
很明显这张图有两个特点：
1.由许多小连通块组成
2.每一个连通块都是基环外向树的形式
我们可以先考虑一下基环外向树的特点：
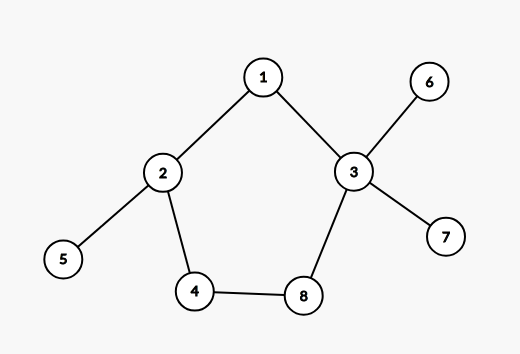
它可以看作是一颗树加一条边组成。
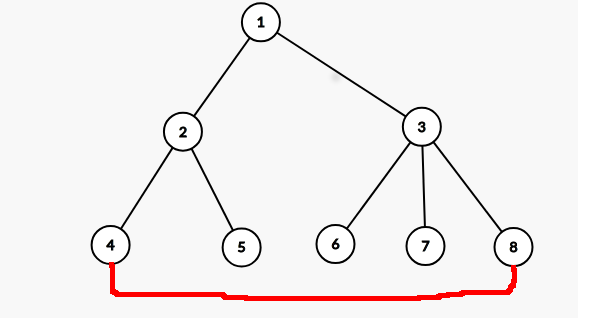
对于树的情况来说这题是很简单的，就是最大独立集的题。
然后考虑一下简单环的做法。
破环成链？
对于这种环状问题，最经典的处理方法就是破环成链：将长度为$n$的环拆成长度为$2n$的链。
但是好像维护限制有些麻烦？因为破环成链逃不开环状的模式，而这时候展开来看就会出现$f[x]=max\{f[x]+d,···\}$的奇怪形式。
拆去一条边！
环在去除一条边后就变成了一条链。而且去除任意一条边的影响都是一样的。
设去除的边为$(u,v)$，那么就代表u,v不能同时选，并且一共就三种情况：选u不选v；选v不选u；两个都不选。要是硬要在环状情况下限制住这一点，是非常麻烦的。但是我们可以用不同的状态来巧妙地回避这一点。
我们在加边时候干脆就不加这条边，这样剩下的就是一条单独的链。然后以u为树根做一次树形dp，得到的$f[u][0],f[u][1]$就分别是这条链不选$u$和选$u$的最大价值。毋庸置疑在动态规划下$f[u][1]$这个状态选没选$v$是我们无法约束的，那么就一共做两次树形dp，令$ans=max(f[u][0],f[v][0])$就好了。
于是基环外向树的情况同理，因为它去除环上任意一边后，就变成一棵树了。
1 #include<bits/stdc++.h> 2 const int maxn = 1000335; 3 4 int n,v[maxn]; 5 int edges[maxn<<1],nxt[maxn<<1],head[maxn],edgeTot; 6 int fa[maxn],lDes[maxn],rDes[maxn],cnt; 7 long long tmp,ans,f[maxn][2]; 8 9 int read() 10 { 11 char ch = getchar(); 12 int num = 0; 13 bool fl = 0; 14 for (; !isdigit(ch); ch = getchar()) 15 if (ch=='-') fl = 1; 16 for (; isdigit(ch); ch = getchar()) 17 num = (num<<1)+(num<<3)+ch-48; 18 if (fl) num = -num; 19 return num; 20 } 21 int get(int x){return x==fa[x]?x:fa[x]=get(fa[x]);} 22 void addedge(int u, int v) 23 { 24 edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 25 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 26 } 27 void dfs(int now, int fa) 28 { 29 f[now][1] = v[now], f[now][0] = 0; 30 for (int i=head[now]; i!=-1; i=nxt[i]) 31 if (edges[i]!=fa){ 32 int v = edges[i]; 33 dfs(v, now); 34 f[now][0] += std::max(f[v][0], f[v][1]); 35 f[now][1] += f[v][0]; 36 } 37 } 38 int main() 39 { 40 register int i,tt; 41 memset(head, -1, sizeof head); 42 n = read(); 43 for (i=1; i<=n; i++) fa[i] = i; 44 for (i=1; i<=n; i++) 45 { 46 v[i] = read(), tt = read(); 47 if (get(tt)!=get(i)){ 48 addedge(i, tt); 49 fa[fa[tt]] = fa[i]; 50 }else lDes[++cnt] = tt, rDes[cnt] = i; 51 } 52 for (int i=1; i<=cnt; i++) 53 { 54 dfs(lDes[i], 0); 55 tmp = f[lDes[i]][0]; 56 dfs(rDes[i], 0); 57 tmp = std::max(tmp, f[rDes[i]][0]); 58 ans += tmp; 59 } 60 printf("%lld\n",ans); 61 return 0; 62 }
END
