【树形dp 最长链】bzoj1912: [Apio2010]patrol 巡逻

富有思维性的树形dp

Description

Input

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1行，每行两个整数 a, b，表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。

Output

输出一个整数，表示新建了K 条道路后能达到的最小巡逻距离。

Sample Input

8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6

Sample Output

HINT

10%的数据中，n ≤ 1000, K = 1；
30%的数据中，K = 1；
80%的数据中，每个村庄相邻的村庄数不超过 25；
90%的数据中，每个村庄相邻的村庄数不超过 150；
100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

题目分析

初看这题觉得毫无头绪，好像怎么也不能把它和最长链联系在一起。特别是新建的边必须经过一次的限制，让人一脸懵逼。

k=0

不过首先挖掘性质：显然的是，若只是树形图，路径最短为$2n-2$；并且实际上起点任意对于答案来说都是一样的。

k=1

然后我们来想一想$k=1$的情况。比如现在我们有一颗树长成这样：

然后我们现在添加一条边：

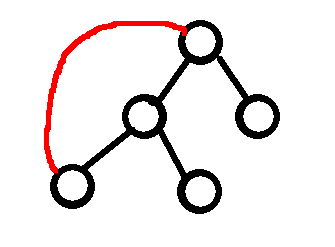
可以发现形成的环上，若环长度为$lens$，那么需要经过的路径就从$2*lens$变为了$lens+1$。并且对于其他节点来说，它们的花费是不改变的。

由此自然想到我们将最长链的首尾相连，就可以得到$k=1$时的答案。

k=2

有了k=1，扩展至k=2的思路大致相同。除了最长链形成的环，我们需要在树上另找一条次长链。

这里有一个技巧就是把最长链上的边权全都改为-1.引用CQzhangyu的一段话：

一开始想的是将直径拎出来，然后跑一个非常复杂的树形DP，但是看了题解。。。直接将直径上的所有边权值设为-1，再求一遍直径即可。正确性如何保证？如果这两条路径不相交，显然正确；如果相交，那么相当于将原路径拆成了两条。所以做法还是很巧妙的~

还有Coco_T的另一段话：

如果我们什么处理都没有，直接求一个次长链（次短路方法），
可能会和最长链重合，那么最长链上的一部分就会走两遍
所以我们在求出最长链之后，把最长链上的边权赋为-1，
这样再跑一个裸的直径就好了
（这样就可以保证可以在新求出的直径中尽量少重合原先的直径）

其实感觉能够感性理解，但是好像依旧不甚明白……？

还有要注意的是：

1     if (k==2){
2         mx = 0;
3         for (int i=s1[dir]; i!=-1; i=s1[edges[i].y])
4             edges[i].val = edges[i^1].val = -1;
5         for (int i=s2[dir]; i!=-1; i=s1[edges[i].y])
6             edges[i].val = edges[i^1].val = -1;
7         dfs(1, 0);
8         ans = ans-mx+1;
9     }

这里第二部分的作用是，将dir的次长链的边权赋为-1.乍一眼看上去好像应该是for (int i=s2[dir]; i!=-1; i=s1[edges[i].y])，不过实际上次长链除了头上是s2，后面的路径走的都是其最大值。

 1 #include<bits/stdc++.h>
 2 const int maxn = 100035;
 3 
 4 struct Edge
 5 {
 6     int y,val;
 7     Edge(int a=0, int b=0):y(a),val(b) {}
 8 }edges[maxn<<1];
 9 int n,k,mx,dir,ans;
10 int edgeTot,nxt[maxn<<1],head[maxn];
11 int s1[maxn],s2[maxn];
12 
13 int read()
14 {
15     char ch = getchar();
16     int num = 0;
17     bool fl = 0;
18     for (; !isdigit(ch); ch = getchar())
19         if (ch=='-') fl = 1;
20     for (; isdigit(ch); ch = getchar())
21         num = (num<<1)+(num<<3)+ch-48;
22     if (fl) num = -num;
23     return num;
24 }
25 void addedge(int u, int v)
26 {
27     edges[++edgeTot] = Edge(v, 1), nxt[edgeTot] = head[u], head[u] = edgeTot;
28     edges[++edgeTot] = Edge(u, 1), nxt[edgeTot] = head[v], head[v] = edgeTot;
29 }
30 int dfs(int now, int fa)
31 {
32     int mx1 = 0, mx2 = 0;
33     for (int i=head[now]; i!=-1; i=nxt[i])
34         if (edges[i].y!=fa){
35             int tt = dfs(edges[i].y, now)+edges[i].val;
36             if (tt > mx1)
37                 mx2 = mx1, mx1 = tt, s2[now] = s1[now], s1[now] = i;
38             else if (tt > mx2) mx2 = tt, s2[now] = i;
39         }
40     if (mx1+mx2 > mx) mx = mx1+mx2, dir = now;
41     return mx1;
42 }
43 int main()
44 {
45     memset(head, -1, sizeof head);
46     memset(s1, -1, sizeof s1);
47     memset(s2, -1, sizeof s2);
48     n = read(), k = read();
49     for (int i=1; i<n; i++)
50         addedge(read(), read());
51     dfs(1, 0);
52     ans = 2*n-mx-1;
53     if (k==2){
54         mx = 0;
55         for (int i=s1[dir]; i!=-1; i=s1[edges[i].y])
56             edges[i].val = edges[i^1].val = -1;
57         for (int i=s2[dir]; i!=-1; i=s1[edges[i].y])
58             edges[i].val = edges[i^1].val = -1;
59         dfs(1, 0);
60         ans = ans-mx+1;
61     }
62     printf("%d\n",ans);
63     return 0;
64 }

END

posted @ 2018-06-30 20:42 AntiQuality 阅读(449) 评论(0) 编辑收藏举报

刷新页面返回顶部

AntiQuality