初涉树形dp

算是一个……复习以及进阶？

什么是树形dp

树形dp是一种奇妙的dp……

它的一个重要拓展是和各种树形的数据结构结合，比如说在trie上、自动机上的dp。

而且有些时候还可以拓展到环加外向树、仙人掌上的酷炫操作。

好吧上面这些我都不会。

树形dp的例题

【简单dp】P2015 二叉苹果树

题目描述

有一棵苹果树，如果树枝有分叉，一定是分2叉（就是说没有只有1个儿子的结点）

这棵树共有N个结点（叶子点或者树枝分叉点），编号为1-N,树根编号一定是1。

我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有4个树枝的树

2   5
 \ / 
  3   4
   \ /
    1

现在这颗树枝条太多了，需要剪枝。但是一些树枝上长有苹果。

给定需要保留的树枝数量，求出最多能留住多少苹果。

输入输出格式

输入格式：

第1行2个数，N和Q(1<=Q<= N,1<N<=100)。

N表示树的结点数，Q表示要保留的树枝数量。接下来N-1行描述树枝的信息。

每行3个整数，前两个是它连接的结点的编号。第3个数是这根树枝上苹果的数量。

每根树枝上的苹果不超过30000个。

输出格式：

一个数，最多能留住的苹果的数量。

 

题目分析

这个的dp是很显然的。

这里我们有两种处理方法：

  1. $f[i][j]$表示$i$子树总共选取$j$根树枝的最大值。不过这样子转移时候就要小处理一下边的转移。
  2. 我们把边权下沉至点权（是的，就像树链剖分时候的边权处理），然后$f[i][j]$表示以$i$为根子树上共选取$j$个节点的最大值。这样处理起来会方便一点。

还有就是，状态转移时候可以用记忆化搜索方式取代要处理拓扑序的非递归。

 1 #include<bits/stdc++.h>
 2 const int maxn = 103;
 3 
 4 int n,q;
 5 int mp[maxn][maxn];
 6 int f[maxn][maxn],l[maxn],r[maxn],a[maxn];
 7 
 8 int read()
 9 {
10     char ch = getchar();
11     int num = 0;
12     bool fl = 0;
13     for (; !isdigit(ch); ch = getchar())
14         if (ch=='-') fl = 1;
15     for (; isdigit(ch); ch = getchar())
16         num = (num<<1)+(num<<3)+ch-48;
17     if (fl) num = -num;
18     return num;
19 }
20 int dp(int x, int y)
21 {
22     if (y==0) return 0;
23     if (l[x]==0&&r[x]==0) return a[x];
24     if (f[x][y]!=-1) return f[x][y];
25     for (int i=0; i<y; i++)
26         f[x][y] = std::max(f[x][y], dp(l[x], i)+dp(r[x], y-i-1)+a[x]);
27     return f[x][y];
28 }
29 void build(int now)
30 {
31     for (int i=1; i<=n; i++)
32         if (mp[now][i]!=-1){
33             l[now] = i, a[i] = mp[now][i];
34             mp[now][i] = -1, mp[i][now] = -1;
35             build(i);
36             break;
37         }
38     for (int i=1; i<=n; i++)
39         if (mp[now][i]!=-1){
40             r[now] = i, a[i] = mp[now][i];
41             mp[now][i] = -1, mp[i][now] = -1;
42             build(i);
43             break;
44         }
45 }
46 int main()
47 {
48     memset(f, -1, sizeof f);
49     memset(mp, -1, sizeof mp);
50     n = read(), q = read()+1;
51     for (int i=1; i<n; i++) 
52     {
53         int x = read(), y = read(), z = read();
54         mp[x][y] = z, mp[y][x] = z;
55     }
56     build(1);
57     printf("%d\n",dp(1, q));
58     return 0;
59 }

 

【权最小边覆盖】P2016 战略游戏

题目描述

Bob喜欢玩电脑游戏，特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。

他要建立一个古城堡，城堡中的路形成一棵树。他要在这棵树的结点上放置最少数目的士兵，使得这些士兵能了望到所有的路。

注意，某个士兵在一个结点上时，与该结点相连的所有边将都可以被了望到。

请你编一程序，给定一树，帮Bob计算出他需要放置最少的士兵.

输入输出格式

输入格式：

第一行 N，表示树中结点的数目。

第二行至第N+1行，每行描述每个结点信息，依次为：该结点标号i，k(后面有k条边与结点I相连)。

接下来k个数，分别是每条边的另一个结点标号r1，r2，...，rk。

对于一个n(0<n<=1500)个结点的树，结点标号在0到n-1之间，在输入数据中每条边只出现一次。

题目分析

这个就是权最小边覆盖的模板题。

我们每一个点的取舍其实可以看做是两种决策：$f[i][0]$表示点$i$不选的最小代价，$f[i][1]$表示选取点$i$的最小代价。

显而易见的是，如果点$i$不选，那么边$(i,j)$的点$j$就必须要选。

于是$f[x][0]=\sum_{son}^{f[son][1]}$

那么如果点$i$选了，边$(i,j)$上的点$j$选不选都无所谓了，不过当然是要取最优的那一个。

于是$f[x][1]=\sum_{son}^{}{min\{f[son][0],f[son][1]\}}$

 1 #include<bits/stdc++.h>
 2 const int maxn = 2003;
 3 
 4 int n;
 5 bool vis[maxn];
 6 int f[maxn][2];
 7 int head[maxn],nxt[maxn<<1],edges[maxn<<1],edgeTot;
 8 
 9 int read()
10 {
11     char ch = getchar();
12     int num = 0;
13     bool fl = 0;
14     for (; !isdigit(ch); ch = getchar())
15         if (ch=='-') fl = 1;
16     for (; isdigit(ch); ch = getchar())
17         num = (num<<1)+(num<<3)+ch-48;
18     if (fl) num = -num;
19     return num;
20 }
21 void addedge(int u, int v)
22 {
23     vis[v] = 1;
24     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
25     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
26 }
27 void dfs(int now, int fa)
28 {
29     for (int i=head[now]; i!=-1; i=nxt[i])
30         if (edges[i]!=fa){
31             dfs(edges[i], now);
32             f[now][0] += f[edges[i]][1];
33             f[now][1] += std::min(f[edges[i]][0], f[edges[i]][1]);
34         }
35 }
36 int main()
37 {
38     memset(head, -1, sizeof head);
39     n = read();
40     for (int i=1; i<=n; i++)
41     {
42         int nd = read()+1, k = read();
43         while (k--) addedge(nd, read()+1);
44         f[i][0] = 0, f[i][1] = 1;
45     }
46     dfs(1, 0);
47     printf("%d\n",std::min(f[rt][0], f[rt][1]));
48     return 0;
49 }

 

【权最小点覆盖】vijos1144皇宫看守

描述

huyichen世子事件后，xuzhenyi成了皇上特聘的御前一品侍卫。

皇宫以午门为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状；某些宫殿间可以互相望见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。

可是xuzhenyi手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。

帮助xuzhenyi布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

格式

输入格式

输入文件中数据表示一棵树，描述如下：

第1行 n，表示树中结点的数目。

第2行至第n+1n+1行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号i（0<i \le n0<i≤n），在该宫殿安置侍卫所需的经费k，该点的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r_1, r_2, \cdots, r_mr1​,r2​,⋯,rm​。

对于一个n（0 < n \le 15000<n≤1500）个结点的树，结点标号在1到n之间，且标号不重复。保证经费总和不超过2^31-1231−1。

输出格式

输出文件仅包含一个数，为所求的最少的经费。

题目分析

乍一看好像跟上面的战略游戏一样，但是实际上一个是要求覆盖所有边，只用考虑边的两端；一个是要求覆盖所有点，需要考虑三种情况。

  1. $f[i][0]$表示$i$节点自身没有安排警卫，但是父节点安排警卫的最小代价
  2. $f[i][1]$表示$i$节点自身没有安排警卫，但是子节点安排警卫的最小代价
  3. $f[i][2]$表示$i$节点自身安排警卫的最小代价

刚开始可能会觉得$f[i][0]$有点鸡肋，好像能删又好像有用。但其实$f[i][0]$和$f[i][1]$的本质区别是：子节点是否必须安排警卫。

那么，怎样才能够保证子节点必须安排警卫的状态呢？

不用说，如果转移时存在$f[son][2]$更优，即子节点安排了警卫，那么就已经符合条件了。

但是如果都是$f[son][1]$更优，即子节点的子节点安排警卫，此时我们需要设$delta=min(f[son][2]-f[son][1])$，最后再加上$max(delta,0)$，就等价于取了一个满足限制的最优解。

（其实这里有一种更加巧妙的写法：$delta=min\{f[son][2]-min\{f[son][1],f[son][2]\}\}$）

动态规划的精髓就是妙在这里，用各种灵活的状态来应对限制条件。

这样，转移方程便不难推出了：

$\begin{cases}f[x][0]=\sum_{son}^{}{min\{f[son][1],f[son][2]\}}\\f[x][1]=\sum_{son}^{}{min\{f[son][1],f[son][2]\}+delta}\\f[x][2]=\sum_{son}^{}{min\{f[son][0],f[son][1],f[son][2]\}+val[x]}\end{cases}$

然后要注意的是，最后的答案是$min\{f[root][1],f[root][2]\}$，而不能够包含进$f[root][0]$。

以下代码：

 

 1 #include<bits/stdc++.h>
 2 const int maxn = 2003;
 3 
 4 int f[maxn][3],a[maxn],n,rt;
 5 int head[maxn],nxt[maxn<<1],edges[maxn<<1],edgeTot;
 6 bool vis[maxn];
 7 
 8 int read()
 9 {
10     char ch = getchar();
11     int num = 0;
12     bool fl = 0;
13     for (; !isdigit(ch); ch = getchar())
14         if (ch=='-') fl = 1;
15     for (; isdigit(ch); ch = getchar())
16         num = (num<<1)+(num<<3)+ch-48;
17     if (fl) num = -num;
18     return num;
19 }
20 inline int min(int a, int b){return a<b?a:b;}
21 inline int min(int a, int b, int c){int t=min(a,b);return t<c?t:c;}
22 void addedge(int u, int v)
23 {
24     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
25     vis[v] = 1;
26 }
27 void dfs(int now)
28 {
29     int delta = 2e9;
30     for (int i=head[now]; i!=-1; i=nxt[i])
31     {
32         int v = edges[i];
33         dfs(v);
34         f[now][0] += min(f[v][1], f[v][2]);
35         f[now][1] += min(f[v][1], f[v][2]);
36         delta = min(f[v][2]-f[v][1], delta);
37         f[now][2] += min(f[v][0], f[v][1], f[v][2]);
38     }
39     delta = std::max(delta, 0);
40     f[now][1] += delta;
41 }
42 int main()
43 {
44     memset(head, -1, sizeof head);
45     n = read();
46     for (int i=1; i<=n; i++)
47     {
48         int p = read(), k;
49         f[p][2] = a[p] = read(), k = read();
50         while (k--) addedge(p, read());
51     }
52     rt = 1;
53     while (vis[rt]) rt++;
54     dfs(rt);
55     printf("%d\n",min(f[rt][1], f[rt][2]));
56     return 0;
57 }

 

【最大独立集】vijos1706舞会

描述

Arthur公司是一个等级森严的公司，它们有着严格的上司与下属的关系，公司以总裁为最高职位，他有若干个下属，他的下属又有若干个下属，他的下属的下属又有若干个下属……现接近年尾，公司组织团拜活动，活动中有一部分是自由舞会，公司的每个职员都有一个搞笑值，现要你制定一套哪些人上台的方案，使得台上所有演员的搞笑值最大。当然，职员们是不会和他们的顶头上司一起上台的。

输入格式

第一行一个整数N，表示这个公司总共的职员个数。

接下来一行有N个整数，由空格隔开，第i个整数表示职员i的搞笑值Ai（-1327670≤Ai≤1327670）。

接下来N-1行，每行一个1到N的整数，第i个整数表示职员i+1的顶头上司是谁，当然总裁就是职员1。

输出格式

一个整数，表示台上所有职员搞笑值之和的最大值。

 

题目分析

这个是最大独立集的板子题。

我们用$f[i][0]$表示$i$这个节点不选，$f[i][1]$表示选这个节点的最大值。

于是转移就和战略游戏很相像了。

 1 #include<bits/stdc++.h>
 2 const int maxn = 5035;
 3 
 4 long long ans,f[maxn][2];
 5 int n,a[maxn];
 6 int edgeTot,edges[maxn],nxt[maxn],head[maxn];
 7 
 8 int read()
 9 {
10     char ch = getchar();
11     int num = 0;
12     bool fl = 0;
13     for (; !isdigit(ch); ch = getchar())
14         if (ch=='-') fl = 1;
15     for (; isdigit(ch); ch = getchar())
16         num = (num<<1)+(num<<3)+ch-48;
17     if (fl) num = -num;
18     return num;
19 }
20 void dfs(int now)
21 {
22     for (int i=head[now]; i!=-1; i=nxt[i])
23     {
24         int v = edges[i];
25         dfs(v);
26         f[now][0] += std::max(f[v][0], f[v][1]);
27         f[now][1] += f[v][0];
28     }
29 }
30 int main()
31 {
32     memset(head, -1, sizeof head);
33     n = read();
34     for (int i=1; i<=n; i++) f[i][1] = a[i] = read();
35     for (int i=1; i<n; i++)
36     {
37         int u = i+1, v = read();
38         edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
39     }
40     dfs(1);
41     printf("%lld\n",std::max(f[1][0], f[1][1]));
42     return 0;
43 }

 

【最长链】poj1985Cow Marathon 

Description

After hearing about the epidemic of obesity in the USA, Farmer John wants his cows to get more exercise, so he has committed to create a bovine marathon for his cows to run. The marathon route will include a pair of farms and a path comprised of a sequence of roads between them. Since FJ wants the cows to get as much exercise as possible he wants to find the two farms on his map that are the farthest apart from each other (distance being measured in terms of total length of road on the path between the two farms). Help him determine the distances between this farthest pair of farms. 

Input

* Lines 1.....: Same input format as "Navigation Nightmare".

Output

* Line 1: An integer giving the distance between the farthest pair of farms. 

Sample Input 

7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S

Sample Output

52 

Hint 

The longest marathon runs from farm 2 via roads 4, 1, 6 and 3 to farm 5 and is of length 20+3+13+9+7=52. 

题目大意

有一颗n个点有边权的树，求树上最长链。

题目分析

这道题是树上最长链的板子题。

求树上最长链其实有两种方法：一是遍历，二是dp。两者的复杂度都是$O(n)$的。先讲bfs。

bfs求最长链

算法流程是这样的：先从任意一点$x$搜索，找到距离它最远的点$dir$。再从$dir$开始搜索一次，找到离它最远的距离$mx$即为答案。

看上去是个挺显然的结论，不过要是为了严格证明也是可以的。

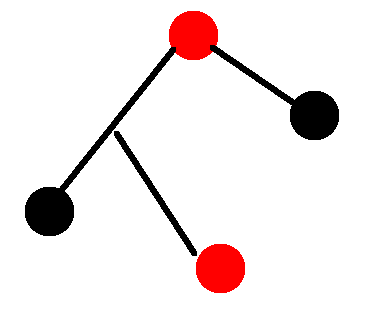
证明挺容易的就不讲了，这里放张图来助于理解吧。红色点代表最初选取的点。

 1 #include<cstdio>
 2 #include<cctype>
 3 #include<cstring>
 4 const int maxn = 100035;
 5 
 6 struct Edge
 7 {
 8     int y,val;
 9     Edge(int a=0, int b=0):y(a),val(b) {}
10 }edges[maxn<<1];
11 int n,m,dir,mx;
12 int edgeTot,nxt[maxn<<1],head[maxn];
13 
14 int read()
15 {
16     char ch = getchar();
17     int num = 0;
18     bool fl = 0;
19     for (; !isdigit(ch); ch = getchar())
20         if (ch=='-') fl = 1;
21     for (; isdigit(ch); ch = getchar())
22         num = (num<<1)+(num<<3)+ch-48;
23     if (fl) num = -num;
24     return num; 
25 }
26 void addedge(int u, int v, int w)
27 {
28     edges[++edgeTot] = Edge(v, w), nxt[edgeTot] = head[u], head[u] = edgeTot;
29     edges[++edgeTot] = Edge(u, w), nxt[edgeTot] = head[v], head[v] = edgeTot;
30 }
31 void dfs(int now, int fa, int w)
32 {
33     if (w > mx) mx = w, dir = now;
34     for (int i=head[now]; i!=-1; i=nxt[i])
35         if (edges[i].y!=fa)
36             dfs(edges[i].y, now, w+edges[i].val);
37 }
38 int main()
39 {
40     memset(head, -1, sizeof head);
41     n = read(), m = read();
42     for (int i=1; i<=m; i++)
43     {
44         int x = read(), y = read(), z = read();
45         addedge(x, y, z);
46     }
47     dfs(1, 0, 0);
48     mx = 0;
49     dfs(dir, 0, 0);
50     printf("%d\n",mx);
51     return 0;
52 }
bfs求最长链

  

dp求最长链

我们先考虑对于点$x$，经过它的最长链怎么求。

如果树根不是$x$，那么就会出现两种最长链的情况：一种是自上而下贯穿的一条链；第二种是仅在其子树内的一条链。

但是如果把$x$设为树根，就不会有这种问题：最长链=子树最长链+子树次长链。

自然想到用$d1[x]$，$d2[x]$分别表示以$x$为根的子树中的最长链和次长链。

但是如果把每一个点为树根都独立地求一遍的话，就浪费掉很多重复的信息，并且复杂度就上升到$O(n^2)$了。

实际上我们可以人为确定一个树根。因为$n$个点同时转移，有大量信息是重叠的。

 

 1 void dfs(int now)
 2 {
 3     vis[now] = 1;
 4     int mx1 = 0, mx2 = 0;
 5     for (int i=head[now]; i!=-1; i=nxt[i])
 6         if (!vis[edges[i].y]){
 7             dfs(edges[i].y);
 8             int val = edges[i].val + f[edges[i].y].mx1;
 9             if (val > mx1) mx2 = mx1, mx1 = val;
10             else if (val > mx2) mx2 = val;
11         }
12     f[now].mx1 = mx1, f[now].mx2 = mx2;
13     ans = std::max(mx1+mx2, ans);
14 }

这个就是转移的代码。

对了，还要注意的就是最后这句$ans = std::max(mx1+mx2, ans)$而不是$ans=f[root].mx1+f[root].mx2$，原因正是：这样的同时转移，等价于把所有节点都当做树根算一遍。这个技巧只意味着节省复杂度，而不意味着答案就是$root$上的答案。

 1 /**************************************************************
 2     Problem: 3363
 3     User: AntiQuality
 4     Language: C++
 5     Result: Accepted
 6     Time:104 ms
 7     Memory:6704 kb
 8 ****************************************************************/
 9  
10 #include<bits/stdc++.h>
11 const int maxn = 100035;
12  
13 struct node
14 {
15     int mx1,mx2;
16 }f[maxn];
17 struct Edge
18 {
19     int y,val;
20     Edge(int a=0, int b=0):y(a),val(b) {}
21 }edges[maxn<<1];
22 int n,m,ans;
23 int edgeTot,nxt[maxn<<1],head[maxn];
24 bool vis[maxn];
25  
26 int read()
27 {
28     char ch = getchar();
29     int num = 0;
30     bool fl = 0;
31     for (; !isdigit(ch); ch = getchar())
32         if (ch=='-') fl = 1;
33     for (; isdigit(ch); ch = getchar())
34         num = (num<<1)+(num<<3)+ch-48;
35     if (fl) num = -num;
36     return num; 
37 }
38 void addedge(int u, int v, int w)
39 {
40     edges[++edgeTot] = Edge(v, w), nxt[edgeTot] = head[u], head[u] = edgeTot;
41     edges[++edgeTot] = Edge(u, w), nxt[edgeTot] = head[v], head[v] = edgeTot;
42 }
43 void dfs(int now)
44 {
45     vis[now] = 1;
46     int mx1 = 0, mx2 = 0;
47     for (int i=head[now]; i!=-1; i=nxt[i])
48         if (!vis[edges[i].y]){
49             dfs(edges[i].y);
50             int val = edges[i].val + f[edges[i].y].mx1;
51             if (val > mx1) mx2 = mx1, mx1 = val;
52             else if (val > mx2) mx2 = val;
53         }
54     f[now].mx1 = mx1, f[now].mx2 = mx2;
55     ans = std::max(mx1+mx2, ans);
56 }
57 int main()
58 {
59     memset(head, -1, sizeof head);
60     n = read(), m = read();
61     for (int i=1; i<=m; i++)
62     {
63         int x = read(), y = read(), z = read();
64         addedge(x, y, z);
65     }
66     dfs(1);
67     printf("%d\n",ans);
68     return 0;
69 }
dp求最长链

 

 

【最长链进阶】bzoj1912: [Apio2010]patrol 巡逻

Description 

Input 

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1行，每行两个整数 a, b， 表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。

Output

输出一个整数，表示新建了K 条道路后能达到的最小巡逻距离。

Sample Input

8 1 
1 2 
3 1 
3 4 
5 3 
7 5 
8 5 
5 6

Sample Output

11

HINT 

10%的数据中，n ≤ 1000, K = 1； 
30%的数据中，K = 1； 
80%的数据中，每个村庄相邻的村庄数不超过 25； 
90%的数据中，每个村庄相邻的村庄数不超过 150； 
100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

题目分析

这题写了题解，就不再写一遍了：https://www.cnblogs.com/antiquality/p/9248589.html

算是最长链的灵活应用。

 

【最长链统计】vijos1476旅游规划(csapc)

描述

W市的交通规划出现了重大问题，市政府下决心在全市的各大交通路口安排交通疏导员来疏导密集的车流。但由于人员不足，W市市长决定只在最需要安排人员的路口安放人员。具体说来，W市的交通网络十分简单，它包括n个交叉路口和n-1条街道，任意一条街道连接两个交叉路口，并且任意两个交叉路口之间都存在一条路径互相连接。经过长期调查结果显示如果一个交叉路口位于W市交通网的最长路径上，那么这个路口必然拥挤不堪，所谓最长路径定义为某条路径p=(v1,v2,v3…vk)，路径经过的路口各不相同且城市中不存在长度>k的路径（因此可能存在着不唯一的最长路径）。因此W市市长希望知道有哪些路口位于城市交通网的最长路径之上。

输入格式

第一行包括一个整数n。

之后的n-1行每行包括两个整数u, v表示编号为u和v的路口之间存在着一条街道（注意：路口被依次编号为0到n-1）

输出格式

输出包括若干行，每行包括一个整数——某个位于最长路上路口的编号。

为了确保解唯一，我们规定位于所有最长路上的路口按编号顺序从小到大输出。

样例输入1

10
0 1
0 2
0 4
0 6
0 7
1 3
2 5
4 8
6 9

样例输出1

0
1
2
3
4
5
6
8
9

提示

这里存在着若干条最长路径，其中的两条是3-1-0-2-5与8-4-0-6-9，他们的长度都是5，但是不存在长度>5的路径且所有最长路径都不包括路口7，所以答案中没有7。

数据范围：
对于50%的数据保证n<=1000
对于100%的数据保证n<=200000

题目分析

这题就是统计直径的板子题。

首先当然要dp算出直径大小。然后再考虑在dp这个结构下，多条直径的形态是怎么样的。

当然只有上图两种情况。

那么有了图就很好理解了：

 

1     if (f[now][1]+f[now][0]==mx||f[now][0]+val==mx)
2         ans[++ans[0]] = now;

 

其中$f[x][0],f[x][1]$分别表示最长链和次长链；$val$表示$x$子树外的最大值。

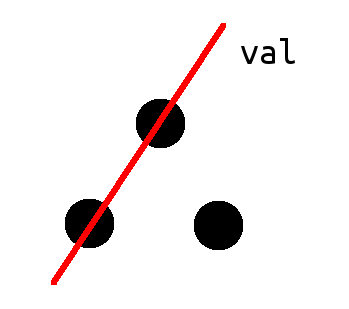
于是大致流程就这样。

 

 1 #include<bits/stdc++.h>
 2 const int maxn = 200035;
 3 
 4 int n,mx;
 5 int f[maxn][2];
 6 int ans[maxn];
 7 int edgeTot,edges[maxn<<1],nxt[maxn<<1],head[maxn];
 8 
 9 int read()
10 {
11     char ch = getchar();
12     int num = 0;
13     bool fl = 0;
14     for (; !isdigit(ch); ch = getchar())
15         if (ch=='-') fl = 1;
16     for (; isdigit(ch); ch = getchar())
17         num = (num<<1)+(num<<3)+ch-48;
18     if (fl) num = -num;
19     return num;
20 }
21 void addedge(int u, int v)
22 {
23     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
24     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
25 }
26 void dp(int now, int fa)
27 {
28     int mx1 = 0, mx2 = 0;
29     for (int i=head[now]; i!=-1; i=nxt[i])
30         if (edges[i]!=fa){
31             dp(edges[i], now);
32             int tt = f[edges[i]][0]+1;
33             if (mx1 < tt) mx2 = mx1, mx1 = tt;
34             else if (mx2 < tt) mx2 = tt;
35         }
36     f[now][0] = mx1, f[now][1] = mx2;
37     mx = std::max(mx1+mx2, mx);
38 }
39 void get(int now, int fa, int val)
40 {
41     if (f[now][1]+f[now][0]==mx||f[now][0]+val==mx)
42         ans[++ans[0]] = now;
43     for (int i=head[now]; i!=-1; i=nxt[i])
44     {
45         int v = edges[i];
46         if (v!=fa){
47             if (f[now][0]==f[v][0]+1)
48                 get(v, now, std::max(val, f[now][1])+1);
49             else get(v, now, std::max(val, f[now][0])+1);
50         }
51     }
52 }
53 int main()
54 {
55     memset(head, -1, sizeof head);
56     n = read();
57     for (int i=1; i<n; i++)
58         addedge(read()+1, read()+1);
59     dp(1, 0);
60     get(1, 0, 0);
61     std::sort(ans+1, ans+ans[0]+1);
62     for (int i=1; i<=ans[0]; i++)
63         printf("%d\n",ans[i]-1);
64     return 0;
65 }

 

 

 

 

END

 

 

posted @ 2018-06-29 15:31  AntiQuality  阅读(586)  评论(0)  编辑  收藏  举报