初涉0/1分数规划
看上去常数很大的二分（？）然而似乎像权闭合子图这样的，每次二分加网络流的玩意都能过……
什么是0/1分数规划
“0/1”表示的是一样物品只有选与不选两种情况；分数规划则是求解一个形如分数式子的多项式的最值问题。而至于处理物品之间的拓扑序（比如说选A那么必须选B、选B不能选C，等等情况），那则是另一回事。
分数规划例题
【分数规划】poj2976Dropping tests
Description
In a certain course, you take n tests. If you get ai out of bi questions correct on test i, your cumulative average is defined to be
.
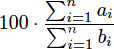Given your test scores and a positive integer k, determine how high you can make your cumulative average if you are allowed to drop any k of your test scores.
Suppose you take 3 tests with scores of 5/5, 0/1, and 2/6. Without dropping any tests, your cumulative average is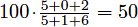 
. However, if you drop the third test, your cumulative average becomes 
.
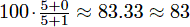Input
The input test file will contain multiple test cases, each containing exactly three lines. The first line contains two integers, 1 ≤ n ≤ 1000 and 0 ≤ k < n. The second line contains n integers indicating ai for all i. The third line contains n positive integers indicating bi for all i. It is guaranteed that 0 ≤ ai ≤ bi ≤ 1, 000, 000, 000. The end-of-file is marked by a test case with n = k = 0 and should not be processed.
Output
For each test case, write a single line with the highest cumulative average possible after dropping k of the given test scores. The average should be rounded to the nearest integer.
题目分析
这道可以说是分数规划的经典入门题吧。给出n个物体，每一个物体$i$有$a_i$与$b_i$两个权值，求丢弃$k$个物品（等于选出$n-k$个物品），使以下式子的值最大：
2^n的暴力
那么我们就枚举每一个物品选或不选吧！显然是最暴力的暴力。
分数规划
考虑有没有一种办法使得我们需要完成的状态数不那么大呢？不妨二分式子最后的值mid。
设，移项得
。由于我们是需要二分这一个单调的答案，二分中的$check()$问题转化为判断存不存在满足
的情况。
那么我们要怎么判断呢？注意到两个$Σ$的$i$都是相等的，很自然地想到设新权值，那么只需要贪心地判断$n-k$个物品新权值和是否大于等于0就可以了。
1 #include<algorithm> 2 #include<cstdio> 3 #include<cmath> 4 const int maxn = 1003; 5 const double eps = 1e-7; 6 7 int a[maxn],b[maxn]; 8 double c[maxn]; 9 int n,k; 10 11 int fcmp(double a, double b) 12 { 13 if (fabs(a-b) < eps) return 0; 14 if (a-b < eps) return -1; 15 return 1; 16 } 17 bool check(double x) 18 { 19 for (int i=1; i<=n; i++) 20 c[i] = a[i]-x*b[i]; 21 std::sort(c+1, c+n+1); 22 double sum = 0; 23 for (int i=k+1; i<=n; i++) 24 sum += c[i]; 25 return fcmp(sum, 0) >= 0; 26 } 27 int main() 28 { 29 while (scanf("%d%d",&n,&k)==2 && (n || k)) 30 { 31 for (int i=1; i<=n; i++) scanf("%d",&a[i]); 32 for (int i=1; i<=n; i++) scanf("%d",&b[i]); 33 double l = 0, r = 1; 34 for (double mid = (l+r)/2; fcmp(l, r)<=0; mid = (l+r)/2) 35 if (check(mid)) l = mid+eps; 36 else r = mid-eps; 37 printf("%.0lf\n",r*100); 38 } 39 return 0; 40 }
【分数规划-最小比例生成树】poj2728Desert King
Description
After days of study, he finally figured his plan out. He wanted the average cost of each mile of the channels to be minimized. In other words, the ratio of the overall cost of the channels to the total length must be minimized. He just needs to build the necessary channels to bring water to all the villages, which means there will be only one way to connect each village to the capital.
His engineers surveyed the country and recorded the position and altitude of each village. All the channels must go straight between two villages and be built horizontally. Since every two villages are at different altitudes, they concluded that each channel between two villages needed a vertical water lifter, which can lift water up or let water flow down. The length of the channel is the horizontal distance between the two villages. The cost of the channel is the height of the lifter. You should notice that each village is at a different altitude, and different channels can't share a lifter. Channels can intersect safely and no three villages are on the same line.
As King David's prime scientist and programmer, you are asked to find out the best solution to build the channels.
Input
Output
题目大意
给出n个在二维上的点，每个点用三元组(x,y,z)描述，表示其在(x,y)上，高度为z。其中两点之间的距离为欧几里得距离；代价为$|z_i-z_j|$。
现在要求你求出一颗生成树，使得它的代价与距离比值最小。
题目分析
看到这种新奇的定义时候，第一眼的确觉得甚是奇怪……不过分析一下就会发现，大致和上一题的模型相同，也是二分$mid$后刷一遍$check()$即可。
1 #include<algorithm> 2 #include<cstdio> 3 #include<cmath> 4 const int maxn = 1003; 5 const double eps = 1e-7; 6 7 int a[maxn],b[maxn]; 8 double c[maxn]; 9 int n,k; 10 11 int fcmp(double a, double b) 12 { 13 if (fabs(a-b) < eps) return 0; 14 if (a-b < eps) return -1; 15 return 1; 16 } 17 bool check(double x) 18 { 19 for (int i=1; i<=n; i++) 20 c[i] = a[i]-x*b[i]; 21 std::sort(c+1, c+n+1); 22 double sum = 0; 23 for (int i=k+1; i<=n; i++) 24 sum += c[i]; 25 return fcmp(sum, 0) >= 0; 26 } 27 int main() 28 { 29 while (scanf("%d%d",&n,&k)==2 && (n || k)) 30 { 31 for (int i=1; i<=n; i++) scanf("%d",&a[i]); 32 for (int i=1; i<=n; i++) scanf("%d",&b[i]); 33 double l = 0, r = 1; 34 for (double mid = (l+r)/2; fcmp(l, r)<=0; mid = (l+r)/2) 35 if (check(mid)) l = mid+eps; 36 else r = mid-eps; 37 printf("%.0lf\n",r*100); 38 } 39 return 0; 40 }
【分数规划-最大比例环】poj3621Sightseeing Cows
Description
Farmer John has decided to reward his cows for their hard work by taking them on a tour of the big city! The cows must decide how best to spend their free time.
Fortunately, they have a detailed city map showing the L (2 ≤ L ≤ 1000) major landmarks (conveniently numbered 1.. L) and the P (2 ≤ P ≤ 5000) unidirectional cow paths that join them. Farmer John will drive the cows to a starting landmark of their choice, from which they will walk along the cow paths to a series of other landmarks, ending back at their starting landmark where Farmer John will pick them up and take them back to the farm. Because space in the city is at a premium, the cow paths are very narrow and so travel along each cow path is only allowed in one fixed direction.
While the cows may spend as much time as they like in the city, they do tend to get bored easily. Visiting each new landmark is fun, but walking between them takes time. The cows know the exact fun values Fi (1 ≤ Fi ≤ 1000) for each landmark i.
The cows also know about the cowpaths. Cowpath i connects landmark L1i to L2i (in the direction L1i -> L2i ) and requires time Ti (1 ≤ Ti ≤ 1000) to traverse.
In order to have the best possible day off, the cows want to maximize the average fun value per unit time of their trip. Of course, the landmarks are only fun the first time they are visited; the cows may pass through the landmark more than once, but they do not perceive its fun value again. Furthermore, Farmer John is making the cows visit at least two landmarks, so that they get some exercise during their day off.
Help the cows find the maximum fun value per unit time that they can achieve.
Input
* Line 1: Two space-separated integers: L and P
* Lines 2..L+1: Line i+1 contains a single one integer: Fi
* Lines L+2..L+P+1: Line L+i+1 describes cow path i with three space-separated integers: L1i , L2i , and Ti
Output
* Line 1: A single number given to two decimal places (do not perform explicit rounding), the maximum possible average fun per unit time, or 0 if the cows cannot plan any trip at all in accordance with the above rules.
题目大意
给出$n$个点，$m$条单向边。每个点有点权$w_i$，每条边有边权$t_i$。求点权比边权最大的环。
题目分析
我们二分枚举mid，再用$wx−mid×t(x,y)$建边，最后跑一遍SPFA看一看有没有正权环就可以了。
一些槽点！
poj的机子速度真的是不敢恭维……一开始用了std::queue和std::vector果不其然在poj上TLE了……（luogu上还是能够过的……）
然后重写了前向星，结果还是TLE？（exm）
后来发现：
和
效率差别还是好一点大的……
1 #include<cmath> 2 #include<queue> 3 #include<cctype> 4 #include<cstdio> 5 #include<vector> 6 #include<cstring> 7 #include<algorithm> 8 const int maxn = 1003; 9 const int maxm = 5003; 10 11 int n,m,pts[maxn],tot[maxn],ql,qr,q[maxn+3],E; 12 int son[maxm],nxt[maxm],lnk[maxn],w[maxm]; 13 double l,r,mid,dis[maxn]; 14 bool vis[maxn]; 15 16 inline int read() 17 { 18 char ch = getchar(); 19 int num = 0; 20 bool fl = 0; 21 for (; !isdigit(ch); ch = getchar()) 22 if (ch == '-') fl = 1; 23 for (; isdigit(ch); ch = getchar()) 24 num = (num<<1)+(num<<3)+ch-48; 25 if (fl) num = -num; 26 return num; 27 } 28 inline int z(int x){return x+1>=maxn?x+1-maxn:x+1;} 29 inline bool check(double x) 30 { 31 memset(vis, 0, sizeof vis); 32 register int i,tt; 33 for (i=1; i<=n; i++) dis[i] = -1e100,tot[i] = 0; 34 dis[1] = 0; 35 ql = 0, qr = 0; 36 q[qr=z(qr)] = 1; 37 while (ql!=qr) 38 { 39 tt = q[ql=z(ql)]; 40 vis[tt] = 0; 41 for (i=lnk[tt]; i; i = nxt[i]) 42 if (dis[son[i]]-(dis[tt]+pts[tt]*1.0-x*w[i]) < 1e-10){ 43 dis[son[i]] = dis[tt]+pts[tt]*1.0-x*w[i]; 44 if (vis[son[i]]==0){ 45 vis[son[i]] = 1; 46 q[qr=z(qr)] = son[i]; 47 if (++tot[son[i]] > n) return 1; 48 } 49 } 50 } 51 return 0; 52 } 53 inline void add(int x, int y, int z) 54 { 55 w[++E] = z,son[E] = y,nxt[E] = lnk[x],lnk[x] = E; 56 } 57 int main() 58 { 59 register int i,x,y,z; 60 n = read(),m = read(); 61 for (i=1; i<=n; i++) pts[i] = read(); 62 for (i=1; i<=m; i++) 63 { 64 x = read(), y = read(), z = read(); 65 add(x, y, z); 66 } 67 l = 0, r = 1e6; 68 for (mid = (l+r)/2; l-r <= 1e-8; mid = (l+r)/2) 69 if (check(mid)) l = mid+1e-4; else r = mid-1e-4; 70 printf("%.2lf\n",l); 71 return 0; 72 }
参考：https://blog.csdn.net/zzkksunboy/article/category/7255714
END
