初涉启发式搜索

高效的一种搜索方式（或许可以叫做一种优化？

什么是启发式搜索

「启发式搜索」这个名字，听上去有些空洞。

想象一下你在去NOIP考场的路上堵车了，但是比赛马上要开始了！你心急火燎地想要找到一条最短路径，但由于此时并不知道整张图（所有到达考场的可行路径），你被迫只能使用搜索的方式。此刻你化出了无数个分身，每个人都往一个特定的方向前进，试图寻找到达考场的最短时间。如果按照传统的BFS/DFS的话，实际上过程中搜索了很多丝毫没有作用的状态——有可能大部分的分身都一直往郊区走去，越走越远，而你却不得不浪费资源去维护他们的状态！这就是「盲搜」。

一种能够使你更快到达考场的方式就是使用「启发式搜索」。

你让每一个分身都维护3个数据：已经花的时间g；预计还要多少时间h；预计最短总共要花时间f。

考虑这个$h$的计算之前先来想一想：$h$在不一定完全等于真正要花时间的情况下（因为h是估计出来的，并不能保证花了h时间之后一定到达），它是应该小于真正的用时$h'$还是要大于真正的用时$h'$。

  1. $h<h'$：估计偏大，“悲观地认为”能够按时到达的点将会超时：搜索范围偏小，搜得快但是不一定是最优解。
  2. $h>h'$：估计偏小，“保守地认为”大部分点能够按时到达（但如果即使这样保守都还会超时，就肯定要舍去了）：搜索范围偏大，效率较低但一定是最优解。

那么由此可得我们应该在小于等于实际距离的情况下，尽可能接近实际距离。

回到寻找NOIP考场路径的问题，我们根据题目条件，自然想到用欧几里得距离充当h()函数。这如同现在有四个方向：一个朝着考场走去；一个背离考场走去；还有两个沿着无关的方向走去。大部分情况下，第一种状态总是能够较为快速地走到终点的，因此我们优先搜索第一种状态。当然，也不排除其他的特殊情况——

 

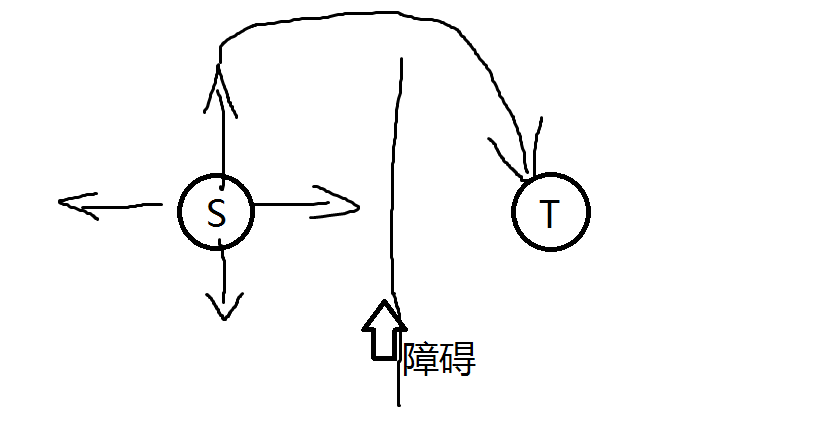
所以我们要在优先搜索f()小的情况下，把所有判断可行的状态都搜索一遍。（当然，这也是搜索必须满足的性质）

启发式搜索板子题

【A*】poj1915Knight Moves

Description

Background 
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him? 
The Problem 
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov. 
For people not familiar with chess, the possible knight moves are shown in Figure 1. 

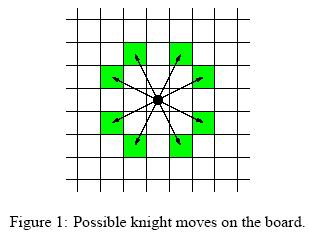
Input

The input begins with the number n of scenarios on a single line by itself. 
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, ..., l-1}*{0, ..., l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.

Output

For each scenario of the input you have to calculate the minimal amount of knight moves which are necessary to move from the starting point to the ending point. If starting point and ending point are equal,distance is zero. The distance must be written on a single line.

题意

求骑士从(x1,y1)->(x2,y2)的最短步数

题目分析

裸的A*题，h()使用欧几里得距离。

 1 #include<cmath>
 2 #include<queue>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<algorithm>
 6 const int dx[] = {0, 1, 1, 2, 2, -1, -1, -2, -2};
 7 const int dy[] = {0, 2, -2, 1, -1, 2, -2, 1, -1};
 8 const int maxn = 303;
 9 
10 struct node
11 {
12     int x,y,step;
13     int f,g,h;
14     bool operator < (node t) const
15     {
16         if (f==t.f)
17             return step > t.step;
18         return f > t.f;
19     }
20 }k;
21 int sx,sy,tx,ty,tt,n,ans;
22 int vis[maxn][maxn];
23 std::priority_queue<node> q;
24 
25 void clear(std::priority_queue<node> &q)
26 {
27     std::priority_queue<node> emt;
28     swap(emt, q);
29 }
30 bool range(node x)
31 {
32     return x.x>=0 && x.y>=0 && x.x<n && x.y<n;
33 }
34 int dis(node x)
35 {
36     return (int)(sqrt((x.x-tx)*(x.x-tx)*1.0+(x.y-ty)*(x.y-ty)*1.0)*1000);
37 }
38 void Astar()
39 {
40     while (q.size())
41     {
42         node tt = q.top();
43         q.pop();
44         if (vis[tt.x][tt.y] && vis[tt.x][tt.y] <= tt.step) continue;
45         vis[tt.x][tt.y] = tt.step;
46         if (tt.x == tx && tt.y == ty)
47         {
48             ans = tt.step;
49             return;
50         }
51         for (int i=1; i<=8; i++)
52         {
53             node t;
54             t.x = tt.x+dx[i], t.y = tt.y+dy[i];
55             if (range(t) && !vis[t.x][t.y])
56             {
57                 t.h = dis(t),t.g = tt.g + 2236;
58                 t.step = tt.step+1;
59                 t.f = t.g+t.h;
60                 q.push(t);
61             }
62         }
63     }
64 }
65 int main()
66 {
67     scanf("%d",&tt);
68     for (int rr=1; rr<=tt; rr++)
69     {
70         memset(vis, 0, sizeof vis);
71         clear(q);
72         scanf("%d",&n);
73         scanf("%d%d%d%d",&sx,&sy,&tx,&ty);
74         k.x = sx, k.y = sy;
75         k.g = 0, k.step = 0;
76         k.h = dis(k), k.f = k.h;
77         q.push(k);
78         Astar();
79         printf("%d\n",ans);
80     }
81     return 0;
82 }

 

【A*】luoguP1379 八数码难题

题目描述

在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

输入输出格式

输入格式：

输入初始状态，一行九个数字，空格用0表示

输出格式：

只有一行，该行只有一个数字，表示从初始状态到目标状态需要的最少移动次数(测试数据中无特殊无法到达目标状态数据)

 

题目分析

此题保证有解，那么就很容易了。

如果存在无解情况，则需要事先判断。参见http://www.cppblog.com/menjitianya/archive/2014/06/23/207386.html SGU 139。

 

  1 #include<set>
  2 #include<queue>
  3 #include<cstdio>
  4 #include<cctype>
  5 #include<cstring>
  6 #include<algorithm>
  7 const int dx[] = {0, 1, -1, 0, 0};
  8 const int dy[] = {0, 0, 0, 1, -1};
  9 const int ff[] = {0,1,2,3,1,2,3,1,2,3};
 10 const int gg[] = {0,1,1,1,2,2,2,3,3,3};
 11 
 12 struct node
 13 {
 14     int a[13],b[13],zr;
 15     int f,g,h,step;
 16     bool operator < (const node &x) const 
 17     {
 18         if (f == x.f)
 19             return x.step < step;
 20         return f > x.f; 
 21     }
 22     inline bool fallsDown()
 23     {
 24         if (zr != 5) return 0;
 25         int f[] = {5, 1, 2, 3, 6, 9, 8, 7, 4};
 26         for (int i=0; i<9; i++)
 27             if (a[i]!=f[i])
 28                 return 0;
 29         return 1;
 30     }
 31     inline int reVal()
 32     {
 33         int num = 0;
 34         for (int i=0; i<9; i++)
 35             num = num*10+a[i];
 36         return num;
 37     }
 38     void print()
 39     {
 40         int f[13];
 41         for (int i=0; i<9; i++)
 42             f[a[i]] = i;
 43         for (int i=1; i<=9; i++)
 44         {
 45             printf("%d ",f[i]);
 46             if (i%3==0) puts("");
 47         }
 48         puts("");
 49     }
 50 }k;
 51 std::set<int> vis;
 52 std::priority_queue<node> q;
 53 int ans;
 54 
 55 inline int abs(int a){return a>0?a:-a;}
 56 inline int evaluate(const node &t)
 57 {
 58     register int cnt = 0,i,x,y,tx,ty;
 59     for (i=1; i<=9; i++)
 60     {
 61         x = gg[i], y = ff[i];
 62         tx = gg[t.a[i]], ty = ff[t.a[i]];
 63         cnt += abs(x-tx)+abs(y-ty);
 64     }
 65     return cnt;
 66 }
 67 void swaps(int &a, int &b)
 68 {
 69     register int t = a;
 70     a = b, b = t;
 71 }
 72 inline int read()
 73 {
 74     char ch = getchar();
 75     for (; !isdigit(ch); ch = getchar());
 76     return ch-48;
 77 }
 78 inline bool range(int a, int b)
 79 {
 80     return a>0 && a<4 && b>0 && b<4;
 81 }
 82 void Astar()
 83 {
 84     register int zrx,zry,i,tx,ty,nzr;
 85     while (q.size())
 86     {
 87         node tt = q.top();
 88         q.pop();
 89         vis.insert(tt.reVal());
 90         if (tt.fallsDown())
 91         {
 92             ans = tt.step;
 93             return;
 94         }
 95         zrx = (tt.zr-1)/3+1, zry = (tt.zr-1)%3+1;
 96         for (i=1; i<=4; i++)
 97         {
 98             tx = zrx+dx[i], ty = zry+dy[i];
 99             if (range(tx, ty))
100             {
101                 node ts = tt;
102                 nzr = tx*3+ty-3;
103                 swaps(ts.a[ts.b[ts.zr]], ts.a[ts.b[nzr]]);
104                 swaps(ts.b[ts.zr], ts.b[nzr]);
105                 if (!vis.count(ts.reVal())){
106                     ts.zr = nzr;
107                     ts.step = tt.step+1;
108                     ts.g = ts.step;
109                     ts.h = evaluate(ts);
110                     ts.f = ts.g+ts.h;
111                     q.push(ts);
112                 }
113             }
114         }
115     }
116 }
117 int main()
118 {
119     for (int i=1; i<=9; i++)
120     {
121         int num = read();
122         k.a[num] = i;
123         k.b[i] = num;
124         if (!num) k.zr = i;
125     }
126     k.h = evaluate(k), k.f = k.h;
127     k.step = 0;
128     q.push(k);
129     Astar();
130     printf("%d\n",ans);
131     return 0;
132 }

 

 

【IDA*/A*】bzoj1085: [SCOI2005]骑士精神

Description

　　在一个5×5的棋盘上有12个白色的骑士和12个黑色的骑士， 且有一个空位。在任何时候一个骑士都能按照骑
士的走法（它可以走到和它横坐标相差为1，纵坐标相差为2或者横坐标相差为2，纵坐标相差为1的格子）移动到空
位上。 给定一个初始的棋盘，怎样才能经过移动变成如下目标棋盘： 为了体现出骑士精神，他们必须以最少的步
数完成任务。

Input

　　第一行有一个正整数T(T<=10)，表示一共有N组数据。接下来有T个5×5的矩阵，0表示白色骑士，1表示黑色骑
士，*表示空位。两组数据之间没有空行。

Output

　　对于每组数据都输出一行。如果能在15步以内（包括15步）到达目标状态，则输出步数，否则输出－1。

Sample Input

2
10110
01*11
10111
01001
00000
01011
110*1
01110
01010
00100

Sample Output

7
-1

题目分析

面对有最大步数限制的题目，更为广泛的想法是使用IDA*（迭代加深A*）。
而IDA*只需在A*的基础上加上小小的改动即可。其主要思想就是把深度为depth的状态全部搜完，若没有找到可行解，那么将depth++再继续搜索。
A*做法（740ms）
  1 #include<set>
  2 #include<queue>
  3 #include<cmath>
  4 #include<cctype>
  5 #include<cstdio>
  6 #include<cstring>
  7 //const int dx[] = {0, 1, 2, 1, 2, -1, -2, -1, -2};
  8 //const int dy[] = {0, 2, 1, -2, -1, 2, 1, -2, -1};
  9 const int dx[] = {0, -2, -2, -1, 1, -1, 1, 2, 2};
 10 const int dy[] = {0, -1, 1, 2, 2, -2, -2, -1, 1};
 11 const int ff[] = {0,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5};
 12 const int gg[] = {0,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5};
 13 const int standard[6][6] = {{0,0,0,0,0,0},{0,2,2,2,2,2},{0,1,2,2,2,2},{0,1,1,0,2,2},{0,1,1,1,1,2},{0,1,1,1,1,1}};
 14 
 15 struct node
 16 {
 17     int step,a[13][13];
 18     int f,g,h,zr;
 19     bool operator < (node x) const 
 20     {
 21         if (x.f == f)
 22             return x.step < step;
 23         return x.f < f;
 24     }
 25     inline int reVal()
 26     {
 27         int sum = 0;
 28         for (int i=1; i<=5; i++)
 29             for (int j=1; j<=5; j++)
 30                 sum = sum*3+a[i][j];
 31         return sum;
 32     }
 33     void print()
 34     {
 35         for (int i=1; i<=5; i++)
 36         {
 37             for (int j=1; j<=5; j++)
 38                 printf("%d ",a[i][j]);
 39             puts("");
 40         }
 41         printf("step:%d f:%d g:%d h:%d\n",step,f,g,h);
 42         puts("");
 43     }
 44 }k;
 45 std::priority_queue<node> q;
 46 std::set<int> vis;
 47 int tts,ans;
 48 
 49 int read()
 50 {
 51     char ch = getchar();
 52     for (; (!isdigit(ch))&&(ch!='*'); ch = getchar());
 53     if (isdigit(ch)) return ch-'0'+1;
 54     return 0;
 55 }
 56 inline int evaluate(node a)
 57 {
 58     int cnt = 0;
 59     register int i,j;
 60     for (i=1; i<=5; i++)
 61         for (j=1; j<=5; j++)
 62             if (standard[i][j]!=a.a[i][j])
 63                 cnt++;
 64     return cnt;
 65 }
 66 inline bool range(int x, int y)
 67 {
 68     return x>0 && y>0 && x<=5 && y<=5;
 69 }
 70 inline void swap(int &a, int &b)
 71 {
 72     int t = a;
 73     a = b, b = t;
 74 }
 75 void clear(std::priority_queue<node> &q)
 76 {
 77     std::priority_queue<node> emt;
 78     std::swap(emt, q);
 79 }
 80 void Astar()
 81 {
 82     clear(q);
 83     q.push(k);
 84     vis.clear();
 85     while (q.size())
 86     {
 87         node tt = q.top();
 88         q.pop();
 89         if (tt.f > 16) continue;
 90         vis.insert(tt.reVal());
 91         int x = ff[tt.zr], y = gg[tt.zr];
 92         if (evaluate(tt)==0)
 93         {
 94             ans = tt.step;
 95             break;
 96         }
 97         for (int i=1; i<=8; i++)
 98         {
 99             int tx = x+dx[i], ty = y+dy[i];
100             if (range(tx, ty))
101             {
102                 node ss = tt;
103                 swap(ss.a[tx][ty], ss.a[x][y]);
104                 ss.zr = tx*5+ty-5;
105                 if (!vis.count(ss.reVal())){
106                     ss.step++;
107                     ss.g = ss.step;
108                     ss.h = evaluate(ss);
109                     ss.f = ss.g+ss.h;
110                     q.push(ss);
111                 }
112             }
113         }
114     }
115 }
116 int main()
117 {
118     scanf("%d",&tts);
119     for (int rr=1; rr<=tts; rr++)
120     {
121         for (int i=1; i<=5; i++)
122             for (int j=1; j<=5; j++)
123             {
124                 k.a[i][j] = read();
125                 if (!k.a[i][j]) k.zr = i*5+j-5;
126             }
127         k.g = 0,k.step = 0;
128         k.h = evaluate(k),k.f = k.h;
129         ans = -1;
130         Astar();
131         printf("%d\n",ans);
132     }
133     return 0;
134 }
A*
IDA*做法（1244ms）
  1 #include<set>
  2 #include<queue>
  3 #include<cmath>
  4 #include<cctype>
  5 #include<cstdio>
  6 #include<cstring>
  7 //const int dx[] = {0, 1, 2, 1, 2, -1, -2, -1, -2};
  8 //const int dy[] = {0, 2, 1, -2, -1, 2, 1, -2, -1};
  9 const int dx[] = {0, -2, -2, -1, 1, -1, 1, 2, 2};
 10 const int dy[] = {0, -1, 1, 2, 2, -2, -2, -1, 1};
 11 const int ff[] = {0,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5};
 12 const int gg[] = {0,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5};
 13 const int standard[6][6] = {{0,0,0,0,0,0},{0,2,2,2,2,2},{0,1,2,2,2,2},{0,1,1,0,2,2},{0,1,1,1,1,2},{0,1,1,1,1,1}};
 14 
 15 struct node
 16 {
 17     int step,a[13][13];
 18     int f,g,h,zr;
 19     bool operator < (node x) const 
 20     {
 21         if (x.f == f)
 22             return x.step < step;
 23         return x.f < f;
 24     }
 25     int reVal()
 26     {
 27         int sum = 0;
 28         for (int i=1; i<=5; i++)
 29             for (int j=1; j<=5; j++)
 30                 sum = sum*3+a[i][j];
 31         return sum;
 32     }
 33     void print()
 34     {
 35         for (int i=1; i<=5; i++)
 36         {
 37             for (int j=1; j<=5; j++)
 38                 printf("%d ",a[i][j]);
 39             puts("");
 40         }
 41         printf("step:%d f:%d g:%d h:%d\n",step,f,g,h);
 42         puts("");
 43     }
 44 }k;
 45 std::priority_queue<node> q;
 46 std::set<int> vis;
 47 int tts,ans;
 48 bool done;
 49 
 50 int read()
 51 {
 52     char ch = getchar();
 53     for (; (!isdigit(ch))&&(ch!='*'); ch = getchar());
 54     if (isdigit(ch)) return ch-'0'+1;
 55     return 0;
 56 }
 57 int evaluate(node a)
 58 {
 59     int cnt = 0;
 60     for (int i=1; i<=5; i++)
 61         for (int j=1; j<=5; j++)
 62             if (standard[i][j]!=a.a[i][j])
 63                 cnt++;
 64     return cnt;
 65 }
 66 bool range(int x, int y)
 67 {
 68     return x>0 && y>0 && x<=5 && y<=5;
 69 }
 70 void swap(int &a, int &b)
 71 {
 72     int t = a;
 73     a = b, b = t;
 74 }
 75 void clear(std::priority_queue<node> &q)
 76 {
 77     std::priority_queue<node> emt;
 78     std::swap(emt, q);
 79 }
 80 void Astar(int depth)
 81 {
 82     if (done) return;
 83     clear(q);
 84     q.push(k);
 85     vis.clear();
 86     while (q.size())
 87     {
 88         node tt = q.top();
 89         q.pop();
 90         if (tt.f > depth+1) continue;　　　　//若大于深度就退出
 91         vis.insert(tt.reVal());
 92         int x = ff[tt.zr], y = gg[tt.zr];
 93         if (evaluate(tt)==0)
 94         {
 95             done = 1;
 96             ans = tt.step;
 97             break;
 98         }
 99         for (int i=1; i<=8; i++)
100         {
101             int tx = x+dx[i], ty = y+dy[i];
102             if (range(tx, ty))
103             {
104                 node ss = tt;
105                 swap(ss.a[tx][ty], ss.a[x][y]);
106                 ss.zr = tx*5+ty-5;
107                 if (!vis.count(ss.reVal())){
108                     ss.step++;
109                     ss.g = ss.step;
110                     ss.h = evaluate(ss);
111                     ss.f = ss.g+ss.h;
112                     q.push(ss);
113                 }
114             }
115         }
116     }
117 }
118 int main()
119 {
120     scanf("%d",&tts);
121     for (int rr=1; rr<=tts; rr++)
122     {
123         for (int i=1; i<=5; i++)
124             for (int j=1; j<=5; j++)
125             {
126                 k.a[i][j] = read();
127                 if (!k.a[i][j]) k.zr = i*5+j-5;
128             }
129         k.g = 0,k.step = 0;
130         k.h = evaluate(k),k.f = k.h;
131         done = 0;ans = -1;
132         for (int i=0; i<=15; i++)　　　　//与A*不同之处
133             Astar(i);
134         printf("%d\n",ans);
135     }
136     return 0;
137 }

 

【IDA*】HDU1560DNA sequence

Problem Description

The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.

For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

 

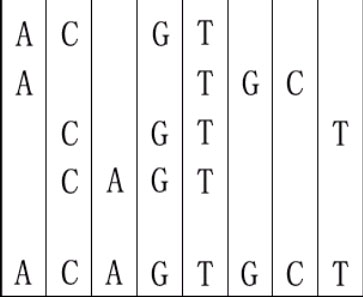
Input

The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

Output

For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

 

题意

构造一个最短的字符串，使得所有给定的n个字符串都是它的字串。

题目分析

自然想到IDA*应对这种问题。那么h()怎么写呢？

一种比较巧妙的方式是用max(lens[i]-match[i])作为h()，其中lens[i]表示第i个字符串的长度；match[i]表示第i个字符串已经匹配了多少位。

 

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 const char seq[] = " ACGT";
 5 
 6 int tt,n,lst;
 7 int lens[13],match[13];
 8 char mp[13][13];
 9 bool done;
10 
11 int evaluate()
12 {
13     int ret = 0;
14     for (int i=1; i<=n; i++)
15         ret = std::max(ret, lens[i]-match[i]);
16     return ret;
17 }
18 void Astar(int left)
19 {
20     if (evaluate()==0) done=1;
21     if (!left || done || left < evaluate()) return;
22     int bkp[13];
23     for (int i=1; i<=n; i++) bkp[i] = match[i];
24     bool ck;
25     for (int i=1; i<=4; i++)
26     {
27         ck = 0;
28         for (int j=1; j<=n; j++)
29             if (mp[j][match[j]]==seq[i]) ck = 1,match[j]++;
30         if (!ck) continue;
31         Astar(left-1);
32         if (done) return;
33         for (int j=1; j<=n; j++) match[j] = bkp[j];
34     } 
35 }
36 int main()
37 {
38     scanf("%d",&tt);
39     for (; tt; tt--)
40     {
41         memset(match, 0, sizeof match);
42         memset(lens, 0, sizeof lens);
43         lst = 0;
44         done = 0;
45         scanf("%d",&n);
46         for (int i=1; i<=n; i++)
47         {
48             scanf("%s",mp[i]);
49             lens[i] = strlen(mp[i]);
50             lst = std::max(lst, lens[i]);
51         }
52         for (;;)
53         {
54             Astar(lst);
55             if (done) break;
56             lst++;
57         }
58         printf("%d\n",lst);
59     } 
60     return 0;
61 }

 

 

 

 

 

END

posted @ 2018-04-18 11:01  AntiQuality  阅读(207)  评论(0)  编辑  收藏  举报