【离线做法】可持久化的书橱
相信那些数据结构题做多的大佬,在看完题之后立马用主席树切了此题
题目描述
Verland 是一个神奇的星球,蒟蒻妹子进入宫殿之后发现了一个 N 层,每层有 M 个格子的神奇书橱,她可以对这个书橱做如下操作:
- 1 i j:在第 i 层的第 j 格放入一本书(如果之前有则这次操作无效)
- 2 i j :将放在第 i 层的第 j 格的书取走(如果之前没有则这次操作无效)
- 3 i:将第 i 层的格子翻转,有书的格子变成没有,没有的变成有
- 4 i:返回第 i 次操作后书橱的状态
蒟蒻妹子想知道每次操作后书橱上的书的总数。
由于蒟蒻妹子觉得数数很累,于是她想让你帮助她解决这个问题.
输入格式
第 1 行三个整数 N,M,Q
接下来 Q 行 第一个数表示操作类型,接下来的输入如题意所说
输出格式
总共 Q 行,每行一个整数,表示这次询问的答案
数据规模与约定
保证数据合法
Subtask 1 (27):N≤1000,M≤1000,Q≤100000,操作 4 的次数≤4
Subtask 2 (25):N≤100,M≤100,Q≤100
Subtask 3 (13):N=1000,M=1000,Q=300000
Subtask 4 (13):N=1000,M=1000,Q=300000
Subtask 5 (13):N=1000,M=1000,Q=300000
时间限制:1s
空间限制:512MB
题目分析
做法一:强行模拟可持久化
记录每一个要被返回到的状态,返回时直接赋值上即可。
处理细节例如操作怎么处理没有什么好说的。
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int MAX_HISTORY = 4103; 4 int n,m,q,ans[300035],k[1003],tot; 5 int lb[300035]; 6 struct node 7 { 8 int tt,x,y; 9 }s[300035]; 10 bitset<1003> f[1003]; 11 bitset<1003> sv[MAX_HISTORY][1003]; 12 int his[MAX_HISTORY][1003]; 13 int read() 14 { 15 char ch = getchar();int num = 0; 16 for (; !isdigit(ch); ch = getchar()); 17 for (; isdigit(ch); ch = getchar()) 18 num = (num<<1)+(num<<3)+ch-48; 19 return num; 20 } 21 int main() 22 { 23 n = read();m = read();q = read(); 24 for (int i=1; i<=q; i++) 25 { 26 s[i].tt = read();s[i].x = read(); 27 if (s[i].tt <= 2)s[i].y = read(); 28 if (s[i].tt==4)if (!lb[s[i].x])lb[s[i].x] = ++tot; 29 } 30 register int i,j; 31 for (i=1; i<=q; i++) 32 { 33 int ansk = ans[i-1],tt = s[i].tt,x = s[i].x,y = s[i].y; 34 if (tt==1){ 35 if (!f[x][y]){ 36 f[x][y] = 1; 37 k[x]++;ansk++; 38 } 39 }else if (tt==2){ 40 if (f[x][y]){ 41 f[x][y] = 0; 42 k[x]--;ansk--; 43 } 44 }else if (tt==3){ 45 f[x].flip(); 46 ansk += m-2*k[x]; 47 k[x] = m-k[x]; 48 }else if (tt==4){ 49 ansk = ans[x]; 50 for (int j=1; j<=n; j++) 51 f[j] = sv[lb[x]][j],k[j]=his[lb[x]][j]; 52 } 53 if (lb[i]){for (j=1; j<=n; j++)sv[lb[i]][j] = f[j],his[lb[i]][j]=k[j];} 54 printf("%d\n",ansk); 55 ans[i] = ansk; 56 } 57 return 0; 58 }
加上bitset乱搞可过52分。
做法二:典型离线题
不一定非得拘泥于「可持久化」的题目名字。
站在另一种角度想一想:把每一个状态看做是一个节点,节点与节点之间的转移就是不同的操作。这样一来,根本无需存储需要返回的状态,而是在这样一张新的图上dfs回溯就可以了。
那么这就是一道典型的离线题。
举个例子,假设现在没有4号操作,那么整张图操作顺序可以看成这样:
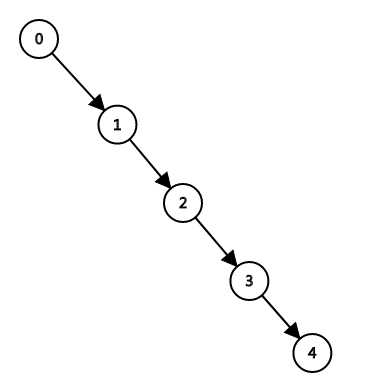
再而,按照每一个节点操作下去就可以了。
又如果有了4号操作,操作顺序可以表示成这样:

其中5号节点的操作是返回2号节点;7号节点操作是返回5号节点。
值得注意的是,有可能返回0号节点(初始状态)
那么只要dfs从0开始就可以了。
1 #include<iostream> 2 #include<cstdio> 3 #include<cctype> 4 #include<vector> 5 #include<bitset> 6 7 struct node 8 { 9 int tt,x,y; 10 }a[300035]; 11 struct scenario 12 { 13 std::bitset<1003> f[1003]; 14 bool fpd; 15 int k[1003]; 16 }f; 17 int n,m,q,ans[300035]; 18 std::vector<int> otd[300035]; 19 20 void dfs(int now) 21 { 22 if (now > q) return; 23 int i = a[now].x, j = a[now].y, delta = 0; 24 if (a[now].tt==1) 25 if (!f.f[i][j]){ 26 delta++; 27 f.k[i]++; 28 f.f[i][j] = 1; 29 } 30 if (a[now].tt==2) 31 if (f.f[i][j]){ 32 delta--; 33 f.k[i]--; 34 f.f[i][j] = 0; 35 } 36 if (a[now].tt==3) 37 { 38 delta = m-2*f.k[i]; 39 f.k[i] = m-f.k[i]; 40 f.f[i].flip(); 41 } 42 ans[now] += delta; 43 for (unsigned int i=0; i<otd[now].size(); i++) 44 { 45 ans[otd[now][i]] = ans[now]; 46 dfs(otd[now][i]); 47 } 48 i = a[now].x, j = a[now].y; 49 if (a[now].tt==1 && delta==1) 50 { 51 f.k[i]--; 52 f.f[i][j] = 0; 53 } 54 if (a[now].tt==2 && delta==-1) 55 { 56 f.k[i]++; 57 f.f[i][j] = 1; 58 } 59 if (a[now].tt==3) 60 { 61 f.k[i] = m-f.k[i]; 62 f.f[i].flip(); 63 } 64 } 65 int read() 66 { 67 char ch = getchar();int num = 0; 68 for (; !isdigit(ch); ch = getchar()); 69 for (; isdigit(ch); ch = getchar()) 70 num = (num<<1)+(num<<3)+ch-48; 71 return num; 72 } 73 int main() 74 { 75 n = read(); 76 m = read(); 77 q = read(); 78 otd[0].push_back(1); 79 for (int i=1; i<=q; i++) 80 { 81 if ((a[i].tt = read()) <= 2) 82 a[i].x = read(),a[i].y = read(); 83 else a[i].x = read(); 84 if (a[i].tt!=4) otd[i-1].push_back(i); 85 else otd[a[i].x].push_back(i); 86 } 87 dfs(0); 88 for (int i=1; i<=q; i++) 89 printf("%d\n",ans[i]); 90 return 0; 91 }
做法三:主席树
END


 浙公网安备 33010602011771号
浙公网安备 33010602011771号