初涉三分法
三分法:大概是一种思想?
何为三分
众所周知,二分可以解决线性函数的极值问题。
那么相应的,三分就是解决凸形/凹形函数的极值问题。
这里有一篇博客讲的不错:二分答案法、三分法
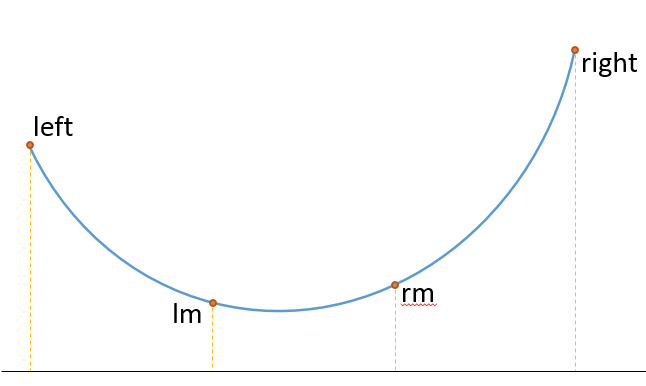
(图自hihocoder)
主要的思路就是选定l,r端点,使 lmid = l+(r-l)/3 ; rmid = r-(r-l)/3 ,继而比较f(lmid)和f(rmid)
显而易见的,若在凹形函数中,f(lmid) < f(rmid),那么$[rmid,r]$这一段一定大于最小值,故$r=rmid$;反之亦然。
至于lmid和rmid为$[l,r]$三等分点的原因,是为了尽量使选取的两点相差较大。
不过群里有人表示,如果函数值比较难求,可以使用黄金分割比例优化lmid和rmid。因为这样子可以重复利用函数值。
三分板子
luoguP3382 【模板】三分法
题目描述
如题,给出一个N次函数,保证在范围[l,r]内存在一点x,使得[l,x]上单调增,[x,r]上单调减。试求出x的值。
输入输出格式
输入格式:
第一行一次包含一个正整数N和两个实数l、r,含义如题目描述所示。
第二行包含N+1个实数,从高到低依次表示该N次函数各项的系数。
输出格式:
输出为一行,包含一个实数,即为x的值。四舍五入保留5位小数。
这个没有什么好说的,直接三分。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const double eps = 0.000001; 4 int n; 5 double l,r,dx[15]; 6 double val(double x) 7 { 8 double ret = dx[1]; 9 for (int i=2; i<=n+1; i++) 10 ret = (ret*x)+dx[i]; 11 return ret; 12 } 13 void three_divide(double l, double r) 14 { 15 while (l+eps < r) 16 { 17 double lmid = l+(r-l)/3; 18 double rmid = r-(r-l)/3; 19 if (val(lmid) > val(rmid)) 20 r = rmid; 21 else l = lmid; 22 } 23 printf("%.5f\n",l); 24 } 25 int main() 26 { 27 scanf("%d%lf%lf",&n,&l,&r); 28 for (int i=1; i<=n+1; i++) 29 scanf("%lf",&dx[i]); 30 three_divide(l, r); 31 return 0; 32 }
HDU2899Strange fuction
F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100)
Can you find the minimum value when x is between 0 and 100.
这个没有讲明是三分,不过我们可以先观察观察,发现F'(x)在[0,+∞)上是一个增函数。
法一:对于F'(x)二分求零点
1 #include<cstdio> 2 #include<cmath> 3 const double eps = 1e-6; 4 double y,l,r,mid; 5 int tt; 6 double dx(double x) 7 { 8 return 42*pow(x,6)+48*pow(x,5)+21*pow(x,2)+10*x-y; 9 } 10 double f(double x) 11 { 12 return 6*pow(x,7)+8*pow(x,6)+7*pow(x,3)+5*x*x-y*x; 13 } 14 int main() 15 { 16 scanf("%d",&tt); 17 for (; tt; tt--) 18 { 19 scanf("%lf",&y); 20 l = 0;r = 100; 21 while (l+eps < r) 22 { 23 mid = (l+r)/2; 24 if (dx(mid) > 0) 25 r = mid; 26 else l = mid; 27 } 28 printf("%.4f\n",f(l)); 29 } 30 return 0; 31 }
法二:发现它在[0,100]上是一个凹形函数,故三分
1 #include<cstdio> 2 const double eps = 0.000001; 3 int tt; 4 double y; 5 double f(double x) 6 { 7 double ret = 6*x*x*x*x*x*x*x+8*x*x*x*x*x*x+7*x*x*x+5*x*x-y*x; 8 return ret; 9 } 10 void three_divide(double l, double r) 11 { 12 while (l+eps < r) 13 { 14 double lmid = l+(r-l)/3; 15 double rmid = r-(r-l)/3; 16 if (f(lmid) < f(rmid)) 17 r = rmid; 18 else l = lmid; 19 } 20 printf("%.4lf\n",f(l)); 21 } 22 int main() 23 { 24 scanf("%d",&tt); 25 for (; tt; tt--) 26 { 27 scanf("%lf",&y); 28 three_divide(0, 100); 29 } 30 return 0; 31 }
hiho1142 : 三分·三分求极值
描述
这一次我们就简单一点了,题目在此:

在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y),求点P到抛物线的最短距离d。
输入
第1行:5个整数a,b,c,x,y。前三个数构成抛物线的参数,后两个数x,y表示P点坐标。-200≤a,b,c,x,y≤200
输出
第1行:1个实数d,保留3位小数(四舍五入)
这道题就比较有趣了。
容易想到定义函数为P点到抛物线上横坐标为$x_0$的点的距离。那么我们来观察一下这个函数:
由于$a$,$b$,$c$,$x$,$y$都是给定的,这个看上去很复杂的东西就是的形式(并且根号下的多项式必定为非负数)。那么就很显然,$f(x)$可以三分查找最值。
接下去的问题就变成了怎么选取三分的$l$,$r$:
一种无脑方法就是直接一个-INF和一个INF拿来做。
另一种方法是分类讨论:若P点被抛物线围住(同向抛物线开口方向),就在y=a(x)的两根之中寻找(a(x)表示抛物线函数);若P点在抛物线外,就是对称轴和x之间寻找。
1 #include<bits/stdc++.h> 2 const double eps = 0.000001; 3 int a,b,c,d,x,y; 4 double calc(double x) 5 { 6 return a*x*x+b*x+c; 7 } 8 double f(double xx) 9 { 10 return sqrt(pow(calc(xx)-y, 2)+(x-xx)*(x-xx)); 11 } 12 void three_divide(double l, double r) 13 { 14 while (r-l > eps) 15 { 16 double lmid = l+(r-l)/3; 17 double rmid = r-(r-l)/3; 18 if (f(lmid) < f(rmid)) 19 r = rmid; 20 else l = lmid; 21 } 22 printf("%.3f\n",f(l)); 23 } 24 int main() 25 { 26 scanf("%d%d%d%d%d",&a,&b,&c,&x,&y); 27 double pl = -b*1.0/(2*a*1.0); 28 double ll = std::min(pl, x*1.0); 29 double rr = std::max(pl, x*1.0); 30 double del = b*b*1.0+4*a*y-4*a*c; 31 if (del >= 0 && ((a > 0 && calc(x) <= y) || (a < 0 && calc(x) >= y))) 32 { 33 ll = (-b-sqrt(del))/(2*a*1.0); 34 rr = (-b+sqrt(del))/(2*a*1.0); 35 } 36 three_divide(ll, rr); 37 return 0; 38 }
END



