收集到的小玩意儿
1.二维数组偏移量读入
int a[1003][1003]; scanf("%d",&a[i][j]); = scanf("%d",a[i]+j);
2.读取无用字符
scanf("%*c%*c");
3.unique函数,用于去重。见www.cnblogs.com/hua-dong/p/7943983.html
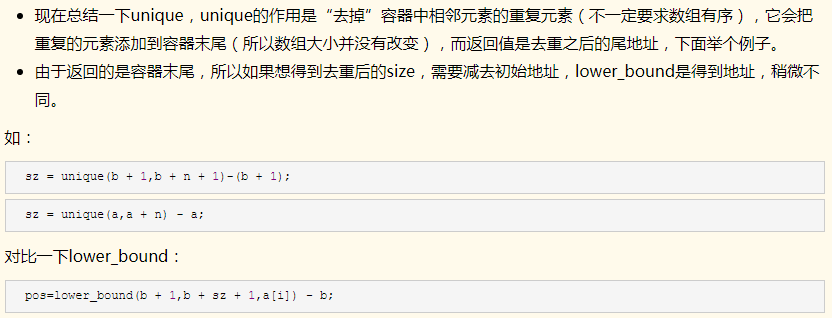
4.vector数组下标默认从零开始!!!
5.priority_queue的自定义使用(例如堆优化Dijkstra)https://www.cnblogs.com/cielosun/p/5654595.html

1 //FROM : https://www.cnblogs.com/cielosun/p/5654595.html 2 int cost[MAX_V][MAX_V]; 3 int d[MAX_V], V, s; 4 //自定义优先队列less比较函数 5 struct cmp 6 { 7 bool operator()(int &a, int &b) const 8 { 9 //因为优先出列判定为!cmp,所以反向定义实现最小值优先 10 return d[a] > d[b]; 11 } 12 }; 13 void Dijkstra() 14 { 15 std::priority_queue<int, std::vector<int>, cmp> pq; 16 pq.push(s); 17 d[s] = 0; 18 while (!pq.empty()) 19 { 20 int tmp = pq.top();pq.pop(); 21 for (int i = 0;i < V;++i) 22 { 23 if (d[i] > d[tmp] + cost[tmp][i]) 24 { 25 d[i] = d[tmp] + cost[tmp][i]; 26 pq.push(i); 27 } 28 } 29 } 30 }
6.set容器的遍历http://blog.csdn.net/wskz876/article/details/17025723

1 set<string>::iterator iter=set_str.begin(); 2 3 while(iter!=set_str.end()) 4 { 5 cout<<*iter<<endl; 6 ++iter; 7 }
7.分治求逆序对https://www.luogu.org/record/show?rid=4756518
8.位运算的优先级http://blog.csdn.net/qq_24489717/article/details/49915281(非常mmp)
9.Meet in the middle http://blog.csdn.net/lishuandao/article/details/49181601
10.如果scanf一个double类型使用了"%f" 你会凉凉的
11.并查集里的补集思想非常非常有趣
12.调试时候如果看上去正常结束但是结果不对不要慌,仔细看看return的数值然后会发现大多数时候return回一个非0的数——某个地方炸了
13.O(1)判断一个数是否为2的幂数:if (x & (x-1)==0) 则x为2的幂数
14.枚举01状态集的子集。for (int x = n; x; x=(x-1)&n)。例如
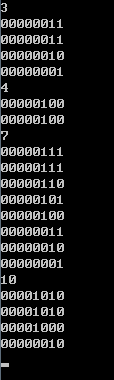
其中初始的1状态表示可选可不选。0状态表示不可选。
15.形如(x+1)&x==0的表达式,似乎并不是按照((x+1)&x)==0的顺序进行的。
16.clock()计时:printf("Time used = %.2f\n", (double)clock() / CLOCKS_PER_SEC).这个CLOCKS_PER_SEC是个跟系统有关的常数,所以最好还是每次使用时候除一下。
17.sprintf向字符串里读入:sprintf(buf, "%d%d", x, y).这里比如说x=10,y=21.那么buf=1021.注意buf是个char*.
18.创建字符串流,从读入字符中读取。例如以下的读取单词:
1 while (cin >> s) 2 { 3 for (int i=0; i<s.length(); i++) 4 s[i]=isalpha(s[i])?tolower(s[i]):' '; 5 stringstream buf(s); 6 while (buf >> s) 7 st.insert(s); 8 }
19.exit()函数在#include<cstdlib>里面
20.给数组赋成一个确定的值。(速度未知)std::fill(f+1,f+n+1,x)其中x为要赋值的数。在<algorithm>里面。
21.对于无环图,一个矩形区域内的连通块个数=点数-边数
22.猜猜这个程序输出什么?
1 #include<bits/stdc++.h> 2 3 int main() 4 { 5 long long sum = 31, x = 1<<sum; 6 printf("%lld\n",x); 7 return 0; 8 }
然而程序输出-2147483648!
事实上,编译器把这里的1看作是int类型,所以是会溢出的!
23.如果 scanf("%s",ch+1); 那么ch的长度就是 strlen(ch+1) 并且不用减一
24.树状数组求区间最值https://www.cnblogs.com/zig-zag/p/4740322.html
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 4 int a[maxn],f[maxn],n,m; 5 6 int read() 7 { 8 int num = 0; 9 char ch = getchar(); 10 bool fl = 0; 11 for (; !isdigit(ch); ch = getchar()) 12 if (ch=='-') fl = 1; 13 for (; isdigit(ch); ch = getchar()) 14 num = (num<<1)+(num<<3)+ch-48; 15 if (fl) num = -num; 16 return num; 17 } 18 inline int lowbit(int x) {return x&-x;} 19 void update(int x, int c){for (; x<=n; x+=lowbit(x)) f[x] = std::max(f[x], c);} 20 int query(int l, int r) 21 { 22 int ret = -2e9; 23 while (l <= r) 24 { 25 ret = std::max(ret, a[r]); 26 for (r-=1; r-lowbit(r)>=l; r-=lowbit(r)) ret = std::max(ret, f[r]); 27 } 28 return ret; 29 } 30 int main() 31 { 32 memset(f, -0x3f3f3f3f, sizeof f); 33 n = read(), m = read(); 34 for (int i=1; i<=n; i++) a[i] = read(), update(i, a[i]); 35 for (int i=1; i<=m; i++) 36 { 37 int l = read(), r = read(); 38 printf("%d\n",query(l, r)); 39 } 40 return 0; 41 }
25.记忆化搜索处理dp的时候:
1 int dp(int x, int y) 2 { 3 if (f[x][y]!=-1) return f[x][y]; 4 dp过程 5 return f[x][y]; 6 } 7 int main() 8 { 9 memset(f, -1, sizeof f); 10 ... 11 printf("%d\n",dp(1, n)); 12 }
这是一种很zz的写法,因为有可能dp过程没处理从而返回f[x][y]=-1。
26.阶乘逆元的处理!(MO=1e9)
1 inv[0] = inv[1] = 1; 2 for (int i=2; i<maxn; i++) 3 inv[i] = (MO-MO/i)%MO*inv[MO%i]%MO; 4 for (int i=2; i<maxn; i++) inv[i] = inv[i-1]*inv[i]%MO;
鬼知道为什么边处理会溢出……
27.有long long的处理尽量还是要加1ll或者(long long),要是溢出的话怎么死的都不知道。
28.tarjan建图时候,如果建了超级源(其实超级汇也要注意)的话,maxm要开大maxn!!!
29.重载二维数组以支持负数下标
1 struct node 2 { 3 int a[103][103]; 4 int *const operator[](int x) 5 { 6 return a[x+50]; 7 } 8 node() {} 9 }f;
30.反三角函数的精度非常差!尽量用其他数学方法而不要用反三角函数!
31.hzq说叶队(叶珈宁)有一种奇妙的树分块:随机选$\sqrt n$个点,然后树上其他点从属于离它最近的选择的点。据说复杂度和块大小可以根据期望保证……
32.hzq:那些转移是O(1)的dp一定要小心空间复杂度。因为如果转移$O(1)$那么时间复杂度就是转移次数,通常来说这样(因为能够在1s跑出来)的空间复杂度是较难接受的。
33.除了费马小定理,还有一个关于互质的欧拉定理了解一下。
34.写treap的时候发现:(!a[x][0]*a[x][1])是不等同(a[x][0]*a[x][1]==0)的!
35.std::random_shuffle至少是$O(n)$的!而且常数特别大。
36.常数方面的问题:
1 for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) 2 { { 3 for (int j=1; j<=m; j++) for (int i=1; i<=n; i++) 4 { { 5 int delta = g[i-1][j-1]; int delta = g[i-1][j-1]; 6 if (t[i]>1) delta -= g[t[i]-2][j-1]; if (t[i]>1) delta -= g[t[i]-2][j-1]; 7 (g[i][j] = g[i-1][j]+delta) %= MO; (g[i][j] = g[i-1][j]+delta) %= MO; 8 } } 9 } }
这两种效率差别极大。
37.从堆删除一个元素:
1.暴力弹,直到堆顶是要删的元素,之后再把弹过的加进去。
2.在堆外标记一个元素已被删除(如果元素重复就用int标记)
3.建一个删除用的堆(简称删除堆),把要删除的元素放进这个堆里。如果当前使用的堆的堆顶等于删除堆的堆顶,就舍弃当前堆顶元素。
38.判断子串[l,r]中i是否为循环节,只需要判断[l,r-i]和[l+i,r]是否相等。
39.当遇到$O(n^3)$暴力题的时候:
1 #include<cstdio> 2 #include<cctype> 3 #include<cstring> 4 const int maxn = 100035; 5 const int base = 233; 6 7 int p,num,ans; 8 char s[maxn]; 9 int n,m,l,r; 10 11 void write(int x) 12 { 13 if (x/10) write(x/10); 14 putchar('0'+x%10); 15 } 16 inline int read() 17 { 18 int ret=0,f=1;char ch=getchar(); 19 while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();} 20 while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();} 21 return ret*f; 22 } 23 inline void read(char* s) 24 { 25 int len=0;char ch=getchar(); 26 while(ch<'0'||ch>'9') ch=getchar(); 27 while(ch>='0'&&ch<='9'){s[++len]=ch-'0';ch=getchar();} 28 } 29 int main() 30 { 31 freopen("bignum.in","r",stdin); 32 freopen("bignum.out","w",stdout); 33 p = read(), scanf("%s",s+1), m = read(); 34 while (m--) 35 { 36 l = read(), r = read(), ans = 0; 37 for (int i=l; i<=r; i++) 38 { 39 num = 0; 40 for (int j=i; j<=r; j++) 41 { 42 num = ((num<<1)+(num<<3)+s[j]-'0')%p; 43 if (!num) ans++; 44 } 45 } 46 write(ans), putchar('\n'); 47 } 48 return 0; 49 }
常数优化是一件非常重要的事情。
40.论位运算优先级的重要性 x2
49 for (int j=1; j<=cnt; j++) 50 for (int i=1; i<=dct; i++) 51 sum[j] += f[i][j][0]+(i==dct?0:f[i][j][1]); 52 // for (int j=1; j<=cnt; j++) 53 // for (int i=1; i<=dct; i++) 54 // sum[j] += f[i][j][0]+(i==dct)?0:f[i][j][1]; //这两个答案是不一样的?……
这里因为 ? : 的运算级比 + 要低……
41.1715: [Usaco2006 Dec]Wormholes 虫洞 判负权环的时候,还是时间戳更保险一点
42.有些时候对拍不是随便就能拍出错的。注意考虑特殊数据范围,比如"ai≥0";"x,y之间"等等。不要轻易地随便调一组参了事。
43.HHHOJ#52. 「NOIP2017模拟赛10.19」Rhyme 这里string map哈希。发现 int &c = mp[s]; 在频繁使用下会使效率大增。在n=300000左右会快个1~2s。
44.右移居然会越位溢出!int类型右移x位==int类型右移x%32位。例如 3>>32==3>>(32%32)==3 非常奇妙。例如线性基处理需要将其转为long long。
45.快输在O2下,1M~2M的数据能够快个0.7s……
46.形如 printf("%d %d",calc(),a-b); 的输出,如果calc()内改变了a,b的值,输出的将会是修改前的a-b值
47.成功获得成就:在模拟赛中以没有AC一题的代价意识到#pragma开在<bits/stdc++.h>下面一行意味着bits库中没有开O2;然后获得了80pts暴力dp的好成绩
50.FFT复数类运算符定义在结构体外面会大大提高效率(其他结构体不知道效果如何),模板题的效率提升是3s左右
51.学了ODT才发现STL的一些奇妙操作:STL的iterator在修改之后所指的对象会改变;set里删iterator之后再使用这个iterator在不同平台上可能发生的后果不同;使用iterator改变所指的结构体元素时,要用mutable修饰。
52.对于一个$10^5$级别的数分解质因数,有如下两种方式:
枚举素数:
1 for (int i=1; pr[i]<=p; i++) 2 if (p%pr[i]==0){ 3 opt.push_back(pr[i]); 4 while (p%pr[i]==0) p /= pr[i]; 5 }
枚举其第二个因数(最小的素因数):
1 for (int pri; p>1; ) 2 { 3 pri = fac[p][1]; 4 if (vis[pri]) break; 5 opt.push_back(pri); 6 while (p%pri==0) p /= pri; 7 }
事实表明,第二种方式的期望常数相当小。具体可以看cf1139d的第一个做法和第二个做法提交记录。
53.一张点数为$n$的完全图生成树个数为$g_i=n^{n-2}$
54.一个串的所有回文后缀可以被划分成不超过log个等差数列
55.布隆过滤器就像是低配版多哈希——但是它误判率在OI好像接受不太了啊。
56.abs()在c++98里面只能int!(但是有些编译器似乎并不)
57.(f[i][j]+1ll*f[k][j-1]*f[i-k-1][j]%MO)%MO多模会影响常数。但是慎用,因为毕竟容易爆int更糟糕。
58.卡常dp可以考虑记忆化搜索,或许能够减少玄学状态。
59.printf("%d%c",ans[i],(i==n)?'\n':' ');如果ans[i]是long long的,输出到文件会乱码



 浙公网安备 33010602011771号
浙公网安备 33010602011771号