【经典dp 技巧】8.13序列

经典的拆绝对值

题目大意

给定$n$个具有顺序的序列，允许对每个序列循环移动。记第$i$个序列尾元素为$x$，$i+1$个序列首元素为$y$，定义其连接收益为$|x-y|*i$，求$n$个序列连接最大收益。

$\sum n \le 10^6$

---

题目分析

经典dp做得少

考虑如何处理绝对值：绝对值按分类讨论分开无非就两种情况$x*i-y*i$或者$y*i-x*i$，并且两者异号，相当于转为$\max$的问题。

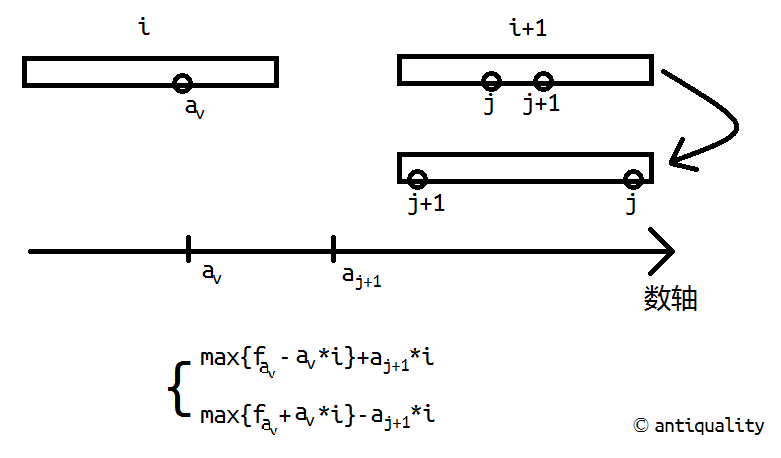
因而不需要管两个元素的相对大小，只需要记录元素$a_v$的$\max\{f_{a_v}-a_v*i\}$和$\max\{f_{a_v}+a_v*i\}$.转移时候两者分开。

意会一下就是如下图

 

#include<bits/stdc++.h>
typedef long long ll;
const ll INF = 1ll<<60;
const int maxn = 1000035;

int T,n,len[maxn],id[maxn];
ll f[maxn],ans,pre,suf;
std::vector<int> a[maxn];

int read()
{
    char ch = getchar();
    int num = 0, fl = 1;
    for (; !isdigit(ch); ch=getchar())
        if (ch=='-') fl = -1;
    for (; isdigit(ch); ch=getchar())
        num = (num<<1)+(num<<3)+ch-48;
    return num*fl;
}
int main()
{
    for (T=read(); T; --T)
    {
        n = read(), id[0] = 1;
        for (int i=1; i<=n; i++)
        {
            a[i].clear(), len[i] = read(), id[i] = id[i-1]+len[i-1];
            for (int j=1; j<=len[i]; j++)
                a[i].push_back(read());
        }
        ans = pre = suf = 0;
        for (int i=1; i<=n; i++)
        {
            ll nxtp = -INF, nxts = 0, val = 0;
            for (int j=0,mx=a[i].size(),lst; j<mx; j++)
            {
                lst = j?(j-1):a[i].size()-1;
                val = std::max(pre+1ll*a[i][j]*(i-1), suf-1ll*a[i][j]*(i-1));
                ans = std::max(ans, val);
                nxtp = std::max(nxtp, val-1ll*a[i][lst]*i);
                nxts = std::max(nxts, val+1ll*a[i][lst]*i);
            }
            pre = nxtp, suf = nxts;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

 

 

 

 

END