【复杂度分析】8.13树(改)
大概是帅气的复杂度分析题
题目大意

$2\le n \le 3\times 10^5$
题目分析
这个是原题的强化版。
话说这种题面给了一个很好的范例去表达一些自然语言难说明的题意。
考虑一个暴力的过程:对于一个确定的$k$,每个点做出最大的$d$,每一层向父亲转移时检查是否有$\ge k$个儿子具有最大值$d_{max}$。
记点$i$的$d$为$f_i$,儿子中$d=d_{max}$的个数为$g_i$。仔细审视这个过程,对于单调增的$k$,$f_i$是一个总体下降的趋势。而每一次的变化,大概就是由于某些最底下的$j$因为$g_j < k'$而向上更新减少$f_i$。而且注意到$k$既然是不断增大,那么一个点如果曾作为最底层节点更新其他节点,它就再也不会主动产生更新了(只可能因为下面的节点变化而影响它)。
于是自然会参照类似暴力ddp的想法,对每次$k$的改变处理一些变化节点。但是这样粗粗看去每次影响到的节点数量是$O(n)$的,难道这不就是$O(nk)$暴力?
简单的复杂度分析
接下去就到了复杂度分析环节。
假设我们是出题人,现在要去卡上面的暴力做法,经典想法无外乎链、菊花图、二叉树、菊花链、竹子等等。
如果是条链——那真是太棒了。$k\ge2$时就再也不用更新了,这怎么跑怎么过。
如果是菊花——那也很不错,$k$只有达到一个定值才会进行唯一一次更新,跟上面一个一样没用。
如果是二叉树——别说了跟上面两个没区别。
如果是菊花链——看上去海星,但是每个交叉点必须花费$k$个节点的代价才能在$k+1$时产生一次更新,比前三个略强一点。
如果是竹子——终于有点头绪了:观察菊花链,会发现链部分除了增加更新深度时的代价以外一点用都没有。把链给缩了的竹子强度就要高一点,但纯随机情况下$k$的种类数不会太大。
进阶复杂度分析
现在的矛盾是一方面想增大有效$k$的种类;一方面又想让每次$k$更新所涉及的节点数量变多。
分析一下二叉树和竹子的优缺点:二叉树可以构造出更大的深度,但是有效$k$就一个;竹子的深度不如二叉树,但是有效$k$可以做出很多。
那么一种结合是贪心地侧重于增大更新涉及的节点数量:
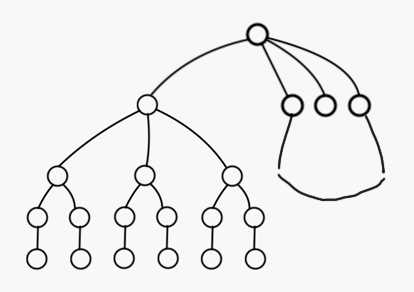
从下往上每一层的有效$k$依次是$1,2,\cdots $。这样的层数$h$是$O(\Gamma^{-1} n)$级别,姑且算是$O(\log n)$的高度,也就是说最多有$\log$级别个的有效$k$。而对于每一次$k+1$的更新,其规模一定是$k$的至多一半。所以更新总涉及节点数量大致是$n+n/2+n/4+\cdots=O(n)$.
另一种结合侧重于增大有效$k$的数量:
为了增大有效$k$,则每种$k$就该只出现一次。同时还可以把每一种依次叠起来增加高度。
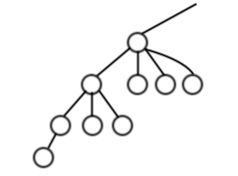
分析一下,因为一个有效$k$需要$k$个空闲的叶子节点,因此这个树高和有效$k$种类是$O(\sqrt n)$的。
所以总涉及节点数是$(\sqrt n)+(\sqrt n-1)+(\sqrt n-2)+\cdots+1$还是$O(n)$的。
总之这么一通hjsakjashdjasd分析之后,我们得到了一个$O(n \log n)$的算法解决这题。
上面的分析或有不到位之处,如果dalao您发现了上面分析的重大问题或者把这个算法用实例卡飞请联系antiquality谢谢!
1 #include<bits/stdc++.h> 2 const int maxn = 300035; 3 const int maxm = 600035; 4 5 int dep[maxn]; 6 struct node 7 { 8 int x; 9 node(int a=0):x(a) {} 10 bool operator < (node a) const 11 { 12 return dep[x] < dep[a.x]; 13 } 14 }; 15 int n,k,f[maxn],g[maxn],fat[maxn]; 16 long long ans,sum; 17 int edgeTot,head[maxn],nxt[maxm],edges[maxm]; 18 int tag[maxn],tim; 19 std::vector<int> fr[maxn]; 20 std::priority_queue<node> q; 21 22 int read() 23 { 24 char ch = getchar(); 25 int num = 0, fl = 1; 26 for (; !isdigit(ch); ch=getchar()) 27 if (ch=='-') fl = -1; 28 for (; isdigit(ch); ch=getchar()) 29 num = (num<<1)+(num<<3)+ch-48; 30 return num*fl; 31 } 32 void addedge(int u, int v) 33 { 34 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 35 edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot; 36 } 37 void pre(int x, int fa) 38 { 39 dep[x] = dep[fa]+1, fat[x] = fa; 40 int ret = 1, cnt = 0; 41 for (int i=head[x]; i!=-1; i=nxt[i]) 42 if (edges[i]!=fa){ 43 pre(edges[i], x); 44 if (f[edges[i]] > ret) cnt = 0, ret = f[edges[i]]; 45 if (f[edges[i]]==ret) ++cnt; 46 } 47 if (cnt >= 1) ++ret; 48 sum += ret, f[x] = ret, g[x] = cnt, fr[cnt].push_back(x); 49 } 50 void maintain(int x) 51 { 52 sum -= f[x], f[x] = 0, g[x] = 0; 53 for (int i=head[x]; i!=-1; i=nxt[i]) 54 { 55 int v = edges[i]; 56 if (v==fat[x]) continue; 57 if (f[v] > f[x]) g[x] = 0, f[x] = f[v]; 58 if (f[v]==f[x]) ++g[x]; 59 } 60 if (g[x] >= k) ++f[x], fr[g[x]].push_back(x); 61 sum += f[x]; 62 } 63 int main() 64 { 65 memset(head, -1, sizeof head); 66 n = read(); 67 for (int i=1; i<n; i++) 68 addedge(read(), read()); 69 pre(1, 1); 70 ans = sum; 71 for (k=2; k<=n; k++) 72 { 73 for (int i=0,mx=fr[k-1].size(); i<mx; i++) 74 if (g[fr[k-1][i]]==k-1) 75 q.push(node(fr[k-1][i])), maintain(fr[k-1][i]); 76 ++tim; 77 for (node tmp; q.size(); ) 78 { 79 tmp = q.top(), q.pop(); 80 if (tag[fat[tmp.x]]==tim) continue; 81 tag[fat[tmp.x]] = tim; 82 maintain(fat[tmp.x]); 83 q.push(node(fat[tmp.x])); 84 } 85 ans += sum; 86 } 87 printf("%lld\n",ans); 88 return 0; 89 }
END


