【思维题 线段树】cf446C. DZY Loves Fibonacci Numbers

我这种maintain写法好zz。考试时获得了40pts的RE好成绩

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation

F1 = 1; F2 = 1; Fn = Fn - 1 + Fn - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an. Moreover, there are mqueries, each query has one of the two types:

  1. Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to each element ai, where l ≤ i ≤ r.
  2. Format of the query "2 l r". In reply to the query you should output the value of 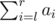 modulo 1000000009 (109 + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

题目分析

注意到形如Fib的数列$a_{n+2}=a_{n+1}+a_n$有相当好的性质。

  1. $a_n=F_{n−2}a_1+F_{n−1}a_2$
  2. $\sum_{i=1}^na_i=a_{n+2}−a_2$

第一条可以用数学归纳法证明；第二条就是将$2\sum_{i=1}^na_i$展开，得到$\sum_{i=1}^na_i+a_{n+2}-a_2$.

回到这一道题上，利用了这两条性质，那么对于每一个修改的区间只需要保留区间前两项增加的Fib值就可以记录下这个操作。所以现在就可以用线段树来维护这一系列询问了。

 

 1 #include<bits/stdc++.h>
 2 #define MO 1000000009
 3 typedef long long ll;
 4 const int maxn = 300035;
 5 
 6 struct node
 7 {
 8     ll tag1,tag2,sum;
 9 }f[maxn<<3];
10 int n,m;
11 ll sum[maxn],fib[maxn];
12 
13 int read()
14 {
15     char ch = getchar();
16     int num = 0, fl = 1;
17     for (; !isdigit(ch); ch=getchar())
18         if (ch=='-') fl = -1;
19     for (; isdigit(ch); ch=getchar())
20         num = (num<<1)+(num<<3)+ch-48;
21     return num*fl;
22 }
23 void maintain(int rt, int lens)
24 {
25     f[rt].tag1 %= MO, f[rt].tag2 %= MO;
26     f[rt].sum = f[rt<<1].sum+f[rt<<1|1].sum;
27     f[rt].sum = (f[rt].sum+f[rt].tag1*fib[lens]+f[rt].tag2*fib[lens+1]-f[rt].tag2)%MO;
28 }
29 void pushdown(int rt, int l, int r)
30 {
31     if (!f[rt].tag1&&!f[rt].tag2) return;
32     int mid = (l+r)>>1, ls = rt<<1, rs = rt<<1|1;
33     f[ls].tag1 += f[rt].tag1, f[ls].tag2 += f[rt].tag2;
34     f[rs].tag1 += f[rt].tag1*fib[mid-l]+f[rt].tag2*fib[mid-l+1];
35     f[rs].tag2 += f[rt].tag1*fib[mid-l+1]+f[rt].tag2*fib[mid-l+2];
36     f[rt].tag1 = f[rt].tag2 = 0;
37     maintain(ls, mid-l+1);
38     maintain(rs, r-mid);
39 }
40 void modify(int rt, int L, int R, int l, int r)
41 {
42     if (L <= l&&r <= R){
43         f[rt].tag1 += fib[l-L+1];
44         f[rt].tag2 += fib[l-L+2];
45         maintain(rt, r-l+1);
46         return;
47     }
48     int mid = (l+r)>>1;
49     pushdown(rt, l, r);
50     if (L <= mid) modify(rt<<1, L, R, l, mid);
51     if (R > mid) modify(rt<<1|1, L, R, mid+1, r);
52     maintain(rt, r-l+1);
53 }
54 ll query(int rt, int L, int R, int l, int r)
55 {
56     if (L <= l&&r <= R) return f[rt].sum;
57     pushdown(rt, l, r);
58     int mid = (l+r)>>1;
59     ll ret = 0;
60     if (L <= mid) ret += query(rt<<1, L, R, l, mid);
61     if (R > mid) ret += query(rt<<1|1, L, R, mid+1, r);
62     return ret%MO;
63 }
64 int main()
65 {
66     n = read(), m = read(), fib[1] = fib[2] = 1;
67     for (int i=1; i<=n; i++) sum[i] = (sum[i-1]+read())%MO;
68     for (int i=3; i<=300005; i++) fib[i] = (fib[i-1]+fib[i-2])%MO;
69     for (int i=1; i<=m; i++)
70     {
71         int opt = read(), l = read(), r = read();
72         if (opt==1) modify(1, l, r, 1, n);
73         else printf("%lld\n",(query(1, l, r, 1, n)+(sum[r]-sum[l-1])%MO+MO)%MO);
74     }
75     return 0;
76 }

 

 

 

 

END

posted @ 2019-02-24 14:17  AntiQuality  阅读(192)  评论(0)  编辑  收藏  举报