【离线 线段树分治】bzoj4025: 二分图
昨天mac的gdb挂了，今天怎么笔记本的gdb也挂了……
Description
神犇有一个n个节点的图。因为神犇是神犇，所以在T时间内一些边会出现后消失。神犇要求出每一时间段内这个图是否是二分图。这么简单的问题神犇当然会做了，于是他想考考你。
Input
输入数据的第一行是三个整数n,m,T。
第2行到第m+1行，每行4个整数u,v,start,end。第i+1行的四个整数表示第i条边连接u,v两个点，这条边在start时刻出现，在第end时刻消失。
Output
输出包含T行。在第i行中，如果第i时间段内这个图是二分图，那么输出“Yes”，否则输出“No”，不含引号。
Sample Input
3 3 3
1 2 0 2
2 3 0 3
1 3 1 2
1 2 0 2
2 3 0 3
1 3 1 2
Sample Output
Yes
No
Yes
No
Yes
HINT
样例说明：
0时刻，出现两条边1-2和2-3。
第1时间段内，这个图是二分图，输出Yes。
1时刻，出现一条边1-3。
第2时间段内，这个图不是二分图，输出No。
2时刻，1-2和1-3两条边消失。
第3时间段内，只有一条边2-3，这个图是二分图，输出Yes。
数据范围：
n<=100000，m<=200000，T<=100000，1<=u,v<=n，0<=start<=end<=T。
题目分析
线段树分治一样的套路
重点在于如何判断一张图是否是二分图。我们知道二分图的充要条件是无奇环的森林：那么奇环的成立条件是在并查集合并时，所连边的两个点在原树中的路径长度为偶数。用$d[x]$表示$x$点在并查集结构中，到其父亲的路径奇偶性；初始每个点独自为根，则$d[x]=0$。每当两个不同的集合合并时，就应该 d[fx]=get(x)^get(y)^1 ，相当于是在并查集中维护了原图的结构。
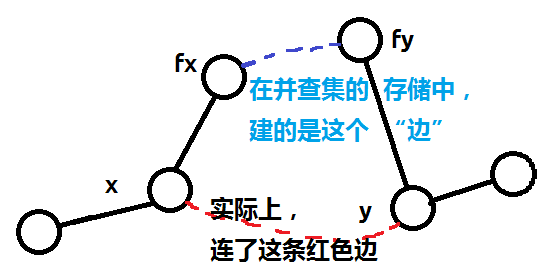
可以用以上这幅图理解。
第一遍写的时候，想当然地混淆了按秩合并并查集和原图这两个树形结构，get的时候直接^1地跳了。
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 const int maxm = 200035; 4 const int maxt = 100035; 5 const int maxOpt = 200035; 6 7 int n,m,T; 8 struct Edge 9 { 10 int u,v,s,t; 11 Edge(int a=0, int b=0, int c=0, int d=0):u(a),v(b),s(c),t(d) {} 12 }tmp; 13 typedef std::vector<Edge> vec; 14 struct Dsu 15 { 16 int top,fat[maxn],size[maxn],d[maxn]; 17 std::pair<int, int> stk[maxOpt]; 18 void init(){for (int i=1; i<=n; i++) fat[i] = i, size[i] = 1;} 19 int find(int x){while (x!=fat[x]) x = fat[x];return x;} 20 int get(int x){int ret = 0;while(x!=fat[x]) ret ^= d[x], x = fat[x];return ret;} 21 bool merge(int x, int y) 22 { 23 int fx = find(x), fy = find(y); 24 if (fx==fy) return get(x)^get(y)^1; 25 if (size[fx] > size[fy]) std::swap(fx, fy); 26 fat[fx] = fy, size[fy] += size[fx]; 27 d[fx] = get(x)^get(y)^1; 28 stk[++top] = std::make_pair(fx, fy); 29 return 0; 30 } 31 void cancel() 32 { 33 int x = stk[top].first, y = stk[top].second; 34 fat[x] = x, size[y] -= size[x], --top, d[x] = 0; 35 } 36 }dsu; 37 bool ans[maxt]; 38 vec opt; 39 40 int read() 41 { 42 char ch = getchar(); 43 int num = 0, fl = 1; 44 for (; !isdigit(ch); ch=getchar()) 45 if (ch=='-') fl = -1; 46 for (; isdigit(ch); ch=getchar()) 47 num = (num<<1)+(num<<3)+ch-48; 48 return num*fl; 49 }
51 void solve(int l, int r, vec opt) 52 { 53 vec L,R; 54 int mid = (l+r)>>1, tmp = dsu.top; 55 for (int i=0, mx=opt.size(); i<mx; i++) 56 { 57 int s = opt[i].s, t = opt[i].t; 58 if (s <= l&&r <= t){ 59 if (dsu.merge(opt[i].u, opt[i].v)){ 60 while (tmp!=dsu.top) dsu.cancel(); 61 return; 62 } 63 }else{ 64 if (s <= mid) L.push_back(opt[i]); 65 if (t > mid) R.push_back(opt[i]); 66 } 67 } 68 if (l==r) ans[l] = 1; 69 else solve(l, mid, L), solve(mid+1, r, R); 70 while (tmp!=dsu.top) dsu.cancel(); 71 } 72 int main() 73 { 74 n = read(), m = read(), T = read(), dsu.init(); 75 for (int i=1; i<=m; i++) 76 { 77 tmp.u = read(), tmp.v = read(), tmp.s = read()+1, tmp.t = read(); 78 if (tmp.s <= tmp.t) opt.push_back(tmp); 79 } 80 solve(1, T, opt); 81 for (int i=1; i<=T; i++) puts(ans[i]?"Yes":"No"); 82 return 0; 83 }
END
