Logistic Regression

Logistic Regression

Logistic Regression是一种分类模型，不是真正用来回归的。

Sigmoid function = Logistic function

\[h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} \]

\(h_\theta(x)=P(y=1|x;\theta)\) ，即 \(h_\theta(x)=\) 对于输入 \(x\) 使得 \(y=1\) 的概率估计。

Desicion boundary: 能够把样本正确分类的一条边界。

不使用线性损失函数 \(J(\theta)=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2\)的原因：函数会变成非凸函数(non-convex function)，不能保证在全局最小值位置收敛。

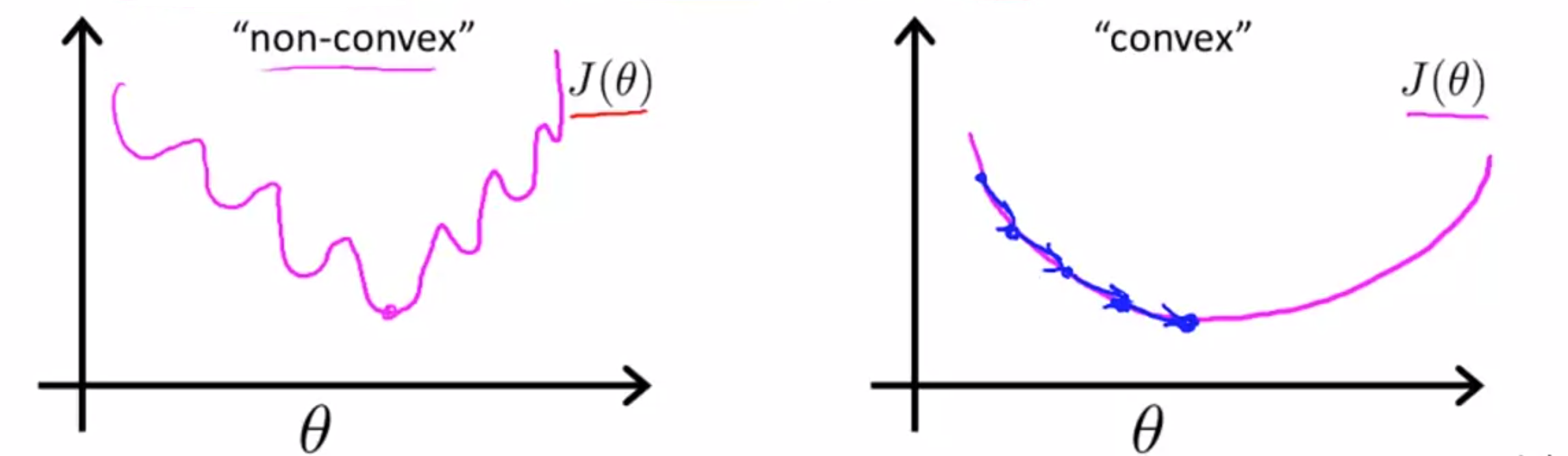
Logistic regression cost function:

\[ Cost(h_\theta(x),y)=\left\{ \begin{aligned} -log(h_\theta(x)) && \text{if}~~y=1 \\ -log(1-h_\theta(x)) && \text{if}~~y=0 \end{aligned} \right. \]

y=1时的损失函数图像
y=0时的损失函数图像

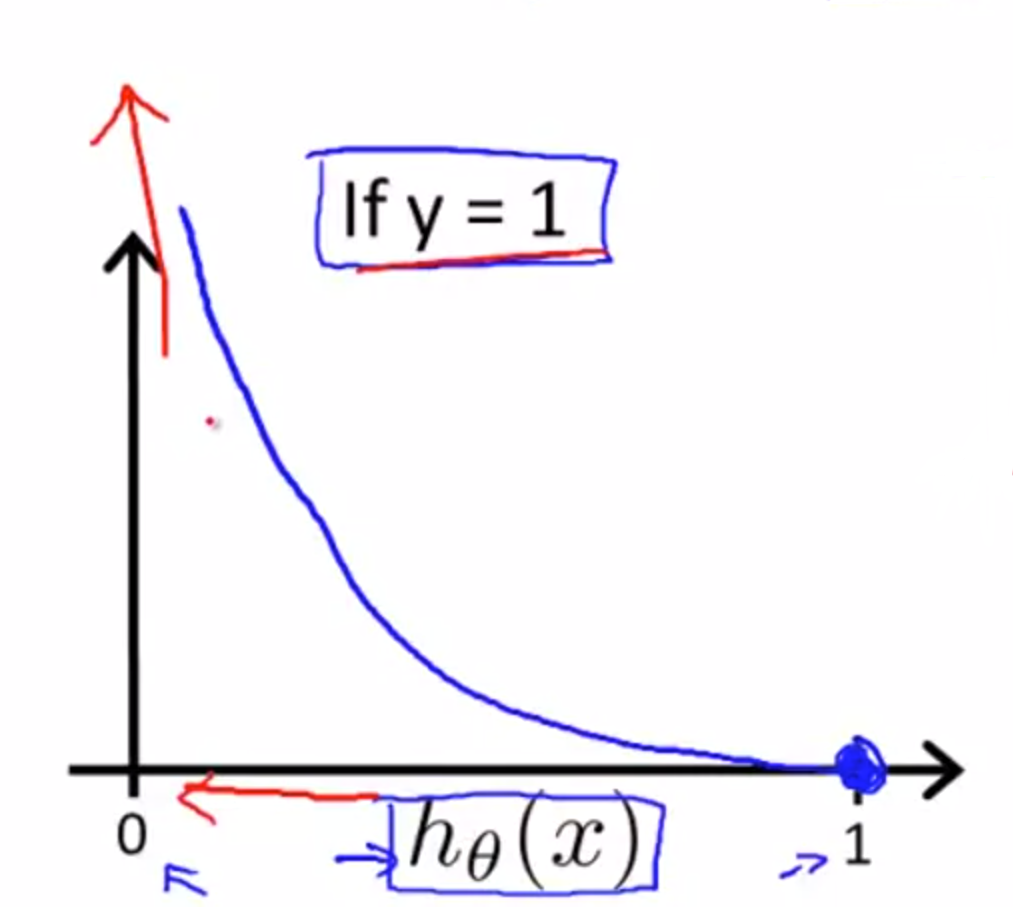
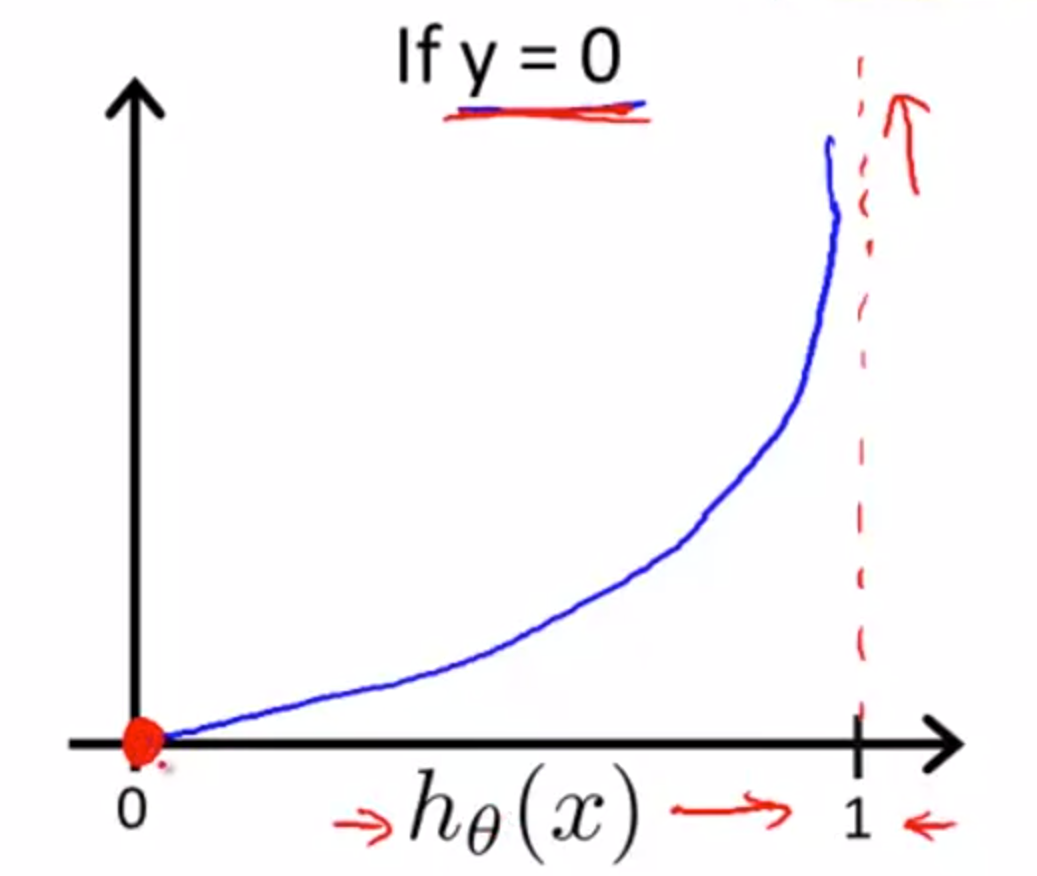
在使用这个损失函数的情况下，判断错误产生的损失会很大。

上述损失函数可以合并成为如下公式：

\[Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x)) \]

最终得到Logistic regression的损失函数为：

\[J(\theta)=-\frac{1}{m}[\sum^m_{i=1}y^{(i)}log(h_\theta(x^{(i)}))+(1-y)log(1-h_\theta(x^{(i)}))] \]

使用梯度下降的方法获得 \(\theta\) 的值的时候，对于 \(\theta\) 偏导的计算结果为：

\[\theta:=\theta-\alpha\frac{1}{m}\sum^m_{i-1}[(h_\theta(x^{(i)})-y^{(i)}) \cdot x^{(i)}] \]

求出 \(\theta\) 的其他方法（不建议学习内部原理，掌握实际应用即可）：

• Conjugate gradient
• BFGS（拟牛顿法）
• L-BFGS

这些算法的优点是：

• 无需人为选择学习率 \(\alpha\)
• 通常比Gradient descent更快

Multiclass Classification: One-vs-all

思想：将多类别分类问题转化为对每一个类别与其余类别分类的问题。
例如，对于类别A、B、C，将其转化为3个不同的分类问题：A与（B,C）,B与（A,C）和C与（A,B)。分别寻找每个问题的分类器。
最后寻找\(\underset{i}{\text{max}}h^{(i)}_\theta(x)\)